IMPORTANCE OF MITOCHONDRIAL P_O2 IN MAXIMAL O₂ TRANSPORT AND UTILIZATION: A THEORETICAL ANALYSIS

Abstract

In previous calculations of how the O₂ transport system limits V̇_O2max, it was reasonably assumed that mitochondrial P_O2 (Pm_O2) could be neglected (set to zero). However, in reality, Pm_O2 must exceed zero and the red cell to mitochondrion diffusion gradient may therefore be reduced, impairing diffusive transport of O₂ and V̇_O2max. Accordingly, we investigated the influence of Pm_O2 on these calculations by coupling previously used equations for O₂ transport to one for mitochondrial respiration relating mitochondrial V̇_O2 to P_O2. This hyperbolic function, characterized by its P₅₀ and V̇_MAX, allowed Pm_O2 to become a model output (rather than set to zero as previously). Simulations using data from exercising normal subjects showed that at V̇_O2max, Pm_O2was usually < 1 mm Hg, and that the effects on V̇_O2max were minimal. However, when O₂ transport capacity exceeded mitochondrial V̇_MAX, or if P₅₀ were elevated, Pm_O2 often reached double digit values, thereby reducing the diffusion gradient and significantly decreasing V̇_O2max.

1. Introduction

At rest or during exercise, production of ATP requires both physical O₂ transport from the environment to the mitochondria and subsequent chemical utilization of O₂ by oxidative phosphorylation. Oxygen transport has been well described (Dejours, 1966; Gnaiger et al., 1998; Weibel et al., 1981) based on the O₂ transport pathway, consisting of the lungs/chest wall, the heart, vascular tree and blood, and the tissues. These structures conduct O₂ as an in-series system in which the main sequential transport steps are ventilation, alveolar-capillary diffusion, circulatory transport, and tissue capillary to mitochondrial diffusion. At each step, the mass of O₂ must be conserved, and this allows a set of simple equations to be defined (Wagner, 1993, 1996b) that quantifies how the transport process at each step integrates with those of the other steps to determine how much O₂ is delivered to the mitochondria per minute (Wagner, 1996a). In this construct, it is shown that each of the four steps contributes to limitation to V̇_O2max and that the quantitative effects of changes at each step are similar.

Systems physiological investigations (Wagner, 1993, 1996b) targeting the understanding of the limits to maximal V̇_O2, have previously been performed on the basis of an important simplifying approximation. This has been that the downstream mitochondrial P_O2 (Pm_O2) is so small in comparison to tissue capillary P_O2 that it can be ignored and therefore set to zero, thus making the analyses of O₂ transport much more tractable. However, because O₂ is one of the molecules that drive oxidative phosphorylation according to the law of mass action, this approximation cannot be physiologically correct, or otherwise V̇_O2 would itself be zero.

Given that Pm_O2 must exceed zero, the P_O2 difference between red cells and mitochondria must be less than when Pm_O2 is assumed to be zero, and thus the diffusive movement of O₂ between them must also be reduced. Therefore, if Pm_O2 is now considered as greater than zero, there is an additional resistance, from the process of mitochondrial respiration, to O₂ movement through the entire pathway of O₂ transport and utilization. We therefore hypothesize that this additional resistance must reduce maximal V̇_O2 below that which would be expected if this resistance were ignored. Clearly, the degree to which V̇_O2max would be reduced will depend on how the high mitochondrial P_O2 rises above zero. This in turn will depend broadly on the capacity for O₂ transport (how many O₂ molecules can be delivered to the mitochondria per minute) compared to the capacity for metabolism (how many O₂ molecules can be consumed by the mitochondria per minute).

The importance of including consideration of oxidative phosphorylation goes beyond asking how much does mitochondrial respiration contribute to the overall impedance to V̇_O2. Because the value of Pm_O2 is dependent on the mitochondrial respiration curve/O₂ transport interaction, hypoxia-induced biological changes may be affected by this interaction. Thus, the significance of the present study is in the degree to which V̇_O2max is reduced by the resistance imparted by oxidative phosphorylation and the consequent effect on mitochondrial P_O2, which in turn may affect processes such as generation of reactive oxygen species and hypoxia-induced gene expression.

The purpose of the present paper is therefore to expand the prior theoretical analysis of the integrated O₂ transport pathway (Wagner, 1993, 1996a) by analyzing the consequences for O₂ transport of allowing mitochondrial P_O2 to be greater than zero. This requires integration of the previously described O₂ transport equations with an equation for mitochondrial respiration, followed by the application of mass conservation principles to solve this new equation system. The same data that were used in (Wagner, 1993, 1996a) are used here.

2. Material and methods

2.1. Principles

Oxidative phosphorylation ensues via the following equation 1 that embodies the law of mass action:

$$3\text{ADP}+3\mathrm{P}i+\text{NADH}+{\mathrm{H}}^{+}+1/2{\mathrm{O}}_2\to 3\text{ATP}+{\text{NAD}}^{+}+{\mathrm{H}}_2\mathrm{O}$$ eq. 1

In this equation, Pm_O2 corresponds to O₂. Clearly, this mass action equation can only move from left to right and produce ATP if Pm_O2 is greater than zero.

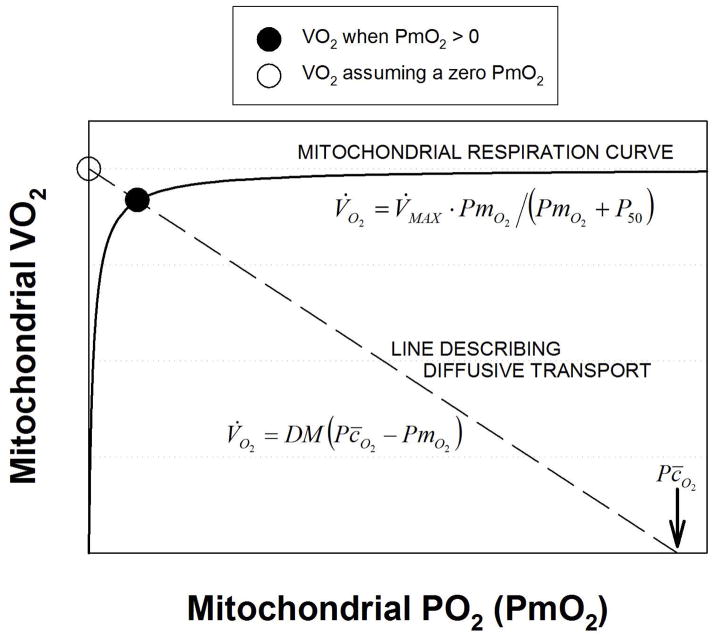
To illustrate this effect, a graphical depiction of mitochondrial respiration is presented in Figure 1. Here, the solid line is the relationship between velocity of the reaction (i.e., mitochondrial V̇_O2), and Pm_O2, similar to what has been found experimentally (Gnaiger et al., 1998; Scandurra and Gnaiger, 2010; Wilson et al., 1977). It shows how V̇_O2 is a positive but non-linear function of mitochondrial P_O2, and indicates that at low Pm_O2, V̇_O2 is very sensitive to (and thus limited by) P_O2, while at higher Pm_O2, V̇_O2 becomes independent of P_O2, and is limited by factors other than O₂.

Figure 1.

Graphical analysis of diffusive transport of O₂ from muscle capillary to the mitochondria (dashed line) and subsequent utilization of O₂ through oxidative phosphorylation (solid line). See text for details.

The hyperbolic curve through the origin displayed in Figure 1 represents mitochondrial respiration. It is of note that despite mitochondrial respiration kinetics is not really a Michaelis-Menten type (Johnson and Goody, 2011; Michaelis and Menten, 1913), experimental data (Gnaiger et al., 1998; Scandurra and Gnaiger, 2010) are well fitted by such a curve. As a hyperbola, it can be represented by equation 2:

$${\stackrel{.}{\mathrm{V}}}_{{\mathrm{O}}_2}={\stackrel{.}{\mathrm{V}}}_{\text{MAX}}·{\text{Pm}}_{{\mathrm{O}}_2}/({\text{Pm}}_{{\mathrm{O}}_2}+{\mathrm{P}}_{50})$$ eq. 2

Where V̇_O2 is mitochondrial V̇_O2 (the ordinate in Figure 1); V̇_MAX is the asymptote of the curve, and represents the maximal rate of use of O₂ when O₂ is in excess; Pm_O2 is mitochondrial P_O2 (the abscissa in Figure 1) and P₅₀ is the P_O2 at 50% of V̇_MAX. Thus, the mitochondrial respiration curve is defined by two parameters: V̇_MAX and P₅₀.

Also shown in Figure 1 is a straight (dashed) line of negative slope. It represents the Fick law of diffusion and depicts diffusive O₂ transport between the tissue capillary and the mitochondria as a function of mitochondrial P_O2 for a given tissue O₂ diffusional conductance (DM) and a given tissue mean capillary P_O2 (Pc̄_O2), both at maximal exercise. We previously utilized this representation as a tool for interpreting intracellular oxygenation data obtained using magnetic resonance spectroscopy (Richardson et al., 1999). The equation is as follows:

$${\stackrel{.}{\mathrm{V}}}_{{\mathrm{O}}_2}=\text{DM}·({\mathrm{P}\overline{\mathrm{c}}}_{{\mathrm{O}}_2}-{\text{Pm}}_{{\mathrm{O}}_2})$$ eq. 3

As the figure indicates, as Pm_O2 is increased, V̇_O2 in eq (3) must fall because the P_O2 difference between mean capillary and mitochondrial P_O2 is reduced. Thus, Figure 1 shows how V̇_O2 increases with mitochondrial P_O2 according to oxidative phosphorylation, but decreases with mitochondrial P_O2 according to the laws of diffusion.

The key concept in Figure 1 is that in a steady state of O₂ consumption, V̇_O2 given by both equations 2 and 3 must be the same at the same mitochondrial P_O2 (i.e., the law of mass conservation applies). This can occur only at the single point of intersection between the two relationships, as indicated by the solid circle placed there. If, as previously approximated (Wagner, 1996b), mitochondrial P_O2 were truly zero, V̇_O2 would be higher, as indicated by the open circle at the left end of the dashed straight line in Figure 1. For a given O₂ transport system defined by the conductances for O₂ allowed by ventilation, alveolar-capillary diffusion, circulation, and capillary to mitochondrial diffusion, the values of mitochondrial V̇_MAX and P₅₀ (equation 2) will thereby influence maximal rate of O₂ utilization, V̇_O2max. In the remainder of this paper, it will be important to distinguish between V̇_MAX (the asymptote to the mitochondrial respiration curve) and V̇_O2max (actual maximal rate of O₂ utilization, solid circle in Figure 1) to avoid confusion. In general, V̇_MAX can exceed V̇_O2max, but V̇_O2max cannot exceed V̇_MAX.

2.2. Modeling the O₂ transport/utilization system

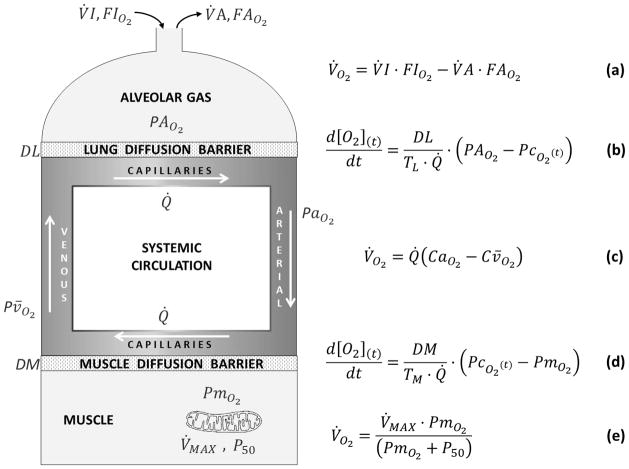
The present study augments our prior approach (Wagner, 1993, 1996b) by adding equation (2) to the equation system used previously. Figure 2 recapitulates the O₂ transport pathway, and the associated four mass conservation equations governing O₂ transport at each step. It adds Equation (2), describing O₂ utilization as a function of Pm_O2. The important point is that in this way, the system has expanded from four equations with four unknowns into a system of five equations and five unknowns.

Figure 2.

Schematic representation of the oxygen transport and utilization system considered in this study and the five associated mass conservation equations governing O₂ transport (equations a–d) and utilization (equation e).

Briefly, using specified input values for O₂ transport step parameters (i.e., values of inspired O₂ fraction (FI_O2), ventilation (V̇I, inspired; V̇A, expired), lung diffusing capacity (DL), cardiac output (Q̇), [Hb], acid base status, tissue (muscle) diffusing capacity (DM), and mitochondrial respiration curve parameters (V̇_MAX and P₅₀)), five mass conservation equations are written for O₂ (see Figure 2). They describe (a) ventilatory transport; (b) alveolar-capillary diffusion; (c) circulatory transport; (d) muscle capillary-mitochondrial diffusion; and (e) mitochondrial respiration. There are five unknowns in these equations: Alveolar P_O2 (PA_O2), arterial P_O2 (Pa_O2), venous P_O2 (Pv̄_O2), mitochondrial P_O2 (Pm_O2) and V̇_O2 itself. In Figure 2, equations (b) and (d) are differential equations describing the process of diffusion across the lung blood: gas barrier and across the tissue capillary wall respectively. They specifically describe the time rate of change of O₂ concentration, [O₂], along the respective capillary as a function of the diffusing capacity, blood flow, red cell capillary transit time (T_L (lungs); T_M (tissues)) and the instantaneous difference between upstream and downstream P_O2 values (alveolar and pulmonary capillary in (b); capillary and mitochondrial in (d)). The two equations are each expressions of the Fick law of diffusion.

The additional inputs of mitochondrial V̇_MAX and P₅₀, and the additional coding for the fifth equation were added to the prior model, and the same (numerical) method of solution employed before (Wagner, 1996b) was used to find the solutions for any set of input variables, defined as the unique values of the five unknowns listed above that simultaneously satisfy all five equations for the given input data defining O₂ transport and utilization.

2.3. Input data for simulations

The input data defining the O₂ pathway parameters used in this analysis were essentially identical to those used previously (Wagner, 1996b), and come from Operation Everest II (Sutton et al., 1988). They reflect maximal exercise by normal subjects at sea level, at a chamber “altitude” of 4,573 m(approximately 15,000 ft.) and at the chamber altitude of the Everest summit, 8,848 m (approximately 29,000 ft.). They are reproduced in Table 1. It is clear that data do not exist for the two new key variables: mitochondrial V̇_MAX and P₅₀. Therefore, for each of the three data sets we computed solutions to the equation system over a systematic range of five mitochondrial V̇_MAX (1000, 2000, 3000, 4000, and 5000 ml/min) and four mitochondrial P₅₀ values (0.1, 0.3, 0.5 and 1.0 mm Hg), resulting in 20 combinations of the two, and thus 20 mitochondrial respiration curves. The values of V̇_MAX were chosen to encompass the range of V̇_O2max from the very sedentary to the elite athlete. Values of P₅₀ on the other hand were based on physiological studies inscribing the mitochondrial respiration curve from samples of normal muscle (Gnaiger et al., 1998; Scandurra and Gnaiger, 2010).

TABLE 1.

	Normal subjects at…
Parameter	Sea Level	15,000 ft.	Everest summit
Barometric pressure (PB), Torr	760	464	253
Fractional Inspired Oxygen (FIO2)	0.2093	0.2093	0.2093
Alveolar ventilation (V̇), BTPS, L·min−1	112	125	165
Blood flow (Q̇), L·min−1	23	21	16
Hemoglobin concentration ([Hb]), g·dl−1	14.5	15.5	18.0
Body temperature (T), °C	38	38	37
O2 dissociation curve P50, Torr	26.8	26.8	26.8
Total Lung O2 diffusing capacity (DL), ml·min−1·Torr−1	51	80	100
Total muscle O2 diffusing capacity (DM), ml·min−1·Torr−1	102	88	62
Maximum O2 uptake (V̇O2 max), L·min−1	3.82	2.81	1.46

A typical example from one of these papers is reproduced with permission in Figure 3, where the hyperbolic character of the curve and its P₅₀ can both be seen by the fitted curve. In this and other similar published cases (Gnaiger et al., 1998; Scandurra and Gnaiger, 2010), P₅₀ is close to 0.3 mm Hg. This accounts for our choice of P₅₀ values - from a third of this typical value to about threefold greater. However it should be stressed that the modeling can be based on any combination of P₅₀ and V̇_MAX, and need not be limited to the choice of specific parameters appearing here.

Figure 3.

Graphical depiction of the hyperbolic equation for oxidative phosphorylation fitted to the data of Scandurra & Gnaiger (Scandurra and Gnaiger, 2010). p16. fig 3B).

2.4. Analysis

Across the matrix of V̇_MAX and P₅₀ values, we posed two questions: First we asked how much would Pm_O2 have to rise above zero to satisfy mass conservation and drive mitochondrial respiration for the given set of physiological O₂ transport variables, V̇_MAX and P₅₀- and as a result, how much would that cause V̇_O2 to be reduced (compared to assuming Pm_O2 = 0) as per Figure 1 (comparing the open and closed circles). This question allows a quantitative description of the theoretical consequences for V̇_O2max of any combination of mitochondrial V̇_MAX and P₅₀. While this is a very useful question to answer, in reality V̇_O2max is a directly measured variable. Therefore, asking how much would it be reduced by any pair of V̇_MAX and P₅₀ values is hypothetical. On the other hand, muscle diffusing capacity, DM, is a variable calculated on the assumption that mitochondrial P_O2 can be neglected and set to zero – the very approximation that the present study is addressing.

Thus, another way to interrogate the model system can be proposed, leading to a second question: It recognizes that the muscle O₂ diffusion step was previously modeled, and muscle diffusing capacity estimated, on the basis of Pm_O2 = 0. However, if Pm_O2 is greater than zero, the capillary to mitochondrial O₂ diffusion gradient would be reduced, and this would necessitate, by the Fick law of diffusion, a higher value of DM to accomplish a given, measured V̇_O2max (compared to the value calculated assuming Pm_O2 = 0).

Therefore, for each of the combinations of V̇_MAX and P₅₀, we asked how much would muscle diffusing capacity have to increase to maintain V̇_O2 constant at the measured value as a result of Pm_O2 being greater than zero.

3. Results

3.1. Effects of mitochondrial respiration on Pm_O2 and maximal V̇_O2

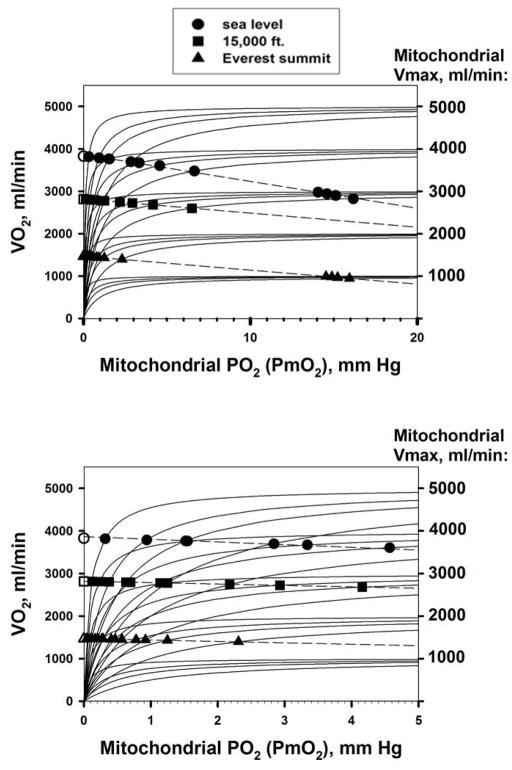
Figure 4 shows how the different combinations of mitochondrial V̇_MAX and P₅₀ affect V̇_O2 max. The upper panel covers the mitochondrial P_O2 (Pm_O2) range from zero to 20 mm Hg; the lower panel shows the same data, but expands the abscissa to better reflect the lower Pm_O2 range between zero and 5 mm Hg. In both panels, each solid curved line emanating from the origin represents one of the twenty mitochondrial respiration curves (as in Figure 3) for a particular V̇_MAX and P₅₀ combination. Solid circles reflect sea level conditions; solid squares represent moderate altitude and solid triangles are for the equivalent of the Everest summit. It turns out that at each altitude, an approximately straight line can be drawn through the resulting V̇_O2max/Pm_O2 solution points for each mitochondrial respiration curve. These are the dashed lines in the figure.

Figure 4.

Effects of considering mitochondrial respiration on maximal V̇_O2 and mitochondrial P_O2. For each V̇_MAX value, the four hyperbolic curves represent P₅₀ values of 0.1, 0.3, 0.5 and 1.0 mm Hg, left to right. See text for details.

The values of V̇_O2max at each altitude at the point where Pm_O2 equals zero (open symbols at zero Pm_O2) are the same as those described in (Wagner, 1996b) where Pm_O2 was taken to be zero. The figure shows how relaxing that approximation affects V̇_O2max for each combination of mitochondrial V̇_MAX and P₅₀.

At sea level (solid circles), results show that allowing for a non-zero Pm_O2 has a small but significant impact on V̇_O2max. For example, V̇_O2max at Pm_O2 = 0 mm Hg (open circle) would be 3,827 ml/min, but if V̇_MAX were 4,000 ml/min and P₅₀ 1.0 mm Hg, V̇_O2max would be significantly less, by 9%, and would be 3,477 ml/min. Moreover, this would require a mitochondrial P_O2 of 6.7 mm Hg to drive oxidative phosphorylation, as the figure shows. In general, for the fixed set of O₂ transport parameters used (see Table 1), the lower the V̇_MAX and the higher the P₅₀, the greater is the reduction in V̇_O2, and the higher is the Pm_O2 required to drive ATP generation. The range of possible values of mitochondrial P_O2 is considerable, from a fraction of a mm Hg to more than 10 mm Hg, depending on V̇_MAX and P₅₀.

The same outcome is seen at each altitude, but with V̇_O2 lower at any Pm_O2 as PI_O2is reduced. The reduction in V̇_O2 per unit change in Pm_O2 is somewhat less at altitude than at sea level, but if examined as a percent of V̇_O2 at Pm_O2 = 0 at each altitude, the effects of allowing for mitochondrial respiration on maximal V̇_O2 are relatively similar across altitudes.

In summary, the higher the mitochondrial V̇_MAX and the lower the P₅₀, the more O₂ can be metabolized for a given upstream (heart, lungs, blood, muscle) transport system. Mitochondrial P_O2 at V̇_O2 can be neglected when considering O₂ transport only when mitochondrial P₅₀ is low and mitochondrial V̇_MAX is high. When V̇_MAX is low and/or P₅₀ is high, the mitochondrial P_O2 required to drive oxidative phosphorylation may reach double digit values, and the impact on V̇_O2max can be considerable.

3.2. Maintenance of maximal V̇_O2 in the face of non-zero Pm_O2

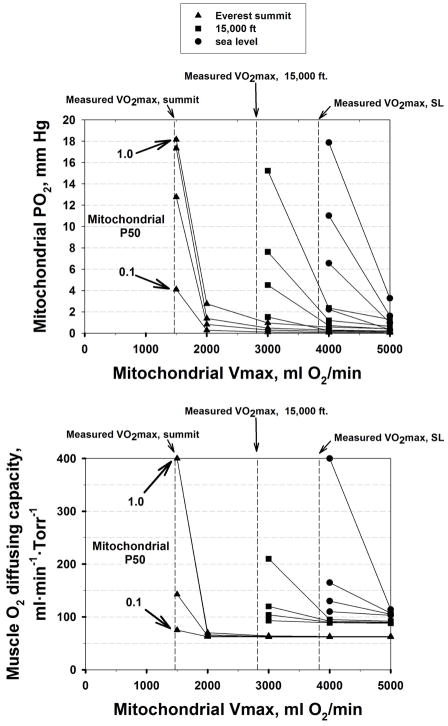
The preceding subsection showed how V̇_O2max would have to decrease as a function of mitochondrial V̇_MAX and P₅₀ with constant values for all O₂ transport conductances. In this subsection we investigate how much higher the muscle O₂ diffusing capacity would have to be to maintain V̇_O2max constant over the same range of V̇_MAX and P₅₀ values as Pm_O2 increases above zero.

The results are shown in Figure 5, which displays the simulation outcomes across the entire matrix of V̇_MAX and P₅₀ values, using V̇_MAX on the abscissa and isopleths for each P₅₀. Results are shown for each altitude as indicated by the different symbols. The top panel shows mitochondrial P_O2 for every combination of V̇_MAX and P₅₀ examined, and the bottom panel the corresponding values of muscle diffusing capacity (DM), that would have to exist to maintain V̇_O2max at measured levels (indicated at each altitude by the vertical dashed lines). Comparing panels shows that when Pm_O2 is high (thus reducing the P_O2 gradient between capillaries and mitochondria), DM must also be high to maintain diffusive O₂ transport.

Figure 5.

Mitochondrial P_O2 (upper panel) and muscle O₂ diffusing capacity (lower panel) required to maintain V̇_O2 constant at the measured value across the domain of V̇_MAX and P₅₀ values at each altitude studied (see text for details).

Also, when mitochondrial V̇_MAX substantially exceeds measured V̇_O2max (at each altitude), Pm_O2 remains low, and therefore DM does not need to be substantially increased to maintain O₂ flux. However, the closer mitochondrial V̇_MAX is to measured V̇_O2max, the higher Pm_O2 must be (see Figure 4), and therefore, DM is also required to be elevated to maintain O₂ transport. When V̇_MAX and actual V̇_O2max are very close, the required DM may be as much as four times the value needed when Pm_O2 is (close to) zero, and the associated Pm_O2 would reach double digit values.

4. Discussion

4.1. Summary of major findings

This study shows that including mitochondrial respiration in analyzing O₂ transport and utilization generally poses a very small additional resistance to the system (over that of the transport pathway alone), only slightly reducing V̇_O2max below that computed ignoring this contribution (Figure 4). The associated mitochondrial P_O2 is also usually low (< 1 mm Hg). If however mitochondrial V̇_MAX is low in relation to O₂ transport capacity, or if mitochondrial P₅₀ is high, V̇_O2max may be considerably reduced. Mitochondrial P_O2 would then increase more, and may reach double digit values.

In order to maintain V̇_O2 max when mitochondrial P_O2 is high, muscle diffusing capacity (DM) would need to be higher than when Pm_O2is assumed to be zero. Under most conditions, the necessary increase in DM would be minimal, being significant only when Pm_O2 is considerably elevated (Figure 5).

4.2. Unifying principles

The main principle demonstrated in the present study is that the final step in the O₂ pathway – mitochondrial respiration – may contribute a non-negligible resistance to O₂ movement through the system from the air to its conversion to CO₂, resulting in a lower V̇_O2max compared to a system where metabolism imposed no resistance to overall O₂ flow. The higher the mitochondrial P_O2 required to drive oxidative phosphorylation, the greater would be the relative resistance and thus the more effect there will be on reduction in V̇_O2max. When mitochondrial P₅₀ is about 0.30 mm Hg as reported by Gnaiger (Gnaiger et al., 1998; Scandurra and Gnaiger, 2010) the effects are generally minor.

The simulations at the three inspired P_O2 values shown here demonstrate that it is the relative capacities (rather than individual absolute values) of the physiological transport system and the mitochondrial respiratory chain that effectively determine both the mitochondrial P_O2 and the associated effect on V̇_O2max, and that both variables, but especially mitochondrial P_O2, may vary over a wide range depending on mitochondrial respiratory function.

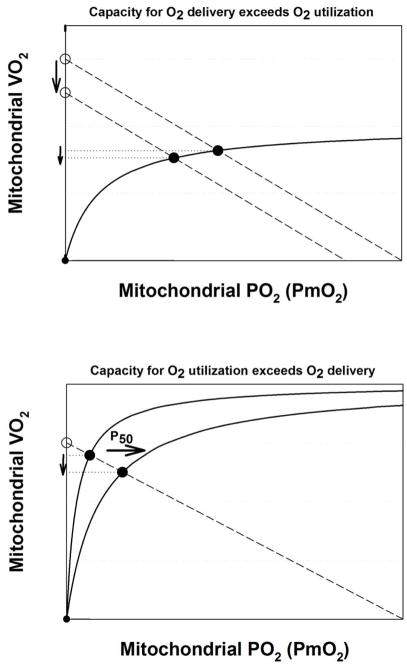
An additional important principle is shown in Figure 6: Even when O₂ transport capacity (i.e., potential for O₂ delivery) is considerably greater than mitochondrial respiratory capacity (i.e., potential for O₂ utilization), as illustrated in concept in the top panel, a change in the former will change overall V̇_O2. The converse is also true – that when mitochondrial respiratory capacity exceeds O₂ transport capacity, (lower panel), a change in the former will have an effect on V̇_O2. It is thus not correct to think that when one component is greater than the other, only the lesser of the two determines overall V̇_O2max. This conclusion is much the same as described for individual components of the physiological transport pathway of the lungs and chest wall, the heart, blood and circulation, and the muscles, where we previously showed (Wagner, 1996a, b) that all components affect V̇_O2max, not just the step with the least transport capacity.

Figure 6.

Graphical depiction of the concept that even when the capacity for O₂ delivery exceeds O₂ utilization (upper panel) a change in O₂ delivery will change actual V̇_O2. Conversely, when the capacity for O₂ utilization exceeds O₂ delivery (lower panel) a change in O₂ utilization (increase in P₅₀ in this example) will change actual V̇_O2. Open circles: maximal O₂ delivery to mitochondria if Pm_O2 was zero. Closed circles: actual V̇_O2. Solid and dashed lines: as in Figure 1.

4.3. Effects of mitochondrial respiration kinetics on both V̇_O2max and Pm_O2 may be small or large

For the examples shown – fit normal subjects – the effects of considering mitochondrial respiration are generally less on V̇_O2 than on the associated Pm_O2 (Figure 4). Examining the sea level results for the example of V̇_MAX = 4,000 ml/min and P₅₀ increasing from 0.1 to 1.0 mm Hg, V̇_O2max would fall by 9% while Pm_O2 would increase by an order of magnitude, from less than 1 mm Hg to more than 6 mm Hg. Just how much variation there is in mitochondrial P₅₀ in the normal population is unknown, let alone whether this may change systematically with training, or in chronic diseases such as chronic obstructive pulmonary disease (COPD) or chronic heart failure. The calculations presented herein however point out that the quantitative nature of the mitochondrial respiration curve may be a critical determinant of the values of mitochondrial P_O2 and V̇_O2max, over and above any influence of upstream O₂ transport.

Even if the effects on V̇_O2max are numerically small, they would likely be important in the competitive endurance athlete where very small differences may separate success from failure. But possibly even more significant might be the potentially large variation in mitochondrial P_O2 depending on P₅₀ and V̇_MAX due to known hypoxia-induced biological effects (Semenza, 2011). Thus, hypoxia-induced gene expression or reactive O₂ species generation may vary according to mitochondrial P_O2.

4.4. Potential for estimating mitochondrial P₅₀ based on the current modeling approach

The analysis presented here suggests a possible method for estimating the characteristics of the mitochondrial respiration curve in vivo. Currently, mitochondrial V̇_MAX and P₅₀ are measured in vitro in respirometers where mitochondria are exposed to different levels of O₂ and V̇_O2 measured (as in Figure 3), (Gnaiger et al., 1998; Scandurra and Gnaiger, 2010; Wilson et al., 1977). To obtain this information in humans would therefore necessitate a muscle biopsy, and even if that were done, the result would be subject to the usual sampling constraints as for any other measure of muscle structure or function determined from a single biopsy.

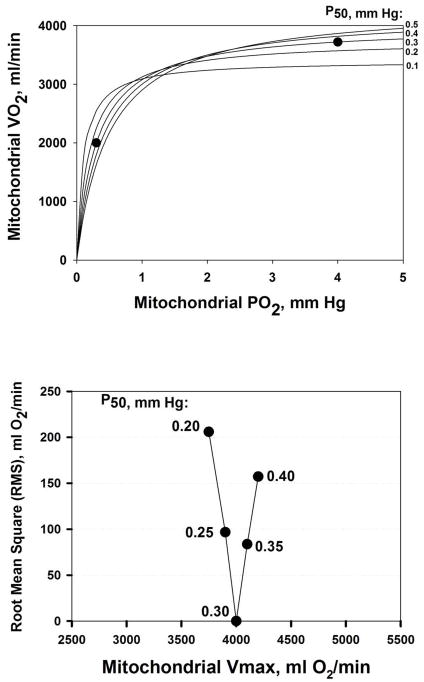
The fitting of a hyperbolic function to paired measured values of V̇_O2max and mitochondrial P_O2 has the potential for estimating P₅₀ and V̇_MAX in vivo, and this is illustrated in Figure 7. The intervention to garner several points on the curve would come from acutely varying FI_O2 and measuring V̇_O2 and mitochondrial P_O2 during maximal exercise at each FI_O2, as indicated by the theoretical example of the two solid circles in the upper panel of Figure 7. These two points reflect a mitochondrial respiration curve with P₅₀ of 0.30 mm Hg and V̇_MAX of 4,000 ml/min. If such data were to span both the steep and flat parts of the respiration curve, as shown in the figure, identifying the V̇_MAX and P₅₀ of a hyperbola that resulted in a least squares best fit to the data points would be possible, as shown in the lower panel of Figure 7. Here, over a range of trial values of both V̇_MAX and P₅₀, the root mean square (RMS) residual V̇_O2 between the data and the hyperbola corresponding to each trial combination of P₅₀ (and the V̇_MAX providing the lowest RMS for that P₅₀) is shown. In this error-free theoretical case, one could quite accurately estimate V̇_MAX (4,000 ml/min) and P₅₀ (0.3 mm Hg) from the values at the nadir of the relationship in the figure. However, if measured data happened to lie on only the flat or only on the steep parts of the curve, ability to estimate V̇_MAX and/or P₅₀ would be considerably reduced.

Figure 7.

Estimation of mitochondrial P₅₀. Upper panel: least squares best fit (solid lines) to data (solid circles) for five trial P₅₀ values. Lower panel: closeness of fit to data reflected by the Root Mean Square error, showing that a P₅₀ of 0.30 mm Hg provides the best estimate.

While whole body or large muscle mass V̇_O2 can be measured relatively easily, the experimental challenge would be to measure mitochondrial P_O2 (during exercise) (Mik, 2013). The closest approach to date in intact subjects has used MRS-based determination of myoglobin O₂ saturation (Jue et al., 1994; Richardson et al., 1995), where the signal comes from a relatively large muscle region. This approach gives intracellular P_O2 estimates of 3–4 mm Hg during exercise (Richardson et al., 1995), but this is the P_O2 associated with myoglobin, inferred from the finding of about 50% myoglobin saturation during peak exercise combined with accepted values of myoglobin P₅₀ of about 3 mm Hg (Rossi-Fanelli and Antonini, 1958). This P_O2 is an order of magnitude greater than that projected at the mitochondria based on the preceding discussion. In the end, a method would have to be developed for direct measurement of mitochondrial P_O2. Whether a candidate signaling atom or molecule can be found for an MRS-based approach is currently unknown.

4.5. Limitations of the analysis

As in previous work (Wagner, 1993, 1996b), the entire analysis is applicable only to steady state conditions (meaning, that O₂ partial pressures are constant in time as is V̇_O2 itself). Therefore, the analysis cannot be used to study transient changes in metabolic rate. Another limitation is not taking into account ventilation-perfusion mismatch in the lung and/or metabolism-perfusion mismatch in the muscle as contributors to impaired oxygen transport. However, using methods to quantify both of these phenomena, this limitation could be removed. A final limitation is that non-muscle blood flow during maximum exercise is neglected.

5. Conclusions

Considering the hindrance to overall O₂ flux caused by mitochondrial respiration using an established model of O₂ transport to the mitochondria revealed that in normal subjects exercising maximally, the step of oxidative phosphorylation, with its requirement for a mitochondrial P_O2 > 0, likely plays only a small role in total O₂ flux resistance. However, we identified conditions in which mitochondrial P_O2 can rise to double digit values. This occurs particularly when the mitochondrial respiration curve has either a low V̇_MAX (relative to O₂ transport), or a high P₅₀, and under such conditions, mitochondrial function may significantly impair O₂ flux and cell function may be affected, for example, in reactive oxygen species generation and/or oxygen-sensitive gene expression.

HIGHLIGHTS.

• We developed an integrative model of O₂ transport and utilization.

• We simulated healthy fit subjects exercising at sea level and altitude.

• Mitochondrial P_O2 likely plays only a small role in total O₂ flux resistance.

• If O₂ transport capacity exceeds V̇_MAX, Pm_O2 may reach double digit values.

• The approach offers the potential for estimating mitochondrial P₅₀ and V̇_MAX.