Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Nov 20;3:3271. doi: 10.1038/srep03271

The Role of Shape Complementarity in the Protein-Protein Interactions

Ye Li 1, Xianren Zhang 1,a, Dapeng Cao 1,b
PMCID: PMC3834541  PMID: 24253561

Abstract

We use a dissipative particle dynamic simulation to investigate the effects of shape complementarity on the protein-protein interactions. By monitoring different kinds of protein shape-complementarity modes, we gave a clear mechanism to reveal the role of the shape complementarity in the protein-protein interactions, i.e., when the two proteins with shape complementarity approach each other, the conformation of lipid chains between two proteins would be restricted significantly. The lipid molecules tend to leave the gap formed by two proteins to maximize the configuration entropy, and therefore yield an effective entropy-induced protein-protein attraction, which enhances the protein aggregation. In short, this work provides an insight into understanding the importance of the shape complementarity in the protein-protein interactions especially for protein aggregation and antibody–antigen complexes. Definitely, the shape complementarity is the third key factor affecting protein aggregation and complex, besides the electrostatic-complementarity and hydrophobic complementarity.

The living cell is an extremely complicated system and comprises hundreds of thousands of types of biological macromolecules, which constantly interact with each other to maintain the function of the cell, reflecting the dynamic of cellular networks1,2. The cluster formation of membrane proteins is also a crucial issue, because it can regulate the protein activity and achieve signal transduction. So it is very significant to research the mechanism of the protein aggregation.

Previous research results revealed that the electrostatic-complementarity, hydrophobic- complementarity and shape-complementarity have a very important effect on the protein aggregation. In many cases, it is unclear how these clusters are formed by specific chemical bonds, or how the assembled structure is driven by unspecific interactions. Some studies suggested that the protein-protein interactions may be electrostatically guided. By calculating the electrostatic potential of protein-protein complexes, McCoy et al. confirmed the general assertion that the protein-protein interfaces display “electrostatic complementarity”3. Sternberg and Gabb also verified that potential complexes are scored on the basis of shape complementartity and favorable electrostatic interaction using Fourier correlation theory4. By performing structural and mutational analyse, Honig et al. have revealed the central role of electrostatic interactions in the protein-protein association5. In another work, Honig et al. also used continuum electrostatics methods to investigate the contribution of electrostatic interaction to the binding of four protein-protein complexes, and found that the electrostatic provides a significant driving force for binding6. In addition, the effects of the salt concentration and pH of the water phase on the protein-protein binding free energy were demonstrated by Alexov et al. They found that the increase of the salt concentration weakens the binding, which is caused by the charge-charge interactions in the interface7. Those studies confirmed the fact that the protein-protein interactions are electrostatically guided or by a long-range force bringing the interacting partners together5,6,7,8,9,10.

Besides the electrostatic complementarity, the hydrophobic mismatch also plays a very important role in the protein aggregation. The “hydrophobic mismatch” denotes the length difference between the hydrophobic domains of the transmembrane protein and the host lipid bilayer. The protein clustering due to hydrophobic mismatch was predicted by both experiments11,12,13 and simulations14,15,16,17,18. In experiment, Matsuzaki and Yano observed the dimerization in a thicker membrane, which is a response to hydrophobic mismatch12. The association of rhodopsin promoted by a reduction in membrane thickness (hydrophobic mismatch) was found by Brown et al.13. Through calculating the potential of mean force between transmembrane proteins, Smit et al. found that the hydrophobic force drives the long-range protein-protein interactions15. Schmid et al. used Monte Carlo simulations to research the mechanisms of membrane-mediated protein-protein interactions by hydrophobic mismatch interactions. The results show that the lipid-mediated interactions are governed by five competing factors: direct interaction; lipid-induced depletion interaction; lipid bridging; lipid packing and a smooth long-range contribution16. Zhang and Yue also used molecular simulation to find that the aggregation of the proteins anchored in different leaflets was caused by the hydrophobic mismatch14.

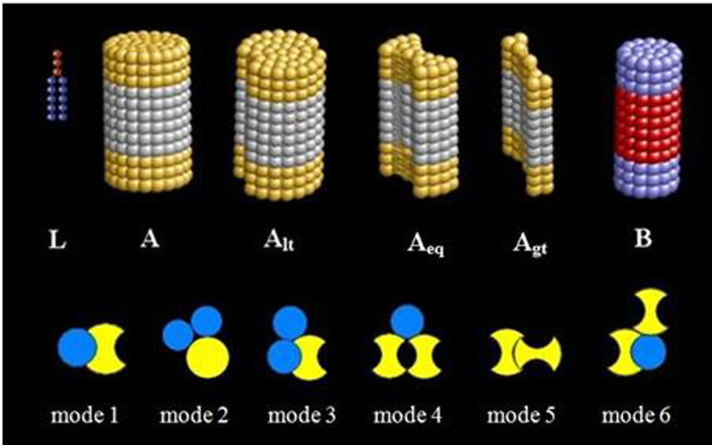
Although the formation of protein cluster has been extensively investigated, it still remains unclear for the mechanism in most cases. In particular, the role of shape complementarity in the protein-protein interactions is still very poorly understood for the case without the electrostatic-complementarity and hydrophobic mismatch. Computer simulation methods have become increasingly valuable to extract information about structural and dynamical properties at a molecular level, and a lot of simulation studies have been performed to explore the interactions of proteins with the membrane14,19,20,21,22,23,24,25. However, to our knowledge, only few studies were focused on the protein shape-complementarity caused by non-specific interactions26,27. For instance, Guigas et al. found that the shape of the hydrophobic domain of the proteins can mediate interactions between proteins. However, the hydrophobic mismatch effect was not eliminated27. So, in this work, we used dissipative particle dynamic (DPD) simulations to investigate the role of protein shape complementarity in the protein aggregation. Two main protein models were designed in this work. One is typically cylindrical protein, and the other is “bowknot” protein with a groove body. Through regulating the size of the groove, we design three kinds of “bowknot” proteins which are larger, equal and smaller than the cylindrical protein radius, as shown in Figure 1.

Figure 1. Models of different proteins and the correct binding modes of proteins.

Figure 1

Open in a new tab

L denotes lipid molecule, A: protein A, Alt: protein Alt (the groove smaller than the radius of protein B), Aeq: protein Aeq (the groove equal to the radius of protein B), Agt: protein Agt (the groove larger than the radius of protein B), B: protein B.

Results

In order to investigate the effect of the shape complementarity on the protein-protein interaction and protein aggregations, we selected the specie of proteins, whose hydrophobic thickness are approximately equal to that of the membrane, in order to eliminate the effect of hydrophobic mismatch between protein and the host lipid membrane. In this work, the hydrophobic domain of the transmembrane protein is constituted by six beads with the space of 0.7.

The shape complementarity is a geometric descriptor, stemming from the practical observation that protein surfaces are complementary to each other at the binding interface. Generally speaking, the shape complementarity can be defined as the match of the convex surface and concave surface of the proteins. First of all, to explore whether the shape complementarity can promote the protein aggregation or not, we investigate four types of protein-protein interaction systems. System 1: protein A (D = 4.5 nm) (D is diameter) and protein B (D = 3.23 nm); system 2: protein Alt (D = 4.5 nm) and protein B (D = 3.23 nm); system 3: protein Aeq (D = 5.81 nm) and protein B (D = 3.23 nm); system 4: protein Agt (D = 7.1 nm) and protein B (D = 3.23 nm). Alt, Aeq, and Agt stands for different types of protein A, but the curvatures of their groove are the smaller, equal and larger than the one of protein B, respectively. In the four systems, the different types of proteins A have the similar volume, aiming at decreasing the excluded volume effect.

After simulating 3840 ns (see Figure 2a), we observed six different protein shape complementarity modes, as shown in Figure 1. Mode 1: the protein B enters the groove of protein A; Mode 2: one protein B and one protein A constitute a concave surface to match the convex surface of the other protein A; Mode 3: two proteins B match the sharp angle of protein A; Mode 4: one protein B is located in the groove formed by two neighboring proteins A; Model 5: one protein A in the groove of another protein A; Model 6: one protein B is located in the groove of protein A and another protein A also matches with them. In this work, the shape complementarity can be judged by the aggregation of the proteins with a convex surface and concave surface match way. We defined the protein binding in the shape complementarity way as “correct binding”. Whereas, the six shape complementarity modes can be devided into two kinds. One is two-body aggregation, and the other is three-body aggregation. The concave surface can come from the protein A itself. At the same time, the concave surface also can be constituted by two protein aggregation. When a protein with a convex surface can enter to the concave the concave of protein A, it is a two-body aggregation such as mode 1 and mode 5. Besides, the protein A with a convex surface also can enter the concave constituted by two proteins to form a three-body aggregation such as mode 2, mode 3, mode 4, and mode 6. These three-body aggregation modes such as mode 2, 3, 4 and 6 can be considered as the especial shape complementarity. The mode 5 and mode 6 are rarely observed in our simulation. So, here we only study the first four kinds of shape complementarity modes.

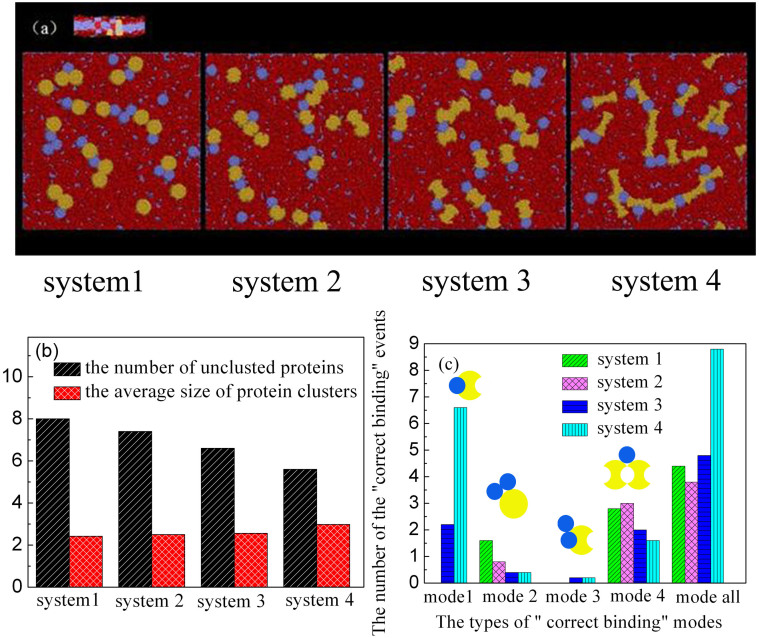
Figure 2. Protein aggregate for the four systems after 3840 ns.

Figure 2

Open in a new tab

System 1: protein A (D = 4.5 nm) and protein B (D = 3.23 nm); System 2: protein Alt (D = 4.5 nm) and protein B (D = 3.23 nm); System 3: protein Aeq (D = 5.81 nm) and protein B (D = 3.23 nm); System 4: protein Agt (D = 7.1 nm) and protein B (D = 3.23 nm) (Protein hydrophobic length: the number of bead is 6. Beads space is 0.7.). (a) Typical top view snapshots of proteins aggregation, where protein A is shown in yellow, protein B in blue, lipid membrane in red. (b) The number of discrete protein and the average size of protein cluster. (c) The number of four “correct binding” modes for the different protein systems.

By simulating the four protein systems, we found that both the aggregation degree of the proteins and average size of protein clusters increase from system 1 to system 4, as shown in Figure 2a and 2b, indicating that an enhanced driving force appears for the protein aggregation from system 1 to system 4. Correspondingly, the fraction of unclustered proteins (i.e. free monomer) decreases (see Figure 2b). To demonstrate the “correct binding” is caused by the enhanced driving force, we show in Figure 2c the number of protein “correct binding” averaged over ten independent runs for the four systems. It is found that the increase of the “correct binding” corresponds to the enhancement of protein aggregation, suggesting that the shape complementarity definitely promotes the protein aggregation. Simultaneously, we also found that the mode 1 and mode 3 only exist in the two cases where the groove of protein A is equal or larger than the radius of protein B, while mode 2 and mode 4 appear for all four systems. On the whole, in the system 4, the number of the protein correct binding caused by the shape complementarity is largest, which is in agreement with the protein aggregation. This observation indicates that the shape complementarity is another key factor affecting protein aggregation, besides the electrostatic interactions, and the hydrophobic mismatch.

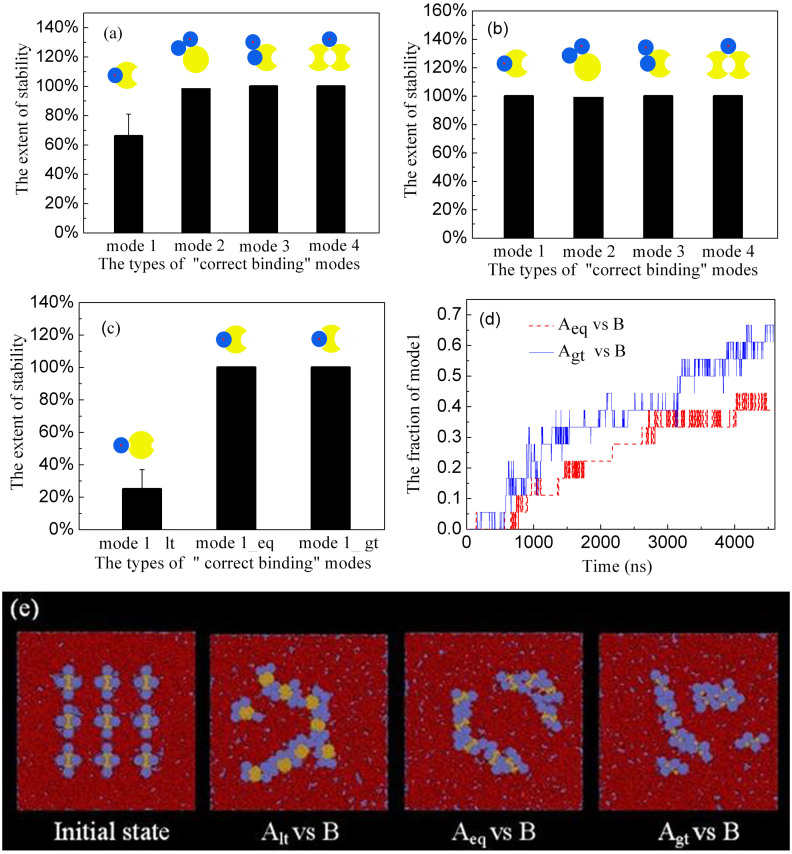
To further explore the stabilities of the “correct binding” of different modes, we monitored the trajectories of a probe protein (protein B marked by red ring) in the presence of its counterpart (protein A), which is fixed in the xy plane of the membrane. For different binding modes, the initial positions of the probe protein were exactly set to bind with its counterpart. At first, all the binding modes were equilibrated for 6.4 ns. The results of the probe protein stability were collected from 100 independent simulation runs of 1600 ns. Then we show the extent of the probe protein stability of different modes in Figure 3a. It is found that all the “correct binding” modes are absolutely stable in which no probe protein is away from its binding site, except for the model 1 (see Figure 3a). However, when we extend the equilibration time of the binding modes to 1600 ns, we found that all the “correct binding” modes are absolutely stable (see Figure 3b). This observation confirms that all the four “correct binding” modes are stable, whereas the mode 1 needs a longer time to reach stable state.

Figure 3.

Figure 3

Open in a new tab

(a) The stability for different “correct binding” modes after balance 6.4 ns (protein A (D = 5.8 nm)), protein B (D = 3.23 nm)). (b) The stability for different “correct binding” modes after balance 1600 ns (protein A (D = 5.8 nm)), protein B (D = 3.23 nm)) (c) The stability for different “correct binding” modes after balance 1600 ns (protein A (D = 5.8 nm)), protein B (D = 3.23 nm)). Mode l_lt: protein Alt and protein B, Mode 1_eq: protein Aeq and protein B, Mode 1_gt: protein Agt and protein B. (d) The fraction of mode 1 as the function of time. (Protein A (D = 4.5 nm)), protein B (D = 3.23 nm)) (e) Initial state and typical top view snapshots of protein aggregation, where protein A (D = 4.5 nm) is shown in yellow, protein B (D = 3.23 nm) in blue, lipid membrane in red.

Sequentially, we further investigated the stability of the “correct binding” in mode 1 but the protein A has different grooves. All the binding modes were equilibrated for 1600 ns. The results of the probe protein stability were collected from 100 independent simulation runs of another 1600 ns. As shown in Figure 3c, for the system containing protein Alt and protein B, the results show that 75 percentage probe proteins are away from its initial site after a simulation run. However, for the system containing protein Aeq and protein B, no probe protein departs from the groove of protein Aeq in one hundred simulations. For the system containing protein Agt and protein B, it shows the same result. This means that the shape complementarity can increase the stability of the protein aggregation. However, when the initial system of the protein Aeq and protein B, and the system of the protein Agt and protein B were equilibrated for 6.4 ns, only the system containing protein Agt and protein B is absolutely stable. That is to say, compared with the binding mode of protein Aeq and protein B, the binding mode of protein Agt and protein B easilier reaches stablility in a short time.

In order to research the kinetics of mode 1 with different grooves, we put the protein Aeq (D = 4.5 nm) (or protein Agt (D = 4.5 nm)) and protein B (D = 3.23 nm) randomly in the membrane. By monitoring the kinetics of mode 1 for different grooves, it is found that the probe protein B is easier to eneter the large groove (protein Agt (D = 4.5 nm)), as shown in Figure 3d. This is consistent with the above observation.

Besides, in order to further confirm the effect of protein shape complementarity on protein aggregation, we used the initial configurations in the first panel of Figure 3e to investigate the protein aggregation. For the system of Alt vs B, the protein B cannot enter the groove of protein Alt. After 4800 ns, we found that all proteins B surround proteins Alt to match the curvature of proteins A that form the mode 2 (see the second panel of the Figure 3e). For the systems of Aeq vs B and Agt vs B (see the third and forth panels of the Figure 3e), the proteins B in the groove of protein Aeq or protein Agt, are still in the groove after simulating 4800 ns, which confirms the system stability. However, the protein B at the bulge of the protein Aeq or protein Agt in the initial state tends to enter into the groove. All the observations indicate that protein aggregation with a shape complementarity is stable. This stable configuration can restrict further movement of protein, and obviously promote protein aggregation.

The mechanism of the enhanced protein aggregations caused by the protein shape complementarity can be interpreted as follows. Since there is no attractive interaction between neighboring proteins in this work, the membrane deformation caused by the protein interaction is minimized. So, the clustering of different proteins does not caused by the protein-protein attraction. When the two proteins with the shape complementarity approach each other, the conformation of lipid chains confined in two proteins would be restricted significantly. Thus, the lipids inside the gap between the proteins would lose their configuration entropy owing to the constraint, compared to their counterparts in an unperturbed bilayer. As a result, the lipid molecules tend to leave the gap to gain more configuration entropy, and yield an effective entropy-induced attraction between the proteins with the shape complementarity, which thus enhances the protein aggregation, similarly to the generation of depletion force in colloid systems. The shape complementarity can be considered as a sub-category of depletion force. However, when the two proteins aggregate with a shape complementarily way, it can increase the contact area of the two proteins. In this case, the number of the lipids inside the gap between the two proteins would increase greatly. So the shape complemetarity between the proteins can enlarge the depletion force between the proteins and promote the protein aggregation. In Figure 2, we can see that with the increase the shape complementarity, the aggregation degree of the system 4 increases compared to system 1. This means that the shape complemetarity promotes the aggregation of the proteins. Besides, the shape complementarity also increases the selective aggregation. Therefore, the shape complementarity may be a special depletion force of proteins with shape matching.

It is not surprising that under driving force toward the minimum of free energy, the misbinding also often occurs. If the aggregation of the protein does not with a shape complementarily way, we call it as an “incorrect binding”. The configurations with “incorrect binding” can be also stabilized, because the high clustering rate leads to the misbinded subunits to be trapped in a growing cluster by further addition of subunits. Therefore, the transformation from a misbinding to a completed “correct binding” becomes extremely slow since the breakage of many misbindings is required. A lot of the assembly pathways leading to incorrect binding are available at these parameter values, so the configuration with minimum free energy of complete “correct binding” is seldom realized.

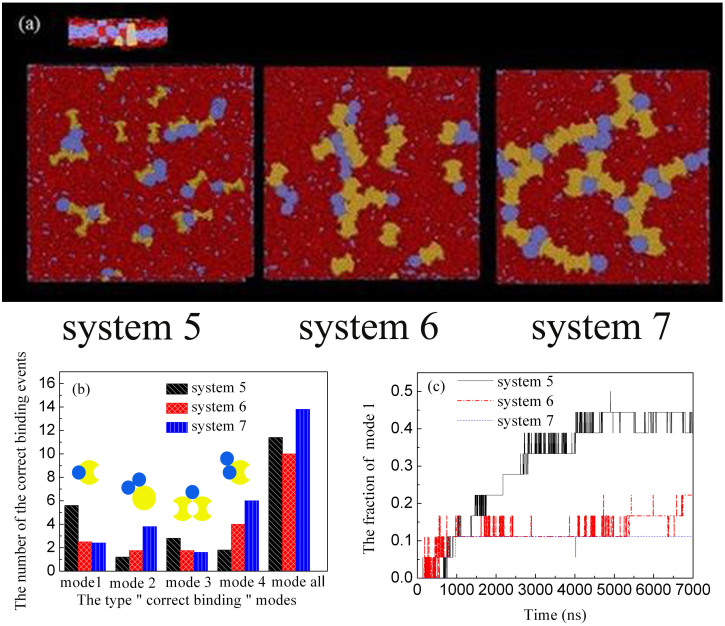
We also study the influence of protein size on protein aggregation. Three different size protein systems are designed. System 5: protein Aeq (D = 4.5 nm) and protein B (D = 3.23 nm); System 6: protein Aeq (D = 5.8 nm) and protein B (D = 3.23 nm); System 7: protein Aeq (D = 7.1 nm) and protein B (D = 4.5 nm). The snapshots from simulation were shown in Figure 4a, where the larger protein exhibits more apparent aggregation. For the three systems studied, the complementarity mode is also different. As shown in Figure 4b, from system 5 to system 7, i.e. with the increase of protein size, the number of “correct binding” from mode 1 and mode 3 decreases, while the number of “correct binding” from mode 2 and mode 4 increases. We also further explored the dependence of the correcting binding on protein size, and investigated the kinetics of mode 1 in the three systems. It is found that the correct binding of larger protein by mode 1 is much slower, i.e. the thermal motion of small proteins is larger, which would gain more chances for the correct binding. However, on the whole, the larger protein is easier to self-assemble into aggregations, as seen in Figure 4a, because the larger protein can optimize four modes together to form dendritic aggregation. It can also be found from Figure 4b that the total number of the correct binding of larger protein by all four modes is highest.

Figure 4. Protein aggregate with different sizes after 3840 ns.

Figure 4

Open in a new tab

System 5: protein Aeq (D = 4.5 nm) and protein B (D = 3.23 nm), System 6: protein Aeq (D = 5.8 nm) and protein B (D = 3.23 nm), System 7: protein Aeq (D = 7. 1 nm) and protein B (D = 4.5 nm). (a) Typical top view snapshots of protein aggregation, where protein Aeq is shown in yellow, protein B in blue, lipid membrane in red. (b) The number of different “correct binding” modes in the three systems. (c) The fraction of mode 1 in different systems as a function of time.

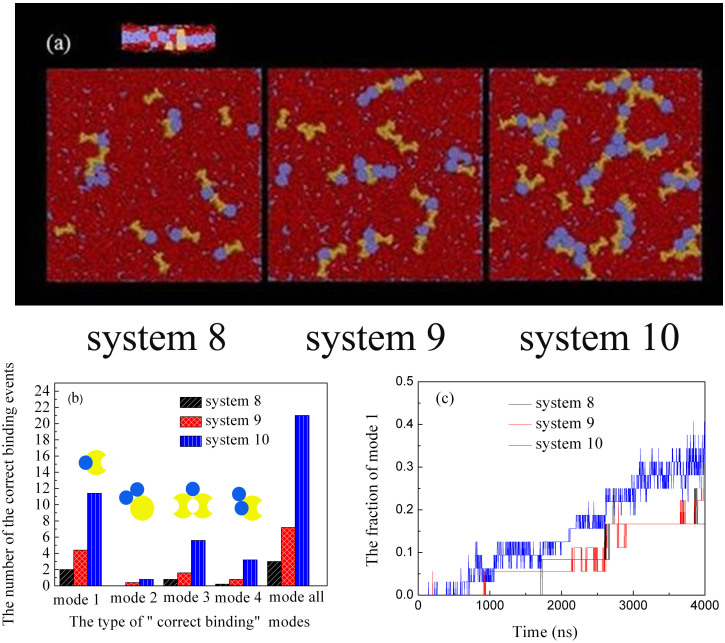
In addition, we also explored the effects of protein density on the aggregations, as shown in Figure 5, where the protein density increases from system 8 to system 10. As seen in the snapshots from Figure 5a, the increase of the protein density promotes the protein aggregation apparently, because the increase in density produces more chances for the protein shape complementarity. This observation is also confirmed by the total number of the correct binding of proteins by all four modes shown in Figure 5b. Moreover, with the increase of the protein density, the dynamic process for protein B into the groove of protein Aeq is also accelerated, as shown in Figure 5c.

Figure 5. Protein aggregate with different densities after 3840 ns.

Figure 5

Open in a new tab

Protein Aeq (D = 4.5 nm) and protein B (D = 3.23 nm). The total number of protein Aeq and protein B from system 8 to system 10 is 25, 36 and 64. (a) Typical top view snapshots of protein self-assembly with different densities, where protein Aeq is shown in yellow, protein B in blue, lipid membrane in red. (b) The number of different “correct binding” modes in the three systems. (c) The fraction of mode 1 in different systems as a function of time.

Discussion

We have systematically investigated the role of the shape complementarity on the protein-protein interaction and the protein aggregation under the condition without the electrostatic-complementarity and hydrophobic complementarity. Results indicate that the shape complementarity significantly promotes the protein aggregation. Importantly, by exploring the shape complementarity of different proteins, we found when the two proteins with shape complementarity approach each other, the conformation of lipid chains between two proteins would be restricted significantly, and the lipid molecules tend to leave from the gap formed by two proteins to maximize the configuration entropy, which yields an effective entropy-induced attraction between the proteins with shape complementarity and thus enhances the protein aggregation. In addition, we also explored the influences of the size and density of proteins with shape complementarity on the aggregation. It is found that the larger protein is easier to self-assemble into the aggregation, because the larger protein can optimize four modes together to form the aggregations. In short, it is expected that this work can trigger scientists' interests in the role of the shape complementarity in the protein-protein interactions especially for protein aggregation and antibody–antigen complexes, besides electrostatic-complementarity and hydrophobic complementarity.

Methods

The dissipative particle dynamics (DPD) method has been extensively used to simulate the hydrodynamic behavior of complex fluids28,29, in which the dynamics of DPD beads are governed by Newton's equation of motion, in a similar way as molecular dynamics (MD) method. DPD is one of the most commonly used computer simulation techniques in the studies of biomembrane systems19,24,25,30,31,32,33,34,35,36,37,38. It can reproduce accurately the dynamic behavior of the lipid bilayer, and also was used to explore the interactions between the biomembranes and proteins14,19.

In this work, a coarse grained model was used to represent the protein, and the protein models were given in Figure 1. To represent dimyristoylphosphatidylcholine (DMPC), a model lipid molecule15 was built by connecting a headgroup with three hydrophilic beads (H) to two hydrophobic tails where each contains five hydrophobic beads (T) (see Figure 1). Although it is slightly different from the DMPC lipid model proposed by Grafmuller et al.39,40, this model can show the typical phase behavior of lipid bilayers41,42.

We have designed two types of transmembrane protein models. One is typical cylindrical protein (B) which have a hydrophobic domain with a length of six layers (PT) and two hydrophilic domains consisting of three layers (PH) distributed at top and bottom of this cylinder. The other is the cylinder (A) and “bowknot” proteins with a groove (i.e. Alt, Aeq and Agt). The groove curvature in Alt, Aeq and Agt proteins is smaller, equal and larger than the one of protein B, respectively (see Figure 1). The protein is a rigid structure constituted by the single beads. The solvent molecule (denoted as W) is also molded as single beads.

The interaction force exerted on beads is composed of conservative, dissipative and random forces. The conservative force between beads i and j, which is soft and repulsive, is determined by

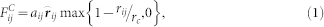graphic file with name srep03271-m1.jpg

where aij is the maximum repulsive force between particles i and j, rij = rj − ri (ri and rj are the positions of particle i and particle j), rij = |rij|, Inline graphic, and rc is the cutoff radius. In this system, the interaction parameters between the same type beads were set to aHH = aTT = aWW = aPHPH = aPTPT = 25, and those between the different types of beads were aHT = aTW = aPHPT = aPTW = 50, aHW = aPHW = 25. The interaction parameter “25” means that there exists no effective attraction between the beads. When the interaction parameter is above than 25, there exists an effectively repulsive interaction between the beads. If it is less than 25, there is an effectively attractive interaction.

For the lipid molecules, the interaction between the neighboring beads is described by a harmonic spring force,

graphic file with name srep03271-m2.jpg

where the spring constant KS was set to 128 kBT and the equilibrium bond length req was set to 0.7rc. The force constraining the variation of bond angle is given by

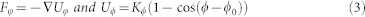graphic file with name srep03271-m3.jpg

where ϕ0 was set to π and Kϕ is the bond bending constant and here Kϕ is 10.0.

Without loss of generality, we set the cutoff radius rc, the bead mass m, and the thermostat temperature kBT to unity for simplifying the calculation. To relate rc to its actual physical size, we used the formula proposed by Groot and Rabone43, rc = 3.107(ρNm)1/3[Å]. Here Nm was set to 3, ρ was set to 3.0 and a water molecule has approximately a volume of 30 cubic Angstroms. Accordingly, we obtained that rc = 6.46 Angstroms.

In this work, we used an N-varied DPD method, a particular variant of DPD method in which the targeted membrane tension is maintained by monitoring the number of lipids per area (LNPA) in a boundary region19,38,44, to simulate internalization processes. In this method, the boundary region, which surrounds the central square region of the membrane, plays an important role as a reservoir of lipids, and the value of LNPA in the boundary region (denoted as Inline graphic) is kept constant by deletion/addition moves. Simultaneously, the corresponding number of water beads are randomly deleted or added to keep the whole density of the simulation box constant.

Since the membrane tension is directly related to 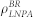Inline graphic, we specified the value of 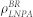Inline graphic hereafter. To keep the membrane flat and to rule out the effect of the membrane curvature on the protein aggregation, we choose a positive surface tension 1.2.

Author Contributions

D.C. and X.Z. co-produced the original idea, designed the study and wrote this paper. Y.L. contributed to perform all the calculations, to collect and analyze data. All authors discussed results and commented on all stages of the paper.

Acknowledgments

This work is supported by National 973 Program (2011CB706900), NSF of China (21274011, 21276007), National Scientific Research Funding (ZZ1304) and Excellent Talents Plan of BUCT.

References

  1. Berger-Wolf T. Y., Przytycka T. M., Singh M. & Slonim D. In Dynamics of Biological Networks–Session Introduction. Pac. Symp. Biocomput. 5, 120–2 (2010). [Google Scholar]
  2. Przytycka T. M., Singh M. & Slonim D. K. Toward the Dynamic Interactome: It's about Time. Brief. Bioinfo. 11, 15–29 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. McCoy A. J., Chandana Epa V. & Colman P. M. Electrostatic Complementarity at Protein/Protein Interfaces. J. Molec. Biol. 268, 570–584 (1997). [DOI] [PubMed] [Google Scholar]
  4. Gabb H. A., Jackson R. M. & Sternberg M. J. Modelling Protein Docking Using Shape Complementarity, Electrostatics and Biochemical Information. J. Molec. Biol. 272, 106–120 (1997). [DOI] [PubMed] [Google Scholar]
  5. Sheinerman F. B., Norel R. & Honig B. Electrostatic Aspects of Protein–Protein Interactions. Current opin. Struct. Biol. 10, 153–159 (2000). [DOI] [PubMed] [Google Scholar]
  6. Sheinerman F. B. & Honig B. On the Role of Electrostatic Interactions in The Design of Protein–Protein Interfaces. J. Molec. Biol. 318, 161–177 (2002). [DOI] [PubMed] [Google Scholar]
  7. Zhang Z., Witham S. & Alexov E. On the Role of Electrostatics in Protein–Protein Interactions. Phys. Biol. 8, 035001 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Elcock A. H., Gabdoulline R. R., Wade R. C. & McCammon J. A. Computer Simulation of Protein-Protein Association Kinetics: Acetylcholinesterase-Fasciculin. J. Molec. Biol. 291, 149–162 (1999). [DOI] [PubMed] [Google Scholar]
  9. Wlodek S. T., Shen T. & McCammon J. A. Electrostatic Steering of Substrate to Acetylcholinesterase: Analysis of Field Fluctuations. Biopolymers. 53, 265–271 (2000). [DOI] [PubMed] [Google Scholar]
  10. Sept D., Elcock A. H. & McCammon J. A. Computer Simulations of Actin Polymerization Can Explain the Barbed-Pointed End Asymmetry. J. Molec. Biol. 294, 1181–1189 (1999). [DOI] [PubMed] [Google Scholar]
  11. Lewis B. A. & Engelman D. M. Lipid bilayer thickness varies linearly with acyl chain length in fluid phosphatidylcholine vesicles. J. Molec. Biol. 166, 211 (1983). [DOI] [PubMed] [Google Scholar]
  12. Yano Y. & Matsuzaki K. Measurement of Thermodynamic Parameters for Hydrophobic Mismatch 1: Self-Association of a Transmembrane Helix. Biochem. 45, 3370–3378 (2006). [DOI] [PubMed] [Google Scholar]
  13. Botelho A. V., Huber T., Sakmar T. P. & Brown M. F. Curvature and Hydrophobic Forces Drive Oligomerization and Modulate Activity of Rhodopsin in Membranes. Biophys. J. 91, 4464–4477 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Yue T. & Zhang X. Signal Transduction Across Cellular Membranes Can Be Mediated by Coupling of the Clustering of Anchored Proteins in Both Leaflets. Phys. Rev. E. 85, 011917 (2012). [DOI] [PubMed] [Google Scholar]
  15. De Meyer F. J. M., Venturoli M. & Smit B. Molecular Simulations of Lipid-Mediated Protein-Protein Interactions. Biophy. J. 95, 1851–1865 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. West B., Brown F. L. H. & Schmid F. Membrane-Protein Interactions in a Generic Coarse-Grained Model for Lipid Bilayers. Biophy. J. 96, 101–115 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Morozova D. & Weiss M. On the Role of Acylation of Transmembrane Proteins. Biophy. J. 98, 800–804 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Parton D. L., Klingelhoefer J. W. & Sansom M. S. P. Aggregation of Model Membrane Proteins, Modulated by Hydrophobic Mismatch, Membrane curvature, and Protein Class. Biophy. J. 101, 691–699 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Yue T., Li S., Zhang X. & Wang W. The Relationship Between Membrane Curvature Generation and Clustering of Anchored Proteins: A Computer Simulation Study. Soft Matter. 6, 6109–6118 (2010). [Google Scholar]
  20. Blood P. D., Swenson R. D. & Voth G. A. Factors Influencing Local Membrane Curvature Induction by N-BAR Domains as Revealed by Molecular Dynamics Simulations. Biophys. J. 95, 1866–1876 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Blood P. D. & Voth G. A. Direct observation of Bin/amphiphysin/Rvs (BAR) domain-induced membrane curvature by means of molecular dynamics simulations. Proc. Natl. Acad. Sci. 103, 15068–15072 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Arkhipov A., Yin Y. & Schulten K. Four-scale description of membrane sculpting by BAR domains. Biophy. J. 95, 2806–2821 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hsin J. et al. Protein-induced membrane curvature investigated through molecular dynamics flexible fitting. Biophy. J. 97, 321–329 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Venturoli M., Smit B. & Sperotto M. M. Simulation studies of protein-induced bilayer deformations, and lipid-induced protein tilting, on a mesoscopic model for lipid bilayers with embedded proteins. Biophy. J. 88, 1778 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Li S., Zhang X. & Wang W. Cluster formation of anchored proteins induced by membrane-mediated interaction. Biophy. J. 98, 2554–2563 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Tsuchiya Y., Kinoshita K. & Nakamura H. Analyses of homo-oligomer interfaces of proteins from the complementarity of molecular surface, electrostatic potential and hydrophobicity. Protein Eng. Design Select. 19, 421–429 (2006). [DOI] [PubMed] [Google Scholar]
  27. Morozova D., Weiss M. & Guigas G. Shape as a determinant of membrane protein cluster formation. Soft Matter. 8, 11905–11910 (2012). [Google Scholar]
  28. Groot R. D. & Warren P. B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 107, 4423 (1997). [Google Scholar]
  29. Hoogerbrugge P. & Koelman J. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. EPL 19, 155 (2007). [Google Scholar]
  30. Yang K. & Ma Y. Q. Computer simulation of the translocation of nanoparticles with different shapes across a lipid bilayer. Nature Nanotech. 5, 579–583 (2010). [DOI] [PubMed] [Google Scholar]
  31. Shillcock J. C. & Lipowsky R. Tension-induced fusion of bilayer membranes and vesicles. Nature Mater. 4, 225–228 (2005). [DOI] [PubMed] [Google Scholar]
  32. Li S., Zhang X. & Wang W. Coarse-grained model for mechanosensitive ion channels. J. Phys. Chem. B. 113, 14431–14438 (2009). [DOI] [PubMed] [Google Scholar]
  33. Smith K. A., Jasnow D. & Balazs A. C. Designing synthetic vesicles that engulf nanoscopic particles. J. Chem. Phys. 127, 084703 (2007). [DOI] [PubMed] [Google Scholar]
  34. Gao L., Lipowsky R. & Shillcock J. Tension-induced vesicle fusion: pathways and pore dynamics. Soft Matter. 4, 1208–1214 (2008). [DOI] [PubMed] [Google Scholar]
  35. Laradji M. & Sunil Kumar P. Dynamics of domain growth in self-assembled fluid vesicles. Phys. Rev. Lett. 93, 198105 (2004). [DOI] [PubMed] [Google Scholar]
  36. Schmidt U., Guigas G. & Weiss M. Cluster formation of transmembrane proteins due to hydrophobic mismatching. Phys. Rev. Lett. 101, 128104 (2008). [DOI] [PubMed] [Google Scholar]
  37. Alexeev A., Uspal W. E. & Balazs A. C. Harnessing Janus nanoparticles to create controllable pores in membranes. ACS Nano. 2, 1117–1122 (2008). [DOI] [PubMed] [Google Scholar]
  38. Li Y., Yue T., Yang K. & Zhang X. Molecular modeling of the relationship between nanoparticle shape anisotropy and endocytosis kinetics. Biomater. 33, 4965–4973 (2012). [DOI] [PubMed] [Google Scholar]
  39. Grafmüller A., Shillcock J. & Lipowsky R. Pathway of membrane fusion with two tension-dependent energy barriers. Phys. Rev. Lett. 98, 218101 (2007). [DOI] [PubMed] [Google Scholar]
  40. Grafmüller A., Shillcock J. & Lipowsky R. The fusion of membranes and vesicles: pathway and energy barriers from dissipative particle dynamics. Biophys. J. 96, 2658–2675 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Venturoli M., Maddalena Sperotto M., Kranenburg M. & Smit B. Mesoscopic models of biological membranes. Phys. Rep. 437, 1–54 (2006). [Google Scholar]
  42. Kranenburg M. & Smit B. Phase behavior of model lipid bilayers. J. Phys. Chem. B. 109, 6553–6563 (2005). [DOI] [PubMed] [Google Scholar]
  43. Groot R. & Rabone K. Mesoscopic simulation of cell membrane damage, morphology change and rupture by nonionic surfactants. Biophy. J. 81, 725–736 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Yue T. & Zhang X. Molecular understanding of receptor-mediated membrane responses to ligand-coated nanoparticles. Soft Matter. 7, 9104–9112 (2011). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES