On the Theory of Reactive Mixtures for Modeling Biological Growth

Abstract

Mixture theory, which can combine continuum theories for the motion and deformation of solids and fluids with general principles of chemistry, is well suited for modeling the complex responses of biological tissues, including tissue growth and remodeling, tissue engineering, mechanobiology of cells and a variety of other active processes. A comprehensive presentation of the equations of reactive mixtures of charged solid and fluid constituents is lacking in the biomechanics literature. This study provides the conservation laws and entropy inequality, as well as interface jump conditions, for reactive mixtures consisting of a constrained solid mixture and multiple fluid constituents. The constituents are intrinsically incompressible and may carry an electrical charge. The interface jump condition on the mass flux of individual constituents is shown to define a surface growth equation, which predicts deposition or removal of material points from the solid matrix, complementing the description of volume growth described by the conservation of mass. A formu-lation is proposed for the reference configuration of a body whose material point set varies with time. State variables are defined which can account for solid matrix volume growth and remodeling. Constitutive constraints are provided on the stresses and momentum supplies of the various constituents, as well as the interface jump conditions for the electrochem cal potential of the fluids. Simplifications appropriate for biological tissues are also proposed, which help reduce the governing equations into a more practical format. It is shown that explicit mechanisms of growth-induced residual stresses can be predicted in this framework.

1 Introduction

The theory of mixtures has been successfully applied to the study of biological tissues and cells for over three decades (Kenyon, 1976; Mow et al, 1980; Lai et al, 1991; Huyghe and Janssen, 1997; Gu et al, 1998; Humphrey and Rajagopal, 2002; Klisch et al, 2003; Lemon et al, 2006). The vast majority of these studies have focused on mechanics and transport of non-reacting mixtures, though more recent studies have addressed problems of tissue growth and remodeling (Baek et al, 2006; Klisch et al, 2003) and tissue engineering (Lemon et al, 2006). Growth and remodeling occur as a result of chemical reactions. Similarly, uptake of nutrients, breakdown into waste products, binding of molecules to tissues and cells, active transport mechanisms in cells, cytoskeletal remodeling, cell motion and taxis and a host of other mechano-transduction and mechanobiological events involve chemical reactions. Mixture theory, which can combine continuum theories for the motion and deformation of solids and fluids with general principles of chemistry, is ideally suited for modeling the complex responses of biological tissues.

Conservation laws for heterogeneous mixtures which can undergo chemical reactions were formulated in a rigorous framework by Truesdell and Toupin (1960). Many authors subsequently built upon this framework (see the review by Bedford and Drumheller, 1983) and helped establish the field of mixture theory. However, much of this classical literature has remained in the realm of theoretical rational mechanics. The field of biomechanics and modeling in mechanobiology is well poised today to adopt the broader formulation of the theory of reactive mixtures and expand upon it.

Mixture theory has been used selectively in the study of biological tissues. The concepts of reactive mixtures of charged constituents have not been applied or summarized comprehensively in the relevant biomechanics literature. Therefore the objective of this study is to present the comprehensive set of governing equations for such mixtures, using a consistent notation. This opportunity is used to clarify and expand on some concepts, particularly in relation to charged constituents and interface jump conditions in the presence of chemical reactions.

The long-term objective is to demonstrate the widespread applicability of mixture theory to tackle the complexities of biological tissues, including the study of biological growth and remodeling. In particular, mixture theory presents an opportunity to identify specific mechanism responsible for growthinduced residual stresses, as addressed in this study, whereas the traditional literature assumes a more phenomenological approach. Other areas of application may include the analysis of active cellular processes, such as the modeling of membrane pumps, resting potentials and action potentials using the framework of continuum theory.

2 Governing Equations for Reactive Mixtures

First, the conservation laws and entropy inequality for reactive mixtures are summarized, along with corresponding interface jump conditions. Next, these equations are formulated for intrinsically incompressible mixture constituents (Bowen, 1980; Mow et al, 1980) which may also carry an electrical charge (Lai et al, 1991; Huyghe and Janssen, 1997), as this representation is most relevant to biological tissues. The assumption of intrinsic incompressibility of the fluid constituents of a mixture is based on the common modeling of aqueous solutions as incompressible in the range of pressures encountered in biological tissues. The assumption of intrinsic incompressibility of the solid constituents represents an idealization which generally holds for most biological tissues. For example, the mixture of collagen type II and proteoglycans which forms the solid matrix of articular cartilag exhibits negligible volume change to hydrostatic pressurization in the range of experimental measurements up to 12 MPa (Bachrach et al, 1998). Most other soft biological tissues are assumed to be incompressible, such as cardiovascular tissues (Humphrey, 2002) and tendons and ligaments (Weiss and Gardiner, 2001). It should be kept in perspective that the porous solid matrix of a mixture may be compressible if fluid enters or leaves its pores.

Modeling of electrical charges on the constituents of a mixture makes it possible to analyze phenomenasuch as Donnan potential and osmotic pressure, streaming and diffusion potentials and electro-osmosis (Overbeek, 1956; Grimshaw et al, 1989, 1990; Gu et al, 1993, 1997, 1998). These phenomena may be relevant to processes at the tissue level as well as at the cellular level. Unlike the more general treatment of Eringen (1998), the analysis adopted here neglects the effects of strongly varying magnetic fields. Consequently only a subset of Maxwell's equations of electromagnetism are needed, which are derived from fundamental principles of conservation of mass (and thus, conservation of charge) and momentum.

2.1 Conservation Laws

The mixtures considered in this study consist of any number of solid and fluid constituents. The derivation of the conservation equations presented in this section was presented by Truesdell and Toupin (1960). The underlying principle of mixture theory is that the continuum is occupied at every point x by all the constituents of the mixture. Each constituent has an independent motion given by the function

$$\mathbf{\text{x}}={\mathbf{\chi }}^{\alpha }({\mathbf{\text{X}}}^{\alpha },t)$$ (1)

where X^α represent the position of constituent α in the reference configuration. At the current configuration, the constituent material points occupying the position x generally originated from different positions X^α. The velocity and acceleration of a material point of constituent α are given by

$${\mathbf{\text{v}}}^{\alpha }=\frac{\partial {\mathbf{\chi }}^{\alpha }}{\partial t}{\mathbf{\text{a}}}^{\alpha }=\frac{{\partial }^2{\mathbf{\chi }}^{\alpha }}{\partial t^2}$$ (2)

In a spatial or Eulerian description, the material derivative of a function may be taken following the motion of constituent α. For example, for a scalar function f (x, t),

$$\frac{D^{\alpha }f}{Dt}=\frac{\partial f}{\partial t}+\text{grad}f\cdot {\mathbf{\text{v}}}^{\alpha }$$ (3)

The conservation of mass for constituent α is given by

$$\frac{D^{\alpha }{\rho }^{\alpha }}{Dt}+{\rho }^{\alpha }\text{div}{\mathbf{\text{v}}}^{\alpha }={\widehat{\rho }}^{\alpha }$$ (4)

where ρ^α (x, t) is the apparent density (mass of constituent α per volume of mixture) and ρ̂^α (x, t) is the mass supply to constituent α due to chemical reactions with, or among other constituents. The units of ρ̂^α are those of mass per unit volume per unit time. A basic principle of the theory of mixtures is that the mean response of a heterogeneous mixture obeys the ordinary equations ofa continuum (Truesdell and Toupin, 1960). Taking the summation of Eq.(4) over all constituents α should thus produce

$$\frac{D\rho }{Dt}+\rho \text{div}\mathbf{\text{v}}=0$$ (5)

A term-by-term comparison shows that the mixture density ρ is given by1

$$\rho =\sum _{\alpha }{\rho }^{\alpha }$$ (6)

and the mixture velocity v is the velocity of the center of mass,

$$\mathbf{\text{v}}=\frac{1}{\rho }\sum _{\alpha }{\rho }^{\alpha }{\mathbf{\text{v}}}^{\alpha }$$ (7)

Moreover, the sum of the mass supply terms over all constituents must reduce to zero,

$$\sum _{\alpha }{\widehat{\rho }}^{\alpha }=0$$ (8)

In the presentation below there are several instances where a mixture property f is related to the corresponding property f^α of the constituents through

$$f=\frac{1}{\rho }{\sum _{\alpha }{\rho }^{\alpha }f}^{\alpha }$$ (9)

The expression ρDf / Dt can be related to the corresponding expression for the individual constituents according to

$$\rho \frac{Df}{Dt}=\sum _{\alpha }{\rho }^{\alpha }\frac{D^{\alpha }{f}^{\alpha }}{Dt}-\text{div}({\rho }^{\alpha }{f}^{\alpha }{\mathbf{\text{u}}}^{\alpha })+{\widehat{\rho }}^{\alpha }{f}^{\alpha }$$ (10)

where the velocity of constituent α relative to the mean mixture velocity,

$${\mathbf{\text{u}}}^{\alpha }\equiv {\mathbf{\text{v}}}^{\alpha }-\mathbf{\text{v}}$$ (11)

is called the diffusion velocity. Similarly it can be shown that

$$\rho \mathbf{\text{a}}=\sum _{\alpha }{\rho }^{\alpha }{\mathbf{\text{a}}}^{\alpha }-\text{div}({\rho }^{\alpha }{\mathbf{\text{u}}}^{\alpha }\otimes {\mathbf{\text{u}}}^{\alpha })+{\widehat{\rho }}^{\alpha }{\mathbf{\text{u}}}^{\alpha }$$ (12)

where a = Dv / Dt and a^α = D^αv^α / Dt.

The conservation of linear momentum for constituent α is given by

$${\rho }^{\alpha }{\mathbf{\text{a}}}^{\alpha }=\text{div}{\mathbf{\text{T}}}^{\alpha }+{\rho }^{\alpha }{\mathbf{\text{b}}}^{\alpha }+{\widehat{\mathbf{\text{p}}}}^{\alpha }$$ (13)

where T^α is the apparent or partial Cauchy stress, b^α represents external body forces acting on constituent α (with units of force per unit mass), and p̂^α is the momentum supply to constituent α from all other constituents (with units of force per unit volume).² The mixture must satisfy

$$\rho \mathbf{\text{a}}=\text{div}\mathbf{\text{T}}+\rho \mathbf{\text{b}}$$ (14)

and the equivalence of this expression with the summation of Eq.(13) over all α requires that the mixture stress T be given by

$$\mathbf{\text{T}}=\sum _{\alpha }{\mathbf{\text{T}}}^{\alpha }-{\rho }^{\alpha }{\mathbf{\text{u}}}^{\alpha }\otimes {\mathbf{\text{u}}}^{\alpha }$$ (15)

and the mixture body force by

$$\mathbf{\text{b}}=\frac{1}{\rho }\sum _{\alpha }{\rho }^{\alpha }{\mathbf{\text{b}}}^{\alpha }$$ (16)

Furthermore, the momentum supplies must satisfy

$$\sum _{\alpha }{\widehat{\mathbf{\text{p}}}}^{\alpha }+{\widehat{\rho }}^{\alpha }{\mathbf{\text{u}}}^{\alpha }=\mathbf{0}$$ (17)

It is noteworthy that the mixture stress is not simply the sum of the stresses of each constituent; the latter quantity is called the inner part of the mixture stress and is given by

$${\mathbf{\text{T}}}^I\equiv \sum _{\alpha }{\mathbf{\text{T}}}^{\alpha }$$ (18)

The conservation of angular momentum for constituent α reduces to

$${({\mathbf{\text{T}}}^{\alpha })}^T-{\mathbf{\text{T}}}^{\alpha }={\widehat{\mathbf{M}}}^{\alpha }$$ (19)

where M̂^α is the antisymmetrictensorwhose dualvector m̂^α is the angular momentum supply to constituent α from all other constituents (with units of moment per unit volume). For a non-polar mixture, the conservation of angular momentum implies that the mixture stress must satisfy

$${\mathbf{\text{T}}}^T-\mathbf{\text{T}}=\mathbf{0}$$ (20)

which implies that

$$\sum _{\alpha }{\widehat{\mathbf{\text{M}}}}^{\alpha }=\mathbf{0}$$ (21)

The conservation of energy for constituent α is given by

$${\rho }^{\alpha }\frac{D^{\alpha }{\varepsilon }^{\alpha }}{Dt}={\mathbf{\text{T}}}^{\alpha }:{\mathbf{\text{L}}}^{\alpha }-\text{div}{\mathbf{\text{q}}}^{\alpha }+{\rho }^{\alpha }{r}^{\alpha }+{\widehat{\varepsilon }}^{\alpha }$$ (22)

where ε^α is the internal energy of constituent α per unit mass, q^α is the heat flux vector (defined positive for heat leaving a control volume), r^α is the heat supply to the mixture from external sources, per unit mass, ε̂^α is the energy supply to constituent α from all other constituents, per unit volume, and L^α = grad v^α. The corresponding relation for the mixture is

$$\rho \frac{D\varepsilon }{Dt}=\mathbf{\text{T}}:\mathbf{\text{L}}-\text{div}\mathbf{\text{q}}+\rho r$$ (23)

where the mixture internal energy is

$$\varepsilon =\frac{1}{\rho }\sum _{\alpha }{\rho }^{\alpha }({\varepsilon }^{\alpha }+\frac{1}{2}{\mathbf{\text{u}}}^{\alpha }\cdot {\mathbf{\text{u}}}^{\alpha })$$ (24)

and the heat flux and heat supply are given by

$$\mathbf{\text{q}}=\sum _{\alpha }{\mathbf{\text{q}}}^{\alpha }-[{({\mathbf{\text{T}}}^{\alpha })}^T-{\rho }^{\alpha }({\varepsilon }^{\alpha }+\frac{1}{2}{\mathbf{\text{u}}}^{\alpha }\cdot {\mathbf{\text{u}}}^{\alpha }\left)\mathbf{\text{I}}\right]{\mathbf{\text{u}}}^{\alpha }$$ (25)

$$r=\frac{1}{\rho }\sum _{\alpha }{\rho }^{\alpha }(r^{\alpha }+{\mathbf{\text{b}}}^{\alpha }\cdot {\mathbf{\text{u}}}^{\alpha })$$ (26)

According to the principle of mixtures, the energy supply terms must satisfy

$$\sum _{\alpha }{\widehat{\varepsilon }}^{\alpha }+{\widehat{\mathbf{\text{p}}}}^{\alpha }\cdot {\mathbf{\text{u}}}^{\alpha }+{\widehat{\rho }}^{\alpha }\left({\varepsilon }^{\alpha }+\frac{1}{2}{\mathbf{\text{u}}}^{\alpha }\cdot {\mathbf{\text{u}}}^{\alpha }\right)=0$$ (27)

These results show that the heat flux q for the mixture is not a simple superposition of the heat fluxes of the constituents, as it also includes terms generated by the diffusion of constituents relative to the mixture velocity. Similarly, the heat supply r includes heat produced by external body forces b^α as a result of diffusion of the mixture constituents. Note that it is also possible to define the inner part of the internal energy as

$${\varepsilon }^I=\frac{1}{\rho }\sum _{\alpha }{\rho }^{\alpha }{\varepsilon }^{\alpha }$$ (28)

and the inner part of the heat flux as

$${\mathbf{\text{q}}}^I=\sum _{\alpha }{\mathbf{\text{q}}}^{\alpha }-{({\mathbf{\text{T}}}^{\alpha })}^T{\mathbf{\text{u}}}^{\alpha }+{\rho }^{\alpha }{\varepsilon }^{\alpha }{\mathbf{\text{u}}}^{\alpha }$$ (29)

The relations summarized in this section are consistent with the presentation of Bowen (1976), with the minor difference that he introduces the term (1/ρ) Σ_αρ^αb^α · u^α on the right-hand-side of Eq.(23) instead of the right-hand-side of Eq.(26).

2.2 Entropy Inequality

Unlike the conservation of mass, momentum and energy, the entropy inequality is not applied separately to each of the individual constituents because it imposes unrealistic constraints on the mixture. Bedford and Drumheller (1983) review the history of the formulation of the entropy inequality and the challenges addressed by various authors, complementing the earlier review of Bowen (1976). The formulation presented below follows that of Bowen (1976) and is reduced to the case where all constituents have the same absolute temperature θ (x, t).

When expressed in terms of the properties of the constituents, the entropy inequality for the mixture is given by

$$\sum _{\alpha }{\rho }^{\alpha }\frac{D^{\alpha }{\eta }^{\alpha }}{\mathit{\text{Dt}}}+\text{div}\left(\frac{{\mathbf{\text{q}}}^{\alpha }}{\theta }\right)-\frac{{\rho }^{\alpha }{r}^{\alpha }}{\theta }+{\widehat{\rho }}^{\alpha }{\eta }^{\alpha }\ge 0$$ (30)

where η^α (x, t) is the entropy of constituent α per unit mass. When expressed in terms of mixture properties, the corresponding expression is given by

$$\rho \frac{D\eta }{\mathit{\text{Dt}}}+\text{div}\frac{\mathbf{\text{h}}}{\theta }-\frac{\rho s}{\theta }\ge 0$$ (31)

where the entropy of the mixture, per unit mass, is

$$\eta =\frac{1}{\rho }\sum _{\alpha }{\rho }^{\alpha }{\eta }^{\alpha }$$ (32)

the heat flux vector h is given by

$$\mathbf{\text{h}}=\sum _{\alpha }{\mathbf{\text{q}}}^{\alpha }+{\rho }^{\alpha }\theta {\eta }^{\alpha }{\mathbf{\text{u}}}^{\alpha }$$ (33)

and the heat supply s is

$$s=\frac{1}{\rho }\sum _{\alpha }{\rho }^{\alpha }{r}^{\alpha }$$ (34)

Note that h and s are not the same as q and r, except in the case of a non-diffusing mixture (u^α = 0).

By introducing the Helmholtz free energy per unit mass for constituent α,

$${\psi }^{\alpha }={\varepsilon }^{\alpha }-\theta {\eta }^{\alpha }$$ (35)

and making use of the conservation of energy in Eq.(22), the inequality of Eq.(30) can be rewritten as

$$\sum _{\alpha }-{\rho }^{\alpha }(\frac{D^{\alpha }{\psi }^{\alpha }}{\mathit{\text{Dt}}}+{\eta }^{\alpha }\frac{D^{\alpha }\theta }{\mathit{\text{Dt}}}))+{\mathbf{\text{T}}}^{\alpha }:{\mathbf{\text{L}}}^{\alpha }-{\widehat{\mathbf{\text{p}}}}^{\alpha }\cdot {\mathbf{\text{u}}}^{\alpha }-\frac{1}{\theta }{\mathbf{\text{q}}}^{\alpha }\cdot \text{grad}\theta -{\widehat{\rho }}^{\alpha }({\psi }^{\alpha }+\frac{1}{2}{\mathbf{\text{u}}}^{\alpha }\cdot {\mathbf{\text{u}}}^{\alpha })\ge 0$$ (36)

This alternative form is more suitable for subsequent formulations of constitutive relations.

2.3 Interface Jump Conditions

To solve the governing partial differential equations presented in Section 2.1 we need to specify a proper set of boundary conditions. Importantly, it is necessary to account for the possibility of chemical reactions occurring on an interface, which may produce mass, momentum, energy and entropy. Such an interface would represent a surface of discontinuity (a singular surface Γ), which requires a specialized treatment and may necessitate the specification of additional constitutive relations. To formulate these interface jump conditions, one has to start from the integral form of the balance equations and properly account for discontinuities, when present (Eringen and Ingram, 1965; Mueller, 1975; Liu, 1980; Hou et al, 1989). Following this approach, the jump conditions for reactive mixtures can be deduced for each individual constituent as well as for the mixture.

The jump condition for mass is given by³

$$[[{\rho }^{\alpha }{\mathbf{\text{u}}}_{\Gamma }^{\alpha }]]\cdot \mathbf{\text{n}}=-{\overline{\rho }}^{\alpha }$$ (37)

where

$${\mathbf{\text{u}}}_{\Gamma }^{\alpha }\equiv {\mathbf{\text{v}}}^{\alpha }-{\mathbf{\text{v}}}_{\Gamma }$$ (38)

v_Γ is the velocity of the interface Γ, u_Γ is the diffusion velocity of constituent α relative to Γ, and n is the unit outward normal to Γ. ρ̄^α is the area density of mass supply from chemical reactions on Γ. Γ may be a boundary surface (or an imaginary surface) separating two regions of the continuum, or it may represent a material surface such as a thin membrane or a monolayer of cells. The jump condition for the mixture is given by

$$[[\rho {\mathbf{\text{u}}}_{\Gamma }]]\cdot \mathbf{\text{n}}=0$$ (39)

where

$${\mathbf{\text{u}}}_{\Gamma }\equiv \mathbf{\text{v}}-{\mathbf{\text{v}}}_{\Gamma }$$ (40)

By summing Eq.(37) over all constituents and equating the result to Eq.(39), we deduce that the area densities of mass supply must satisfy

$$\sum _{\alpha }{\overline{\rho }}^{\alpha }=0$$ (41)

For example, Γ may be a bone surface on which osteoblasts produce bony matrix (or osteoclasts resorb it), with ρ̄^bone representing the rate of bone growth or removal; or Γ may represent a mineralization front between bone and cartilage as in growth plates and centers of ossification; or it may represent the boundary between ice and liquid water and ρ̄^ice would represent the rate at which ice is melting (ρ̄^ice < 0) or water is freezing (ρ̄^ice > 0). These examples illustrate the case where Γ is a boundary separating two constituents, with surface growth or resorption of one constituent as a result of chemical reactions with the other. For instance, if the ice is assumed to be stationary, v^ice = 0, and since ρ^ice = 0 on the liquid water side of the interface, Eq.(37) can be used to determine the normal component of velocity of the growing or receding ice-water interface Γ, v_Γ · n = ρ̄^ice/ρ^ice, where n is the unit outward normal to the ice surface.⁴ Therefore, the evolving geometry of the solid ice in response to chemical reactions at its surface is determined entirely by the motion of the interface Γ along its local unit outward normal, at a rate controlled by the local value of ρ̄^ice/ρ^ice.

The jump condition for linear momentum is given by

$$[[{\mathbf{\text{T}}}^{\alpha }-{\rho }^{\alpha }{\mathbf{\text{u}}}_{\Gamma }^{\alpha }\otimes {\mathbf{\text{u}}}_{\Gamma }^{\alpha }]]\mathbf{\text{n}}=-{\overline{p}}^{\alpha }$$ (42)

where p̄^α is the area density of momentum supply (units of force per area) representing a discontinuity in the momentum supply to constituent α across Γ. This discontinuity may arise from a number of different factors, including chemical processes. In formulating Eq.(42), it was assumed that the surface of discontinuity Γ is either immaterial or has negligible mass so that its linear momentum does not enter into the jump condition; furthermore, surface tension has been neglected.⁵ The momentum jump condition for the mixture is given by

$$[[\mathbf{\text{T}}-\rho {\mathbf{\text{u}}}_{\Gamma }\otimes {\mathbf{\text{u}}}_{\Gamma }]]\mathbf{\text{n}}=\mathbf{0}$$ (43)

from which it can be shown that

$$\sum _{\alpha }{\overline{\rho }}^{\alpha }=\mathbf{0}$$ (44)

The corresponding relations for angular momentum are

$$[[\mathbf{\text{x}}\times ({\mathbf{\text{T}}}^{\alpha }-{\rho }^{\alpha }{\mathbf{\text{u}}}_{\Gamma }^{\alpha }\otimes {\mathbf{\text{u}}}_{\Gamma }^{\alpha })]]\mathbf{\text{n}}=-\mathbf{\text{x}}\times {\overline{\mathbf{\text{p}}}}^{\alpha }-{\overline{\mathbf{\text{m}}}}^{\alpha }$$ (45)

$$[[\mathbf{\text{x}}\times (\mathbf{\text{T}}-\rho {\mathbf{\text{u}}}_{\Gamma }\otimes {\mathbf{\text{u}}}_{\Gamma })]]\mathbf{\text{n}}=\mathbf{0}$$ (46)

$$\sum _{\alpha }{\overline{\mathbf{\text{m}}}}^{\alpha }=\mathbf{0}$$ (47)

where m̄^α is the area density of angular momentum supply on Γ. It may include, but is not limited to, angular momentum supply imparted to constituent α from chemical reactions as it passes throughthe interface.

The interface jump conditions for energy satisfy

$$\left[\right[{\left({\mathbf{\text{T}}}^{\alpha }\right)}^{\mathit{T}}{\mathbf{\text{u}}}_{\Gamma }^{\alpha }-{\rho }^{\alpha }({\varepsilon }^{\alpha }+\frac{1}{2}{\mathbf{\text{u}}}_{\Gamma }^{\alpha }\cdot {\mathbf{\text{u}}}_{\Gamma }^{\alpha }){\mathbf{\text{u}}}_{\Gamma }^{\alpha }-{\mathbf{\text{q}}}^{\alpha }\left]\right]\cdot \mathbf{\text{n}}={\overline{\varepsilon }}^{\alpha }$$ (48)

$$\left[\right[{\mathbf{\text{T}}}^T{\mathbf{\text{u}}}_{\Gamma }-\rho (\varepsilon +\frac{1}{2}{\mathbf{\text{u}}}_{\Gamma }\cdot {\mathbf{\text{u}}}_{\Gamma }){\mathbf{\text{u}}}_{\Gamma }-\mathbf{\text{q}}\left]\right]\cdot \mathbf{\text{n}}=0$$ (49)

$$\sum _{\alpha }{\overline{\varepsilon }}^{\alpha }=\mathbf{0}$$ (50)

where ε̄^α is the area density of energy supply resulting from discontinuities across Γ, which may include energy supply to constituent α from chemical reactions on the interface.

From the entropy inequality, the interface jump condition for the mixture is given by

$$\sum _{\alpha }\left[\right[{\rho }^{\alpha }{\eta }^{\alpha }{\mathbf{\text{u}}}_{\Gamma }^{\alpha }+\frac{1}{\theta }{\mathbf{\text{q}}}^{\alpha }\left]\right]\cdot \mathbf{\text{n}}\le 0$$ (51)

or equivalently,

$$\left[\right[\rho \eta {\mathbf{\text{u}}}_{\Gamma }+\frac{1}{\theta }\mathbf{\text{h}}\left]\right]\cdot \mathbf{\text{n}}\le 0$$ (52)

Unlike the area density of mass supply ρ̄^α on Γ, which can be defined constitutively in a straightforward manner, the supply terms p̄^α, m̄^α and ε̄^α have contributions from multiple mechanisms which cannot be isolated until further constitutive assumptions are made, even in the absence of chemical reactions. Since the jump conditions onthe mixture, together with the mass jump conditions on individual constituents, are not sufficient to define a complete set of boundary conditions, it is necessary to make additional constitutive assumptions to help guide the formulation of appropriate jump conditions. Some common assumptions for biological tissues are provided in Section 3.6.

2.4 Incompressibility and Electroneutrality Constraints

The approach described in this section for enforcing constraints on a mixture is a generalization of that presented by several authors (Bowen, 1980; Lai et al, 1991; Huyghe and Janssen, 1997) to the case of reacting mixtures. We now consider the case where each of the mixture components is intrinsically incompressible, with constant and homogeneous true density ${\rho }_{\mathit{\text{T}}}^{\alpha }$ (which implies $D^{\alpha }{\rho }_T^{\alpha }/\mathit{\text{Dt}}=0$). The true density of constituent α is the ratio of mass to volume of the constituent. It is thus related to the apparent density via

$${\rho }^{\alpha }={\phi }^{\alpha }{\rho }_T^{\alpha }$$ (53)

where φ^α is the volume fraction of constituent α in the mixture, 0 ≤ φ^α ≤ 1. Substituting this relationinto the conservation of mass for each constituent, Eq.(4), taking the summation over all constituents and making use of the saturation condition⁶

$$\sum _{\alpha }{\phi }^{\alpha }=1$$ (54)

produces an alternative expression for the mixture conservation of mass,

$$\sum _{\alpha }\text{div}({\phi }^{\alpha }{\mathbf{\text{v}}}^{\alpha })-\frac{{\widehat{\rho }}^{\alpha }}{{\rho }_T^{\alpha }}=0$$ (55)

This expression, which can also be rearranged as

$$\sum _{\alpha }\frac{1}{{\rho }_T^{\alpha }}(\text{grad}{\rho }^{\alpha }\cdot {\mathbf{\text{u}}}^{\alpha }+{\rho }^{\alpha }\mathbf{\text{I}}:{\mathbf{\text{L}}}^{\alpha }-{\widehat{\rho }}^{\alpha })=0$$ (56)

represents a constraint on the mixture.

If a mixture conducts electricity, it satisfies the electroneutrality condition,

$$\sum _{\alpha }{z}^{\alpha }\frac{{\rho }^{\alpha }}{M^{\alpha }}=0$$ (57)

where z^α is the valence and M^α is the molecular weight of constituent α. In this treatment, we consider that that the net effect of all simultaneous chemical reactions which occur in a mixture is to preserve electroneutrality; thus, negative and positive charges are produced or removed at equal rates such that

$$\sum _{\alpha }{z}^{\alpha }\frac{{\widehat{\rho }}^{\alpha }}{M^{\alpha }}=0$$ (58)

This relation places a constraint on the supply terms ρ̂^α, which complements that of Eq.(8). Differentiating Eq.(57) with respect to time and using the conservation of mass for each mixture constituent, Eq.(4), along with Eq.(58) produces

$$\sum _{\alpha }\frac{z^{\alpha }}{M^{\alpha }}\text{div}({\rho }^{\alpha }{\mathbf{\text{v}}}^{\alpha })=0$$ (59)

Noting that

$${\mathbf{\text{I}}}_e\equiv F_c\sum _{\alpha }{z}^{\alpha }\frac{{\rho }^{\alpha }}{M^{\alpha }}{\mathbf{\text{v}}}^{\alpha }$$ (60)

is the electrical current density, where F_c is Faraday's constant, we find from Eq.(59) that the current density is divergence free in the presence of chemical reactions which preserve electroneutrality,

$$\text{div}{\mathbf{\text{I}}}_e=0$$ (61)

consistent with the equation of conservation of charge derived from Maxwell's equations. Multiplying the jump condition on the mass, Eq.(37), with F_cz^α/M^α, taking the sum of the resulting relation over all constituents, assuming that chemical reactions on an interface Γ preserve electroneutrality,

$$\sum _{\alpha }\frac{z^{\alpha }}{M^{\alpha }}{\overline{\rho }}^{\alpha }=0$$ (62)

and making use of Eqs.(57) and (60), produces a jump condition on the current density,

$$[[{\mathbf{\text{I}}}_e]]\cdot \mathbf{\text{n}}=0$$ (63)

Taking the dot product of the gradient of Eq.(57) with the mean velocity v and subtracting the result from Eq. (59) yields the constraint equation

$$\sum _{\alpha }\frac{z^{\alpha }}{M^{\alpha }}({\rho }^{\alpha }{\mathbf{\text{L}}}^{\alpha }:\mathbf{\text{I}}+{\mathbf{\text{u}}}^{\alpha }\cdot \text{grad}{\rho }^{\alpha })=0$$ (64)

The incompressibility constraint of Eq.(56) and the above electroneutrality constraint canbe introduced into the entropy inequality of Eq.(36) using Lagrange multipliers. As shown in previous studies (Bowen, 1980; Huyghe and Janssen, 1997), the multiplier for the incompressibility constraint represents a pressure p, while that for the electroneutrality constraint is F_cψ, where ψ is an electric potential,

$$\sum _{\alpha }-{\rho }^{\alpha }(\frac{D^{\alpha }{\psi }^{\alpha }}{\mathit{\text{Dt}}}+{\eta }^{\alpha }\frac{D^{\alpha }\theta }{\mathit{\text{Dt}}})-\frac{1}{\theta }{\mathbf{\text{q}}}^{\alpha }.\text{grad}\theta +[{\mathbf{\text{T}}}^{\alpha }+{\rho }^{\alpha }\left(\frac{p}{{\rho }_T^{\alpha }}+\frac{z^{\alpha }}{M^{\alpha }}{F}_c\psi \right)\mathbf{\text{I}}]:{\mathbf{\text{L}}}^{\alpha }-[{\widehat{\mathbf{\text{p}}}}^{\alpha }-(\frac{p}{{\rho }_T^{\alpha }}+\frac{z^{\alpha }}{M^{\alpha }}{F}_c\psi )\text{grad}{\rho }^{\alpha }\left]\right]\cdot {\mathbf{\text{u}}}^{\alpha }-{\widehat{\rho }}^{\alpha }({\psi }^{\alpha }+\frac{p}{{\rho }_T^{\alpha }}+\frac{1}{2}{\mathbf{\text{u}}}^{\alpha }\cdot {\mathbf{\text{u}}}^{\alpha })\ge 0$$ (65)

Had the mixture not been assumed to satisfy electroneutrality, it would carry a net electrical charge density ρ_e ≠ 0 whose time-rate-of-change would enter into the equation of conservation of charge, Eq.(61), consistent with Maxwell's equations of electromagnetism. The mixture would also be subjected to a net body force in the presence of electromagnetic fields.

In this treatment it is assumed that externally applied and self-induced magnetic fields exhibit negligible temporal and spatial variations, which precludes the need for Maxwell's equations which involve the magnetic field (the absence of magnetic monopoles, and Faraday's law of induction). The remaining equation, Gauss's law, states that the electric displacement vector, which is the sum of the electric field and polarization vectors, is divergence-free in an electroneutral mixture. Ionic polarization arises from the relative displacement of ions carrying opposite charges (Dugdale, 1993), and the resulting polarization vector is not divergence-free; therefore neither is the electric field grad ψ, so that ∇²ψ ≠ 0 in general.

3 Constitutive Restrictions

In this section a constitutive relation is formulated for the Helmholtz free energy of a reactive mixture. Some early work on this topic was presented by Bowen (1968) and reviewed by Truesdell (1984), which addressed mixtures of non-diffusing constituents (no relative motion among constituents). In a subsequent study Bowen (1969) formulated a framework for reacting and diffusing mixtures where no explicit distinction was made between the solids and fluids in the constitutive formulation of the Helmholtz free energy function. In that treatment, no particular consideration was given to growth and remodeling of the solid constituents. Conversely, a number of classical studies have explored growth and remodeling of tissues modeledas solids (Skalaketal, 1982; Cowin, 1983; Rodriguez et al, 1994), with no explicit reference to chemical reactions. More recently, studies have combined mixture analysis with chemical reactions (Humphrey and Rajagopal, 2002; Klisch et al, 2003; Garikipati et al, 2004), though they have been applied in narrower contexts than presented here.

In addition, a constitutive relation is formulated for the momentum supply among the diffusing constituents of a mixture, in the presence of chemical reactions.

3.1 Mixture of Solid and Fluid Constituents

Consider that the mixture consists of m solid and n fluid constituents. With only limited loss of generality, assume that there is no relative motion among the solid constituents, so that their individual velocities v^σ (σ = 1 to m) are equal at all times, and representedby v^s.⁷ There is a benefit to modeling the solid matrix of biological tissues as a constrained heterogeneous mixture of solid constituents (Humphrey and Rajagopal, 2002), such as collagen, elastin, proteoglycans, etc.⁸ To maintain consistency with the equations of conservation of mass, it follows that the density ρ^s, volume fraction φ^s and mass supply terms ρ̂^s of the mixture of solid constituents are given by

$${\rho }^s=\sum _{\sigma =1}^m{\rho }^{\sigma }{\phi }^s=\sum _{\sigma =1}^m{\phi }^{\sigma }{\widehat{\rho }}^s=\sum _{\sigma =1}^m{\widehat{\rho }}^{\sigma }$$ (66)

Note that unlike the true density of its individual constituents, the true density of the solid mixture,

$${\rho }_T^s=\frac{1}{{\phi }^s}\sum _{\sigma =1}^m{\phi }^{\sigma }{\rho }_T^{\sigma }$$ (67)

is not constant in the presence of chemical reactions since the proportion φ^σ/φ^s of each constituent of the solid matrix may vary over time and at various locations. Since the conservation of mass for the whole solid mixture is not needed in any analysis (only that for each solid constituent), there is no adverse consequence to this observation. However, this is an insightful observation because classical porous media studies of intrinsically incompressible constituents which include only one solid constituent constrain the analyst to assume that the solid is homogeneous in order not to violate the intrinsic incompressibility assumption. The above result shows that modeling the solid matrix as a mixture does not impose this constraint, even while the individual solid constituents have a constant and homogeneous true density.

3.2 Surface growth and volume growth

There are two kinds of growth processes which can be described in continuum theory: Surface (orappositional) growth, and volume (or interstitial) growth. Surface growth of the solid matrix occurs when ρ̄^s ≠ 0 on an interface Γ, whereas volume growth occurs when ρ̂^s ≠ 0 in the body. Surface growth redefines the boundary of the solid matrix as addressed in Section 2.3, whereas volume growth may change the local apparent density ρ^s of the solid. Given that ${\rho }^s={\phi }^s{\rho }_T^s$, volume growth implies primarily that φ^s may be changing; in other words, the pore volume of the solid matrix increases or decreases during volume growth. As described in the previous section however, ${\rho }_T^s$ may also change with chemical reactions when the solid matrix consists of a mixture of more than one solid constituent.

When ρ̂^s < 0, it is possible through volume resorption to reduce the solid matrix apparent density to zero at locations inside the body, ρ^s = 0, potentially creating internal cavities and altering the body's topology. We can refer to the opening of a cavity inside the volume as cavitation. Importantly, cavitation does not imply the appearance of a region of vacuum inside the mixture; it simply means that the mixture in a cavity consists only of fluids, as the solid volume fraction reduces to zero, φ^s → 0.⁹ Conversely, we can refer to the process of solid volume growth in a neighborhood initially occupied only by fluid constituents as nucleation.

In general, despite suggestions from earlier studies, neither surface growth nor volume growth is fully amenable to a description using a deformation gradient or growth tensor. In the case of surface growth, the evolving solid boundary may recruit new material point or release others. Thus, in the intuitive example of freezing water, molecules of ice are gained from liquid water as the solid-liquid boundary evolves. In other words, new solid regions may be formed which do not correspond to previously existing solid material points. Therefore, a one-to-one spatial mapping of material points from a reference time to the current time is not possible over the entire solid matrix, nullifying the usefulness of a growth tensor. In the case of volume growth, one-to-one mapping is possible only if there is no cavitation or nucleation; otherwise, the connectivity of the solid matrix may change, rendering the mapping non-invertible and meaningless. Since the applicability of a growth tensor is limited, a framework which does not rely upon it is preferable.

3.3 Reference Configuration

For the fluid constituents the reference configuration is taken to be the current configuration. In classical solid mechanics, in the absence of chemical reactions which can produce or remove mass from the solid constituent, it is common to define the reference state of the solid as a traction-free or stress-free state at the time origin. In the more general treatment of growth and remodeling, more subtle descriptions of the reference configuration have been proposed. Since the early work of Hsu (1968), Cowin and Hegedus (1976) and Skalak et al (1982), considerable advances have been made in the field of growth and remodeling of biological tissues. Some of the recent developments address various challenges in the identification of natural reference configurations for the tissue, whether modeled as a single solid constituent (Rodriguez et al, 1994; Chen and Hoger, 2000; Guillou and Ogden, 2006), a mixture of solid constituents (Humphrey and Rajagopal, 2002, 2003), or a mixture of solid and fluid constituents (Klisch et al, 2003).

The present treatment of the reference configuration will deviate somewhat from these prior studies for two principal reasons. First, since the use of a one-to-one mapping for tracking growth is considered either too restrictive or inappropriate for some applications, as reviewed in the previous section, the concomitant assumption that the deformation gradient F^s = ∂x/∂X^s canbeconstructed from the convolution of an elastic deformation and a growth deformation relative to a reference configuration suffers from the same limitations. Second, in the alternative approach which considers that the natural configuration κ_n (t) of the solid matrix evolves with time so that F^s may be evaluated via ∂x/∂x_κn, the governing equations to solve for the evolving reference configuration have not been made explicit.

Based on these concerns this study adopts a more conventional approach, with an extension to account for mass deposition and removal. The basic premise is that the reference configuration of a material point is immutable; there cannot be any evolution in this configuration. What evolves is the set of material points describing the body, since material points may be added or removed as a result of growth. This immutability is necessary so that the place X^s of a material point in the reference configuration remains constant, or else the kinematics of the continuum can no longer be described by the standard approach. This approach does not preclude tissue remodeling, which can be described by an evolution of the material texture as presented below. However, changes in material texture at a material point do not alter its reference place X^s. The reference configuration of a material point is defined at the time it is deposited. In practice, if the initial time of material deposition is not known, the reference configuration may be selected as the (typically traction-free) state of the body at some arbitrary time t₀, representing the time origin for the purposes ofthat analysis.

The general analysis presented in this paper applies to surface growth and volume growth. Surface growth implies the deposition of new material points onto an existing body.

Therefore the reference configuration of these new material points must be defined at the time of surface growth. Volume growth implies changes in the apparent density at an existing material point, whose reference configuration was already determined at an earlier time (when it was deposited by surface growth). Thus, exceptforthe case of nucleation, only surface growth requires an explicit definition of the reference configuration.

The capture and release of solid material points by surface growth is determinedby Eq.(37), specialized to the case of solid constituents. Since the normal component of solid velocity is continuous at an interface Γ,¹⁰

$$[[{\mathbf{\text{v}}}^s]]\cdot \mathbf{\text{n}}=0$$ (68)

the specialization of Eq.(37) to the solid matrix yields

$$({\mathbf{\text{v}}}_{\Gamma }-{\mathbf{\text{v}}}^s)\cdot \mathbf{\text{n}}=\frac{{\overline{\rho }}^s}{[[{\rho }^s]]}\equiv {\xi }^s$$ (69)

where it is understood from Eqs.(37) and (68) that [[ρ^s]] = 0 implies ρ̄^s = 0 and (v_Γ - v^s) ⋅ n = 0, or equivalently, ξ^s = 0. When ξ^s > 0, the region whose outward normal is n is gaining solid material points; when ξ^s < 0, solid material points are being lost. The relation of Eq.(69) applies even when there is solid matrix only on one side of the interface Γ, in which case [[ρ^s]] = ρ^s.

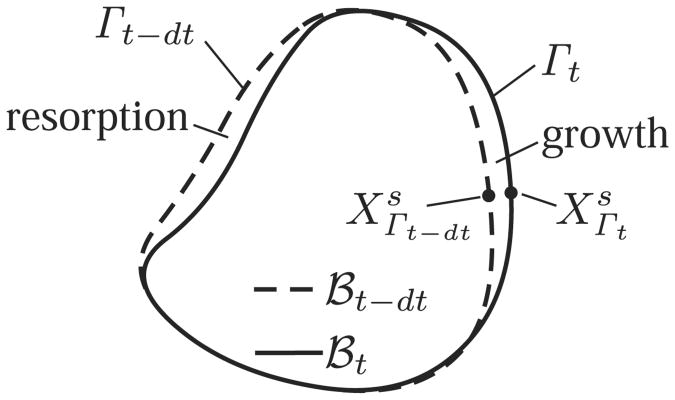
Let ℬ represent the set of solid material points X^s in the body. Since material points may be added or removed from the body at different time points, the point set ℬ is not fixed, unlike the conventional approach of solid mechanics. Therefore, let ℬ_t represent the material point set at time t. In general, due to growth, ℬ_t ≠ ℬ_τ when t ≠ τ. Similarly, let Γ_t represent a surface growth boundary on ℬ_t (Figure 1).

Figure 1.

Point sets defining the body ℬ at consecutive time points t − dt and t. Due to surface growth or resorption, ℬ_{t − dt} and ℬ_t do not contain the same material points.

Let a material point which is on Γ_t-dt be denoted by $X_{{\Gamma }_{t-\mathit{\text{dt}}}}^s$. At a subsequent time t, as a result of surface growth, $X_{{\Gamma }_{t-\mathit{\text{dt}}}}^s$ is no longer on the boundary; however a new material point $X_{{\Gamma }_t}^s\in {\Gamma }_t$ has been added to the body ℬ_t whose position in the current configuration is deduced from Eq.(69),

$${\mathbf{\chi }}^s(X_{{\Gamma }_t}^s,t)={\mathbf{\chi }}^s(X_{{\Gamma }_{t-\mathit{\text{dt}}}}^s,t-\mathit{\text{dt}})+{\mathbf{\text{v}}}^s(X_{{\Gamma }_{t-\mathit{\text{dt}}}}^s,t-\mathit{\text{dt}})\mathit{\text{dt}}+{\xi }^s(X_{{\Gamma }_{t-\text{dt}}}^s,t-\text{dt})\mathbf{\text{n}}(X_{{\Gamma }_{t-\mathit{\text{dt}}}}^s,t-\mathit{\text{dt}})\mathit{\text{dt}}$$ (70)

This relation indicates that in the absence of surface growth, ξ^s = 0, the material point $X_{{\Gamma }_t}^s$ is the same as $X_{{\Gamma }_{t-\mathit{\text{dt}}}}^s$, and the above relation would simply summarize the motion of that material point arising from the solid matrix velocity. If ξ^s < 0 the body is in fact losing the material point $X_{{\Gamma }_{t-\mathit{\text{dt}}}}^s$, and $X_{{\Gamma }_t}^s$ actually represents a material point already in the body ℬ_t−dt but not on its boundary Γ_t−dt, now being exposed on Γ_t. These are semantic distinctions between deposition and removal, but the mathematical analysis remains the same.

For a smooth boundary there is a one-to-one relation between Γ_t-dt and Γ_t and thus a one-to-one relation between the material points $X_{{\Gamma }_{t-\mathit{\text{dt}}}}^s$ and $X_{{\Gamma }_t}^s$, which is represented by Eq.(70). This one-to-one relation persists over sequential generations of material point deposition or resorption, unless Γ_t collapses on itself (complete resorption of the solid body), self-intersects (separation of the body into multiple regions), or intersects with the boundary of another body (merging of two regions). Therefore, in-between such special events, Eq.(70) can be generalized to

$${\mathbf{\chi }}^s(X_{{\Gamma }_t}^s,t)={\mathbf{\chi }}^s(X_{{\Gamma }_{t0}}^s,t_0)+\underset{t_0}{\overset{t}{\int }}[{\mathbf{\text{v}}}^s(X_{{\Gamma }_{\tau }}^s,\tau )+{\xi }^s(X_{{\Gamma }_{\tau }}^s,\tau )\mathbf{\text{n}}(X_{{\Gamma }_{\tau }}^s,\tau )]d\tau$$ (71)

where t₀ represents some initial time for the analysis of interest. In this relation $X_{{\Gamma }_{\tau }}^s$ represents a family of material points either deposited onto or exposed on the surface, over the period t₀ ≤ τ ≤ t.

The process of nucleation, which is initiated by volume growth at a point initially containing only fluid constituents, deposits a solid material point X^s at some time t, which initiates the definition of the point set ℬ.¹¹ Subsequently, the boundary of this nucleating region may expand by surface growth (not by volume growth, which only implies that the apparent density ρ^s of the solid material points X^s inside ℬ evolves over time). Thus the above analysis applies for surface growth emanating from a site of nucleation.

This presentation demonstrates that the current configuration of the boundary of a solid matrix undergoing surface growth is uniquely defined by Eq.(71). This equation accounts for the conditions prevailing at the interface Γ_t via the constitutive dependence of ξ^s on these conditions. However, absent from this relation is information about the reference configuration of material points deposited into ℬ_t, as addressed next.

The reference configuration of a material point $X_{{\Gamma }_t}^s$ deposited on Γ_t at time t depends on modeling assumptions. Since the current configuration is known, it is more convenient to define the deformation gradient F^s ( $X_{{\Gamma }_t}^s$, t), and then determine the place ${\mathbf{\text{X}}}_{{\Gamma }_t}^s$ of the material point $X_{{\Gamma }_t}^s$ in the reference configuration by inversion of the relation

$$d\mathbf{\text{x}}={\mathbf{\chi }}^s(X_{{\Gamma }_t}^s,t)-{\mathbf{\chi }}^s(X_{{\Gamma }_{t-\mathit{\text{dt}}}}^s,t)={\mathbf{\text{F}}}^s\cdot d{\mathbf{\text{X}}}^s={\mathbf{\text{F}}}^s(X_{{\Gamma }_t}^s,t)\cdot ({\mathbf{\text{X}}}_{{\Gamma }_t}^s-{\mathbf{\text{X}}}_{{\Gamma }_{t-\mathit{\text{dt}}}}^s)$$ (72)

to yield the reference place of $X_{{\Gamma }_t}^s$ relative to that of the preceding point $X_{{\Gamma }_{t-\mathit{\text{dt}}}}^s$ in the genealogy. Since F^s ( $X_{{\Gamma }_t}^s$, t) is proposed by modeling assumptions, let's consider the three most representative cases:

(a) Inherited Strain

F^s ( $X_{{\Gamma }_t}^s$, t) is inherited from the nearest ancestor $X_{{\Gamma }_{t-\mathit{\text{dt}}}}^s$ via

$${\mathbf{\text{F}}}^s(X_{{\Gamma }_t}^s,t)={\mathbf{\text{F}}}^s(X_{{\Gamma }_{t-\mathit{\text{dt}}}}^s,t-\mathit{\text{dt}})+\frac{\partial \mathbf{\text{F}}}{\partial t}\mathit{\text{dt}}+\left(\text{grad}\mathbf{\text{F}}\right)d\mathbf{\text{x}}$$ (73)

where dx is given in Eq.(72), and ∂F/∂t and grad F are evaluated at ( $X_{{\Gamma }_{t-\mathit{\text{dt}}}}^s$, t − dt). According to this relation, F^s is a continuous function across Γ_t−dt. This modeling assumption applies to problems where surface growth occurs without producing additional residual stresses upon unloading. It also applies to surface resorption, when $X_{{\Gamma }_t}^s$ is a material point originally inside the body, which now is exposed on its boundary Γ_t.

(b) Stress-Free Growth

F^s ( $X_{{\Gamma }_t}^s$, t) is prescribed to be equal to I, on the basis that the new material region Γ_t−Γ_t−dt being deposited on Γ_t−dt is in a stress-free state. Then, according to Eq.(72), the reference place of $X_{{\Gamma }_t}^s$ is given by

$${\mathbf{\text{X}}}_{{\Gamma }_t}^s={\mathbf{\text{X}}}_{{\Gamma }_{t-\mathit{\text{dt}}}}^s+d\mathbf{\text{x}}={\mathbf{\text{X}}}_{{\Gamma }_{t-\mathit{\text{dt}}}}^s+{\mathbf{\chi }}^s({\mathit{\text{X}}}_{{\Gamma }_t}^s,t)-{\mathbf{\chi }}^s(X_{{\Gamma }_{t-\mathit{\text{dt}}}}^s,t)$$ (74)

This case applies to analyses where the newly-growing region is unaffected by the prior state of strain on Γ_t−dt (no inheritance). Therefore, this case generally implies that there will be a jump in F^s across Γ_t−dt (unless Γ_t−dt happened to be in a stress-free state at the time of new material deposition). It also implies that, generally, the traction-free configuration of ℬ_t will be residually stressed.

(c) Adhesion of Pre-Formed Material

F^s ( $X_{{\Gamma }_t}^s$, t) is prescribed such that it will conform the newly deposited material region Γ_t − Γ_t−dt from a known stress-free configuration to the shape of Γ_t−dt in the current configuration. This case applies to problems where surface growth occurs by adhesion of a pre-formed material region to the body under consideration. For example, a layer of tissue-engineered skin, originally in a stress-free state, is stretched to conform to a graft region, onto which it is adhered. This problem can be viewed as a surface growth of the graft region. In this case as well, there will be a jump in F^s across Γ_t−dt.

Depending on the mode of surface growth and the evolution of growth and resorption, the above presentation implies that discontinuities in the spatial distribution of the reference place X^s of material points in the body may occur, even though the motion χ^s (X^s, t) is always continuous. Consequently, the deformation gradient F^s = ∂χ^s/∂X^s and the corresponding right Cauchy-Green tensor C^s = (F^s)^T F^s may be only piecewise-continuous; however there is no adverse consequence to this outcome, which is common in classical elasticity, such as at the interface of two dissimilar solids.

As usual, the reference configuration may be hypothetical in the sense that the material may never pass through that state in a given history. In all cases, the place X^s of a material point X^s is defined at the time of deposition and remains constant. Thus, in this framework, the reference configuration does not evolve with time. Since X^s for each material point is constant, the conventional kinematic analysis of a continuum can be applied.

The deformation gradient of the solid matrix, F^s, and the corresponding right Cauchy-Green tensor C^s are measures of deformation relative to the reference configuration. To help distinguish between changes in density from growth and deformation at a point, it is convenient to define the solid density in the reference configuration, ${\rho }_r^s$, where

$${\rho }_r^s=J^s{\rho }^s{J}^s=\text{det}{\mathbf{\text{F}}}^s$$ (75)

This approach was adopted by Bowen (1969) in his study of reactive mixtures and by several authors subsequently (Klisch et al, 2003; Guillou and Ogden, 2006).¹² Using Eqs.(4) and (75), it can be shown that

$$\frac{D^s{\rho }_r^s}{\mathit{\text{Dt}}}={\widehat{\rho }}_r^s$$ (76)

where

$${\widehat{\rho }}_r^s=J^s{\widehat{\rho }}^s$$ (77)

It follows from these relations that the solid matrix density can be represented as ρ^s = ρ^s (C^s, ${\rho }_r^s$) and that

$$\frac{\partial {\rho }^s}{\partial {\mathbf{\text{C}}}^s}=-\frac{{\rho }^s}{2}{({\mathbf{\text{C}}}^s)}^{-1}$$

In the limiting case of an inert solid matrix (ρ̂^s = 0), ${\rho }_r^s$ is constant and ρ^s = ρ^s (C^s).

By the definitions of Eqs.(53) and (75), it is evident that

$$0\le {\rho }_r^s(\mathbf{\text{x}},t)\le {\rho }_T^s$$ (78)

The lower bound of zero implies that solid matrix is not present at that location and time (φ^s = 0), whereas the upper bound of ${\rho }_T^s$ implies that the mixture consists entirely of solid matrix (φ^s = 1). The relations of Eqs.(75)-(78) are equally applicable to the individual solid constituents σ of the solid matrix. A practical implication of this presentation is that the spatial distribution of solid matrix content (and thus, the evolution of the solid matrix geometry) can be deduced from the scalar function ${\rho }_r^s(\mathbf{\text{x}},t)$. Because of the presence of fluid constituents, this framework can conceivably describe a continuum which grows a solid matrix from an initial state with no solid content (nucleation), or equally, one where the solid content reduces to zero (cavitation).

It is evident that the density of the solid matrix constituents changes in response to two driving factors: deformation and growth. Deformation can be factored out by using ${\rho }_r^s$ instead of ρ^s, leaving the rate of growth to be described by ${\widehat{\rho }}_r^s$ which is simply the material derivative of ${\rho }_r^s$. Clearly, the function ${\widehat{\rho }}_r^s$ would need to be provided by a constitutive relation (Bowen, 1969).

By a similar analogy, it is possible to describe the material texture of the solid matrix as being dependent on the same two factors. For example, if a specific material texture were described by the texture tensor A^s = a^s ⊗ a^s, where a^s is a unit vector along a preferred material direction in the current configuration, the corresponding material texture in the reference configuration would be given by ${\mathbf{\text{A}}}_r^s={\mathbf{\text{a}}}_r^s\otimes {\mathbf{\text{a}}}_r^s$, where ${\mathbf{\text{a}}}^{\text{s}}={\mathbf{\text{F}}}^s{\mathbf{\text{a}}}_r^s/\Vert {\mathbf{\text{F}}}^s{\mathbf{\text{a}}}_r^s\Vert$. The evolution of ${\mathbf{\text{A}}}_r^s$ as a result of chemical reactions, which represents remodeling (Guillou and Ogden, 2006), could thus be given by the function ${\widehat{\mathbf{\text{A}}}}_r^s\equiv D^s{\mathbf{\text{A}}}_r^s/\mathit{\text{Dt}}$, which should be provided by a constitutive relation.

3.4 State Variables

We are now ready to propose a set of state variables for the constitutive relations needed in this analysis. For ψ^α, η^α, T^α, q^α,p̂^α, ρ̂^α, ${\widehat{\mathbf{\text{A}}}}_r^s$, ρ̄^α, p̄^α, and ε̄^α represented generically by f^α, we have

$$f^{\alpha }=f^{\alpha }(\theta ,\mathbf{\text{g}},{\mathbf{\text{C}}}^s,{\mathbf{\text{G}}}^s,{\rho }_r^s,{\mathbf{\text{d}}}_r^s,{\mathbf{\text{A}}}_r^s,{\rho }^{\gamma },{\mathbf{\text{d}}}^{\gamma },{\mathbf{\text{L}}}^{\beta },{\mathbf{\text{u}}}^{\beta })\gamma \ne s$$ (79)

Here, g = grad θ, G^s = grad C^s (a third-order tensor), ${\mathbf{\text{d}}}_r^s=\text{grad}{\rho }_r^s$ and d^γ = grad ρ^γ. This type of constitutive relation represents materials devoid of memory (Truesdell and Noll, 1992), able to describe thermoelasticity and viscoelasticity of the Voigt type (Bowen, 1968). While this list of dependent variables seems daunting, it is justified by our effort to consider both solid and fluid constituents (hence the need for C^s, ${\rho }_r^s$ and ${\mathbf{\text{A}}}_r^s$ for the solid, and ρ^γ for the fluids), and the fact that the entropy inequality of Eq.(65) involves the gradient of the densities (hence the need for G^s and ${\mathbf{\text{d}}}_r^s$ for the solid, and d^γ for the fluids) as well as L^β and u^β.

Taking the material derivative of ψ^α and substituting the result into Eq.(65), as shown in the Appendix, it is found that the entropy inequality is satisfied if and only if

$${\eta }^{\alpha }=-\frac{\partial {\psi }^{\alpha }}{\partial \theta }$$ (80)

$$\frac{\partial {\Psi }^{\alpha }}{\partial \mathbf{\text{g}}}=\mathbf{0}\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{G}}}^s}=\mathbf{0}\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{d}}}^{\gamma }}=\mathbf{0}\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{L}}}^{\beta }}=\mathbf{0}\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{u}}}^{\beta }}=\mathbf{0}$$ (81)

$${\mathbf{\text{T}}}^s=-{\rho }^s(\frac{p}{{\rho }_T^s}+\frac{z^s}{M^s}{F}_c\psi -{\psi }^s)\mathbf{\text{I}}+2{\mathbf{\text{F}}}^s\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{C}}}^s}{(F^s)}^T+{\mathbf{\text{T}}}_d^s$$ (82)

$${\mathbf{\text{T}}}^{\gamma }=-{\rho }^{\gamma }({\stackrel{\sim }{\mu }}^{\gamma }-{\psi }^{\gamma })\mathbf{\text{I}}+{\mathbf{\text{T}}}_d^{\gamma }\gamma \ne s$$ (83)

$${\widehat{\mathbf{\text{p}}}}^s={\text{grad}}^T{\mathbf{\text{d}}}_r^s\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{d}}}_r^s}+\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{A}}}_r^s}:\text{grad}{\mathbf{\text{A}}}_r^s+{\stackrel{\sim }{\mu }}^s\text{grad}{\rho }^s-\text{grad}{\Psi }^s+\frac{\partial {\Psi }^s}{\partial \theta }\mathbf{\text{g}}+{\widehat{\mathbf{\text{p}}}}_d^s$$ (84)

$${\widehat{\mathbf{\text{p}}}}^{\gamma }={\stackrel{\sim }{\mu }}^{\gamma }{\mathbf{\text{d}}}^{\gamma }-\text{grad}{\Psi }^{\gamma }+\frac{\partial {\psi }^{\gamma }}{\partial \theta }\mathbf{\text{g}}+{\widehat{\mathbf{\text{p}}}}_d^{\gamma }\gamma \ne s$$ (85)

$$\sum _{\alpha }{\widehat{\mathbf{\text{p}}}}_{\mathbf{\text{d}}}^{\alpha }\cdot {\mathbf{\text{u}}}^{\alpha }-{\mathbf{\text{T}}}_d^{\alpha }:{\mathbf{\text{L}}}^{\alpha }+{\widehat{\rho }}^{\alpha }({\mu }^{\alpha }+\frac{1}{2}{\mathbf{\text{u}}}^{\alpha }\cdot {\mathbf{\text{u}}}^{\alpha })+\frac{1}{\theta }{\mathbf{\text{q}}}^{\alpha }\cdot \mathbf{\text{g}}+\frac{2{\widehat{\rho }}^s}{{\rho }^s}\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{C}}}^s}:{\mathbf{\text{C}}}^s+\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{d}}}_r^s}\cdot \text{grad}{\widehat{\rho }}_r^s+\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{A}}}_r^s}:{\widehat{\mathbf{\text{A}}}}_r^s\le 0$$ (86)

where

$${\Psi }^{\alpha }={\rho }^{\alpha }{\psi }^{\alpha }$$ (87)

is the Helmholtz free energy density of constituent α,

$${\Psi }^I=\sum _{\alpha }{\Psi }^{\alpha }$$ (88)

is the inner part of the mixture Helmholtz free energy density,

$${\mu }^{\alpha }=\frac{p}{{\rho }_T^{\alpha }}+\frac{\partial {\Psi }^I}{\partial {\rho }^{\alpha }}$$ (89)

is the chemical potential and

$${\stackrel{\sim }{\mu }}^{\alpha }={\mu }^{\alpha }+\frac{z^{\alpha }}{M^{\alpha }}{F}_c\psi$$ (90)

is the electrochemical potential of constituent α. ${\mathbf{\text{T}}}_d^{\alpha }$ are stresses which may represent dissipative mechanisms such as viscous stresses; similarly, ${\widehat{\mathbf{\text{p}}}}_d^{\alpha }$ are dissipative momentum supply terms which represent frictional drag acting on constituent α due to all other constituents. ${\mathbf{\text{T}}}_d^{\alpha }\text{and}{\widehat{\mathbf{\text{p}}}}_d^{\alpha }$ are generally dependent on the state variables outlined in Eq.(80). Based on the above relations it is found that the inner part of the mixture Helmholtz free energy density is given by

$${\Psi }^I={\Psi }^I(\theta ,{\mathbf{\text{C}}}^s,{\rho }_r^s,{\mathbf{\text{d}}}_r^s,{\mathbf{\text{A}}}_r^s,{\rho }^{\gamma })$$ (91)

We also note that the inner part of the total stress is given by

$${\mathbf{\text{T}}}^I=\sum _{\alpha }{\mathbf{\text{T}}}^{\alpha }=-(p-{\Psi }^I+\sum _{\gamma \ne s}{\rho }^{\gamma }\frac{\partial {\Psi }^I}{\partial {\rho }^{\gamma }})\mathbf{\text{I}}+2{\mathbf{\text{F}}}^s\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{C}}}^s}{({\mathbf{\text{F}}}^s)}^{\mathbf{\text{T}}}+\sum _{\alpha }{\mathbf{\text{T}}}_d^{\gamma }$$ (92)

and the momentum supplies satisfy

$$\sum _{\alpha }{\widehat{\mathbf{\text{p}}}}^{\alpha }=\sum _{\alpha }{\widehat{\mathbf{\text{p}}}}_d^{\alpha }$$ (93)

where we have made use of the mixture saturation and electroneutrality conditions. The form of Eq.(92) can be further simplified by following the approach advocated by Biot (1972) and adopted by Bowen (1980), whereby the Helmholtz free energy density is expressed relative to the volume of the mixture in the reference configuration, ${\Psi }_r^I$, where

$${\Psi }_r^I(\theta ,{\mathbf{\text{C}}}^s,{\rho }_r^s,{\mathbf{\text{d}}}_r^s,{\mathbf{\text{A}}}_r^s,{\rho }_r^{\gamma })=J^s{\Psi }^I(\theta ,{\mathbf{\text{C}}}^s,{\rho }_r^s,{\mathbf{\text{d}}}_r^s,{\mathbf{\text{A}}}_r^s,{\rho }^{\gamma })\gamma \ne s$$ (94)

and the fluid densities are similarly evaluated in the reference configuration,

$${\rho }_r^{\gamma }=J^s{\rho }^{\gamma }\gamma \ne s$$ (95)

It can be shown that

$$\frac{\partial {\Psi }^I}{\partial \theta }=\frac{1}{J^s}\frac{\partial {\Psi }_r^I}{\partial \theta }\frac{\partial {\Psi }^I}{\partial {\rho }_r^s}=\frac{1}{J^s}\frac{\partial {\Psi }_r^I}{\partial {\rho }_r^s}\frac{\partial {\Psi }^I}{\partial {\rho }^{\gamma }}=\frac{\partial {\Psi }_r^I}{\partial {\rho }_r^{\gamma }}\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{d}}}_r^s}=\frac{1}{J^s}\frac{\partial {\Psi }_r^I}{\partial {\mathbf{\text{d}}}_r^s}\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{A}}}_r^s}=\frac{1}{J^s}\frac{\partial {\Psi }_r^I}{\partial {\mathbf{\text{A}}}_r^s}\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{C}}}^s}=\frac{1}{J^s}[\frac{\partial {\Psi }_r^I}{\partial {\mathbf{\text{C}}}^s}-({\Psi }^I-\sum _{\gamma \ne s}{\rho }^{\gamma }\frac{\partial {\Psi }_r^I}{\partial {\rho }_r^{\gamma }}\left)\frac{\partial J^s}{\partial {\mathbf{\text{C}}}^s}\right]$$ (96)

so that

$${\mathbf{\text{T}}}^I=-p\mathbf{\text{I}}+\frac{2}{{\mathit{J}}^s}{\mathbf{\text{F}}}^s\frac{\partial {\Psi }_r^I}{\partial {\mathbf{\text{C}}}^s}{({\mathbf{\text{F}}}^s)}^T+\sum _{\alpha }{\mathbf{\text{T}}}_d^{\alpha }$$ (97)

In this standard form, the inner part of the total mixture stress reduces to the sum of a hydrostatic fluid pressure term, a hyperelastic solid stress, and stresses which may include viscous effects. With this representation, the chemical potential of the fluid constituents is given by

$${\mu }^{\gamma }=\frac{p}{{\rho }_T^{\gamma }}+\frac{\partial {\Psi }_r^I}{\partial {\rho }_r^{\gamma }}\gamma \ne s$$ (98)

The residual entropy inequality of Eq.(86) summarizes the irreversible mechanisms that may arise in the class of mixtures considered here, which include dissipative stresses, frictional drag between constituents, heat flow, and chemical reactions involving mass supply and solid matrix remodeling. This inequality serves as the basis for formulating acceptable constitutive relations for ${\mathbf{\text{T}}}_d^{\alpha },{\widehat{\mathbf{\text{p}}}}_d^{\alpha }$, and q^α. It also expresses the conditions which must prevail in order for a chemical reaction to proceed. For example, standard biology and physical biochemistry textbooks (Tinoco Jr. et al, 1995; van Holde et al, 1998; Alberts et al, 2002) state that a chemical reaction can proceed spontaneously at constant temperature and pressure only if the net change in the Gibbs free energy G of a system is negative (ΔG < 0); the reaction is in equilibrium when ΔG = 0. The Gibbs free energy density is the sum of the chemical potentials of all the constituents, weighted by their density (Σ_α ρ^α μ^α). This statement rests on a number of assumptions (sometimes implicit) which we can clarify in the context of Eq.(86). First, in the elementary textbook treatment, it is assumed that isothermal conditions prevail in most biological reactions (g = 0); second, it is implicitly assumed that all reactants and products are fluids or behave as such (∂Ψ^I/∂C^s = 0, $\partial {\Psi }^I/\partial {\mathbf{\text{d}}}_r^s=\mathbf{0}$ ,and $\partial {\Psi }^I/\partial {\mathbf{\text{A}}}_r^s=\mathbf{0}$); third, energy dissipation from viscous effects or diffusive drag is neglected ( ${\mathbf{\text{T}}}_d^{\alpha }:{\mathbf{\text{L}}}^{\alpha }=\mathbf{0}$ and ${\widehat{\mathbf{\text{p}}}}_d^{\alpha }\cdot {\mathbf{\text{u}}}^{\alpha }=\mathbf{0}$); finally, the quadratic diffusive term (u^α · u^α/2) is generally ignored (it is usually negligible for biological systems). Under these assumptions, Eq.(86) states that a chemical reaction can proceed if and only if ${\sum }_{\alpha }{\widehat{\rho }}^{\alpha }{\mu }^{\alpha }\le 0$. This expression represents the continuum version of the classical textbook treatment. It is more general in the sense that it is expressed in local form, valid at any instant in time and space. It is also not limited to constant pressure processes since μ^α incorporates the term $p/{\rho }_T^{\alpha }$ as seen in Eq.(89).

3.5 Constitutive Relation for the Momentum Supply

Substituting the expression for the fluid stresses from Eq.(83) and the momentum supply from Eq.(85) into the conservation of linear momentum for the fluid constituents, Eq.(13), yields

$${\rho }^{\gamma }{\mathbf{\text{a}}}^{\gamma }=-{\rho }^{\gamma }\text{grad}{\stackrel{\sim }{\mu }}^{\gamma }+\text{div}{\mathbf{\text{T}}}_d^{\gamma }+{\rho }^{\gamma }{\mathbf{\text{b}}}^{\gamma }+\frac{\partial {\Psi }^{\gamma }}{\partial \theta }\mathbf{\text{g}}+{\widehat{\mathbf{\text{p}}}}_d^{\gamma }\gamma \ne s$$ (99)

This form of the linear momentum equation (Bowen, 1982) is often more convenient to use for mixture problems in biological tissues (Lai et al, 1991). To formulate a constitutive relation for ${\widehat{\mathbf{\text{p}}}}_d^{\alpha }$, the inequality constraint of Eq.(86) must be satisfied. Furthermore, substituting the relation of Eq.(93) into Eq.(17), we find that ${\widehat{\mathbf{\text{p}}}}_d^{\alpha }$ must additionally satisfy

$$\sum _{\alpha }{\widehat{\mathbf{\text{p}}}}_d^{\alpha }+{\widehat{\rho }}^{\alpha }{\mathbf{\text{u}}}^{\alpha }=0$$ (100)

Extending the approach of previous authors to the case of reactive mixtures, a proposition for a constitutive relation for ${\widehat{\mathbf{\text{p}}}}_d^{\alpha }$ which satisfies the constraints of Eqs.(86) and (100) is given by

$${\widehat{\mathbf{\text{p}}}}_d^{\alpha }=-\frac{{\rho }^{\alpha }}{\rho }\sum _{\beta }{\widehat{\rho }}^{\beta }{\mathbf{\text{u}}}^{\beta }+{\sum _{\beta \ne \alpha }\mathbf{\text{f}}}^{\alpha \beta }({\mathbf{\text{u}}}^{\beta }-{\mathbf{\text{u}}}^{\alpha })$$ (101)

where f^αβ and f^βα are second-order tensors (diffusive drag coefficients) which must be positive semi-definite and satisfy

$${\mathbf{\text{f}}}^{\alpha \beta }={\mathbf{\text{f}}}^{\beta \alpha }$$ (102)

These coefficients depend on the same variables as provided in Eq.(80). The term ${\sum }_{\beta \ne \alpha }{\mathbf{\text{f}}}^{\alpha \beta }({\mathbf{\text{u}}}^{\beta }-{\mathbf{\text{u}}}^{\alpha })$ in Eq.(101) represents the frictional interactions (diffusive drag) of constituent β with constituent α, with the components of the tensor f^αβ representing the frictional coefficients; generally, this represents a dissipative term (irreversible mechanism) in the response of mixtures. For the term −(ρ^α / ρ) Σ_βρ̂^βu^β, the summation represents the momentum supply generated by mass production from all the constituents. The factor ρ^α / ρ indicates that this resulting body force is imparted on constituent α in proportion to its mass fraction. Unlike the diffusive drag, this term represents a conservative mechanism because, when substituted into the entropy inequality of Eq.(86), the resulting expression reduces to zero.

Substituting Eq.(101) into Eq.(99) and making use of Eq.(8), it can be shown that

$$({\mathbf{\text{f}}}^{\alpha }+\frac{{\rho }^{\alpha }}{\rho }{\widehat{\rho }}^{\alpha }\mathbf{\text{I}})({\mathbf{\text{v}}}^{\alpha }-{\mathbf{\text{v}}}^s)-\sum _{\beta \ne \alpha ,s}({\mathbf{\text{f}}}^{\alpha \beta }-\frac{{\rho }^{\alpha }}{\rho }{\widehat{\rho }}^{\beta }\mathbf{\text{I}})({\mathbf{\text{v}}}^{\beta }-{\mathbf{\text{v}}}^s)=-{\rho }^{\alpha }{\mathbf{\text{a}}}^{\alpha }-{\rho }^{\alpha }\text{grad}{\stackrel{\sim }{\mu }}^{\alpha }+\text{div}{\mathbf{\text{T}}}_d^{\alpha }+\frac{\partial {\Psi }^{\alpha }}{\partial \theta }\mathbf{\text{g}}+{\rho }^{\alpha }{\mathbf{\text{b}}}^{\alpha }\alpha \ne s$$ (103)

where

$${\mathbf{\text{f}}}^{\alpha }\equiv \sum _{\beta \ne \alpha }{\mathbf{\text{f}}}^{\alpha \beta }$$ (104)

3.6 Interface Jump Condition on the Electrochemical Potential

This section extends some of the concepts of Mueller (1975) and Liu (1980) in an effort to better formulate the jump condition on μ̃^α across an interface Γ in the presence of chemical reactions. The basic constitutive assumption needed to formulate this jump condition is to let

$$[[\theta ]]=0$$ (105)

The assumption that temperature does not suffer a jump at an interface is common in many applications, including in heat transfer analyses (Incropera and DeWitt, 1981). Using this relation, let the jump condition of Eq. (51) be equivalently formulated for each constituent α as

$$[[{\rho }^{\alpha }\theta {\eta }^{\alpha }{\mathbf{\text{u}}}_{\Gamma }^{\alpha }+{\mathbf{\text{q}}}^{\alpha }]]\cdot \mathbf{\text{n}}=-\theta {\overline{\eta }}^{\alpha }$$ (106)

Where η̄^α is the area density of entropy supply of constituent α on Γ, which satisfies

$$\sum _{\alpha }{\overline{\eta }}^{\alpha }\ge 0$$ (107)

on a dissipative interface. Adding the expression of Eq.(106) to Eq. (48) yields

$$\left[\right[{\rho }^{\alpha }({\mathbf{\text{K}}}^{\alpha }+\frac{1}{2}({\mathbf{\text{u}}}_{\Gamma }^{\alpha }\cdot {\mathbf{\text{u}}}_{\Gamma }^{\alpha }\left)\mathbf{\text{I}}\right){\mathbf{\text{u}}}_{\Gamma }^{\alpha }\left]\right]\cdot \mathbf{\text{n}}=-{\overline{\psi }}^{\alpha }$$ (108)

where

$${\overline{\psi }}^{\alpha }\equiv {\overline{\varepsilon }}^{\alpha }-\theta {\overline{\eta }}^{\alpha }$$ (109)

is the area density of Helmholtz free energy supply, which satisfies

$$\sum _{\alpha }{\overline{\psi }}^{\alpha }\le 0$$ (110)

and

$${\mathbf{\text{K}}}^{\alpha }={\psi }^{\alpha }\mathbf{\text{I}}-\frac{{\left({\mathbf{\text{T}}}^{\alpha }\right)}^T}{{\rho }^{\alpha }}$$ (111)

has been called the chemical potential tensor by Bowen (1976), though in the current context it may be more aptly called the electrochemical potential tensor. Indeed, using the expression for the fluid stress tensor from Eq.(83), we find that

$${\mathbf{\text{K}}}^{\gamma }={\stackrel{\sim }{\mu }}^{\gamma }\mathbf{\text{I}}-\frac{{({\mathbf{\text{T}}}_d^{\gamma })}^T}{{\rho }^{\alpha }}\gamma \ne s$$ (112)

and in the case when viscous stresses are negligible, K^γ = μ̃^γI.

Equation (108) represents the jump condition on the electrochemical potential K^α of any constituent (fluid or solid), in the presence of chemical reactions, on an interface Γ which may be dissipative. The free energy supply Ψ̄^α can represent a variety of phenomena. For example, if Γ represents a membrane, Ψ̄^α may represent the loss of free energy in constituent α due to frictional diffusive drag resulting from the flow through the membrane. Another possibility is that Ψ̄^α represents free energy supply on the membrane due to chemical reactions (which may not necessarily involve constituent α). An important example includes membrane pumps in cells, such as the sodium-potassium pump (Na⁺/K⁺– ATPase), where the hydrolysis of ATP produces free energy which drives the mechanical work of translocating ions across the membrane. Perhaps a more familiar example illustrating free energy supply on an interface Γ would be a voltaic cell, where the chemical reaction between a metal electrode and an acid bath produces free energy in the form of an electric potential. In general, Eq.(108) needs to be combined with the jump condition on the mass, Eq.(37), along with a suitable constitutive assumption on Ψ̄^α, to yield the jump condition on the electrochemical potential in the presence of chemical reactions.

In the case of fluid constituents γ ≠ s, in the absence of chemical reactions producing free energy or dissipative mechanisms consuming free energy on Γ, we may let Ψ̄^γ = 0, in which case Eq.(108) leads to

$$\left[\right[{\rho }^{\gamma }({\mathbf{\text{K}}}^{\gamma }+\frac{1}{2}({\mathbf{\text{u}}}_{\Gamma }^{\gamma }\cdot {\mathbf{\text{u}}}_{\Gamma }^{\gamma })\mathbf{\text{I}}){\mathbf{\text{u}}}_{\Gamma }^{\gamma }\left]\right]\cdot \mathbf{\text{n}}=0\gamma \ne s$$ (113)

Neglecting viscous stresses and recognizing that $\left[\right[{\rho }^{\gamma }{\mathbf{\text{u}}}_{\Gamma }^{\gamma }\left]\right]\cdot \mathbf{\text{n}}=0$ in the absence of chemical reactions involving constituent γ on Γ according to Eq.(37), while ${\rho }^{\gamma }{\mathbf{\text{u}}}_{\Gamma }^{\gamma }\cdot \mathbf{\text{n}}\ne 0$ under general conditions, this expression reduces to

$$\left[\right[{\stackrel{\sim }{\mu }}^{\gamma }+\frac{1}{2}{\mathbf{\text{u}}}_{\Gamma }^{\gamma }\cdot {\mathbf{\text{u}}}_{\Gamma }^{\gamma }\left]\right]=0\gamma \ne s$$ (114)

which further reduces to [[μ̃^γ]] = 0 when neglecting the quadratic diffusive term. This is the familiar relation of classical physical chemistry which states that the electrochemical potential of a fluid is continuous across an interface which is permeable to it (Katzir-Katchalsky and Curran, 1965). The present analysis clarifies the special circumstances under which this relation holds (Ψ̄^γ = 0, ρ̄^γ = 0).

There is one more remark to be made regarding kinematic jump conditions on Γ, which is not directly related to the electrochemical potential jump but complements the conditions needed for a well-posed problem. If the viscous stresses in fluids are not neglected, it is necessary to provide additional constitutive kinematic assumptions regarding the jump in the components of the velocity of each constituent tangential to Γ, called pseudo-no-slip conditions (Hou et al, 1989), which generalize the well-known no-slip condition of classical fluid mechanics to the case of solid and fluid mixtures.

4 Common Assumptions for Biological Tissues

The aim of this section is to make simplifications appropriate for biological tissues and help reduce the governing equations into a practical and familiar format.

4.1 Concentration

In studies of chemical reactions and transport in fluid solutions, it is more common to use concentrations instead of densities to describe the amount of various constituents in moles per unit volume. For solid-fluid mixtures, it becomes necessary to distinguish between mixture volume-based measures and solution volume-based measures of concentration, and to clarify which of the two measures is being used. In the current treatment, we adopt a solution volume-based measure. Thus, the concentration of constituent α in the mixture is given by

$$c^{\alpha }=\frac{{\rho }^{\alpha }}{(1-{\phi }^s)M^{\alpha }}$$ (115)

which represents the number of moles of constituent α per volume of solution.¹³ The concentration in the reference configuration is given by

$$c_r^{\alpha }=\frac{{\rho }_r^{\alpha }}{(1-{\phi }_r^s)M^{\alpha }}$$ (116)

where $c_r^{\alpha }=c^{\alpha }(J^s-{\phi }_r^s)/(1-{\phi }_r^s)$ according to Eqs.(95) and (135) below. The mass supplies may be similarly replaced with the molar supplies

$${\widehat{c}}^{\alpha }=\frac{{\widehat{\rho }}^{\alpha }}{(1-{\phi }^s)M^{\alpha }}{\widehat{c}}_r^{\alpha }=\frac{{\widehat{\rho }}_r^{\alpha }}{(1-{\phi }_s^r)M^{\alpha }}$$ (117)

4.2 Angular Momentum Supply, Dissipative Stresses, Dilute Solutions, Diffusion and Permeation, Inertia Terms

This presentation extends the approach of Lai et al (1991) and Ateshian et al (2006) to the case of reactive mixtures. Depending on the intended application of the general equations presented above, it is possible to make a number of simplifying assumptions which are relevant to biological tissues. In most biological applications, diffusion velocities u^α are sufficiently small so that quadratic terms u^α · u^α and u^α ⊗ u^α are negligible compared to other terms involving these expressions; then T ≈ T^I, ε ≈ ε^I, q ≈ q^I. Similarly, in the expressions for the jump conditions on the momentum, energy, and chemical potential, terms involving ${\text{u}}_{\Gamma }^{\alpha }\cdot {\text{u}}_{\Gamma }^{\alpha },{\text{u}}_{\Gamma }^{\alpha }\otimes {\text{u}}_{\Gamma }^{\alpha }$, u_Γ · u_Γ and u_Γ ⊗ u_Γ may also be neglected.

Though the governing equations of mixture theory allow for non-symmetric constituent stresses even while the mixture stress is symmetric, it is commonly assumed that the angular momentum supply term is negligible, m̂^α = 0, implying from Eq.(19) that (T^α)^T = T^α. When dissipative stresses are neglected in the solid and fluid constituents, then

$${\mathbf{\text{T}}}_d^{\alpha }=0$$ (118)

When the mixture of fluid constituents is assumed to be a dilute aqueous solution, where the solvent is denoted by α = w, the mixture saturation condition simplifies to

$$\sum _{\alpha }{\phi }^{\alpha }=1\approx {\phi }^s+{\phi }^w$$ (119)

which signifies that only the solid matrix and the solvent occupy significant volume fractions (φ^α≪ 1,α≠s,w). Then, assuming that the true densities of the constituents are all on the same order of magnitude, the mass fractions of the solutes may also be assumed to satisfy

$$\frac{{\rho }^{\alpha }}{\rho }\ll 1\alpha \ne s,w$$ (120)

As shown below, the friction coefficients f^αβ are related to the diffusivities of solutes in the mixture and the permeability of the solvent in the porous solid matrix. For most applications to biological tissues, an order of magnitude analysis on the coefficients of the relative velocities in Eq.(103) demonstrates that

$${\mathbf{\text{f}}}^{\alpha }+\frac{{\rho }^{\alpha }}{\rho }{\widehat{\rho }}^{\alpha }\mathbf{\text{I}}\approx {\mathbf{\text{f}}}^{\alpha }{\mathbf{\text{f}}}^{\alpha \beta }-\frac{{\rho }^{\alpha }}{\rho }{\widehat{\rho }}^{\beta }\mathbf{\text{I}}\approx {\mathbf{\text{f}}}^{\alpha \beta }$$ (121)

implying that the mass supply terms contribute negligibly to the momentum exchange among constituents. The friction coefficients may be assumed to be isotropic, as a first-order approximation,¹⁴

$${\mathbf{\text{f}}}^{\alpha \beta }=f^{\beta \alpha }\mathbf{\text{I}}$$ (122)

Since the solutions are assumed dilute, the friction between various solutes may be considered negligible compared to that between solutes and solvent, or solutes and solid, thus

$$\Vert {\mathbf{\text{f}}}^{\gamma \nu }\Vert \ll \text{min}(\Vert {\mathbf{\text{f}}}^{\alpha w}\Vert ,\Vert {\mathbf{\text{f}}}^{\beta s}\Vert )\gamma ,\nu \ne s,w$$ (123)

We may also assume that isothermal conditions prevail in most biological tissue applications, grad θ = 0, and that inertia forces can be neglected in the momentum equations. Incorporating these simplifying assumptions into Eq.(103) yields

$$f^w({\mathbf{\text{v}}}^w-{\mathbf{\text{v}}}^s)-\sum _{\beta \ne w,s}{\mathit{\text{f}}}^{w\beta }({\mathbf{\text{v}}}^{\beta }-{\mathbf{\text{v}}}^s)=-{\rho }^w\text{grad}{\stackrel{\sim }{\mu }}^{\text{w}}+{\rho }^w{\mathbf{\text{b}}}^w$$ (124)

$$f^{\alpha }({\mathbf{\text{v}}}^{\alpha }-{\mathbf{\text{v}}}^s)-f^{\alpha w}({\mathbf{\text{v}}}^w-{\mathbf{\text{v}}}^s)=-{\rho }^{\alpha }\text{grad}{\stackrel{\sim }{\mu }}^{\alpha }+{\rho }^{\alpha }{\mathbf{\text{b}}}^{\alpha }\alpha \ne w,s$$ (125)

As shown previously (Lai et al, 1991; Meerveld et al, 2003; Ateshian et al, 2006), the friction coefficients can be related to solute diffusivities according to

$$\begin{array}{c}{D}_0^{\alpha }=\frac{R\theta }{f^{\alpha w}}{\phi }^w{c}^{\alpha }\\ D^{\alpha }=\frac{R\theta }{f^{\alpha w}+f^{\alpha s}}{\phi }^w{c}^{\alpha }\end{array}\alpha \ne w,s$$ (126)

where D^α is the diffusion coefficient of solute α in the mixture, $D_0^{\alpha }$ is its diffusion coefficient in free solution, and R is the universal gas constant. Furthermore, the friction between the solvent and solid is related to the hydraulic permeability of the solid matrix to the solvent,

$$k=\frac{{({\phi }^w)}^2}{f^{\mathit{\text{ws}}}}$$ (127)

The system of equations in Eqs.(124)-(125) can be solved for the relative velocities and rearranged to produce the volume flux of solvent relative to the solid, w, and the molar flux of solute relative to the solid, j^α,

$$\mathbf{\text{w}}\equiv {\phi }^{\mathit{w}}({\mathbf{\text{v}}}^{\mathit{w}}-{\mathbf{\text{v}}}^{\mathit{s}})=-\stackrel{\sim }{k}{\rho }_T^{\mathit{w}}(\text{grad}{\stackrel{\sim }{\mu }}^{\mathit{w}}-{\mathbf{\text{b}}}^{\mathit{w}})-\stackrel{\sim }{k}\sum _{\alpha \ne w,s}{M}^{\alpha }\frac{D^{\alpha }}{D_0^{\alpha }}{c}^{\alpha }(\text{grad}{\stackrel{\sim }{\mu }}^{\alpha }-{\mathbf{\text{b}}}^{\alpha })$$ (128)

$${\mathbf{\text{j}}}^{\alpha }\equiv {\phi }^{\mathit{w}}{c}^{\alpha }({\mathbf{\text{v}}}^{\alpha }-{\mathbf{\text{v}}}^s)=\frac{D^{\alpha }}{D_0^{\alpha }}{c}^{\alpha }\mathbf{\text{w}}-\frac{{\phi }^{\mathit{w}}}{\mathit{R}\theta }{\mathit{M}}^{\alpha }{D}^{\alpha }{c}^{\alpha }(\text{grad}{\stackrel{\sim }{\mu }}^{\alpha }-{\mathbf{\text{b}}}^{\alpha })\alpha \ne s,w$$ (129)

where

$$\stackrel{\sim }{k}\equiv {[\frac{1}{k}+\frac{1}{{\phi }^w}\sum _{\alpha \ne w,s}R\theta (1-\frac{D^{\alpha }}{D_0^{\alpha }}\left)\frac{c^{\alpha }}{D_0^{\alpha }}\right]}^{-1}$$ (130)

is the hydraulic permeability of the solid matrix to the solution. These equations are complemented by the conservation of linear momentum for the mixture, Eq.(14),

$$\text{div}{\mathbf{\text{T}}}^I+\rho \mathbf{\text{b}}=\mathbf{0}$$ (131)

where inertia forces, and the quadratic diffusive term in the mixture stress, Eq.(15), have been neglected.

Additional equations are the conservation of mass equations for the mixture, Eq.(55), the solid constituents and the solutes, Eq.(4),

$$\text{div}({\mathbf{\text{v}}}^s+\mathbf{\text{w}})=\frac{{\widehat{\rho }}^{\mathit{w}}}{{\rho }_T^{\mathit{w}}}+\sum _{\sigma =1}^{\mathit{m}}\frac{{\widehat{\rho }}^{\sigma }}{{\rho }_T^{\sigma }}+{\phi }^{\mathit{w}}\sum _{\alpha \ne \mathit{w},\mathit{s}}{\nu }_T^{\alpha }{\widehat{\mathit{c}}}^{\alpha }$$ (132)

$$\frac{\partial {\rho }^{\sigma }}{\partial t}+\text{div}({\rho }^{\sigma }{\mathbf{\text{v}}}^s)={\widehat{\rho }}^{\sigma }$$ (133)

$$\frac{\partial ({\phi }^w{c}^{\alpha })}{\partial t}+\text{div}({\mathbf{\text{j}}}^{\alpha }+{\phi }^w{c}^{\alpha }{\mathbf{\text{v}}}^s)={\phi }^w{\widehat{c}}^{\alpha }\alpha \ne w,s$$ (134)

where ${\nu }_T^{\alpha }=M^{\alpha }/{\rho }_T^{\alpha }$ is the molar volume of solute α (which is constant for intrinsically incompressible materials); the conservation of mass for the solid mixture,

$${\phi }^s=\frac{{\phi }_r^s}{J^s}{\phi }^w=1-\frac{1-{\phi }_r^w}{J^s}$$ (135)

where the lower bound on J^s is ${\phi }_r^s$;¹⁵ the electro neutrality condition, Eq.(57),

$$\sum _{\sigma =1}^m{z}^{\sigma }\frac{{\rho }^{\sigma }}{M^{\sigma }}+{\phi }^w\sum _{\alpha \ne w,s}{z}^{\alpha }{c}^{\alpha }=0$$ (136)

where it is assumed that the solvent does not carry charge (z^w = 0); and the conservation of charge, Eqs.(60)-(61),

$$\text{div}{\mathbf{\text{I}}}_e=\text{div}{F}_c\sum _{\alpha \ne w,s}{z}^{\alpha }{\mathbf{\text{j}}}^{\alpha }=0$$ (137)

Equations (128)-(137), along with an appropriate constitutive relation for ${\Psi }_r^I$ requisite boundary conditions as described in Sections 2.3 and 3.6, and equations of reaction kinetics, are needed to solve problems of reactive mixtures.

4.3 Constitutive Relation for the Chemical Potential of Fluids

For ideal fluids, classical physical chemistry proposes that

$${\mu }^{\alpha }={\mu }_0^{\alpha }(\theta )+\frac{p-p_0}{{\rho }_T^{\alpha }}+\frac{R\theta }{M^{\alpha }}\text{ln}{x}^{\alpha }\alpha \ne s$$ (138)

where x^α is the mole fraction of constituent α in the solution; ${\mu }_0^{\alpha }(\theta )$ and p₀ are the chemical potential and pressure, respectively, at the standard state x^α = 1.¹⁶ Given that x^α may be represented in terms of the concentrations of the fluid constituents of the solution as

$$x^{\alpha }=\frac{c_r^{\alpha }}{\sum _{\beta \ne s}{c}_r^{\beta }}\alpha \ne s$$ (139)

it may be noted, based on Eqs.(98) and (116), that the relation of Eq.(138) can be derived from the constitutive assumption

$${\Psi }_r^I=\sum _{\alpha \ne s}{M}^{\alpha }{c}_r^{\alpha }({\mu }_0^{\alpha }(\theta )-\frac{p_0}{p_T^{\alpha }}+\frac{R\theta }{M^{\alpha }}\text{ln}\frac{c_r^{\alpha }}{\sum _{\beta \ne s}{c}_r^{\beta }})+W_r(\theta ,{\mathbf{\text{C}}}^s,{\rho }_r^s,{\mathbf{\text{d}}}_r^s,{\mathbf{\text{A}}}_r^s)$$ (140)

where W_r is a generic strain energy density function which remains to be specified when we consider a constitutive relation for the elastic stress in the solid matrix. Note that since W_r is not a function of the fluid densities, and since the solution is ideal, we can also refer to the mixture as being ideal.¹⁷

Experimentally, ideal behavior is generally expected only for very dilute solutions in a single solvent. For non-ideal solutions, the constitutive relation of Eq.(138) is generalized to

$${\mu }^{\alpha }={\mu }_0^{\alpha }\left(\theta \right)+\frac{p-p_0}{{\rho }_T^{\alpha }}+\frac{R\theta }{M^{\alpha }}\text{ln}{a}^{\alpha }\alpha \ne s$$ (141)

where a^α = γ^αx^α is called the activity of constituent α and γ^α is called the activity coefficient, which satisfies

$$\underset{x^{\alpha }\to 1}{lim}{\gamma }^{\alpha }=1$$ (142)

It follows that γ^α = 1 for ideal solutions. In principle, γ^α may be a function of all of the state variables listed in Eq.(80). Therefore, a closed-form expression for ${\Psi }_r^I$ of the form given in Eq.(140) is usually not available for real solutions.

For most biological applications, fluid solutions may be considered dilute, with x^ι << 1, ι ≠ s,w, where w denotes the solvent and ι denotes solutes. The standard state for the solvent is defined as above (a^w = 1); however, since the mole fraction of solutes never approaches unity, the solute standard state is defined at a standard concentration $c_0^{\iota }$ (usually, $c_0^{\iota }=1\text{M}$) (Tinoco Jr. et al, 1995).¹⁸ Under these conditions, the chemical potential of the solvent and solutes may be approximated by

$${\mu }^w={\mu }_0^w(\theta )+\frac{1}{{\rho }_T^w}(p-p_0-R\theta \Phi \sum _{\alpha \ne s,w}{c}^{\alpha })$$ (143)

$${\mu }^{\iota }={\mu }_0^{\iota }(\theta )+\frac{R\theta }{M^{\iota }}\text{ln}\frac{{\gamma }^{\iota }{c}^{\iota }}{c_0^{\iota }}\iota \ne s,w$$ (144)

where Φ is called the osmotic coefficient, given by

$$\Phi =1+\frac{\text{ln}{\gamma }^w}{\text{ln}{x}^w}$$ (145)

From this relation it may be noted that Φ = 1 for ideal solutions.

4.4 Rule of Mixture for the Solid Matrix

While it has been assumed that all the solid constituents share the same motion, they may not share the same constitutive relation. As the proportion of each solid constituent in the solid matrix evolves due to chemical reactions, the stresses resulting from the deformation may evolve accordingly. Humphrey and Rajagopal (2002) proposed to use a simple rule of mixtures for evaluating the stress resulting from the matrix deformation. To apply their approach to the hyperelastic stress term in Eq.(97), it may be postulated that

$$\frac{2}{J^s}{\mathbf{\text{F}}}^s\frac{\partial {\Psi }_r^I}{\partial {\mathbf{\text{C}}}^s}{({\mathbf{\text{F}}}^s)}^T=\frac{2}{J^s}{\mathbf{\text{F}}}^s\left(\sum _{\sigma =1}^m\frac{{\rho }_r^{\sigma }}{{\rho }_r^s}\frac{\partial W_r^{\sigma }}{\partial {\mathbf{\text{C}}}^s}\right){({\mathbf{\text{F}}}^s)}^T$$ (146)

where $W_r^{\sigma }$ is the strain energy density of solid constituent σ and the summation is taken over all solid constituents.

4.5 Chemical Reactions

Chemical reactions are characterized by their stoichiometry, order and mechanism (Tinoco Jr. et al, 1995). Stoichiometry enforces conservation of mass in each individual chemical reaction. Let N represent the number of independent reactions and let ${\varsigma }_{\nu }^{\alpha }$ be the stoichiometric coefficient of constituent α in reaction ν (ν = 1 to N). The conservation of mass in reaction ν is given by

$$\sum _{\alpha }{\varsigma }_{\nu }^{\alpha }{M}^{\alpha }=0$$ (147)

where M^α is the molecular weight of constituent α (Mueller, 1975). The molar supply ${\widehat{c}}_r^{\alpha }$ to constituent α is the resultant of all simultaneous chemical reactions occurring at any given time,

$${\widehat{c}}_r^{\alpha }=\sum _{\nu =1}^N{\widehat{c}}_{r\nu }^{\alpha }$$ (148)

where ${\widehat{c}}_{r\nu }^{\alpha }$ is the molar supply to constituent α in the ν—th reaction.

The order of a reaction is determined experimentally based on a constitutive relation for ${\widehat{c}}_{r\nu }^{\alpha }.$. For example, for many reactions a constitutive relation for the rate law is given by

$${\widehat{c}}_{r\nu }^{\alpha }=k_{\nu }\prod _{\beta }{(c_r^{\beta })}^{m_{\nu }^{\beta }}$$ 149

where $m_{\nu }^{\beta }$ are often, but not always, integers (Tinoco Jr. et al, 1995). The product is taken over all constituents in the mixture; if a particular constituent β is not involved in the reaction ν, or if it only serves as a catalyst, its corresponding power is $m_{\nu }^{\beta }=0$. The order of the reaction is then given by ${\sum }_{\beta }{m}_{\nu }^{\beta }$. Thus, a reaction of order zero exhibits a mass supply equal to k_ν. k_ν is known as the rate coefficient (or rate ’constant’) of the reaction; in principle it can be a function of any of the state variables listed in Eq.(80). In particular, in problems of growth and remodeling, it may be dependent on the state of strain in the solid matrix.

The mechanism of a reaction pertains to how molecules react to form a product; it describes these elementary reactions consistent with the stoichiometric reaction (Tinoco Jr. et al, 1995). Knowledge of the mechanism may help determine the rate law of a reaction. However, even without a precise knowledge of the mechanism, the rate law may be determined experimentally.

5 Discussion

The objective of this study is to present the comprehensive set of governing equations for reactive mixtures of charged constituents, for the purpose of investigating active processes in biological tissues. This presentation extends the existing literature by providing explicit equations for a growing solid matrix, and a common framework for analyzing surface and volume growth. By using a mixture framework, the mechanisms of growth must explicitly satisfy the conservation of mass of fluid and solid constituents; thus, growth of a constituent must be accompanied by resorption of others. This approach makes it possible to analyze solid matrix growth starting from only a fluid mixture; no starting solid matrix geometry is needed to initiate an analysis.

The approach advocated here places considerable emphasis on the definition of the reference configuration for material points of the solid matrix. Based on the formulation of the governing equations, the mechanisms of surface growth and volume growth are associated with the area density of mass supply ${\overline{\rho }}_r^s$ and volume density of mass supply ${\widehat{\rho }}_r^s$, respectively. Since ${\overline{\rho }}_r^s$ involves the deposition of new material points onto the body, whereas ${\widehat{\rho }}_r^s$ alters the apparent density ${\rho }_r^s$ (X^s, t) of existing material points X^s in the body, it follows that the definition of a reference configuration only occurs during surface growth. Furthermore, this framework is built on the foundation that the reference configuration of a material point is immutable, so that the standard definition of the deformation gradient may be applied. Once a material point X^s has been deposited, its place X^s in the reference configuration does not change with time, even if volume growth (altering of the apparent density ${\rho }_r^s$) and remodeling (altering of the texture tensor ${\text{A}}_r^s$) occur at this material point over time.

This framework differs in a number of important details from that adopted by previous investigators (Rodriguez et al, 1994; Chen and Hoger, 2000; Klisch et al, 2003; Humphrey and Rajagopal, 2002; Guillou and Ogden, 2006). Some of these earlier descriptions have been explicitly limited to volume growth, to ensure a one-to-one mapping between the reference and current configurations, thereby allowing a decomposition of the motion into a contribution from growth and a contribution from loading. Others refer explicitly to evolving natural configurations, which the current approach precludes. In the study of Skalak et al (1982), specific attention is given to surface growth, though their approach differs from the one followed here. In particular, these authors define a vector growth rate on an interface between two solids, rather than the scalar area density of mass supply appearing in the current analysis.

The framework of mixture theory provides opportunities to explore growth mechanisms in more subtle ways than the analysis of a single solid constituent, by suggesting a specific pathway for the development of residual stresses. By allowing the inclusion of fluid constituents, including charged or neutral solutes in an interstitial fluid solution, it is possible to account for residual stresses arising from osmotic effects. In the cartilage literature, significant consideration has been given to the concept of swelling stress in the cartilage matrix arising from Donnan osmotic pressure in the interstitial fluid (Maroudas, 1976; Eisenberg and Grodzinsky, 1987; Mow and Lai, 1990; Lai etal, 1991; Settonetal, 1998; Basser et al, 1998; Narmoneva et al, 1999; Chahine et al, 2004). This pressure difference with the ambient bathing environment occurs primarily because of the negatively charged proteoglycan molecules trapped within the collagen matrix, which attract anions and cations in different concentrations to maintain electroneutrality. The resulting imbalance in the concentration of mobile ions with the external bath must be compensated by an increased pressure to maintain balance in the chemical potential of the interstitial water. This increased pressure places the traction-free solid matrix in a state of tensile stress. Since the proteoglycan distribution is inhomogeneous through the thickness of the articular layer, the resulting inhomogeneity in osmotic pressure manifests itself as a residual stress. To a significant extent, the osmotic pressure may be alleviated by placing the tissue in a hypertonic bath. For example, Setton et al (1998) have demonstrated that curling of an explanted cartilage strip can be altered by the tonicity of the bathing solution, an observation which confirms the presence of osmotically-induced residual stresses. This type of response can be predicted using the mixture theory framework presented here and in the earlier literature (Lai et al, 1991).

While the mechanism of osmotic pressurization in articular cartilage has been widely recognized, only limited attention has been paid to it in other biological soft tissues (Grodzinsky, 1983). In particular, it is well known that the arterial wall contains a significant amount of proteoglycans and that these are inhomogeneously distributed across the arterial wall (Wight and Ross, 1975; Yao et al, 1994). Less well-known is that they carry a significant amount of negative charge (Porterfield et al, 1968). It is entirely plausible that this inhomogeneous fixed charge distribution plays a significant role in regulating the well-recognized residual stresses across the arterial wall (Fung, 1990; Humphrey, 2002), particularly since the synthesis of proteoglycans by arterial smooth muscle cells is known to be regulated by their strain environment (Lee etal, 2001).

In the framework presented in this study, the growth and evolution of such residual stresses can be entirely accounted for by the deposition and removal of charged proteoglycans, modeled as one of the constituents of the solid matrix. Since the fixed charge density of a tissue may evolve over time, either due to synthesis or degradation of charged molecules which are bound to, or trapped in the solid matrix, the resulting residual matrix stresses may also change. The osmotic pressure can be predicted from the concentrations ρ^α of the various constituents in the matrix, which depend on ${\rho }_r^{\alpha }$ and J^s (Lai et al, 1991; Ateshian et al, 2004). Experimentally, it may be possible to assess the significance of these residual stresses by osmotic unloading (balancing the inner and outer concentrations of solutes) while keeping the tissue intact, if a tissue exhibits low cellularity. Alternatively, enzymatic digestion of the charged species may induce changes in tissue swelling and mechanical properties which may be attributed to alterations in the residual stresses. This approach is also applicable to uncharged mixtures, where the imbalance in solute concentration may arise from the selective partitioning of solutes between the tissue and its external bathing environment, and between intracellular and extracellular compartments.¹⁹

Another mechanism available to account for residual stresses in this framework relates to surface growth, as explained in Section 3.3. For example, surface growth of a stress-free material region upon a stressed substrate will produce residual stresses upon unloading. Adhesion of pre-stressed, pre-formed material regions onto a stress-free or stressed substrate will also result in residual stresses under traction-free conditions. Explicit expressions for determining the reference configuration of newly-deposited material regions have been provided.

The above examples indicate that the framework presented here can provide explicit mechanisms for the development of growth-induced residual stresses from volume growth or surface growth, whereas the majority of earlier studies have adopted a more phenomenological approach for the prediction of such stresses. In the case of volume growth, the proposed mechanism of osmotically-induced residual stresses is particularly enhanced by the charged nature of biological mixtures, which emphasizes the benefits of including such effects in a modeling framework. More detailed presentations of these concepts will be covered in future theoretical and experimental studies.

Appendix.

The material derivative of ψ^α with respect to the α—constituent, which is needed for the entropy inequality, is obtained using the chain rule of differentiation,

$$\frac{D^{\alpha }{\psi }^{\alpha }}{\mathit{\text{Dt}}}=\frac{\partial {\psi }^{\alpha }}{\partial \theta }\frac{D^{\alpha }\theta }{\mathit{\text{Dt}}}+\frac{\partial {\psi }^{\alpha }}{\partial \mathbf{\text{g}}}\cdot \frac{D^{\alpha }\mathbf{\text{g}}}{\mathit{\text{Dt}}}+\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{\text{C}}}^s}:\frac{D^{\alpha }{\mathbf{\text{C}}}^s}{\mathit{\text{Dt}}}+\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{\text{G}}}^s}⋮\frac{D^{\alpha }{\mathbf{\text{G}}}^s}{\mathit{\text{Dt}}}+\frac{\partial {\psi }^{\alpha }}{\partial {\rho }_r^s}\frac{D^{\alpha }{\rho }_r^s}{\mathit{\text{Dt}}}+\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{\text{d}}}_r^s}\cdot \frac{D^{\alpha }{\mathbf{\text{d}}}_r^s}{\mathit{\text{Dt}}}+\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{\text{A}}}_r^s}:\frac{D^{\alpha }{\mathbf{\text{A}}}_r^s}{\mathit{\text{Dt}}}+\sum _{\gamma \ne s}\frac{\partial {\psi }^{\alpha }}{\partial {\rho }^{\gamma }}\frac{D^{\alpha }{\rho }^{\gamma }}{\mathit{\text{Dt}}}+\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{\text{d}}}^{\gamma }}\cdot \frac{D^{\alpha }{\mathbf{\text{d}}}^{\gamma }}{\mathit{\text{Dt}}}+\sum _{\beta }\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{\text{L}}}^{\beta }}\cdot \frac{D^{\alpha }{\mathbf{\text{L}}}^{\beta }}{\mathit{\text{Dt}}}+\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{\text{u}}}^{\beta }}\cdot \frac{D^{\alpha }{\mathbf{\text{u}}}^{\beta }}{\mathit{\text{Dt}}}$$ (A1)

where ⋮ denotes the triple dot product of third-order tensors.²⁰ It can be shown that

$$\frac{D^{\alpha }{\mathbf{\text{C}}}^s}{\mathit{\text{Dt}}}={\left({\mathbf{\text{F}}}^s\right)}^T({\left({\mathbf{\text{L}}}^s\right)}^T+{\mathbf{\text{L}}}^s){\mathbf{\text{F}}}^s+{\mathbf{\text{G}}}^s({\mathbf{\text{u}}}^{\alpha }-{\mathbf{\text{u}}}^s)$$ (A2)

$$\frac{D^{\alpha }{\mathbf{\text{G}}}^s}{\mathit{\text{Dt}}}=\left[{({\mathbf{\text{F}}}^s)}^T\underset{\_}{\otimes }{\left({\mathbf{\text{F}}}^s\right)}^T\right]:\text{grad}[{({\mathbf{\text{L}}}^s)}^T+{\mathbf{\text{L}}}^s]+[{({\mathbf{\text{L}}}^s)}^T+{\mathbf{\text{L}}}^s]:\text{grad}\left({\mathbf{\text{F}}}^s\underset{\_}{\otimes }{\mathbf{\text{F}}}^s\right)+\left(\text{grad}{\mathbf{\text{G}}}^s\right):({\mathbf{\text{u}}}^{\alpha }-{\mathbf{\text{u}}}^s)$$ (A3)

$$\frac{D^{\alpha }{\rho }_r^s}{\mathit{\text{Dt}}}={\widehat{\rho }}_r^s+{\mathbf{\text{d}}}_r^s\cdot ({\mathbf{\text{u}}}^{\alpha }-{\mathbf{\text{u}}}^s)$$ (A4)

$$\frac{D^{\alpha }{\mathbf{\text{d}}}_r^s}{\mathit{\text{Dt}}}=\text{grad}{\widehat{\rho }}_r^s+\left(\text{grad}{\mathbf{\text{d}}}_r^s\right)({\mathbf{\text{u}}}^{\alpha }-{\mathbf{\text{u}}}^s)$$ (A5)

$$\frac{D^{\alpha }{\mathbf{\text{A}}}_r^s}{\mathit{\text{Dt}}}={\widehat{\mathbf{\text{A}}}}_r^s+(\text{grad}{\mathbf{\text{A}}}_r^s)({\mathbf{\text{u}}}^{\alpha }-{\mathbf{\text{u}}}^s)$$ (A6)

$$\frac{D^{\alpha }{\rho }^{\gamma }}{\mathit{\text{Dt}}}={\widehat{\rho }}^{\gamma }-{\rho }^{\gamma }\mathbf{\text{I}}:{\mathbf{\text{L}}}^{\gamma }+{\mathbf{\text{d}}}^{\gamma }\cdot ({\mathbf{\text{u}}}^{\alpha }-{\mathbf{\text{u}}}^{\gamma })$$ (A7)

$$\frac{D^{\alpha }{\mathbf{\text{d}}}^{\gamma }}{\mathit{\text{Dt}}}=\text{grad}{\widehat{\rho }}^{\gamma }-(\mathbf{\text{I}}:{\mathbf{\text{L}}}^{\gamma }){\mathbf{\text{d}}}^{\gamma }-{\rho }^{\gamma }\mathbf{\text{I}}:\text{grad}{\mathbf{\text{L}}}^{\gamma }+(\text{grad}{\mathbf{\text{d}}}^{\gamma })({\mathbf{\text{u}}}^{\alpha }-{\mathbf{\text{u}}}^{\gamma })$$ (A8)

$$\frac{D^{\alpha }{\mathbf{\text{L}}}^{\beta }}{\mathit{\text{Dt}}}=\text{grad}{\mathbf{\text{a}}}^{\beta }+(\text{grad}{\mathbf{\text{L}}}^{\beta })({\mathbf{\text{u}}}^{\alpha }-{\mathbf{\text{u}}}^{\beta })$$ (A9)

$$\frac{D^{\alpha }{\mathbf{\text{u}}}^{\beta }}{\mathit{\text{Dt}}}={\mathbf{\text{a}}}^{\beta }-\mathbf{\text{a}}+(\text{grad}{\mathbf{\text{u}}}^{\beta }){\mathbf{\text{u}}}^{\alpha }-{\mathbf{\text{L}}}^{\beta }{\mathbf{\text{u}}}^{\beta }$$ (A10)

In Eq.(A3), the tensor dyadic product ⊗ of second order tensors A and B is the fourth-order tensor (A ⊗ B)_ijkl = A_ikB_jl (Curnier et al, 1995), and the double-dot product of a fourth-order tensor V with a third-order tensor W is the third-order tensor (V:W)_ijk = V_ijlmW_lmk. In anticipation of substituting these relations into Eq.(A1), it can be shown that

$$\sum _{\alpha }{\rho }^{\alpha }\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{\text{C}}}^s}:\frac{D^{\alpha }{\mathbf{\text{C}}}^s}{\mathit{\text{Dt}}}=(2{\mathbf{\text{F}}}^s\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{C}}}^s}{({\mathbf{\text{F}}}^s)}^T+{\Psi }^s\mathbf{\text{I}}):{\mathbf{\text{L}}}^s-(\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{C}}}^s}:{\mathbf{\text{G}}}^s)\cdot {\mathbf{\text{u}}}^s+\sum _{\alpha }(\frac{\partial {\Psi }^{\alpha }}{\partial {\mathbf{\text{C}}}^s}:{\mathbf{\text{G}}}^s)\cdot {\mathbf{\text{u}}}^{\alpha }$$ (A11)

$$\sum _{\alpha }{\rho }^{\alpha }\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{\text{G}}}^s}⋮\frac{D^{\alpha }{\mathbf{\text{G}}}^s}{\mathit{\text{Dt}}}=[2({\mathbf{\text{F}}}^s\underset{\_}{\otimes }{\mathbf{\text{F}}}^s):\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{G}}}^s}]⋮\text{grad}{\mathbf{\text{L}}}^s+[2\text{grad}({\mathbf{\text{F}}}^s\underset{\_}{\otimes }{\mathbf{\text{F}}}^s)⋮\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{G}}}^s}]:{\mathbf{\text{L}}}^s-(\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{G}}}^s}⋮\text{grad}{\mathbf{\text{G}}}^s)\cdot {\mathbf{\text{u}}}^s+\sum _{\alpha }(\frac{\partial {\Psi }^{\alpha }}{\partial {\mathbf{\text{G}}}^s}⋮\text{grad}{\mathbf{\text{G}}}^s)\cdot {\mathbf{\text{u}}}^{\alpha }$$ (A12)

$$\sum _{\alpha }{\rho }^{\alpha }\frac{\partial {\psi }^{\alpha }}{\partial {\rho }_r^s}\frac{D^{\alpha }{\rho }_r^s}{\mathit{\text{Dt}}}={\widehat{\rho }}_r^s(\frac{\partial {\Psi }^I}{\partial {\rho }_r^s}-\frac{1}{J^s}{\psi }^s)-\frac{\partial {\Psi }^I}{\partial {\rho }_r^s}{\mathbf{\text{d}}}_r^s\cdot {\mathbf{\text{u}}}^s+\sum _{\alpha }\frac{\partial {\Psi }^{\alpha }}{\partial {\rho }_r^s}{\mathbf{\text{d}}}_r^s\cdot {\mathbf{\text{u}}}^{\alpha }$$ (A13)

$$\sum _{\alpha }{\rho }^{\alpha }\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{\text{d}}}_r^s}\cdot \frac{D^{\alpha }{\mathbf{\text{d}}}_r^s}{\mathit{\text{Dt}}}=\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{d}}}_r^s}\cdot \text{grad}{\widehat{\rho }}_r^s-\left({\text{grad}}^T{\mathbf{\text{d}}}_r^s\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{d}}}_r^s}\right)\cdot {\mathbf{\text{u}}}^s+\sum _{\alpha }\left({\text{grad}}^T{\mathbf{\text{d}}}_r^s\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{d}}}_r^s}\right)\cdot {\mathbf{\text{u}}}^{\alpha }$$ (A14)

$$\sum _{\alpha }{\rho }^{\alpha }\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{\text{A}}}_r^s}:\frac{D^{\alpha }{\mathbf{\text{A}}}_r^s}{\mathit{\text{Dt}}}=\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{A}}}_r^s}:{\widehat{\mathbf{\text{A}}}}_r^s-(\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{A}}}_r^s}:\text{grad}{\mathbf{\text{A}}}_r^s)\cdot {\mathbf{\text{u}}}^s+\sum _{\alpha }\left(\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{A}}}_r^s}:\text{grad}{\mathbf{\text{A}}}_r^s\right)\cdot {\mathbf{\text{u}}}^{\alpha }$$ (A15)

$$\sum _{\alpha }{\rho }^{\alpha }\frac{\partial {\psi }^{\alpha }}{\partial {\rho }^{\gamma }}\frac{D^{\alpha }{\rho }^{\gamma }}{\mathit{\text{Dt}}}=({\widehat{\rho }}^{\gamma }-{\rho }^{\gamma }\mathbf{\text{I}}:{\mathbf{\text{L}}}^{\gamma })(\frac{\partial {\Psi }^I}{\partial {\rho }^{\gamma }}-{\psi }^{\gamma })-\frac{\partial {\Psi }^I}{\partial {\rho }^{\gamma }}{\mathbf{\text{d}}}^{\gamma }\cdot {\mathbf{\text{u}}}^{\gamma }+\sum _{\alpha }\frac{\partial {\Psi }^{\alpha }}{\partial {\rho }^{\gamma }}{\mathbf{\text{d}}}^{\gamma }\cdot {\mathbf{\text{u}}}^{\alpha }$$ (A16)

$$\sum _{\alpha }{\rho }^{\alpha }\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{\text{d}}}^{\gamma }}\cdot \frac{D^{\alpha }{\mathbf{\text{d}}}^{\gamma }}{\mathit{\text{Dt}}}=\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{d}}}^{\gamma }}\cdot \text{grad}{\widehat{\rho }}^{\gamma }-(\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{d}}}^{\gamma }}\cdot {\mathbf{\text{d}}}^{\gamma })\mathbf{\text{I}}:{\mathbf{\text{L}}}^{\gamma }-({\rho }^{\gamma }\mathbf{\text{I}}\otimes \frac{\partial {\Psi }^I}{\partial {\mathbf{\text{d}}}^{\gamma }})⋮\text{grad}{\mathbf{\text{L}}}^{\gamma }-\left({\text{grad}}^T{\mathbf{\text{d}}}^{\gamma }\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{d}}}^{\gamma }}\right)\cdot {\mathbf{\text{u}}}^{\gamma }+\sum _{\alpha }\left({\text{grad}}^T{\mathbf{\text{d}}}^{\gamma }\frac{\partial {\Psi }^{\alpha }}{\partial {\mathbf{\text{d}}}^{\gamma }}\right)\cdot {\mathbf{\text{u}}}^{\alpha }$$ (A17)

$$\sum _{\alpha }{\rho }^{\alpha }\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{\text{L}}}^{\beta }}:\frac{D^{\alpha }{\mathbf{\text{L}}}^{\beta }}{\mathit{\text{Dt}}}=\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{L}}}^{\beta }}:\text{grad}{\mathbf{\text{a}}}^{\beta }-(\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{L}}}^{\beta }}:\text{grad}{\mathbf{\text{L}}}^{\beta })\cdot {\mathbf{\text{u}}}^{\beta }+\sum _{\alpha }(\frac{\partial {\Psi }^{\alpha }}{\partial {\mathbf{\text{L}}}^{\beta }}:\text{grad}{\mathbf{\text{L}}}^{\beta })\cdot {\mathbf{\text{u}}}^{\alpha }$$ (A18)

$$\sum _{\alpha }{\rho }^{\alpha }\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{\text{u}}}^{\beta }}\cdot \frac{D^{\alpha }{\mathbf{\text{u}}}^{\beta }}{\mathit{\text{Dt}}}=\frac{\partial {\Psi }^I}{\partial {\mathbf{\text{u}}}^{\beta }}\cdot ({\mathbf{\text{a}}}^{\beta }-\mathbf{\text{a}})-({\mathbf{\text{u}}}^{\beta }\otimes \frac{\partial {\Psi }^I}{\partial {\mathbf{\text{u}}}^{\beta }}):{\mathbf{\text{L}}}^{\beta }+\sum _{\alpha }\left({\text{grad}}^T{\mathbf{\text{u}}}^{\beta }\frac{\partial {\Psi }^{\alpha }}{\partial {\mathbf{\text{u}}}^{\beta }}\right)\cdot {\mathbf{\text{u}}}^{\alpha }$$ (A19)

where Ψ^α = ρ^αψ^α is the Helmholtz free energy density of constituent α and Ψ^I = Σ_α Ψ^α is the inner part of the mixture Helmholtz free energy density.

Substituting these relations into Eq.(A1) and the resulting expression into Eq.(65) yields

$$\sum _{\alpha }\left[{\rho }^{\alpha }\right(\frac{\partial {\Psi }^{\alpha }}{\partial \theta }+{\eta }^{\alpha })\frac{D^{\alpha }\theta }{\mathit{Dt}}+\frac{\partial {\Psi }^{\alpha }}{\partial \mathbf{g}}\cdot \frac{D^{\alpha }\mathbf{g}}{\mathit{Dt}}+\frac{1}{\theta }{\mathbf{q}}^{\alpha }\cdot \mathbf{g}]+[2{\mathbf{F}}^s\frac{\partial {\Psi }^I}{\partial {\mathbf{C}}^s}\left({\mathbf{F}}^s\right)T+{\Psi }^s\mathbf{I}+2\mathrm{grad}({\mathbf{F}}^s\underset{\_}{\otimes }{\mathbf{F}}^s)⋮\frac{\partial {\Psi }^I}{\partial {\mathbf{G}}^s}-{\mathbf{u}}^s\otimes \frac{\partial {\Psi }^I}{\partial {\mathbf{u}}^s}]:{\mathbf{L}}^s-\sum _{\gamma \ne s}\left[{\rho }^{\gamma }\right(\frac{\partial {\Psi }^{\mathbf{I}}}{\partial {\rho }^{\gamma }}-{\psi }^{\gamma })\mathbf{I}+(\frac{\partial {\Psi }^{\mathbf{I}}}{\partial {\mathbf{d}}^{\gamma }}\cdot {\mathbf{d}}^{\gamma })I+{\mathbf{u}}^{\gamma }\otimes \frac{\partial {\Psi }^I}{\partial {\mathbf{u}}^{\gamma }}]:{\mathbf{L}}^{\gamma }-\sum _{\alpha }[{\mathbf{T}}^{\alpha }+{\rho }^{\alpha }(\frac{p}{{\rho }_T^{\alpha }}+\frac{z^{\alpha }}{M^{\alpha }}{\mathbf{F}}_c\psi \left)I\right]:{\mathbf{L}}^{\alpha }+\left[2\right({\mathbf{F}}^s\otimes F^s):\frac{\partial {\Psi }^I}{\partial {\mathbf{G}}^s}]⋮\mathrm{grad}{\mathbf{L}}^s-\sum _{\gamma \ne s}({\rho }^{\gamma }I\otimes \frac{\partial {\Psi }^I}{\partial d^{\gamma }})⋮\text{grad}{\mathbf{L}}^{\gamma }-[\frac{\partial {\Psi }^I}{\partial C^s}:G^s+\frac{\partial {\Psi }^I}{\partial G^s}⋮\text{grad}{\mathbf{G}}^s+\frac{\partial {\Psi }^I}{\partial {\rho }_r^s}{\mathit{d}}_{\mathit{r}}^{\mathit{s}}+{\text{grad}}^T{\mathit{d}}_{\mathit{r}}^{\mathit{s}}\frac{\partial {\Psi }^I}{\partial {\mathit{d}}_{\mathit{r}}^{\mathit{s}}}+\frac{\partial {\Psi }^I}{\partial {\mathit{A}}_{\mathit{r}}^{\mathit{s}}}:\text{grad}{\mathit{A}}_{\mathit{r}}^{\mathit{s}}+\frac{\partial {\Psi }^I}{\partial L^s}:\text{grad}{L}^s]\cdot u^s-\sum _{\gamma \ne s}[\frac{\partial {\Psi }^I}{\partial {\rho }^{\gamma }}{\mathbf{d}}^{\gamma }+{\text{grad}}^T{}^{\gamma }\frac{\partial {\Psi }^I}{\partial {\mathbf{d}}^{\gamma }}+\frac{\partial {\Psi }^I}{\partial {\mathbf{L}}^{\gamma }}:\text{grad}{\mathbf{L}}^{\gamma }]\cdot {\mathbf{u}}^{\gamma }+\sum _{\alpha }[{\widehat{p}}^{\alpha }-(\frac{p}{{\rho }_T^{\alpha }}+\frac{z^{\alpha }}{M^{\alpha }}{F}_c\psi )\text{grad}{\rho }^{\alpha }+\text{grad}{\Psi }^{\alpha }-\frac{\partial {\Psi }^I}{\partial \theta }\mathbf{g}-{\text{grad}}^T\mathbf{g}\frac{\partial {\Psi }^I}{\partial \theta }]\cdot {\mathbf{u}}^{\alpha }+{\widehat{\rho }}_r^s\frac{\partial {\Psi }^I}{\partial {\rho }_r^s}+\frac{\partial {\Psi }^I}{\partial {\mathit{d}}_{\mathit{r}}^{\mathit{s}}}\cdot \text{grad}{\widehat{\rho }}_r^s+\frac{\partial {\Psi }^I}{\partial {\mathit{A}}_{\mathit{r}}^{\mathit{s}}}:{\widehat{A}}_r^s+\sum _{\gamma \ne s}{\widehat{\rho }}^{\gamma }\frac{\partial {\Psi }^I}{\partial {\rho }^{\gamma }}+\sum _{\gamma \ne s}\frac{\partial {\Psi }^I}{\partial d^{\gamma }}\cdot \text{grad}{\widehat{\rho }}^{\gamma }+\sum _{\alpha }{\widehat{\rho }}^{\alpha }(\frac{p}{{\rho }_T^{\alpha }}+\frac{z^{\alpha }}{M^{\alpha }}{F}_c\psi +\frac{1}{2}{u}^{\alpha }\cdot u^{\alpha })+\sum _{\alpha }\frac{\partial {\Psi }^I}{\partial {\mathbf{L}}^{\alpha }}:\text{grad}{a}^{\alpha }+\sum _{\alpha }\frac{\partial {\Psi }^I}{\partial u^{\alpha }}\cdot (a^{\alpha }-a)\le 0$$ (A20)

Terms with a common factor of: L^s are grouped together and denoted by ${\mathbf{T}}_d^s$, whereas terms with a common factor of: L^γ (γ ≠ s) are grouped together and denoted by ${\mathbf{T}}_d^{\gamma }$. Similarly, terms with a common factor of u^s are grouped into ${\widehat{p}}_d^s$ and those with a common factor of u^γ (γ ≠ s) are grouped into ${\widehat{p}}_d^{\gamma }$.In order for this inequality to be satisfied for arbitrary changes in D^αθ/Dt, D^αg/Dt, grad L^s, grad L^γ, grad a^α and a – a, the relations of Eqs.(80)-(81) must hold.