Do Bayesian adaptive trials offer advantages for comparative effectiveness research? Protocol for the RE-ADAPT study

Abstract

Background

Randomized clinical trials, particularly for comparative effectiveness research (CER), are frequently criticized for being overly restrictive or untimely for health-care decision making.

Purpose

Our prospectively designed REsearch in ADAptive methods for Pragmatic Trials (RE-ADAPT) study is a ‘proof of concept’ to stimulate investment in Bayesian adaptive designs for future CER trials.

Methods

We will assess whether Bayesian adaptive designs offer potential efficiencies in CER by simulating a re-execution of the Antihypertensive and Lipid Lowering Treatment to Prevent Heart Attack Trial (ALLHAT) study using actual data from ALLHAT.

Results

We prospectively define seven alternate designs consisting of various combinations of arm dropping, adaptive randomization, and early stopping and describe how these designs will be compared to the original ALLHAT design. We identify the one particular design that would have been executed, which incorporates early stopping and information-based adaptive randomization.

Limitations

While the simulation realistically emulates patient enrollment, interim analyses, and adaptive changes to design, it cannot incorporate key features like the involvement of data monitoring committee in making decisions about adaptive changes.

Conclusion

This article describes our analytic approach for RE-ADAPT. The next stage of the project is to conduct the re-execution analyses using the seven prespecified designs and the original ALLHAT data.

Introduction

Bayesian and adaptive trial designs have been used to support Food and Drug Administration (FDA) approval of drugs and medical devices and are proposed as an efficient way to achieve valid and reliable evidence from comparative effectiveness research (CER) [1 –9] as defined by the Institute of Medicine [10]. To our knowledge, there have been no Bayesian adaptive CER trials performed and just one such trial plan published [11].

We initiated a project, ‘REsearch in ADAptive methods for Pragmatic Trials’ (RE-ADAPT), funded by the National Heart, Lung and Blood Institute (NHLBI), whose aim is a proof-of-concept that Bayesian adaptive methods may have potential benefits for CER trials. RE-ADAPT will re-execute the Antihypertensive and Lipid Lowering Treatment to Prevent Heart Attack Trial (ALLHAT) [12] using patient-level data to evaluate whether a Bayesian adaptive design might have accomplished the original ALLHAT objectives more efficiently in terms of the number of patients enrolled and the calendar time of the trial.

The aim of the RE-ADAPT study is to emulate the actual process of designing a Bayesian adaptive design tailored to the original aims of the ALLHAT trial (as opposed to performing a Bayesian reanalysis of ALLHAT). The aim of this article is to describe in detail the design process of the simulation protocol. We describe a systematic review of pre-ALLHAT literature and derivation of priors to guide the designs, the specific designs that will be considered, the adaptive mechanisms (e.g., adaptive randomization) that are considered, the criteria on which adaptation decisions will be based, and factors on which the designs will be compared (e.g., final allocation of patients, duration of trial, total sample size, and final conclusions).

By prospectively publishing our protocol before we execute our new designs, we hope to address possible concern of hindsight bias – simply choosing the best design from a set of designs that would have led to a more efficient trial. To further reduce potential/concern for bias, during the design process, the two primary designers (JTC and KRB) remained blinded to the ALLHAT dataset, did not read the clinical outcome articles, and relied only on the original ALLHAT protocol and clinical discussions with cardiovascular experts regarding what cardiologists and trial designers would have known prior to the design of ALLHAT. These discussions, as well as input from the ALLHAT clinical trials center director and statistician (B.R.D.), were used to design our simulation study as though it were occurring historically at the time of ALLHAT.

ALLHAT was selected as a case study because it was large, nationally prominent, evaluated active comparators within community care settings, a public-use patient-level dataset [13] was available, was costly (US$135 million) [14], and was sufficiently lengthy (8 years) that practice patterns and thus clinical questions (e.g., combination versus monotherapy becoming more standard) may have changed during the course of the trial [15].

Co-sponsored by NHLBI and the Department of Veterans Affairs, ALLHAT enrolled 42,418 patients (aged 55 years or above, 47% women and 36% African–American) with at least one cardiovascular disease risk factor besides hypertension [16] to compare three newer antihypertensive medications to a diuretic for reducing fatal coronary heart disease (CHD) and nonfatal myocardial infarction (MI) [3,4,12]. ALLHAT incorporated several adaptive design features including conditions for early study termination and arm dropping [17]. ALLHAT monitored each comparison with its own monitoring guideline with alpha = 0.027 according to the Dunnet procedure. Early success and early futility were both based on stochastic curtailment. The number of looks depended on the information times and the calendar times of the Data and Safety Monitoring Board (DSMB) meetings. In the ‘Discussion’ section of this article, we contrast the adaptive features employed by the ALLHAT investigators with those we have designed.

The RE-ADAPT simulation protocol

The RE-ADAPT protocol consists of developing a series of potential redesigns of ALLHAT followed by simulating them to measure efficiency and performance using de-identified ALLHAT patient data. There are five steps to the process:

1. Conducting a systematic literature review and derivation of priors based on literature existing when ALLHAT was designed to provide the data upon which prior evidence distributions could be derived.

2. Identifying possible adaptations that may improve trial efficiency involves specifying possible adaptive features (e.g., adaptive randomization or arm dropping) that might be included in such a trial.

3. Constructing candidate set of Bayesian adaptive designs for ALLHAT by selecting combinations of priors distributions and specific adaptive features from steps 1 and 2. This includes prespecifying designs, including timing and frequency of interim analyses when adaptations may occur, and thresholds (e.g., early stopping bounds).

4. Selecting an optimal design for implementation from those developed in step 3. A total of 1000 replications of each design created in step 3 were simulated under different scenarios (e.g., no difference between treatments, different effect sizes). The design providing the best operating characteristics (e.g., smallest sample size, shortest trial duration, highest power, and most patients randomized to better therapy) over the widest range of possible efficacy scenarios is chosen for implementation.

5. Executing all designs using actual ALLHAT data to assess the performance of the chosen optimal design and all others considered, comparing each with the original ALLHAT design. Whereas, in reality, a single design must be chosen for implementation, since this is a simulation exercise, we can/will execute the chosen design as well as those we opted ‘not’ to implement.

Details of these steps are explained in the following sections. The first 4 items have been completed; we describe the fifth prospectively.

Systematic literature review and derivation of priors

Priors are required for the Bayesian analysis. They can be classified as non-informative (‘vague’) roughly corresponding to classical analysis in which only new trial data inform the inference; or ‘informative’ (‘historical’) where the evidence distribution is formally incorporated with the new trial data.

We originally planned to create one set of designs with non-informative priors and another using historical priors for each of the four drugs under study. Our formal literature review, however, revealed that no such studies using the ALLHAT primary end point were available for any of the three comparators (angiotensin-converting enzyme (ACE) inhibitors, calcium-channel blockers (CCBs), and alpha-blockers). Therefore, the historical prior effectively matched the non-informative prior for the three comparator drugs, and we chose to incorporate only designs using non-informative priors for all four drugs.

Identify possible adaptations that may improve trial efficiency

Three types of adaptations are considered: adaptive randomization, arm dropping, and early stopping. Adaptive randomization and arm dropping may occur in the accrual stage. All designs allow early stopping of the trial for futility or success, either of which may occur in the accrual or follow-up stages (criteria for early stopping are discussed in detail in the section ‘Early Stopping of the Trial for Success or Futility’). Adaptive randomization and arm dropping (during accrual) serve two key purposes: they increase the probability that patients randomized later in the trial receive a beneficial therapy; and they can increase statistical power by prioritizing data gathering for treatments where the research question remains more uncertain. Furthermore, by performing multiple prospectively defined interim analyses during accrual and follow-up phases, the trial may stop early if primary goals are met or it becomes evident that additional information is unlikely to lead to a significant conclusion.

The following sections describe the different rules with which adaptive randomization, arm dropping, and study termination may be incorporated into designs. These rules involve predetermined thresholds that govern when and which adaptations would be made. These were determined based on simulations testing a range of potential thresholds to find those values offering the most beneficial trade-offs. The statistical and clinical benefits of designs based on the various potential thresholds were discussed between the statistical designers and the clinicians involved to replicate the actual trial design process. This included discussing the overall operating characteristics and also discussing many individual trial simulations to illustrate how the trial would proceed and the nature of possible realizations and the adaptations that would result. This, like an actual adaptive trial design, was an iterative process between the statistical team and clinical team.

All thresholds/decision points were based upon simulation and chosen before the lead statisticians acquired the ALLHAT data. Thresholds for early success stopping were chosen to conserve Type I error to less than 2.5% (one-sided). Thresholds for arm dropping were chosen to balance the probability of correctly dropping a poorly performing arm with incorrectly dropping an arm that was performing poorly early due to natural variability. Thresholds were also chosen to optimize power, trial duration, and percentage of patients randomized to the best therapy. The process of choosing thresholds is analogous to choosing a cutoff threshold for a diagnostic test when weighing sensitivity and specificity – higher, more aggressive values will lead to correctly stopping a trial early or dropping a poor arm sooner, but will also lead to increased Type I errors or an increased likelihood of erroneously dropping efficacious arms.

These decisions are subjective, and different designers and clinicians may have chosen other values. This is similar to trial designers choosing more or less aggressive stopping boundaries in a group sequential trial to match the clinical situation. For instance, we simulate data from the five scenarios discussed below (not ALLHAT data but plausible scenarios) and tuned the thresholds to behave well over this range of plausible ‘truths’. Once the values/decisions points are set, the real ALLHAT data will be used to execute the trial. Another example is provided below in the section describing adaptive arm dropping.

Adaptive randomization

Trials with adaptive randomization begin with an initial assignment probability for each study arm and are later updated at predetermined times based on ‘real time’ observed treatment effects. ALLHAT used fixed randomization with a greater proportion of patients allocated to the diuretic arm to increase power for each pair-wise comparison. We will compare this original fixed randomization approach to two alternative approaches: randomize patients proportional to the probability that each comparator arm offers the higher probability of being the best arm (probability-weighting), and randomize patients proportional to both the observed treatment effects and the uncertainty in those treatment effects (information-weighting). In both cases, randomization to the diuretic arm remains fixed at one-third of patients since this is considered standard treatment to which others are compared. Due to the low incidence of the primary end point (fatal CHD + nonfatal MI), randomization probabilities will first be updated after the 10,000th patient is enrolled and then again every 3 months until the end of accrual. Starting adaptive randomization at 10,000 patients, like other thresholds, was chosen based on comparing the operating characteristics of a variety of alternatives (e.g., 20,000 patients).

The three randomization schemes explored are as follows:

1. Fixed randomization (reference case): Patients are randomized according to the original allocation rules in ALLHAT throughout enrollment: 36.55% to diuretic and 21.15% to each of the three comparator arms [12].

2. Probability-weighted adaptive randomization: Beginning with the 10,000th patient and every 3 months thereafter, randomization probabilities are updated to be proportional to the probability that each comparator offers the best (lowest) hazard ratio (HR) compared to diuretic. Probabilities are derived from posterior distributions of HRs of each treatment at interim analyses. Thus, if all comparators have similar posterior distributions, then randomization to non-diuretic arms would occur with approximate equal probability, and the more dramatic the benefit to a particular arm, the higher the randomization probability to that arm.

   The result is that the comparator arms performing better will receive more patients and overall event rates will be lower than with fixed randomization [18 –22]. However, statistical power for the comparison of the best two arms in a multi-arm trial is increased since the comparator arms of most interest receive larger numbers of patients [23].

3. Information-weighted adaptive randomization: This approach is similar to the probability-weighted approach, but further incorporates the precision of the HRs in the derivation of revised randomization ratios. Thus, in addition to favoring arms with the lowest observed event rates, this approach also prioritizes arms where precision is lowest, and hence, the need for additional data is highest. For example, if CCBs and alpha-blockers appear to be equally efficacious but there is greater variability surrounding the estimate for alpha-blockers, more patients would be randomized to that arm in the next cohort in order to refine its estimate. Adaptive randomization here will tend to be less aggressive than with probability-weighting [24 –26].

Many have criticized adaptive randomization [27,28] for its lack of power compared to fixed randomization. However, these criticisms focus on the two-arm case and are not relevant to this four-arm trial. We acknowledge that 1:1 randomization tends to optimize power in the two-arm case. However, as Berry [23] describes, adaptive randomization tends to increase study power for trials of three or more arms. Furthermore, he suggests that we tend to do two-armed trials because it is hard and expensive to do multi-armed balanced trials, but then having limited most of our thinking to two-arm trials, we criticize adaptive trials in the two-armed setting, which is clearly not where they shine brightest.

Adaptive arm dropping

Another adaptation type that enhances treatment allocation is arm dropping (i.e., suspension of enrollment). This can be viewed as an extension of adaptive randomization in which one or more arms are assigned a zero probability of randomization. The following four adaptive arm-dropping approaches are explored:

1. No arm dropping (reference case) whereby enrollment is never stopped completely, but if the adaptive allocation is allowed in the design, randomization ratios can become very small, effectively zero, if one or more of the CCB, ACE inhibitor, and alpha-blocker arms is performing poorly compared to the others.

2. Posterior probability-based adaptive arm dropping extends designs with adaptive randomization by suspending enrollment into arms with low randomization probabilities. This threshold is set at 0.05 with probability-weighted adaptive randomization and 0.10 with information-weighted adaptive randomization. If randomization probabilities fall below these thresholds, accrual to the arm is suspended, and the remaining arms will receive a proportional increase in randomization. At the next interim analysis, the suspended arm may resume accrual if randomization probabilities increase above the thresholds. Patients in the suspended arms continue treatment and follow-up as usual.

   Arm dropping can be incorporated in the design even if randomization ratios are fixed. Instead of basing the decision to discontinue enrollment on randomization probabilities, adaptation is based on the posterior probability of effectiveness – that is, the probability that the HR of a comparator arm to the diuretic is less than 1. If this probability drops below 0.2, enrollment into the arm is stopped without possibility of resuming and both treatment and follow-up also stops.

   For the 20% threshold, we looked at individual simulations and considered the frequency with which beneficial arms were erroneously terminated (due to natural variability and usually occurring at early interim analyses) versus the proportion of terminations that occurred to truly inferior arms. The higher (more aggressive) this threshold, the greater the likelihood of both good and bad arms being terminated. Therefore, this value was chosen to most often suspend poorly performing arms while rarely suspending better arms that were just at a random low. No formal utility rule was used in the decision process.

3. Predictive probability-based arm dropping is employed when arm dropping can occur, but is based upon predictive probabilities of trial success. In this approach, no adaptive randomization is used, and control arm randomization is fixed at 1/3 with the remaining 2/3 being divided equal between the remaining available arms. This decision rule is based upon predictive power that incorporates data observed (at the time of the interim analysis) and data likely to be observed if each arm stays in the trial. An arm is terminated if predictive power versus diuretic is ever less than 10% and patients who would have been randomized to that arm are redistributed to the remaining arms [29].

Early stopping of the trial for success or futility

Early stopping of the trial for success or futility, a feature of all the designs, will be assessed at interim analyses during the accrual and follow-up phases. Up to nine early stopping interim analyses are planned: when the 20,000th, 30,000th, and 40,000th patients are enrolled (i.e., the latter being the end of accrual), and then at 9, 18, 27, 36, 45, and 54 months after the end of accrual, as noted in Table 1. Final analysis occurs 60 months after final patient enrollment. Early stopping for futility may occur at any interim look, but early stopping for success begins at the 30,000th patient look. Even with 20,000 patients accrued, few events are observed and there is large variability in the observed treatment effects. Thus, early success stopping is not allowed at the first interim analysis.

Table 1.

Planned interim analyses for potential early stopping

Analysis	Sa	Fa
20,000 enrolled	None	0.15
30,000 enrolled	0.9999	0.20
40,000 enrolled	0.9999	0.35
End of accrual + 9 months	0.99975	0.50
End of accrual + 18 months	0.9995	0.60
End of accrual + 27 months	0.99925	0.70
End of accrual + 36 months	0.9990	0.80
End of accrual + 45 months	0.99875	0.90
End of accrual + 54 months	0.9985	0.95
End of trial (End of accrual + 60 months)	0.9985

S_a: success; F_a: failure.

This serves to control Type I error rate in two ways. First, initiating adaptive randomization after 10,000 patients are enrolled but not allowing early success stopping until the 30,000-patient analysis eliminates the possibility of a Type I error at the early analyses. Meanwhile, all design variants that include adaptive randomization will increase the number of patients on arms performing best at that point in time. Thus, these arms will be more rapidly ‘tested’, and if we are truly observing a random high, more patients will be randomized to those arms and we will observe regression to the mean more rapidly, thus decreasing the likelihood of a Type I error at a subsequent analysis. If the effect is real, additional patients to the most effective arm will increase power between the best arm and the comparator.

At each early stopping analysis, the comparator arm with the best (lowest) HR is compared to the diuretic arm, and the posterior probability that the HR is below 1 is compared to the stopping boundaries for success (S_a) and failure (F_a) (Table 1). The trial is stopped early for success if this probability exceeds S_a, and for futility if this probability is below F_a.

Therefore, as soon as one comparator meets a stopping criterion, the trial stops. Two or all three comparators could cross a threshold simultaneously, in which case it would be reported that two or all comparators offer a significant improvement compared to diuretic. Similarly, the best comparator might cross a stopping boundary with the second best close, but not quite, achieving statistical significance. The trial would nevertheless stop as the goal is to most rapidly identify an alternative to diuretic that offers improvements on the primary cardiac outcome.

Stopping boundaries are identical across all designs. Success criteria (S_a) have been calibrated to adjust for both multiple comparisons and frequent interim analyses such that the overall one-sided Type I error rate is less by 2.5%.

Construct candidate set of Bayesian adaptive designs for ALLHAT

Seven different adaptive designs are created by combining the three randomization types with the three-arm-dropping approaches, as noted in Table 2. These include each of the three randomization schemes (none, probability-weighted, and information-weighted) paired with each of the three-arm-dropping schemes (none, posterior probability based, and predictive probability based). The predictive probability arm-dropping scheme incorporates the distribution of outcomes for future subjects, which is dependent upon their randomization assignments. Therefore, this strategy is more complicated if randomization assignments for future subjects vary. Consequently, the predictive-probability-based arm-dropping approach was used only in the context of fixed randomization leaving a total of seven designs.

Table 2.

Planned adaptive trial designs

Design	Allocation	Arm dropping
1	(a) Fixed	(d) None
2	(b) Probability wt	(d) None
3	(c) Information wt	(d) None
4	(b) Probability wt	(e) Posterior probability
5	(c) Information wt	(e) Posterior probability
6	(a) Fixed	(f) Posterior probability
7	(a) Fixed	(g) Predictive probability

Select optimal design for implementation

After the seven candidate designs (each individually optimized via simulation) were identified, we compared them to one another by simulating trials across a variety of plausible effectiveness scenarios. This involves testing each design via simulation to understand the potential performance measured in terms of expected (mean) sample size and duration of the trial, power, probability of stopping early for success or futility, and proportion of patients randomized to the best therapy for five different efficacy scenarios:

• Null: no comparators arms better than control;

• Alternative: all equally better than control (HR = 0.837);

• One Works: one better than control (HR = 0.837) and the other two equal to control;

• Better & Best: one best (HR = 0.837), one slightly better (0.9185), and one equal to control;

• Worse: all are equally worse than control (HR = 1/0.837 =1.195).

These scenarios are based on a range of plausible effectiveness scenarios including the null and alternative hypotheses from the original ALLHAT designs and other variants on these two scenarios. In this manner, we seek to identify an optimal design: one which offers the best trade-off of highest power and most likely to terminate a futile trial early, to identify a successful treatment fastest, and to randomize the highest proportion of patients to the best treatment, all while maintaining Type I error control.

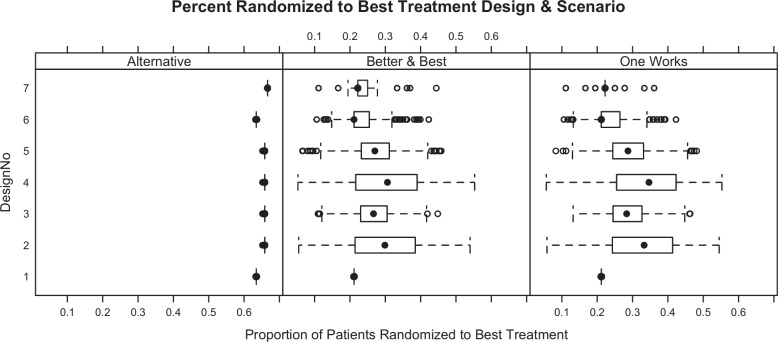
Simulating 1000 trials from each scenario for each of the seven designs produces operating characteristics for each scheme (Table 3). Note that power in the null scenario is the one-sided Type I error rate, and controlled at less than 2.5% (Table 3). In addition to studying average operating characteristics, understanding the range of possibilities for single trials is important. Numerous individual simulated trials were shown to the clinical team. Additionally, Figures 1 and 2 show distributions for study duration and the proportion of patients within each simulation randomized to the best treatment (according to the primary end point). Because each design variant uses the same stopping rules (the key differences are randomization assignment algorithms), trial durations do not change drastically across designs.

Table 3.

Operating characteristics for planned adaptive trial design variants

	Mean subjects	Power	Early success	Early futility	% Randomized to best arm	Mean trial duration (months)
Design 1: early stopping only
Null	39487	0.03	0.023	0.875	1.00	60
Alternative	39513	0.93	0.895	0.005	0.63	56
One Works	39637	0.70	0.657	0.112	0.21	66
Better & Best	39649	0.73	0.669	0.082	0.21	66
Worse	35286	0.00	0.000	1.000	0.37	29
Design 2: probability-weighted adaptive randomization; no arm dropping
Null	39504	0.02	0.020	0.905	1.00	59
Alternative	39400	0.93	0.900	0.016	0.66	56
One Works	39537	0.75	0.708	0.091	0.32	63
Better & Best	39634	0.75	0.707	0.091	0.30	64
Worse	34755.3	0.00	0.000	1.000	0.34	28
Design 3: information-weighted adaptive randomization; no arm dropping
Null	39624	0.02	0.018	0.896	1.00	60
Alternative	39443	0.93	0.901	0.012	0.66	56
One Works	39595	0.75	0.708	0.093	0.28	66
Better & Best	39711	0.78	0.742	0.075	0.27	65
Worse	35118	0.00	0.000	1.000	0.34	29
Design 4: probability-weighted adaptive randomization; 5% arm dropping
Null	39557	0.02	0.018	0.897	1.00	60
Alternative	39395	0.91	0.889	0.01	0.66	57
One Works	39658	0.79	0.728	0.094	0.34	64
Better & Best	39641	0.76	0.707	0.09	0.30	65
Worse	34683	0.00	0	1	0.34	28
Design 5: information-weighted adaptive randomization; 10% arm dropping
Null	39377	0.03	0.022	0.905	1.00	59
Alternative	39503	0.92	0.885	0.013	0.66	56
One Works	39622	0.74	0.704	0.088	0.29	66
Better & Best	39726	0.74	0.7	0.07	0.27	66
Worse	35142	0.00	0	1	0.34	29
Design 6: no adaptive randomization; arm dropping 20% vs control
Null	38568	0.02	0.022	0.736	1.00	56
Alternative	39369	0.92	0.901	0.012	0.79	55
One Works	39256	0.69	0.645	0.104	0.20	63
Better & Best	39404	0.71	0.656	0.103	0.22	64
Worse	31700	0.00	0.000	0.190	0.00	26
Design 7: no adaptive randomization; predictive probability-based arm dropping
Null	38630	0.022	0.020	0.88	1.00	57
Alternative	34337	0.91	0.87	0.012	0.67	57
One Works	37303	0.69	0.64	0.11	0.25	67
Better & Best	37032	0.70	0.65	0.08	0.24	68
Worse	34323	0.00	0.00	>0.99	1.00	27

Figure 1.

Distribution of trial duration (in years) for each design/scenario combination.

Figure 2.

Distribution of proportion of patients randomized to the best therapy (according to primary end points) for each design/scenario combination. The null scenario (all doses equal) and scenario where all comparators are worse than control are not shown since they are the same for all designs (100% and 33%, respectively).

After considering operating characteristics of all candidate designs, we chose Design 4 (probability-weighted adaptive randomization, and probability-based adaptive arm dropping) as the design we would have implemented. Its power is high (91%, 79%, and 76%) for each scenario with an effective comparator. Design 4 offers 79% power versus 70% for a fixed randomization trial when just one comparator is superior to control and 76% versus 73% when one is clearly better and another is in between (one better, one best). In scenarios where one treatment is preferable (One Works and Better & Best), a greater proportion of patients are randomized to the better arm (34% and 30%) compared to trials with fixed randomization (including the original design) in which 21% of patients are randomized to the superior treatment. In the ‘Better & Best’ scenario, 14%, 21%, and 30% of patients are randomized to the inferior, middle, and best comparator, respectively.

The effect of adding an arm-dropping component to adaptive randomization is small but important. Without arm dropping, poor arms are eventually dropped as their probability of being the best arm approaches zero. With arm dropping, these probabilities are truncated to zero anytime they are less than 5%, and then the randomization probabilities are redistributed, thus the arm-dropping component is a bit more aggressive in assigning patients to better performing arms. For instance, when comparing Design 2 with Design 4, 2% more patients are assigned to the best therapy in the One Works scenario producing an increase in power from 75% to 79%.

This highlights the double benefit of adaptive randomization: a higher proportion of patients randomized to the more effective therapy and by the end of the trial resources (patients) are being assigned to the treatment that increases statistical power and randomized away from treatments (the one equal to control) for which we do not desire an increase in statistical power. The Technical Appendix A includes a full description of each design, including additional operating characteristics for each design. An example trial of Design 4 is also detailed there and illustrates how this design would be conducted.

Execution of Bayesian adaptive designs

The first four steps have been completed and are described in this article and in Technical Appendix A. The final step is to execute the chosen Bayesian adaptive design using the actual ALLHAT data.

We believe the best way to judge a trial (adaptive or fixed) is by simulating the trial’s conduct over a broad range of potential scenarios (efficacy scenarios, accrual rates, patient populations, etc.) and studying which trial offers the best operating characteristics over the broadest range of deviations from the primary trial assumptions. However, we understand that simulation, particularly to many clinicians, is sometimes not the most convincing tool. Therefore, until a large-scale CER trial is performed using the adaptive techniques described here, we will implement each of our seven proposed designs using the original ALLHAT data to illustrate how an actual Bayesian adaptive CER trial would likely proceed and how the inferences that result will compare to the traditional alternative (the actual ALLHAT trial).

In addition to executing Design 4, we will also execute the other six designs to understand how each would likely have performed had it been chosen. Actual ALLHAT data will be used to replicate the trial conduct including enrollment, randomization, follow-up, and end-point ascertainment. Should one comparator arm perform particularly well, the adaptive randomization process may call for more patients than were contained in its original ALLHAT arm, in which case we will resample subjects in a bootstrap fashion.

To ensure proper timing for interim analyses, special attention will be given to ensure simulated time reflects actual time between enrollment and timing of end points. Thus, only end points that had occurred and were recorded and available for analysis may inform an interim adaptation. Accumulated data at each prespecified interim looks will be analyzed to test criteria for adaptation or early trial termination. Resulting changes are incorporated and applied to the next patient cohort of enrollees. This virtual process continues until an early stopping criterion is met or the study reaches its administrative end defined by its maximum sample size and maximum follow-up time.

Evaluation criteria

Simulated outcomes of each scheme will be compared in terms of total sample size, trial duration, percentage of patients to each arm, and trial conclusions – how each trial’s inferences compare to the original ALLHAT design’s inferences. We will also look at total numbers of events, both primary and secondary, across all arms in the different designs and we will identify which components of the adaptive trial are leading to benefits or drawbacks compared with the original ALLHAT design.

Discussion

This article illustrates the redesign process we developed and will employ to simulate ALLHAT as a Bayesian adaptive trial. ALLHAT was chosen strictly for convenience as a proof of concept case study. The overall RE-ADAPT project includes several additional components presently under consideration but not addressed here, including an economic analysis of efficiency differences (e.g., trial duration or size) we may detect, and demonstrating how a combination therapy arm could have been added (if desired) during the course of the ALLHAT trial.

In this article, we describe the selected adaptive schemes we will use, stopping rules, and randomization probability updates that may increase power by allocating more patients to better performing study arms, possibly decrease trial duration and sample size, and improve other aspects of trial efficiency. We intentionally make public our protocol prior to executing the reanalysis.

Typically in designing adaptive trials, several candidate designs are developed and tested via simulation based upon a range of possible outcome parameters and one design is selected for implementation. Selecting a single adaptive design in RE-ADAPT is not necessary, however, since the actual ALLHAT data are available and, thus, all candidate designs can easily be executed, including a variant that corresponds closely to the original design of the study. However, we do identify one preferred design that our study group would have implemented if an actual trial were being executed. This eliminates a multiplicity: executing all seven designs and simply comparing the best to the original ALLHAT design. Now, we will focus on one chosen design, prospectively identified, versus the original ALLHAT design.

The original ALLHAT trial was adaptive in that it offered early stopping at loosely defined times that were to be based on Data Monitoring Committee (DMC) meeting times. The early stopping strategies here are slightly more aggressive and not based on DMC meeting times. The major difference, however, is that adaptive randomization was not permitted under the ALLHAT protocol but is a focus here. This may offer increased power to the trial and offer patients, particularly those entering the trial at later stages, the opportunity to receive a better treatment. A final key difference is that our redesign focuses on one-sided tests versus ALLHAT, which was a two-sided trial. We believe, particularly in a case where a cheaper, better understood control arm is studied versus newer, more expensive comparators, that a DMC is unlikely to allow patients to be continually exposed to a comparator arm that is performing poorly merely to show it is statistically significantly worse. In this sense, we believe a one-armed trial better reflects how a DMC would behave.

The benefit of adaptive randomization is most obvious when one arm is superior to others, in which case a larger proportion of patients get randomized to the best treatment. In our pretrial simulation exercise, on average, 34% of patients are randomized to the best treatment arm when adaptive randomization and arm dropping were allowed (Design 4) compared with only 21% with fixed design (Design 1) and original ALLHAT design. Furthermore, power also increased with adaptation (79% in Design 4 vs 70% in Design 1). This occurs because in the fixed design, patients continue to be randomized to inferior treatments in the later stages of enrollment. In contrast, in Design 4, nearly all patients are randomized to diuretics and the best comparator in the later stages of enrollment. This is clinically beneficial for patients and provides increased statistical power for the primary question of interest.

While our aim is to understand how Bayesian adaptive applications may perform in CER trials, we realize that adaptive designs are situation specific, tailored to each unique clinical situation and research question. Therefore, we realize that findings from RE-ADAPT will not generalize to all CER situations that may be encountered.

The exercise described here will require some simplifications and assumptions. In reality, this decision would be based on results from interim data analyses and other factors that may be difficult to capture quantitatively. For instance, the DMC may also consider the safety profile of treatments, important secondary outcomes, or exogenous data that become available during the study. While one key task of the DMC is ensuring proper implementation of the protocol – including resulting adaptations – it may use its prerogative to make deviations to ensure patient safety (e.g., if adaptive randomization would increase randomization probability to an arm that was seeing an increase in a serious adverse event that was not part of the adaptive algorithm). We believe, however, that a DMC’s role in adaptive trials extends to ensuring that the protocol is followed unless there is strong reason to do otherwise. This means ensuring the implementation of all adaptive components. A DMC should not view protocol-defined adaptations as guidelines they may or may not choose to implement. Overruling protocol-defined adaptations leads to poorly understood operating characteristics and unknown Type I and Type II error rates.

This article discusses the primary aims of the RE-ADAPT study. Future articles will explore broader applications of Bayesian adaptive designs, for instance, by simulating the addition of new arms into the study or modeling other adaptations that were not consistent with the original aims of ALLHAT.

Limitations

Although our simulations will rely on actual patient data from ALLHAT and will emulate the original enrollment and follow-up process, the obvious main limitation is that it is a simulation and not a ‘live’ study. However, until a large-scale CER study is conducted using Bayesian adaptive trial methodologies, we hope this exercise will serve to illustrate their potential benefits and challenges. Most notably, we will not simulate the decision process a DMC may use in interpreting findings from interim analyses and approving changes in design, including early stopping. Our simulations will algorithmically apply changes based on adaptation rules without consideration of other contextual factors.

An important challenge with our study has been to omit the benefit of hindsight and knowledge gained from the results of ALLHAT in retrospectively formulating new designs for the trial. Although we went to some lengths to maintain a ‘veil of ignorance’, that effort was undoubtedly imperfect. In some instances, this ‘veil’ may have worked against our aim of making this simulation as realistic as possible.

Our goal is to re-execute these designs using the original ALLHAT data to make the designs’ outcomes directly comparable with the original findings. In some instances, however, adaptive randomization to better performing arms may call for a larger number of patients on an arm than was observed in ALLHAT. Our plan is to resample patients in these situations, and this can lead to an underestimation of the uncertainty of the results from these arms.

Finally, the ability to incorporate prior information is a fundamental advantage of the Bayesian approach, particularly in CER where we might expect high-quality phase-3 data are available on the therapies of interest. Unfortunately, data limitations precluded our planned systematic review and meta-analysis from providing historical priors on the primary outcome for beta-blockers, ACE inhibitors, and CCBs. Therefore, the designs described here used only non-informative priors. However, the sensitivity of CER trial designs to incorporation of historical information is the subject of a future article.

Conclusion

For CER to achieve its lofty aims, investment in comparative trials is needed. Since randomized controlled trials (RCTs) are expensive and time-consuming and not always tailored to achieve CER objectives, the RE-ADAPT project was initiated to test the degree to which Bayesian adaptive trial designs may be useful in increasing CER trial efficiency and utility.

Although the FDA has issued guidance documents [5,6] and both the FDA and manufacturers have gained increasing experience and acceptance of Bayesian and adaptive designs, they have not been tested in CER settings. We hope our effort will be viewed as a valid proof-of-concept of the potential for such designs to be useful for CER and will stimulate investment in them for future CER trials.

This article describes our plans for a redesigned and re-executed ALLHAT. By publishing the details of our prespecified plans, we hope to engender reader confidence that the process can be considered a reasonable approximation of what we would have done had we designed ALLHAT itself as a Bayesian adaptive trial.

Finally, we wish to emphasize that our goal is not to criticize the ALLHAT study (it also contained aims not mentioned here, for example, a statin study component that affected the design) or to claim it should have been designed differently. Rather, we chose to re-execute the ALLHAT study using Bayesian adaptive trial methods because it was a well-designed and conducted trial that provides high-quality data in a CER setting.

Technical Appendix A

Design details

Further details of each design and the prior specifications are shown here. We also demonstrate an example trial for Design 4, our preferred design.

The non-informative priors used for all cases are

$${\lambda }_c~\text{Gamma}(0.001,1)$$

for the diuretic equivalent to 0.001 patients’ worth of information with a mean of 1 day and

$$\log ({\theta }_t)~\text{Normal}(0,{100}^2)$$

for each of the three comparator arms (t = 1,2,3) where θ_t represents the log-hazard ratio (HR):λ_t = λ_c exp(θ_t).

Scenarios

The following five scenarios are used in the design stage. ‘Null’ represents the scenario where no comparator offers benefit over the diuretic. ‘Alternative’ is that all offer an equally large benefit with a HR of 0.837 versus diuretic. ‘One works’ is that one offers benefit while the other two are similar to control. ‘Middle’ is a case where one drug is equal to diuretic, one offers HR 0.9185 versus diuretic, and the third offers HR 0.837 versus diuretic. Worse implies that all three are worse than diuretic with HR 1.195. For all three cases, we assume the diuretic event rate is 6.7% at 6 years.

	Hazard ratio: arm 1	Hazard ratio: arm 2	Hazard ratio: arm 3
Null	1	1	1
Alternative	0.837	0.837	0.837
One Works	1	1	0.837
Middle	1	0.9185	0.837
Worse	1.195	1.195	1.195

Design 1: fixed randomization with no arm dropping

Randomization

The original Antihypertensive and Lipid Lowering Treatment to Prevent Heart Attack Trial (ALLHAT) trial design specified that 1.7 times as many patients would be allocated to the diuretic arm than each of the comparator arms. Thus, patients will be randomized 36.55:21.15:21.15:21.15 to diuretic and each of the comparator arms. As such, a maximum of 14,620 patients will be randomized to diuretic and 8460 patients will be randomized to each of the comparator arms.

Arm dropping

None.

Operating characteristics

Trial success and futility

	Mean subjects	Mean duration (months)	Total Pr(success)	Probability of early success	Probability of success at final evaluation	Probability of early futility	Probability of futility at final evaluation
Null	39,487	60	0.025	0.023	0.002	0.88	0.10
Alternative	39,513	56	0.93	0.90	0.036	0.005	0.064
One Works	39,637	66	0.70	0.66	0.046	0.11	0.19
Middle	39,649	66	0.73	0.67	0.061	0.082	0.19
Worse	35,286	29	0.00	0.00	0.00	1.00	0.00

Mean randomization

	Mean randomization control	Mean randomization arm 1	Mean randomization arm 2	Mean randomization arm 3
Null	14,432	8351	8351	8351
Alternative	14,442	8357	8356	8357
One Works	14,487	8383	8383	8383
Middle	14,491	8385	8385	8385
Worse	12,897	7463	7463	7463

Treatment arm comparisons

	Probability maximum effective arma			Probability superior to diuretic
	Arm 1	Arm 2	Arm 3	Arm 1	Arm 2	Arm 3
Null	0.33	0.36	0.31	0.47	0.46	0.46
Alternative	0.30	0.35	0.34	0.97	0.97	0.97
One Works	0.01	0.02	0.97	0.53	0.52	0.95
Middle	0.01	0.11	0.88	0.54	0.83	0.97
Worse	0.37	0.32	0.31	0.09	0.09	0.09

^aProbability maximum effective arm does not imply the arm chosen as the maximum effective arm is identified as statistically significant compared to the control.

Design 2: probability-weighted randomization with no arm dropping

Randomization

In an initial randomization phase, we will randomize a total of 10,000 patients to the four treatment arms based on the original ALLHAT randomization ratios. Thus 3655 patients will be randomized to diuretic and 2115 will be randomized to each comparator of interest. After this initial phase, adaptive randomization will begin. During adaptive randomization, patients will be randomized in blocks of 6, where 2 patients will be randomized to the diuretic and 4 patients will be randomized to the comparator arms. Adaptive randomization probabilities will be updated every 3 months. Randomization probabilities for each of the comparator arms will be weighted according to the probability that the arm is the maximum effective treatment arm. The randomization probability for treatment arm t is

$$r_t\propto \sqrt{\text{Pr}(t=t_{max})}$$

where

$$\text{Pr}(t=t_{max})=\text{Pr}({\theta }_t=min({\theta }_1,{\theta }_2,{\theta }_3))\mathrm{for}t\in \{1,2,3\}$$

Arm dropping

None.

Operating characteristics

Trial success and futility

	Mean subjects	Mean duration (months)	Total Pr(success)	Probability of early success	Probability of success at final evaluation	Probability of early futility	Probability of futility at final evaluation
Null	39,504	59	0.021	0.020	0.001	0.91	0.074
Alternative	39,400	56	0.93	0.90	0.027	0.016	0.057
One Works	39,537	63	0.75	0.71	0.046	0.091	0.15
Middle	39,634	64	0.75	0.70	0.040	0.091	0.16
Worse	34,755	28	0.00	0.00	0.00	1.00	0.00

Mean randomization

	Mean randomization control	Mean randomization arm 1	Mean randomization arm 2	Mean randomization arm 3
Null	13,489	8798	8544	8671
Alternative	13,455	8576	8684	8685
One Works	13,500	6560	6629	12846
Middle	13,533	6110	8158	11831
Worse	11,906	7587	7542	7718

Treatment arm comparisons

	Probability maximum effective arma			Probability superior to diuretic
	Arm 1	Arm 2	Arm 3	Arm 1	Arm 2	Arm 3
Null	0.35	0.31	0.34	0.44	0.43	0.43
Alternative	0.31	0.35	0.34	0.94	0.94	0.94
One Works	0.02	0.01	0.97	0.51	0.50	0.96
Middle	0.01	0.10	0.89	0.51	0.80	0.95
Worse	0.32	0.34	0.34	0.08	0.08	0.08

^aProbability maximum effective arm does not imply the arm chosen as the maximum effective arm is identified as statistically significant compared to the control.

Design 3: information-weighted randomization with no arm dropping

Randomization

In an initial randomization phase, we will randomize a total of 10,000 patients to the four treatment arms based on the original ALLHAT randomization ratios. Thus 3655 patients will be randomized to diuretic and 2115 will be randomized to each comparator of interest. After this initial phase, adaptive randomization will begin. During adaptive randomization, patients will be randomized in blocks of 6, where 2 patients will be randomized to the diuretic and 4 patients will be randomized to the comparator arms. Adaptive randomization probabilities will be updated every 3 months. Information weighting for the maximum effective treatment arm will be used to determine the adaptive randomization probabilities. Information is a measure of the expected reduction in variance from adding an additional patient and is defined for an arm t as

$$r_t\propto \sqrt{\frac{\text{Pr}(t=t_{max})\mathrm{Var}\left({\theta }_t\right)}{n_t+1}}$$

where $\mathrm{Var}\left({\theta }_t\right)$ is the posterior variance of the log-HR, and n_t is the current number of subjects allocated to arm t.

Arm dropping

None.

Operating characteristics

Trial success and futility

	Mean subjects	Mean duration (months)	Total Pr(success)	Probability of early success	Probability of success at final evaluation	Probability of early futility	Probability of futility at final evaluation
Null	39,624	60	0.019	0.018	0.001	0.896	0.085
Alternative	39,443	56	0.93	0.90	0.024	0.012	0.063
One Works	39,595	66	0.75	0.71	0.045	0.093	0.15
Middle	39,711	65	0.78	0.74	0.039	0.075	0.14
Worse	35,118	29	0.00	0.00	0.00	1.00	0.00

Mean randomization

	Mean randomization control	Mean randomization arm 1	Mean randomization arm 2	Mean randomization arm 3
Null	13,529	8720	8611	8761
Alternative	13,469	8623	8663	8686
One Works	13,519	7361	7445	11267
Middle	13,558	6953	8595	10604
Worse	12,027	7660	7697	7732

Treatment arm comparisons

	Probability maximum effective arma			Probability superior to diuretic
	Arm 1	Arm 2	Arm 3	Arm 1	Arm 2	Arm 3
Null	0.33	0.32	0.34	0.45	0.44	0.44
Alternative	0.33	0.32	0.35	0.96	0.96	0.95
One Works	0.01	0.01	0.98	0.52	0.52	0.96
Middle	0.01	0.09	0.90	0.53	0.83	0.97
Worse	0.32	0.35	0.34	0.08	0.08	0.08

^aProbability maximum effective arm does not imply the arm chosen as the maximum effective arm is identified as statistically significant compared to the control.

Design 4: probability-weighted randomization with arm dropping based on posterior probability

Randomization

In an initial randomization phase, we will randomize a total of 10,000 patients to the four treatment arms based on the original ALLHAT randomization ratios. Thus 3655 patients will be randomized to diuretic and 2115 will be randomized to each comparator or interest. After this initial phase, adaptive randomization will begin. During adaptive randomization, patients will be randomized in blocks of 6, where 2 patients will be randomized to the diuretic and 4 patients will be randomized to the comparator arms. Adaptive randomization probabilities will be updated every 3 months. Randomization probabilities for each of the comparator arms will be weighted according to the probability that the arm is the maximum effective treatment arm. The randomization probability for treatment arm t is

$$r_t\propto \sqrt{\text{Pr}(t=t_{max})}$$

where

$$\text{Pr}(t=t_{max})=\text{Pr}({\theta }_t=min({\theta }_1,{\theta }_2,{\theta }_3))\mathrm{for}t\in \{1,2,3\}$$

Arm dropping

If the adaptive randomization probability for an arm is less than 5%, the randomization probability for this arm will be set to zero, and the remaining arms may receive a proportional increase in randomization probability. In this manner, arms may be dropped, but may be reintroduced if the adaptive randomization probability increases above 5%.

Operating characteristics

Trial success and futility

	Mean subjects	Mean duration (months)	Total Pr(success)	Probability of early success	Probability of success at final evaluation	Probability of early futility	Probability of futility at final evaluation
Null	39,557	59	0.022	0.018	0.004	0.90	0.081
Alternative	39,395	56	0.91	0.89	0.023	0.01	0.078
One Works	39,658	66	0.79	0.73	0.057	0.094	0.12
Middle	39,641	66	0.76	0.71	0.049	0.09	0.15
Worse	34,683	29	0.00	0	0	1	0

Mean randomization

	Mean randomization control	Mean randomization arm 1	Mean randomization arm 2	Mean randomization arm 3
Null	13,507	8567	8645	8837
Alternative	13,453	8505	8703	8733
One Works	13,541	6321	6426	13369
Middle	13,535	5926	8153	12026
Worse	11,882	7594	7560	7645

Treatment arm comparisons

	Probability maximum effective arma			Probability superior to diuretic
	Arm 1	Arm 2	Arm 3	Arm 1	Arm 2	Arm 3
Null	0.33	0.32	0.36	0.44	0.43	0.44
Alternative	0.33	0.33	0.35	0.94	0.94	0.94
One Works	0.01	0.02	0.97	0.52	0.52	0.96
Middle	0.01	0.10	0.89	0.52	0.79	0.95
Worse	0.33	0.33	0.34	0.08	0.08	0.08

^aProbability maximum effective arm does not imply the arm chosen as the maximum effective arm is identified as statistically significant compared to the control.

Arm dropping

	Probability arm dropped (at least once)
	Arm 1	Arm 2	Arm 3
Null	0.51	0.48	0.51
Alternative	0.51	0.51	0.50
One Works	0.75	0.73	0.20
Middle	0.78	0.55	0.28
Worse	0.48	0.47	0.45

Design 5: information-weighted randomization and arm dropping based on posterior probability

Randomization

In an initial randomization phase, we will randomize a total of 10,000 patients to the four treatment arms based on the original ALLHAT randomization ratios. Thus, 3655 patients will be randomized to diuretic and 2115 will be randomized to each comparator or interest. After this initial phase, adaptive randomization will begin. During adaptive randomization, patients will be randomized in blocks of 6, where 2 patients will be randomized to the diuretic and 4 patients will be randomized to the comparator arms. Adaptive randomization probabilities will be updated every 3 months. Information weighting for the maximum effective treatment arm will be used to determine the adaptive randomization probabilities. Information is a measure of the expected reduction in variance from adding an additional patient and is defined for a treatment arm t as

$$r_t\propto \sqrt{\frac{\text{Pr}(t=t_{max})\mathrm{Var}\left({\theta }_t\right)}{n_t+1}}$$

where $\mathrm{Var}\left({\theta }_t\right)$ is the posterior variance of the log-HR, and n_t is the current number of subjects allocated to arm t.

Arm dropping

If the adaptive randomization probability for an arm is less than 10%, the randomization probability for this arm will be set to zero and the remaining arms may receive a proportional increase in randomization probability. In this manner, arms may be dropped, but may be reintroduced if the adaptive randomization probability increases above 10%.

Operating characteristics

Trial success and futility

	Mean subjects	Mean duration (months)	Total Pr(success)	Probability of early success	Probability of success at final evaluation	Probability of early futility	Probability of futility at final evaluation
Null	39,377	56	0.025	0.022	0.003	0.91	0.070
Alternative	39,503	55	0.92	0.89	0.03	0.013	0.072
One Works	39,622	63	0.74	0.70	0.04	0.088	0.17
Middle	39,726	64	0.74	0.70	0.042	0.07	0.19
Worse	35,142	26	0.00	0.00	0.00	1.00	0.00

Mean randomization

	Mean randomization control	Mean randomization arm 1	Mean randomization arm 2	Mean randomization arm 3
Null	13,447	8573	8689	8666
Alternative	13,489	8642	8732	8638
One Works	13,529	7454	7325	11313
Middle	13,563	6902	8613	10646
Worse	12,035	7666	7702	7737

Treatment arm comparisons

	Probability maximum effective arma			Probability superior to diuretic
	Arm 1	Arm 2	Arm 3	Arm 1	Arm 2	Arm 3
Null	0.30	0.34	0.36	0.42	0.43	0.42
Alternative	0.36	0.32	0.33	0.96	0.96	0.96
One Works	0.014	0.012	0.97	0.51	0.51	0.96
Middle	0.008	0.094	0.90	0.52	0.83	0.97
Worse	0.31	0.36	0.33	0.08	0.08	0.08

^aProbability maximum effective arm does not imply the arm chosen as the maximum effective arm is identified as statistically significant compared to the control.

Arm dropping

	Probability arm dropped (at least once)
	Arm 1	Arm 2	Arm 3
Null	0.25	0.25	0.25
Alternative	0.28	0.25	0.25
One Works	0.42	0.47	0.10
Middle	0.53	0.29	0.14
Worse	0.23	0.22	0.21

Design 6: fixed randomization with arm dropping based on posterior probability

Randomization

The original ALLHAT trial design specified that 1.7 times as many patients would be allocated to the diuretic arm than each of the comparator arms. Thus, patients will be randomized 36.55:21.15:21.15:21.15 to diuretic and each of the comparator arms. As such, a maximum of 14,620 patients will be randomized to diuretic and 8460 patients will be randomized to each of the comparator arms.

Arm dropping

After 20,000 patients have been randomized to the four treatment arms, looks for arm dropping will begin. Looks for arm dropping will occur every 3 months. At each look, an arm may be dropped if the posterior probability it is superior to diuretic is less than 20%

$$\mathrm{Pr}\left({\theta }_t<0\right)<20\%$$

The diuretic arm may not be dropped. If all three comparator arms are dropped, the trial will stop. If an arm is dropped, it may not re-renter the trial, but the total sample size of the trial will remain the same, and as such accrual to the remaining arms will increase.

Operating characteristics

Trial success and futility

	Mean subjects	Mean duration (months)	Total Pr(success)	Probability of early success	Probability of success at final evaluation	Probability of early futility	Probability of futility at final evaluation
Null	38,568	60	0.023	0.022	0.001	0.736	0.080
Alternative	39,369	57	0.92	0.90	0.021	0.012	0.060
One Works	39,256	64	0.69	0.65	0.049	0.10	0.15
Middle	39,404	65	0.71	0.66	0.049	0.10	0.17
Worse	31,700	28	0.00	0.00	0.00	0.19	0.00

Mean randomization

	Mean randomization control	Mean randomization arm 1	Mean randomization arm 2	Mean randomization arm 3
Null	14,097	8021	8149	8300
Alternative	14,389	8344	8305	8329
One Works	14,348	7743	7811	9352
Middle	14,401	7417	8486	9099
Worse	11,586	6696	6737	6679

Treatment arm comparisons

	Probability maximum effective arma			Probability superior to diuretic
	Arm 1	Arm 2	Arm 3	Arm 1	Arm 2	Arm 3
Null	0.31	0.35	0.34	0.38	0.39	0.40
Alternative	0.32	0.35	0.33	0.92	0.92	0.92
One Works	0.04	0.04	0.93	0.45	0.45	0.90
Middle	0.02	0.14	0.85	0.42	0.73	0.91
Worse	0.33	0.34	0.33	0.10	0.10	0.11

^aProbability maximum effective arm does not imply the arm chosen as the maximum effective arm is identified as statistically significant compared to the control.

Arm dropping

	Probability arm dropped
	Arm 1	Arm 2	Arm 3
Null	0.49	0.50	0.46
Alternative	0.079	0.084	0.078
One Works	0.50	0.48	0.095
Middle	0.55	0.22	0.092
Worse	0.93	0.92	0.92

Design 7: fixed randomization with arm dropping based on predictive probabilities

Randomization

Patients are randomized 1/3 to diuretic for the entire trial. The remaining 2/3 of patients are randomized evenly to the available arms. This is 2/9 for each arm for the first 10,000 patients, then 2/9 (if all arms remain available), 1/3 (if 2 arms remain available), or 2/3 (if one arm remains available).

Arm dropping

At the time 20,000 and 30,000 patients are enrolled, arm-dropping analyses are performed. We calculate the predictive probability of demonstrating superiority to diuretic at the end of the trial. If this probability is less than 10% assuming the current randomization probabilities, the comparator arm is dropped. If all three arms are dropped, the trial stops for futility.

If accrual reaches 40,000 patients, post accrual follow-up proceeds as described in the articles with early stopping possible for success or futility.

Operating characteristics

	Mean subjects	Mean duration (months)	Total Pr(success)	Probability of early success	Probability of success at final evaluation	Probability of early futility	Probability of futility at final evaluation
Null	38,630	57	0.022	0.020	0.002	0.88	0.094
Alternative	34,337	57	0.91	0.87	0.04	0.012	0.080
One Works	37,303	67	0.69	0.64	0.05	0.11	0.20
Middle	37,032	68	0.70	0.65	0.05	0.08	0.21
Worse	34,323	27	0.00	0.00	0.00	>0.99	>0.99

Mean randomization

	Mean randomization control	Mean randomization arm 1	Mean randomization arm 2	Mean randomization arm 3
Null	12,878	8565	8602	8585
Alternative	11,447	7630	7637	7622
One Works	12,436	7798	7831	9237
Middle	12,346	7613	8275	8798
Worse	11,442	7589	7627	7665

Treatment arm comparisons

	Probability maximum effective arma			Probability superior to diuretic
	Arm 1	Arm 2	Arm 3	Arm 1	Arm 2	Arm 3
Null	0.30	0.34	0.36	0.42	0.43	0.42
Alternative	0.357	0.318	0.325	0.96	0.96	0.96
One Works	0.014	0.012	0.974	0.51	0.51	0.96
Middle	0.008	0.094	0.898	0.519	0.827	0.967
Worse	0.31	0.36	0.33	0.08	0.08	0.08

^aProbability maximum effective arm does not imply the arm chosen as the maximum effective arm is identified as statistically significant compared to the control.

Arm dropping

	Probability arm dropped (at least once)
	Arm 1	Arm 2	Arm 3
Null	0.30	0.30	0.30
Alternative	0.06	0.05	0.06
One Works	0.31	0.30	0.06
Middle	0.30	0.14	0.05
Worse	0.76	0.76	0.76

Example trial

This is a single simulation of Design 4 to illustrate the adaptive algorithm.

The first interim analysis occurs when 10,000 patients have been enrolled (Table A1). In this example, this occurs 34 weeks after the start of the study. Early stopping is not allowed, only an update of the adaptive allocation probabilities. The 10,000 patients have been allocated according to the initial allocation ratios. Very few events have been observed in each arm. Currently, Arm 2 has the greatest observed treatment effect and Arm 1 has the smallest observed treatment effect. The probability that Arm 1 is the maximum effective arm is 4%. This translates to a probability of allocation less than 5% and allocation to Arm 1 is suspended.

Table A1.

Adaptive allocation update: 10,000 patients and 34 weeks

	N Pts	N Events	Total Exp (years)	Hazard ratio	Pr(Max)	Pr(Alloc)
Diuretic	3655	13	1165	–	–	0.33
Arm 1	2115	7	677	0.91	0.04	0.00
Arm 2	2115	3	675	0.39	0.65	0.46
Arm 3	2115	4	676	0.54	0.30	0.21

The next update to the adaptive allocation probabilities occurs 3 months later (47 weeks) (Table A2). At this time, 14,118 patients have been enrolled. Arm 1 continues to have the smallest observed treatment effect, but the treatment effects for Arms 2 and 3 are now smaller and appear more similar. The probability Arm 1 is the maximum effective arm increases to 8%, and allocation to this arm resumes, but with only a 6% probability of allocation. The next interim analysis, conducted at 60 weeks, is similar.

Table A2.

Adaptive allocation update: 14,118 patients (47 weeks)

	N Pts	N Events	Total Exp (years)	Hazard ratio	Pr(Max)	Pr(Alloc)
Diuretic	5028	21	2247	–	–	0.33
Arm 1	2115	13	1203	1.15	0.08	0.06
Arm 2	4012	11	1438	0.82	0.46	0.31
Arm 3	2963	10	1312	0.83	0.45	0.30

An interim analysis for early futility stopping is conducted when 20,000 patients have been enrolled, but with promising arms, the early futility criteria are not met and enrollment continues. Now at 73 weeks from the start of the study, 22,097 patients have been enrolled (Table A3). Arm 1 is still performing poorly relative to the other two arms, and again, allocation to Arm 1 is suspended. Allocation to Arm 1 remains suspended at the interim analyses conducted at 86 weeks and 99 weeks. The interim analysis at 99 weeks also coincides with the early stopping look after 30,000 patients have been enrolled. At this early stopping look, stopping for either futility or success is allowed. Arm 3 is the mostly likely maximum effective treatment, and the probability its HR relative to diuretic is less than 1 is 0.9964. This is less than the 0.9999 required for early success stopping and enrollment continues.

Table A3.

Adaptive allocation update: 22,097 patients (73 weeks)

	N Pts	N Events	Total Exp (years)	Hazard ratio	Pr(Max)	Pr(Alloc)
Diuretic	7689	55	5403	–	–	0.33
Arm 1	2590	29	2361	1.20	0.03	0.00
Arm 2	6770	37	4077	0.89	0.37	0.26
Arm 3	5048	28	3350	0.83	0.60	0.41

By the interim analysis at 112 weeks, accrual is nearly complete (34,283 patients), and Arm 3 is highly likely to be the maximum effective arm (Table A4). Allocation to Arms 1 and 2 is suspended. Patients are now allocated 1:2 to diuretic and Arm 3.

Table A4.

Adaptive allocation update: 34,283 patients (112 weeks)

	N Pts	N Events	Total Exp (years)	Hazard ratio	Pr(Max)	Pr(Alloc)
Diuretic	11,753	133	12623	–	–	0.33
Arm 1	2590	53	4272	1.17	0.00	0.00
Arm 2	9184	104	10179	0.97	0.02	0.00
Arm 3	10,756	68	9074	0.72	0.98	0.67

Accrual is completed (40,000 patients) by the next interim analysis, 138 weeks after the start of the study (Table A5). In all, 34% of patients have been allocated to the diuretic and 36% have been allocated to Arm 3, the most likely maximum effective arm. A third early stopping analysis is conducted now that accrual is complete. The probability that Arm 3 has a HR relative to diuretic less than 1 is 0.9996, which is less than the 0.9999 required to stop early. The trial continues following all patients, and early stopping looks will be conducted every 9 months.

Table A5.

Adaptive allocation update: 40,000 (138 weeks)

	N Pts	N Events	Total Exp (years)	Hazard ratio	Pr(Max)	Pr(Alloc)
Diuretic	13,659	208	19031	–	–	0.33
Arm1	2590	68	5537	1.12	0.01	0.00
Arm 2	9184	160	14705	0.99	0.01	0.00
Arm 3	14,567	119	15642	0.70	0.99	0.67

At the first interim analysis conducted after accrual is complete, this trial stops early for success (Table A6). While the treatment effect for Arm 3 is not as large as observed at the previous early stopping look, additional patient years of follow-up have reduced the uncertainty around the estimate. The probability that Arm 3 has a HR relative to diuretic is less than 1 is > 0.9999, which is greater than the 0.99975 required for early stopping.

Table A6.

Interim analysis 9 months after complete accrual: stop early for success

	N Pts	N Events	Total Exp (years)	Hazard ratio	Pr(Max)	Pr(Alloc)
Diuretic	13,659	328	29076	–	–	–
Arm1	2590	84	7421	1.01	0.01	–
Arm 2	9184	239	21441	0.98	0.002	–
Arm 3	14,567	225	26438	0.75	0.98	–