A Comparison of In Vivo Cellular Responses to Cs-137 Gamma Rays And 320-kV X Rays

Abstract

Research reported here relates to comparing the relative effectiveness of 320-kV X rays compared to Cs-137 gamma rays for two in vivo endpoints in C.B-17 mice after whole-body exposure: (1) cytotoxicity to bone marrow cells and splenocytes evaluated at 24-hours post exposure and (2) bone marrow and spleen reconstitution deficits (repopulation shortfalls) evaluated at 6 weeks post exposure. We show that cytotoxicity dose-response relationships for bone marrow cells and splenocytes are complex, involving negative curvature (decreasing slope as dose increases), presumably implicating a mixed cell population comprised of large numbers of hypersensitive, modestly radiosensitive, and resistant cells. The radiosensitive cells appear to respond with 50% being killed by a dose < 0.5 Gy. The X-ray relative biological effectiveness (RBE), relative to gamma rays, for destroying bone marrow cells in vivo is > 1, while for destroying splenocytes it is < 1. In contrast, dose-response relationships for reconstitution deficits in the bone marrow and spleen of C.B-17 mice at 6 weeks after radiation exposure were of the threshold type with gamma rays being more effective in causing reconstitution deficit.

INTRODUCTION

Self-shielded cesium-137 chloride (¹³⁷CsCl) irradiators with radioactivity levels in the International Atomic Energy Agency Categories 1 and 2 (i.e., greater than 27 Ci) are widely used in three major applications (NRC 2008): (1) blood sterilization, (2) bio-medical research involving cells in culture and small animals, and (3) calibration. Cesium-137 chloride was selected for the irradiators because of the radiological properties of Cs-137, including its desirable single (662 keV, for unshielded photons) energy, long half-life, relative low cost, and moderate shielding requirements relative to other radionuclides. A report by the National Research Council (NRC 2008) recommended that careful consideration be given to the possibility of replacing Cs-137 irradiators with X-ray irradiators for homeland security purposes.

Research reported here relates to possibly replacing ¹³⁷CsCl irradiators used in radiobiological research involving small animals with an X-RAD 320 Unit (X-ray source [PXINC 2010]) with energies higher than for a typical X-ray irradiator. The objective of the research reported here was to demonstrate the feasibility of achieving the same success in mouse radiobiology studies employing a 320-kV X-ray unit spectrum as has been achieved with higher energy gamma rays from Cs-137. Success would be expected if the X-ray relative effectiveness compared to gamma rays is not a limiting factor for the radiobiological endpoint of interest. The focus of the studies reported here were on (1) bone marrow and spleen cell destruction shortly (24 hours) after irradiating C.B-17 mice (males and females) and (2) on reconstitution deficits in both organs at 6 weeks post exposure of female C.B-17 mice. Reconstitution deficit refers to the repopulation shortfall in the cell count after allowing time for recovery from radiation-induced cell killing (cytotoxicity). Our emphasis was on determining if the X-Ray relative effectiveness compared to gamma rays was a limiting factor in achieving study success.

METHODS

Animals

Female and male C.B-17 mice (10 – 18 weeks old) were either bred at Lovelace Respiratory Institute or purchased from Taconic (Germantown, NY). Animals were housed in sterile microisolator caging with autoclaved bedding. They received irradiated food (Teklad Global 18% Protein Rodent Diet 1918 Irradiated, Harlan Laboratories, Madison, WI) and antibiotic treated water (enrofloxacin, 175 mg/mL) (Baytril 100, Bayer HealthCare) for the duration of our studies. For the first 14 days post-irradiation, mice were supplemented with moistened food daily. Lab gel (Banana flavored enrichment gel, no sugar added 71-01-1081, ClearH2O, Portland, ME) was provided as necessary. All experiments were approved by the Institutional Animal Care and Use Committee and were conducted at Lovelace Respiratory Research Institute, an AAALAC-approved facility.

Irradiators

Gammacell-1000 Unit

The Gammacell-1000 unit (AECL 1984) used is a self-contained irradiator that was designed to deliver large radiation doses to small biological samples. The irradiator consists of a stationary Cs-137 doubly-encapsulated radiation source permanently secured within a steel-encased, lead biological shield. The biological shield is mounted on a steel frame and covered with sheet-metal panels. The biological shield contains the sample chamber rotor. By turning the rotor through an arc of up to 180 degrees, the sample chamber is either exposed to or removed (except for leakage radiation) from the radiation field. The radioactive source consists of an array of two ¹³⁷CsCl pencils (Model ISO-1000; AECL 1984).

X-RAD 320 Unit

The X-RAD 320 Unit (PXINC 2010) is a self-contained X-ray irradiation system that is designed for use in biology and medical research. The X-RAD 320 Irradiation System is used in conjunction with the GE ISO-VOLT 320 TITAN X-ray unit. A Cathode Generator with a Power Electronics Module and Anode Generator are used to generate the negative and positive high voltages used to excite the X-ray tube. For our unit, an oil-to-air cooling system is employed.

Animal Irradiation

Just before the first of two dose fractions, mice were anesthetized with 75 – 100 mg/kg ketamine (Putney and/or Fort Dodge Animal Health, Inc) and 5 mg/kg xylazine (Anased, Akorn, Inc.) delivered in a maximum of 0.20 mL saline i.p. Anesthetized mice were placed in 50 mL polypropylene conical centrifuge tubes with the conical end removed to allow a 7 mm hole for breathing. They were secured in the tubes with absorbent wipes placed in front of the tube cap. All radiation doses were delivered as a split dose (i.e., two separate dose fractions) with 50% of the dose being delivered in each of two sessions separated by 4 hours. Between the two irradiation sessions, mice were allowed to wake up from their anesthesia on temperature controlled warming pads and once awake were placed back in their cages with access to food and water. Just before the second dose fraction, mice were again anesthetized with the indicated amount of ketamine and xylazine. No adverse effects were observed related to the two applications of anesthesia.

Tubes were secured horizontally on a turntable in the X-RAD 320 Unit whereas they were positioned vertically in the stainless steel sample canister in the Gammacell 1000 Unit. Mice were rotated on turntables for the duration of the radiation exposures to allow for more uniform distribution of dose. In addition, because the X-ray source was above the mice, the tubes were positioned with the ventral side of the mouse facing the source during the first irradiation session and during the second session the tubes were positioned such that their dorsal side was facing the source. The rotation reduces the risk of damage to the skin.

For our 24-hour study of cytotoxicity to bone marrow and spleen, 21 mice (males and females combined) were used. For our 6-week study of organ reconstitution (recovery/repopulation), data for 13 female mice are reported in this paper. Data for 7 male mice were inconsistent and are excluded.

Dosimetry

Radiation absorbed doses to mice were evaluated using Thermoluminescent Dosimeters (TLD, Quantaflux, Oregonia, OH) which were read on-site using a Victoreen 2800 Thermoluminescent Reader. Dose calibration relationships for the X-RAD 320 unit were established based on Victoreen ionization chamber wands and a Condenser R-Meter Model 570 (Fluke Biomedical, Cleveland, OH). Gammacell 1000 Unit exposure readings based on TLDs were confirmed using nanoDots (Optically Stimulated Luminescence Technology, Landauer, Glenwood, IL). Initial dosimetry was performed by inserting TLDs into mouse carcasses in the inguinal area near femurs to estimate the dose to the bone marrow. These values were used to determine the exposure times for experimental runs. Experimental doses were measured by TLDs taped either to center of turntable (X-RAD 320 Unit) or taped to the outside of exposure tubes (Gammacell 1000 Unit). Gamma-ray doses ranged from 0 to 7.11 Gy. X-ray doses ranged from 0 to 4.74 Gy.

Bone Marrow and Spleen Isolation

Mice were euthanized by i.p. injection of an overdose of Euthasol (0.5 cc 10% Euthasol, Virbac AH, Inc., 300 – 500 mg/kg). Spleen and hind legs were aseptically removed. For bone marrow isolation, femur and tibia bones were isolated and cleaned of muscle and soft tissue. Bones were cut at the ends and the marrow was flushed into 50 ml tubes with complete RPMI (Cellgro) with 5% FBS (Atlanta Biologicals) using a 25 gauge needle and 10 cc syringe.

Splenocytes were isolated by pressing the spleen between frosted ends of sterile microscope slides and collecting cells into 15 mL tubes by rinsing with complete RPMI plus 5% FBS. Bone marrow and spleen cells were spun at 300 × g, for 10 minutes, and resuspended in ACK Lysis Buffer (hypotonic ammonium chloride) to remove RBC. Cells were washed in HBSS and resuspended in complete RPMI with 5% FBS, and filtered through a 40 μm pore size cell strainer (Falcon, BD Biosciences). Cell counts were made under a compound microscope using a hemocytometer and dilutions of Trypan Blue.

Modeling Approaches

An empirical model developed based on exploratory analyses was used for characterizing in vivo cytotoxicity dose-response relationships for bone marrow cells and splenocytes at 24 hours after radiation exposure of C.B-17 mice. A Bayesian approach implemented via Markov chain Monte Carlo was used to obtain model parameter values (Gilks et al. 1996; Gamerman 1997; Siva 1998). An Appendix is provided summarizing the Bayesian approach discussed. A separate empirical model, also developed based on exploratory analyses, was used for characterizing reconstitution deficits in bone marrow and spleen at 6 weeks after radiation exposure of C.B-17 mice. Linear regression was used with applying the second model. More details on the modeling conducted are provided in the section titled Results and Discussion and in the Appendix.

RESULTS AND DISCUSSION

Data Used in Modeling

Table 1 shows the in vivo 24-hour post-exposure, bone-marrow cytotoxicity data (cytotoxicity hazard) used in our analyses. Bone marrow data derived from male and female mice were similar as expected and both were used. The cytotoxicity hazard was evaluated as explained in the next section. Table 2 shows the corresponding splenocyte data. Splenocyte data for males and females were similar as expected and both were used. Table 3 shows the week 6, post-exposure bone marrow cellularity data for female C.B-17 mice used in our analyses of cell count deficits. Table 4 shows the corresponding splenocyte cellularity data.

TABLE 1.

In vivo bone marrow cytotoxicity hazard data evaluated at 24 hours after whole-body Cs-137 gamma- or 320-kV X-ray exposure of male and female C.B-17 mice.^a

X-Ray Data		Gamma-Ray Data
Dose (Gy)	Observed Hazard	Dose (Gy)	Observed Hazard
0	0	0	0
0	0	0	0
0	0	0	0
1.94	1.17	2.42	1.56
1.94	2.18	2.42	1.47
1.94	1.04	2.42	1.64
3.35	2.06	4.7	1.83
3.35	1.89	4.7	1.48
3.35	1.67	4.7	1.68
4.74	1.89	6.11	2.06
4.74	2.15	6.11	1.69
4.74	1.72	6.11	2.24

^aCytotoxicity hazard was evaluated relative to the average number of cells scored in control mice. Data for male and female mice were similar so all the data were used. Each data entry relates to a single animal.

TABLE 2.

In vivo splenocyte cytotoxicity hazard data evaluated at 24 hours after Cs-137 gamma- or 320-kV X-ray exposure of female C.B-17 mice.^a

X-Ray Data		Gamma-Ray Data
Dose (Gy)	Observed Hazard	Dose (Gy)	Observed Hazard
0	0	0	0
0	0	0	0
0	0	0	0
1.94	1.68	2.42	2.92
1.94	2.11	2.42	2.66
1.94	1.97	2.42	2.55
3.35	3.07	4.7	4.54
3.35	2.53	4.7	3.39
3.35	2.31	4.7	3.21
4.74	2.92	6.11	3.31
4.74	3.06	6.11	3.64
4.74	3.51	6.11	3.46

^aCytotoxicity hazard evaluated relative to the average number of cells scored in control mice. Data for male and female mice were similar so all the data were used. Each data entry relates to a single animal.

TABLE 3.

Bone marrow cell counts in female C.B-17 mice and body weights of the mice at 6 weeks after gamma-ray exposure.^a

Dose (Gy)	Cells (millions)	Weight (g)
0	15.69	23.7
0	15.17	24.8
2.68	17.13	25.2
2.68	15.00	29.5
2.70	22.79	21.9
2.83	20.94	23.1
4.64	15.63	30.1
4.79	14.94	24.7
5.16	10.38	23.8
6.15	9.69	25.2
6.38	14.78	25.6
6.38	14.50	23.0
7.11	8.69	22.1

^aEach data entry relates to a single animal.

TABLE 4.

Splenocyte counts in female C.B-17 mice and body weights of the mice at 6 weeks after gamma-ray exposure.^a

Dose (Gy)	Cells (millions)	Weight (g)
0	130.31	23.7
0	161.88	24.8
2.68	155.00	25.2
2.68	130.21	29.5
2.70	177.71	21.9
2.83	156.04	23.1
4.64	142.81	30.1
4.79	127.81	24.7
5.16	90.21	23.8
6.15	82.81	25.2
6.38	69.06	23.0
6.38	127.5	25.6
7.11	84.06	22.1

^aEach data entry relates to a single animal.

Relative Biological Effectiveness Evaluation

Exploratory analyses of 24-hour, post-exposure splenocyte and bone marrow cell survival (in vivo) data were conducted to help select a plausible model to use for relative biological effectiveness (RBE) evaluation for 320 kV X rays vs. Cs-137 gamma rays. In carrying out the exploratory analyses the surviving fraction data were converted to corresponding cytotoxicity hazard data using the following equation

$$H(D_{\text{j}})=-\text{ln}[S(D_{\text{j}})],$$ (1)

where S(D_j) is the surviving fraction and H(D_j) is the cytotoxicity hazard as a function of the radiation dose D_j for radiation of type j (X rays or gamma rays). Equation 1 follows from the fundamental relationship between the survival probability and the cumulative hazard function as they relate to all-or-none biological effects (Scott 1984, 1986, 2004). The effect modeled can be cell death, neoplastic transformation, cancer occurrence, organ dysfunction, acute lethality, etc. (Scott 2004). Because of its allowance for a variety of different curve shapes, we used the following empirical model with parameters D_50,j (median effective dose) and v (shape parameter) (Scott 2004):

$$H(D_{\text{j}})=[\text{ln}(2)]{[D_{\text{j}}/D_{50,\text{j}}]}^v.$$ (2)

For v = 1, a linear no-threshold (LNT) relationship arises for the cytotoxicity hazard. For v = 2, a quadratic relationship (i.e., positive curvature, with the slope progressively increasing as dose increases) arises. Linear (no curvature) and positive curvature dose-response relationships are typical for in vitro studies of cell survival after exposure to low-LET photon radiation when the surviving fraction is plotted using a logarithmic scale and dose is plotted using a linear scale (Scott 1977; Fertil et al. 1984; Fertil and Malaise 1985). For v < 1, negative curvature (i.e., decreasing slope with increasing dose) arises which is unusual for in vitro studies of homogeneous populations exposed to low-LET photon radiation but appears to be the case for our in vivo data presented here which can be presumed to be explained on the basis of a heterogeneous population. For ionizing photon radiation, the shape parameter v is expected to be independent of the type of radiation (Scott 2004), which was assumed here.

We used the Bayesian approach, implemented via Markov chain Monte Carlo (MCMC, Lunn et al. 2000), to estimate model parameters D₅₀ and v (see Appendix for more details). The cytotoxicity hazard H(D_j) was modeled as being normally distributed for a given value of D_j with a standard deviation equal to the standard deviation for the experimental data fitted with the model. With this approach, one obtains not only a posterior distribution mean (central estimate) for a given parameter but also the standard deviation and percentiles (e.g., 5%, 10%, 50%, 90%, 95%) of the posterior distribution. The prior distribution used for D_50,j for splenocytes was uniform from 0.01 to 5.0 Gy. For bone marrow cells, the corresponding distribution was uniform from 0.01 to 2.0 Gy. For both cell types, the prior distribution used for v was uniform from 0.05 to 1.0, because of negative curvature in the dose-response data revealed by exploratory analysis.

The 320 kV X-ray and Cs-137 gamma-ray data for a given cell type were simultaneously fit to facilitate evaluating a common value for the parameter v. One hundred thousand iterations (single chain) were used for the MCMC analysis for bone marrow cells and 140 thousands iterations for splenocytes, with only the last 20,000 results retained for each cell type for analysis. The number of iterations and data discarding were based on autocorrelations observed over the first 5000 iterations. The discarded MCMC-generated data represents what is called burn-in (see Appendix for more discussion).

The X-ray RBE for in vivo cytotoxicity relative to gamma rays was evaluated based on the following equation:

$$\text{RBE}=D_{50,\text{g}}/D_{50,\text{x}}.$$ (3)

Because D_50,g and D_50,x have posterior distributions, RBE also has a posterior distribution. We used the mean of the posterior distribution as our central estimate of RBE.

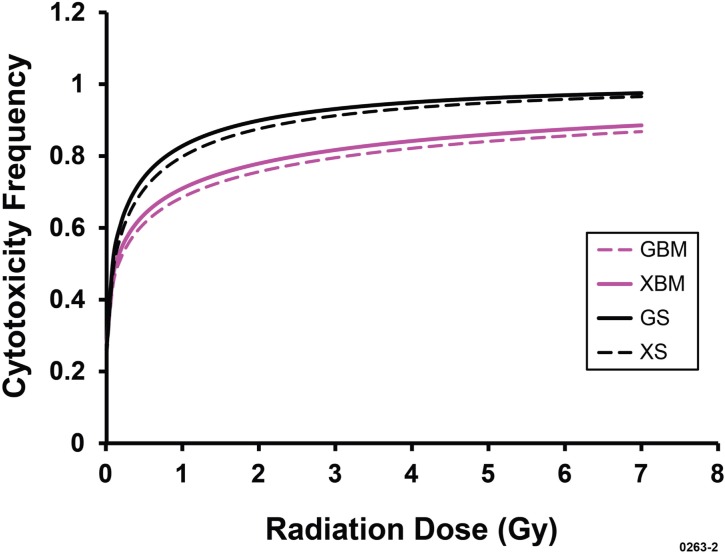
Table 5 and Figures 1A and 1B show results (cytotoxicity hazards) obtained in our MCMC analyses of data for early-on (24-hours after exposure) cytotoxicity for the two cell and two radiation types. Negative-curvature, dose-response relationships were observed for both X rays and gamma rays and for both cell types and implicate heterogeneous (mixed) cell populations as is known to be the case. While the doses D_50,x and D_50,g for killing 50% of the target cells were < 0.5 Gy, the added dose needed to kill the remaining 50% of the cells exceeded 6 Gy. Thus, a large number of cells in the target populations appear to be radiosensitive, a large number appear modestly radiosensitive, and a large number appear quite resistant to being killed.

TABLE 5.

Summary of MCMC results obtained for splenocytes and bone marrow cells evaluated in vivo after whole-body exposure of male and female C.B-17 mice to Cs-137 gamma rays or 320-kV X rays.

Cells	Parameter	mean	sd	5%	10%	50%	90%	95%
Splenocytes	D50,g in Gy	0.0871	0.040	0.0326	0.0399	0.0818	0.141	0.161
Splenocytes	D50,x in Gy	0.112	0.043	0.05	0.0593	0.107	0.169	0.19
Splenocytes	v	0.382	0.044	0.311	0.324	0.381	0.439	0.456
Splenocytes	RBEa	0.763	0.109	0.583	0.623	0.763	0.902	0.943
Bone marrow	D50,g in Gy	0.17	0.077	0.0681	0.0811	0.158	0.276	0.32
Bone marrow	D50,x in Gy	0.134	0.072	0.0444	0.0553	0.121	0.233	0.277
Bone marrow	v	0.288	0.045	0.223	0.233	0.284	0.348	0.370
Bone marrow	RBEa	1.346	0.283	0.965	1.026	1.305	1.709	1.862

^aRBE values refer to X rays relative to gamma rays.

FIGURE 1A.

Cytotoxicity hazard for bone marrow cells in vivo at 24 hours after X-ray or gamma-ray exposure of C.B-17 mice (combined data for males and females): HazG, fitted line for gamma rays; DataG, gamma-ray data; HazX, fitted line for X rays; DataX, X-ray data. FIGURE 1B. Corresponding results for splenocytes: HazG, fitted line for gamma rays; DataG, gamma-ray data; HazX, fitted line for X rays; DataX, X-ray data.

X rays were found to be more effective (RBE = 1.35, posterior distribution mean) than gamma rays in damaging bone marrow cells inside the body. In contrast, X rays were found to be less effective (RBE = 0.76, posterior distribution mean) than gamma rays in damaging splenocytes inside the body. Similar estimates of RBE can also be obtained based on the separate posterior distribution means for D_50,g and D_50,x presented in Table 5. Figure 2 shows the corresponding dose-response relationships for the cytotoxicity frequency (i.e., cell killing frequency) which was evaluated as 1 – S(D_j), where based on Equation 1,

$$S(D_{\text{j}})=\text{exp}[-H(D_{\text{j}})].$$ (4)

FIGURE 2.

Central estimates of the frequency of cytotoxicity (cell killing) to bone marrow cells and splenocytes in vivo for X-ray and gamma-ray exposure of female C.B-17 mice based on curves presented in Figures 1A and 1B. GBM, for gamma rays and bone marrow; XBM, for X rays and bone marrow; GS, for gamma rays and splenocytes; XS, for X rays and splenocytes.

Exploratory-Analysis-Based Equations for Evaluating Reconstitution Deficit

Data in Tables 3 and 4 were first evaluated for correlations between key variables (D_j, C(D_j), and body weight). Because C(D_j) might be influenced by organ weight, data for C(D_j) in millions of cells were first evaluated against body weight in grams. This approach is based on the assumption that at the end of a fixed follow-up time, organ weight and body weight are correlated for animals of similar ages. For the female C.B-17 mice studied and related ages, no significant correlations were observed (p > 0.05) as indicated in Table 6. In contrast, significant correlations were found when data for C(D_j) were evaluated against the gamma-ray dose D_g but not when evaluated against the X-ray dose D_x (for the lower dose range studied for X rays based on a study design RBE of 1.3), as indicated in Table 6. This along with other results from data exploratory analyses was interpreted to indicate that cell reconstitution deficit increases with gamma-ray dose above the threshold (i.e., for the excess dose D – T) but not for X-ray exposure over the dose-range studied (implicating T > maximum D_x used). Thus, our analyses revealed that Cs-137 gamma rays appear to be more effective (lower threshold T) than 320-kV X rays in causing reconstitution deficit at 6 weeks after radiation exposure. Full reconstitution is implicated after the X-ray doses used. These observations are consistent with the splenocyte cytotoxicity hazard data in Figure 1B (X-ray RBE = 0.76) but not the bone marrow cytotoxicity data in Figure 1A (X-ray RBE = 1.3).

TABLE 6.

Results of correlation analyses related to bone marrow and spleen cellularity at 6 weeks after whole-body exposure of female C.B-17 mice to gamma or X rays

Radiation Type	Tissue	Comparison	Correlation Coefficient	Degrees of Freedom	Significance (p value)
Gamma	Bone marrow	Cell count vs. weight	−0.075	11	> 0.5
Gamma	Bone marrow	Cell count vs. dose	−0.54	11	< 0.05a
Gamma	Spleen	Cell count vs. weight	0.145	11	> 0.5
Gamma	Spleen	Cell count vs. dose	−0.712	11	< 0.01a
X rays	Bone marrow	Cell count vs. weight	0.03	12	> 0.5
X rays	Bone marrow	Cell count vs. dose	0.19	12	> 0.5b
X rays	Spleen	Cell count vs. weight	0.377	12	> 0.1
X rays	Spleen	Cell count vs. dose	−0.296	12	> 0.2b

^aResults implicate an increasing deficit in cellularity as the gamma-ray dose increases.

^bResults implicate no deficit in the cellularity irrespective of dose.

Additional exploratory analyses of bone marrow and spleen cellularity (cell counts) at 6 weeks after gamma-ray exposure of female C.B-17 mice were conducted to provide guidance on a plausible dose-response model. In the analysis, dose-response relationships were expressed using log vs. linear, linear vs. log, and log vs. log scales. These analyses revealed two components to the dose-response relationship for the cell count: (1) a low-dose range where cellularity was the same as for controls; (2) a high-dose range where there was a deficit in the cell count relative to controls (i.e., reconstitution deficit) and the cell count decreased exponentially as dose increased above a threshold dose T for a deficit. The low dose range comprised only two doses (controls and lowest non-zero dose group). Based on the indicated observations, the following model was used to characterize the expected cell count C(D) (in millions) in spleen and bone marrow of C.B-17 mice as a function of the radiation dose D that was received 6 weeks earlier:

$$C(D)=N_0,\text{for}\hspace{0.17em}D<T.$$

Otherwise,

$$C(D)=N_0\text{exp}[-\alpha (D-T)].$$ (5)

The threshold T was estimated as the largest dose applied that was not associated with a deficit in the cell count at 6 weeks after radiation exposure. This however corresponded to the lowest non-zero dose group as already indicated. The reconstitution deficit, deficit(D), of the cell count in millions was evaluated based on the following relationships:

$$\mathit{deficit}(D)=0,\text{when}\mathit{ }D<T.$$

Otherwise,

$$\mathit{deficit}(D)=N_0-C(D)=N_0(1-\text{exp}[-\alpha (D-T)]).$$ (6)

Model parameter N₀ and α were estimated based on linear regression of data for ln[C(D)] against the excess dose “D – T” for doses D ≥ T. With this approach, the intercept obtained is an estimate of ln[N₀] and the slope multiplied by −1 is an estimate of α. N₀ is then evaluated by exponentiation of the estimate obtained for ln[N₀].

Dose-Response Relationships for C(D_j) and deficit(D_j)

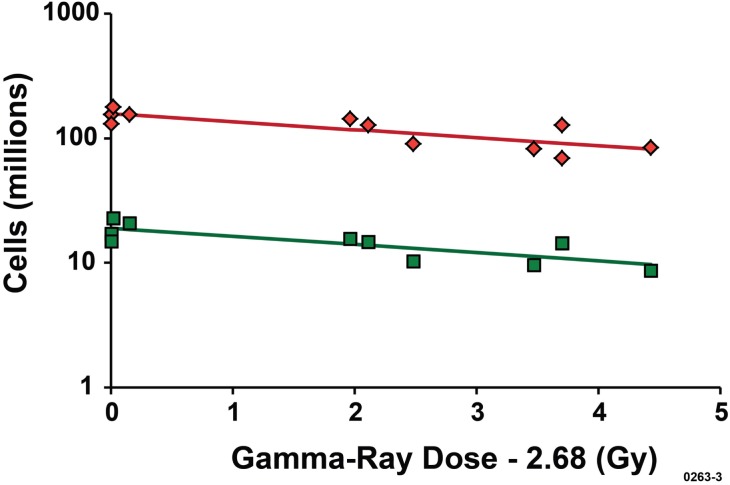
Dose-response relationships for C(D_j) are presented in Figure 3 for both bone marrow cells and splenocytes with T estimated to be 2.68 Gy. Data for C(D_j) are plotted against the excess dose (D – T) for D ≥ 2.68 Gy. C(D) (cells in millions) is plotted on a logarithmic scale against the excess dose “D – 2.68” Gy on a linear scale. The slope parameter α was not significantly different (p > 0.3) for bone marrow cells and splenocytes (see Table 7 for values). The intercept N₀ for splenocytes was 157 million cells (rounded central estimate) and for bone marrow cells the rounded central estimate was 19 million cells (see footnotes ^a and ^b for Table 7).

FIGURE 3.

Dose-response relationships for bone marrow (lower line) and spleen (upper line) cellularity for female C.B-17 mice exposed to gamma rays 6 weeks prior to animal sacrifices. The upper line has the intercept N₀ = 157 million cells. The lower line has the intercept N₀ = 19 million cells. These values for N₀ were used to obtain results presented in Figure 4.

TABLE 7.

Results of regression of data for ln[C(D_g)] vs. “D_g – 2.68”, for D_g ≥ 2.68 Gy, for bone marrow cells and splenocytes at 6 weeks after whole-body, gamma-ray exposure of female C.B-17 mice.

Parameter	Tissue	Parameter Value and Standard Error
ln[N0]	Bone marrow	2.933 ± 0.098 a
ln[N0]	Spleen	5.056 ± 0.093b
α (Gy−1)	Bone marrow	0.134 ± 0.038
α (Gy−1)	Spleen	0.15 ± 0.04c

^aN₀ = exp(2.933) = 19 million cells (rounded).

^bN₀ = exp(5.056) = 157 million cells (rounded).

^cNot significantly different from bone marrow, p > 0.3.

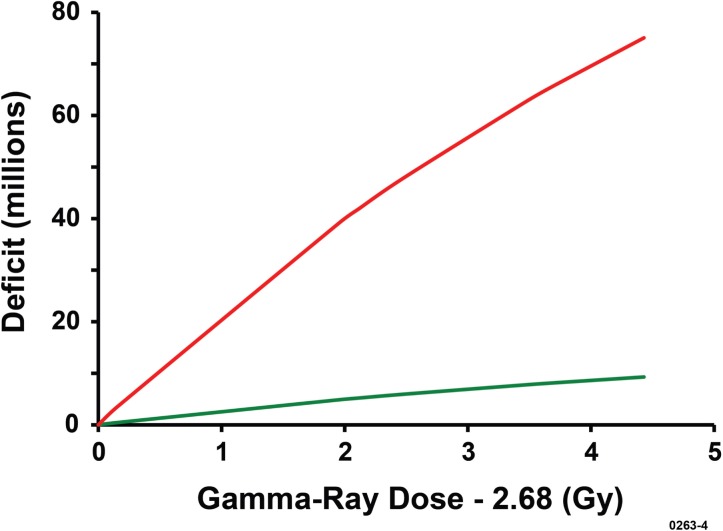
The indicated central estimates of N₀ were used to evaluate deficit(D_g) for both bone marrow cells and splenocytes at 6 weeks after Cs-137 gamma-ray exposure of female C.B-17 mice. Results obtained are presented in Figure 4 as a function of the excess dose, for D_g ≥ 2.68 Gy. Much larger reconstitution deficits were revealed for splenocytes compared to bone marrow cells. For a given dose D_g, deficit(D_g) was a factor of 157/19 = 8.3 larger (central estimate) for splenocytes than for bone marrow cells. This was not the case for X rays for which the data for C(D_x) did not reveal any significant negative correlations of C(D_x) with dose D_x for the more limited range of doses studied for both bone marrow cells and splenocytes (Table 6). We interpret this to mean that T for X-ray exposure is larger and/or α is much smaller than for gamma-ray exposure. If so, larger X-ray doses would be needed to demonstrate a reconstitution deficit in bone marrow cells and splenocytes at 6 weeks after radiation exposure of female C.B-17 mice. Larger X-ray doses than used in our studies may be needed for successful bone marrow transplantation studies using 320-kV X rays or lower energy X rays (Scott et al. 2012).

FIGURE 4.

Central estimates of reconstitution deficits for splenocyte (upper red curve) and bone marrow cells (lower curve) in female C.B-17 mice at 6 weeks after exposure to gamma rays. No deficits were found for mice exposed to X rays for the shorter range of doses used for X rays (data not presented).

CONCLUSIONS

Early (24-hour, post-exposure) in vivo cytotoxicity dose-response relationships for bone marrow cells and splenocytes of C.B-17 mice are complex, showing negative curvature, implicating a mixed cell population comprised of large numbers of hypersensitive, modestly radiosensitive, and resistant cells. The radiosensitive cells appear to respond without a threshold radiation dose, however additional studies are needed to confirm this. Modest and high doses of both Cs-137 gamma rays and 320-kV X rays can destroy large numbers of both bone marrow cells and splenocytes of C.B-17 mice. The X-ray RBE relative to gamma rays for destroying bone marrow cells in vivo is > 1 while for destroying splenocytes is < 1. In contrast, dose-response relationships for reconstitution deficits in the bone marrow and spleen of C.B-17 mice at 6 weeks after radiation exposure were of the threshold type with gamma rays being more effective (lower threshold) in causing reconstitution deficits in both the bone marrow and spleen. It is important to consider these reconstitution deficit differences for Cs-137 gamma-ray and 320-kV X-ray exposures when designing mouse bone marrow transplantation studies using 320-kV X rays.

APPENDIX. Estimating Cytotoxicity Model Parameters using Bayesian Inference Implemented with MCMC

With the Bayesian approach, model parameters and the biological effects for data of interest (e.g., cytotoxicity hazard) are considered random variables (Gamerman 1997; Siva, 1998). If “data” is used to denote the observed biological effects vector and θ is used to denote a model parameters vector, then formal Bayesian inference requires setting up a joint probability distribution P(data,θ) over the quantities in the two vectors (biological effects and model parameters). This joint distribution comprises two parts: a prior distribution, P(θ), and a likelihood, P(data|θ). The vertical bar indicates that the data vector is conditional on the parameter vector θ. The joint probability distribution is specified as

$$P(\mathbf{data},\mathbf{\theta })=P(\mathbf{data}|\mathbf{\theta })P(\mathbf{\theta })=P(\mathbf{\theta }|\mathbf{data})P(\mathbf{data}).$$ (A1)

Both P(θ) and P(data) are unconditional distributions. When new observations are available, Bayes theorem is used to update the distribution of the parameters P(θ|data) given (i.e., conditional on) the new data. The Bayesian updating relationship can be expressed as (Siva, 1998):

$$\begin{array}{c}P(\mathbf{\theta }|\mathbf{data})=P(\mathbf{data}|\mathbf{\theta })P(\mathbf{\theta })/\int P(\mathbf{data}|\mathbf{\theta })P(\mathbf{\theta })d\mathbf{\theta }=\\ P(\mathbf{data}|\mathbf{\theta })P(\mathbf{\theta })/\text{P}(\mathbf{data}).\end{array}$$ (A2)

Depending on the complexities of the model being addressed, analytical solutions to Equation A2 may exist. Analytical solutions do not exist for many complex stochastic models. However, whether or not an analytical solution exists, the integral can be estimated numerically using MCMC (Gilks et al. 1996; Lunn et al. 2000).

MCMC methods are a group of sophisticated methods that are often used in complex Bayesian analyses. The most common implementation uses what are called the Metropolis-Hastings algorithm and Gibbs sampling. Markov chains provide a framework under which simulation techniques may be used to explore various distribution properties, generally focused on the posterior distribution. Gibbs sampling is iterative and allows the marginal distribution of model parameters (e.g., v, D_50,g, D_50,x) to be directly sampled. The Markov chain component of Gibbs sampling provides the framework from which the random samples are generated. However, it is required that the distribution of all parameters, conditional on all other influential parameters and the data fitted, to be specified to allow Monte Carlo sampling. Generally, single or multiple chains are used and data from the initial portion from a Markov chain sample is discarded so that the effect of the initial values on the posterior inference is minimized. The discarded data are called burn-in.