Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2013 Sep 9;29(23):2964–2970. doi: 10.1093/bioinformatics/btt521

Precise inference of copy number alterations in tumor samples from SNP arrays

Gary K Chen 1,*, Xiao Chang 2, Christina Curtis 1, Kai Wang 1,2,3,*
PMCID: PMC3834792  PMID: 24021380

Abstract

Motivation: The accurate detection of copy number alterations (CNAs) in human genomes is important for understanding susceptibility to cancer and mechanisms of tumor progression. CNA detection in tumors from single nucleotide polymorphism (SNP) genotyping arrays is a challenging problem due to phenomena such as aneuploidy, stromal contamination, genomic waves and intra-tumor heterogeneity, issues that leading methods do not optimally address.

Results: Here we introduce methods and software (PennCNV-tumor) for fast and accurate CNA detection using signal intensity data from SNP genotyping arrays. We estimate stromal contamination by applying a maximum likelihood approach over multiple discrete genomic intervals. By conditioning on signal intensity across the genome, our method accounts for both aneuploidy and genomic waves. Finally, our method uses a hidden Markov model to integrate multiple sources of information, including total and allele-specific signal intensity at each SNP, as well as physical maps to make posterior inferences of CNAs. Using real data from cancer cell-lines and patient tumors, we demonstrate substantial improvements in accuracy and computational efficiency compared with existing methods.

Availability: Source code, documentation and example datasets are freely available at http://sourceforge.net/projects/penncnv-2.

Contact: gary.k.chen@usc.edu or kaichop@gmail.com

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Copy number alterations (CNAs) refer to the copy number change of a chromosomal segment that is of somatic origin, often observed in tumor tissues (Albertson et al., 2003; Pollack et al., 2002). In contrast to inherited copy number variants (CNVs) present in the germline, CNAs tend to be longer and occupy a significantly larger proportion of the genome. The recent application of single nucleotide polymorphism (SNP) genotyping arrays has led to the characterization of genomic aberrations associated with cancer development and prognosis (Beroukhim et al., 2007; Caren et al., 2010; Waddell et al., 2010; Weir et al., 2007), and some studies have investigated CNAs in cancer cell lines (Bignell et al., 2010) and tumor subtypes (Beroukhim et al., 2010; Curtis et al., 2012). The comprehensive characterization of CNAs in cancer genomes is critical for understanding disease etiology and for advancing the development of targeted therapies for individual cancer patients (Attiyeh et al., 2005; Perez et al., 2011; Slamon et al., 1987; Zhang et al., 2009).

A number of methods have been proposed to detect both CNVs and CNAs using SNP genotyping array-based technologies such as those from Affymetrix or Illumina. Compared with array-comparative genomic hybridization (CGH) platforms, which measure only the total intensity at each marker, SNP arrays report both the overall intensities of the probe hybridization reaction for each SNP, as well as the ratio of the intensities between the two alleles. Recent versions of high-density SNP arrays have incorporated non-polymorphic markers to better interrogate genomic regions for which SNP information is not adequate or not available. By leveraging signal intensity data from SNP arrays, statistical methods can measure both total copy number and allelic states with high resolution due to the high density of SNPs featured on these microarrays (typically ranging from 500 000 to >2.5 million markers across the genome). Dozens of computational algorithms have been developed for CNV detection on SNP arrays, and these methods have already been widely used in human genetics research (Winchester et al., 2009). However, the problem of CNA detection is considerably more difficult than CNV detection for several reasons. First, whereas germline CNVs can be inferred based on the assumption of a baseline copy number of two, calibration of the baseline in tumors is not obvious, as tumor cells may be aneuploid (i.e. have an abnormal number of chromosomes). A second complication, known as stromal contamination, arises from the fact that samples derived from malignant tissue are often contaminated with adjacent normal tissue. Simply modeling the copy number state of the tumors may lead to inaccurate estimates, as the true copy number state is distributed as a mixture of normal and one or more tumor cells populations. Third, intra-tumor heterogeneity is now appreciated as a common feature of cancer genomes (Gerlinger et al., 2012; Michor and Polyak, 2010), and sub-populations of cancer cells may harbor distinct copy number changes. Fourth, although CNAs and CNVs can both be recurrent events, CNA boundaries may be more variable in a region across samples, so sensitivity may be an issue for CNA methods. Continuous time hidden Markov Models (HMMs) are traditionally favored for modeling the underlying state space (i.e. copy number and allelic state) for CNV/CNA inference, as they integrate over all parameters in the model, including the spatial relationship between SNPs along the genome, allowing one to obtain both point estimates and their confidence intervals for the parameters of interest. In the current study, we present an HMM-based solution to CNA detection that addresses each of the issues specific to tumor genomes. Because several previously published methods have also considered some of these complications, we compare these with our approach and highlight its advantages.

2 METHODS

2.1 Overview

Our CNA calling algorithm, PennCNV-tumor, is an HMM-based method that is loosely based on the model used in PennCNV (Wang et al., 2007), an algorithm developed specifically for germline CNV detection. Later in the text, we describe the key features that are unique to the proposed method.

For each sample, we include global parameters that model stromal contamination (γ) and aneuploidy (via a correction factor β), and SNP specific parameters that model intra-tumor heterogeneity (αi), allelic imbalance (baci) and copy number (cni) at each SNP i. Aneuploidy estimation is an essential a component of chip-wide normalization in tumor samples so that a baseline Log R ratio (LRR) of 0 is assigned to SNPs whose CN corresponds to the overall DNA index (which may not equal 2 as in hypo- or hyper- diploid tumor samples). Formally, stromal contamination is the overall fraction of normal cells among a mixture of tumor and normal cells. In contrast, we characterize intratumor heterogeneity, at each SNP i, based on the fraction of subclones in addition to the dominant tumor clone. Such events may suggest functionally important somatic events during tumor progression. Allelic imbalance provides information as to which germline allele is more likely to have somatic gain/loss at heterozygous sites, offering biological insights into the functional role of germline mutations (Wang et al., 2011). Furthermore, unlike CNVs that typically represent single-copy deletions or duplications, tumor CNAs often involve amplification of multiple copies. Finally, our current HMM accommodates the fact that CNA events are more prevalent and usually much larger than CNVs in cancer samples.

2.2 Estimation of stromal contamination

Although stromal contamination and CNA calls can in principle be simultaneously estimated, our analyses on real data suggest that CNA calls are more reliable if we first estimate stromal contamination (γ) in a pre-processing step. The parameter γ can then be used in the HMM for CNA detection. To estimate γ, we apply a maximum likelihood estimation procedure at each contiguous k non-overlapping window (e.g. 100 markers) across the genome. We exclude non-polymorphic markers, as well as SNP markers in the sex chromosomes and mitochondria from the estimation procedure. The method leverages the fact that at regions where there is a single copy number loss or an amplification event, a mixture of tumor and stromal samples will likely shift the B allele frequency (BAF; i.e. the ratio of intensities between the B allele and both alleles) distributions for heterozygous SNPs. By default, half of the windows with the lowest average LRR values are considered. Our model assumes a baseline average heterozygosity level for the genome is already known, derived from empirical evidence (e.g. h = 0.3 for Illumina 550 K array for any given Caucasian sample). For this model, rather than using the BAF, we consider the B minor allele frequency (BMAF), which is equivalent to BAF for BAF < .5 and 1-BAF in all other cases. Suppose that s is the index of the first marker of a window. We consider w candidate values for γk ranging from 0 to 1 (e.g. w = 50 candidates provide a resolution for γk of 0.02). At each candidate c (c = 1, 2, … , w), we compute the log-likelihood γkc at a sliding window with m markers and finally choose c that maximizes the expression:

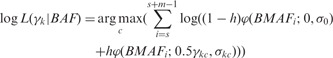graphic file with name btt521m1.jpg (1)

where φ() is the density function of a univariate Gaussian distribution. Assuming that higher BMAF values have higher variance, σkc is assigned from a linear interpolation of σhomo and σhet, the standard deviations of BMAF for homozygous and heterozygous SNPs, respectively (both parameters are pre-specified in PennCNV for Illumina or Affymetrix arrays). For windows where tumor and normal copy numbers are concordant (e.g. CN = 2), γk is not informative and is uniformly distributed across the set of candidate values c. For informative regions however, γk will be consistent. Hence, we select the mode of γk, taken across all windows, as our estimate of the global parameter γ. The standard deviation parameters σhomo and σhet can also be estimated from the data, but from our experience, these estimates do not vary substantially from pre-specified values. Similarly, choosing alternative values for h between 0.1 and 0.5 has little impact on estimation of γ. These findings suggest that our procedure for estimating γ is robust to prior assumptions.

2.3 Adjustment of signal intensity by aneuploidy and genomic waves

For SNP genotyping arrays, values for the LRRi and BAFi at each SNP can be generated from the Illumina GenomeStudio software for Illumina arrays or from the PennCNV-Affy pipeline for Affymetrix arrays at each SNP (indexed by i in our notation). LRRi is a normalized measure of total signal intensity of two alleles (i.e. sum of A and B allele intensities) and BAFi is a normalized measure of allelic intensity ratio. Further details can be found in (Wang et al., 2007). We now describe our pre-processing procedure, which adjusts observed LRRi values to account for both aneuploidy and genomic waves.

Tumor samples may have large-scale duplications and deletions of one or more chromosomes, so the average ploidy levels cannot safely be assumed to be two, as is the case for germline samples. After evaluating several aneuploidy estimation methods, we adopted a straightforward method of exploiting the empirical LRRi distribution for SNPs with BAFi values within a narrow range. The approach is an integral part of the PennCNV-tumor algorithm. We estimate the aneuploidy correction factor β by taking a weighted average of all possible copy numbers at sites where BAFi is near .5 (e.g. | BAFi −.5|<.01), where the weight is the emission probability (described in the following section) at the HMM state associated with the copy number. The expected intensity value associated with β is then added to the LRRi at each SNP, which is similar in spirit to previously described methods (Attiyeh et al., 2009; Yau et al., 2010).

In addition to aneuploidy adjustment, a second adjustment procedure eliminates the phenomenon known as ‘genomic waves’ (Diskin et al., 2008; Marioni et al., 2007). Genomic waves refer to the variation in hybridization intensity that is related to the genomic position of the clones. In practice, real datasets usually exhibit genomic waves and would result in erroneous CNA calls (see examples later in the text). Our solution entails fitting a regression model where GC content is included as a predictor variable (Diskin et al., 2008). This technique complements our aneuploidy adjustment procedure. Briefly, given M markers in a genotyped sample, we collect all the m autosome markers that are at least 1 Mb away from each other. For each of the m markers, we collect its LRR value as Lj (j = 1, … , m) and the average GC percentage in the 1 Mb window around the marker, then fit a linear regression model: Lj = α + βGj + εj. After obtaining these estimated regression parameters, for each of the M marker in the genotyping array, we then calculate the expected signal intensity value based on the GC percentage in the 1 Mb window around the marker. The adjusted signal intensity value is then simply calculated as the observed LRR value minus the expected value (residual in the regression model).

2.4 Hidden states in HMM

The hidden states of our HMM model copy number counts, LOH status and intra-tumor heterogeneity. Typical CNV algorithms for SNP arrays model copy number ranging from 0 to 4, but higher level values may also be discernable for large CNAs. Unlike other software tools, we consider tumor copy numbers ranging from 0 to 4 by default but make this parameter user-adjustable. For copy numbers of zero and two copies, we do not model intra-tumor heterogeneity levels (αi) for the reason of identifiability. However, we include an additional LOH state for two copy numbers. For all other copy numbers, we include additional states that consider values for αi ranging from 0 to 1, in increments of .25 by default. Supplementary Table S1 recapitulates our state definition, but we emphasize that this is merely an example, and users have the flexibility to adjust the models based on prior beliefs.

2.5 Emission probability

For tumor samples, the observed LRRi and BAFi values are assumed to arise from an unobserved mixture distribution of normal cells (stromal contamination) and tumor sub-clones. We denote the true underlying CN-aware genotypes of the tumor and the contaminating normal cells at each marker as gt,i and gn,i, respectively. CN-aware genotype refers to the genotype call that takes into account of allelic copy numbers, such as A (copy = 1), ABB (copy = 3) and AABB (copy = 4). To accommodate stromal contamination (γ) and intra-tumor heterogeneity (αi), we define the latent distribution as a Gaussian mixture with means that reflect contributions from stromal and tumor tissue. At any SNP i, we define the expected value of the R ratio (RR) as

graphic file with name btt521m2.jpg (2)

where the function cn() counts the total number of copies for a genotype, and rmean() maps a copy number to an expected RR (based on linear interpolation of the observed RR at copy number of 0, 1, 2 and 3 from real datasets). The intra-tumor heterogeneity measure can essentially be considered as a refinement parameter that is locus specific. When αi = 0, there is no heterogeneity, and all tumor cells have the same copy number at each marker in the population of tumor cells. The standard deviation of RRi, sr,i, at each SNP is assigned from a linear interpolation of the observed RR at copy number of 0, 1, 2 and 3 from real datasets, given the composite copy number of tumor and normal cells as (1-γ-αi)cn(gt,i) + (γ + αi)cn(gn,i).

Conditional on μr,i, the emission probability of the RR is modeled as a mixture of a uniform and Gaussian distribution:

graphic file with name btt521m3.jpg (3)

where ϕ() is the density function of a Gaussian distribution with mean μr,i and standard deviation sr,i, and λi is a vector for the state parameters (i.e. gt,i, gn,i, γ, αi). The uniform distribution πr accommodates the random fluctuation of signal measures in chemical assays and possible genome mis-annotation. By default, πr is assigned as 0.01. We now discuss the component of the likelihood that involves the observed BAF signal.

In our method for CNA detection, the main challenge lies in accurately defining μb,i in the model. For germline CNV calling, the peaks of these distributions are fixed at given intervals: for example, the peaks of the BAF distribution are located at 0, 0.33, 0.67 and 1 for three-copy regions. For CNA calling, the numbers need to be modified: for example, when γ = 0.2 and αi = 0, the peaks of the distribution becomes 0, 0.29, 0.71 and 1 for three-copy regions (assuming paired germline sample is not available, or gn,I = 2). In the simpler case where homozygous genotypes (AA or BB) in normal tissues are observed, the mean μb,i is constrained to be 0 and 1, respectively, as it is reasonable to assume that it is extremely rare for a new allele to arise de novo. In the case of a heterozygous genotype, we model the conditional BAF mean (μb,i) for a given SNP i as:

graphic file with name btt521m4.jpg (4)

where bac() counts the number of B alleles for a CNV-aware genotype (e.g., bac(“AAAB”) = 1 and bac(“ABB”) = 2). For copy numbers greater than zero, we define the emission probability for BAFi as a mixture of uniform and a Gaussian distribution conditioned on μb,i. We review the model first described by the original PennCNV article (Wang et al., 2007). Let I() be an indicator function so that when BAFi is 0 or 1, we multiply the binomial likelihood density BN() by a mixture of point mass M at 0 or 1, respectively, and a truncated Gaussian distribution.

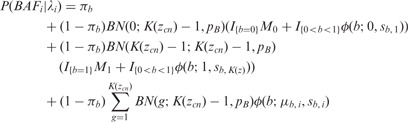graphic file with name btt521m5.jpg (5)

where K(zcn) denotes the number of total possible genotypes for copy number state zcn, and

graphic file with name btt521m6.jpg (6)

is the probability of observing g copies of allele B, and pB is the population frequency of the B allele, estimated from a large ethnically matched reference panel. As indicated in we integrate over all possible genotypes for any copy number state greater or equal to two.

Because there is no contribution to signal from tumor cells when copy number is zero, in the case of copy number zero, we define the emission probability for BAFi simply as

graphic file with name btt521m7.jpg (7)

As mentioned earlier, our method can account for tumor heterogeneity, which manifests as values of αi that differ from the global stromal contamination value γ. To calculate the emission probability for a particular value of αi, we assume a Gaussian density function centered at α:

graphic file with name btt521m8.jpg (8)

The final emission probability (likelihood) is simply the product of the RR, BAF and tumor heterogeneity emission probabilities.

2.6 Transition probability

For whole-genome SNP arrays, the transition probabilities can be calculated in the same manner as in PennCNV by considering the distance between SNPs on the array. We estimate the transition matrix that defines all possible pairs of states by applying the forward-backward and Baum–Welch algorithms.

2.7 Incorporating datasets with tumor-normal pairs

It is reasonable to assume that in some cases, detection of CNAs in tumor cells is confounded by copy number changes mapping to the same regions in the germline. For instances where germline and tumor DNA is available on the same individuals, one can easily disentangle CNAs that are unique to tumors versus those shared with germline. Statistically, information from germline DNA is straightforward to incorporate, as has been done in other software tools (Sun et al., 2009; Yau et al., 2010). In this case, where paired samples are available, site-specific copy number counts enter through the parameter cn(gn,i), whereas in the more general case when the germline component in unavailable, we simply fix the parameter at value 2.

2.8 Posterior inference

The Viterbi algorithm, used by programs such as PennCNV, infers copy number by tracing the most likely state path across all markers. However, this approach can be unsatisfactory in some cases (such as when stromal contamination levels are high), as several candidate models can plausibly explain the data. To account for this uncertainty, in the method proposed here, we use the posterior probabilities derived from the forward–backward algorithm. Copy number calls and model parameters are therefore posterior averaged values. The HMM reports absolute copy number for tumor samples, which can be divided by aneuploidy levels to obtain a relative copy number, which is usually more informative.

3 RESULTS

In this section, we report comparisons between PennCNV-tumor and existing software for calling CNAs, namely, ASCAT (Van Loo et al., 2010), GAP (Popova et al., 2009), GenoCN (Sun et al., 2009), OncoSNP (Yau et al., 2010) and GPHMM (Li et al., 2011).

3.1 Estimating stromal contamination

Stromal contamination is commonly observed for tumor samples, as the sample collection procedure may inadvertently result in the inclusion of normal cells. To evaluate CNA detection methods under varying levels of stromal contamination, we examined a previously published (Staaf et al., 2008) dilution series, which includes 12 samples with mixtures of known proportions of the normal cell line HCC1395BL and the paired breast carcinoma cell line HCC1395 for a variety of values (0, 10, 14, 21, 23, 30, 34, 45, 47, 50, 79, 100). Stromal contamination estimates made using GAP and GPHMM have been previously reported in (Li et al., 2011), and these results were incorporated into our comparison. For other programs, we ran the software using recommended settings. Program settings and full output for each method in this analysis can be downloaded from https://sourceforge.net/projects/penncnv-2/files/supplementary_files/.

This comparative analysis demonstrated the superior performance of our method over other competing approaches. Figure 1 shows the plot of expected versus actual estimates for each method. Both GPHMM and our estimation procedure were able to recover known stromal contamination levels across a broad range of values (correlation coefficient of ρ = 0.99). GAP produced accurate estimates at higher levels of stromal contamination, but over estimated at lower levels (ρ = .28). The remaining programs overall did not recover the true values as well: OncoSNP (ρ = 0), GenoCN (ρ = −.23) and ASCAT (ρ = .02). We also note that other programs that require user-specified priors do not perform as well either. For example, PICNIC (Greenman et al., 2010) can be overly sensitive to user-specified priors such that they significantly influence the final computational predictions. In summary, our maximum likelihood method resulted in the accurate estimation of stromal contamination, which is essential for the optimal detection of CNAs in subsequent steps.

Fig. 1.

Fig. 1.

Open in a new tab

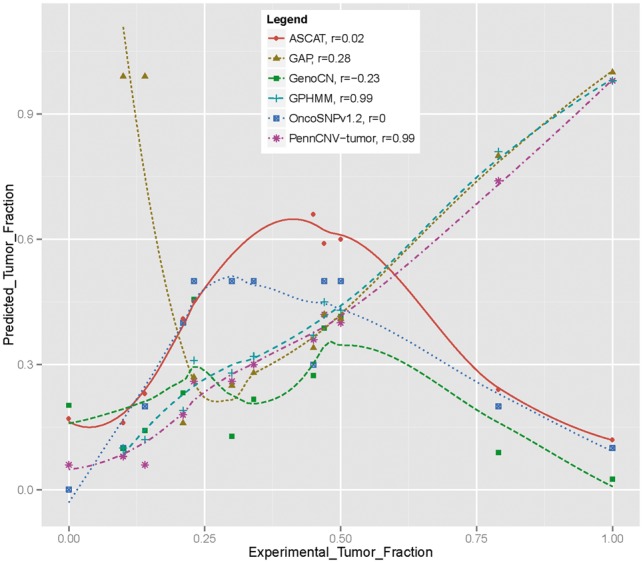
Comparison of several methods’ ability to estimate the tumor cell fraction from the breast cancer dilution series data. Lowes smoothed curves are superimposed on the predictions. Results on GPHMM and GAP were obtained from Li et al. (2011). PennCNV-tumor achieves better correlation (r = 0.99, L1norm = 0.05, L2norm = 0.06) with experimental data than most other methods

3.2 CNA calling on tumor samples with known aberrations

To evaluate our ability to call CNAs, we compared our method and others on the breast cancer cell line SUM159. These data were generated on the Illumina CNV370-Duo array and were previously characterized extensively on four different technical platforms (Curtis et al., 2009). SUM159 is known to harbor CNAs at multiple different scales on chromosome 5, including a whole-arm amplification of the p-arm, a megabase-level deletion at ∼100 Mb, and two kilobase-level complex duplication toward the telomere of 5p (Fig. 3 in Curtis et al., 2009). Supplementary Figure S1 illustrates a comparison of copy number estimates using different methods. For large events, inference was nearly identical in terms of localization of aberrations (albeit some differences in their magnitude) for GenoCN, OncoSNP, ASCAT, GPHMM and PennCNV-tumor. However, different algorithms yielded discordant calls for small CNAs, perhaps reflecting the different sensitivity of each algorithm under default settings.

3.3 CNA inference in the presence of stromal contamination

To further evaluate the sensitivity and consistency in calls using different methods, we tested the concordance rate of CNAs calls on the breast cancer dilution series. As we do not know the true CNA profile, for each algorithm, we treat the calls generated on the tumor cell line HC1395 as the reference and tested how many of these calls can be recovered for each diluted sample in the face of noise from stromal contamination (Supplementary Fig. S2). We ran each program using the recommended settings except for GAP, which we were not able to successfully run. However, we integrated into our comparison previously published results (specifically CNA calls for this data made using GAP, which are available at http://bioinfo-out.curie.fr/projects/snp_gap/.) For each program, we calculate the proportion of calls concordant with the reference sample. An ideal method would have high concordance, and the concordance is expected to monotonically decrease as a function of stromal contamination. Qualitatively, PennCNV-tumor performs most similarly to GAP and GPHMM. The other programs show a noticeable drop in concordance across various levels of stromal contamination. It is also important to note each method’s sensitivity to detect aberrations across various levels of stromal contamination. A method that is not sufficiently sensitive may call nearly every site copy neutral for a pure tumor sample, which in turn can artificially produce perfect concordance when applied to samples with higher levels of stromal contamination. Supplementary Figure S3 illustrates the distribution of percentage of sites aberrant across different stromal contamination levels. The figure indicates that sensitivity levels for the methods were calibrated similarly. Finally, we were also interested in how these methods compare in terms of concordance and percentage aberration when considering only large CNA events. We filtered results across methods on only CNAs greater than 10 MB and plot the comparison of concordance and percent aberrations in Supplementary Figures S4 and S5. Interestingly, the programs appear to diverge in their distribution of percentage sites aberrant when only large (>10 MB) CNA events are considered in contrast to all sized events.

Finally, we also tested a dilution series dataset simulated by CnaGen (Mosen-Ansorena et al., 2012), as the ground truth is known. The dataset contains 11 samples, with tumor purities ranging from 0.01 to .99. Each sample contains a region with intratumor heterogeneity of 80%, and PennCNV-tumor correctly identified the region from those samples with tumor purity >50%. In contrast, other methods were not able to predict stromal contamination with reasonable accuracy, as summarized in Supplementary Table S2.

3.4 CNA inference in presence of intra-tumor heterogeneity

We assessed the ability of PennCNV-tumor to call tumors in the presence of intratumor heterogeneity, which is characterized by proportions of normal cells that can differ across sites. We are not aware of existing datasets in which the true profile of intratumor heterogeneity is known, so we evaluated the performance of our program and others through the same simulated datasets, which have previously been described earlier for evaluating stromal contamination. For each scenario (modeling a specific level of stromal contamination), we simulated intratumor heterogeneity in random regions covering 12% of the genome, where each of these regions span ∼15 Mb. We compared the accuracy of CNV calls against other methods, where OncoSNP was the only other competing program that could account for intratumor heterogeneity. Supplementary Table S2 lists the L1 errors for estimates of tumor copy number and intratumor heterogeneity, calculated as the sum of the absolute value of deviations between the true and estimated values, taken across all sites. PennCNV-tumor generally had better concordance with respect to copy number estimates as compared with OncoSNP, whereas OncoSNP had slightly better accuracy in estimating intratumor heterogeneity when stromal contamination levels were lower. Additionally, OncoSNP has better performance to predict stromal contamination when the values are below 50%. Interestingly, ASCAT performed well for CN inference, but was not able to complete analyses for tumor purities outside the range of .4 to .9. GPHMM appeared to have the lowest sensitivity, calling most sites as copy neutral.

3.5 Computational efficiency

One dimension of performance for CNA calling that is often overlooked is computational efficiency. As the availability of large multi-dimensional datasets (e.g. The Cancer Genome Atlas) increases, the ability to complete analyses in a timely fashion is becoming more important. We recorded run times and memory usage across the programs GenoCNA, OncoSNP, GPHMM, ASCAT and PennCNV-tumor. Table 1 highlights the computational demands of these programs for the analysis of 12 samples used in the dilution series analysis across more than 370,000 SNPs. One should keep in mind though that these are based on default settings, which we have assumed the authors have suggested to give a good balance between accuracy and run time performance. ASCAT and GenoCN required 66 and 72 times more memory, respectively, than PennCNV-tumor. However GPHMM and ASCAT were slightly faster than PennCNV-tumor.

Table 1.

Computational requirements of various programs benchmarked on the same machine with two Intel X5680 CPUs at 3.33 GHz

Program Run-time in minutes Memory
OncoSNP 328 605 MB
GenoCN 104 1013 MB
PennCNV-tumor 35 14 MB
GPHMM 21 647 MB
ASCAT 20 930 MB
Open in a new tab

Note: Twelve samples across 24 chromosomes were analyzed.

4 DISCUSSION

Over 10 software tools have now been published for identifying CNAs from SNP arrays. Most are based on HMMs, but several use segmentation algorithms. Our proposed algorithm uses SNP genotyping arrays to identify CNAs and estimate their magnitude in tumor samples, while accounting for intratumor heterogeneity, stromal contamination and aneuploidy. When compared against other popular methods, our approach performs comparably in terms of the detection and estimation of CNAs but shows marked improvements in the estimation of stromal contamination and runtime efficiency. Later in the text, we discuss the major differences between various algorithms and potential avenues for future improvements.

  1. Capability of integrating multiple sources of ‘prior’ information in the likelihood calculation step. To our knowledge, only OncoSNP and our program PennCNV-tumor comprehensively account for stromal contamination, tumor heterogeneity, aneuploidy and genomic waves when inferring CNAs, whereas other tools consider only a subset of these issues.

  2. A unique but simple approach for estimating stromal contamination. Although we estimate the global γ (stromal contamination) and the aneuploidy offset parameter β in a data pre-processing step, in principle, it should be possible to estimate these parameters in an integrated analysis (e.g. learning the HMM parameters). However, our preliminary results have suggested that for reasons of identifiability, it is difficult to get consistent estimates: for example, disentangling global γ from local α (intra-tumor heterogeneity) estimation when both are included as free parameters in the model. As domain knowledge is critical in most statistical learning problems, we incorporate an a priori heterozygosity rate for each given sample in our pre-processing step. A good approximation of this fixed parameter can lead to superior accuracy over competing methods, as demonstrated in the real breast cancer dataset with known dilutions of stromal tissue. Our simulation study suggested that this method might not be optimal in certain contexts however. For instance, when we simulated a large proportion of sites that had tumor heterogeneity, our stromal contamination estimates did not perform as well as in the real breast cancer data. Because this example was based on simulated data, it is possible that the simulated data did not properly reflect realistic distributions of intratumor heterogeneity, CNAs or other phenomena. Furthermore, these simulation study results should be balanced against our program’s ability to make predictions that were more robust across the entire spectrum of stromal contamination levels (other methods we tested were unable to make reliable estimates beyond 50% stromal contamination). Inference of high stromal contamination levels can be of great interest in certain cancer contexts. In late stages of pancreatic cancer, typically malignant cancer cells represent only 25% of the cells in the tumor on average (Boyd et al., 2009). The authors of GPHMM found that among fresh breast cancer biopsies, ‘About 91% tumor samples (87 of 96) are mixed with >50% normal cells, of which 60 have normal cell proportions larger than 0.7, and 12 have normal cell proportions greater than 0.85’ (Li et al., 2011).

  3. The need for some users to fine-tune calling algorithms to achieve the desired resolution and granularity: We have provided users with flexibility in specifying the state space in the HMM. Previous studies show that copy number states up to 6 can be readily discerned by eye in the signal intensity plots (Attiyeh et al., 2009). It is possible that even higher copy number can be detected by sophisticated computational means, though they may not have much practical value. Among the features described earlier in the text, (ii) is unique to our algorithm, to be best of our knowledge.

Several further improvements may be made to the proposed method. For instance, different researchers have varied requirements for the sensitivity and specificity of CNV calling, depending on their research needs. Many software tools, including PennCNV-tumor, rely on post-calling QC to control sensitivity and specificity (e.g. minimum number of probes thresholds and the log likelihood threshold). However, it is possible to directly control the sensitivity within the HMM model by arbitrarily setting a different set of noise parameters and transition parameters. CNV filtering may also be introduced post hoc using a suitable ethnically matched reference. We plan to introduce tools in our software that can automate parameter tuning by applying supervised learning procedures on ‘gold standard’ datasets. Third, it is a known problem that HMM-based algorithms tend to over-segment the data, resulting in long CNV regions being broken into several small calls. This depends on the HMM parameters, so it cannot be directly adjusted from the algorithm per se. However, several post-calling adjustment procedures have been developed before; for example, PLINK and PennCNV both have CNV-processing steps that merge neighboring CNV calls if the ‘bridge’ between the two neighboring calls are less than a certain threshold (such as 20%) of the total combined call. For tumor CNA calling, this post-processing procedure can also be used. Fourth, our current approach estimates stromal contamination in a pre-processing step, rather than treating it as a parameter in the HMM. We have previously attempted to discretize alpha (e.g. from 0 to 1 in increments of 0.1) and estimate it in HMM; however, this increases the HMM states by ∼11-fold, but the estimation per marker is highly unstable.

Finally, we wish to stress that a variety of genome-wide approaches, and technical platforms have been developed for CNV detection (Alkan et al., 2011). Although next-generation sequencing may soon replace SNP arrays in certain areas, it is still cost-prohibitive for genome-wide screening. In addition, the accurate detection of CNVs/CNAs from sequencing data is non-trivial, dependent on sequencing depth, and represents an area of ongoing development. Hence, SNP arrays remain a cost-effective and popular approach to interrogate CNAs, as evidenced by recent large-scale oncogenomic profiling studies such as TCGA (TCGA, 2012) and METABRIC (Curtis et al., 2012).

Supplementary Material

Supplementary Data
supp_29_23_2964__index.html (963B, html)

ACKNOWLEDGEMENTS

The authors thank members of the Wang laboratory for helpful discussions and comments.

Funding: The study is supported by NIH/NHGRI grant R01HG006465.

Conflict of Interest: None declared.

REFERENCES

  1. Albertson DG, et al. Chromosome aberrations in solid tumors. Nat. Genet. 2003;34:369–376. doi: 10.1038/ng1215. [DOI] [PubMed] [Google Scholar]
  2. Alkan C, et al. Genome structural variation discovery and genotyping. Nat. Rev. Genet. 2011;12:363–376. doi: 10.1038/nrg2958. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Attiyeh EF, et al. Genomic copy number determination in cancer cells from single nucleotide polymorphism microarrays based on quantitative genotyping corrected for aneuploidy. Genome Res. 2009;19:276–283. doi: 10.1101/gr.075671.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Attiyeh EF, et al. Chromosome 1p and 11q deletions and outcome in neuroblastoma. N. Engl. J. Med. 2005;353:2243–2253. doi: 10.1056/NEJMoa052399. [DOI] [PubMed] [Google Scholar]
  5. Beroukhim R, et al. Assessing the significance of chromosomal aberrations in cancer: methodology and application to glioma. Proc. Natl Acad. Sci. USA. 2007;104:20007–20012. doi: 10.1073/pnas.0710052104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Beroukhim R, et al. The landscape of somatic copy-number alteration across human cancers. Nature. 2010;463:899–905. doi: 10.1038/nature08822. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bignell GR, et al. Signatures of mutation and selection in the cancer genome. Nature. 2010;463:893–898. doi: 10.1038/nature08768. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Boyd ZS, et al. A tumor sorting protocol that enables enrichment of pancreatic adenocarcinoma cells and facilitation of genetic analyses. J. Mol. Diagn. 2009;11:290–297. doi: 10.2353/jmoldx.2009.080124. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Caren H, et al. High-risk neuroblastoma tumors with 11q-deletion display a poor prognostic, chromosome instability phenotype with later onset. Proc. Natl Acad. Sci. USA. 2010;107:4323–4328. doi: 10.1073/pnas.0910684107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Curtis C, et al. The pitfalls of platform comparison: DNA copy number array technologies assessed. BMC Genomics. 2009;10:588. doi: 10.1186/1471-2164-10-588. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Curtis C, et al. The genomic and transcriptomic architecture of 2,000 breast tumours reveals novel subgroups. Nature. 2012;486:346–352. doi: 10.1038/nature10983. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Diskin SJ, et al. Adjustment of genomic waves in signal intensities from whole-genome SNP genotyping platforms. Nucleic Acids Res. 2008;36:e126. doi: 10.1093/nar/gkn556. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gerlinger M, et al. Intra-tumor heterogeneity and branched evolution revealed by multiregion sequencing. N. Engl. J. Med. 2012;366:883–892. doi: 10.1056/NEJMoa1113205. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Greenman CD, et al. PICNIC: an algorithm to predict absolute allelic copy number variation with microarray cancer data. Biostatistics. 2010;11:164–175. doi: 10.1093/biostatistics/kxp045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Li A, et al. GPHMM: an integrated hidden Markov model for identification of copy number alteration and loss of heterozygosity in complex tumor samples using whole genome SNP arrays. Nucleic Acids Res. 2011;39:4928–4941. doi: 10.1093/nar/gkr014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Marioni JC, et al. Breaking the waves: improved detection of copy number variation from microarray-based comparative genomic hybridization. Genome Biol. 2007;8:R228. doi: 10.1186/gb-2007-8-10-r228. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Michor F, Polyak K. The origins and implications of intra-tumor heterogeneity. Cancer Prev. Res. (Phila) 2010;3:1361–1364. doi: 10.1158/1940-6207.CAPR-10-0234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Mosen-Ansorena D, et al. Comparison of methods to detect copy number alterations in cancer using simulated and real genotyping data. BMC Bioinformatics. 2012;13:192. doi: 10.1186/1471-2105-13-192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Perez EA, et al. C-MYC alterations and association with patient outcome in early-stage HER2-positive breast cancer from the north central cancer treatment group N9831 adjuvant trastuzumab trial. J. Clin. Oncol. 2011;29:651–659. doi: 10.1200/JCO.2010.30.2125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Pollack JR, et al. Microarray analysis reveals a major direct role of DNA copy number alteration in the transcriptional program of human breast tumors. Proc. Natl Acad. Sci. USA. 2002;99:12963–12968. doi: 10.1073/pnas.162471999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Popova T, et al. Genome Alteration Print (GAP): a tool to visualize and mine complex cancer genomic profiles obtained by SNP arrays. Genome Biol. 2009;10:R128. doi: 10.1186/gb-2009-10-11-r128. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Slamon DJ, et al. Human breast cancer: correlation of relapse and survival with amplification of the HER-2/neu oncogene. Science. 1987;235:177–182. doi: 10.1126/science.3798106. [DOI] [PubMed] [Google Scholar]
  23. Staaf J, et al. Normalization of Illumina Infinium whole-genome SNP data improves copy number estimates and allelic intensity ratios. BMC Bioinformatics. 2008;9:409. doi: 10.1186/1471-2105-9-409. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Sun W, et al. Integrated study of copy number states and genotype calls using high-density SNP arrays. Nucleic Acids Res. 2009;37:5365–5377. doi: 10.1093/nar/gkp493. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. TCGA. Comprehensive molecular characterization of human colon and rectal cancer. Nature. 2012;487:330–337. doi: 10.1038/nature11252. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Van Loo P, et al. Allele-specific copy number analysis of tumors. Proc. Natl Acad. Sci. USA. 2010;107:16910–16915. doi: 10.1073/pnas.1009843107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Waddell N, et al. Subtypes of familial breast tumours revealed by expression and copy number profiling. Breast Cancer Res. Treat. 2010;123:661–677. doi: 10.1007/s10549-009-0653-1. [DOI] [PubMed] [Google Scholar]
  28. Wang K, et al. PennCNV: an integrated hidden Markov model designed for high-resolution copy number variation detection in whole-genome SNP genotyping data. Genome Res. 2007;17:1665–1674. doi: 10.1101/gr.6861907. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Wang K, et al. Convergent mechanisms of somatic mutations in polycythemia vera. Discov. Med. 2011;12:25–32. [PMC free article] [PubMed] [Google Scholar]
  30. Weir BA, et al. Characterizing the cancer genome in lung adenocarcinoma. Nature. 2007;450:893–898. doi: 10.1038/nature06358. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Winchester L, et al. Comparing CNV detection methods for SNP arrays. Brief. Funct. Genomic Proteomic. 2009;8:353–366. doi: 10.1093/bfgp/elp017. [DOI] [PubMed] [Google Scholar]
  32. Yau C, et al. A statistical approach for detecting genomic aberrations in heterogeneous tumor samples from single nucleotide polymorphism genotyping data. Genome Biol. 2010;11:R92. doi: 10.1186/gb-2010-11-9-r92. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Zhang Y, et al. Copy number alterations that predict metastatic capability of human breast cancer. Cancer Res. 2009;69:3795–3801. doi: 10.1158/0008-5472.CAN-08-4596. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_29_23_2964__index.html (963B, html)
supp_btt521_supplementary_data.doc (523.5KB, doc)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES