Integrated profiling of three dimensional cell culture models and 3D microscopy

Abstract

Motivation: Our goal is to develop a screening platform for quantitative profiling of colony organizations in 3D cell culture models. The 3D cell culture models, which are also imaged in 3D, are functional assays that mimic the in vivo characteristics of the tissue architecture more faithfully than the 2D cultures. However, they also introduce significant computational challenges, with the main barriers being the effects of growth conditions, fixations and inherent complexities in segmentation that need to be resolved in the 3D volume.

Results: A segmentation strategy has been developed to delineate each nucleus in a colony that overcomes (i) the effects of growth conditions, (ii) variations in chromatin distribution and (iii) ambiguities formed by perceptual boundaries from adjacent nuclei. The strategy uses a cascade of geometric filters that are insensitive to spatial non-uniformity and partitions a clump of nuclei based on the grouping of points of maximum curvature at the interface of two neighboring nuclei. These points of maximum curvature are clustered together based on their coplanarity and proximity to define dissecting planes that separate the touching nuclei. The proposed curvature-based partitioning method is validated with both synthetic and real data, and is shown to have a superior performance against previous techniques. Validation and sensitivity analysis are coupled with the experimental design that includes a non-transformed cell line and three tumorigenic cell lines, which covers a wide range of phenotypic diversity in breast cancer. Colony profiling, derived from nuclear segmentation, reveals distinct indices for the morphogenesis of each cell line.

Availability: All software are developed in ITK/VTK and are available at https://vision.lbl.gov/Software/3DMorphometry.

Contact: b_parvin@lbl.gov or hchang@lbl.gov

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

High content screening of cell culture models continue to play a major role in evaluating therapeutic targets, elucidating aberrant pathways and identifying novel biomarkers. Traditionally, cell culture models are based on 2D monolayers that are grown on plastic, but recent research indicates that cells grown in a 3D culture often behave more like cells in living organisms. This is partly due to the cellular organization, cell–cell contact and unique cell–extracellular matrix (ECM) adhesions and motility phenotype. 3D cell culture models offer many advantages over the 2D monolayer systems: (i) Each cell forms an ellipsoid with dimensions of 10–30 microns (Pampaloni et al., 2007), whereas in the monolayer system, each cell remains flat with a thickness of a few microns; (ii) In a 3D system, the entire cell surface is exposed to neighboring cells and extracellular matrix. In contrast, in a 2D system, a small percentage of the cell surface is exposed to the other cells. These differences in shape and surfaces are significant given that ∼30% of the genome is known to encode membrane-bound macromolecules (Wallin and Heijme, 1998). (iii) Studies have shown that 3D morphological organizations have a profound impact on cellular function, such as morphogenesis (Fournier et al., 2009), development (Park et al., 2000), response to therapy (Liu et al., 2004) and patterns of gene expression (Han et al., 2010). (iv) Unlike conventional 2D models, 3D culture assays distinguish tumor phenotypes from non-malignant ones, where the tumor phenotype is often manifested as multicellular organizations (Peterson et al., 1992). Owing to these differences, there is a greater need for characterizing and quantifying organizations through the delineation of each cell. Because the protocols for nuclear staining are well established, we focus on delineating nuclear regions, which also provides context for quantifying multiple endpoints in high content screening. In addition, cell-by-cell analysis enables characterization of heterogeneity, which is one of the central challenges and a fundamental property in cellular systems (Altschuler and Wu, 2010). It has been suggested that heterogeneity enables cellular systems to explore a wide range of phenotypic responses, where a specific subpopulation may serve as a predictor of response to perturbations. An example is shown in Supplementary Figure S1 in the Supplementary Section.

Given the aforementioned motivation, there is clear gap in quantitative methods for characterizing multicellular organizations for the next generation of high content screening systems. This is partly due to the massive amounts of 3D data that have to be acquired through confocal or deconvolution microscopy, and the ambiguities that were present in the 2D assays (Coelho et al., 2009) must now be resolved in the 3D volume space. In this article, we propose a pipeline, implemented within the Insight Segmentation and Registration Toolkit (ITK) and The Visualization Toolkit (VTK) framework, to delineate each nucleus and to profile morphometric and colony organization. At an abstract level, our approach is an extension of a previously developed method for monolayer cell culture models (Wen et al., 2009). Nevertheless, such an extension has proven to be challenging because of structural heterogeneity and partitioning of clumped nuclei in a 3D volume. Our approach consists of a series of filters that remove ambiguities in (i) the nuclear stain through prior modeling; (ii) the structural heterogeneity through object level adaptive smoothing; and (iii) the perceptual boundaries within a clump of cells by detecting and grouping points of maximum curvature. These processes are intrinsically compute-intensive in a 3D volume. As a result, the segmentation strategy initially detects isolated nuclei and groups of nuclei that are clumped together prior to subsequent partitioning. The net result is increased throughput for processing a large amount of data. The proposed method is referred to as curvature-based partitioning (CBP) in the remainder of the article.

Organization of the article is as follows. Section 2 provides a brief review of the motivation, issues and prior research. Section 3 discusses details of the experimental design and computational approach. Section 4 provides validation results on synthetic and real data, and compares performance of CBP with the previous techniques. Section 5 compares morphogenesis of multiple cell lines in terms of the colony organization. Section 6 concludes the article.

2 BACKGROUND

In Section 1, we reviewed the prior literature to suggest that the 3D cell culture models are in fact functional assays. As a result, the utility of these model systems have been on the rise. For example, in 2008, the growth rate for the number of publications exploiting 3D cell culture models increased by 153% of the previous year (www.3dcellculture.com), i.e. from approximately 370–930 publications. This trend indicates the growing importance for multicellular segmentation and profiling. Challenges for segmenting the 3D colonies are similar to those involving the 2D assays; they include (i) variation in cellular state and cell shape, and (ii) the traditional issue of the perceptual boundaries between adjacent nuclei. Moreover, segmentation of 3D colonies is aggravated by complex volumetric analysis and cellular growth in the Matrigel.

The key concepts in delineating nuclei have been watershed (Chawla et al., 2004) with user intervention, active surface models (Padfield et al., 2009), gradient flow tracking (GFT) (Li et al., 2007), atlas-based methods (Qu et al., 2011) and hybrid methods of seed detection through iterative voting (IV) and geometric partitioning (Han et al., 2011). Interactive techniques are not amenable for large scale data, and the watershed method is prone to erroneous partitioning of the image space. On the other hand, level set method, while having a solid analytical foundation, requires robust initialization and stopping criterion; they can also benefit from the prior shape models. Of course, any segmentation technique can benefit from additional constraints, but creating the necessary diversity of prior models can add to the complexity. GFT, which is conceptually similar, at an abstract level, to the radial centroid transform (Yang and Parvin, 2003), is sensitive to morphometric aberrations and internal structure within the nucleus. Whereas, the atlas-based models assume a prior model of organization, which is (i) nonexistent for the growth of 3D cell culture models, and (ii) difficult to generate as a result of cellular and organizational heterogeneity. The general strategy for segmentation has been to detect a distinct seed per nucleus [e.g. LoG, radial centroid transform, (IV)] that is followed through geometric partitioning. These techniques work well in live cell assays and when each cell, in a whole organism, has a similar morphology. In contrast, fixed cell assays may have artifacts that lead to dislocation of constituents, and cancer cells are well known to have aberrant morphologies. In addition, multicellular systems, cultured in Matrigel can have higher background intensity within the colony than outside of the colony, which complicates cell-by-cell segmentation. The novelty of our approach is that it incorporates these insights and overcomes intrinsic barriers associated with the segmentation of 3D cell culture models.

3 APPROACH

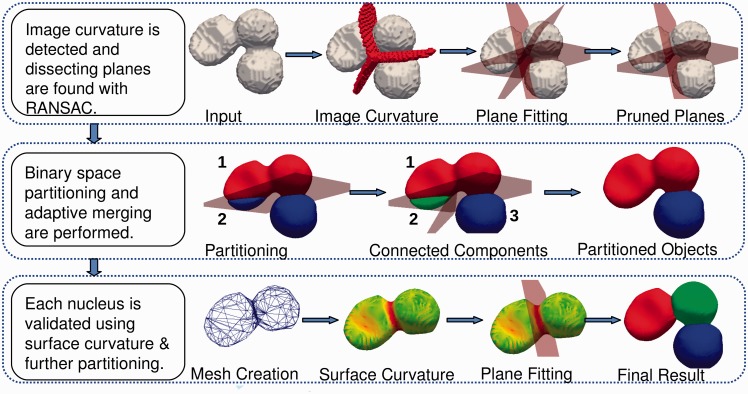
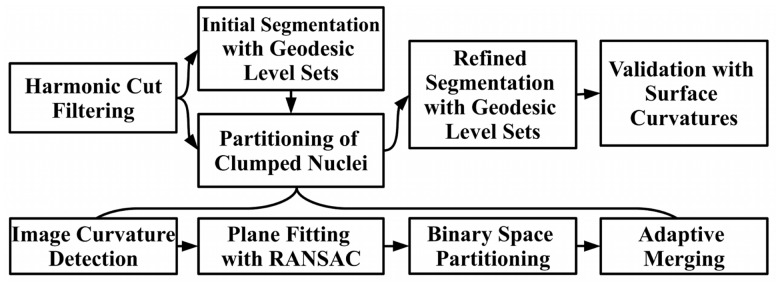
One of the barriers in delineating a multicellular colony system has to do with separating touching nuclei in 3D. The basic idea for segmentation is to use curvature feature to detect perceptual boundaries (e.g. touching adjacent nuclei); however, curvature can be noisy as a result of structural nucleoli, which is responsible for transcribing ribosomal RNA. Therefore, the first step is to interpolate nucleoli (e.g. smoothing) through harmonic cut (Yang and Parvin, 2003). Furthermore, 3D segmentation is intrinsically compute intensive, which motivates for a more opportunistic policy for quantitative analysis. These insights are the basis of the organization and integration of filters shown in Figure 1. Accordingly, the method integrates a cascade of filter operations to eliminate ambiguities in a stepwise fashion. (i) The approach replaces the original image with harmonic cut, where inter-nuclei structural details (e.g. nucleoli) are interpolated for smoothness. (ii) An initial segmentation delineates isolated nuclei or clumps of nuclei from the background. These segmented regions provide the basis for decomposing the space through Voronoi partitioning. (iii) Simultaneously, the clumped nuclei are separated along their overlapping regions. These overlapping regions are detected using curvature maxima and clustered to define dissecting planes. (iv) The aggregate of dissecting planes and Voronoi partitioning are then combined to define polytopes where segmentation can be refined locally. Lastly, each delineated nucleus is validated with its surface curvature properties. Each of these steps is discussed below.

Fig. 1.

Steps in segmentation of nuclei in a 3D cell culture model. The partitioning of the clumped nuclei consists of four distinct operations

3.1 Materials and methods

3D cell cultures are grown in Matrigel using on-top method (Lee et al., 2007) for one non-transformed line MCF10A (Michigan Cancer Foundation), and three malignant lines of MCF7, MDA-MB-231 (Monroe Dunaway Anderson metastatic breast) and MDA-MB-468. All cell lines are breast epithelial lines that have been obtained from American Type Culture Collection. The malignant lines are selected for their genetic and morphometric diversity. From a genetic perspective, MCF7 is estrogen and progesterone positive (ER+, PR+) as well as ERBB2−; MDA-MB-468 is ERBB2+; and MDA-MB-231 is triple negative (e.g. ER−, PR− and ERBB2−). From a morphometric perspective, MCF7, MDA-MB-468 and MDA-MB231 maintain a ‘mass’, ‘grape-like’ and ‘stellate’ colony organization per nomenclature (Han et al., 2010). All colonies are fixed and stained with 4′,6-diamidino-2-phenylindole (DAPI). These diverse cell lines were specifically selected, as they provide a wide range of phenotypic diversity for validation and sensitivity analysis. For MCF10A and MCF7, samples were collected on days 2, 5, 7 and 12. For MDA-MB-231 and MDA-MB-468, samples were fixed and stained for days 2, 5 and 7. For the latter two lines, the experiment was discontinued after day 7 as a result of nearby colonies merging because of their invasive growth property. Samples were imaged with a Zeiss LSM710 confocal with pixel size of 0.25 in X and Y and 1 micron in Z dimensions. All images were scaled isotropically for processing and visualization.

3.2 Elliptic features and harmonic cut filtering

The first step is to replace the original scaled image stack (e.g. isotropic representation of the image) with a smooth version by removing the structural heterogeneity. It is important that smoothing is performed at object level as opposed to pixel level (e.g. anisotropic diffusion). In this context, smoothing aims at detecting and interpolating subcellular structures such as nucleoli. These structures are detected using elliptic features, and interpolation is performed with the harmonic cuts (Yang and Parvin, 2003).

Let I, I_m and I_mn be the image intensity, with image partial derivatives in m and mn directions, respectively. In scale-space theory, the elliptic features are defined by 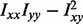. This definition is extended to 3D, and the elliptic points are then found using 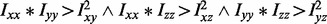. These elliptic features correspond to bright punctate regions within the nucleus when the determinant of the Hessian is negative. The bright elliptic features are interpolated with their immediate background through harmonic cut, which minimizes the functional 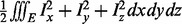. The Euler–Lagrange solution to this optimization is the Laplace equation 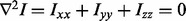, which defines a harmonic function. This step has a single parameter that corresponds to the scale of smoothing, and is set at . Figure 2b and c shows the original image and the effect of harmonic cut, respectively. The solution to the Laplacian is included in the Supplementary Section S2.

Fig. 2.

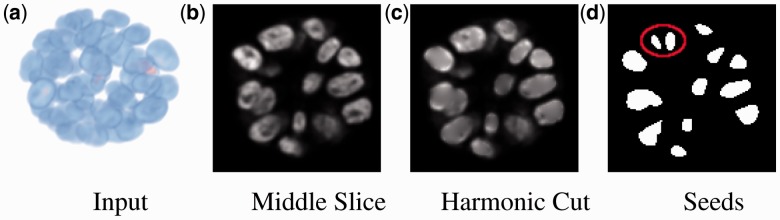
Harmonic cut filtering and seed detection on a 2D slice: (a, b) original 3D volume and a slice in the middle of the stack; (c) detection of dark elliptic regions followed by harmonic cuts removes small punctate internal structures corresponding to nucleoli; and (d) results of initial seed detection from bright elliptic regions. Initial seeds, labeled in red, are fragmented within one of the nuclei; however, these seeds are merged through the application of geodesic level set to hypothesize an initial segmentation

3.3 Initial segmentation

To increase computational throughput, individual nucleus and clumps of nuclei are delineated from the background using an initial segmentation. The staining is highly variable as a result of the cell states. The problem is further complicated with heterogeneous background signal within and outside of the colony. These complications hinder any type of global thresholding (e.g. Otsu); therefore, delineation must be within a local neighborhood. Simultaneously, the initial segmentation increases computational throughput, as a complex problem is reduced to smaller subproblems. One strategy for detecting of the initial seeds is through application of the bright elliptic features, as outlined in section 3.2. These feature detectors (i) respond to the local spatial topography, (ii) are invariant to the signal strength (e.g. variable staining) and (iii) have improved noise immunity because of Gaussian smoothing kernel. An example of initial seed detection for one slice of image is shown in Figure 2d. These initial seeds are subsequently refined through geodesic level sets, where fragmented blobs, within a nucleus, can be merged. Let I be in the image intensity, u be the implicit representation of the evolving surface, g be the image gradient, then the initial segmentation of the nuclear regions are estimated by solving the following evolution equation 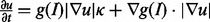where 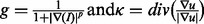(Caselles et al., 1997). The net result is that fragmented seeds, within a nucleus, are merged subject to the gradient constraint.

3.4 Partitioning clumped nuclei

The partitioning approach builds on the observation that when two adjacent nuclei overlap they form folds, and principle curvature along the fold is significantly increased (e.g. curvature maxima). These points of maximum curvature are used to detect the boundaries between the overlapping nuclei and separate them. Once identified, these points are clustered on the basis of proximity and coplanarity. A plane is then fit to each cluster. These planes are used to partition the volume into subdivisions, whereby a local segmentation could be performed more faithfully. Each of these steps is shown in Figure 3 and summarized in the next sections.

Fig. 3.

Steps in delineating the nuclear architecture

3.4.1 Curvature computation

Curvature can be estimated either from 3D volumetric data or calculated from segmented surfaces. In the proposed pipeline, curvature features are first estimated from volumetric data for initial partitioning the space. Having segmented each nucleus, we then use surface curvature, in section 3.6, for validation. Volumetric curvature is computed from differential geometric properties (e.g. partial derivative) of a 3D image stack (Thirion and Gourdon, 1995). Once the maximum principal curvature values are localized, they are thresholded to identify the curvature maxima. These maxima points correspond to regions between two overlapping adjacent nuclei. The details of curvature computation are included in the Supplementary Section S3.

3.4.2 Clustering points of maximum curvature and plane fitting

Computed curvature maxima convey the boundaries between the touching nuclei. Points of maximum curvature form a ring on a specific plane P for two adjacent nuclei. Using this observation, we group points of maximum curvature to find a set of planes for decomposing the colony into individual nuclei. Geometric grouping is performed on the basis of proximity and coplanarity of the points using Euclidean clustering and RANdom SAmple Consensus (RANSAC) (Fischler and Bolles, 1981). To fit planes to the points of maximum curvature, the iterative RANSAC method is used. In this approach, a model is fitted to the points of maximum curvature using the RANSAC algorithm; the inliers are found and removed from the dataset. The remaining dataset is used for fitting more models when possible. The output of this step is a set of plane models that will be used to partition the clumps of nuclei.

3.4.3 Binary space partitioning of clumped nuclei

RANSAC provides a natural way to cluster points of maximum curvature based on coplanarity and proximity. The clustered points of curvature maxima define planes that can partition a clump of nuclei into individual nucleus. It should be noted that the partitioning space is exponential in the number of planes, i.e. for n planes there are 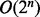subdivisions. Therefore, we use an approach similar to binary space partitioning with auto-partitions, which allows the partition complexity to become 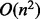(De Berg et al., 2008).

Denote the volume to be partitioned by V. Also denote each cluster of points of maximum curvature by C and the set of all clusters by S_C. Each cluster of points of maximum curvature defines a plane P with the set of all the planes defined by the clusters by S_P. In our partitioning algorithm, the volume V is divided by a plane 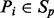into two halves, with one half falling to the negative side of the dividing plane 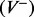, and the other half falling on the positive side of the plane 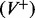. The plane P_i also separates the set S_C into two 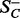and 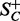, respectively. Each subdivision is further divided with the planes into their respected subspace recursively. Within each subdivision, defined by the intersecting planes computed from points of maximum curvature, connected components are performed and the disconnected objects are further partitioned using Voronoi partitioning.

3.4.4 Adaptive Merging

Despite a robust set of geometric operations, previous steps may lead into fragmentation of a nucleus via binary space partitioning. Therefore, a policy to validate each of the hypothesized subdivisions is needed. A dissecting plane for a subdivision is considered invalid when the corresponding points of maximum curvature for that plane lie on a different subdivision. For example, in Figure 3, polytope 2 is invalid as there are no curvature maxima on the polytope. Partitions with invalid planes are identified and merged back to an adjacent partition in the opposite side of the plane.

3.5 Refinement of the initial segmentation

As a result of the (i) variations in the background signal within and outside of the colony, (ii) intrinsic artifacts in imaging a 3D colony at different Z positions and (iii) heterogeneity in the cell states, refinement of the initial segmentation is needed for a more accurate representation. In this step, the geodesic level sets method is applied one more time within the refined space of the polytope for improved delineation.

3.6 Validation of geometric constraints

The computational pipeline can benefit from additional validation to assure that geometric constraints are satisfied. For example, our analysis reveals that the computation of the image curvature, described in section 3.4.1, may miss a clump of nuclei because of the scale of the fold between two adjacent nuclei. This problem is more significant in the Z direction because of its lower resolution and potential accidental alignment of two overlapping nuclei along the Z direction. Validation of the geometric constraints is based on building surface meshes and computing surface curvatures. The same partitioning strategy, as in section 3.4.2, is also used to partition a polytope further.

After building a triangular mesh (e.g. discrete marching cubes), the discrete Gaussian surface curvature at vertex v is found by measuring the excess angle at vertex v made by the incident triangles. Specifically, 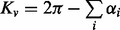, where 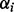’s are the interior angles of all triangles meeting at vertex v. On the other hand, the mean curvature for the surface is the sum of the dihedral angles at e made by the incident triangle normals weighted by the edge lengths, . Having calculated the mean and Gaussian curvatures, the principal curvatures are calculated, these values are then thresholded, and if enough data points exist, they are used to partition the polytopes as described previously. Details and visual examples are given in Supplementary Section S4.

4 VALIDATION AND COMPARISON

Quantification of the multicellular organization requires successful delineation of each nucleus. The proposed computational pipeline was (i) evaluated with synthetic and manually annotated images, (ii) compared with alternative methods and (iii) applied to a dataset of MCF10A, MCF7, MDA-MB-231 and MDA-MB-468 cell lines that are fixed in culture at days 2, 5 and 7 for quantifying morphogenesis. The importance of this experimental design is that genetically diverse cell lines provide a significant phenotypic diversity for proof of concept and validation. Comparison is performed against watershed-based techniques such as marker-based watershed, IV and GFT (Li et al., 2007) based on the availability of the source code.

Synthetic Data: The efficacy of the proposed method is evaluated using synthetically generated datasets. The experimental setup involves 50 randomly generated colonies where nuclei, with ellipsoidal geometry, are placed on the surface of a sphere that represents a colony. Each ellipsoidal nucleus is randomly placed and rotated on the colony sphere. Having constructed a synthetic volume, the images are corrupted with four types of noise models: (i) additive Gaussian noise, (ii) speckle noise, (iii) shot noise and (iv) salt and pepper noise. A peak signal-to-noise ratio (PSNR) of 9 dB is used for all the experiments. PSNR is given by 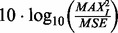, where 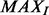is the maximum intensity value and MSE is the mean squared error between the noise and the input signal. The parameter setting for the experiments is as follows: for initial segmentation 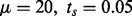; for image curvature detection 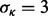; and for plane fitting 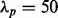and 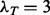are used. In all four cases, the nuclei are correctly delineated from each other. A sample of each test case is shown in Figure 4 along with segmentation using proposed method and classical watershed technique. Table 1 summarizes precision and recall for all of the experiments subject to multiple noise conditions.

Fig. 4.

First column illustrates Gaussian, speckle, shot and salt and pepper noise models on four randomly generated colonies. The segmentation of each colony is provided in the second column, and the watershed results are given in the third column

Table 1.

Object level precision for synthetic data

Algorithm	Gaussian	Shot	Speckle	Median
CBP precision	1.0	1.0	1.0	1.0
CBP recall	1.0	1.0	1.0	1.0
CBP F-measure	1.0	1.0	1.0	1.0
IV precision	0.96	0.90	0.99	0.93
IV recall	0.97	1.0	1.0	0.84
IV F-measure	0.97	0.95	0.99	0.88
GFT precision	0.84	0.81	0.75	0.91
GFT recall	0.59	0.49	0.50	0.64
GFT F-measure	0.69	0.61	0.60	0.75

Note: Object level precision recall values for the synthetic datasets with different noise models are given. PSNR is set to 9 dB.

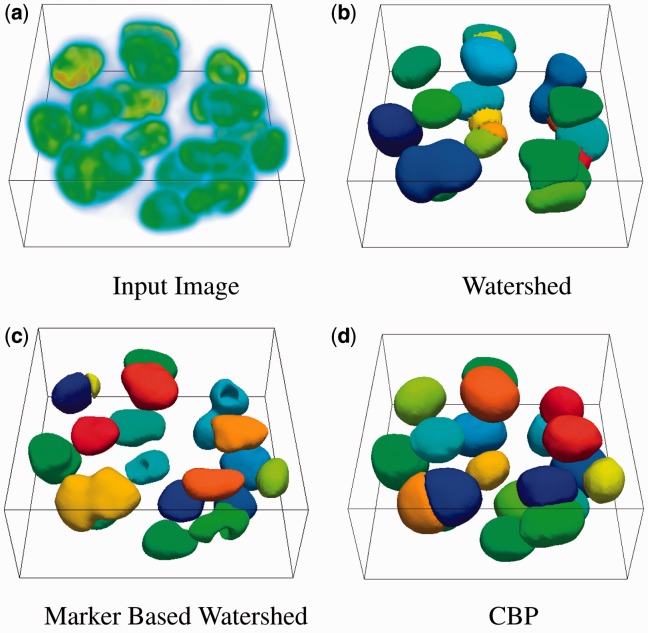
Real Data: In all, 70 image stacks (e.g. 70 colonies) were manually annotated from two independent datasets for validation and comparative analysis. Results are represented at three levels: (i) comparison with the watershed-based techniques, (ii) visualization of colony organization for different cell lines and (iii) precision and recall over annotated dataset. The parameter setting for processing the real data was identical to the synthetic dataset as in the previous section. Variations up to 20% had no impact on the final outcome. (i) Figure 5 shows a sample of segmentation results and comparison with variants of watershed-based method. (ii) Figure 6 shows a sample of segmented colony organization for each of the four cell lines. (iii) Table 2 shows superior precision and recall against alternative methods for the annotated dataset. Potential failures are (a) accidental alignment between two adjacent nuclei that form a partial fold with insufficient information for partitioning them (shown in Supplementary Section S5) and (b) sequential RANSAC inferring incorrect partitioning because of its greedy nature; however, multi-RANSAC (Isack and Boykov, 2012) should reduce the frequency of incorrect plane fitting. On average, each stack is about 512 × 512 × 80 pixels and the processing time is ∼2 min/stack with an 800 Mb of memory usage.

Fig. 5.

Comparison with watershed-based methods on a stack of MCF10A cell line. (a) An example input is given. The results of watershed, marker based watershed and the proposed curvature-based partitioning (CBP) is provided in (b), (c) and (d) respectively

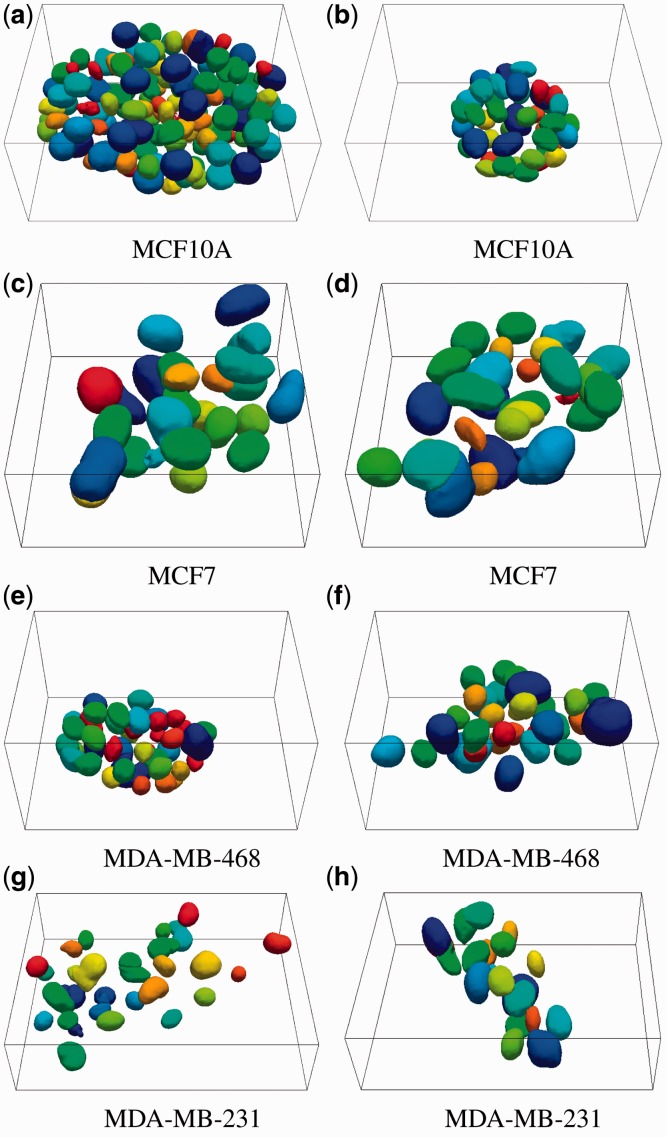
Fig. 6.

Two examples of MCF10A (a,b), MCF7 (c,d), MDA-MB-468 (e,f) and MDA-MB-231 (g,h) cell lines on day 7

Table 2.

Pixel and object level precision recall values for the annotated dataset

Measurement Type	Watershed	Marker-based watershed	GFT	IV	CBP
B/F precision	0.95	0.84	0.95	0.97	0.86
B/F recall	0.44	0.52	0.82	0.79	0.84
B/F F-measure	0.60	0.58	0.88	0.87	0.85
Object precision	0.75	0.88	0.88	0.87	0.97
Object recall	0.67	0.72	0.87	0.86	0.95
Object F-measure	0.71	0.80	0.88	0.87	0.96

Note: B/F stands for Background/Foreground.

5 MORPHOGENESIS COMPARISON

Comparison needs to be performed in context. For example, it is well known that MCF10A and MCF7 have a well-contained symmetrical organization, whereas MDA-MB-231 and MDA-MB-468 have more invasive growth properties. Therefore, morphogenesis analysis is performed by comparing (i) MCF10A against MCF7 and (ii) all four lines simultaneously. In both cases, colony organization is multiparametrically profiled with the Delaunay triangulation.

In the first case, the MCF10A line is a non-transformed line, whereas the MCF7 line is tumorigenic one. Non-transformed lines should form a hollow sphere by day 10, i.e. cells inside the colony should go through apoptosis. Thus, a potential index for lumen formation is the distribution of distances of nuclei to the center of the convex hull (CH) in a colony. Depending on the type of cell lines, during the colony growth, the distance of some of the nuclei to the center of the CH is increased, whereas others may remain unchanged. There are a number of ways to visualize cellular organization for quality control, as seen in Figure 7a, which shows a distribution of distance of nuclei to the center of the CH for MCF10A. Our investigation indicates that a preferred index for lumen formation, lumenosity, is the volume of the CH that excludes nuclear information, where the CH is generated from the centroids of nuclei in a colony. Computation of CH is supported by the VTK library. The evolutions of the lumenosity indices for MCF10A and MCF7 are shown in Figure 7b, which is consistent with the published literature as MCF7 does not form a lumen (e.g. a hollow sphere) (Kenny et al., 2007).

Fig. 7.

(a) A computed morphogenesis index corresponding to the distance of each nucleus to the center of the CH of the MCF10A colony; (b) another computed index indicating an index that represents percentages of nuclei being at a specific distance to the center of the colony for MCF7 and MCF10A. It is clear that MCF10A forms a lumen, but MCF7 does not. (c, d) MDA-MB-468 and MDA-MB-231 have non-symmetrical growth properties

In the second case, colony organization is quantified across the four cell lines, as shown in Figure 7c and d. In contrast to MCF10A and MCF7, the other two lines have an invasive morphogenesis. Among computed colony indices, ‘Colony Elongation’ and ‘Mean Edge Length’ were identified to be discriminative between the four cell lines. Colony Elongation is calculated as the ratio of 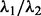where 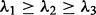are the lengths of principal moments of the colony. For MCF10A and MCF7 lines, the elongation of the colony is significantly lower compared with the 231 and 468 cell lines at day 7. There is also a 2-fold difference between the 231 and 468 cell lines and MCF10A, which indicates invasiveness of these cell lines. The mean edge length of these colonies is used as an index to measure the dispersion of the nuclei in the colony space. Both 231 and 468 lines are showing increased mean edge lengths in our experiments as a result of increased proliferation (Fig. 7(d)).

6 CONCLUSION

With the increasing demand for high content screening of 3D cell culture models, the CBP method is a highly effective approach for segmentation and subsequent profiling. Evaluation and testing of CBP have been tightly coupled with the experimental design that consists of four cell lines with a significant genetic diversity and distinct phenotypic signatures. Comparison of CBP with the alternative methods demonstrates superior performance in terms of the error rates. Furthermore, multiparametric representation for the colony organization has identified indices that capture aberrant and normal morphogenesis in these four cell lines. The software has been developed in ITK/VTK framework for improved portability and memory use.