Molecular and Subcellular-Scale Modeling of Nucleotide Diffusion in the Cardiac Myofilament Lattice

Abstract

Contractile function of cardiac cells is driven by the sliding displacement of myofilaments powered by the cycling myosin crossbridges. Critical to this process is the availability of ATP, which myosin hydrolyzes during the cross-bridge cycle. The diffusion of adenine nucleotides through the myofilament lattice has been shown to be anisotropic, with slower radial diffusion perpendicular to the filament axis relative to parallel, and is attributed to the periodic hexagonal arrangement of the thin (actin) and thick (myosin) filaments. We investigated whether atomistic-resolution details of myofilament proteins can refine coarse-grain estimates of diffusional anisotropy for adenine nucleotides in the cardiac myofibril, using homogenization theory and atomistic thin filament models from the Protein Data Bank. Our results demonstrate considerable anisotropy in ATP and ADP diffusion constants that is consistent with experimental measurements and dependent on lattice spacing and myofilament overlap. A reaction-diffusion model of the half-sarcomere further suggests that diffusional anisotropy may lead to modest adenine nucleotide gradients in the myoplasm under physiological conditions.

Introduction

Spatiotemporal diffusion of adenine nucleotides regulates cardiac energetics and excitation-contraction coupling, by transporting ATP as a substrate for myosin ATPase, ion channels, and transporters (ATP-sensitive K⁺ channel, Na⁺/K⁺ pump, and sarcolemmal and sarcoplasmic reticulum Ca²⁺ ATPases) and the phosphocreatine shuttling pathway (1,2). Under physiological and pathological conditions, the irregular subcellular ultrastructure may lead to the development of nucleotide gradients that could affect nucleotide-dependent processes (3,4). Experimental and theoretical studies suggest that diffusion of ATP, its metabolites, and other small molecules is hindered within muscle cells (5–8). Recent studies have also implicated subcellular structures including mitochondria, transverse tubules, and the sarcoplasmic reticulum among the barriers contributing to hindered ionic and nucleotide diffusion within myocytes (5,9).

Within the myofibril, the thick and thin filaments form a dense hexagonal lattice (with <20-nm interfilament spacing) that, independent of organelle-scale features, has been suggested to influence the rate of nucleotide diffusion (7), and hence the development of concentration gradients, within a substantial fraction of the cell volume (4). The hexagonal lattice of the myofibril is aligned with the radial axis of the cell, and evidence suggests (9,10) that nucleotide diffusion along radial axis is slower than the longitudinal axis, along which the largely linear filaments are aligned. In particular, Shorten and Sneyd (9) have predicted, using cryo-electromagnetic (cryo-EM) resolution models of the thin and thick filaments, that the skeletal myofibril lattice imparts diffusional anisotropy, in line with spectroscopic evidence (6,7,11). Given that ATP consumption is highly regulated in cardiac cells and dysregulated under pathological conditions (12,13), we sought to quantify the magnitude of diffusional anisotropy in cardiac cells and its impact on nucleotide dynamics during pulsatile ATPase activity.

The extrapolation of Shorten and Sneyd’s findings in skeletal muscle cells to heart cells likely depends on specific structural properties of the cardiac myofilaments and sarcomere. For example, wider myosin and actin filament distances, d_ma, are reported for cardiac myocytes compared with skeletal muscle (18.3 nm (14) vs. 16.5 nm (15)). Furthermore, because diffusion is inherently a macroscopic phenomenon dependent on molecular-scale attributes such as the molecular structure, solvent-accessible surface area, and conformation, there may be a benefit in using atomic-resolution structural data. For instance, even at cryo-EM resolution, the inclusion of approximate geometries of the myosin heads in the myofibril was shown by Shorten and Sneyd (9) to significantly reduce the rate of diffusion in the myofibril. Hence, by utilizing recently available atomistic structural data (16–18) and myofibril lattice spacings appropriate for cardiac cells, refined estimates for nucleotide diffusion in the cardiomyocyte may be possible.

Our recent successes in describing small molecule diffusion in atomistic systems (19,20), and the availability of reconstructions of the thin filament from x-ray crystallographic structures (17), enable the investigation of molecular structure on cellular scale diffusion, such as for nucleotides. Recent studies on Ca²⁺ diffusion in cardiac myocytes (21,22) and diffusion within the actin/myosin myofilament lattice (9) have used homogenization theory in describing diffusion of small molecules such as Ca²⁺ and ATP. This technique provides a simultaneous description of molecular and cellular length-scales, specifically by spreading out, or homogenizing the contribution of a periodic microscopic domain comprising a macroscopic domain (23–25). Hence, we extend our approaches with homogenization theory (26–28), to integrate microscopic myofibril geometries of arbitrary resolution into macroscopic, sarcomere-scale models of diffusion.

In this study:

• 1.We estimate the diffusional anisotropy of nucleotides in the cardiac myofibril using atomic resolution reconstructions of sarcomeric proteins, and
• 2.We investigate the effects of diffusional anisotropy on ADP gradients under physiological conditions.

We applied the homogenization approach proposed for skeletal myofibrils in Shorten and Sneyd (9), to the cardiac myofibril, utilizing newly available atomic-resolution models of the thin filament. Using a molecular-scale homogenization approach, we examined the extent to which variations in the diffusion constant due to filament overlap, cross-bridges density, and lattice spacing influence the transport of ATP and its reaction partners. We furthermore investigated the propensity for the formation of ADP gradients within a finite-element model of the half-sarcomere, in which ATP hydrolysis by the myosin ATPase and ADP/ATP exchange with the mitochondrion are included. We find that anisotropic adenine nucleotide diffusion, originating from the configuration of atomistic-resolution myofibril proteins, may promote radial concentration gradients within the cardiac sarcomere.

Methods

Geometries

Two-dimensional (primitive) and three-dimensional (atomistic) lattices were created. The software GMSH, Ver. 2.7 (30), was used to create the primitive lattice unit cell based on Fig. 1 of Tanner et al. (31) (see Fig. S1 a in the Supporting Material) and includes two intact actin filaments at its center, four myosin thick filaments, and four actin thin filament halves at the cell boundary; cell boundaries are coaligned with the macroscopic axes, $\hat{e}$.

The filaments are invariant along the z axis, thus the effective diffusivity may be completely described using a two-dimensional formulation of Michailova et al. (2). Three reference models of the atomistic myofibril unit cell were created:

• 1.Both thin and thick filaments;
• 2.Only thin filaments; and
• 3.Only thick filaments.

All filaments were aligned along z. The reference distance between the thick (M) and thin (A) filaments, d_ma, is 18.3 nm, which was varied to investigate lattice spacing effects. An atomic-resolution reconstruction (PDB:2W4U) (32) and the myosin heads from the myosin-bound thin filament model (PDB:4A7F) (33) were used for the thin filament (TF) geometry (Fig. 1). Up to three bound myosin head pairs (at 120° angles) were fitted to the TF based on the PDB:4A7F structure (33). The thick filament was represented by a cylinder of radius 6 Å, because molecular reconstructions were unavailable at the time. We refer the reader to Liao et al. (34) and the Supporting Material for mesh generation details.

Figure 1.

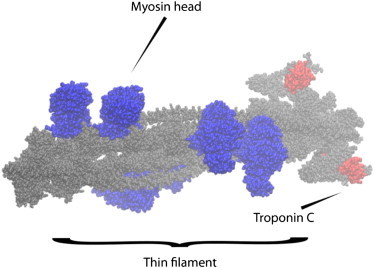
Atomistic thin filament model. Side view of thin filament (gray) with six bound myosin heads (three cross-bridges, blue). Troponin C is marked (red) for reference.

Homogenization

We numerically solve the homogenized diffusion partial differential equation for χ_k in Equation 7 and compute the effective diffusivity D_ij from Equation 8 using the finite-element solver FENICS (35). The solver assumes surfaces at the mesh outer boundary belong to the unit cell (Γ\Γ_ϵ); all other boundaries are impermeable and thus belong to Γ_e. We solved the weak form of the homogenization equation using a piecewise linear Galerkin finite-element method with the default direct linear solver. The solution is then applied to Equation 8 to yield the ith components of D (D_ii). We report the effective diffusion constant by its normalized value, D ≡ D/D^ϵ. The protocol is validated in the Supporting Material. The code will be released at https://bitbucket.org/huskeypm/homogenization.

Reaction-diffusion model

To examine the impact of altered nucleotide diffusion within the sarcomere, we created a finite-element reaction diffusion model (4–9),

$$\frac{\partial ATP}{\partial t}=-\nabla \cdot D_{\text{ATP}}\nabla ATP-J_{\text{hydrolysis}}-J_{CK},$$ (1)

$$\frac{\partial ADP}{\partial t}=-\nabla \cdot D_{\text{ADP}}\nabla ADP+J_{\text{hydrolysis}}+J_{CK},$$ (2)

where ATP and ADP are MgATP and free ADP, respectively, J_hydrolysis is the rate of ATP hydrolysis,

$$ATP\to ADP+P_i.$$ (3)

and J_CK is the rate of cytosolic creatine kinase reaction,

$$ATP+Cr\leftrightarrow ADP+PCr.$$ (4)

P_i, Cr, and PCr are inorganic phosphate, creatine, and phosphocreatine. We assumed that ATPase heads interacted with thin filament but activity was continuously distributed and restricted to the overlap region of the A-band (see Fig. 1 B of Vendelin et al. (36)); similarly, creatine-kinase (CK) activity was concentrated along the boundaries normal to the mitochondrion intermembrane space, and decreased linearly toward the center of the myofibril. At the interface between the cytosol and intermembrane space, we applied the boundary conditions

$$D_N\nabla N=J_{N,\text{diff}}\text{for}N=ATP,ADP,$$ (5)

which control the rate of ADP entry into the mitochondrion and flow of synthesized ATP into the cytosol. The concentration of substrates P_i, Cr, PCr, as well as ATP/ADP in the intermembrane space, were treated as whole-cell values by our implementation of the ordinary differential equation model of van Beek (37). D_ATP and D_ADP in Selivanov et al. (4) represent the diffusion coefficients for ATP and ADP; we consider both an isotropic diffusion constant (D_ii = D^ϵ ⋅ 1.0, where D^ϵ = 145 [μm²/s]) and an anisotropic diffusion constant for the diffusing species determined from our homogenization models.

We modeled myosin ATPase activity, creatine kinase activity, and nucleotide exchange between the sarcomere and mitochondrion, using a myocardial metabolism model from van Beek (37). The van Beek model included mitochondrial synthesis of ATP from ADP via oxidative phosphorylation, hydrolysis of ATP (J_hydrolysis) in the myofibril, and diffusion of nucleotides between the intermembrane space (intermembrane space) and the myofibril (J_diff) as well as fluxes due to the creatine-kinase (CK) pathway (J_CK). The contribution of the adenosine nucleotide transporter (ANT) was implicitly represented by the intermembrane space diffusional fluxes, because reduced models and full models of mitochondrial coupling (e.g., via explicit models of ANT (36)) have been shown to yield similar results (37). Further details of the model geometry, integration of the ordinary and partial differential equation models, and their solution are in the Supporting Material.

Theory

We present a brief mathematical formulation of the homogenized diffusion equations; a lengthier treatment of this approach can be found in the literature (21,22,24). Given a macroscale geometry Ω_m ⊂ $\mathbb{R}$³, the time-dependent diffusion problem is to find an ionic concentration function c:Ω_m × [0,T]→$\mathbb{R}$ such that

$$\begin{array}{l}\frac{\partial c}{\partial t}=\nabla \cdot D\nabla c\hfill \\ {\text{on Ω}}_m,\hfill \end{array}$$ (6)

where D is an unknown effective diffusion tensor. A function f representing the net effect of any ionic sinks or sources is given for the initial condition c(x,0) = f(x,0) for all x ∈ Ω_m and the boundary conditions c(x,t) = f(x,t) for x ∈ ∂Ω_m, t ∈ [0,T]. The forcing term f represents the net effect of any ionic sinks or sources on ∂Ω.

We assume that Ω_m has two length scales of interest, x and y:= x/ϵ. Here, ϵ is small compared to the dimensions of Ω and it is assumed that Ω is periodic at the y scale; a unit cell in this lattice is denoted Ω, and the accessible region therein as Ω_ϵ. We further assume that D is a function of the y scale only, i.e., that D(x,y) can be written as D^ϵ(y) (in the application context here, this assumption on D implies that a Ca²⁺ ion’s diffusion is governed by its location relative to nearby myosin and actin molecules, but not its location in the larger lattice of thick and thin filaments). The homogenization is carried out by expanding c in terms of powers of ϵ (i.e., $c={\sum }_i{c}_i{\mathit{ϵ}}^i$) and writing ∇ as a scaled gradient operator (i.e., ∇ = ∂_x + ϵ−1∂_y). This results in the y-scale steady-state problem: find χ:Ωϵ→$\mathbb{R}$ such that

$$\begin{array}{ll}\nabla \cdot \left(D_{ij}^{\mathit{ϵ}}\left({\delta }_{jk}+\frac{\partial {\chi }_k}{\partial y_j}\right)\right)=0,\hfill & {\text{on Ω}}_{\mathit{ϵ}},\hfill \\ \left(D_{ij}^{\mathit{ϵ}}\left({\delta }_{jk}+\frac{\partial {\chi }_k}{\partial y_j}\right)\right)\cdot \hat{n}=0,\hfill & {\text{on Γ}}_{\mathit{ϵ}}:=\partial {\text{Ω}}_{\mathit{ϵ}},\hfill \\ \left(D_{ij}^{\mathit{ϵ}}\left(\frac{\partial {\chi }_k}{\partial y_j}\right)\right)\cdot \hat{n}=0,\hfill & \text{on Γ}\setminus {\text{Γ}}_{\mathit{ϵ}}:=\partial \text{Ω}\setminus \partial {\text{Ω}}_{\mathit{ϵ}},\hfill \end{array}$$ (7)

where Γ_ϵ corresponds to a molecular boundary and ∂Ω\∂Ω_ϵ refers to all other boundaries, the diffusion coefficients D^ϵ are experimental inputs, and periodicity of χ with respect to opposite sides of Γ_ϵ is enforced. Given solutions for χ, the coefficients of the effective diffusion tensor can be computed via

$$D_{ij}=\frac{1}{\left|\text{Ω}\right|}\underset{{\text{Ω}}_{\mathit{ϵ}}}{\int }{D}_{ij}^{\mathit{ϵ}}\left(y\right)\left({\delta }_{jk}-\frac{\partial {\chi }_k}{\partial y_j}dy\right),$$ (8)

where Ω is the unit cell volume.

Results

Validation of homogenization model

As a preliminary step, we show that our implementation of the homogenization protocol applied to a layered n-dimensional system and a lattice of cylinders of varying diameters is in strong agreement with analytical predictions (see the Supporting Material). We then compared our homogenization implementation against results predicted by Shorten and Sneyd (9). In their study, a unit cell containing two myosin filament quarters and two actin filament halves arranged with a myosin/actin spacing, d_ma of 16.5 nm (typical of skeletal muscle (15)), was used for the solution of the homogenization equation (see Fig. S1 b). We used a larger unit cell (the primitive mesh) to facilitate integrating intact molecular models in the next section. We solved Eq. 7 on the primitive mesh and report the homogenized field along x, χ_x, for particles of diameter 0 and 6 nm in Fig. S2. The χ_i field indicates the relative impact of diffusional barriers on the effective transport along the ith direction. Generally speaking, χ_x ≈ 0 signifies regions where diffusion essentially unhindered, whereas deviations from zero signify strong diffusional hindrance. Based on Eq. 8, if the gradient ∂χ_x/∂y_x is zero (as one expects for χ_x = 0), the effective diffusion constant, D_ij, is equal to its reference value, D^ϵ_ij. When χ_x! = 0 in the neighborhood of diffusional obstacles, nonzero values for ∂χ_x/∂y_x will in general reduce the integrand of Eq. 8 and yield a smaller effective diffusion constant relative to its reference value.

We observed that positive gradients predominated over negative gradients arising from the filament diffusional barriers, which reduced the integrand in Eq. 8 and hence, D_ij. The predominance of nonzero gradients for the 6-nm substrate modeled relative to a 0-nm substrate suggests that the former has a smaller effective diffusion constant. The magnitude and profile of χ_x predicted by our implementation for the large unit cell qualitatively agree with solutions shown in Fig. 5 of Shorten and Sneyd (9) (not shown).

Fig. 2 compares our predictions for the x component (orthogonal to filament axis) of the effective diffusion constant, D_xx, at d_ma =16.5 nm using Eq. 8 with estimates from the literature (Fig. 6 of Shorten and Sneyd (9)). In qualitative agreement with Shorten and Sneyd, we observe that D_xx decreases linearly with increasing particle sizes until converging to zero as the particle diameter (8 nm) approaches the mean free distance between filaments. For substrates smaller than 1 nm, such as the nucleotides at the focus of our study, D_xx ≈ 68% of its bulk value. We also compared our predictions against the Hashin-Shtrikman (HS) bound from Auriault et al. (26) (D = ϕ/(2 − ϕ)), where ϕ is the accessible volume fraction), and found exceptional agreement for all but the smallest volume fractions (near 8-nm particle diameters). The deviation is likely due to the nonuniform filament radii. For a d_ma value typical of cardiac tissue (18.3 nm) (14), we report a lesser extent of hindrance along the x direction, which is still less than hindrance along the z axis. D_xx ≈ 0.72, D_zz ≈ 0.82, for substrate diameters <1 nm.

Figure 2.

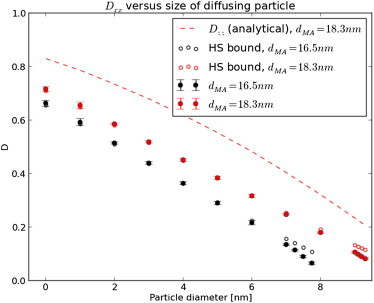
Effect of myofibril lattice spacing on D. Predictions of the effective diffusion constant for myosin/actin spacings of 16.5 and 18.3 nm along the transverse direction based on the primitive unit cell in Fig. S1a in the Supporting Material as a function of diffusing particle size. Error bars represent the 95% confidence interval based on three trials of differing mesh resolutions. We include an analytical estimate for D parallel to the filaments (Dzz) for comparison. To see this figure in color, go online.

Diffusivity on large unit cell with atomistic-representation of thin filaments

We incorporated an atomistic representation of the thin filament into the unit cell geometry to determine its impact on diffusion. Solutions for χ_x and χ_z are shown in Fig. 3. The value χ_x for the atomistic mesh resemble those for the primitive mesh, with positive gradients predicted to the left of molecular boundaries, and negative on the right. Notable differences, however, are reported for the thin filament, as the protruding Troponin complex and bound myosin heads perturb χ_x and χ_z. Inclusion of the molecular geometries reduce D_xx and D_zz, in a similar fashion to the estimates of Shorten and Sneyd (9) when cryo-EM resolution myosin heads were included. Our predictions indicate D_xx = 0.42 (Table 1) and D_zz = 0.59, versus 0.72 and 0.82 predicted for the primitive mesh (Fig. 2); our estimate are within 5% of the HS bound. The 95% confidence interval in D_ii based on varying the mesh resolution was <0.03 (see the Supporting Material), thus we believe differences in reported the D_xx values are significant.

Figure 3.

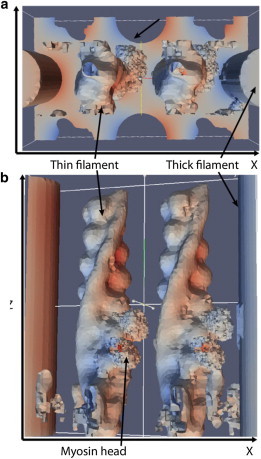
Solutions of the homogenized fields for a unit cell with atomistic-resolution geometries: (a) χ_x; (b) χ_z. Thin filament geometries of outer boundary are hidden for clarity.

Table 1.

Predicted effective diffusion constants with respect to myosin/actin overlap

Region	[Dxx, Dyy, Dzz]	ϕ	HSa bound (Dxx)
A-band (filament overlap)	[0.42, 0.45, 0.59]	0.61	0.44
I-band (thin filament only)	[0.59, 0.64, 0.75]	0.77	0.62
H-zone (thick filament only)	[0.70, 0.71, 0.82]	0.82	0.69

^aHS is Hashin-Shtrikman bound for transverse diffusion rate based on volume fraction, ϕ.

Influence of lattice geometry on ATP diffusional anisotropy

We hypothesized that increased thin and thick filament overlap influences diffusional anisotropy. Table 1 provides D_ii for the I-band (thin filament-only), the filament overlap region of the A-band, and H-zone (thick filament only). The overlap region presented the largest hindered diffusion (D_ii = [0.42, 0.45, 0.59]), the I-band less so (D_ii = [0.59, 0.64, 0.75]), and the H-zone with the least (D_ii = [0.70, 0.71, 0.82]). The magnitude of D was correlated with the accessible volume fraction and HS bound. We further hypothesized that altered interfilament spacing within the overlap region would modulate D; indeed, in Table 2 we demonstrate for a myosin-bound filament that a 10% decrease in d_ma leads to a reduction in D_xx (0.26 vs. 0.34) versus an increase in D_xx (0.34 vs. 0.44) for a commensurate increase in d_ma.

Table 2.

Predicted effective diffusion constants with respect to myosin/actin lattice spacing, d_ma, for the thin filament with bound myosin heads

dma, nm	[Dxx, Dyy, Dzz]	ϕ	HSa bound (Dxx)
16.43	[0.26, 0.26, 0.37]	0.45	0.29
18.26	[0.34, 0.35, 0.46]	0.53	0.36
20.08	[0.44, 0.44, 0.57]	0.61	0.44

^aHS is Hashin-Shtrikman bound for transverse diffusion rate based on volume fraction, ϕ.

We sought to understand the influence of thin filament-bound myosin heads on diffusivity. We estimated D_ii for zero to three cross-bridges formed between myosin heads and each thin filament. Our results in Table 3 indicate that D_ii decreases with increasing cross-bridge density based on d_ma = 18.3 μm. Although the differences in D between sequential additions of myosin heads are comparable to our estimates of standard error (see the Supporting Material), there is a 20% difference between the zero- and three cross-bridge states, which we deem significant.

Table 3.

Predicted effective diffusion constants for actin with varying number of bound myosin heads

dma, nm	Cross-bridges	[Dxx, Dyy, Dzz]	ϕ	HSa bound (Dxx)
18.26	0	[0.42, 0.45, 0.59]	0.61	0.44
18.26	1	[0.38, 0.41, 0.54]	0.58	0.41
18.26	2	[0.38, 0.37, 0.50]	0.56	0.39
18.26	3	[0.34, 0.35, 0.46]	0.53	0.36

^aHS is Hashin-Shtrikman bound for transverse diffusion rate based on volume fraction, ϕ.

Anisotropic diffusion in a sarcomere reaction-diffusion model

We speculated that hindered, anisotropic diffusion would enhance ADP gradients in the myofibril lattice relative to the unhindered, isotropic constant. We thus simulated nucleotide diffusion within a half-sarcomere model for the isotropic bulk and anisotropic diffusion constants, D^ϵ and D, where D is based on the three cross-bridge lattice, d_ma = 16.4 nm model, as well as with (+CK) and without (−CK) creatine kinase activity. Resting levels of ATP and ADP (+CK, [ATP] ≈ 5.92 mM, [ADP] ≈ 0.055 mM) were sustained for each 300-ms beat interval through 6 s of simulation (independent of the diffusion constant) and evidence the stability of the model (see Fig. S8 a); moreover, while the concentration of ATP changes <3%, peak [ADP] is twofold larger than resting levels (≈0.11 mM) and consistent with predictions from Van Beek (see Fig. 10 in van Beek (37)). In Fig. 4 a we report a 300-ms beat interval, over which [ADP] follows the time course of J_hydrolysis (see Fig. S9) with a maximum at 5.27 s; [ADP] is marginally higher in the overlap region relative to the I-band and near the intermembrane space, with the largest variations observed for the anisotropic diffusion constant (red) versus isotropic (black). We report the two-dimensional ADP distribution at peak J_ATP in Fig. S10, which suggests a [ADP] gradient develops along the radial (y) direction, stemming from the higher concentration of ADP in the myofibril relative to the intermembrane space. The radial ADP gradient summarized in Fig. 5 was approximately twofold higher for D relative to D^ϵ (∇ [ATP] ≈ 10 μM/μm for isotropic relative to ∼20 μM/μm for anisotropic).

Figure 4.

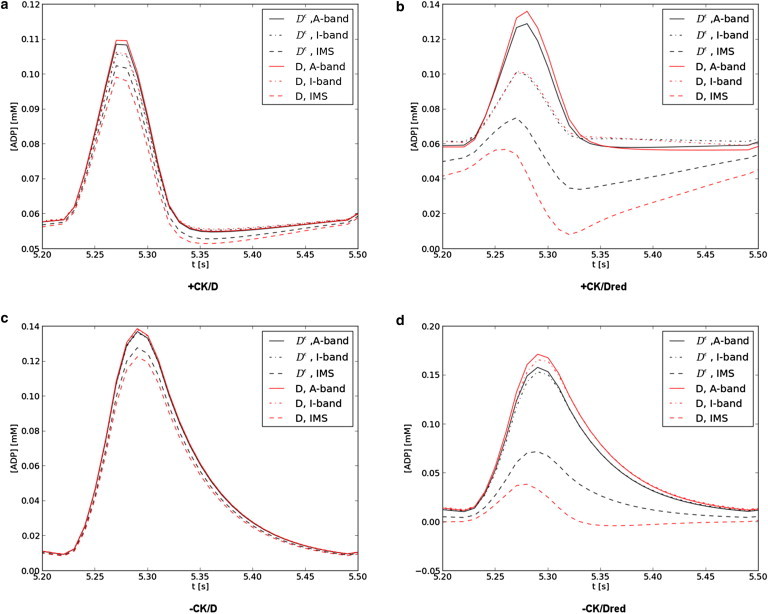
ADP concentration profiles. [ADP]at several sarcomere locations with CK (a and b) and without (c and d), and with a normal (a and c) or 10-fold reduced (b and d) diffusion constant are given. [ADP] is reported at the filament overlap region of the A-band (solid), I-band (dashed), and adjacent to the intermembrane space (dot dash) for the isotropic (black) and anisotropic (red) diffusion constants. ADP profiles are in agreement with Fig. 10 of Van Beek (37). To see this figure in color, go online.

Figure 5.

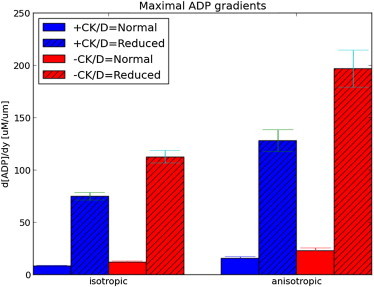
Maximal ADP gradients. Comparison of ADP gradients at t ≈ 5.3 s in the presence (blue) and absence (red) of CK activity, and with normal (solid) and 10-fold reduced (patterned) diffusion coefficients. Gradients are defined based on [ADP] at the A-band relative to the interface with the intermembrane space. Error bars represent 95% confidence interval based on 10 trials where the diffusion constant was randomly varied within one standard deviation (0.035) of the estimated values from homogenization (see the Supporting Material). To see this figure in color, go online.

It was reported in van Beek (37) that CK buffers ADP fluctuations arising from pulsatile ATPase activity, thus we compared the scale of ADP gradients in absence of CK (−CK) and their dependence on the anisotropic diffusion constant. We reduced the CK rate constants by 98%, which decreased the resting [ADP] (to 0.01 mM from almost 0.06), and nearly doubled the peak [ADP] (to 0.14 mM from 0.11). Without the consumption of ADP by the myofibril CK pathway, elevated ADP pools persisted in the cytosol and increased the time required to restore resting levels of the nucleotide (0.20 s relative to 0.08 s for CK present). Radial ADP gradients were negligibly increased for the isotropic CK-absent case relative to CK-present, whereas the gradients for the anisotropic case increased by <30% (see Fig. S10 and Fig. 5).

It has been speculated that nucleotide diffusion rates within the myofibril may deviate significantly from measurements in bulk water (36). Indirect estimates have ranged considerably, with a recent study suggesting reductions as low as one-thousandth of the bulk rate are necessary for consistency with observations of ATP compartmentalization in the myofibril (4). We reduced the diffusion constant by 90% to examine its impact on ADP distribution. We observed a substantial increase in peak [ADP] within the myofibril (≈20%) and reduction in ADP at the intermembrane space (≈30–40%). When CK was active, [ADP] was reduced by 30% within the I-band (where CK activity is assumed to be maximal) and the intermembrane space [ADP] appeared to overshoot the resting concentration. This overshot may be a limitation of the model, as we applied fluxes based on the average concentration of the nucleotides in the sarcomere (J_average), not their local concentrations (J_local), which would locally deplete ADP when J_average > J_local. Nevertheless, we observe clear distinctions between the anisotropic and isotropic diffusion constants that arise when the constant was reduced significantly, as shown in Fig. 5 (and see Fig. S11).

Discussion

Atomistic-scale features induce diffusional anisotropy in myofibril lattice

Prior studies successfully applied homogenization to estimate diffusional anisotropy in cellular and subcellular environments (9,21,22). Homogenization requires the macroscopic (cellular) and microscopic (subcellular or molecular) spatial scales to be decoupled, as quantified by the y = x/ϵ limit (see Theory). This condition is satisfied for the myofibrils, because the unit cell (∼50 nm per side) is an order-of-magnitude smaller than the μm-scale dimensions of the sarcomere. Hence, the success of Shorten and Sneyd (9) in providing compelling evidence that the myofibril lattice contributes significant diffusion hindrance and anisotropy. Our studies extend their work by adding atomistic-resolution detail for the thin filament and indicate greater diffusional hindrance than estimated by lower resolution geometries. Moreover, our technique provides what we believe is a novel bridge between atomistic-resolution reconstructions of macromolecules and cellular-scale signaling processes.

The ratio of our D_xx to D_zz estimates in the filament overlap region were ∼70% ± 0.027 under a variety of lattice spacings and cross-bridge densities, which agrees with recent image correlation spectroscopy estimates (0.69–0.70, Table 1 (11)) and observations of other small molecules (0.72–0.74) (6,7). In fact, our predictions using three cross-bridges per filament at 18.3 μm (D_xx = 0.34 and D_zz = 0.46) are strikingly close to the recent image correlation spectroscopy estimates, which revealed radial and longitudinal diffusion constants that are 28 and 45% of the 183 [μm²/s] isotropic rate measured in water. In contrast, our primitive unit cell predicts a D_xx/D_zz ratio of ∼82%, which clearly overestimates transverse diffusion rates. This finding demonstrates that atomistic-resolution, macromolecular models of the filaments yield superior predictive power for modeling diffusion in complex environments.

Interestingly, our estimate of diffusional anisotropy along x (D_xx = 0.26) at d_ma = 16.43 nm, which approximates the distance used by Shorten and Sneyd (9), is significantly smaller than predicted by their approach (D_xx = 0.72). We suspect that the accessible volume fraction in our model is significant smaller than the model of Shorten and Sneyd, which would lead to a different scale for the effective diffusion constant. One explanation for the difference is that our molecular resolution geometries occupy a greater volume than the cryo-EM structures used in their study. Hence, accurate determination of the diffusivity is contingent upon a reasonable assessment of the molecular volume, for which we believe atomistic-resolution data are ideally suited. At a larger d_ma typical of cardiac tissue (18.3 nm), D_xx is 30% of the bulk value, the less restrictive packing may permit the diffusion of larger substrates than accommodated by the skeletal muscle myofibril; it is possible that the more rapid diffusion rates help maintain myofilament energetics in a reaction-limited regime (3), especially given the high oxidative demands of cardiomyocytes.

Nucleotide diffusion is dependent on myofibril configuration

During contraction, the myofibril lattice spacing decreases and concomitantly drives the myosin heads toward the actin subunits on the thin filament (14); given appropriate substrates, cross-bridges may be formed and drive contraction. Three regions of the sarcomere—the I-band, the filament overlap region of the A-band, and the H-zone—differ with respect to the presence or absence of thin and thick filaments. We anticipated that each region would have a sufficiently different volume fraction depending on the filaments present, and this in turn would influence D. Our results confirm this hypothesis, as we observed decreases of 30–40% between the filament overlap region and the I-band or H-zone. We hypothesize that nucleotide diffusion depends on the longitudinal position along the myofilament, yet a firm conclusion awaits a more complete model of the I- and H-zones, including structurally important structural proteins such as titin, obscurin, and nebulin (38).

In the overlap region of the A-band, the myosin-actin filament spacing varies as a function of sarcomere length; this property provides a structural basis for the Frank-Starling law, whereby increased sarcomere length is associated with enhanced force generation (39). Because the cell is stretched during diastole, transverse constriction will reduce the effective volume fraction, while systolic shortening of the sarcomere and expansion of the myofilament lattice would have the opposite effect; hence, we hypothesized that these structural changes would hinder diffusion to greater and lesser degrees, respectively, relative to the resting configuration. Indeed, our results demonstrate a positive correlation between effective diffusivity and myofilament spacing, with smaller myosin-actin distances demonstrating a greater extent of hindered diffusion and anisotropy. Thus, regardless of other proteins that may exist between the filaments, nucleotide diffusion may be modestly sensitive to changes in lattice spacing; this sensitivity may be more apparent for conditions in which myofibril strain and sarcomere length are increased by elevated diastolic pressures, such as dilated cardiomyopathy and heart failure (40).

The sliding of filaments is driven in part by the association of myosin heads to actin subunits comprising the thin filament. In Shorten and Sneyd (9), the presence of myosin heads in the skeletal myofibril was found to reduce D_xx by ∼15% relative to the filament-only geometry. In agreement with their findings, we observe a 20% decrease in D_xx between the three-crossbridge-per-TF case relative to the crossbridge-free case (0.34 vs. 0.42); our prediction is also consistent with estimates from analytical bounds (26,41) using the corresponding accessible volumes (D_xx = 0.36 vs. D_xx = 0.43). In fact, we find that a linear-least-squares fit of D_xx from the HS bound to our estimated D_xx (and D_yy) across all overlapping geometries is in quantitative agreement with an R² = 0.97 (not shown). That is, the diffusivity is determined almost exclusively by the accessible volume fraction. Hence, our predictions are unlikely to change significantly if the myosin heads were solely tethered to the thick filament and not bound to the thin filament, as would be expected during relaxation of the myofibril. In theory we could predict D_xx based on the volume of proteins in the myofibril using the HS bound, including those not directly associated with the filaments, regardless of their location or binding configuration. However, we observed that the bound underestimated the extent of hindered diffusion for large particles corresponding to volume fractions below roughly 20% (Fig. 2). Given that the volume fraction of a cell may fall within this range (0.19–0.27) (42), it is likely the HS bound would underestimate the extent of diffusional hindrance for even small particles. This shortcoming provides strong justification for advanced models of diffusion in crowded environments, such as Brownian dynamics (42,43), Monte Carlo simulations (9,10), and homogenization (9).

Nucleotide diffusional anisotropy impacts the spatial-temporal distribution of ADP in sarcomere

As the byproduct of ATPase activity during contraction, ADP is an important substrate for the reestablishment of resting ATP concentrations, directly through oxidative phosphorylation within the mitochondrion and indirectly through the creatine kinase pathway. The interplay among the distribution and activity of metabolic enzymes, the localization of substrates, and substrate diffusion rates between enzymatically active regions, are important constraints for energy delivery within the cell (8). Early numerical studies of mitochondrial respiration in a two-dimensional representation of the sarcomere suggested the development of slight cytosolic ADP gradients (≈20 μM/μm) (36). These gradients were significantly amplified when a 10-fold reduced diffusion constant was used, based on estimates from confocal imaging of redox (44) and mitochondrial membrane potentials under substrate-deprived conditions (45). More recently, by fitting a reaction-diffusion model to experimental measurements of myosin ATPase activity (4), it was suggested that the diffusion constant may be up to three orders-of-magnitude smaller than its bulk value, which was then shown to promote significant radial ADP gradients in the sarcomere. While there are apparent discrepancies between these indirect measurements of the nucleotide diffusion constant and direct spectroscopic measurements, our homogenization method provides a framework for quantifying the molecular-scale contributions to hindered diffusion and anisotropy for a given reference diffusion constant, and describing their impact on diffusion gradients within the sarcomere.

Our simplified sarcomere model demonstrates localization of ADP and the development of ADP gradients under physiological conditions, similar to findings from prior studies (4,36). To estimate the magnitude of ADP gradients, we performed reaction diffusion simulations comparable to those performed by Vendelin et al. (36), using the directly-measured bulk rate (145 μm²/s) and a 10-fold reduced rate (1.45 μm²/s) motivated by indirect measurements (4,36,44,45). Our findings confirm that radial ADP gradients develop during contraction (36), due to the localization of myosin ATPases within the myofibril bundle versus the mitochondrial intermembrane space (46), as well as along the longitudinal direction CK activity concentrated along the I-band and M-line (46); these longitudinal ADP gradients are all but abolished upon cessation of CK activity.

Our predictions of the effective diffusion tensor within the myofibril, which suggest substantially greater diffusional hindrance transverse to the myofilaments relative to parallel, nearly double the magnitude of radial ADP gradients in the sarcomere for all cases we considered. Upon reduction of creatine kinase activity, a pathway known for dampening ADP oscillations during contraction (8,37), we found that radial ADP gradients were increased upwards of 30%. A 10-fold reduction of the diffusion constant toward values inferred indirectly from measurements of ATPase activity lead to the largest enhancement of ADP gradients, which were maximized with the anisotropic diffusion constant. While direct methods suggest reduced diffusion coefficients within one order of magnitude of its value in dilute solution, it has been suggested that substantially slower constants inferred from myosin ATPase activity may reflect the average diffusional rate between the catalytic sites and cell periphery. Hence, the results here may characterize a range in potential ADP gradients encountered in the cytosol. Additionally, whereas the localization of ADP is dependent on our assumptions of protein distributions and sarcomere geometry based on Vendelin et al. (36), our predictions of metabolite distribution shed insight into important constraints for oxidative phosphorylation (4) and metabolism as a whole.

Despite these observations, there is considerable evidence to suggest that ATP hydrolysis is reaction-, not diffusion-limited (3). At the myofibril level, it is probably no accident that ATP hydrolysis and synthesis machinery are not diffusion-limited, because it relieves the constraint that the contractile fibers could impose on the diffusion of substrates. Nevertheless, conditions that significantly alter diffusion distances, such as large myofibrils (47) and pathological remodeling (48), or significant deviations in oxygenation at high workload (3), could shift metabolism to a diffusion-limited regime. In which case, ADP gradients may develop within the myofibril; to understand their impact on metabolic signaling, accurate estimates of anisotropic diffusion constants from experiments (6,7,11) or theoretical constants such as ours may be of considerable importance.

Limitations

The relative compactness of the myofibril lattice gives rise to substantial anisotropy in the diffusion of small molecules, which is further modulated by changes in lattice spacing and cross-bridge configuration. Lattice changes were done independently of any molecular changes, such as known conformational changes of the troponin complex (49,50) during rigor, but we anticipate that their effects on diffusivity are likely secondary to changes in lattice spacing and overlap. Lastly, substitution of our simplistic model of the thick filament with a molecular-scale reconstruction could improve our estimates of its contribution to hindered diffusion (51).

The primary nonsteric factors that could additionally influence diffusional anisotropy include hydrodynamic effects and electrostatic interactions (42). Hydrodynamic interactions scale roughly with the relative size of the diffusing substrate to the separation between obstacles (52); based on our filament model, the nucleotide radii are one-tenth of the filament spacing and thus we believe hydrodynamic effects are modest. Larger diffusing molecules, such as CaM, and diffusion adjacent to walls, would lead to more appreciable effects (9). Electrostatics may also influence the nature of diffusion (19,20), especially given the net negative charges of the nucleotides. Based on our model, the distance between fibers is almost 20 nm, which is several fold greater than the Debye length (7 Å at physiological ionic strength) and thus electrostatic interactions are likely to be modest.

However, the cell cytosol is a crowded domain where interactions between diffusing substrates and crowders can significantly impact reaction-diffusion dynamics (42,53). Similarly, additional structures intertwining with the thin/thick filament lattice, such as myosin binding protein C, as well as other molecular players including kinases associated with phosphorylation of troponin and myosin and diffusing entities like calmodulin (1), could impact substrate diffusion. Explicit consideration of crowders would be expected to decrease the accessible volume and in turn, the effective diffusion rate. Concurrently, crowding results in reduced intermolecular separations that may approach the Debye length expected at physiological ionic strengths. Under such conditions, electrostatic and hydrodynamic interactions may be more significant factors, particularly for charged substrates like the nucleotides. Extension of the homogenization approach to include external fields and hydrodynamic considerations could address these limitations.

Our half-sarcomere model does not explicitly consider the spatial-temporal dynamics of the CK substrates Cr and PCr, nor P_i, of which at least PCr demonstrates anisotropic diffusion (54). We further assumed a spatially uniform diffusional flux of nucleotides across the intermembrane space, which may be inadequate if the distribution of adenosine nucleotide transporters responsible for nucleotide exchange between the mitochondrion and intermembrane space is heterogeneous. Related to this point is our use of a simplified mitochondrial model; more sophisticated models such as Cortassa et al. (55) and Beard (56), for which the mitochondrial potential and NADH-dependent reactions are considered, as well as the contribution of the adenylate kinase pathway, may improve the accuracy of our predictions.

Furthermore, we used a coarse description for the nonuniform distribution of ATPase and CK activity, which could be improved with more detailed data. Our simulation domain was represented by a simple geometry, although studies such as ours (20,57,58) and those of others (59,60) have demonstrated a significant influence of realistic geometries on small-molecule diffusion. These factors all have the potential to alter the location and magnitude of the substrate gradients developing during the course of a heartbeat, and warrant further refinement. Nevertheless, the integration of molecular-scale based predictions of diffusional anisotropy with a simplified model of nucleotide dynamics constitutes an important step toward a realistic depiction of metabolism within the sarcomere.

Conclusions and Future Work

We have demonstrated the contribution of myofibril macrostructures to the apparent anisotropic diffusion of ATP and ADP. The anisotropy arises due to the diffusional restrictions imposed by the impermeable surfaces of molecular structures. Long-range forces, such as electrostatic interactions, and substantial conformational flexibility can be expected to further nuance the diffusional picture. We have demonstrated that the contribution of atomistic-resolution, macromolecular structural data to macroscopic diffusional processes can be readily integrated into conventional subcellular models of diffusion. Although the necessity of including atomistic-resolution details for accurate cellular modeling may seem to be a daunting task, the fact that homogenization of molecular scale features over a macroscopic region yields surprising accurate results suggests that simultaneous modeling molecular and cellular features in some cases could be pursued by homogenizing representative unit cells at several separable length-scales. As such, homogenization simulations can inform cellular simulations (58) and leverage macromolecular electrostatic descriptions (19) in regimes where molecular-scale physiochemical properties profoundly influence diffusion-dependent aspects of molecular signaling.