Selection of examples in case-based computer-aided decision systems

Abstract

Case-based computer-aided decision (CB-CAD) systems rely on a database of previously stored, known examples when classifying new, incoming queries. Such systems can be particularly useful since they do not need retraining every time a new example is deposited in the case base. The adaptive nature of case-based systems is well suited to the current trend of continuously expanding digital databases in the medical domain. To maintain efficiency, however, such systems need sophisticated strategies to effectively manage the available evidence database. In this paper, we discuss the general problem of building an evidence database by selecting the most useful examples to store while satisfying existing storage requirements. We evaluate three intelligent techniques for this purpose: genetic algorithm-based selection, greedy selection and random mutation hill climbing. These techniques are compared to a random selection strategy used as the baseline. The study is performed with a previously presented CB-CAD system applied for false positive reduction in screening mammograms. The experimental evaluation shows that when the development goal is to maximize the system’s diagnostic performance, the intelligent techniques are able to reduce the size of the evidence database to 37% of the original database by eliminating superfluous and/or detrimental examples while at the same time significantly improving the CAD system’s performance. Furthermore, if the case-base size is a main concern, the total number of examples stored in the system can be reduced to only 2–4% of the original database without a decrease in the diagnostic performance. Comparison of the techniques shows that random mutation hill climbing provides the best balance between the diagnostic performance and computational efficiency when building the evidence database of the CB-CAD system.

1. Introduction

Computer-aided decision (CAD) systems typically rely on intelligent methods for providing a second opinion to physicians when diagnosing patients. For example, CAD systems have been widely developed and utilized for the diagnosis of various forms of cancer such as breast (Cheng et al 2003, Sampat et al 2005, Doi 2005, Lo et al 2006), lung (Li et al 2005, Doi 2005, 2007, Sluimer et al 2006, Katsuragawa and Doi 2007) and colon (Doi 2005, Perumpillichira et al 2005) from radiologic images. In a typical CAD system, the task is to classify an incoming query case to one of several predefined groups (e.g. normal/abnormal, normal/benign/malignant) based on information acquired from the patient. The main CAD paradigms utilized for such a classification task are rule-based and case-based reasoning. The fundamental difference between these two paradigms lies in the way they utilize previously acquired examples for constructing the CAD system and for classifying incoming query cases.

In rule-based systems, the acquired examples are used to construct decision rules. These rules are further used to make decisions regarding new, unknown cases. Popular examples of this approach are artificial neural networks (Zurada 1992), where knowledge about the previous cases is incorporated into the weights of the inter-neuron connections. Other examples are systems based on statistical principles (Duda et al 2000) or decision trees (Mitchell 1997). In rule-based systems, the training examples are used exclusively for training the CAD system. As soon as the system is trained, it is applied independently to the new, incoming cases using only the rules found during training.

In contrast, there is virtually no training in case-based systems. Instead, the available examples are stored in the database of the system to serve as established knowledge during the classification stage. When a new query case is presented to a case-based system, it is compared with knowledge examples. Then, classification of the query case is done based on these pair-wise comparisons. This type of decision making is also known as evidence-based since it relies on prior evidence of established cases. CAD schemes that were built upon content-based image retrieval concepts fall under this category (Chang et al 2001, Tourassi et al 2003, 2007b, El-Naqa et al 2004, Park et al 2007). Note that in this context, the case base is often referred to as a knowledge database or reference library.

In this study we focus on one of the distinct issues tied with case-based systems, namely managing the case base (i.e. database of known examples). Storing examples directly in the database of the system has one major advantage over the rule-based approach. The case base can be updated without retraining the system. On the other hand, there are some drawbacks as well, such as the ever-increasing storage requirement. Data storage becomes a major problem when a large number of examples needs to be stored in the system to maintain case-base variety while each example requires a lot of storage space. This is a typical scenario when storing clinical images. Another problem arising in a large case-based system is the computational cost of classification due to the need for comparing the query case to many examples from the case base. This problem is intensified when a single comparison incurs a large computational cost due to an elaborate (dis)similarity measure. An example of a case-based medical decision support system facing such challenges is the information-theoretic CAD (IT-CAD) system proposed by our group (Tourassi et al 2003, 2007b) for mass detection in screening mammograms. The system uses the information theoretic concept of mutual information to assess the similarity between two mammographic cases. The first practical difficulty is the fact that the examples are stored in the database in the form of full images and not feature vectors causing large storage requirements. The second difficulty is the longer calculation time of assessing the mutual information between two mammographic images instead of just comparing the extracted image features.

The disadvantages of case-based systems can be alleviated by proper management of the system’s case base. In fact, careful selection of the examples included in the database may not only decrease the decision time and storage requirements, but could possibly improve the CAD performance by removing redundant or even misleading examples.

Case base optimization is a long-standing problem in artificial intelligence (Blum and Langley 1997, Wilson and Martinez 2000). The problem can be stated in several different ways depending on the ultimate optimization goal. In medical CAD systems, two main properties should be taken into account: (i) system performance and (ii) response time per query. For a case-based CAD system, both properties are directly tied to the size of the case base. These two properties can be of different importance in different environments. Priority is typically given to system performance, measured often by receiver operator characteristic (ROC) analysis (Bradley 1997, Metz et al 1998b, Obuchowski 2003). In such a scenario, certain minimal conditions on system performance may have to be met and the system designer chooses the smallest subset of available examples that meets such conditions. In another scenario, system performance needs to be maximized at any expense. Then, the case base size is of no concern. In most situations, the case base size should be reasonably controlled while ensuring that the diagnostic performance of the system is not compromised. In our study, we account for all of these scenarios in the formalization of the problem, the applied techniques and the experimental evaluation.

The existing case base reduction algorithms can be classified into three general groups. The first group comprises algorithms based on the nearest-neighbor editing rule. These algorithms rely on the distances between examples and their class membership to remove those on the borders of classes, noisy examples, etc (Hart 1968, Aha et al 1991, Aha 1992). The algorithms from the first group are well suited to feature-based systems and metric spaces. The second group is iterative algorithms that evaluate the classification performance of the case-based system when relying on subsets of examples. A typical algorithm falling into this group is random mutation hill climbing (Skalak 1994), where the subsets are randomly modified and the old set is replaced if the performance obtained by the new set is strictly better. This group of algorithms is easily applicable with feature-based and featureless systems as well as suitable for metric/nonmetric spaces (Pekalska et al 2006). Finally, the algorithms belonging to the third group operate under very different principles. Instead of selecting the most useful examples from the available pool, they modify the existing examples or create new, more representative ones. Such an algorithm is called the prototypes (Chan 1974), which merges examples that are close to each other using weighted averaging. Since these algorithms rely on feature-based representation of cases, they are not applicable to featureless systems. Furthermore, this third group of case selection algorithms seems inappropriate for clinical evidence-based systems since it alters clinical evidence. Regardless, case-base selection algorithms are typically developed and evaluated using classification accuracy (number of correctly classified queries versus total number of queries) as the figure of merit.

Recently, case-base optimization gained some interest in the CAD community. For example, Park et al (2007) proposed a variation of the edited nearest-neighbor rule (Wilson and Martinez 2000) for case-base reduction. The authors evaluated the technique with a feature-based CAD system for false positive reduction in screening mammograms. The method uses the leave-one-out (LOO) technique to assign a decision variable to each examplein the case base. Then, two thresholds T₁ and T₂ are set. Given these thresholds, the reduction is performed such that an example is removed if it depicts a mass and the corresponding value of the decision variable is lower than T₁ as well as if it depicts a normal tissue and the corresponding value of the decision variable is higher than T₂. In this way, nontypical examples are removed from the case base. In their experiments, the authors examine some thresholds such that T₁ + T₂ = 1. The second study on case-base reduction for a CAD system was that reported by our group (Tourassi et al 2007a) for the same clinical problem as the previous study. This technique implements an entropy-based selection scheme where only examples with the highest entropy (i.e. highest information content) are preserved in the case base. The technique was proposed and investigated strictly within the context of our IT-CAD system and as such it is not necessarily generalizable to feature-based CAD systems.

Choosing an example selection algorithm for a particular clinical problem is not trivial. As discussed before, each of the previously proposed algorithms has its own advantages and disadvantages and many of them are limited to specific types of case representation. The aims of this study were to investigate algorithms previously proposed in machine learning that are suitable to a variety of CAD systems, adapt them for optimization based on clinically relevant objectives and evaluate them with respect to our own evidence-based IT-CAD system for false positive reduction in screening mammograms. Specifically, we chose to investigate three different intelligent techniques that fall into the second group of case selection algorithms described before. Our criteria of choosing the techniques are discussed in more detail in the following section. Overall, we chose to focus on intelligent techniques that are not only well suited to our own featureless CAD system but also easily generalizable to other types of evidence-based CAD systems.

This paper is organized as follows. Section 2.1 formalizes the problem of case selection and describes in detail the methods employed in this study. Section 2.2 introduces the IT-CAD system that serves as the test bed for the study. Sections 2.3 and 2.4 describe the dataset and experimental design, respectively. Section 3 presents the experimental results. The paper is concluded with discussion in section 4.

2. Case-base optimization methods

To formalize the problem, we assume that T is an initial set of available examples and S is a subset of T. Then, given a desired number of examples in the final case base (k), the problem is to find such S^* that among all the subsets of T containing k examples, S^* provides the best performance. Formally, find

$$S^{\ast }=arg\underset{\{S:S\subset T,\mid S\mid =k\}}{max}\mathrm{A}(S),$$ (1)

where A(S) is a measure of the classification performance of the system given S as its case base. Note that the desired number k is imposed by the case-base storage restrictions or by the response time requirement for efficient, real-time application of the system. We selected to investigate three different intelligent methods of case-base reduction to improve the efficiency of our own CAD system. The selection criteria used were as follows:

• applicability to both feature-based and featureless-case-based CAD systems, independent of their (dis)similarity measure and decision function;

• adaptability of the selection algorithm to optimize clinically relevant performance measures such as area under the ROC curve and partial ROC area;

• adaptability of the selection algorithm to specific storage limitations;

• simplicity of implementation.

Consequently, the intelligent algorithms selected for comparative investigation in this study were genetic algorithm selection (GAS), greedy selection (GREEDY) and random mutation hill climbing (RMHC). A random selection (RANDOM) technique was also applied as the default strategy to establish whether a more sophisticated strategy is indeed necessary.

All intelligent algorithms are based on the same principle. In each algorithm, the selected case-base subsets of a given size are evaluated using the chosen figure of merit. Each algorithm, however, applies a different exploration technique to find the most diagnostically useful case-base subset. The exploration techniques are not dependent on case representation (feature-based or featureless), distance measure (metric or non-metric) or decision algorithm. Therefore, the intelligent techniques presented here are applicable to any case-based CAD classifier. Furthermore, since the case-based system is included in the intelligent selection process, it is feasible that intelligent case selection may result in improvement of the system’s diagnostic performance.

Although different metrics could be used as the figure of merit for performance evaluation, we used ROC analysis-based assessment. Namely, the area under the curve (AUC) is chosen as the evaluation index since it is widely used with CAD systems. Specifically, the Wilcoxon approach (Bradley 1997) was utilized to calculate the AUC. Thus, the problem was to find

$$S^{\ast }=arg\underset{\{S:S\subset T,\mid S\mid =k\}}{max}\text{AUC}(S),$$ (2)

where AUC(S) is the area under the ROC curve for the system with the case base S.

For each of the intelligent algorithms, the LOO technique was used to calculate AUC(S). Given a candidate subset S_C ∈ T at each step i (i = 1, …, |T|), one example E_i is removed from T and used as a query to the system based on the candidate subset S_C. Whenever the left-out example E_i belongs to the selected candidate subset S_C, this example is temporarily excluded from S_C for the purpose of calculating the response of the system. This way, example E_i is not compared to itself. ${DI}_i^{S_C}$ denotes the decision variable, for example E_i, based on subset S_C. Accordingly, a vector of decision variables is obtained for all examples from the development dataset $\left(\mathbf{D}{\mathbf{I}}^{{\mathbf{S}}_{\mathbf{C}}}=\left[{DI}_1^{S_C},\dots ,{DI}_i^{S_C},\dots ,{DI}_{n_T}^{S_C}\right]\right)$. This vector, together with the corresponding ground-truth values for these examples, is used to calculate the area under the ROC curve (AUC(S)) using the Wilcoxon approach.

2.1. Genetic-algorithm-based case selection

Genetic algorithm-based selection (GAS) is a technique utilizing evolutionary computation to find an optimal case-base subset. Genetic algorithms (GAs) have been applied to select a subset of features in feature-based systems as well as optimization of the case base (Cano et al 2003, Llora and Garrell 2003, Mazurowski et al 2007). Initial investigations on the applicability of GAs to the case weighting (Mazurowski et al 2008) and case selection (Mazurowski et al 2007) problem with our IT-CAD system have been presented before for discrimination of true masses from normal breast parenchyma. Here, a more extensive study is presented by applying several case base reduction algorithms and by using a more elaborate data handling scheme as well as a new, more clinically challenging dataset.

In GAs, each candidate solution for a problem is coded in a chromosome of one individual. The algorithm starts with typically randomly generated population of individuals (usually 50–200). Then, best solutions are evolved by means of crossover, mutation and natural selection. More details about the mechanics of the GA can be found elsewhere (Michalewicz 1999, Eiben and Smith 2003). The rest of this subsection is devoted to the description of solution representation and the genetic operators used specifically in this study.

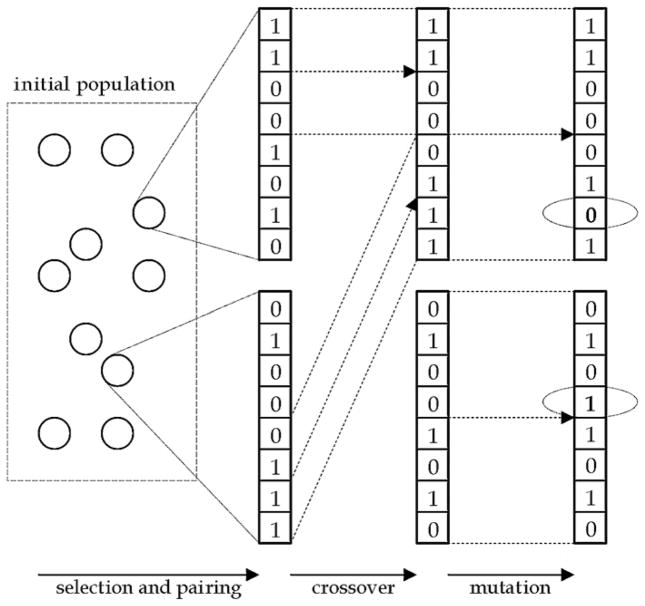
The diagram illustrating the progress of the genetic algorithm used in this study is shown in figure 1. A candidate solution for the problem at hand is a k-element subset S of the original n_T -element set of available cases T. To represent such a solution in a chromosome (i.e. a sequence of numbers), all the examples in the original case base T are numbered. Given such numbering, the chromosome representing a subset of T is an n-element sequence containing ‘1’ on the ith position of the sequence if the ith example belongs to S and ‘0’ if it does not. Therefore, each chromosome contains exactly k 1’s and (n_T − k) 0’s (Cano et al 2003). To generate an offspring from the best-adapted individuals, a one-point crossover recombination technique is utilized. Given two parents, a single point (called locus) is chosen randomly in the chromosome. Then, chromosomes of parents are split into two parts in the locus, generating two offspring individuals. The first offspring inherits the first part of the chromosome of the first parent and the second part of the chromosome of the second parent. The second offspring inherits the first part of the chromosome of the second parent and the second part of the chromosome of the first parent.

Figure 1.

Diagram illustrating steps of the genetic algorithm.

Such a crossover, even though shown efficient in various applications, has a significant drawback for our application. The problem at hand is a constrained optimization problem because only candidate solutions of a certain form (i.e. sets of a given size k) are proper candidate solutions to the problem. Such a constraint on the candidate solution incurs a constraint on the chromosome, namely a chromosome representing a proper solution must contain exactly k 1’s. The one-point crossover operator used in this study does not guarantee that when the parents satisfy the constraint, the offspring satisfies it as well. To deal with this issue, a repair function is applied to the offspring chromosomes. The repair function randomly changes 1’s to 0’s if the number of 1’s is too large or 0’s to 1’s if the number of 1’s is too small in order to obtain the proper number of 0’s and 1’s and respectively a subset with the required number of elements.

At every iteration of the GA algorithm, each chromosome is subject to random mutation as well. The mutation is performed by allowing each position in the chromosome to flip (i.e. change 1 to 0 or 0 to 1) with a certain probability. Typically, the mutation probability is kept very small. Such an operator, similar to the presented crossover operator, is ‘constraints-blind’. Therefore, the chromosome repair function described in the previous paragraph is applied. Note that the repair function could be applied only once at the end of the mutation step. We chose, however, to apply the repair function twice, at the end of the crossover and mutation steps separately, so that the two aspects of the GA algorithm are clearly delineated. Crossover and mutation operations are a fundamental aspect of GAs. The repair function is just a modification to ensure that the solutions satisfy the constraints imposed by the specific problem. Actually, a repair function is one of the standard ways of approaching constrained optimization problems and has been previously described in the GA literature (Michalewicz 1999, Eiben and Smith 2003). Finally, to select the parents and individuals to survive, proportional selection with windowing was applied and a roulette rule was used to implement it (Eiben and Smith 2003). As a fitness function, simply the ROC area index AUC(S) was used.

2.2. Greedy case selection

The greedy case selection algorithm (GREEDY) is an incremental algorithm which chooses the best possible available solution at each step. The algorithm starts with an empty subset S. In the first step, the algorithm chooses an example $E_1^{\ast }$ such that S₁ containing only $E_1^{\ast }$ provides the highest AUC(S₁). Then, in each subsequent step i, the algorithm finds an example $E_i^{\ast }$ such that the set S_i containing all the examples selected in the previous steps and the example $E_i^{\ast }$ provide the best AUC(S_i) among all possible selections during that step. The algorithm stops after k steps providing a subset of the desired size. Note that GREEDY is similar to forward selection techniques (Blum and Langley 1997). It is guaranteed to find a globally optimal subset only for k = 1 since at any step, previously selected cases cannot be eliminated.

2.3. Random mutation hill climbing

Random mutation hill climbing was first applied to case-base reduction by Skalak (1994). The steps of this iterative technique are as follows. First, a random subset S of a desired size is selected. Then, in each iteration, one randomly chosen element from S is switched with one randomly chosen element from the remaining cases (T – S). If such a change improves the objective (i.e. it strictly increases AUC(S)), it is accepted. Otherwise, the change is reversed. The algorithm terminates when the maximum number of iterations is reached.

2.4. Random selection

The random selection algorithm randomly selects a subset of a given size without replacement and equal probability of selection of each example. As mentioned before, the RANDOM selection algorithm was implemented for comparison purposes to establish whether more sophisticated selection strategies are indeed superior.

3. Information-theoretic CAD system

For this study, we focus on an IT-CAD system presented by our group before (Tourassi et al 2003, 2007b). The task of the system is to distinguish between true masses and normal tissue in screening mammograms. In IT-CAD, the information-theoretic concept of mutual information (MI) is utilized to assess similarity between images. In information theory, mutual information between two random variables I(X, Y) is defined as

$$I(X,Y)=\sum _x\sum _y{P}_{XY}(x,y){log}_2\frac{P_{XY}(x,y)}{P_X(x)P_Y(y)}$$ (3)

and describes the statistical dependence between two discrete random variables. To apply such a similarity index to images, the probability distributions P_x(x) and P_y(y) can be replaced by intensity histograms of images X and Y and the joint probability distribution P_xy can be replaced with a joint histogram of the two images. Here, the normalized mutual information (NMI) is used as the similarity measure:

$$\text{NMI}=\frac{2I(X,Y)}{H(X)+H(Y)}.$$ (4)

Such a normalized index is equal to 1 when the images are identical and 0 when there is no statistical relationship between them.

Given similarity evaluations between a query image and all images stored in the case base, the system is asked to make a decision regarding the query case. In order to do so, a decision index (DI) is calculated as follows:

$$\text{DI}(Q_i)=\frac{1}{m}\sum _{j=1}^m\text{NMI}(Q_i,M_j)-\frac{1}{n}\sum _{j=1}^n\text{NMI}(Q_i,N_j),$$ (5)

where Q_i is a query case, m is the number of mass examples and n is the number of normal examples stored in the system’s case base. The first part of the DI evaluates the average similarity between the query and the known mass cases while the second part evaluates the average similarity between the query and the known normal cases. After the decision index is calculated for the query, a decision threshold needs to be applied. If the decision index is larger than the threshold, then the query case is classified as a mass case. If not, then the query case is classified as normal.

Thus far, the IT-CAD has been shown to be quite effective for the detection of masses (Tourassi et al 2003, 2007b) and architectural distortions (Tourassi and Floyd 2004) in mammograms. Its main advantage over feature-based CAD systems is that no image preprocessing and feature extraction are necessary for the decision-making process. These advantages however come with a higher than desired computational cost (due to the computational complexity of NMI) and large storage requirements (since entire images have to be stored). Such a drawback can be dealt with effectively by reducing the number of examples stored in the case base of the system. In IT-CAD, both the case base storage requirements and the computational cost of classifying the query are linearly proportional to the number of examples stored in the case base.

4. Databases and study design

4.1. Databases

For this study, the Digital Database of Screening Mammography (Heath et al 1998) was utilized. The original mammograms were digitized using a Lumisys scanner to 12 bit images at 50 μm per pixel. From the mammograms, 512 pixels × 512 pixels regions of interest (ROIs) were extracted around mass and normal mammographic locations. Three separate databases of ROIs were created. One database was used for developmental purposes and proof of concept while the other two databases were used for additional validation. There was no overlap between the development database (Database 1) and the validation databases (Databases 2 and 3).

Database 1, used in the main part of the experimental evaluation, consisted of 600 ROIs, 300 depicting biopsy-proven malignant and benign masses (positive class) and 300 depicting normal breast parenchyma (negative class). Mass ROIs were centered on the physician annotation provided in the DDSM truth files. The normal ROIs were regions indicated as suspicious by a prescreening CAD system developed at our laboratory (Catarious et al 2004) to operate at four false positives per image on average. Note that these suspicious ROIs were considered normal according to the DDSM truth files and belonged to the negative class. Thus, the IT-CAD system was essentially tested as a second-level analysis scheme for reduction of computer-generated false positives. To avoid any bias, we ensured that this database did not include different views of the same mass. Therefore, all 300 mass ROIs corresponded to completely different masses. The same was true for all 300 normal ROIs.

Database 2, used for the final validation, consisted of 200 ROIs, 101 depicting biopsy-proven masses and 99 depicting normal breast parenchyma. The ROIs were obtained in exactly the same way as the ROIs in database 1. In other words, they did not include multiple views of the same mammographic locations.

Database 3, also used for additional validation of our conclusions, consisted of 98 ROIs, 58 depicting biopsy-proven masses and 40 depicting normal breast parenchyma. These ROIs were extracted around locations indicated as suspicious by a breast imaging specialist with more than 15 years of experience. The radiologist was blinded to the ground truth. The radiologist was asked to report any suspicious locations using a specially designed graphical user interface (GUI) that displayed one mammographic view at a time. 512 × 512 pixels ROIs were extracted around the reported locations. Database 3 was used to evaluate how the results obtained by the intelligent techniques translate to a slightly different clinical task—reduction of perceptually generated false positives.

4.2. Study design

In the main stage of the study, a ten-fold cross-validation scheme was applied using Database 1 to assess the effectiveness of each case selection method. The data were randomly split into ten folds. Nine folds (540 examples, 270 masses and 270 normals) were used as the development set while the tenth fold (60 examples, 30 masses and 30 normals) was reserved as the test set. The same experiments were repeated ten times so that each fold served for testing once. We ensured that at each data split, the train and test sets included ROIs from completely different mammograms.

For each case selection method, the dataset folds were used in the following way. Given each data split, the development dataset (i.e., the nine folds) was used as a pool of examples available for building the knowledge case base of the CAD system. In the example selection process, the leave-one-out approach was implemented within the development dataset as described in the methodology section 2.1. With the case-base selection step complete, the IT-CAD system was applied using the resulting case base on the test set (i.e. the tenth fold reserved for testing only). This process was repeated ten times, till each fold served as a test set. The whole experiment was also repeated separately for various desired case-base sizes k: 10–500 (see equation (1)). To assess the statistical significance of the CAD performance differences between the example selection methods and the original CAD (i.e. using the full case base), we used the ROCKIT software allowing for comparison of ROC areas for correlated data using a parametric estimation of the ROC curves (Metz et al 1998a, 1998b).

For further validation of our conclusions, additional experiments were conducted such that the entire Database 1 was used as the development dataset (utilized for construction of the case base as described in methodology section 2.1). Databases 2 and 3 were used only for testing. To account for the variability introduced by the relatively small size of these two databases, AUC performance was estimated using bootstrap sampling (Efron and Tibshirani 1993).

5. Experimental results

In the experiments, the following implementation parameter values were employed. For GAS, the number of chromosomes was set to 50, the number of offsprings was set to 50 and the probability of mutation was 0.0005. The maximum number of iterations for GAS was 100. For RMHC, a 2000 iteration limit was used. The above parameters were optimized empirically to obtain the best performance while keeping the computation time reasonable. In the analysis of the experimental results we took into account two different design paradigms, namely one where the CAD system designer imposes a constraint on the case-base size (k) either because of a limited storage capacity or restricted response time, and another where the system designer aims for the best possible system performance regardless of the resulting case-base size and its implications on computational efficiency. The underlying assumption of the first paradigm is that there may be superfluous cases present in the case base. The second paradigm is based on the assumption that some cases may have detrimental effect in the overall diagnostic performance of the CAD system. Both superfluous and detrimental examples could be eliminated, providing a system optimized in terms of diagnostic performance and computational efficiency. Results of the experiments based on Database 1 are presented separately for each design paradigm in sections 3.1 and 3.2. Section 3.3 presents additional validation of the conclusions drawn using Database 1 on Databases 2 and 3.

5.1. Satisfying limited storage requirements

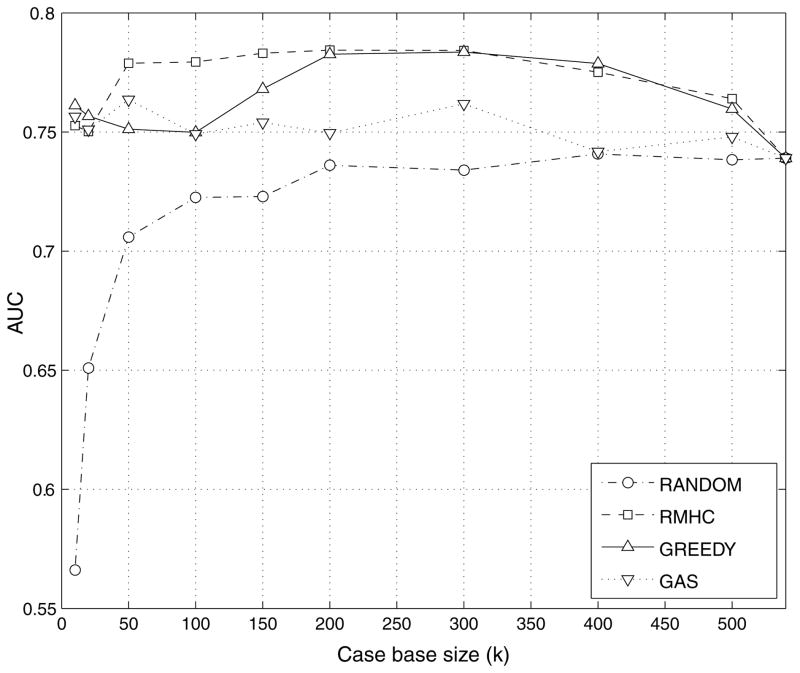
In this design scenario, a CAD system designer can only afford to store a limited number (k) of examples in the case base of the system. This number is essentially dictated by the system’s storage and computational power limitations. Figure 2 compares the IT-CAD system’s performance obtained by each case-base selection method for various desired sizes k of the case base. Performance is shown in terms of the average AUC(S) obtained by a particular example selection method across all cross-validation folds. The horizontal axis of the graph shows the desired size k of the case-base subset (as defined in equation (2)).

Figure 2.

Average IT-CAD performance obtained with each case-base selection method at various desired case-base sizes.

Overall, the three intelligent methods outperform the random selection in a wide range of desired database sizes. The difference becomes more dramatic as the allowable case base size is further restricted. This finding suggests that if only a very small number of cases can be stored in the case base, then intelligent selection of cases is critical to ensure optimized performance. At the upper limit (i.e. using all available examples), all techniques provide the same results (0.745 ± 0.020), as expected. For the problem at hand, the RMHC algorithm consistently provides the best results. Average RMHC results were better than random selection for all examined desired database sizes. Statistical comparison of the methods was performed for three representative case base sizes of 20, 100 and 200 examples. Table 1 shows the two-tailed p-values for pair-wise comparisons of the obtained AUC by different selection methods. These p-values were obtained using the ROCKIT software (Metz et al 1998a, 1998b) after merging the IT-CAD prediction responses across all cross-validation folds.

Table 1.

Two-tail p-values for the AUC pairwise comparison of techniques for three representative case-base sizes in Database 1.

Case base size (k)	20	100	200
RMHC versus GREEDY	0.6698	0.0088	0.7065
RMHC versus GAS	0.5848	0.025	0.0167
GREEDY versus GAS	0.2568	0.7932	0.0249
RMHC versus RANDOM	0.0000	0.0004	0.0003
GREEDY versus RANDOM	0.0000	0.0655	0.0004
GAS versus RANDOM	0.0000	0.1178	0.0478

Table 1 shows that for very small case-base sizes (i.e. 20 examples), all intelligent techniques statistically significantly outperformed random selection (p < 0.0001). For such low k, the difference in performance between the intelligent techniques and random selection is most apparent. However, no statistically significant differences are observed among the intelligent techniques for such low k values. For larger case base sizes (i.e. 100 examples), RMHC statistically significantly outperforms all other techniques. At this size, even though the difference between the other two intelligent techniques (GREEDY and GA) and RANDOM were substantial, they did not reach statistical significance. When the allowable case base size increases (i.e. 200 examples), no statistically significant difference is observed between RMHC and GREEDY but both techniques significantly outperform GAS and RANDOM. Although the performance obtained for this case using GAS is lower than for other intelligent methods, GAS is still statistically significantly better than RANDOM.

An interesting finding of this study is that with as few as 10 or 20 intelligently selected cases, the IT-CAD system achieves performance comparable to that when relying on the full case base. This finding may seem inconsistent with general wisdom that a large case base is essential in clinical applications. However, such dramatic reduction has been previously shown in the machine learning field (Wilson and Martinez 2000, Skalak 1994, Pekalska et al 2006). Furthermore, it must be noted that most CAD studies assessing the impact of the number of training examples were based on the assumption that the examples are drawn from their populations randomly. Our study approaches this problem from a different perspective and shows that application of intelligent techniques can identify a set of only few examples that are critical for the system to maintain its diagnostic capability at the same level as when using the entire case base.

In addition, we examined the examples that were more frequently selected in the early stages of the case selection process (k = 20). Figure 3 presents the seven most frequently selected examples (ROIs) when the case base was optimized with RMHC and the resulting case base contained 20 examples. Note that for the applied data handling scheme, each example was in the pool of cases nine times (i.e. nine possible folds). The ROIs presented in figure 3 were selected at least four times. These are ROIs that were consistently selected as the most useful diagnostically. It is interesting that five out of the seven examples represent masses. Furthermore, the overwhelming majority are malignant masses. The shape, size and margin characteristics are quite diverse and span a wide range. Specifically, figures 3(a) and (c) show lobulated masses with ill-defined and microlobulated margins, respectively. Figure 3(d) depicts an irregular mass with spiculated margins and associated architectural distortion. Figures 3(e) and (f) show round masses with circumscribed and microlobulated margins, respectively. Interestingly, the mass shown in figure 3(e) turns out to be malignant while that shown in figure 3(f) was the only benign one. Finally, the two most frequently selected false positive examples are also rather different. Overall, figure 3 shows that given the requirement of a very small resulting case base, the intelligent techniques select a diverse subset of examples with a wide range of characteristics. It must also be noted that the performance for low k, even though comparable to the performance of the system with a full case base, is lower than the best performance that can be achieved by the system. In fact, CB-CAD performance can be further improved by expanding the variety of examples using one of the intelligent selection techniques.

Figure 3.

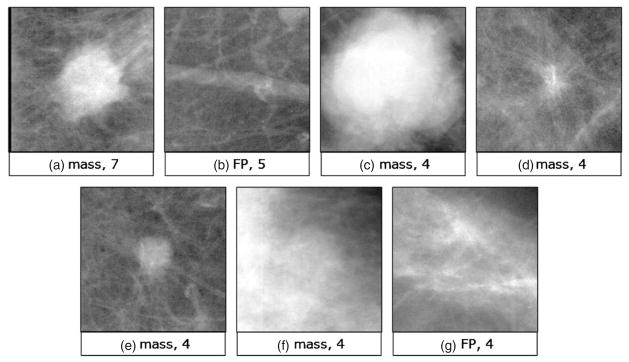
The most frequently selected examples by RMHC in Database 1 when the resulting case-base size was 20.

Also note that since we do not impose a rule for equal prevalence, it is not necessary that the reduced set will contain an equal number of mass and normal examples. We believe that not imposing a constraint on class prevalence is more consistent with the clinical problem where the CAD designer does not know a priori the number of examples from each class that may be detrimental or the class that will contain more clinically useful examples. However, all three algorithms can be easily modified to impose an equal number of mass and normal examples in the selected case base (or any other ratio for that matter).

To address further the issue of imbalance in the selected subsets, we examined more carefully various subsets of intelligently selected examples. We noted that even though typically for selected case bases of very small sizes the number of positive examples exceeds the number of negative examples, as the number of desired examples k increases, the ratio of mass to normal examples gets closer to 1.

5.2. Maximizing diagnostic performance

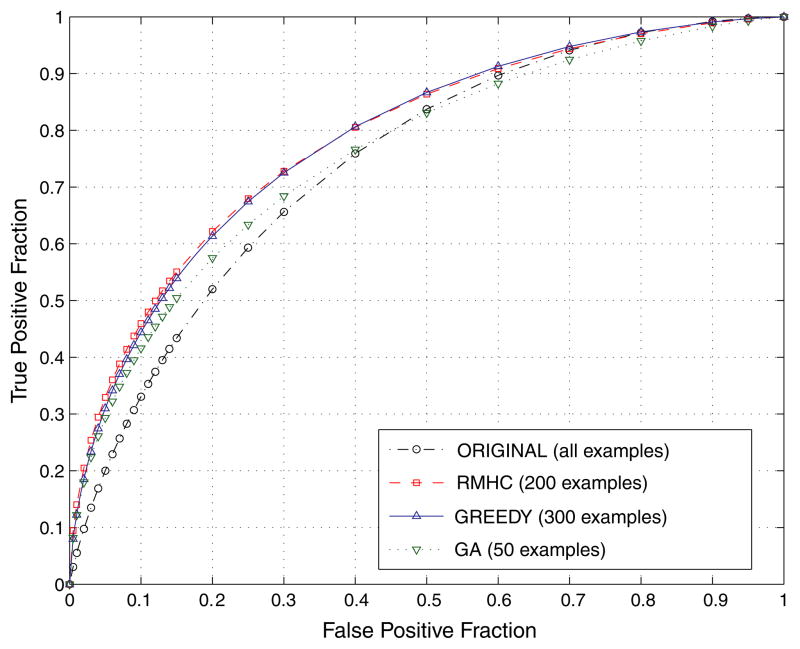
In this scenario, no limitations are imposed on the resulting case base size (k). The main goal is to select examples that provide the best possible CAD performance. Table 2 shows the best performance in terms of AUC obtained by the system developed with a different example selection algorithm. Figure 4 shows the corresponding ROC curves. These curves were derived according to the ROCKIT software. To obtain the curves, we used all decision indices from ten test sets (normalized to a common mean of 0 and standard deviation of 1 within a split). The best overall performance (AUC = 0.789 ± 0.018) was obtained by RMHC for 200 examples. The same performance level (AUC = 0.787 ± 0.018) was reached by GREEDY for 300 examples. A comparison of the ROC performance obtained by these two methods to the performance of the original IT-CAD system (AUC = 0.745 ± 0.020) indicates statistically significant improvement in both cases (two-tailed p-value < 0.005). However, the improvement obtained by GAS (AUC = 0.760 ± 0.019) did not reach statistical significance (p = 0.3).

Table 2.

Best AUC performance on Database 1 obtained by the IT-CAD system developed with different case-base selection algorithms. For each algorithm, the numbers in parentheses indicate the number of case-base examples for which the best performance was obtained.

	Original CAD	RMHC (200)	GREEDY (300)	GAS (50)
AUC	0.745 ± 0.020	0.789 ± 0.018	0.787 ± 0.018	0.760 ± 0.019

Figure 4.

ROC curves for the best IT-CAD performance obtained with each case-base selection method.

(This figure is in colour only in the electronic version)

5.3. Additional validation

To provide further validation of our observations on Database 1, we performed an experiment using the entire Database 1 as a development dataset and then tested the system using Databases 2 and 3. This additional validation simulates an actual clinical scenario where the case base is built using the preferred intelligent example selection strategy and then the case-based CAD system is put to practice. Since RMHC emerged as the intelligent selection technique that provided the best and most robust results in Database 1, these additional validation studies were performed using only RMHC.

The baseline performance of IT-CAD using the entire Database 1 as a case base and tested on Database 2 was AUC = 0.748 ± 0.034 (estimate based on 5000 bootstrap samples). To account for the variability due to the stochastic nature of the RMHC and RANDOM methods, we repeated the selection 50 times for each k. Applying RMHC resulted in an improvement for all three case-base sizes explored in this study (median values for 50 RMHC runs are given): AUC = 0.812 ± 0.030 for k = 20, AUC = 0.778 ± 0.033 for k = 100 and 0.767 ± 0.033 for k = 200. It is notable that in Database 2, the improvement in AUC performance for k = 20 was considerably higher than the baseline performance. However, this could be attributed to the specific database. The variability introduced by the stochastic nature of RMHC, as expressed by the standard deviation of the performance in the 50 runs, was relatively low: 5.5%, 4.9% and 4.2% of the performance value for 20,100 and 200 desired examples in case base respectively. This variability decreases with increasing k. Random selection resulted in median performance of AUC = 0.659 ± 0.039 for k = 20, AUC = 0.718 ± 0.036 for k = 100 and AUC = 0.739 ± 0.036 for k = 200. The variability introduced by RANDOM was much higher than the variability associated with RMHC and was 16.3% for k = 20, 7.3% for k = 100 and 4.3% for k = 200. Overall, the validation experiment on Database 2 confirms our conclusions: (i) intelligent selection techniques allow for a significant reduction of the case base while sustaining or improving the diagnostic performance of the CAD system and (ii) the intelligent techniques outperform the random selection, especially when a small case base size is desired.

Testing on Database 3 showed a baseline performance of AUC = 0.562 ± 0.061. This is a significantly lower performance than what was observed in Databases 1 and 2. However, this is not unexpected. Databases 1 and 2 are more homogeneous since both contain computer-generated false positives. Database 3 contains false positives generated by a highly expert radiologist, thus representing a particularly challenging set. The performance of the system after applying RMHC was improved to AUC = 0.654 ± 0.059 for k = 20, AUC = 0.680 ± 0.057 for k = 100 and AUC = 0.681 ± 0.056 for k = 200. The variability of AUC over 50 RMHC runs was 5.0% for k = 20, 3.2% for k = 100 and 2.0% for k = 200. The performance for RANDOM was AUC = 0.554 ± 0.062 for k = 20, AUC = 0.544 ± 0.062 for k = 100 and AUC = 0.564 ± 0.060 for k = 200. The AUC variability with RANDOM over 50 runs (10.5% for k = 20, 6.8% for k = 100 and 6.5% for k = 200) was again larger than the variability with RMHC selection. Note that again, as expected, the variability introduced by the selection method (for both RMHC and RANDOM) decreases with increasing k. These results confirm that case-base optimization translates very well to a database that is more loosely related to the one used for developing the case base. The results obtained on Database 3 further support our hypothesis that a substantial improvement in classification performance of the IT-CAD can be obtained by applying RMHC while at the same time reducing the case base.

5.4. Comparison to previously reported case-base reduction techniques in CAD

We have also compared the presented algorithms to already proposed ones in the CAD field (Park et al 2007, Tourassi et al 2007a). To compare the techniques presented here to that recently proposed by Park et al (2007), we implemented the latter with parameter values examined by the authors, i.e. thresholds varying from 0.05 to 0.35 for true positive ROIs and from 0.65 to 0.95 for false positive ROIs. For all examined thresholds, the obtained AUC was lower than that of the original system (AUC = 0.745 ± 0.020). However, a small reduction of the database by 15% was observed with a non-significant drop of performance (AUC = 0.720 ± 0.020).

Comparison of the entropy-based selection technique proposed by our group (Tourassi et al 2007a) using Database 1 resulted in small improvement of the overall performance (AUC improved from 0.745 ± 0.020 to 0.752 ± 0.019). Applying this technique allowed for case base size reduction by 26% (to 400 examples) without compromising the performance of the system.

6. Discussion

This study focused on the problem of building a database of examples for case-based medical decision support systems. The significance of the problem was discussed, and three intelligent techniques were experimentally evaluated for solving the problem. Although the study was performed with respect to our own information-theoretic CAD system, the proposed techniques are applicable to virtually all case-based CAD systems, irrespective of the type of case representation (i.e. feature-based or featureless), case (dis)similarity functions (i.e. metric or non-metric) and/or decision algorithms they employ.

The experimental results show high efficiency of the examined techniques for the IT-CAD system with a significant advantage of the intelligent techniques over random selection. The techniques studied can be applied in various ways, depending on the ultimate optimization goal. If the main goal is to reduce the available case base with no loss of diagnostic performance or with limited loss, intelligent techniques such as the random mutation hill climbing algorithm are very promising. For our study, all intelligent techniques were able to build a concise database of 10–20 cases (less than 4% of its original size) without compromising the overall performance of the system. This finding may seem controversial; however, it is consistent with evidence provided in machine learning with a variety of benchmark databases. For example, (Wilson and Martinez 2000) showed that the case base can be reduced to less than 1% of the original database without loss of performance. Skalak (1994) showed on some benchmark problems that for the k-nearest-neighbor (k-NN) rule, the number of examples can be reduced to as few as 1% of the original database. Recently, Pekalska et al (2006) demonstrated that the database of examples in case-based systems can be in some cases reduced to about 20 examples when using the k-nearest-neighbor classification rule without a decrease of performance. The study by Pekalska et al is of particular relevance to our own study as it demonstrates a similar finding using a non-metric, dissimilarity-based classifier. The same authors also show that when more sophisticated classification rules are applied, the database can be reduced to as few as three examples without compromising the performance of the system.

Our result may appear inconsistent with findings of previous studies which demonstrated that a large and diverse database is needed to develop a successful CAD classifier. Note, however, that these studies assume that the examples available for the development of the CAD system are drawn randomly from the available population. In fact, our results concur with these previous findings by showing that as more examples are selected randomly from the available pool, the CAD performance increases consistently and that random selection of just a few examples is insufficient, resulting in a significant decrease of performance (figure 2). Our investigations extend these previous results by showing that given a large collection of available examples, sophisticated rather than random case base selection results in a significantly smaller case base with similar or better predictive power. Nevertheless, the amount of case base reduction depends on the size and diversity of the original case base as well as the complexity of the decision problem at hand.

The techniques studied can also be applied when the main goal is to maximize the diagnostic performance regardless of the case base size. In such a scenario, applying the intelligent techniques such as RMHC or GREEDY selection are also well justified. For our study, both techniques resulted in statistically significant improvement of the performance while reducing the database size to just 200 or 300 examples (37% and 56% of the original database respectively). This result suggests that system designers need to keep in mind that some knowledge examples may have detrimental effect on the overall performance of the system. This finding was also confirmed by other investigators (Park et al 2007). Careful data mining is certainly warranted to determine when and why some examples may have detrimental effect, but such analysis is beyond the scope of this paper. Overall, our comparative study showed that random mutation hill climbing is the most effective technique for case selection.

Additionally, we have compared the presented intelligent algorithms to those that have been previously reported in the CAD field and we showed that the intelligent techniques we investigated in this paper are superior for the task at hand. The technique proposed by Park et al was less effective with respect to our own evidence-based CAD system. We believe that this is mainly because the technique by Park et al is tailored to metric-based similarity measures. Our CAD system does not satisfy this condition due to the non-metric nature of the NMI similarity measure. Similarly, the superior performance of the intelligent techniques implemented in this paper over the entropy-based selection technique can be attributed to the fact that the CAD system is always part of the case selection process during the intelligent selection which allows for tailoring the selected case base to the system. The entropy-based selection method operates independently of the system. Also, it must be noted that the entropy-based selection technique is specifically applicable to our own IT-CAD system and not necessarily effective with other evidence-based CAD schemes.

Comparing the computational complexity of the intelligent algorithms is difficult as they highly depend on the algorithm parameters (e.g. number of chromosomes, iterations, etc). In this study, however, the RMHC was roughly tenfold faster than the GAS. This result even further reinforces that RMHC is truly the superior technique for the task at hand, not only in terms of improving system performance but also in terms of time complexity. Although more careful optimization of the GAS may have led to better performance, this is not a trivial issue from the computational point of view. RMHC as well as GREEDY is considerably simpler to implement compared to the GA-based selection technique.

While the time complexity and implementation time of the algorithms are independent of the database, system performance obtained with a particular algorithm varies depending on the clinical application. For example, our experience with the GREEDY selection algorithm was that it is particularly sensitive to overfitting when only a small pool of examples is provided to develop a CAD system. Consequently, a CAD designer should carefully choose the reduction method considering the specifics of the particular problem. Ideally, designers should compare various different algorithms before finalizing the case-base selection process.

In conclusion, this study presented a comparative analysis of three intelligent techniques for case base optimization in evidence-based CAD systems. Although the analysis was based on a specific CAD system and clinical task, the techniques are applicable to a wide variety of case-based CAD systems regardless of their case representation, similarity measure and/or decision-making algorithms. The study clearly demonstrated the advantage of intelligent case base optimization over conventional random selection. Furthermore, random mutation hill climbing emerged as the superior choice. It not only markedly improved the efficiency of our evidence-based CAD system but also improved significantly its diagnostic performance.