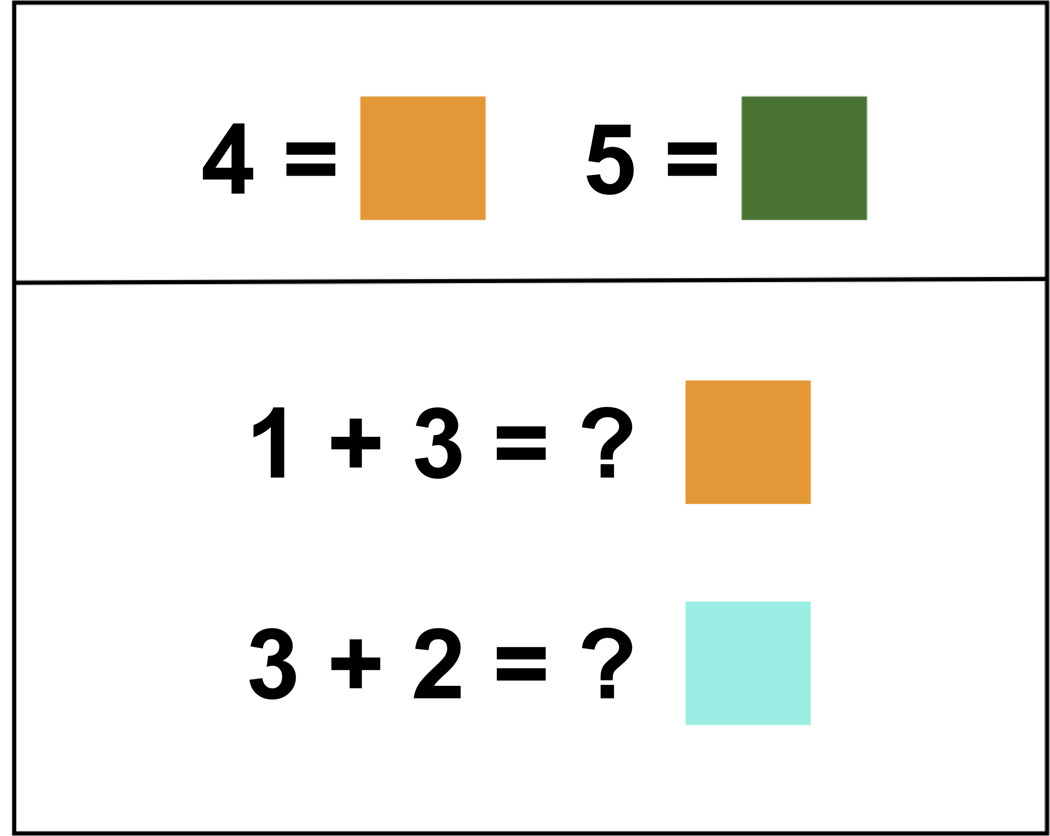Abstract
In grapheme-color synesthesia, graphemes (e.g., numbers or letters) evoke color experiences. It is generally reported that the opposite is not true: colors will not generate experiences of graphemes or their associated information. However, recent research has provided evidence that colors can implicitly elicit symbolic representations of associated graphemes. Here, we examine if these representations can be cognitively accessed. Using a mathematical verification task replacing graphemes with color patches, we find that synesthetes can verify such problems with colors as accurately as with graphemes. Doing so, however, takes time: ~250ms per color. Moreover, we find minimal reaction time switch-costs for switching between computing with graphemes and colors. This demonstrates that given specific task demands, synesthetes can cognitively access numerical information elicited by physical colors, and they do so as accurately as with graphemes. We discuss these results in the context of possible cognitive strategies used to access the information.
Keywords: Synesthesia, Mental Arithmetic, Bidirectionality, Numerical Cognition
1.1 Introduction
Synesthesia is a perceptual phenomenon in which stimulation of one sensory modality (e.g., sight or taste) evokes additional sensory experiences (e.g., sounds or colors). In a common form of synesthesia, grapheme-color synesthesia, graphemes (i.e., letters, punctuation marks or numbers) evoke percepts of color (Cohen Kadosh et al., 2005; Day, 2005; Simner et al., 2006). The percepts can be quite vivid and are cognitively accessible in the sense that they are verbally reportable and can be used by the synesthete to perform certain perceptual and cognitive tasks ranging from color matching (Arnold, Wegener, Brown, & Mattingley, 2012; Blake, Palmeri, Marois, & Kim, 2005) to visual search (Palmeri, Blake, Marois, Flanery, & Whetsell, 2002; Ramachandran & Hubbard, 2001; Ramachandran & Hubbard, 2001) and facilitate learning and memory (Gibson, Radvansky, Johnson, & McNerney, 2012; Gross, Neargarder, Caldwell-Harris, & Cronin-Golomb, 2011; Rothen, Meier, & Ward, 2012; Watson, Blair, Kozik, Akins, & Enns, 2012). However, past accounts of grapheme-color synesthetes generally suggest that the inverse is not the case. Namely, that colors viewed in isolation do not provide cognitive access to percepts of graphemes or their associated symbolic information (Callejas, Acosta, & Lupianez, 2007; Cytowic, 1989). Thus, although for a given synesthete, viewing the grapheme ‘3’ may elicit a perceptual experience of the color of a blue sky, it is commonly reported that viewing a blue sky will not necessarily give rise to a similarly vivid experience of the number three, let alone give the synesthete cognitive access to the numerosity of the number. However, little empirical work has been done to test whether this is the case in all circumstances. Here we empirically test the possibility that, given specific task demands, colors can indeed provide cognitive access to information that is ordinarily symbolically represented by a grapheme.
Recent evidence suggests that the asymmetry of grapheme-color synesthesia may not be as stark as previously thought. A number of studies have demonstrated that the presentation of colors can implicitly influence a grapheme-color synesthete’s behavior in a manner that is consistent with their grapheme-color associations across a wide range of contextual, numerical lexical and memory tasks (Brang, Edwards, Ramachandran, & Coulson, 2008; Cohen Kadosh et al., 2005; Dixon, Smilek, Cudahy, & Merikle, 2000; Gevers, Imbo, Cohen Kadosh, Fias, & Hartsuiker, 2010; Ghirardelli, Mills, Zilioli, Bailey, & Kretschmar, 2010; Johnson, Jepma, & de Jong, 2007; Knoch, Gianotti, Mohr, & Brugger, 2005; Smilek, Dixon, Cudahy, & Merikle, 2002; Weiss, Kalckert, & Fink, 2009). For example, it has been shown that the physical presence of a grapheme is not necessary for color associations to have an influence on behavior (Dixon et al., 2000). Specifically, a synesthete was presented with simple arithmetic problems followed by a color patch that was either congruent or incongruent with the true solution (See Figure 1). The task was to name the color of the square as quickly as possible and then report the correct solution. Despite the grapheme for the solution (e.g., 4) never being displayed, the synesthete responded faster if the physical color square matched the color associated with the solution. Further evidence (Cohen Kadosh et al., 2005) for colors implicitly evoking numerical information was derived using a modified distance effect paradigm (Moyer & Landauer, 1967). The distance effect reflects the observation that magnitude judgments (e.g., which number is larger) are easier when the numerical separation between two items is larger. In their task, synesthetes performed magnitude judgments on numerical graphemes presented in colors that were either congruent or incongruent with the associated synesthetic colors (Cohen Kadosh et al., 2005). The subjects were faster at performing the task if the physical colors were associated with more numerically distant digits than the digits actually presented (e.g., 3 and 4 were judged faster if they were presented in colors corresponding to the digits 1 and 8). Additionally, priming effects have also been demonstrated using contextual (Brang et al., 2008), numerical (Gebuis, Nijboer, & van der Smagt, 2009) and lexical (Weiss et al., 2009) tasks. Interestingly, Brang et al. (2008) demonstrated that the congruity of synesthetic colors induced by contextual statements altered the brain response for synesthetes compared to controls suggesting that synesthesia may be an automatic perceptual phenomenon with bidirectional connections between numbers and synesthetically associated colors.
Figure 1.
An example of the color-priming task used by (Dixon et al., 2000). They demonstrated that RTs were faster for naming the color patch that matched the correct solution compared to a color patch that did not match the correct solution. Adapted from Figure 2.11 in Cytowic & Eagleman, 2009.
These studies demonstrate that physical colors can produce interference or facilitatory effects on behavior; however, little evidence to suggest that synesthetes report being able to cognitively access the information (e.g., the experience of ‘fourness’) correlated with particular graphemes when viewing associated colors. This is unlike the case of graphemes that give rise to specific color percepts that can be verbally described and matched to colors on a screen with extraordinary precision. As such, these studies have only reported effects that are implicit in nature, and without an explicit measure of numerical or mnemonic processing on the basis of the physical color it is impossible to know whether such interference and facilitation effects were due to synesthetes cognitively accessing their associated graphemes. Indeed it has been directly argued in some cases that the synesthetes did not have explicit cognitive access to the symbolic information and that the reported effects were strictly implicit in nature (Cohen Kadosh et al., 2005; Gevers et al., 2010; Knoch et al., 2005; Weiss et al., 2009). Thus, the questions that remain unanswered are: Are there circumstances in which color information alone is sufficient to give synesthetes cognitive access to the information associated with a corresponding grapheme, and if so, what is the nature of this access compared to the accessing the information via the grapheme itself? Simply stated: can a grapheme-color synesthete compute/spell/read using only colors?
One plausible reason why synesthetes do not generally report that colors elicit experiences of their associated graphemes is that colors are cognitively associated with countless other sources of information. For example, the color red is commonly associated with stop lights, candy, fruit, fire trucks, etc. In contrast, a grapheme is typically only associated with the symbolic information it represents. As such, a synesthetic color represents one of very few associations with the grapheme whereas the grapheme likely represents only one of many associations with the color. As such, one may not expect that viewing a color would elicit an associated grapheme any more that it would elicit any other associated source of information. In the sections that follow we describe an experiment that is designed to explicitly test whether synesthetes can indeed cognitively access the symbolic information normally associated with a grapheme solely on the basis of viewing a patch of color. The experiment applies a mathematical verification task in which one, two or all of the digits in an equation are replaced with the corresponding color patch (Figure 2). This design places a distinct constraint on the context in which the color patches are viewed, increasing the likelihood that of all possible associations the synesthete may have with a given color, its synesthetic association with a given grapheme will be preferentially accessible. In order to accurately perform the task, the synesthetes would have to use their color associations to explicitly access the numerosity linked with the associated grapheme and use that information to determine if the presented equation was correct or incorrect. If they are able to cognitively access the information, they should be able to perform simple math well above chance regardless of how many of the numbers in the equation are replaced with color patches.
Figure 2.
A sample math problem used in the experiment for each of the four conditions. The color patches used here represent S3’s color associations for 2, 3 and 5, respectively. This represents a trial where the presented solution was true. On a given trial, a fixation cross appeared for 500ms followed by the presentation of one of the four conditions until participants responded.
Our results demonstrate that the synesthestes (and not the controls) we tested can indeed perform simple mathematical operations using patches of color rather than explicit numerical graphemes. Moreover, we observe minimal differences in accuracy despite how many graphemes are replaced, including when all or none of the numbers in the equation are explicitly presented. We find that reaction times are generally slower when numbers are replaced with color (~250ms per item). Moreover, reaction time costs associated with switching from computing solely with graphemes to computing with colors only occurred when equations containing graphemes followed color trials. Taken together, these findings demonstrate that provided with an appropriate context, the presentation of an associated color can provide explicit cognitive access to the symbolic information represented in a grapheme. Although the exact mechanism by which the numerosity is accessed remains unknown it is important to note that such access is relatively flexible as there are minimal costs associated with switching between computing with numbers or colors.
1.2 Material and Methods
1.2.1 Participants
Ten grapheme-color synesthetes (8 women, 2 men; mean age: 24.8 years) and 10 non-synesthetes (6 women, 4 men; mean age: 24.3 years) participated in the experiment. Each participant provided informed consent in accordance with either the Institutional Review Board at the University of Nevada, Reno and the University of California, Berkeley. All reported normal or corrected-to-normal vision. All participants were volunteers and some received course credit for participating.
1.2.2 Apparatus and display
Stimuli were presented on a Dell Trinitron P991 monitor (19 inches, 1024 × 768) with an 85 Hz refresh rate. The stimulus computer was a 2.4 GHz Mac Mini with an NVIDIA GeForce Video Card. Stimuli were generated and presented using the Psychophysics toolbox (Brainard, 1997) for MATLAB (MathWorks, Inc., Natick, MA).
1.2.3 Stimuli and procedures
Color associations for each synesthete were obtained using a standardized test battery for synesthesia research (Eagleman, Kagan, Nelson, Sagaram, & Sarma, 2007). Participants were randomly presented with black numbers (0–9) and letters (A–Z) and picked the corresponding color from a color palette (for more information, see Eagleman et al., 2007). Immediately prior to the experiment, color associations were re-computed for each synesthete so that the average RGB values obtained for each grapheme and used to create the stimuli used in the main experiment were calibrated the monitor. Supplementary Figure 1 shows the approximate color associations for each of the 10 synesthetes.
For the main experiment, trials consisted of simple mathematical problems using randomly generated single digits ranging from 0 to 9 in the form X [+ – × ÷] Y = Z. For four synesthetes, only digits ranging from 1 to 9 were used as they did not have a color association for the number ‘0’ that could be represented on a computer display (all of these synesthetes described the color as being clear or transparent). As illustrated in Figure 2, four distinct forms of the equations were presented. In the control condition, all three numbers were presented without any color substitutions. In the other conditions one, two or all three of the graphemes were replaced with a square color patch (3.5° visual angle). The color of each patch matched the synesthetic color the subject associates with the number it replaced. For controls, we randomly chose the color associations of a synesthete and used those colors to create the color patches. The grapheme(s) were replaced randomly in the one- and two-color on each trial. The numerical stimuli subtended a vertical visual angle of 2.7° and a horizontal visual angle of 0.9–1.5°. The operators subtended a vertical visual angle of 0.3–0.9° and a horizontal visual angle of 0.8–1.1°. All problems had a true integer answer of 9 or less (e.g., 3 + 4 = 7). This restricted range of numbers was selected because several of the synesthetes in our study did not report having distinct color associations for numbers greater than nine. The numbers associated with the color patches and explicitly presented numbers formed an equation that could either be true (e.g., color corresponding to the number ‘3’ + 4 = 7) or false (e.g., color corresponding to the number ‘9’÷3 = 4). The numbers and colors that made up the equations on each trial were randomly selected in an iterative process until the constraints described above were satisfied.
On each trial, a fixation cross appeared for 500ms followed by an equation that was presented until the participant responded. The task was to press ‘T’ if the presented solution was true and ‘F’ if the presented solution was false. Feedback on the accuracy of response was not provided and no instructions on which hand to use when responding were given. Participants were simply instructed to respond as quickly and accurately as possible. Reaction times (RTs) for each trial were recorded starting at the time the problem appeared on the screen. 64 trials each of the zero-, one-, two- or three-color conditions were presented in a pseudorandom order for a total of 256 trials. Each condition contained an equal amount of problem types (16 of each: addition, multiplication, subtraction and division) and an equal amount of true and false trials. The type of problem (e.g., true division) and number of color patches was pseudorandomly chosen on each trial.
It is important to note that to non-synesthetes, the equations in all but the zero-color condition make no sense: is blue + 7 = 8? As such the untrained non-synesthetes in our study had to guess whether or not each equation were true and be expected to perform at a chance level of 50% for all color conditions.
Prior to the main experiment, each subject completed a practice session containing 16 proble with all black numbers presented on a grey background. This was done to (a) put the subject in the mindset of doing math problems and (b) to our great relief, confirm that the subjects could accurately perform simple math problems. A grey background was used throughout the experiment because none of the synesthetes in our study had graphemes that evoked this color.
1.3 Results
1.3.1 Accuracy
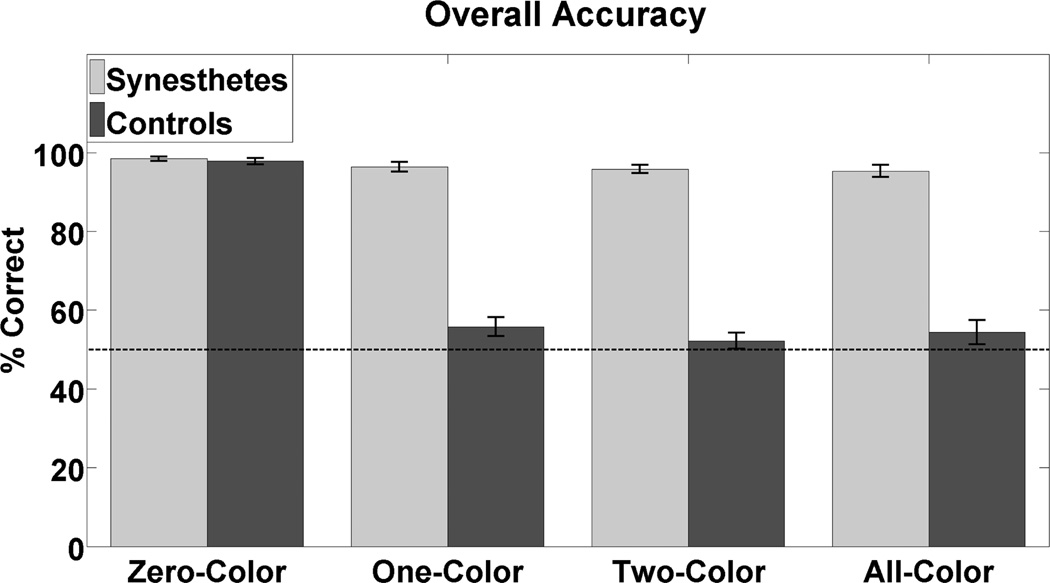
Not surprisingly, averaging across all true, false and problem type (addition,subtraction, multiplication and division) conditions, all participants performed very well in the zero-color condition (synesthetes: 98.4%, controls: 97.8%). There was no significant difference in accuracy between synesthetes and controls (t(9) = 0.69, n.s. in the zero-color condition. Mean accuracy for synesthetes in the one-, two- and three-color conditions was 96.5%, 95.8% and 95.3%, respectively (Figure 3). One-sample t-tests revealed that performance for synesthetes was significantly above chance (50%) for all the colored conditions: one-color (t(9) = 40.97, p < 0.001), two-color (t(9) = 42.14, p < 0.001), three-color (t(9) = 28.23, p < 0.001). As expected, accuracy for the controls was near 50% in all color conditions (one-color: 55.8%; two-color: 52.2%; three-color: 54.4%) and was only significantly above chance for the one-color condition (t(9) = 2.49, p = 0.03); given the nature of the task and the small observed effect, it is most likely this simply reflects random response variation.
Figure 3.
Mean accuracy for each of the four conditions. The light grey bars indicate accuracy for synesthetes and the dark grey bars indicate accuracy for controls. The dashed line represents chance level performance. Error bars represent ±1 SEM.
Additionally, for the synesthetes a 2 (trial-type: true or false) ×4 (number of color patches: none, one, two, three) ×4 (equation type: addition, subtraction, multiplication, division) repeated measures ANOVA was performed. The main effect of number of color patches was significant (F(3, 27) = 4.75, p = 0.009, η2 = 0.35). Follow-up analyses revealed that synesthetes performed significantly better in the no-color condition relative to the one- (t(9) = 2.33, p = 0.045), two- (t(9) = 3.79, p = 0.004) and three-color (t(9) = 2.86, p = 0.02) conditions. The linear trend for a decline in performance as colors were substituted was also significant (F(1,9) = 9.03, p = 0.015, η2 = 0.5). Though these differences reached statistical significance, it is important to note that the actual performance difference between the no-color and the one-, two- and three-color conditions was only 2.0%, 2.6% and 3.1%, respectively and each participant was performing near ceiling (Supplemental Figure 2). The main effects of trial-type (F(1, 9) = 3.58, n.s.) and equation type (F(3, 27) = 0.46, n.s.) did not reach significance. Additionally, no significant interactions were observed (All F < 1.0, n.s.). These results demonstrate that the synesthetes we tested performed well above chance at a similar level of accuracy regardless of whether they verified equations containing only black digits or one, two or three of those digits was replaced with a color patch and these effects were not being driven by specific equation/trial types.
1.3.2 Reaction Time
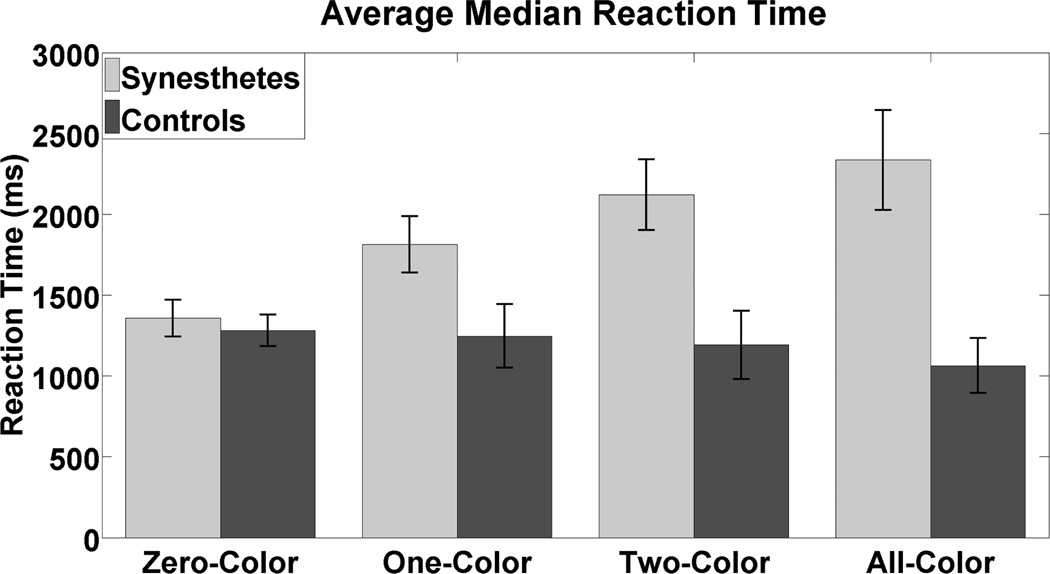
The median reaction time data averaged across trial and equation type are illustrated in Figure 4. In the no-color condition, there was no difference in RT between the synesthetes and controls (t(9) = 0.54, n.s.). For the controls, replacing the graphemes with one, two or three color patches had little effect on reaction time. Given the chance level accuracy, it is likely that the RTs derived from these trials simply reflect the time it takes to guess whether the equations are true or false. In contrast, inspection of the average median reaction times shown in Figure 4 suggests that for the synesthetes there is a linear increase in RT as the number of substituted colors increased from zero to three. On average, RTs increase by ~250ms with the addition of each color patch. This trend appears to be case for most of the individual subjects (Supplementary Figure 2).
Figure 4.
Overall median RTs for each of the four conditions. The light grey bars indicate accuracy for synesthetes and the dark grey bars indicate accuracy for controls. Error bars for individual subjects represent the interquartile range. Error bars for the overall mean represent ±1 SEM.
As was done for the accuracy data, we sub-divided the data on the basis of trial-type (true/false), number of colors (zero-three), and equation type (+ – ×÷) and performed a 2 ×4 ×4 repeated measures ANOVA on the median RTs and found a significant effect of the number of colors in the equation on reaction time (F(3, 27) = 10.85, p < 0.001, η2 = 0.55). The linear trend for an increase in RT with the addition of color patches was also significant (F(3, 27) = 19.74, p = 0.002, η2 = 0.69). Combined with the near perfect accuracy performance on the task, it is reasonable to conclude that the observed increase in reaction times reflect cognitive processing associated with accessing the numerosity associated with the color and using it to correctly verify the equations. Similarly to accuracy, no significant main effects were observed for trial type (F(1, 9) = 0.28, n.s.) or equation type (F(3, 27) = 2.51, n.s.). Additionally, no other interactions reached significance (All F < 2.0, n.s.). Thus, the data indicate that there are RT increases (~250ms per item) associated with verifying the equations using colors rather than graphemes and these effects are not driven by specific equation/trial types.
1.3.3 Switch Costs
1.3.3.1 Color trials preceded by zero-color (switch) or color (no-switch) trials
Here, for synesthetes, we examined RT data for one-, two- or three-color trials that were preceded by either another color substitution trial (no-switch) and compared them to data from trials that were preceded by a zero-color trial (switch). Controls would not be expected to actively perform the task on color trials as they did not have grapheme-color associations, and as such were excluded from this analysis.
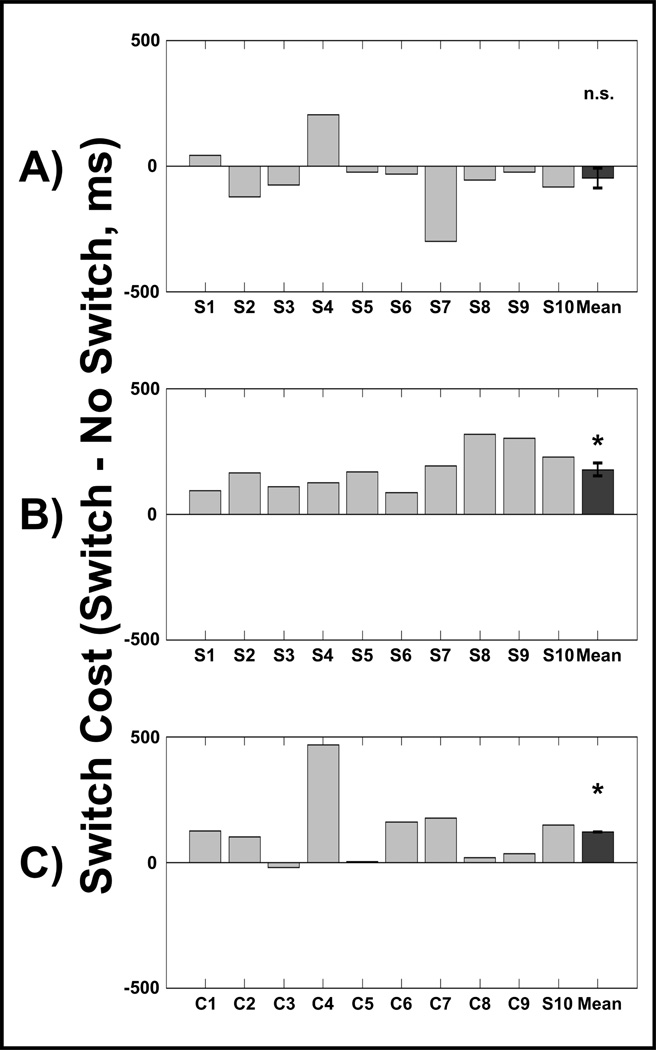
The degree to which the synesthetes can efficiently switch between accessing numerosity via a grapheme vs. color should be reflected in differences in RT on switch trials (slower) and no-switch trials (faster). As shown in Figure 5A, we found no evidence for switch costs across synesthetes when color trials were preceded by zero-color trials (paired-samples t-test: t(9) = −1.22, n.s.). However, we note that by the nature of the experimental design, there are more color trials than zero-grapheme trials. Because of this, potential costs associated with task switching could potentially be offset by an expectancy for a forth-coming color trial.
Figure 5.
A) Switch cost for each synesthete and the overall mean across all synesthetes when grapheme trials preceded color trials. B) Switch cost for each synesthete and the overall mean across all synesthetes when color trials preceded grapheme trials. C) Switch cost for each control subject and the overall mean across all conrols when grapheme trials preceded color trials. Switch cost was computed by subtracting the median RT for repeat trials from task switch trials. A bar in the positive direction is indicative of a switch cost. Light grey bars indicate individual subjects and the dark grey bar indicates the mean across subjects. Error bars represent ±1 SEM.
1.3.3.2 Grapheme trials preceded by color (switch) or zero-color (no-switch) trials
Additionally, we examined RTs in response to zero-color trials that were preceded by a color trial (switch) or another zero-color trial (no-switch). As controls can perform zero-color trials, this analysis was performed in both groups. On these zero-color trials, both synesthetes (t(9) = 6.85, p < 0.001) and controls (t(9) = 2.70, p = 0.02) showed significant switch costs when zero-color trials were preceded by equations containing color patches (Figure 5B & C). The magnitude of this switch cost effect, did not differ between the two groups (t(18) = 1.12, n.s.). As noted above, it is possible that these observed switch costs may be exaggerated by the expectancy of a forth-coming color trial and may thus represent an upper limit of the switch cost.
1.4 Discussion
This study was inspired in part by an anecdotal report from a synesthete that she thought everyone used color when performing arithmetic: “I thought everyone did math with colors—that yellow plus yellow was red for everyone” (Blake et al., 2005). This stands in contrast to the generally held view that although grapheme-color synesthetes often describe vivid experiences of color when viewing numbers or letters, they do not usually report experiencing a grapheme when viewing its associated color (Callejas et al., 2007; Cytowic, 1989). Here, we empirically investigated the degree to which colors alone can provide cognitive access to the symbolic numerical representation of synesthetically associated graphemes. There are three primary conclusions to be drawn from the current data. First, when presented with patches of color, the synesthetes we tested were indeed able to cognitively access the symbolic numerical representation of the synesthetically associated graphemes and use that information to verify simple math problems as accurately as when graphemes are explicitly presented. Secondly, this cognitive access does not come without cost. Accessing numerosity via color takes longer (~250ms per item) than via graphemes. Finally, the data demonstrate that synesthetes can flexibly switch between computing with numbers or colors without cost, but only when switching to computing with graphemes following trials with one or more color patches and not vice versa. This final result, however, is constrained by the nature of the experimental design, which included a different number of color and zero-color trials.
One intuitive explanation for the current results is that when presented with a color, the subjects are using mnemonic information to recall the associated grapheme, and are subsequently able to verify the equation. This could occur in either of two distinct ways. For example, when presented with the equation 2 + 3 = ‘the color blue’, the participant could solve the equation 2 + 3, derive the correct answer ‘5’ and then recall from memory the color associated with ‘5’ and use it to verify the equation as presented. While this approach is certainly feasible for the 1-color trials, it is unclear how this process would work for the two- and three-color trials. That said, as described in the introduction, RTs tend to be slower in response to incongruent pairings of graphemes and colors compared to congruent pairings across a variety of tasks (Dixon et al., 2000; Gebuis et al., 2009; Ghirardelli et al., 2010; Johnson et al., 2007). If in fact the synesthetes were using this approach to verify the equations then we would expect to find slower RTs in response to false trials (incongruent) than true trials (congruent). However, as described above, no main effect of trial type (true/false) was observed in either the accuracy or RT data suggesting that this method of solving the equation and matching the solution to one’s color was not being used, at least for the case of 1-color trials. However, we note that the hand and/or finger with which participants responded was not explicitly controlled for nor counterbalanced. As such, handedness effects could obscure potential RT differences in response to true versus false.
Alternatively, when presented with the above equation, the participant could use a search and check strategy to recall from memory the grapheme they associate with the color blue and use it to access the numerosity needed to verify the equation. Indeed, as would be predicted by this hypothesis, almost all of the synesthetes tested show a systematic increase in reaction time as the number of color-substitutions increases with an average of ~250ms per item. This RT increase is consistent with a serial cognitive strategy in which the grapheme associated with each color is referenced in memory thereby giving access to the associated numerosity. The sequential nature of such a strategy would lead to a linear increase in reaction time as more color patches are substituted. Alternatively, this mnemonic access may operate in parallel but be mediated by a capacity-limited resource (Townsend, 1972; Townsend, 1974, 1990). For example, multiple color-grapheme associations may be recalled at once but doing so is harder and thus takes longer as more items are retrieved in parallel. Moreover, there is some variability across the synesthetes we tested (Supplemental Figure 3). This could alternately reflect either greater efficiency of access within a serial process or greater resource capacity in a parallel one. We note that the cognitive access to numerosity hypothesized above is indirect in nature, with the access being granted by the recollection of the grapheme associated with the presented colors. Another possibility is that the access to numerosity is direct in nature without the intermediate representation of a grapheme. Unfortunately, the current data does not allow us to distinguish whether the synesthetes’ route of access was indirect or direct in nature. However, we note that the synesthetes we tested did not report experiencing vivid percepts of graphemes when presented with the color patches. For example, when presented with the light-blue color S3 associates with the grapheme ‘3’, she did not report experiencing a pictoral representation of the grapheme. Instead, she reported that when performing the task it is as if the color itself symbolically represents the numerical value ‘three’.
When asked prior to participation if colors in general evoke numerical experiences, each subject responded ‘no’. For example, seeing a red fire truck does not automatically evoke a sensation of a specific number. This suggests that being able to cognitively access the numerosity associated with a given color is likely context specific. This is in contrast to the synesthetic color evoked by a given grapheme that is seemingly automatic and relatively context free. This asymmetry in cognitive access to the synesthetically associated color/grapheme may arise from the fact that color is commonly associated with many environmental objects (e.g., red can be associated with apples, roses, etc.) (Nijboer, van Zandvoort, & de Haan, 2006) and actions (e.g., green means go). For synesthetes, it may be that numerical representations are simply one of many associates of color. One reason why colors are not often reported to evoke experiences of numerosity may simply be that the context (i.e., a stop light) in which a color is seen may lead a non-numerical associate to be more strongly activated. In contrast, numerical graphemes are not typically associated with many objects in memory; instead, they are almost singly associated with a numerical value, and for grapheme-color synesthetes, with a specific color. Thus, when a synesthete views a grapheme, it strongly activates a color association and can more easily lead to an intense experience of that color (Brang et al., 2008; Callejas et al., 2007; Gebuis et al., 2009; Weiss et al., 2009). Indeed, in addition to perceptual associations, grapheme-color synesthetes may have declarative associations for their colors in that 5 is red is just as true as the sky is blue.
A question arises as to how flexibly synesthetes can switch from one access-route to another. To address this question, we examined the response data of the synesthetes looking for evidence of switch costs (Kiesel et al., 2010). It is well established that it takes longer for a person to respond to a novel response mapping than to a repeated response mapping (Jersild, 1927). For example, (Wylie & Allport, 2000) employed a color-word Stroop task using a block of incongruent color-word Stroop stimuli followed by a mixed block containing color-neutral stimuli (colored squares) and incongruent color-word stimuli. They demonstrated that if participants completed a block of only incongruent trials prior to the mixed block, they were slower on incongruent color-word trials than if they did not complete an incongruent only trial block prior to the mixed trials. Although extreme practice can reduce switch costs, there is little evidence supporting the idea that people can switch between alternative stimulus-response mappings without any associated switch cost (Berryhill & Hughes, 2009; Stoet & Snyder, 2007). Interestingly, we found that the synesthetes experienced no significant switch costs when performing math with colors (one-, two- or three- color trials) following grapheme trials (zero-color). Conversely, following color trials, both synesthetes and controls experienced significant costs when switching back to using digits. For synesthetes, this may reflect a switch cost in switching back to computing with graphemes following color trials. Because there were three times as many color trials, there are many instances in which several color trials would appear before switching back to graphemes trials and this may have resulted in a cost when switching computational modes. Alternatively, the fact that both groups experienced this cost may suggest that they were simply expecting more color trials throughout the experiment and it was only the anticipation of a subsequent color trial that resulted in slowed reaction times.
One interpretation is that the synesthetes have simultaneous access to the symbolic meaning of a digit and the synesthetic color corresponding to a particular magnitude. However, as stated above we are somewhat cautious of this interpretation of the task-switch analysis and additional testing would needed to determine if cognitive access to numerosity using color alone is a serial or capacity-limited, parallel process. Based on these data, however, we conclude that each synesthete was able to switch from computing graphemes to using colors to access numerosity in a manner that is not commonly observed in other response-mapping experiments (Kiesel et al., 2010).
A final unanswered question is whether the current results reflect a cognitive process that is unique to synesthetic individuals or whether they are indicative of a lifelong learning process of associating graphemes with specific colors and vice-versa. Could non-synesthetic individuals be trained to form such associations and accurately perform tasks like those described here? Such a process would be analogous to learning a new alphabet—something humans are readily capable of doing with the exception that the new characters being learned are already strongly associated with many other items in memory (i.e., a native English speaker does not have numerous associations with the Chinese character for the number three, as is the case for the color red). Importantly, however, the synesthetes and controls in this experiment received no prior training with the task and each reported never having attempted to perform math problems using colors. Even without such training the synesthetes were immediately able to perform the task with minimal speed or accuracy tradeoffs and were able to switch from computing with graphemes to computing with colors with negligible switch costs. Additional research is needed to determine if training non-synesthetes to associate particular colors with numbers can reach a similar level of performance.
In conclusion, we report ten grapheme-color synesthetes who can verify simple mathematical equations using the colors they synesthetically associate with specific graphemes in the complete absence of the graphemes themselves. Moreover, they performed the task with comparable accuracy to equations containing digit information in the absence of color and can switch from using graphemes to using colors to access numerical information with minimal cost. Specifically, given appropriate context, color associations can provide synesthetes with explicit cognitive access to the numerosity associated with a particular grapheme without viewing the grapheme itself. The answer is yes to the fundamental question posed in this paper: can a grapheme-color synesthete compute/spell/read using only colors? So while the statement Yellow plus Blue equals Red may make a color scientist cringe, to a grapheme-color synesthete it may make perfect sense.
Supplementary Material
Highlights.
Grapheme-color synesthetes verified mathematical equations when 1–3 of the digits were replaced with color patches.
Accuracy was similar to when all digits were explicitly presented.
Time to verify equations increased as digits were replaced (~250ms per color).
Acknowledgements
This work was supported in part by grants awarded to GPC from the National Institute of Health: NIGMS 5P20GM103650-02 and NEI 1R15EY022775. We would like to thank our anonymous reviewers for their helpful comments.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Arnold DH, Wegener SV, Brown F, Mattingley JB. Precision of synesthetic color matching resembles that for recollected colors rather than physical colors. Journal of experimental psychology. Human perception and performance. 2012;38(5):1078–1084. doi: 10.1037/a0028129. [DOI] [PubMed] [Google Scholar]
- Berryhill ME, Hughes HC. On the minimization of task switch costs following long-term training. Attention, perception & psychophysics. 2009;71(3):503–514. doi: 10.3758/APP.71.3.503. [DOI] [PubMed] [Google Scholar]
- Blake R, Palmeri TJ, Marois R, Kim C-Y. On the perceptual reality of synesthetic color. Synesthesia: Perspectives from cognitive neuroscience. 2005:47–73. [Google Scholar]
- Brainard DH. The Psychophysics Toolbox. Spat Vis. 1997;10(4):433–436. [PubMed] [Google Scholar]
- Brang D, Edwards L, Ramachandran VS, Coulson S. Is the sky 2? Contextual priming in grapheme-color synaesthesia. Psychological science. 2008;19(5):421–428. doi: 10.1111/j.1467-9280.2008.02103.x. [DOI] [PubMed] [Google Scholar]
- Callejas A, Acosta A, Lupianez J. Green love is ugly: emotions elicited by synesthetic grapheme-color perceptions. Brain research. 2007;1127(1):99–107. doi: 10.1016/j.brainres.2006.10.013. [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R, Sagiv N, Linden DE, Robertson LC, Elinger G, Henik A. When blue is larger than red: colors influence numerical cognition in synesthesia. Journal of cognitive neuroscience. 2005;17(11):1766–1773. doi: 10.1162/089892905774589181. [DOI] [PubMed] [Google Scholar]
- Cytowic RE. Synesthesia and mapping of subjective sensory dimensions. Neurology. 1989;39(6):849–850. doi: 10.1212/wnl.39.6.849. [DOI] [PubMed] [Google Scholar]
- Day S. Some demographic and socio-cultural aspects of synesthesia. In: Lynn C, editor. Robertson and Noam Sagiv. 2005. [Google Scholar]
- Dixon MJ, Smilek D, Cudahy C, Merikle PM. Five plus two equals yellow. Nature. 2000;406(6794):365. doi: 10.1038/35019148. [DOI] [PubMed] [Google Scholar]
- Eagleman DM, Kagan AD, Nelson SS, Sagaram D, Sarma AK. A standardized test battery for the study of synesthesia. Journal of neuroscience methods. 2007;159(1):139–145. doi: 10.1016/j.jneumeth.2006.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gebuis T, Nijboer TC, van der Smagt MJ. Of colored numbers and numbered colors: interactive processes in grapheme-color synesthesia. Experimental psychology. 2009;56(3):180–187. doi: 10.1027/1618-3169.56.3.180. [DOI] [PubMed] [Google Scholar]
- Gevers W, Imbo I, Cohen Kadosh R, Fias W, Hartsuiker RJ. Bidirectionality in synesthesia: evidence from a multiplication verification task. Experimental psychology. 2010;57(3):178–184. doi: 10.1027/1618-3169/a000022. [DOI] [PubMed] [Google Scholar]
- Ghirardelli TG, Mills CB, Zilioli MK, Bailey LP, Kretschmar PK. Synesthesia affects verification of simple arithmetic equations. The Journal of general psychology. 2010;137(2):175–189. doi: 10.1080/00221301003645152. [DOI] [PubMed] [Google Scholar]
- Gibson BS, Radvansky GA, Johnson AC, McNerney MW. Grapheme-color synesthesia can enhance immediate memory without disrupting the encoding of relational cues. Psychonomic bulletin & review. 2012;19(6):1172–1177. doi: 10.3758/s13423-012-0306-y. [DOI] [PubMed] [Google Scholar]
- Gross VC, Neargarder S, Caldwell-Harris CL, Cronin-Golomb A. Superior encoding enhances recall in color-graphemic synesthesia. Perception. 2011;40(2):196–208. doi: 10.1068/p6647. [DOI] [PubMed] [Google Scholar]
- Jersild AT. Mental set and shift. Archives of psychology. 1927 [Google Scholar]
- Johnson A, Jepma M, de Jong R. Colours sometimes count: awareness and bidirectionality in grapheme-colour synaesthesia. Quarterly journal of experimental psychology. 2007;60(10):1406–1422. doi: 10.1080/17470210601063597. [DOI] [PubMed] [Google Scholar]
- Kiesel A, Steinhauser M, Wendt M, Falkenstein M, Jost K, Philipp AM, et al. Control and interference in task switching--a review. Psychological bulletin. 2010;136(5):849–874. doi: 10.1037/a0019842. [DOI] [PubMed] [Google Scholar]
- Knoch D, Gianotti LR, Mohr C, Brugger P. Synesthesia: when colors count. Cognitive Brain Research. 2005;25(1):372–374. doi: 10.1016/j.cogbrainres.2005.05.005. [DOI] [PubMed] [Google Scholar]
- Moyer RS, Landauer TK. Time required for judgements of numerical inequality. Nature. 1967;215(5109):1519–1520. doi: 10.1038/2151519a0. [DOI] [PubMed] [Google Scholar]
- Nijboer TC, van Zandvoort MJ, de Haan EH. Seeing red primes tomato: evidence for comparable priming from colour and colour name primes to semantically related word targets. Cognitive processing. 2006;7(4):269–274. doi: 10.1007/s10339-006-0153-8. [DOI] [PubMed] [Google Scholar]
- Palmeri TJ, Blake R, Marois R, Flanery MA, Whetsell W., Jr The perceptual reality of synesthetic colors. Proceedings of the National Academy of Sciences of the United States of America. 2002;99(6):4127–4131. doi: 10.1073/pnas.022049399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramachandran VS, Hubbard EM. Psychophysical investigations into the neural basis of synaesthesia. Proceedings. Biological sciences / The Royal Society. 2001;268(1470):979–983. doi: 10.1098/rspb.2001.1576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramachandran VS, Hubbard EM. Synaesthesia--a window into perception, thought and language. Journal of consciousness studies. 2001;8(12):3–34. [Google Scholar]
- Rothen N, Meier B, Ward J. Enhanced memory ability: Insights from synaesthesia. Neuroscience and biobehavioral reviews. 2012;36(8):1952–1963. doi: 10.1016/j.neubiorev.2012.05.004. [DOI] [PubMed] [Google Scholar]
- Simner J, Mulvenna C, Sagiv N, Tsakanikos E, Witherby SA, Fraser C, et al. Synaesthesia: the prevalence of atypical cross-modal experiences. Perception. 2006;35(8):1024–1033. doi: 10.1068/p5469. [DOI] [PubMed] [Google Scholar]
- Smilek D, Dixon MJ, Cudahy C, Merikle PM. Synesthetic color experiences influence memory. Psychological science. 2002;13(6):548–552. doi: 10.1111/1467-9280.00496. [DOI] [PubMed] [Google Scholar]
- Stoet G, Snyder LH. Extensive practice does not eliminate human switch costs. Cognitive, Affective, & Behavioral Neuroscience. 2007;7(3):192–197. doi: 10.3758/cabn.7.3.192. [DOI] [PubMed] [Google Scholar]
- Townsend JT. Some results concerning the identifiability of parallel and serial processes. British Journal of Mathematical and Statistical Psychology. 1972;25(2):168–199. [Google Scholar]
- Townsend JT. Issues and models concerning the processing of a finite number of inputs. Human information processing: Tutorials in performance and cognition. 1974:133–168. [Google Scholar]
- Townsend JT. Serial vs. parallel processing: Sometimes they look like Tweedledum and Tweedledee but they can (and should) be distinguished. Psychological science. 1990;1(1):46–54. [Google Scholar]
- Watson MR, Blair MR, Kozik P, Akins KA, Enns JT. Grapheme-color synaesthesia benefits rule-based Category learning. Consciousness and cognition. 2012;21(3):1533–1540. doi: 10.1016/j.concog.2012.06.004. [DOI] [PubMed] [Google Scholar]
- Weiss PH, Kalckert A, Fink GR. Priming letters by colors: evidence for the bidirectionality of grapheme-color synesthesia. Journal of cognitive neuroscience. 2009;21(10):2019–2026. doi: 10.1162/jocn.2008.21166. [DOI] [PubMed] [Google Scholar]
- Wylie G, Allport A. Task switching and the measurement of"switch costs". Psychol Res. 2000;63(3–4):212–233. doi: 10.1007/s004269900003. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.