The biological effectiveness of targeted radionuclide therapy based on a whole-body pharmacokinetic model

Abstract

Biologically effective dose (BED) may be more of a relevant quantity than absorbed dose for establishing tumour response relationships. By taking into account the dose rate and tissue-specific parameters such as repair and radiosensitivity, it is possible to compare the relative biological effects of different targeted radionuclide therapy (TRT) agents. The aim of this work was to develop an analytical tumour BED calculation for TRT that could predict a relative biological effect based on normal body and tumour pharmacokinetics. This work represents a step in the direction of establishing relative pharmacokinetic criteria of when the BED formalism is more applicable than absorbed dose for TRT. A previously established pharmacokinetic (PK) model for TRT was used and adapted into the BED formalism. An analytical equation for the protraction factor, which incorporates dose rate and repair rate, was derived. Dose rates within the normal body and tumour were related to the slopes of their time–activity curves which were determined by the ratios of their respective PK parameters. The relationships between the tumour influx-to-efflux ratio (k₃₄:k₄₃), central compartment efflux-to-influx ratio (k₁₂:k₂₁), central elimination (k_el), and tumour repair rate (μ), and tumour BED were investigated. As the k₃₄:k₄₃ ratio increases and the k₁₂:k₂₁ ratio decreases, the difference between tumour BED and D increases. In contrast, as the k₃₄:k₄₃ ratios decrease and the k₁₂:k₂₁ ratios increase, the tumour BED approaches D. At large k₃₄:k₄₃ ratios, the difference between tumour BED and D increases to a maximum as k_el increases. At small k₃₄:k₄₃ ratios, the tumour BED approaches D at very small k_el. At small μ and small k₃₄:k₄₃ ratios, the tumour BED approaches D. For large k₃₄:k₄₃ ratios, large μ values cause tumour BED to approach D. This work represents a step in the direction of establishing relative PK criteria of when the BED formalism is more applicable than absorbed dose for TRT. It also provides a framework by which the biological effects of different TRT agents can be compared in order to predict efficacy.

1. Introduction

Targeted radionuclide therapy (TRT) aims to deliver therapeutic doses to a tumour while sparing normal tissues by selective retention of a radionuclide-carrying agent within a tumour (Carlsson et al 2002). Unlike external radiotherapy, the efficacy of TRT is dependent on a targeting moiety—the molecular constituent that either binds onto or is sequestered by tumour cells (Roberson and Buchsbaum 1995, Wessels and Meares 2000, Zeng et al 2002). To be an effective targeting agent, the moiety must have a propensity for tumours over normal tissues thus increasing its therapeutic efficacy. The pharmacokinetics (PK) of a targeting agent includes not only the biological path that the agent takes through the body but also the uptake and clearance characteristics within the tumour. Along with the physical characteristics of the chosen radionuclide, physical half-life and dose deposition, the synergy between large body clearance and small tumour clearance can effectively deliver tumour therapeutics while preventing normal tissue complications. Pharmacokinetic modelling for TRT is advantageous because it simplifies the complicated physiology and dosimetry of TRT to predict normal tissue complications.

TRT of solid tumours has shown less promise than for haematological malignancies (DeNardo and Denardo 2006, Oyen et al 2007). This can be attributed to many factors such as the reduced radiosensitivity of solid tumours (DeNardo and Denardo 2006, Williams et al 2008), the reduced radiobiological effect of the decreased dose rate associated with TRT (Fowler 1990, Dale 1996, Chapman 2003) and the non-uniform uptake of radiopharmaceuticals which ultimately leads to non-uniform dose distributions (O'Donoghue 1999, Zanzonico 2000, Strigari et al 2006, Kalogianni et al 2007). To improve radiosensitivity of solid tumours, it has been shown that combination with molecular radiosensitizers or pre-targeting molecules is advantageous (Zhu et al 1998, Aft et al 2003, Ma et al 2003). The heterogeneous distributions and small dose rates (10–20 cGy h⁻¹) of TRT require 20% greater tumour doses than those used in external beam therapy (Fowler 1990) which ultimately delivers more normal tissue dose. Because the small dose and heterogeneous distribution of TRT lead to a low effective uniform dose (EUD), the tumour control probability (TCP) is less than favourable (O'Donoghue 1999). Therefore, it is advantageous to combine TRT with a conformal therapy such as external beam therapy (XRT) in order to increase the TCP by delivering higher doses and creating a more uniform dose distribution. Since similar absorbed doses from TRT and XRT have different biological effects, it is necessary to convert their absorbed doses to biologically effective doses (BED) by taking into account the dose rate and tissue-specific parameters such as repair rate and radiosensitivity (Bodey 2004, Bodey et al 2003, 2004). The aim of this work was to develop an analytical tumour BED calculation for TRT that could predict a relative biological effect based on normal body and tumour PK. In addition, this work aims to establish relative pharmacokinetic criteria of when the BED formalism is more applicable than absorbed dose for TRT.

2. Model derivation

2.1. Standard biologically effective dose formalism

The absorbed dose in radiotherapy is a physical quantity that describes the energy per unit mass (J kg⁻¹) without considering biological effects. It is known, however, that the same dose, but delivered at different rates, can have a substantial influence on the biological effect caused to tissue. In radiotherapy, the linear-quadratic (LQ) formalism is commonly used for quantitatively comparing different fractionation/protraction schemes (Brenner etal 1998). For this reason, the LQ model of cell survival has been adopted to derive an equivalent parameter that may be used to represent the effects of total dose and dose rate. In addition, the LQ model estimates the fraction of cells surviving the irradiation (SF) as a function of the dose delivered, D (Thames and Hendry 1987, Thames et al 1988, Roberson and Buchsbaum 1995, Lazarescu and Battista 1997, Barone et al 2005, Yang and Xing 2005):

$$ln(\text{SF})=-\alpha D-\beta D^2.$$ (1)

Equation (1) assumes insufficient time for cellular repair during the irradiation. For the large dose rates and short treatment times of external beam therapy, equation (1) is very appropriate. In contrast, when treatments are carried out at smaller dose rates as with TRT, the treatment duration can be protracted to a time scale over which repair can take place, resulting in a reduction in the level of damage. At smaller dose rates there will generally be a greater temporal separation between events, and the probability increases that sub-lethal damage will be repaired. The α component of damage, which represents the single-hit cell kill, is independent of dose rate. Consequently, the β term is affected by changes in dose rate, and a dose-protraction or Lea–Catcheside factor, G (Sachs et al 1997, Brenner et al 1998, Hobbs and Sgouros 2009), has been incorporated to introduce a correction to the level of damage due to the relationship between dose rate and repair (Dale 1985, 1989, 1996, Bodey et al 2004, Dale and Carabe-Fernandez 2005):

$$ln(\text{SF})=-\alpha D-\beta G{D}^2.$$ (2)

The BED formalism allows one to convert doses delivered using any fractionation scheme or dose rate to their biologically effective levels delivered at an ultra-small dose rate over infinitely long time. This means that once different schedules, which have been delivered at different dose rates, are converted to BED they can be compared or combined if desired. The BED may be determined using the LQ model:

$$\text{BED}=-\frac{ln(\text{SF})}{\alpha }=D\left(1+\frac{D\cdot G}{(\alpha /\beta }\right).$$ (3)

Typical values for the alpha–beta ratio (α/β) are about 5–25 Gy for early-responding normal tissues and tumours and about 2–5 Gy for late-responding normal tissues (Hall and Giaccia 2006). In the TRT BED formalism, the slope of the time–activity curve (TAC) of a particular organ of interest can affect G because it determines the dose rate. Therefore, G can vary between 0 and 1 for TRT. The generalized Lea–Catcheside (Hobbs and Sgouros 2009) factor for a time-dependent dose rate, Ḋ(t), is defined as follows:

$$G(T)=\frac{2}{D^2}{\int }_0^T\dot{D}(t)\mathrm{d}t{\int }_0^t\dot{D}(w)\cdot {\mathrm{e}}^{-\mu (t-w)}\mathrm{d}w.$$ (4)

The second integration over the time parameter, w, refers to the exponential repair of first sublethal damage and μ is the constant of sub-lethal damage repair (Dale 1985, Millar 1991). The first integral term expresses the second event that can combine with the first event remaining after repair to produce a lethal lesion. As opposed to a single lethal event, sublethal damage is dependent on the rate of dose delivery. Therefore, the tumour dose rate, defined by the TAC, in conjunction with μ, determines tumour BED.

The extension of a TRT pharmacokinetic model for tumour BED calculations makes it possible to investigate the relationship of normal body and tumour PK on tumour BED.

2.2. An analytical pharmacokinetic model for targeted radionuclide therapy

In this work, we used a classical two-compartment open model assuming bolus intravenous administration and central compartment elimination (Wagner 1975, 1993) shown in figure 1. The tumour compartment within the linear system was assumed not to perturb the two-compartment open model of the body because of its negligible volume compared to the other two body compartments; therefore, the tumour compartment was decoupled from the normal body compartments. The transfer of radioactivity between comparments is described by linear differential equations created from figure 1:

Figure 1.

Depicted is a classical two-compartment pharmacokinetic model of the body decoupled from the tumour compartment. The plasma concentration, C_p, becomes the forcing function for the tumour. The units for the transfer constants are h⁻¹.

$$\begin{array}{l}\frac{\mathrm{d}{C}_1}{\mathrm{d}t}=k_{21}{C}_2-(k_{12}+k_{\text{el}}+\mathrm{\lambda })C_1\\ \frac{\mathrm{d}{C}_2}{\mathrm{d}t}=k_{12}{C}_1-(k_{21}+\mathrm{\lambda })C_2\\ \frac{\mathrm{d}{C}_4}{\mathrm{d}t}=k_{34}{C}_p(t)-(k_{43}+\mathrm{\lambda })C_4.\end{array}$$ (5)

Because the tumour is decoupled from system, the TAC for compartment 1, C_p(t), is forced into the tumour compartment. The negligible volume of the tumour prevents the tumour efflux to have an effect on either of the normal body compartments. Furthermore, the amount of radioactivity within each compartment at any given time is determined by the magnitude of the physical decay, λ, central compartment elimination, k_el, normal body inter-compartmental rate constants, k₁₂ and k₂₁, and tumour inter-compartmental rate constants, k₃₄ and k₄₃. The integral of radioactivity within a compartment over all time is the first step in determining absorbed dose within a compartment. As derived in the appendix of a previous work (Grudzinski et al 2010), the maximum tumour absorbed dose, D_tumor, based on a total body dose threshold, D_thresh, is described by equation (6):

$$D_{\text{tumour}}=D_{\text{thresh}}\left[\frac{k_{34}}{k_{43}}\right(\frac{1}{w_1+w_2\left(\frac{k_{12}}{k_{21}}\right)}\left)\right],$$ (6)

where w₁ and w₂ are the proportions of total body volume composed of compartments 1 and 2, respectively. Our model assumes bone marrow to be the dose-limiting organ. Because whole body dose is a surrogate for bone marrow dose, the whole body dose threshold, D_thresh, is set according to a bone marrow limit of 2 Gy (Lassmann et al 2005). Our model also assumes homogeneous uptake within each compartment, homogeneous dose deposition and homogeneous tissue within each compartment. Lastly, each compartment only experiences self-dose, and neighbouring dose deposition is neglected.

2.3. Extension of BED formalism into a pharmacokinetic model

The dose rate to the tumour is the activity within the tumour at time t, A(t), multiplied by a dose conversion term, δ:

$$\dot{D}(t)=A(t)\cdot \delta .$$ (7)

Substituting equation (7) into (4) yields

$$G(T)=\frac{2}{D^2}{\int }_0^T\delta \cdot A(t)\mathrm{d}t{\int }_0^t\delta \cdot A(w)\cdot {\mathrm{e}}^{-\mu (t-w)}.$$ (8)

This time varying dose rate can be incorporated into the pharmacokinetic model by inserting equation (8) into (3). For the tumour we get

$$G_{\text{tumour}}=\frac{1}{{(\delta \cdot A_0\cdot \frac{V_4}{V_1}\cdot k_{34}\left(\frac{\zeta }{\varepsilon \eta \sigma }\right))}^2}{\delta }^2{\left(A_0\cdot \frac{V_4}{V_1}\cdot k_{34}\right)}^2\times \left(\frac{\begin{array}{l}{\varepsilon }^2{\zeta }^2\mu +{\varepsilon }^2{\zeta }^2\sigma +{\varepsilon }^2\eta {\zeta }^2+{\varepsilon }^2\eta \sigma \mu +\varepsilon {\eta }^2\sigma \mu \\ +2\varepsilon {\zeta }^2\sigma \eta +2\varepsilon {\zeta }^2\eta \mu +\varepsilon \beta {\sigma }^2\mu +\varepsilon {\zeta }^2{\sigma }^2+\varepsilon {\zeta }^2{\eta }^2\\ +2\varepsilon {\zeta }^2\sigma +\varepsilon {\zeta }^2{\mu }^2+\varepsilon \eta \sigma {\mu }^2+{\eta }^2{\zeta }^2\sigma +\eta {\zeta }^2{\mu }^2\\ +{\zeta }^2\sigma {\mu }^2+\eta {\zeta }^2{\sigma }^2+2\eta {\zeta }^2\sigma \mu +{\zeta }^2{\sigma }^2\mu +{\eta }^2{\zeta }^2\mu \end{array}}{((\varepsilon +\mu )(\sigma +\mu )(\eta +\mu )(\sigma +\varepsilon )(\eta +\varepsilon )(\sigma +\eta )(\varepsilon \eta \sigma ))}\right),$$

where A₀=injected activity (when t = 0), V₁= compartment 1 volume and V₄= compartment 4 volume ζ = k₂₁ + λ, and σ = k₄₃ + λ, γ = k₁₂ + k_el + λ; λ = physical decay rate

$$\begin{array}{l}\varepsilon =\frac{1}{2}((\gamma +\zeta )+\sqrt{{(\gamma +\zeta )}^2-4(\gamma \zeta -k_{21}{k}_{12}))},\\ \eta =\frac{1}{2}((\gamma +\zeta )+\sqrt{{(\gamma +\zeta )}^2-4(\gamma \zeta -k_{21}{k}_{12}))}.\end{array}$$ (9)

We assumed that δ is a dose conversion factor which is spatially invariant. We also assumed that the tumour only experiences self-irradiation and does not experience any cross-fire radiation from neighbouring compartments. This is a valid assumption because the contribution from the remainder of the body is orders of magnitude smaller than is associated with self-irradiation for radionuclides such as ¹³¹I and ⁹⁰Y (Pacilio et al 2010). Therefore, equation (9) simplifies:

$$G_{\text{tumour}}=\left(\frac{\begin{array}{l}({\mu }^2(\varepsilon {\zeta }^2+\varepsilon \eta \sigma +\eta {\zeta }^2+{\zeta }^2\sigma )+\mu ({\varepsilon }^2{\zeta }^2+{\varepsilon }^2\eta \sigma +\varepsilon {\eta }^2\sigma \\ +\varepsilon \eta {\sigma }^2+{\zeta }^2{\sigma }^2+{\eta }^2{\zeta }^2+2\varepsilon {\zeta }^2\eta +2\eta {\zeta }^2\sigma )+{\varepsilon }^2{\zeta }^2\sigma +{\varepsilon }^2\eta {\zeta }^2\\ +2\varepsilon {\zeta }^2\sigma \eta +\varepsilon {\zeta }^2{\sigma }^2+\varepsilon {\zeta }^2{\eta }^2+2\varepsilon {\zeta }^2\sigma +{\eta }^2{\zeta }^2\sigma +\eta {\zeta }^2{\sigma }^2)\varepsilon \eta \sigma \end{array}}{((\varepsilon +\mu )(\sigma +\mu )(\eta +\mu )(\sigma +\varepsilon )(\eta +\varepsilon )(\sigma +\eta ){\zeta }^2)}\right).$$ (10)

An equation for maximum tumour BED that takes into account total body absorbed dose limits as well as total body PK was derived by inserting equations (10) and (6) into (3):

$${\text{BED}}_{\text{tumour}}=D_{\text{tumour}}\left(1+\frac{D_{\text{tumour}}\cdot G_{\text{tumour}}}{(\alpha /\beta )}\right).$$ (11)

Our whole-body pharmacokinetic model maximizes the tumour BED by limiting the total body dose, D_thresh, which is a surrogate for bone marrow toxicity (Siegel 2005). Pharmacokinetic modelling has also been considered for maximizing doses to target tissues by limiting renal toxicity (Wessels et al 2008). The motivation behind this modelling was to find a dose–response relationship that was predictive of renal toxicity. BED was used because it combined kidney dosimetry with biologic response parameters. The results obtained from a model that limits renal toxicity would differ greatly from a whole-body model because central compartment elimination, k_el, is the only inter-compartment pharmacokinetic parameter considered; the renal model mainly focuses on intra-compartment transfer. We chose a whole-body model because k₁₂, k₂₁ and k_el are pharmacokinetic parameters that describe inter-compartment transfer of radioactivity throughout the entire body.

3. Materials and methods

The relationship between the individual parameters within our model and tumour BED was investigated. In each investigation, the α/β ratio for the tumour was assumed to be 10 Gy and the physical decay, λ, was assumed to be 0.003 61 h⁻¹, which is representative of the long-lived radionuclide, ¹³¹I.

To investigate the relationship between the tumour influx-to-efflux ratio, k₃₄:k₄₃, and tumour BED, the central compartment efflux-to-influx ratio, k₁₂:k₂₁, was fixed according to the PK data within the literature while the k₃₄:k₄₃ ratio was varied. Because k₁₂:k₂₁ ratios for most TRT agents are unknown, a landscape of k₁₂:k₂₁ ratios was developed for a variety of pharmaceuticals (Grudzinski et al 2010). The relationship between the k₁₂:k₂₁ ratio and tumour BED was determined by fixing the k₃₄:k₄₃ ratio and varying the k₁₂:k₂₁ ratio. k_el was assumed to be 1.0 h⁻¹ and the tumour repair rate, μ, was assumed to be 1.4 h⁻¹ (Dale 1996). To determine the impact of k_el on tumour BED, k₃₄:k₄₃ was fixed while k_el was varied. The k₁₂:k₂₁ ratio was assumed to be 1.0 h⁻¹ and the tumour repair rate was assumed to be 1.4 h⁻¹. The relationship between μ and tumour BED was investigated by fixing the k₃₄:k₄₃ ratio and varying μ. The k₁₂:k₂₁ ratio was assumed to be 1.0 and k_el was assumed to be 1.0 h⁻¹.

4. Results

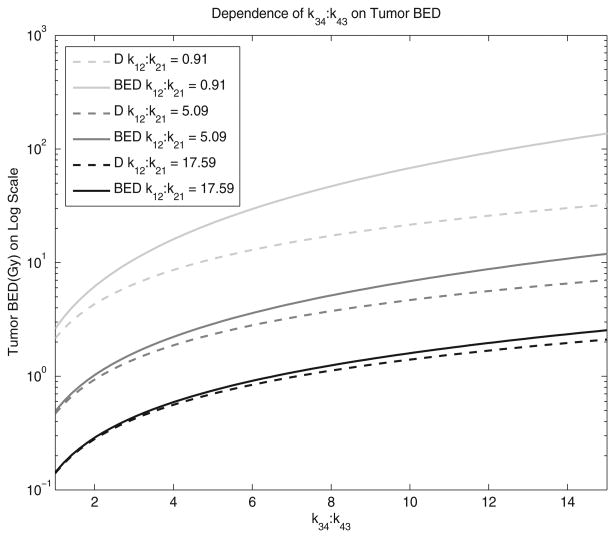
Figure 2 shows the relationship between the k₃₄:k₄₃ ratio and tumour BED when the k₁₂:k₂₁ ratio is fixed with respect to pharmaceuticals from the literature. The three representative pharmaceuticals were chosen to show the range of variability within radiopharmaceuticals. Cefazolin, with a k₁₂:k₂₁ ratio of 0.91, was used to represent a TRT agent with a small k₁₂:k₂₁ ratio. Sulpiride, with a k₁₂:k₂₁ ratio of 5.09, was included to show a medium k₁₂:k₂₁ ratio. To represent a large k₁₂:k₂₁ ratio, Doxorubicin, with a k₁₂:k₂₁ ratio of 17.59, was used. The solid lines represent the tumour BED while the dotted lines represent the tumour absorbed dose, D. The difference between tumour BED and D increases as the k₃₄:k₄₃ ratio increases. As the k₁₂:k₂₁ ratio increases, the difference between BED and D decreases; BED has more of an impact at smaller k₁₂:k₂₁ ratios and larger k₃₄:k₄₃. k_el was assumed to be 1.0 h⁻¹ and the tumour repair rate, μ, was assumed to be 1.4 h⁻¹. The k_el is a reasonable average of many reported pharmaceuticals (Grudzinski et al 2010).

Figure 2.

The dependence of the tumour influx-to-efflux ratio, k₃₄:k₄₃, on tumour BED is shown. The solid lines represent the tumour BED while the dotted lines represent the tumour absorbed dose, D. k_el was assumed to be 1.0 h⁻¹ and the tumour repair rate, μ, was assumed to be 1.4 h⁻¹.

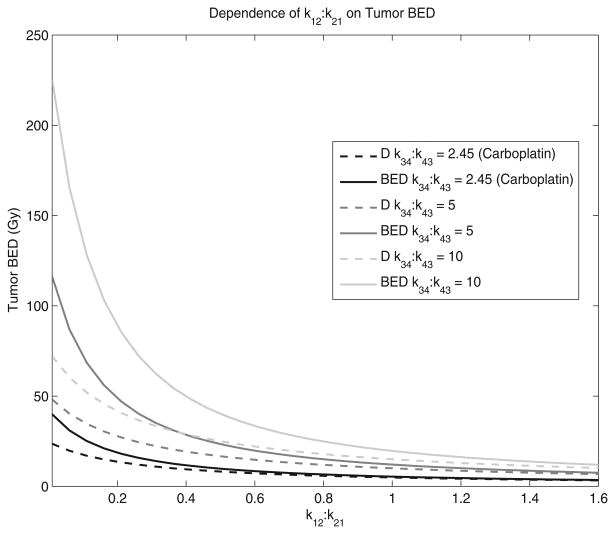
Figure 3 shows the relationship between k₁₂:k₂₁ and tumour BED when the k₃₄:k₄₃ ratio is fixed. The k₃₄:k₄₃ ratios that are shown were chosen to establish a range of realistic values. Topotecan and Carboplatin (Gallo et al 2004) are shown because they are two tumour agents whose parameters were measured using the same model and were reported. The solid lines represent the tumour BED while the dotted lines represent the tumour D. For small k₁₂:k₂₁ ratios and large k₃₄:k₄₃ ratios, the difference between BED and D is significant. In contrast, for large k₁₂:k₂₁ ratios and small k₃₄:k₄₃ ratios, the difference between BED and D is insignificant; D and BED are insensitive to the k₃₄:k₄₃ ratio when the k₁₂:k₂₁ ratio is small. k_el was assumed to be 1.0 h⁻¹ and the tumour repair rate, μ, was assumed to be 1.4 h⁻¹. k_el was assumed to be 1.0 h⁻¹ which is a reasonable average of many reported pharmaceuticals (Grudzinski et al 2010).

Figure 3.

The dependence of the central compartment efflux-to-influx ratio, k₁₂:k₂₁, on tumour BED is shown. The solid lines represent the tumour BED while the dotted lines represent the tumour absorbed dose, D. k_el was assumed to be 1.0 h⁻¹ and the tumour repair rate, μ, was assumed to be 1.4 h⁻¹.

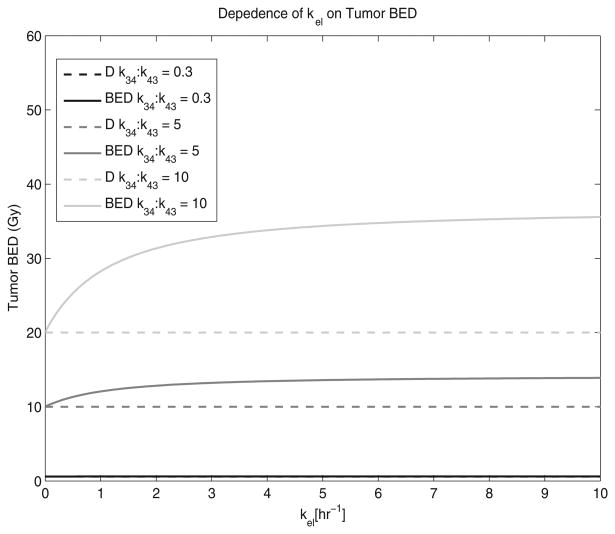
Figure 4 shows the relationship between k_el and tumour BED when the k₁₂:k₂₁ and k₃₄:k₄₃ ratios are fixed. The k₃₄:k₄₃ ratios that are shown were chosen to establish a range of realistic values. Topotecan and Carboplatin (Gallo et al 2004) are shown for reference to real tumour therapy agents. The effect that k_el has on tumour BED depends on the magnitude of the k₃₄:k₄₃ ratio. At small k₃₄:k₄₃ ratios, there is little change in tumour BED with an increase in k_el; therefore, the BED approaches D. For large k₃₄:k₄₃ ratios and small k_el values, the difference between tumour BED and D increases drastically but eventually reaches a maximum, or horizontal asymptote, at large k_el values.

Figure 4.

The dependence of central compartment elimination, k_el, on tumour BED is shown. The solid lines represent the tumour BED while the dotted lines represent the tumour absorbed dose, D. The k₁₂:k₂₁ ratio was assumed to be 1.0 and the tumour repair rate was assumed to be 1.4 h⁻¹.

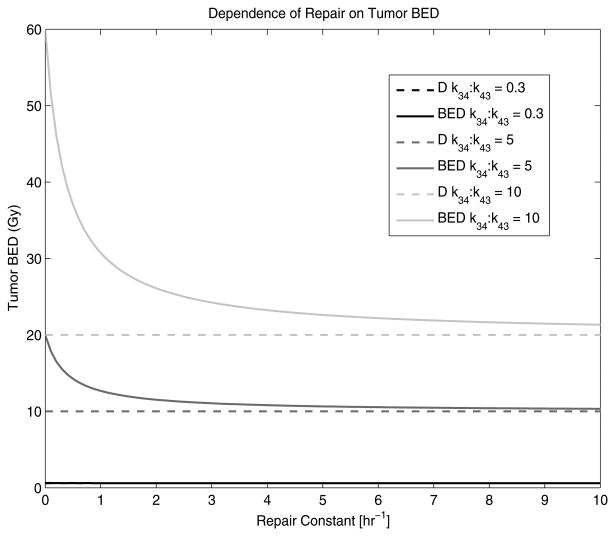
Figure 5 shows the relationship between μ and tumour BED when the k₁₂:k₂₁ and k₃₄:k₄₃ ratios are fixed. The k₁₂:k₂₁ ratio was assumed to be 1.0 h⁻¹ which is a reasonable average of many reported pharmaceuticals (Grudzinski et al 2010). The difference between tumour BED and D is maximized at large k₃₄:k₄₃ ratios and small μ. As μ increases, the difference between tumour BED and D decreases and eventually the tumour BED approaches D. At small k₃₄:k₄₃ ratios, the tumour BED approaches D at very small μ.

Figure 5.

The dependence of the repair rate, μ, on tumour BED is shown. The solid lines represent the tumour BED while the dotted lines represent the tumour absorbed dose, D. The k₁₂:k₂₁ ratio was assumed to be 1.0 and k_el was assumed to be 1.0 h⁻¹.

5. Discussion

As the tumour influx-to-efflux ratio increases, the difference between D and BED increases because the dose rates become significant. At small tumour influx-to-efflux ratios, there are little noticeable differences between D and BED, which is due to the countering effects of increased μ and α/β. When the combined effects of μ and α/β are significant, the dose rate becomes negligible, causing G to approach zero and BED to equal D. A small k₁₂:k₂₁ ratio increases the activity within compartment 1 that can then be transferred to the tumour. A large central compartment efflux-to-influx ratio indicates that more activity is transferred into compartment 2 which does not have the capability of being transferred into the tumour.

Central compartment clearance, k_el, has varying effects on tumour BED depending on the magnitude of the tumour influx-to-efflux ratio. Because central compartment clearance is directly related to compartment 1 through γ of equation (9), it has potential to indirectly affect tumour BED by influencing the effect of k₃₄:k₄₃. The increase in tumour BED caused by increasing k_el for large tumour influx-to-efflux ratios suggests that the tumour dose rate is increasing. In contrast, the dose rate delivered by small tumour influx-to-efflux ratios may not be significant enough for an increase in k_el to enhance it; therefore, the BED approaches D. Furthermore, for each k₃₄:k₄₃ ratio there is a horizontal asymptote that is reached as k_el increases.

An increase in repair rate, μ, results in a decrease in tumour BED. Small tumour influx-to-efflux ratios deliver such small dose rates that very small μ have the capability of repairing all sub-lethal damage. This causes the BED to approach D at very small μ values. Conversely, large k₃₄:k₄₃ ratios deliver larger dose rates that require larger μ to repair all sub-lethal damage. When μ = 0 h⁻¹, the tumour BED is at a maximum because no sub-lethal damage is repaired. When the tumour BED reaches D with increasing μ, this means that all sub-lethal damage has been repaired. However, the degree to which μ affects tumour BED is dependent on α/β as well. As α/β increases, the maximum tumour BED—when μ = 0 h⁻¹—decreases. This is due to the fact that the dose rate becomes less important than the absolute absorbed dose; therefore, the degree to which μ affects tumour BED is proportional to the magnitude of α/β. To increase BED when the α/β increases requires an increase in k₃₄:k₄₃ as well.

Our previous study established criteria for effective TRT based on absorbed dose: a k₃₄:k₄₃ ratio greater than 5 and a k₁₂:k₂₁ ratio less than 1 (Grudzinski et al 2010). Our current study has shown that PK of these magnitudes deliver a BED that is significantly greater than the delivered D because the dose rates are sufficient for increasing biological effects. In contrast, unfavourable PK produce insignificant dose rates that cause the BED to approach the D thus rendering the BED calculation unnecessary when comparing schedules or combining them.

Furthermore, relatively large values for k_el and small μ will contribute to an increase in biological effects. Large values for k_el increase the biological effect because compartment 1 directly influences the tumour. k_el steepens the slope of the TAC within compartment 1 which in turn steepens the slope of the tumour TAC. Because the dose rate within the tumour is related to its TAC, there is an increased biological effect with a steeper sloped TAC. In addition, small μ values increase the biological effect because binary misrepair of sublethal lesions can lead to the formation of dicentrics or asymmetric chromosomal repair resulting in cell death through mitotic catastrophe the next time these cells try to divide.

Because the model only considers self-irradiation of compartments, different radionuclides will only possess different physical decay rates, λ. How much λ affects BED is dependent on the biological clearance of the TRT agent. If the physical clearance is faster than the biological clearance, λ will greatly affect BED by changing the tumour TAC. If the physical clearance is slower than the biological clearance, λ will have less of an effect on BED because the tumour TAC will be the result of the biological clearance. When considering only physical decay, which is representative of brachytherapy, a radionuclide with a larger λ will have a larger BED than a radionuclide with a smaller λ.

6. Conclusions

The BED may be a biologically relevant quantity in terms of establishing response or toxicity relationships. It also normalizes differing dose rates of multiple modalities so that dose combination is possible. This work represents a step in the direction of establishing relative pharmacokinetic criteria of when the BED formalism is more applicable than absorbed dose for TRT. By writing a pharmacokinetic model in terms of BED, we have extended the applicability of the BED concept for use in TRT. Our model affords the possibility of comparing the biological effect of targeted radionuclide agents based on their pharmacokinetic parameters. In addition, we have also developed a methodology that could be used for combined multi-modality radiation therapy.