Abstract
Reaction networks are commonly used to model the dynamics of populations subject to transformations that follow an imposed stoichiometry.
This paper focuses on the efficient characterisation of dynamical properties of Discrete Reaction Networks (DRNs). DRNs can be seen as modeling the underlying discrete nondeterministic transitions of stochastic models of reaction networks. In that sense, a proof of non-reachability in a given DRN has immediate implications for any concrete stochastic model based on that DRN, independent of the choice of kinetic laws and constants. Moreover, if we assume that stochastic kinetic rates are given by the mass-action law (or any other kinetic law that gives non-vanishing probability to each reaction if the required number of interacting substrates is present), then reachability properties are equivalent in the two settings.
The analysis of two types of global dynamical properties of DRNs is addressed: irreducibility, i.e., the ability to reach any discrete state from any other state; and recurrence, i.e., the ability to return to any initial state. Our results consider both the verification of such properties when species are present in a large copy number, and in the general case. The necessary and sufficient conditions obtained involve algebraic conditions on the network reactions which in most cases can be verified using linear programming.
Finally, the relationship of DRN irreducibility and recurrence with dynamical properties of stochastic and continuous models of reaction networks is discussed.
1 Introduction
Reaction networks describe the possible transformations between species in a system, subject to stoichiometry constraints (e.g. 2A + B → C + D). They are widely used for fine-grained modelling of various complex dynamical systems, and in particular biochemical dynamical systems. Typically, reaction network models are equipped with kinetic laws in order to take into account the influence of the various speeds and propensities of the reactions involved on the overall dynamics. Depending on the nature of the systems and interacting species, those kinetics may follow different laws. These reaction networks and kinetic rules are then generally interpreted either in continuous frameworks, such as ODEs (Feinberg, 1979; Craciun et al., 2006; Shinar and Feinberg, 1987), which relates the dynamics of the concentration of the species; or in stochastic frameworks, such as continuous-time Markov chains (Wilkinson, 2006; Anderson et al., 2010), which precisely track the population (copy number) of each species along time.
In practice, such modelling techniques face two challenges: the actual kinetics are most often unknown and may substantially vary between systems sharing the same reaction network; and formal analysis of the emerging dynamical properties is computationally intractable for large-scale continuous and stochastic models.
In this paper, we propose a more abstract level of interpretation of reaction networks, by focusing on the nondeterministic discrete evolution of the population of the species. Given the population of each species (discrete state), the system can evolve due to the application of any reaction, if the minimum required amount of each substrate species for that reaction is present. We consider that only one discrete reaction can be applied at a time. Such nondeterministic systems can be formally considered as the discrete underlying dynamics of stochastic models of reaction networks (Fages and Soliman, 2008).
In such a setting, dynamics of Discrete Reaction Networks (DRNs) naturally delimit the dynamics of concrete stochastic systems, whatever the kinetic laws and constants: if a reachability is proved impossible in a DRN, it is also impossible for any particular stochastic model of the network. In the case where the rate (or probability) of a reaction in the stochastic model never becomes zero, the (discrete) reachability properties of the stochastic model are equivalent with the corresponding properties of the underlying DRN. In general, one can think of a DRN as underlying any discrete stochastic model of the reaction network.
Here, we demonstrate that some general dynamical reachability properties can be efficiently derived from a DRN: the capacity to reach any discrete state from any other state (irreducibility); and the reversibility of the reachability properties (recurrence). Such properties are both considered in the case where species are present in a large copy number as well as in the general case. These results help provide an understanding of the possible global dynamics of reaction networks, and give a direct relationship between the structure of the set of reactions and the verification of the dynamical properties mentioned, without any assumption on kinetic laws.
The main objects and results presented in this paper are summarised below.
Notations
For any a, b in ℤ, [a; b] denotes the set of integers between a and b, i.e., {a, a + 1,…,b}. For any x, x′ in ℤd, we say that x is greater than x′, denoted x ≥ x′, if every component of x is greater or equal than the corresponding component in x′, i.e., for any i in [1; d], we have
. The set of matrices of elements in some set G ⊆ ℝ having n rows and d columns is denoted by Gn×d. If the matrix
 is in Gn×d, then for any j ∈ [1; n],
is in Gn×d, then for any j ∈ [1; n],
 j is the jth row, and
j is the jth row, and
 j is in Gd. Given a set F ⊆ ℝ, and a matrix
j is in Gd. Given a set F ⊆ ℝ, and a matrix
 ∈ Gn×d, the span of
∈ Gn×d, the span of
 over F is denoted by spanF
over F is denoted by spanF
 ≜ { λ
≜ { λ
 | λ∈Fn } and is a subset of ℝd. Finally, the null vector in ℝd is denoted 0.
| λ∈Fn } and is a subset of ℝd. Finally, the null vector in ℝd is denoted 0.
Discrete Reaction Networks We consider a set of reactions between d species Ai, i ∈ [1; d] of the form
| (1) |
where for any i in [1; d] the numbers ci and are in ℤ≥0. Such a reaction can be applied as soon as the population of species Ai is at least ci, for any i in [1;d]. Its application decreases the population of species Ai by ci and then increases it by . Such a reaction can be summarised by two vectors of dimension d: , the drift vector describing the population changes after application of the reaction; and o = (c1,…,cd), the origin of the reaction, i.e., the minimum required population for applying the reaction.
In this setting, a Discrete Reaction Network (DRN) of n reactions between d species can be defined by a couple (
 ,
,
 ) of two matrices having d columns and n rows: (
) of two matrices having d columns and n rows: (
 ,
,
 ) gathers the drift vectors of the n reactions and
) gathers the drift vectors of the n reactions and
 gathers their origins (Def. 1.1). The definition considers only reactions that can be applied at least once from their origin, i.e. ∀i ∈ [1; n],
gathers their origins (Def. 1.1). The definition considers only reactions that can be applied at least once from their origin, i.e. ∀i ∈ [1; n],
 i +
i +
 i ≥ 0.
i ≥ 0.
Definition 1.1 (Discrete Reaction Network). A Discrete Reaction Network (DRN) is a couple (
 ,
,
 ), where
), where
 ∈ℤn×d,
, and ∀i ∈ [1; n],
∈ℤn×d,
, and ∀i ∈ [1; n],
 i +
i +
 i ≥ 0. The number n is the size and d is the dimension of the DRN.
i ≥ 0. The number n is the size and d is the dimension of the DRN.
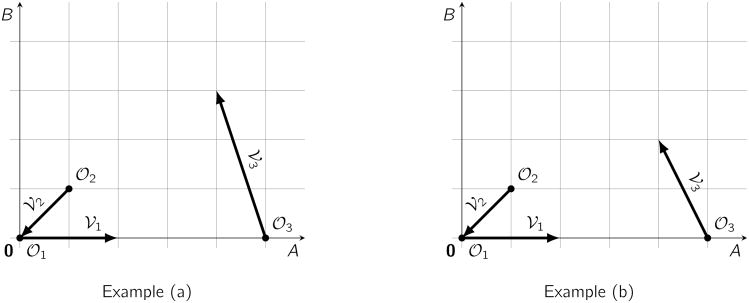
Example. Fig. 1 shows two examples of DRNs with 3 reactions between 2 species.
Figure 1.
Two DRNs with 3 reactions involving 2 species A and B.
Example (a). reactions: .
Example (b). reactions: .
We will see in Sect. 3 and 4 that these similar-looking DRNs have different dynamical properties.
Discrete transitions The population of the d species of the DRN forms a discrete state (or point) of the DRN, and is represented as a vector x in
. At state x, only the reactions j in [1; n] such that x ≥
 j can occur. The occurrence of a single reaction leads to the state x′ = x +
j can occur. The occurrence of a single reaction leads to the state x′ = x +
 j, with necessarily x′ in
.The transition relation → (see Def. 1.2) is defined such that x → x′ if and only if x′ can be reached by the occurrence of a single reaction from x. The binary relation →* extends the binary relation → by considering the successive occurrence of any finite number of reactions. Hence for any x, x′ in
, x →* x′ if and only if there exists a sequence of reaction occurrences from x leading to exactly x′, which never causes the population of any species to become negative.
j, with necessarily x′ in
.The transition relation → (see Def. 1.2) is defined such that x → x′ if and only if x′ can be reached by the occurrence of a single reaction from x. The binary relation →* extends the binary relation → by considering the successive occurrence of any finite number of reactions. Hence for any x, x′ in
, x →* x′ if and only if there exists a sequence of reaction occurrences from x leading to exactly x′, which never causes the population of any species to become negative.
Definition 1.2 (Transition relation →). Given a DRN (
 ,
,
 ) and two points x,
, we write x →(
) and two points x,
, we write x →(
 ,
,
 )
x′ if and only if Σi ∈ [1; n] such that x ≥
)
x′ if and only if Σi ∈ [1; n] such that x ≥
 i and x +
i and x +
 i = x′. We denote by→*(
i = x′. We denote by→*(
 ,
,
 ) the transitive closure ofthe binary relation →(
) the transitive closure ofthe binary relation →(
 ,
,
 ). When clear from context, →(
). When clear from context, →(
 ,
,
 ) is written as →.
) is written as →.
DRNs may be regarded as discrete Petri nets (Petri, 1962; Murata, 1989), where the places are the species, the transitions are the reactions, and arc multiplicites reflect the stoichiometry. This connection has been used previously for the study of ODE models of chemical networks (Angeli et al., 2007; Shiu and Sturmfels, 2010).
Irreducibility and Recurrence In this paper, we focus on two dynamical properties of DRNs:
Irreducibility: a DRN is irreducible if and only if one can reach any point x′ ∈ ℤ≥0 from any point x ∈ ℤ≥0 (Def. 1.3).
Recurrence: a DRN is recurrent if and only if one can always reverse the application of any sequence of reactions (Def. 1.4).
It is worth noticing that any irreducible DRN is recurrent (Remark 1).
Definition 1.3 (Irreducibility). DRN (
 ,
,
 ) is irreducible if and only if ∀x,
, x →* x′ and x′ →* x.
) is irreducible if and only if ∀x,
, x →* x′ and x′ →* x.
Definition 1.4 (Recurrence). DRN (
 ,
,
 ) is recurrent if and only if ∀x,
, x →* x′ ⇒ x′ →* x.
) is recurrent if and only if ∀x,
, x →* x′ ⇒ x′ →* x.
Remark 1. Irreducibility ⇒ Recurrence.
The terms irreducibility and recurrence have the same meaning as in the Markov chain literature (Lawler, 2006). The term irreducibility is motivated by the fact that is not possible to reduce the state space of the network by ignoring the states that are not reachable from a given initial state x, or states that cannot reach x. Hence, if the reachability class of x (composed of all states y such that y →* x and x →* y) is , we say the DRN is irreducible. The term recurrence comes from the fact that if we leave a state along some path, it is always possible for that state to occur again (i.e., to recur). In the Petri net literature, recurrence is usually referred to as reversibility.
In addition to considering irreducibility and recurrence from any possible population of species of the DRN, we also investigate a less restrictive version of these dynamical properties, when assuming the species are present at a Large Copy Number (LCN). This basically restricts the above dynamical properties to population of species greaterthan a certain threshold M0 in . We refer to these less restrictive properties as LCN irreducibility (Def. 1.5) and LCN recurrence (Def. 1.6). Note that the inclusion relationship between irreducibility and recurrence still holds (Remark 2).
Definition 1.5 (LCN Irreducibility). DRN (
 ,
,
 ) is LCN irreducible if and only if
such that ∀x,
with x ≥ M0 and x′ ≥ M0, x →* x′ and x′ →* x.
) is LCN irreducible if and only if
such that ∀x,
with x ≥ M0 and x′ ≥ M0, x →* x′ and x′ →* x.
Definition 1.6 (LCN Recurrence). DRN (
 ,
,
 ) is LCN recurrent if and only if
such that ∀x,
with x ≥ M0 and x′ ≥ M0, x →* x′ ⇒ x′ →* x.
) is LCN recurrent if and only if
such that ∀x,
with x ≥ M0 and x′ ≥ M0, x →* x′ ⇒ x′ →* x.
Remark 2. LCN Irreducibility ⇒ LCN Recurrence.
Note that a reaction network that has any conservation laws cannot be irreducible or LCN irreducible.
Main Results
In Sect. 3 we prove that LCN irreducibility is equivalent to having both the strictly positive real span of drift vectors being ℝd and the integer span of drift vectors being ℤd.
Theorem (3.4). DRN (
 ,
,
 ) is LCN irreducible if and only if span ℝ>0
) is LCN irreducible if and only if span ℝ>0
 = ℝd and spanℤ
= ℝd and spanℤ
 = ℤd.
= ℤd.
Verifying spanℝ>0
 = ℝd can be done using linear programming, and verifying spanℤ
= ℝd can be done using linear programming, and verifying spanℤ
 = ℤd can be also efficiently done by computing, for instance, the Hermite normal form of
= ℤd can be also efficiently done by computing, for instance, the Hermite normal form of
 .
.
Then, we point out additional properties that characterize full irreducibility: self-starting (capability to reach a strictly positive point from 0) and self-stopping (capability to reach 0 from a strictly positive point).
Theorem (3.8). DRN (
 ,
,
 ) is irreducible if and only if (
) is irreducible if and only if (
 ,
,
 ) is LCN irreducible, self-starting and self-stopping.
) is LCN irreducible, self-starting and self-stopping.
Self-starting and self-stopping properties can be decided using a backtracking algorithm combined with linear programming to find a particular order of reactions
In Sect. 4, we prove that LCN recurrence is equivalent to the presence of 0 in the strictly positive real span of drift vectors. This property is also considered in a different context, where it was called positive dependence of drift vectors (Feinberg, 1987). Surprisingly, no integer constraints need to be checked for LCN recurrence, so this property can be easily decided using only linear programming.
Theorem (4.2). DRN (
 ,
,
 ) is LCN recurrent if and only if 0 ∈ spanℝ>0
) is LCN recurrent if and only if 0 ∈ spanℝ>0
 .
.
Sect. 5 applies those results to DRNs modelling biological systems. The results and their relationships with stochastic and continuous models of reaction networks are discussed in Sect. 6. For example, we show how we can use the theorems above to check that common phosphorylation chain networks are LCN recurrent and some circadian clock networks are LCN irreducible.
2 Additional definitions and basic properties
2.1 Set of points and paths manipulation
We introduce the following notations to manipulate sets of points and paths (sequences of reactions):
lowerpoint Given a set of m points {x1,…,xm} ⊂ ℤd, we denote by lowerpoint({x1,…,xm}) the largest point that is lower than all the given points:
orderings Given with , we denote by orderings(λ) all the mappings π: [1;ℓ] → [1; n] which map exactly λi distinct values to i, ∀i ∈ [1; n]:
where #S denotes the cardinality of the finite discrete set S.
Hereafter, we use such mappings π: [1;ℓ] → [1; n] to refer to paths, i.e., sequences of reactions. In such a context, should be understood as the vector giving the number of times each reactions in [1; n] has to be used in a path; and orderings(λ) as all the possible realizations of such paths.
path application (x • π) Given a DRN (
 ,
,
 ) of size n and dimension d, a path π: [1;ℓ] → [1; n], and an initial point x ∈ ℤd, x • π is the set of points resulting from the sequential application of π from x:
) of size n and dimension d, a path π: [1;ℓ] → [1; n], and an initial point x ∈ ℤd, x • π is the set of points resulting from the sequential application of π from x:
We remark that lowerpoint(x • π) = x + lowerpoint(0 • π).
2.2 Inverse DRN
The inverse DRN (Def. 2.1) is defined by the negative drift vectors and the origins shifted by the original drift vector. For instance, the inverse of the reaction described in Eq. (1) results in:
| (2) |
Definition 2.1 (Inverse DRN). Given a DRN (
 ,
,
 ), then (
), then (
 ,
,
 )−1 ≜ (−
)−1 ≜ (−
 ,
,
 +
+
 ) is the inverse DRN.
) is the inverse DRN.
Lemma 2.2. x →(
 ,
,
 )
x′ ⇔ x′ →(
)
x′ ⇔ x′ →(
 ,
,
 )−1x.
)−1x.
2.3 Basic properties
From the definition of transitions between the discrete states of the DRN (Def. 1.2), one can easily derive that if x →* x′ then any succession of reactions from x to x′ can be applied from x (positively) shifted by any , leading to x′ + δ (Lemma 2.3). In the particular case when 0 →*x′, one can instantiate the latter property with δ = x′, which by transitivity of →* leads to 0 →* αx′ with α ∈ ℤ>0 (Lemma 2.4).
Lemma 2.3. Given x, .
Lemma 2.4. 0 →* x′ ⇒ ∀α∈ ℤ>0, 0 →*αx′.
3 Deciding Irreducibility
DRN (
 ,
,
 ) is irreducible if any point in
can be reached from any other point in
(Def. 1.3). We first address the LCN irreducibility, and then exhibit supplementary properties that lead to full irreducibility.
) is irreducible if any point in
can be reached from any other point in
(Def. 1.3). We first address the LCN irreducibility, and then exhibit supplementary properties that lead to full irreducibility.
3.1 LCN Irreducibility
Recall that DRN (
 ,
,
 ) is LCN irreducible if and only if any point above a certain
can be reached from any other point above M0 (Def. 1.5).
) is LCN irreducible if and only if any point above a certain
can be reached from any other point above M0 (Def. 1.5).
Before using the LCN hypothesis, we remark that the DRN is irreducible if (and only if) one can reach each elementary point ei,∀i ∈ [1;d] from 0 and vice-versa (Lemma 3.1). Here ei is the d-dimensional vector having 0 at each of its component, except the ith component being 1.
Lemma 3.1. DRN (
 ,
,
 ) is irreducible if and only if ∀i ∈ [1; d], 0 →* ei and ei →* 0.
) is irreducible if and only if ∀i ∈ [1; d], 0 →* ei and ei →* 0.
Note that a necessary condition for LCN irreducibility is that spanℤ≥0(
 ,
,
 ) = ℤd. This property is actually sufficient for LCN irreducibility (Lemma 3.2) by choosing M0 big enough such that for any i ∈ [1; d] at least one reachability path from M0 to M0 ± ei never goes outside
, and such that M0 is greater than all the reaction origins.
) = ℤd. This property is actually sufficient for LCN irreducibility (Lemma 3.2) by choosing M0 big enough such that for any i ∈ [1; d] at least one reachability path from M0 to M0 ± ei never goes outside
, and such that M0 is greater than all the reaction origins.
Remarking that spanℚ>0
 = ℚd ⇔ spanℝ>0
= ℚd ⇔ spanℝ>0
 = ℝd (Lemma 3.3), Theorem 3.4 establishes that verifying spanℤ≥0
= ℝd (Lemma 3.3), Theorem 3.4 establishes that verifying spanℤ≥0
 = ℤd is equivalent to verifying both spanℤ
= ℤd is equivalent to verifying both spanℤ
 = ℤd and spanℝ>0
= ℤd and spanℝ>0
 = ℝd.
= ℝd.
While the verification of spanℤ≥0
 = ℤd involves integer programming techniques, verifying if spanℝ>0
= ℤd involves integer programming techniques, verifying if spanℝ>0
 = ℝd and spanℤ
= ℝd and spanℤ
 = ℤd can be done more efficiently: the former can be decided using linear programming, for instance by first checking whether 0 ∈ spanℝ>0
= ℤd can be done more efficiently: the former can be decided using linear programming, for instance by first checking whether 0 ∈ spanℝ>0
 and then whether spanℝ≥0
and then whether spanℝ≥0
 = Rd; the latter can be decided, for instance, by computing the Hermite normal form of
= Rd; the latter can be decided, for instance, by computing the Hermite normal form of
 (Cohen, 1993).
(Cohen, 1993).
Lemma 3.2. DRN (
 ,
,
 ) is LCN irreducible ⇔ spanℤ≥0
) is LCN irreducible ⇔ spanℤ≥0
 = ℤd.
= ℤd.
Proof. spanℤ≥0
 = ℤd ⇒ ∀i ∈ [1; d], Σλi,+, λi,− ∈
: λi,+
= ℤd ⇒ ∀i ∈ [1; d], Σλi,+, λi,− ∈
: λi,+
 = ei and λi,−
= ei and λi,−
 = −ei.
= −ei.
For each i ∈ [1; d] and s ∈ {+, −}, we pick an arbitrary ordering πi,s ∈ orderings(λi,s).
If M0 is defined such that ∀i ∈ [1; d], ∀s ∈ {+, −},∀j ∈ [1; n], M0 + lowerpoint(0 • πi,s) ≥
 j, then it is clear that ∀i ∈ [1; d], M0 →* M0 + ei and M0 + ei →* M0.
j, then it is clear that ∀i ∈ [1; d], M0 →* M0 + ei and M0 + ei →* M0.
Lemma 3.3. spanℝ>0
 = ℝd ⇔ spanℚ>0
= ℝd ⇔ spanℚ>0
 = ℚd.
= ℚd.
Proof. (⇒) Let us consider
such that λ
 = w, where w ∈ ℚd.
= w, where w ∈ ℚd.
Consider a basis (βα)α∈I of ℝ over ℚ such that βα0 = 1 (i.e. ∀r ∈ ℝ, ∃ a unique choice of rα ∈ ℚ:r = Σα∈Irαβα). Then with λα ∈ ℚn. On the other hand, w = wβα0 + Σα∈I\{α0} 0βα. Hence, and ∀ α ∈ I, α ≠ α0, .
(⇐) Because spanℚ>0
 = ℚd, ℚd ⊆ spanℝ≥0
= ℚd, ℚd ⊆ spanℝ≥0
 . This implies that the convex hull of ℚd is a subset of spanℝ≥0
. This implies that the convex hull of ℚd is a subset of spanℝ≥0
 , hence ℝd ⊆ spanℝ≥0
, hence ℝd ⊆ spanℝ≥0
 which implies spanℝ≥0
which implies spanℝ≥0
 = ℝd. Finally, we conclude that spanℝ≥0
= ℝd. Finally, we conclude that spanℝ≥0
 =spanℝ>0
=spanℝ>0
 because, from hypothesis, 0 is a positive linear combination of elements rows of
because, from hypothesis, 0 is a positive linear combination of elements rows of
 : 0 ∈ spanℚ>0
: 0 ∈ spanℚ>0
 ⇒ ∃ λ̃ ∈
: λ ˜
⇒ ∃ λ̃ ∈
: λ ˜
 = 0. Hence, for any w ∈ ℝd, there exists
such that w = w + 0 = λ
= 0. Hence, for any w ∈ ℝd, there exists
such that w = w + 0 = λ
 + λ̃
+ λ̃
 = (λ + λ̃)
= (λ + λ̃)
 , with (λ + λ̃) ∈ ℝ>0.
, with (λ + λ̃) ∈ ℝ>0.
Theorem 3.4. spanℤ≥0
 = &ℤd ⇔ spanℝ>0
= &ℤd ⇔ spanℝ>0
 = ℝd and spanℤ
= ℝd and spanℤ
 = ℤd. Therefore, DRN (
= ℤd. Therefore, DRN (
 ,
,
 ) is LCN irreducible if and only if spanℝ>0
) is LCN irreducible if and only if spanℝ>0
 = ℝd and spanℤ
= ℝd and spanℤ
 = ℤd.
= ℤd.
Proof. (⇐) spanℝ>0
 = ℝd ⇔ spanℚ>0
= ℝd ⇔ spanℚ>0
 = ℚd (Lemma 3.3). Therefore,
such that λ
= ℚd (Lemma 3.3). Therefore,
such that λ
 = 0 and ∃α ∈ ℤ>0 such that
. Moreover, ∀i ∈ [1; d] and ∀s ∈ {+, −}, ∃λi,s ∈ ℤn such that λi,s
= 0 and ∃α ∈ ℤ>0 such that
. Moreover, ∀i ∈ [1; d] and ∀s ∈ {+, −}, ∃λi,s ∈ ℤn such that λi,s
 = sei. Hence, there exists β ∈ ℤ>0 such that λ* = βαλ + λi,s with
, resulting in λ*
= sei. Hence, there exists β ∈ ℤ>0 such that λ* = βαλ + λi,s with
, resulting in λ*
 = sei. (⇒) use the fact that spanℤ≥0
= sei. (⇒) use the fact that spanℤ≥0
 = ℤd ⇒ spanℤ>0
= ℤd ⇒ spanℤ>0
 = ℤd, which follows from −
= ℤd, which follows from −
 j ∈ spanℤ≥0
j ∈ spanℤ≥0
 .
.
Example. One can check that both examples of Fig. 1 verify spanℝ>0
 = ℝd. However, the computation of Hermite normal forms shows that only example (b) verifies the second necessary condition spanℤ
= ℝd. However, the computation of Hermite normal forms shows that only example (b) verifies the second necessary condition spanℤ
 = ℤd. Hence, example (a) is not LCN irreducible whereas example (b) is LCN irreducible.
= ℤd. Hence, example (a) is not LCN irreducible whereas example (b) is LCN irreducible.
3.2 Full Irreducibility
In this subsection, we demonstrate that a DRN is totally irreducible if and only if it is LCN irreducible and is both self-starting (Def. 3.5) and self-stopping (Def. 3.6). A DRN is self-starting if at least one strictly positive point can be reached from 0, and is self-stopping if there exists at least one strictly positive point from which 0 can be reached – which is equivalent to the inverse DRN being self-starting.
Definition 3.5 (Self-starting DRN). DRN (
 ,
,
 ) is self-starting if and only if
such that 0 →* x.
) is self-starting if and only if
such that 0 →* x.
Definition 3.6 (Self-stopping DRN). DRN (
 ,
,
 ) is self-stopping if and only if inverse DRN (
) is self-stopping if and only if inverse DRN (
 ,
,
 )−1 is self-starting.
)−1 is self-starting.
Lemma 3.7 establishes that a DRN is self-starting if and only if there exists a sequence of d reactions (not necessarily unique) such that for each dimension at least one reaction of this sequence has a positive drift along that dimension, and such that the origin of the kth reaction belongs to the positive real span of the K − 1 preceding drift vectors (the first reaction having necessarily 0 as origin). Therefore, one can derive a backtrack algorithm to determine if such an ordering of reactions exists.
Then, Theorem 3.8 states that if an LCN irreducible DRN is both self-starting and self-stopping then it is irreducible. Indeed, if the DRN is self-starting, then there exists a strictly positive point x ∈ℤ>0 such that 0 →* x. From Lemma 2.4, the self-starting property implies that there exists a point x′ ≥ M0 such that 0 →* x′. Then, if the DRN is self-stopping, one can show similarly that there exists a point x″ ≥ M0such that x″ →* 0. Because the DRN is LCN recurrent, we know that any pair of points above M0 is reversibly reachable. Hence, by using Lemma 2.3, one can verify the existence of a reversible path from 0 to all ei, i ∈ [1;d].
Informally, the self-starting property allows to reach the LCN region, and the self-stopping allows to reach any ±ei or 0 from any point in the LCN region. The LCN irreducibility property finally ensures that those two paths can be connected. This is illustrated in Fig. 2.
Figure 2.
Illustration of the reasoning for Theorem 3.8 on irreducibility. If the DRN is self-starting, by repeating the reactions, we eventually reach the LCN region from 0. In the same manner, if the DRN is self-stopping, we eventually reach 0 from a point in the LCN region. If the DRN is LCN irreducible, any point in the LCN region can be reached by any other point in the LCN region. Therefore, one can construct a path from 0 to each elementary vector, and vice-versa.
Lemma 3.7. a mapping σ: [1; d] → [1; n] with:
∀k ∈ [1; d], ∃i ∈ [1; d],
 σ(i),k ≥ 1, and
σ(i),k ≥ 1, and σ(1) = 0
and ∀k ∈ [2; d],
.
σ(1) = 0
and ∀k ∈ [2; d],
.
Proof. (⇐) Let us define ∀k ∈ [1; d], and xk such that ∀i ∈ [1; d], and . We show by induction that ∀k ∈ [1; d], ∃x′ ≥ xk s.t. 0 →* x′:
k = 1: 0 →
 σ(1) with ∀j ∈ Ω1,
σ(1) with ∀j ∈ Ω1,
 σ(1),j ≥ 1.
σ(1),j ≥ 1.k + 1: by induction, (2), and Lemma 2.4, ∃α ∈ℤ>0 such that αxk ≥
 σ(k+1) (with 0 →* αxk). Hence, αxk → αxk +
σ(k+1) (with 0 →* αxk). Hence, αxk → αxk +
 σ(k+1). We remark that if ∃i ∈ Ωk+1 such that (αxk +
σ(k+1). We remark that if ∃i ∈ Ωk+1 such that (αxk +
 σ(k+1))i < 1, then necessarily i ∈ Ωk. Hence, ∃β ∈ℤ>0 such that (βαxk +
σ(k+1))i < 1, then necessarily i ∈ Ωk. Hence, ∃β ∈ℤ>0 such that (βαxk +
 σ(k+1)) ≥ xk+1. Therefore, 0
→* x′ with x′ ≥ xk+1.
σ(k+1)) ≥ xk+1. Therefore, 0
→* x′ with x′ ≥ xk+1.
Finally, as
(⇒) 0 →* x ⇒ ∃ℓ ∈ℤ>0, ∃ a path π: [1;ℓ] → [1; n] with , and . Let us define the mapping ς: [1; d] → [1;ℓ] iteratively, starting with ς(1) ≜ 1 and ∀k ∈ [2; d]:
with wk ≜ {j ∈ [1; d] | ∄i ∈ [1; k − 1],
 πς(i)),j ≥ 1},
πς(i)),j ≥ 1},if wk = ∅, ς(k) ≜ 1;
otherwise, ς(k) ≜ min{m ∈ [ς(k−1) + 1; l] | ∃j ∈ wk,
 π(m),j ≥ 1}. We remark that this minimum necessarily exists (otherwise
), and ∀m ∈ [ς(k−1); ς(k)−1],
.
π(m),j ≥ 1}. We remark that this minimum necessarily exists (otherwise
), and ∀m ∈ [ς(k−1); ς(k)−1],
.
From construction, σ ≜ ς ◦ π verifies (1) and (2).
Theorem 3.8. DRN (
 ,
,
 ) is irreducible if and only if (
) is irreducible if and only if (
 ,
,
 ) is LCN irreducible and
and
(i.e. (
) is LCN irreducible and
and
(i.e. (
 ,
,
 ) is self-starting and self-stopping).
) is self-starting and self-stopping).
Proof. (⇒) obvious.
(⇐) For any fixed M0, from Lemma 2.4, ∃α ∈ ℤ>0 such that αx ≥ M0 and αx′ ≥ M0, with and . Hence, ∀i ∈ [1; d], from Lemma 2.3,
, and
.
Example. One can easily show that the two examples in Fig. 1 are self-starting and self-stopping. Using LCN irreducibility criteria from the previous subsection, we conclude that example (b) is irreducible (recall that example (a) is not LCN irreducible, so it is not irreducible).
4 Deciding Recurrence
Recall that DRN (
 ,
,
 ) is recurrent if and only if for all pair of points x,
, x →* x′ implies x′ →* x (Def. 1.4). First, we show that the LCN recurrence is equivalent to the presence of the null vector in the strictly positive real span of drift vectors. Then, we discuss sufficient conditions to obtain the recurrence, and reduce the full recurrence property to a set of reachability properties.
) is recurrent if and only if for all pair of points x,
, x →* x′ implies x′ →* x (Def. 1.4). First, we show that the LCN recurrence is equivalent to the presence of the null vector in the strictly positive real span of drift vectors. Then, we discuss sufficient conditions to obtain the recurrence, and reduce the full recurrence property to a set of reachability properties.
4.1 LCN Recurrence
Let us ignore reaction origins and population positivity constraints. If 0 ∈ spanℤ>0
 , it is clear that from any point x, one can undo any reaction application and then go back to x:
such that λ
, it is clear that from any point x, one can undo any reaction application and then go back to x:
such that λ
 = 0. Hence ∀i ∈ [1; d], we obtain (λ − ei)
= 0. Hence ∀i ∈ [1; d], we obtain (λ − ei)
 = −
= −
 i.
i.
By following the proof of Lemma 3.3, we remark in Lemma 4.1 that 0 ∈ spanℚ>0
 (hence 0 ∈ spanℤ>0
(hence 0 ∈ spanℤ>0
 ) is equivalent to 0 ∈ spanℝ>0
) is equivalent to 0 ∈ spanℝ>0
 . This can be verified with linear programming.
. This can be verified with linear programming.
Lemma 4.1. 0 ∈ spanℚ>0
 ⇔ 0 ∈ spanℝ>0
⇔ 0 ∈ spanℝ>0
 .
.
Proof. (⇒) obvious. (⇐) same proof as for Lemma 3.3 with w = 0.
Finally, Theorem 4.2 establishes that LCN recurrence is equivalent to 0 ∈ spanℝ>0
 . The main difficulty is to prove that there exists a
such that it is possible to reverse all the reactions connecting any pair of points above M0 by staying in
. For that, we consider a basis ℬ = {b1,…,bk} of the free ℤ-module generated by
. The main difficulty is to prove that there exists a
such that it is possible to reverse all the reactions connecting any pair of points above M0 by staying in
. For that, we consider a basis ℬ = {b1,…,bk} of the free ℤ-module generated by
 . It is worth noticing that, because 0 ∈ spanℤ>0
. It is worth noticing that, because 0 ∈ spanℤ>0
 , it follows that bi ∈ spanℤ>0
, it follows that bi ∈ spanℤ>0
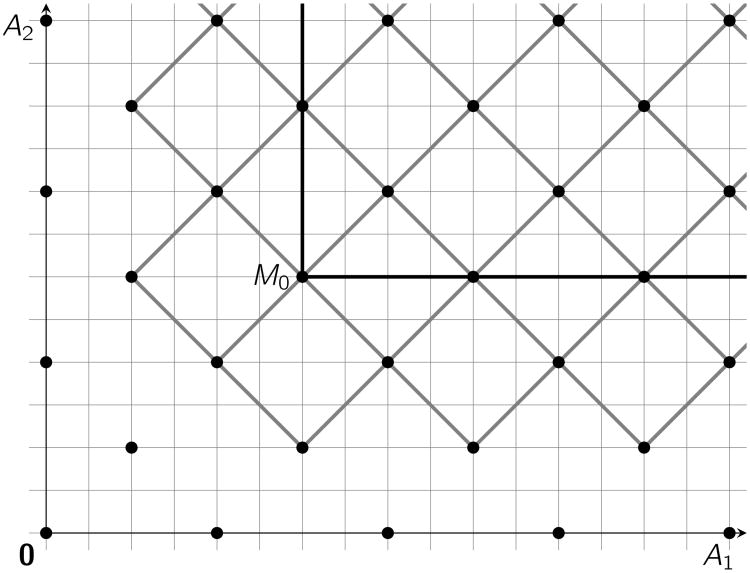
 ,∀i ∈ [1; k]. Let us pick M0 large enough such that there exists a sequence of reactions from M0 that can be successively applied (i.e., never below their origins) and that goes to all the vertices of the fundamental region formed by B that are adjacent to M0. Then any pair of points above M0 that is connected can be reversibly reached from each other. Fig. 3 illustrates this reasoning.
,∀i ∈ [1; k]. Let us pick M0 large enough such that there exists a sequence of reactions from M0 that can be successively applied (i.e., never below their origins) and that goes to all the vertices of the fundamental region formed by B that are adjacent to M0. Then any pair of points above M0 that is connected can be reversibly reached from each other. Fig. 3 illustrates this reasoning.
Figure 3.
Black dots are the points of the lattice generated by
 . The lattice fundamental regions (formed by the basis) are delimited by the gray lines.
. The lattice fundamental regions (formed by the basis) are delimited by the gray lines.
The proof of Theorem 4.2 also indicates that the reachability graph above M0 becomes in a sense maximal, or saturated: if x + δ→*x′ + δ when x ≥ M0, x′ ≥ M0, , then x →* x′. This is stated by Corollary 4.3.
Theorem 4.2. (
 ,
,
 ) is LCN recurrent ⇔ 0 ∈ spanℝ>0
) is LCN recurrent ⇔ 0 ∈ spanℝ>0
 .
.
Proof. (⇒) straightforward.
(⇐) Let us consider ℬ = {b1,…, bk}, a basis of the free ℤ-module generated by
 .
.
From Lemma 4.1, 0 ∈ spanℤ>0
 , which implies ±bi, ∈ spanℤ>0
, which implies ±bi, ∈ spanℤ>0
 , ∀i ∈ [1;k]. Hence, ∀i ∈ [1;k], ∀s ∈ {+, −}, ∃λ i,s ∈
such that λi,s
, ∀i ∈ [1;k]. Hence, ∀i ∈ [1;k], ∀s ∈ {+, −}, ∃λ i,s ∈
such that λi,s
 = bi,s ≜ sbi,. Let us pick an arbitrary ordering πi,s ∈ orderings(λi,s).
= bi,s ≜ sbi,. Let us pick an arbitrary ordering πi,s ∈ orderings(λi,s).
Let us define such that for any mapping Π: [1: 2k] → [1; k] × {+, − }, and ∀l, l′ ∈ [1; 2k], Π(l) = Π(l′) =>l = l′, then ∀l ∈ [1; 2k], ∀j ∈ [1; n], M0 + lowerpoint .
From M0 construction, the set of lattice fundamental regions formed by b1,…,bk intersecting
is connected and fits inside
. Moreover, each edge of those fundamental regions can be translated to a sequence of drift vectors v ∈
 in
. Therefore, ∀x, x′ ≥ M0 we have x →′ x′ ⇒ x′ → x.
in
. Therefore, ∀x, x′ ≥ M0 we have x →′ x′ ⇒ x′ → x.
Corollary 4.3 (Reachability Graph Saturation). If 0 ∈ spanℤ>0
 then there exists
such that the reachability graph on the set
becomes constant in the sense that: if x →* x′, and x − δ, x′ − δ ≥ M0 for some
, then x − δ →* x′ − δ.
then there exists
such that the reachability graph on the set
becomes constant in the sense that: if x →* x′, and x − δ, x′ − δ ≥ M0 for some
, then x − δ →* x′ − δ.
We refer to this property as “saturation” of the reachability graph, because it means that, for M0 large enough, and any , the reachability graph in the region above is identical (up to a shift) to the reachability graph in the region above M0.
Example. From the previous section we know that example (b) in Fig. 1 is irreducible hence recurrent, but example (a) is not irreducible. Using the characterization above one can verify that example (a) is LCN recurrent.
4.2 Full Recurrence
Assume a DRN (
 ,
,
 ) is LCN recurrent. If ∃x* ∈
such that 0 →* x* →* 0, then (
) is LCN recurrent. If ∃x* ∈
such that 0 →* x* →* 0, then (
 ,
,
 ) is recurrent (Lemma 4.4). Indeed, using Lemma 2.4, ∃α ∈ ℤ>0 such that αx* ≥ M0. Then, for any pair of points x,
If x→* x′, then, by Lemma 2.3, x + αx* →* x′ + αx*. Because the DRN is LCN recurrent, x′ + αx* →* x + αx*. Hence, x′ →* x. We remark however that, to our knowledge, there is no efficient general method to verify if
such that 0 →* x* →* 0. Moreover, this condition is sufficient but not necessary, in order to insure that an LCN recurrent network is fully recurrent.
) is recurrent (Lemma 4.4). Indeed, using Lemma 2.4, ∃α ∈ ℤ>0 such that αx* ≥ M0. Then, for any pair of points x,
If x→* x′, then, by Lemma 2.3, x + αx* →* x′ + αx*. Because the DRN is LCN recurrent, x′ + αx* →* x + αx*. Hence, x′ →* x. We remark however that, to our knowledge, there is no efficient general method to verify if
such that 0 →* x* →* 0. Moreover, this condition is sufficient but not necessary, in order to insure that an LCN recurrent network is fully recurrent.
Lemma 4.4. If DRN (
 ,
,
 ) is LCN recurrent and
such that 0→*x* and x* → * 0, then (
) is LCN recurrent and
such that 0→*x* and x* → * 0, then (
 ,
,
 ) is recurrent.
) is recurrent.
Proof. Consider α ∈ ℤ>0 such that αx* ≥ M0. If x →* x′ then x′ →* x′ + αx* →* x + αx* →* x.
In the general case, and independently of LCN recurrence, we notice that recurrence is equivalent to the reachability of the origin of each reaction from the point that is its origin plus drift vector (Lemma 4.5). Again, there is currently no efficient general method to verify these reachability properties.
Lemma 4.5. DRN (
 ,
,
 ) is recurrent if and only if ∀j ∈ [1; n],
) is recurrent if and only if ∀j ∈ [1; n],
 j +
j +
 j →*
j →*
 j.
j.
Proof. (⇒) straightforward. (⇐)
, ∀j ∈ [1; n]: x ≥
 j, x → x +
j, x → x +
 j →* x.
j →* x.
The above lemma allowsto conclude that any weakly reversible reaction network is recurrent (Lemma 4.6). A reaction network is weakly reversible if each reaction is part of a cycle of reactions Johnston et al. (2012); for instance X → Y; Y → Z; Z → X is a weakly reversible reaction network.
Lemma 4.6. Any weakly reversible reaction network is recurrent.
Proof. A DRN models a weakly reversible reaction network if and only if each reaction is part of a cycle of m ≤ n reactions where the origin of a reaction matches with the origin plus the drift vector of the previous reaction, i.e. ∀j ∈ [1; n], ∃m ∈ [1; n] and a path π: [1; m] → [1; n] such that ∀k ∈ [1; m],
. Therefore, ∀j ∈ [1; n],
 j +
j +
 j →*
j →*
 j.
j.
Example. The sufficient condition for recurrence depicted in Lemma 4.4 is verified by example (a) of Fig. 1. Indeed, 0 →* (6, 6) →* 0 (applying 3
 1 then 2
1 then 2
 3 from 0 results in (6,6), then applying 6
3 from 0 results in (6,6), then applying 6
 2 results in 0). Hence, example (a) is recurrent (but not irreducible), whereas example (b) is irreducible (and recurrent).
2 results in 0). Hence, example (a) is recurrent (but not irreducible), whereas example (b) is irreducible (and recurrent).
5 Biological Examples
This section applies the results of this paper to show that a model of circadian clock is LCN irreducible, and a generic model of phosphorylation chain is LCN recurrent.
5.1 Circadian clock
We study here a model of PER and TIM circadian oscillations from Leloup and Goldbeter (1999), extracted from the BioModels database (Le Novère et al., 2006). This model involves 10 species and 26 reactions (including 6 reversible). The list of reactions is given in Fig. 4
Figure 4. Reaction network of the PER/TIM circadian oscillations (Leloup and Goldbeter, 1999).
One can check that the necessary and sufficient conditions for LCN irreducibility of Theorem 3.4 are verified by this DRN. Hence, there exists a threshold on the population of species such that there exists a succession of reactions connecting any pair of states above this threshold.
Because no reaction has an origin being 0, the DRN is not self-starting, hence not fully irreducible; and because of the presence of degradation reaction, the DRN is not fully recurrent (for instance, 0 is reachable from the state where all species are 0 except PER_mRNA being 1, but the converse is false).
5.2 Phosphorylation chains
We consider a generic model of chains of phosphorylation, where an enzyme E can progressively phosphorylate a protein up to a certain level k. In concurrence, a kinase F can progressively de-phosphorylate this protein (Angeli et al., 2007).
Because of mass conservation properties (for example
being constant), such a DRN is not irreducible – in particular, spanℝ>0
 ≠ ℝd.
≠ ℝd.
Assuming LCN, one can notice that the irreversible reactions such as SmE → Sm+1 + E can be undone using the chain of reaction Sm+1 + F → Sm+1F → Sm + F followed by Sm + E → SmE. The undoing of Sm + F ← SmF irreversible reactions is achieved similarly. This shows that the DRN is LCN recurrent as 0 ∈ spanℝ>0
 . In addition, we remark that it is actually sufficient that all the species are present with at least one copy in order to undo any irreversible reaction of this network (i.e., M0 can be the vector having all its components being 1).
. In addition, we remark that it is actually sufficient that all the species are present with at least one copy in order to undo any irreversible reaction of this network (i.e., M0 can be the vector having all its components being 1).
Removing the LCN hypothesis, and in particular considering that F is absent (0 copy), it becomes impossible to revert the reaction S0E → S1 + E. Hence, the DRN is not fully recurrent.
LCN irreducibility depends both on stoichiometry properties (as highlighted by the two examples in Fig. 1) and on the dimension of the lattice generated by
 : if the free ℤ-module generated by
: if the free ℤ-module generated by
 has a lower dimension than
has a lower dimension than
 , the DRN is not LCN irreducible. This typically occurs in the presence of mass conservation properties, as highlighted by the example on phosphorylation chains.
, the DRN is not LCN irreducible. This typically occurs in the presence of mass conservation properties, as highlighted by the example on phosphorylation chains.
In addition, as stated in Lemma 4.6, we recall that any weakly reversible reaction networks is recurrent, as they verify necessarily 0 ∈ spanℝ>0
 .
.
6 Discussion
Relationships between DRNs and stochastic models dynamics Markov chains are a widely used modelling framework for analysing dynamics of biochemical reaction networks. Typically, the discrete states of such Markov chains represent the population of each biochemical species, and the transitions follow the drift vectors of reactions, when applicable (population of species greater than the reaction origin). Then, Markov chains associate either probabilities (DTMCs) or continuous rates (CTMCs) to transitions following biochemical laws, for instance.
In that sense, a DRN can be considered as the underlying discrete dynamics of any Markov chain modelling the same set of reactions (Fages and Soliman, 2008). If we assume that the probabilities or rates associated to reactions are never null, we obtain the following correspondence between DRNs and Markov chains dynamical properties:
DRN is irreducible if and only if the associated Markov chain is irreducible.
DRN is recurrent if and only if all states in the associated Markov chain are recurrent.
In the case where probability or rates may become null, DRN irreducibility (resp. recurrence) is still a necessary condition for Markov chain irreducibility (resp. recurrence).
We note that a DRN which is not recurrent implies that there exist some irreversible reactions. On the other hand, weak reversibility allows, in some cases, an efficient characterization of the stationary distribution in the associated Markov chain models (Anderson et al., 2010).
Relationships between DRNs and continuous models dynamics Continuous models of reaction networks, such as ODE systems, typically evolve in the continuous space of concentrations of species and implicitly assume that species are present in large copy numbers. In that way, we may want to relate dynamical properties of such continuous models of reaction networks to LCN properties of DRNs.
In particular, one can remark that if a DRN is not LCN recurrent, i.e. 0 ∉ spanℝ>0
 , then there exists a hyperplane H in ℝd such that all reaction vectors point on the same side of this hyperplane, and at least one reaction vector points strictly inside the corresponding half-space. This implies that no oscillation is possible in the continuous dynamics, i.e. there cannot exist any periodic solution. Indeed, if 0 ∉ spanℝ>0
, then there exists a hyperplane H in ℝd such that all reaction vectors point on the same side of this hyperplane, and at least one reaction vector points strictly inside the corresponding half-space. This implies that no oscillation is possible in the continuous dynamics, i.e. there cannot exist any periodic solution. Indeed, if 0 ∉ spanℝ>0
 , then there exists a vector vH perpendicular to the hyperplane H which gives rise to the linear function L(x) = vHx which is a strict Lyapunov function for the ODE model (there we assume that reaction rate functions do not vanish if reactant concentrations are strictly positive).
, then there exists a vector vH perpendicular to the hyperplane H which gives rise to the linear function L(x) = vHx which is a strict Lyapunov function for the ODE model (there we assume that reaction rate functions do not vanish if reactant concentrations are strictly positive).
Future work One possible future direction following the results presented is the derivation of necessary or sufficient conditions for persistence of DRNs.
Informally, persistent dynamical systems are ones where no species “goes extinct”, i.e., if we start with all species being present in the system, then no trajectory will wipe out some species in the long run.
The notion of persistence for continuos systems has been of great interest recently (Angeli et al., 2007; Craciun et al., 2012). It is not obvious how to define persistence for discrete systems, but one possible definition is given in Def. 6.1. Note that recurrence is a particular case of this notion of persistence (Remark 3).
Definition 6.1 (Persistence) DRN (
 ,
,
 ) is persistent if and only if
such that ∃k ∈ [1; d] with
,
such that x′ → x″.
) is persistent if and only if
such that ∃k ∈ [1; d] with
,
such that x′ → x″.
Remark 3. Recurrence ⇒ Persistence.
More generally, the study of DRNs may allow to efficiently prove the absence of certain dynamical properties in a wide-range of concrete models, independent of rate laws or kinetic parameters.
Acknowledgments
We thank Andrei Caldararu for helpful comments and suggestions. The work of GC was supported by NIH grant R01GM086881.
References
- Anderson D, Craciun G, Kurtz T. Product-form stationary distributions for deficiency zero chemical reaction networks. Bulletin of Mathematical Biology. 2010;72:1947–1970. doi: 10.1007/s11538-010-9517-4. [DOI] [PubMed] [Google Scholar]
- Angeli D, Leenheer PD, Sontag ED. A petri net approach to the study of persistence in chemical reaction networks. Mathematical Biosciences. 2007;210(2):598–618. doi: 10.1016/j.mbs.2007.07.003. [DOI] [PubMed] [Google Scholar]
- Cohen H. A course in computational algebraic number theory. Springer-Verlag; 1993. [Google Scholar]
- Craciun G, Nazarov F, Pantea C. SIAM Journal on Applied Mathematics. 2012. Persistence and permanence of mass-action and power-law dynamical systems. to appear. [Google Scholar]
- Craciun G, Tang Y, Feinberg M. Understanding bistability in complex enzyme-driven reaction networks. Proceedings of the National Academy of Sciences. 2006;103(23):8697–8702. doi: 10.1073/pnas.0602767103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fages F, Soliman S. Abstract interpretation and types for systems biology. Theoretical Computer Science. 2008;403(1):52–70. [Google Scholar]
- Feinberg M. Lectures on chemical reaction networks Notes of lectures given at the Mathematics. Research Center of the University of Wisconsin; 1979. available online at http://www.chbmeng.ohio-state.edu/∼feinberg/LecturesOnReactionNetworks/ [Google Scholar]
- Feinberg M. Chemical reaction network structure and the stability of complex isothermal reactors—i. the deficiency zero and deficiency one theorems. Chemical Engineering Science. 1987;42(10):2229–2268. [Google Scholar]
- Johnston M, Siegel D, Szederkényi G. A linear programming approach to weak reversibility and linear conjugacy of chemical reaction networks. Journal of Mathematical Chemistry. 2012;50:274–288. [Google Scholar]
- Lawler GF. Introduction to Stochastic Processes. second Chapman & Hall/CRC; 2006. [Google Scholar]
- Le Novère N, Bornstein B, Broicher A, Courtot M, Donizelli M, Dharuri H, Li L, Sauro H, Schilstra M, Shapiro B, Snoep JL, Hucka M. BioModels Database: a free, centralized database of curated, published, quantitative kinetic models of biochemical and cellular systems. Nucleic Acids Research. 2006;34(Database issue):D689–D691. doi: 10.1093/nar/gkj092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leloup, Goldbeter Chaos and birhythmicity in a model for circadian oscillations of the PER and TIM proteins in drosophila. J Theor Biol. 1999;198(3):445–459. doi: 10.1006/jtbi.1999.0924. [DOI] [PubMed] [Google Scholar]
- Murata T. Petri nets: Properties, analysis and applications. Proceedings of the IEEE. 1989;77(4):541–580. [Google Scholar]
- Petri CA. PhD thesis. University of Bonn; 1962. Kommunikation mit Automaten. [Google Scholar]
- Shinar G, Feinberg M. Concordant chemical reaction networks. Mathematical Biosciences. 1987;240(2):92–113. doi: 10.1016/j.mbs.2012.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shiu A, Sturmfels B. Siphons in chemical reaction networks. Bulletin of Mathematical Biology. 2010;72(6):1448–1463. doi: 10.1007/s11538-010-9502-y. [DOI] [PubMed] [Google Scholar]
- Wilkinson DJ. Stochastic Modelling for Systems Biology. Chapman and Hall/CRC; 2006. [Google Scholar]