Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Nov 21;3:3283. doi: 10.1038/srep03283

Fermi-edge superfluorescence from a quantum-degenerate electron-hole gas

Ji-Hee Kim 1, G Timothy Noe II 1, Stephen A McGill 2, Yongrui Wang 3, Aleksander K Wójcik 3, Alexey A Belyanin 3, Junichiro Kono 1,a
PMCID: PMC3836032  PMID: 24257510

Abstract

Nonequilibrium can be a source of order. This rather counterintuitive statement has been proven to be true through a variety of fluctuation-driven, self-organization behaviors exhibited by out-of-equilibrium, many-body systems in nature (physical, chemical, and biological), resulting in the spontaneous appearance of macroscopic coherence. Here, we report on the observation of spontaneous bursts of coherent radiation from a quantum-degenerate gas of nonequilibrium electron-hole pairs in semiconductor quantum wells. Unlike typical spontaneous emission from semiconductors, which occurs at the band edge, the observed emission occurs at the quasi-Fermi edge of the carrier distribution. As the carriers are consumed by recombination, the quasi-Fermi energy goes down toward the band edge, and we observe a continuously red-shifting streak. We interpret this emission as cooperative spontaneous recombination of electron-hole pairs, or superfluorescence (SF), which is enhanced by Coulomb interactions near the Fermi edge. This novel many-body enhancement allows the magnitude of the spontaneously developed macroscopic polarization to exceed the maximum value for ordinary SF, making electron-hole SF even more “super” than atomic SF.

Recent advances in optical studies of condensed matter systems have led to the emergence of a variety of phenomena that have conventionally been studied in the realm of quantum optics, including the Rabi flopping behavior1,2, the Autler-Townes splitting and dressed states3,4,5, electromagnetically induced transparency6, and the Mollow triplet7,8. These studies have not only deepened our understanding of light-matter interactions but also introduced aspects of many-body correlations inherent in optical processes in condensed matter systems9,10.

Here, we study nonequilibrium dynamics of high-density electron-hole (e-h) pairs in photo-excited semiconductor quantum wells at low temperature. The e-h pairs are incoherently prepared, but a macroscopic polarization spontaneously emerges and cooperatively decays, emitting a giant pulse of coherent light. This phenomenon, known as superfluorescence (SF)11,12 in quantum optics, is a nonequilibrium many-body process, in which order emerges in a self-organized manner via quantum fluctuations13. A giant dipole grows as inverted atomic dipoles interact with each other by exchanging spontaneously emitted photons. As predicted by Dicke in 195414 and verified experimentally in atomic gases15,16, the resultant macroscopic polarization produced by N atomic dipoles with an individual decay rate of 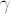Inline graphic can cooperatively decay at an accelerated rate 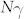Inline graphic and an intensity 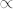Inline graphic N2 17,18,19.

We demonstrate that Coulomb interactions, i.e., virtual-photon exchange, among photo-excited carriers have a profound influence on the collective superradiant decay of the dense e-h plasma. Contrary to a typical interband emission spectrum of semiconductors, which is concentrated near the band gap, the observed SF spectra of this Coulomb-correlated ensemble of e-h pairs show that the dominant emission originates from the recombination of electrons and holes at their respective quasi-Fermi energies. Consequently, we observe a red-shifting streak of SF at zero magnetic field and sequential SF bursts from different Landau levels in a quantizing magnetic field. The photon energy of the emitted SF mirrors the instantaneous location of the quasi-Fermi energy, which continuously decreases with time toward the band edge as the e-h pairs at the Fermi edge are consumed by SF; this dynamic red-shift is opposite to what we expect from band-gap renormalization, which should decrease as the carriers are consumed, leading to a dynamic blue-shift. Overall, the many-body effects in this system are not just small corrections that require exotic conditions to be observed; rather, they completely dominate the electron dynamics and emission spectra. Thus, ultrabright SF from a dense e-h plasma is one of the most vivid displays of many-body physics in semiconductors.

Results

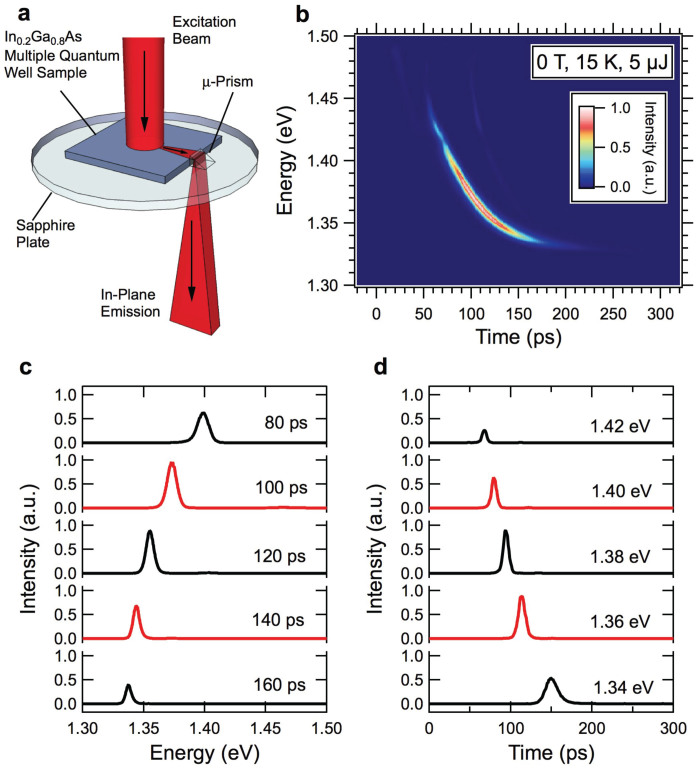
Figure 1a shows the experimental geometry used in this work. Photoluminescence (PL) travels in all directions, but some of the emission travels in the plane of the quantum wells, which is reflected by the micro-prism towards our collection optics. Figure 1b shows the result of time-resolved measurements of in-plane-emitted PL taken at 15 K at zero magnetic field with a pump pulse energy of 5 μJ. The dominant feature is a line of emission starting from ~1.45 eV and ending at ~1.325 eV, i.e., the emitted photon energy changes continuously with time. There is a kink in the line at ~1.42 eV, which corresponds to the E1L1 transition; the curvature of the line also changes slightly at that kink. Figure 1c shows some “vertical” slices of the data in Fig. 1b at various time delays. We see that for a given time delay there is an emission peak with a spectral width of 5–10 meV, which dynamically shifts to lower energy as time passes. Figure 1d shows some “horizontal” slices of the data in Fig. 1b at various photon energies, demonstrating an ultrashort pulse of light emitted at a given photon energy at a certain time delay after excitation.

Figure 1. Observation of intense ultrashort pulses of radiation from a photo-excited InGaAs quantum well sample with photon energy and time delay continuously changing with time.

Figure 1

Open in a new tab

(a), The experimental geometry. The in-plane emission is redirected with a micro-prism towards the collection optics. The sample was kept at 15 K and 0 T. The excitation photon energy, pulse width, and pulse energy were ~1.6 eV, ~150 fs, and 5 μJ, respectively. (b), Photoluminescence intensity as a simultaneous function of time delay and photon energy. The peak emission red-shifts as a function of time. (c), Spectral slices of the map in (b) for various time delays. (d), Temporal slices of the map in (b) for various photon energies, showing pulses of radiation whose delay time with respect to the pump pulse becomes longer with decreasing photon energy.

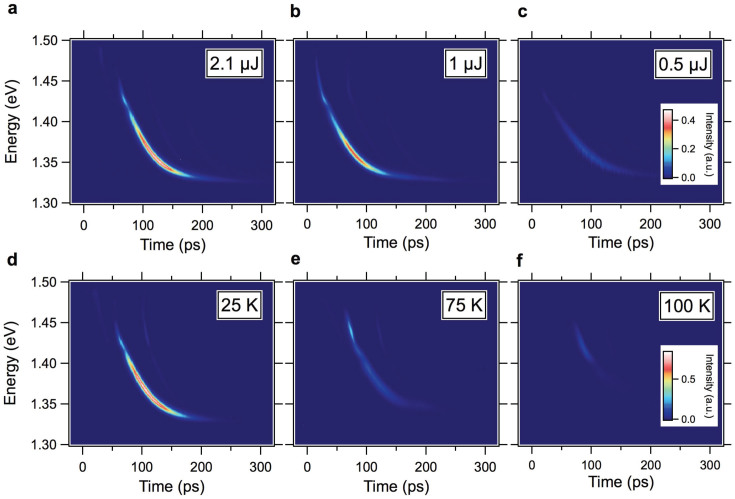
We found that the spectral and temporal behavior of the emission line sensitively depends on the excitation pulse energy and temperature. Figures 2a–c show time-resolved PL maps taken with different excitation pulse energies at zero magnetic field. The map constructed with 2.1 μJ pulse energy looks very similar to the map constructed with 5 μJ (Fig. 1b). When the power is further decreased, there is a non-monotonic temporal shift in the line of emission. For a given photon energy close to the middle of the line, say 1.37 eV, we see that the line moves to earlier time from 2.1 to 1 μJ and then back to a later time at 0.5 μJ excitation pulse energy with a change in curvature. At the highest photon energy for strong emission in the line, at ~1.45 eV, the emission moves to earlier time delays with decreasing power and then stays there for the lowest power. For all excitation powers, the emission line ends at 1.325 eV, which corresponds to the E1H1 band-edge. We also varied the temperature while fixing the excitation pulse energy at 5 μJ, as shown in Figs. 2d–f. With increasing temperature, there is a smearing of the emission line at the lowest photon energies of the line, until all of the emission from the E1H1 contribution of the line is ‘washed out’, and only the slightest signal at the E1L1 portion remains at 100 K. It is clear that the emission burst moves to later times as it is ‘washed out’ at high temperatures.

Figure 2. Excitation pulse energy and temperature dependence of the observed pulsed radiation at zero magnetic field.

Figure 2

Open in a new tab

Photoluminescence intensity versus time delay and photon energy for excitation pulse energies of (a) 2.1 μJ, (b) 1 μJ, and (c) 0.5 μJ at 15 K and 0 T. Photoluminescence intensity versus time delay and photon energy at (d) 25 K, (c) 75 K, and (e) 100 K, with 5 μJ excitation pulse energy at 0 T. The intense pulsed emission of radiation becomes weaker with decreasing (increasing) excitation power (temperature) and eventually disappears when the excitation power (temperature) becomes too low (high).

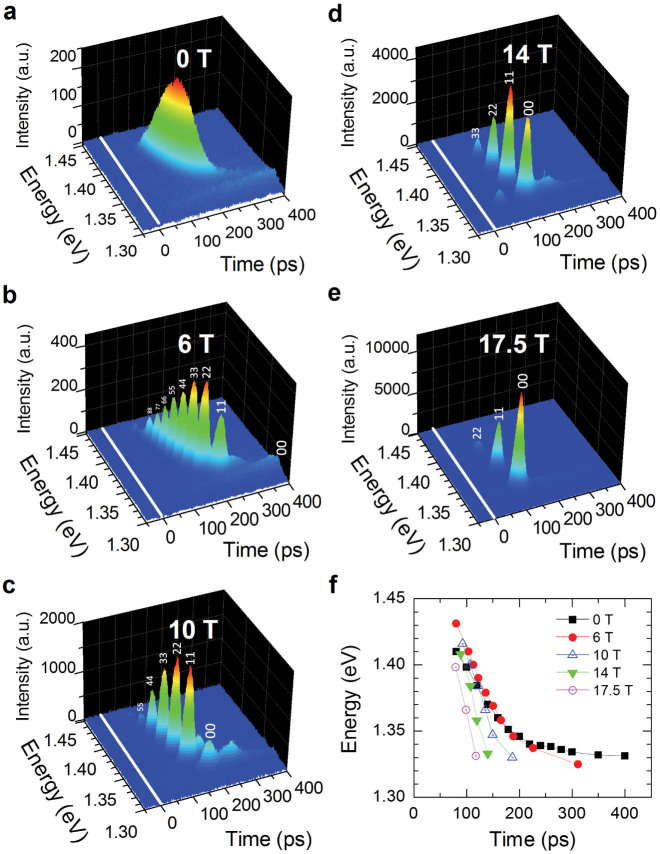
The emission spectrum and dynamics drastically change when a magnetic field perpendicular to the quantum well plane is applied. Figures 3a–e show streak camera images of emission as a function of photon energy and time delay at different magnetic fields. With increasing magnetic field, the number of peaks decreases, and the energy separation between adjacent peaks increases due to increasing Landau quantization energy (i.e., the cyclotron energy). Previously we demonstrated the superradiant nature of the individual emission peaks by streak-camera and pump-probe measurements20. Here we observe that at a given magnetic field the delay is longer for emission from lower Landau levels, and the (NN) = (00) SF emission occurs only after the higher-energy SF emissions occur. This means that the relative timing of the bursts coming from different Landau levels is not random. Rather, these data clearly indicate that e-h pairs in the highest occupied energy states near the quasi-Fermi edge at a given time always recombine first; e-h pairs in lower and lower energy states then emit bursts sequentially. Figure 3f summarizes the peak positions of the SF bursts as a function of photon energy and time.

Figure 3. Magnetic-field evolution of the observed pulsed coherent emission as a function of photon energy and time delay.

Figure 3

Open in a new tab

Time-resolved emission spectra at (a), 0 T, (b), 6 T, (c), 10 T, (d), 14 T, and (e), 17.5 T with 2 μJ of excitation pulse energy at 5 K. Each (N, N) recombination is observed as a delayed burst of superfluorescence (N: Landau level index). With increasing magnetic field, the number of peaks decreases, and the energy separation between adjacent peaks increases due to increasing Landau quantization energy. At a fixed magnetic field, the delay is longer for smaller N. Note that the N = 0 state is the last to burst. (f), Peak shift of emission as a function of time at different magnetic fields.

Discussion

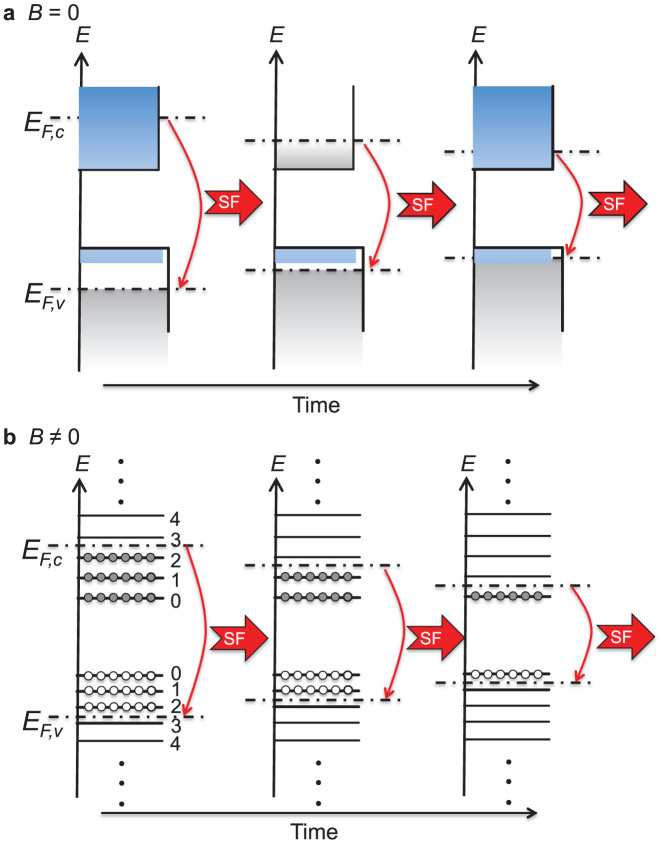
We interpret these phenomena in terms of Coulomb enhancement of gain near the Fermi energy in a high-density e-h system, which results in a preferential SF burst near the Fermi edge, as schematically shown in Fig. 4. After relaxation and thermalization, the photo-generated carriers form degenerate Fermi gases with respective quasi-Fermi energies inside the conduction and valence bands. The recombination gain for the e-h states just below the quasi-Fermi energies is predicted to be enhanced due to Coulomb interactions among carriers21, which causes a SF burst to form at the Fermi edge most easily. As a burst occurs, a significant population is depleted, resulting in a decreased Fermi energy. Thus, as time goes on, the Fermi level moves toward the band edge continuously. This results in a continuous line of SF emission at zero field (Figs. 1 and 2) and a series of sequential SF bursts in a magnetic field (Fig. 3).

Figure 4. Interpretation of the burst of emission with dynamically red-shifting wavelength: coherent Fermi-edge emission via ultrafast superradiant recombination of an electron-hole plasma.

Figure 4

Open in a new tab

(a), Zero magnetic field. Carriers near the instantaneous quasi-Fermi energies are consumed through ultrafast cooperative recombination, due to many-body enhancement of gain21, leading to both a burst of radiation with continuously red-shifting wavelength and a continuously decreasing Fermi energy towards the band edge. (b), Finite magnetic field. Electron-hole pairs at the highest occupied Landau levels recombine first, again due to many-body enhancement of gain, leading to sequential bursts of superfluorescece from higher to lower Landau levels toward the (00) level.

We model the recombination dynamics of the photo-excited e-h plasma using semiconductor Bloch equations derived from a general two-band e-h Hamiltonian in the Hartree-Fock approximation (see Methods and Supplementary Information for more details). At the linear stage of SF, when the field grows exponentially, the gain spectrum is given by 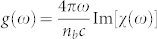Inline graphic, where nb is the background refractive index, c is the speed of light, 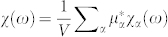Inline graphic is the optical susceptibility, and V is the normalization volume. The functions χα(ω) satisfy a set of linear equations

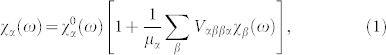graphic file with name srep03283-m1.jpg

where

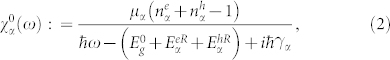graphic file with name srep03283-m2.jpg

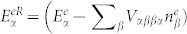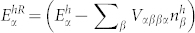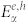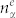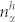each Greek subscript (α, β, …) denotes a set of quantum numbers for a given single-particle state (e.g., wave vector, Landau level index, and spin), μα is the dipole matrix element of the optical transition between electron and hole states with index α, Inline graphic and Inline graphic are the renormalized energies of single-particle states, Inline graphic, Inline graphic and Inline graphic are e-h occupation numbers, and 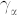Inline graphic is the phenomenological dephasing term for the interband polarization. Matrix elements 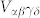Inline graphic of the screened Coulomb interaction are specified in Supplementary Information; screening is calculated using the Lindhard formula.

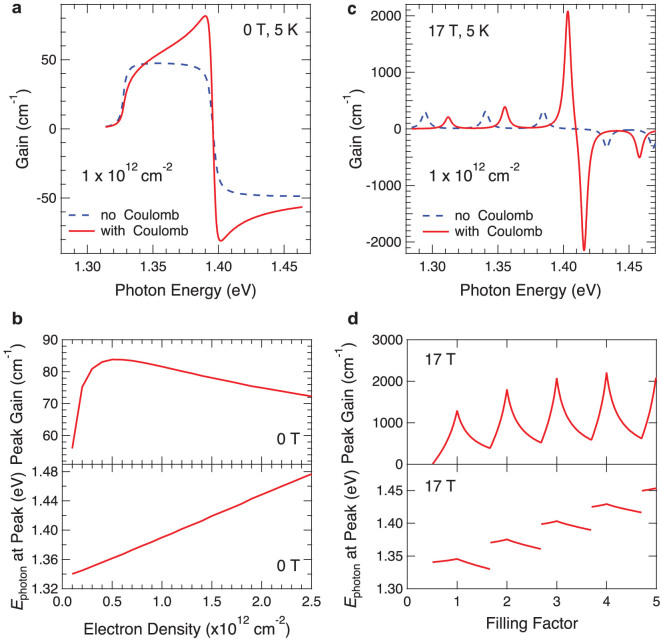
An example of Coulomb-induced modification of gain for quantum wells at zero magnetic field is shown in Fig. 5a (solid line), together with a gain spectrum neglecting all Coulomb effects except band gap renormalization (dashed line); the latter was obtained by replacing χα(ω) by 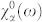Inline graphic. A relaxation time of 2 meV is assumed. It is seen that Coulomb interactions lead to an enhancement of gain just below the energy that corresponds to the difference between the quasi-Fermi levels of electrons and heavy holes. Previously, a related effect of “Fermi-edge singularity” has been observed in the spontaneous PL spectra of n-doped quantum wells in a steady state22. In the present case, the many-body gain enhancement is completely due to a nonequilibrium photo-excited e-h plasma. Stimulated emission occurs in the quantum well plane, and the light intensity grows exponentially, both in space and time. As a result, the rather broad many-body enhancement in the gain spectrum around Fermi energy translates into a sharp peak in the instantaneous intensity spectrum. The subsequent time evolution of the spectrum is dominated by an ultrafast collective recombination process: the peak continuously follows the red-shift of the quasi-Fermi level as the carriers at the Fermi edge are consumed by the SF. This behavior, observed in our samples according to Fig. 2, is in agreement with Fig. 5b, which shows the calculated evolution of the peak gain and peak gain energy as a function of e-h pair density. Furthermore, the highest gain, which leads to the fastest decay, is seen to be achieved at some intermediate density, which explains the observed non-monotonic temporal shift as a function of pump power (Figs. 2a–c).

Figure 5. Theoretical calculations of Coulomb-induced many-body enhancement of gain at the Fermi energy at zero magnetic field and 17 T.

Figure 5

Open in a new tab

(a), Gain spectrum for the InGaAs sample without a magnetic field, calculated using Eq. (1) (solid line), in comparison with the spectrum obtained by replacing 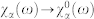Inline graphic, i.e., neglecting all Coulomb effects except band-gap renormalization (dashed line). Separate Fermi distributions for electrons and holes of density 1 × 1012 cm−2 and temperature 5 K are assumed. A relaxation rate of 2 meV is assumed. (b), Peak gain (upper panel) and peak gain energy (lower panel) as a function of e-h density at zero magnetic field. Other parameters are the same as in (a). (c), Calculated gain spectrum in a magnetic field of 17 T (solid line), in comparison with the spectrum obtained by replacing 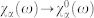Inline graphic, i.e., neglecting all Coulomb effects except band-gap renormalization (dashed line). A filling factor ν = 3 and a temperature of 5 K are assumed. A relaxation rate of 3 meV is adopted. (d), Peak gain (upper panel) and peak gain energy (lower panel) at 17 T as a function of filling factor, defined as the number of filled Landau levels. Other parameters are the same as in (c).

In a strong magnetic field, the gain spectrum exhibits strong peaks when the Landau level filling factor is an integer, and for a given filling factor, the gain is largest for the highest filled Landau level (Figs. 5c and 5d). A snapshot of the gain for a fixed filling factor ν = 3, corresponding to three filled Landau levels, is shown in Fig. 5c for a magnetic field of 17 T. A relaxation time of 3 meV is adopted. It can be seen that the peak gain for e-h pairs at the N = 3 Landau level is much higher than that for completely filled, lower Landau levels. Note that the peak gain value is strongly enhanced compared to quantum wells without a magnetic field due to an increase in the transition matrix element and density of states. This provides a natural explanation for the trend observed in Fig. 3f, i.e., SF develops faster in a stronger magnetic field. Figure 5d shows the calculated peak gain and peak gain energy as a function of filling factor at a fixed magnetic field of 17 T. The peculiar many-body dynamics of the peak gain lead to isolated SF bursts that are fired consecutively from higher to lower Landau levels, as observed in Fig. 3.

In summary, the results of this study not only provide new insight into the nonequilibrium dynamics of Coulomb-correlated e-h pairs in semiconductors but also open up new possibilities of controlling, and enhancing, collective emission properties of many-body states. Specifically, we showed that superfluorescence, a well-known phenomenon in quantum optics of atoms based on photon exchange between inverted atomic dipoles, takes a new turn when it occurs in a condensed matter system, where Coulomb correlations (i.e., virtual-photon exchange) create enormous gain concentrated at the Fermi edge, which becomes better defined at lower temperatures (Figs. 2d–f). Thus, this work demonstrates a unique method of producing ultrashort pulses of radiation from a semiconductor, based on the existence of Fermi-degenerate, nonequilibrium electrons and holes.

Methods

Experimental methods

The sample studied was an undoped multiple quantum well structure, consisting of fifteen layers of 8-nm In0.2Ga0.8As wells and 15-nm GaAs barriers. By using an amplified Ti:sapphire laser with with a pulse width of ~150 fs, a repetition rate of 1 kHz, and a photon energy of ~1.6 eV, we generated carriers with energies higher than the band gap of the GaAs barriers20. The experimental data shown in Figs. 1 and 2 was taken utilizing the optical Kerr gate method at Rice University using a 1 kHz amplified Ti:sapphire laser (Clark-MXR: CPA-2001). The Kerr medium used was Toluene. The photoluminescence was collected and imaged with off-axis parabolic mirrors onto the Kerr medium. A split-off portion of the excitation beam was used as the optical Kerr gate pulse. The time-resolved photoluminescence was measured by a CCD camera attached to a grating spectrometer after incrementally changing the time delay between the excitation and gate pulses using a one-dimensional linear stage. The experimental data shown in Fig. 3 was taken at the National High Magnetic Field Laboratory in Tallahassee, utilizing a 17.5-T superconducting magnet. The sample was mounted in the Faraday geometry, where the magnetic field was parallel to the optical excitation and perpendicular to the plane of the quantum wells. We observed time-resolved photoluminescence using a streak camera with 2 ps time resolution.

Theoretical methods

We used the semiconductor Bloch equations (SBEs) to study SF from a high-density e-h plasma in the presence of Coulomb interactions. The usual form of the SBEs23 is for a bulk or 2D semiconductor, where the states can be labeled by a 3D or 2D wave vector 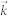Inline graphic. Here we rederive SBEs following the same basic Hartree-Fock and random-phase approximations but in a more general form, which accommodates the effects of a finite well width and the quantization of motion in a strong magnetic field. The Supplemental Information section outlines the derivation and explains all notations. The resulting equations of motion for the distribution functions of electrons 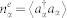Inline graphic and holes 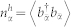Inline graphic, and the polarization 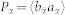Inline graphic are as follows:

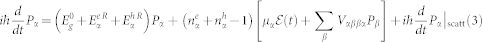graphic file with name srep03283-m3.jpg
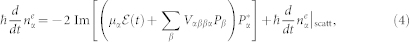graphic file with name srep03283-m4.jpg
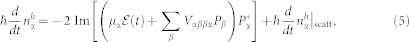graphic file with name srep03283-m5.jpg

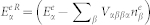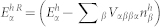where Inline graphic and Inline graphic are the renormalized energies, and the scattering terms account for higher-order contributions beyond the Hartree-Fock and other scattering processes such as scattering with LO-phonons. Here we replace 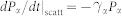Inline graphic for simplicity. The band structure for our sample consisting of undoped 8-nm In0.2Ga0.8As wells and 15-nm GaAs barriers on a GaAs substrate is calculated using the parameters given by Vurgaftman et al.24. Strain effects are included using the results of Sugawara et al.25.

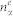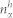These equations, together with Maxwell's equations for the electromagnetic field, can be applied to study the full nonlinear dynamics of interaction between the e-h plasma and radiation. Here we derive the gain for given carrier distributions Inline graphic and Inline graphic. Assuming a monochromatic and sinusoidal time dependence for the field 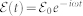Inline graphic and the polarization 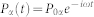Inline graphic, we can find Pα from Eq. (3) and define the quantity 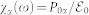Inline graphic, which satisfies Eq. (1). The optical susceptibility is then 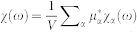Inline graphic, where V is the normalization volume. The gain spectrum is given by 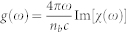Inline graphic, where nb is the background refractive index, and c is the speed of light. We use the above general results to calculate the gain spectra shown in Fig. 5.

Author Contributions

J.-H.K. and G.T.N. equally contributed to the measurements presented in this manuscript under the supervision and guidance of J.K. S.A.M. provided assistance in some of the measurements performed at the National High Magnetic Field Laboratory. Y.W., A.K.W. and A.A.B. developed the theoretical model and performed simulations. All authors contributed to data analysis and interpretation as well as the writing of the manuscript.

Supplementary Material

Supplementary Information

Supplementary Informaton

srep03283-s1.pdf (170KB, pdf)

Acknowledgments

This work was supported by the National Science Foundation through grants DMR-1006663, DMR-1310138, and ECS-0547019. A portion of this work was performed at the National High Magnetic Field Laboratory, supported by NSF Co-operative Agreement No. DMR-0084173 and by the State of Florida. We thank G. S. Solomon for providing us with the InGaAs/GaAs quantum well sample used in this study.

References

  1. Kamada H., Gotoh H., Temmyo J., Takagahara T. & Ando H. Exciton Rabi oscillation in a single quantum dot. Phys. Rev. Lett. 87, 246401 (2001). [DOI] [PubMed] [Google Scholar]
  2. Choi H. et al. Ultrafast Rabi flopping and coherent pulse propagation in a quantum cascade laser. Nat. Photon. 4, 706–710 (2010). [Google Scholar]
  3. Shimano R. & Kuwata-Gonokami M. Observation of Autler-Townes splitting of biexcitons in CuCl. Phys. Rev. Lett. 72, 530–533 (1994). [DOI] [PubMed] [Google Scholar]
  4. Muller A., Fang W., Lawall J. & Solomon G. S. Emission spectrum of a dressed exciton-biexciton complex in a semiconductor quantum dot. Phys. Rev. Lett. 101, 027401 (2008). [DOI] [PubMed] [Google Scholar]
  5. Wagner M. et al. Observation of the intraexciton Autler-Townes effect in GaAs/AlGaAs semiconductor quantum wells. Phys. Rev. Lett. 105, 167401 (2010). [DOI] [PubMed] [Google Scholar]
  6. Phillips M. & Wang H. Spin coherence and electromagnetically induced transparency via exciton correlations. Phys. Rev. Lett. 89, 186401 (2002). [DOI] [PubMed] [Google Scholar]
  7. Vamivakas A. N., Zhao Y., Lu C.-Y. & Atatüre M. Spin-resolved quantum-dot resonance fluorescence. Nat. Phys. 5, 198–202 (2009). [DOI] [PubMed] [Google Scholar]
  8. Flagg E. B. et al. Resonantly driven coherent oscillations in a solid-state quantum emitter. Nat. Phys. 5, 203–207 (2009). [Google Scholar]
  9. Toyozawa Y. Optical Properties of Solids (Cambridge University Press, Cambridge, 2003). [Google Scholar]
  10. Kira M. & Koch S. W. Semiconductor Quantum Optics (Cambridge University Press, Cambridge, 2012). [Google Scholar]
  11. Bonifacio R. & Lugiato L. A. Cooperative radiation processes in two-level systems: Superfluorescence. Phys. Rev. A 11, 1507–1521 (1975). [Google Scholar]
  12. Vrehen Q. H. F. & Gibbs H. M. Superfluorescence experiments. In Bonifacio, R. (ed.) Dissipative Systems in Quantum Optics, Topics in Current Physics, chap. 6, 111–147 (Springer-Verlag, Berlin, 1982). [Google Scholar]
  13. Nicolis G. & Prigogine I. Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order through Fluctuations (Wiley, New York, 1977). [Google Scholar]
  14. Dicke R. H. Coherence in spontaneous radiation processes. Phys. Rev. 93, 99–110 (1954). [Google Scholar]
  15. Skribanowitz N., Herman I. P., MacGillivray J. C. & Feld M. S. Observation of Dicke superradiance in optically pumped HF gas. Phys. Rev. Lett. 30, 309–312 (1973). [Google Scholar]
  16. Gibbs H. M., Vrehen Q. H. F. & Hikspoors H. M. J. Single-pulse superfluorescence in cesium. Phys. Rev. Lett. 39, 547–550 (1977). [Google Scholar]
  17. Andreev A. V., Emel'yanov V. I. & Il'inskii Y. A. Collective spontaneous emission (Dicke superradiance). Sov. Phys. Usp. 23, 493–514 (1980). [Google Scholar]
  18. Gross M. & Haroche S. Superradiance: An essay on the theory of collective spontaneous emission. Phys. Rep. 93, 301–396 (1982). [Google Scholar]
  19. Zheleznyakov V. V., Kocharovsky V. V. & Kocharovsky V. V. Polarization waves and superradiance in active media. Sov. Phys. Usp. 32, 835–870 (1989). [Google Scholar]
  20. Noe II G. T. et al. Giant superfluorescent bursts from a semiconductor magneto-plasma. Nat. Phys. 8, 219–224 (2012). [Google Scholar]
  21. Schmitt-Rink S., Ell C. & Haug H. Many-body effects in the absorption, gain, and luminescence spectra of semiconductor quantum-well structures. Phys. Rev. B 33, 1183–1189 (1986). [DOI] [PubMed] [Google Scholar]
  22. Skolnick M. S. et al. Observation of a many-body edge singularity in quantum-well luminescence spectra. Phys. Rev. Lett. 58, 2130–2133 (1987). [DOI] [PubMed] [Google Scholar]
  23. Haug H. & Koch S. W. Quantum Theory of the Optical and Electronic Properties of Semiconductors (World Scientific, Singapore, 2004), fourth edn. [Google Scholar]
  24. Vurgaftman I., Meyer J. R. & Ram-Mohan L. R. Band parameters for III-V compound semiconductors and their alloys. J. Appl. Phys. 89, 5815 (2001). [Google Scholar]
  25. Sugawara M., Okazaki N., Fujii T. & Yamazaki S. Conduction-band and valence-band structures in strained In1−xGaxAs/InP quantum wells on (001) InP substrates. Phys. Rev. B 48, 8102–8118 (1993). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Informaton

srep03283-s1.pdf (170KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES