Abstract
Minimal physiologically-based pharmacokinetic (mPBPK) models provide a sensible modeling approach when fitting only plasma (or blood) data yielding physiologically-relevant PK parameters that may provide more practical value than parameters of mammillary models. We propose a second-generation mPBPK model specifically for monoclonal antibodies (mAb) by including (lumping) several essential components of mAb PK used in full PBPK models. These components include convection as the primary mechanism of antibody movement from plasma into tissues and return to plasma with interstitial fluid as the major extravascular distribution space. The model divides tissue spaces into two groups according to their vascular endothelial structure, leaky and tight, which consequently allows discernment of two types and general sites of distribution. This mPBPK model was applied to two mAbs in mice and ten mAbs with linear kinetics in humans. The model captured their plasma PK profiles well with predictions of concentrations in interstitial fluid for two types of tissues. Predictions of tissue concentrations for mAb 7E3 and 8C2 were consistent with actual measurements in mice, indicating the feasibility of this model in assessing extravascular distribution in the two categories of tissues. The vascular reflection coefficients (σ1) of tight tissues (Vtight) ranged 0.883 to 0.987 and coefficients (σ2) for leaky tissues (Vleaky) ranged 0.311 to 0.837. The plasma clearance (CLp) varied among the mAbs in humans from 0.0054 to 0.03 L/hr. In addition, applying this model generates parameters for mAb transcapillary escape rates and assesses major sites of elimination. Four of ten mAbs exhibited better fitting statistics premised on elimination from interstitial fluid than from plasma. This approach allows comparisons of mAb PK when only plasma data are available, provides more realistic parameters and predictions than mammillary models, and may provide an intermediate step towards utilizing full PBPK models for mAbs.
Keywords: PBPK, minimal PBPK, mammillary model, monoclonal antibody
Introduction
Physiologically-based pharmacokinetic models (PBPK) offer more mechanistic characterization of drug disposition than ‘classical’ compartment models by incorporating a comprehensive array of anatomical and physiological properties [1]. In general, employment and validation of PBPK models requires information from estimates or measurements of drug concentrations in numerous tissues. When only plasma (or blood) data is available, a minimal PBPK model (mPBPK), which inherits the major physiologic attributes from full PBPK models and represents the system as a substantially lumped PBPK model, provides a simpler approach than full-PBPK models, but provides parameters with more practical value than mammillary models [2]. mPBPK models provide separation of system- and drug-specific parameters and allow evaluation of known physicochemical and metabolic properties in determination of drug PK parameters. These parameters from mPBPK models can be compared among congeneric drugs and across species. Additionally, as with full-PBPK models, the mPBPK models have the flexibility in handling different clearance sites and mechanisms and absorption processes.
Applications of the mPBPK models were demonstrated in our earlier publication for several situations and types of drugs [1], including monoclonal antibodies (mAb). Nevertheless, our original mPBPK model was established as a generalized approach mainly applied to small molecules and did not make specific accommodations of the unique PK features of mAb. Our ‘second-generation’ mPBPK model gives particular considerations to these PK features by adapting and ‘lumping’ more features from original mPBPK models for evaluation of mAb PK.
The mAbs market has had impressive growth and is the leading segment of the development pipeline [3]. More than 25 mAbs and derivatives have been approved for a variety of diseases and around 500 mAbs and other biologics are currently at different stages of development. Because of their large size and relatively poor membrane permeability, mAbs exhibit distinct PK behaviors compared with small molecules [4, 5]. Therefore, PK models with specific appreciation of these PK features will be helpful in better description of mAb disposition. However, the two-compartment mammillary model (2CM) remains the most commonly employed approach in assessing mAb PK [6, 7]. The 2CM fails to properly represent the underlying processes of mAb disposition and lacks clear interpretation of their PK characteristics. For instance, mammillary models often assign the same rate or clearance (CLd) to inward and outward distribution. This makes concentrations equate between plasma and ‘tissue’ compartments at equilibrium. However, convection is the predominant mechanism for mAb extravascular distribution and different reflection coefficients on vascular and lymphatic sides yield lower concentrations of mAb in interstitial fluids [8]. Also, mammillary models, by definition, assume that all clearances occur from the central compartment; however, peripheral clearance is frequently indicated for mAbs [9]. Our original mPBPK model evaluated the possibility of peripheral clearance and the present ‘second-generation’ mPBPK pursues this avenue further by more closely utilizing several mAb PK characteristics to establish a mAb-specific mechanistic PK modeling approach.
Theoretical
The ‘second-generation’ mPBPK model in this paper was proposed by adapting the original mPBPK model [1] with considerations of specific PK characteristics of mAbs. The mAb have several unique PK features different from small molecules such as poor transcapillary and cellular permeability, less renal filtration and hepatic metabolism, clearance possible from peripheral tissues, salvage by Brambell receptors, and often nonlinearity caused by receptor binding [4,5]. Full-PBPK models seek to accommodate these features with a ‘bottom up’ approach [10, 11]. In contrast, our mPBPK modeling takes a reductionist approach to develop models incorporating only essential PK components and offering system-average rather than tissue-specific PK parameters in fitting of only plasma concentration versus time data (‘top down’ view).
It is important to identify the essential PK components that largely govern mAb disposition. In blood, mAbs are largely confined to plasma without distribution into blood cells [10, 11]. Therefore, modeling questions are primarily about evaluating distribution in extravascular spaces. Two factors need attention: one is distribution rate, also known as transcapillary escape rate (TER) [12], and the other is how mAbs localize in the extravascular space.
The mAb can escape the vascular space by both diffusion and convection. In the PBPK model developed by Baxter et al, both mechanisms were evaluated by fitting tissue data, but it was concluded that convection largely mediated TER with insignificant diffusion [8]. Several other studies also provided evidence supporting this [13, 14]. Thus, our mPBPK models only considered convection as the distribution pathway and the one-pore formalism was employed as in several full-PBPK models [10, 11].
About half of native IgG was found distributed in extravascular space [12] and interstitial fluid (ISF) is generally believed to be the primary extravascular distributable space given the limited cellular permeability of mAbs. The vascular endothelial endosome is frequently included in full-PBPK models to assess the influence of FcRn salvage [10, 15]. However, it is known that an adult has about 1.0 kg of endothelial cells, which comprise around 1.6×1013 cells with a surface area of 1–7 m2 [16]. Given that the endosome is only a small part of cell space (about 0.6 ~ 2%) [17, 18], the overall volume of vascular endothelial endosomes in adults may be estimated to be only about 0.4% of plasma and less than 0.1% of ISF volume. As such, even if endosomes have slightly higher concentrations of mAb than plasma, only a small fraction of the total mass of antibody will reside within vascular endothelial endosomes at any moment of time. The interaction between FcRn and antibody within the endosomal space clearly plays an important role in mAb elimination (and IgG homeostasis); however, this may be explained by the rapid time course of endosomal transit (described in detail in the full PBPK model of Chen and Balthasar [19]). Given that extravascular distribution appears to be primarily determined by mAb in ISF, with little contribution relating to the mass of mAb within endothelium endosomes, the mPBPK model takes only ISF into consideration as the extravascular distribution space.
The model structure is shown in Figure 1. Model A is described by the differential equation structure similar to full-PBPK models:
| (1) |
| (2) |
| (3) |
| (4) |
where Cp is mAb concentration in Vp (plasma volume), Ctight and Cleaky are mAb ISF concentrations in tissue Vtight and Vleaky. The Vtight and Vleaky are volumes of ISF in tissues that have continuous and discontinuous or fenestrated capillaries. Based on the report of Sarin [20], we have assigned the muscle, skin, adipose and brain to Vtight, and all other tissues to Vleaky (liver, kidney, heart, etc). The Vlymph is lymph volume, assumed equal to blood volume [21]. The L is total lymph flow equal to the sum of L1 and L2, the lymph flow for Vtight and Vleaky. The σ1 and σ2 are vascular reflection coefficients for Vtight and Vleaky. The σL is the lymphatic capillary reflection coefficient, which is assumed to be 0.2. The CLi and CLp are clearances from ISF and plasma. Model B has CLi from Vtight and Vleaky while all other equation structures are the same as Model A. All Initial Conditions are concentrations = 0.
Figure 1.
Second-generation minimal-PBPK model for monoclonal antibody pharmacokinetics Symbols and physiological restrictions are defined with Eq (1–7) Clearance is applied either to plasma (Model A) or to interstitial fluid (Model B). The plasma compartment in the left box represents the venous plasma as in full PBPK models, but is not applied in the present model.
The critical elements of the mPBPK model are the physiologic attributes where Vp is plasma volume, L is total lymph volume, and:
| (5a,b) |
| (6a,b) |
| (7a,b) |
where ISF is total system interstitial fluid and Kp is available fraction of ISF for mAb distribution, which is largely determined by antibody size, charge, structure and other physiochemical properties. Given the similar size and structure of most mAbs, charge will be the primary factor influencing Kp, which was designated as 0.8 for native IgG1 and 0.4 for native IgG4 according to previous studies [22, 23]. As shown in equations (6) and (7), the relative fractions of Vtight (0.65) and Vleaky (0.35) to total ISF were calculated based upon the values used in full-PBPK models, as were the fractions of L1 (0.33) and L2 (0.67) to L [11]. These physiological parameters were found in the literature [24] and are listed in Table 1. The volume of ISF was assigned as 15.6 L and lymph flow was assumed as 2.9 L/day at basal state for a 70 kg BW person [24, 25].
Table 1.
Pharmacokinetic parameters of monoclonal antibodies (mAb) in micea
| Parameter (CV%) | 7E3 | 8C2 | |||
|---|---|---|---|---|---|
| Model A | Model B | Model A | Model B | ||
| σ1 (−) | 0.95 (−) b | 0.95 (−) | 0.943 (30.7) | 0.918 (32.7) | |
| σ2 (−) | 0.421 (10.4) | 0.340 (10.6) | 0.378 (34.2) | 0.311 (52.6) | |
| CLp (or CLi) (×10−5 L/hr) | 0.499 (14.1) | 0.666 (18.3) | 0.525 (46.5) | 0.618 (56.7) | |
| Objc | 5057 | 4868 | 772053 | 753499 | |
| Vp (mL) | Plasma volume | 0.85 | |||
| L (ml/hr) | Total lymph flow | 0.12 | |||
| ISF (mL) | Total interstitial volume | 4.35 | |||
In this model, only three parameters need to be estimated: σ1, σ2 and CLp (or CLi). Two clearances are not employed together, but the modeler can test which one works better. Like the first-generation mPBPK models, the model serves in fitting of only plasma profiles, but has flexibilities in adding other tissue compartments when more information is available.
The total tissue concentrations were simulated and compared with measured values to assess model predictive performance. The output of total tissue concentrations is:
| (8) |
Where Rs is the summed volume of residual blood and Vt is the summed physical volume for each group of tissues. The Rs of tight and leaky tissues for a 20 g mouse in our simulations were 0.00045 and 0.00020 L; Vt were 0.0131 and 0.005435 L according to values used in full PBPK models [10, 11].
Data Analysis
The proposed model was applied to diverse published mAb PK data. Actual data were used for 7E3 [10] and 8C2 [26] in mice. Data for several therapeutic mAbs in human subjects were digitized: adecatumumab [27], mepolizumab [28], gevokizumab [29], GNbAC1 [30], MEDI-528 [31], tefibazumab [32], PAmAb [33], PRO95780 [34], siltuximab [35], and visilizumab [36]. Models with CLi or CLp were both fitted and compared in terms of parameter estimates and several other model performance criteria.
Simulations of 7E3 and 8C2 tissue concentrations were compared with experimental measurements to evaluate model performance. The areas under the concentration versus time curves (AUC0-t) were calculated using the NCA module in Phoenix 2.0 (Pharsight Corporation, Mountain View, CA) and compared for predictions vs observations.
Fittings utilized the maximum likelihood method in ADAPT 5 [37]. The variance model was:
| (9) |
where: Vi is the variance of the response at the ith time point, ti is the actual time at the ith time point, and Y(ti) is the predicted response at time ti from the model. Variance parameter intercept and slope were estimated together with system parameters.
Model performance was evaluated by goodness-of-fits, visual inspection, sum of square residuals, Akaike Information Criterion (AIC), Schwarz Criterion (SC), and Coefficient of Variation (CV) of the estimated parameters.
Results
General evaluation
Similar to the first-generation mPBPK model, this model uses plasma volume as initial distribution space as found in full PBPK models, which is supported by the fact that initially mAb only circulate in plasma without distribution into red blood cells [10, 11]. This assumption worked well in our examples showing less dependency on the timing and frequency of blood sampling than mammillary models. Specific values of the plasma volume should be considered with respect to species, gender, and age differences [38].
The critical difference of this model from our original mPBPK is in regard to extravascular distribution. This model accounts for specific distribution behaviors of mAb, such as convection as the primary extravasation mechanism. The reflection coefficients σ1 and σ2 being less than 1 make the extravasation rate no higher than total lymph flow (L). Another latent assumption is setting σ1 larger than σ2, as tight vascular endothelium is expected to have higher reflection than leakier vessels. Lymphatic capillaries are very porous with little restriction of antibody movement into lymph and, subsequently, σL is assigned as 0.2, a value that has been assumed in some full-PBPK models [10].
A separate lymph compartment is defined as in previous full-PBPK models. An important difference is that this model applies known or assumed lymph flow (L) and lymph volume (Vlymph) [24] rather than an empirical parameter τ to account for the delay of lymph drainage in recirculation of mAb back to plasma.
The transcapillary escape rate TER is the sum of two routes,
| (9) |
The concentration ratios at equilibrium between ISF and plasma can be calculated as,
| (10a,b) |
in Model A. In model B, the ratios are:
| (11a,b) |
7E3 PK in mice
The PK of 7E3 [10] in mice was analyzed based on the proposed mPBPK model. Only plasma data was used for the mPBPK fittings. The L and ISF volumes used in the model are listed in Table 1. As the lymph flow in mice has been reported to range 0.06 to 0.8 ml/hr for 18–31 g mice [24], we selected a midrange value of 0.12 ml/hr for a 20 g mouse. The Kp was assigned as 0.8 for 7E3 as for other IgG1 [22, 23]. The fitted profile is shown in Figure 2a and the parameters are summarized in Table 1. The model captured the observed PK profiles quite well with reasonable CV% of the estimated parameters. The original estimate of σ1 was close to 1 requiring an assigned value of 0.95 according to the estimation of σ1 for other antibodies (Table 2). Model B performed slightly better in capturing the profile (smaller Obj) than model A, but such a small difference is not conclusive regarding where the antibody is primarily cleared. The CLp is 0.499×10−5 L/hr, close to the estimate from Non-compartmental Analysis. In model B, the distributional rates L1·(1-σ1) and L2·(1-σ2) are 0.198×10−5 and 0.531×10−4 L/hr. Compared with CLi 0.666×10−5 L/hr, it is suggested that distribution rather than clearance is the rate-limiting step in tissues with tight endothelium, while in tissues with leaky endothelium, clearance appears to be the slower process. A simulation was performed based on Model B. As shown in Figure 2, the predictions of total tissue concentrations correlated well with experimental measurements [10]. The AUC ratios (observed / predicted) averaged 0.98 ± 0.89, suggesting reasonable estimates of σ1 and σ2. Model A predicted similar AUC ratios (1.01± 0.96). For clarification, the simulated total tissue concentrations include trapped plasma as originally reported. This also pertains to the next case study. As expected, leaky tissues have higher concentrations than tissues with tight endothelia, indicated by smaller values of σ1 than σ2. The Vleaky was predicted with about 13-fold higher leakage than Vtight (1-σ2 vs 1-σ1) for 7E3. The simulated concentrations of 7E3 in ISF are shown in Figure 2b, with earlier peaking and higher concentrations of 7E3 in Vleaky than in Vtight.
Figure 2.
A. Plasma and total tissue profiles of 7E3 in mice; B. Predicted interstitial fluid (Vleaky and Vtight) profiles based on estimates using only plasma data. Symbols are observations and curves are model fittings or predictions.
Table 2.
Pharmacokinetic parameters (CV%) for ten monoclonal antibodies in human subjectsa
| Model A: CL from plasma | Model B: CL from ISF | |||||||
|---|---|---|---|---|---|---|---|---|
| Compound | σ1 (−) | σ2 (−) | CLp (L/hr) | Objb | σ1 (−) | σ2 (−) | CLi (L/hr) | Obj |
| Adecatumumab | 0.883 (9.64) | 0.524 (7.37) | 0.0300 (3.19) | 6266 | 0.416 (44.8) | 0.296 (33.1) | 0.0318 (8.29) | 6238 |
| Mepolizumab | 0.950 (−)c | 0.750 (1.48) | 0.00851 (1.50) | 1327 | 0.950 (−) | 0.591 (1.96) | 0.0193 (2.44) | 938 |
| Gevokizumab | 0.931 (2.58) | 0.837 (2.63) | 0.00668 (1.87) | 309 | 0.757 (6.82) | 0.834 (4.67) | 0.0193 (4.53) | 322 |
| GNbAC1 | 0.915 (5.21) | 0.831 (5.71) | 0.00714 (2.93) | 1574 | 0.776 (15.2) | 0.787 (11.7) | 0.0189 (6.72) | 1381 |
| MEDI-528 | 0.987 (6.17) | 0.754 (7.00) | 0.00537 (6.88) | 2204 | 0.942 (10.9) | 0.735 (10.3) | 0.0182 (9.82) | 2214 |
| Tefibazumab | 0.902 (7.37) | 0.815 (7.56) | 0.00933 (4.19) | 60625 | 0.644 (23.8) | 0.819 (14.0) | 0.0215 (8.25) | 59439 |
| PAmAb | 0.950 (−) | 0.779 (5.24) | 0.00867 (2.29) | 68643 | 0.950 (−) | 0.621 (3.16) | 0.0224 (5.29) | 52639 |
| PRO95780 | 0.984 (22.2) | 0.638 (19.4) | 0.0124 (18.3) | 25967 | 0.575 (48.4) | 0.702 (25.5) | 0.0189 (32.7) | 27601 |
| Siltuximab | 0.964 (10.3) | 0.673 (9.27) | 0.0115 (5.19) | 184681 | 0.950 (−) | 0.467 (6.41) | 0.0218 (8.25) | 179121 |
| Visilizumab | 0.949 (3.63) | 0.834 (5.44) | 0.0152 (3.02) | 0.419 | 0.567 (34.0) | 0.806 (17.1) | 0.0390 (6.93) | 0.433 |
Plasma volume (Vp) was assumed 2.6 L, the volume of ISF was assigned as 15.6 L, and total lymph flow (L) was assumed as 2.9 L/day at basal state for a 70 kg BW person;
Value of objective function in ADAPT-5;
Not applicable
8C2 PK in mice
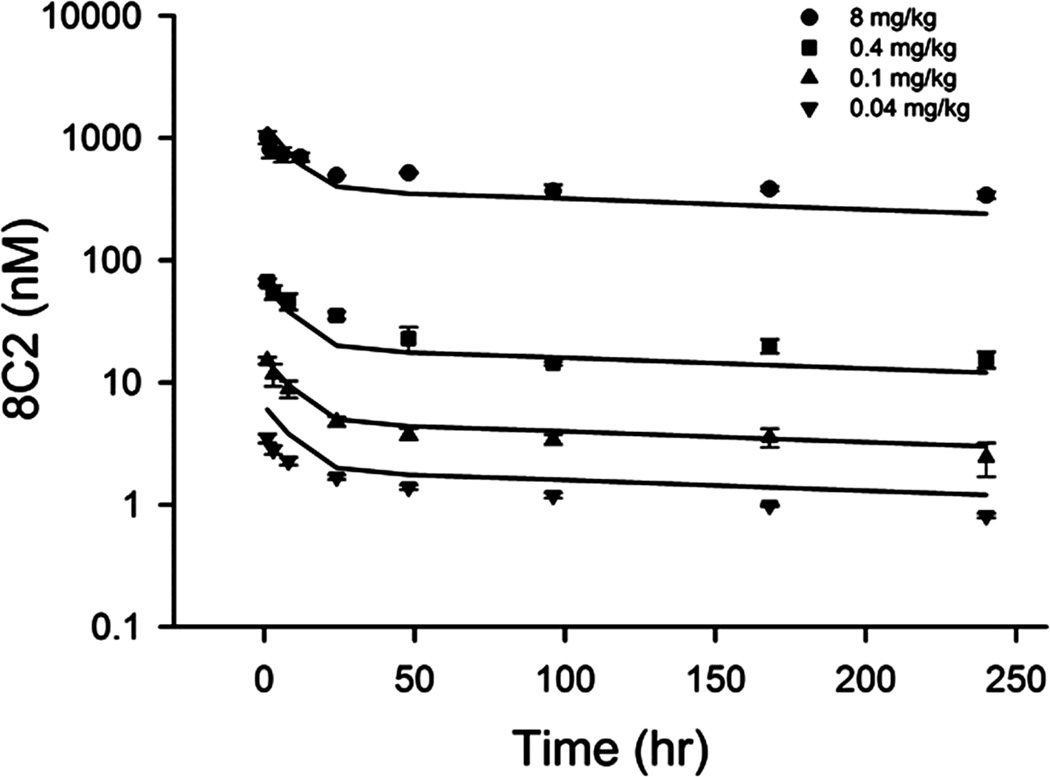
The PK of 8C2 in mice was reassessed [26]. Physiological and estimated parameters are listed in Table 1. Models A and B both captured the profiles well, but model B has a lower Obj. The CLp is 0.525×10−5 L/hr and CLi is 0.618 ×10−5 L/hr. The fittings and predictions from Model B are shown in Figures 3 and 4. The predicted tissue concentrations are consistent with measurements in the two types of tissues. The AUC ratios (observed / predicted) averaged 1.02 ± 0.81 for model B and 1.03 ± 0.84 for model A, suggesting reasonable estimations of σ1 and σ2. The Vleaky had about 8-fold higher concentrations of 8C2 than Vtight.
Figure 3.
Pharmacokinetic profiles of 8C2 in mice. Symbols are observations and curves are model fittings or predictions.
Figure 4.
Simulated tissue and interstitial fluid (Vleaky and Vtight) profiles of 8C2 in mice. The simulated tissue and interstitial fluid concentrations were for a dose of 8 mg/kg. Symbols are observations and curves are model fittings or predictions.
mAb PK in man
The PK profiles of 10 mAbs assessed in humans were found in the literature. Estimated parameters using Models A and B are listed in Table 3 showing reasonable CV% of all parameters. The fitted profiles using Model A are shown in Figure 5. The estimate of σ1 is in the range of 0.883 to 0.987 in Model A and the predicted Vtight concentrations are 1.6% to 14.6% of plasma concentration at equilibrium. The σ2 range is 0.524 to 0.837 with Vleaky concentrations of 20.4% to 59.5% of plasma. No significant correlation was found between values of σ1 and σ2. The estimate CLp varied among these mAbs from 0.0054 to 0.03 L/hr, of which adecatumumab had the highest CLp, corresponding to its 15 day shorter half-life [27]. Based on the Obj value, Model A showed better performance for the PK of 4 mAbs while Model B worked better for the remaining 6. However, the latent relationship of σ1 > σ2 should be another criteria to compare Models A and B. At this point, Model A would be more reasonable for tefibazumab and GNbAC1, even with a higher Obj than Model B.
Figure 5.
Pharmacokinetic profiles of 10 monoclonal antibodies in human subjects. Symbols are observations and curves are model fittings or predictions.
Discussion
Previously published full-PBPK models for mAbs utilize mass balance to include almost all tissues. This is imperative to consider all distribution spaces to allow assessment of target sites of mAbs for treatment of various diseases [3]. Full-PBPK models have become the gold standard of delineating all processes affecting mAb disposition. When only plasma (or blood) data are available, full-PBPK models with a diverse array of assigned parameters often allow accurate fitting or prediction of plasma and tissue concentration-time data, with few fitted parameters [10, 11, 39] or, in some cases, with no fitted parameters [40]. The mPBPK models provide a mathematically and computationally simpler alterative allowing fitting of only plasma data to generate physiologically-relevant parameters. Our ‘second-generation’ mPBPK model incorporates several essential determinants of mAb PK to reduce full-PBPK models and offers system-average evaluations of mAb disposition. These essential PK components include convection as the major extravasation mechanism and ISF as the primary distribution space. The ISF concentrations were found to differ among antibodies and in tissues in our estimations as well as in previous publications [41, 42]. This mPBPK approach provides antibody-specific and tissue-average predictions of ISF distribution. Concentrations of two mAbs in two sets of tissues of mice were used to partially validate this modeling approach. If a full PBPK model is not selected, then this mPBPK model may be preferable to the commonly used 2CM which fails to incorporate key elements and may be mechanistically inappropriate for mAb PK analysis.
This mPBPK model divides tissues into two groups according to their vascular endothelium structures giving predictions of ISF concentrations in the two types of tissues [20]. Many mAb targets are known to be located in ISF but directly measuring mAb in ISF is an experimental challenge [43]. A PK model that can appropriately predict ISF concentrations would be helpful. The ‘second-generation’ mPBPK model considers ISF as an important component and provides direct predictions of mAb concentrations in ISF of two types of tissues by fitting plasma data. As indicated for 7E3 and 8C2, this mPBPK model may reasonably approximate total mAb concentrations in tissues. Here we did not make direct comparison of predicted and measured ISF concentrations because the measured ISF concentrations of the two antibodies are not available.
One question needs to be addressed in characterization of mAb PK: TER. The TER is often determined by the Initial Decline Rate (IDR) of plasma curves [12] but a more accurate relation should be: IDR = TER + CLp (if existent). For the mAbs in our analysis, CLp was five to ten-fold less than TER and therefore the IDR was largely defined by TER. In model B, no CLp is applied and TER equals IDR. These relations rely on the fact that at very early times post IV dosing, the extravascular mAb that is recycled back to the systemic circulation is negligible because of the delay caused by the slow transport of mAb in lymph. This makes the IDR mostly dependent on TER with an insignificant influence by the recycling process.
This mPBPK model makes a prior definition of distribution fraction Kp, of which Kp = 0.8 for native IgG1 and 0.4 for native IgG4, meaning only part of ISF is accessible for mAb distribution [22, 23]. The exclusion fraction (1-Kp) of mAb in ISF is generally influenced by two factors: size and charge [44]. The slightly negatively charged ISF matrix makes IgG4 less distributable than IgG1 due to the lower isoelectric point (pI) of IgG4 (6.6) than IgG1 (8.7) [45]. It has been experimentally shown that an increase in net positive charge could result in increased tissue distribution and increased systemic clearance [45]. The ISF distributable fractions vary among tissues and mAbs, and even probably across species. This mPBPK model utilizes an average Kp as a simple starting point, but more investigation is warranted regarding the tissue- and mAb- differences of the distributable fractions.
Only three parameters (σ1, σ2, and CLp or CLi) need to be estimated in this mPBPK model. Vascular reflection coefficients (σ1 and σ2) are parameters that not only reflect TER but also predict the extent of distribution. Given the low value of σL, concentration ratios at equilibrium between ISF and plasma are primarily determined by σ1 and σ2 as in Eq. (10–11). Therefore, a high extravasation rate would produce greater distribution of mAb in ISF. In model B, this relation is also associated with L and CLi. At certain σ1 and σ2 values, high CLi would produce low concentrations in ISF. The two types of tissues display distinct profiles, where leaky tissues show earlier peaking and higher concentrations than tissues with tight vascular junctions.
Where are mAbs primarily eliminated from the system? This mPBPK model allows a comparison of models with clearances from either ISF or plasma and allows for assessment according to model performance and parameter estimation. Multiple elimination mechanisms have been elucidated for mAb [46], but which mechanism dominates the elimination for a specific mAb remains an unanswered question. Antigen-mediated elimination is often a significant pathway for many mAbs and the locality of antigen would likely indicate the major site of elimination. Our mPBPK modeling results compare major sites of elimination (Tables 1 and 2), which may offer hypotheses towards mAb disposition mechanisms. The major site of elimination may be selected based on fitting statistics. However, both models often performed similarly, as for mAb 7E3 and 8C2; in such cases, conclusions cannot be easily made based on just fitting plasma data.
In both full PBPK and our original mPBPK models, the assignment of plasma (or blood) volume as the initial distribution space worked well. The ‘second-generation’ mPBPK model retains this feature. This is especially important for mAb, as it reduces fitting dependency on the early sampling schedule but, more importantly, offers a better evaluation of distribution rates which is vital for mAb as the distribution rate is also closely related to the distribution extent as in Eq. (10–11). The endothelium endocytosis appears efficient [19, 47] allowing rapid uptake of mAb into endothelial endosomes and a quick ‘equilibrium’ between the endothelial endosome and plasma. This rapid uptake may lead to a higher apparent initial distribution volume than plasma. This influence may not be significant owing to the small volume of endothelial endosomes. Additionally, rapid endocytosis makes the subsequent lysosomal degradation operate similarly to clearance from plasma (CLp) rather than from extravascular space (CLi). The interpretation of CLp should not only include elimination from plasma but probably reflects degradation in endothelial lysosomes.
The role of FcRn has been well characterized in protection of IgG from lysosomal degradation. It has become a common strategy to modify FcRn binding affinity with the aim of either improving the plasma half-life of therapeutic mAbs or reducing the half-life of pathogenic antibodies [48]. The mPBPK model does not incorporate the endosomal compartment and thus may not reflect the functioning of FcRn, but it should be anticipated that improved affinity to FcRn would likely reduce estimates of CLp in this model. However, in contrast to several previous models [49, 50], interaction with FcRn would not be expected to affect mAb extravascular distribution in this model context. This is in line with observations that the tissue-to-plasma exposure ratios of mAb were not noticeably different between FcRn-knockout and wild-type mice in the majority of tissues examined [10], suggesting the limited impact of FcRn on mAb tissue distribution.
The parameters generated in mPBPK models have low dimensionality and ease of interpretation. The across-species scalability of those parameters in our original mPBPK model was demonstrated for one drug [2]. Whether this mPBPK model is useful for translation and can be used to predict clinical mAb PK from preclinical data requires further evaluation.
The application of the present mPBPK model is largely dependent on the stated assumptions. Some of them need more experimental evidence to validate further. This model may not be appropriate to characterize the PK of other macromolecules when diffusion is not negligible compared to convection for extravasation. As in full-PBPK models, plasma volume, lymph and ISF volumes, and lymph flow are taken from literature sources. These physiological components could be specified or serve as covariates for subjects with varying ages, sex, body weights, and disease status. Lymph flow is a process having high variation [24]; even the same person may have different lymph flows at basal or exercise states [51]. The lymph volume increases markedly in patients with edema [52]. All these factors should be carefully considered in applications of both this mPBPK and full PBPK models in various physiological or pathological states. The next step in application of this model will be the incorporation of site-related target-mediated disposition which is important for many mAbs.
The mPBPK manifests a ‘reductionist’ approach for analyzing mAb PK. The simple and physiological consideration of essential PK components in the mPBPK model provides general perspectives on the distributional and elimination features of mAb. However, the reductionist nature of the mPBPK would preclude its use in addressing some mAb PK problems, such as predicting mAb distribution in a specific tissue, assessing the role of FcRn binding affinities, and evaluating relative contributions of convection and diffusion. These specific questions would best be addressed using a full PBPK model which accommodates these elements.
In summary, the second-generation mPBPK model improves upon our original mPBPK model by inclusion of the major distributional characteristics of mAbs allowing for discernment of the two major groups of organs and tissues with ‘tight’ and ‘leaky’ vascular structures. The mPBPK model well anticipates actual tissue mAb concentrations measured in mice and were applied to human data sets with a range of doses and dosing conditions allowing for more certainty in model fitting than using single-dose profiles. This mPBPK model offers more realism in capturing mAb PK than compartment models and can serve an intermediary role when moving towards application of full PBPK models for mAbs.
Supplementary Material
Acknowledgments
The authors acknowledge Drs. Lubna Abuqayyas and Amit Garg for kindly sharing the original datasets of mAb 7E3 and 8C2. This research was supported by the National Institutes of Health Grant GM57980, the University at Buffalo - Pfizer Strategic Alliance, and the UB Center for Protein Therapeutics.
References
- 1.Rowland M, Peck C, Tucker G. Physiologically-based pharmacokinetics in drug development and regulatory science. Annu Rev Pharmacol Toxicol. 2011;51:45–73. doi: 10.1146/annurev-pharmtox-010510-100540. [DOI] [PubMed] [Google Scholar]
- 2.Cao Y, Jusko WJ. Applications of minimal physiologically-based pharmacokinetic models. J Pharmacokinet Pharmacodyn. 2012;39:711–723. doi: 10.1007/s10928-012-9280-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nelson AL, Dhimolea E, Reichert JM. Development trends for human monoclonal antibody therapeutics. Nat Rev Drug Discov. 2010;9:767–774. doi: 10.1038/nrd3229. [DOI] [PubMed] [Google Scholar]
- 4.Wang W, Wang EQ, Balthasar JP. Monoclonal antibody pharmacokinetics and pharmacodynamics. Clin Pharmacol Ther. 2008;84:548–558. doi: 10.1038/clpt.2008.170. [DOI] [PubMed] [Google Scholar]
- 5.Mould DR, Green B. Pharmacokinetics and pharmacodynamics of monoclonal antibodies: concepts and lessons for drug development. BioDrugs. 2010;24:23–39. doi: 10.2165/11530560-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 6.Weisman MH, Moreland LW, Furst DE, Weinblatt ME, Keystone EC, et al. Efficacy, pharmacokinetic, and safety assessment of adalimumab, a fully human anti-tumor necrosis factor-alpha monoclonal antibody, in adults with rheumatoid arthritis receiving concomitant methotrexate: a pilot study. Clin Ther. 2003;25:1700–1721. doi: 10.1016/s0149-2918(03)80164-9. [DOI] [PubMed] [Google Scholar]
- 7.Xu Z, Bouman-Thio E, Comisar C, Frederick B, Van Hartingsveldt B, Marini JC, Davis HM, Zhou H. Pharmacokinetics, pharmacodynamics and safety of a human anti-IL-6 monoclonal antibody (sirukumab) in healthy subjects in a first-in-human study. Br J Clin Pharmacol. 2011;72:270–281. doi: 10.1111/j.1365-2125.2011.03964.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Baxter LT, Zhu H, Mackensen DG, Jain RK. Physiologically based pharmacokinetic model for specific and nonspecific monoclonal antibodies and fragments in normal tissues and human tumor xenografts in nude mice. Cancer Res. 1994;54:1517–1528. [PubMed] [Google Scholar]
- 9.Lammerts van Bueren JJ, Bleeker WK, Bogh HO, Houtkamp M, Schuurman J, van de Winkel JG, Parren PW. Effect of target dynamics on pharmacokinetics of a novel therapeutic antibody against the epidermal growth factor receptor: implications for the mechanisms of action. Cancer Res. 2006;66:7630–7638. doi: 10.1158/0008-5472.CAN-05-4010. [DOI] [PubMed] [Google Scholar]
- 10.Garg A, Balthasar JP. Physiologically-based pharmacokinetic (PBPK) model to predict IgG tissue kinetics in wild-type and FcRn-knockout mice. J Pharmacokinet Pharmacodyn. 2007;34:687–709. doi: 10.1007/s10928-007-9065-1. [DOI] [PubMed] [Google Scholar]
- 11.Shah DK, Betts AM. Towards a platform PBPK model to characterize the plasma and tissue disposition of monoclonal antibodies in preclinical species and human. J Pharmacokinet Pharmacodyn. 2012;39:67–86. doi: 10.1007/s10928-011-9232-2. [DOI] [PubMed] [Google Scholar]
- 12.Rossing N. Intra- and extravascular distribution of albumin and immunoglobulin in man. Lymphology. 1978;11:138–142. [PubMed] [Google Scholar]
- 13.Flessner MF, Lofthouse J, Zakariael R. In vivo diffusion of immunoglobulin G in muscle: effects of binding, solute exclusion, and lymphatic removal. Am J Physiol. 1997;273:H2783–H2793. doi: 10.1152/ajpheart.1997.273.6.H2783. [DOI] [PubMed] [Google Scholar]
- 14.Baxter LT, Jain RK. Transport of fluid and macromolecules in tumors. I. Role of interstitial pressure and convection. Microvasc Res. 1989;37:77–104. doi: 10.1016/0026-2862(89)90074-5. [DOI] [PubMed] [Google Scholar]
- 15.Ferl GZ, Wu AM, Distefano JJ., 3rd A predictive model of therapeutic monoclonal antibody dynamics and regulation by the neonatal Fc receptor (FcRn) Ann Biomed Eng. 2005;33:1640–1652. doi: 10.1007/s10439-005-7410-3. [DOI] [PubMed] [Google Scholar]
- 16.Augustin HG, Kozian DH, Johnson RC. Differentiation of endothelial cells: analysis of the constitutive and activated endothelial cell phenotypes. Bioessays. 1994;16:901–906. doi: 10.1002/bies.950161208. [DOI] [PubMed] [Google Scholar]
- 17.Parton RG, Schrotz P, Bucci C, Gruenberg J. Plasticity of early endosomes. J Cell Sci. 1992;103(Pt 2):335–348. doi: 10.1242/jcs.103.2.335. [DOI] [PubMed] [Google Scholar]
- 18.Griffiths G, Back R, Marsh M. A quantitative analysis of the endocytic pathway in baby hamster kidney cells. J Cell Biol. 1989;109:2703–2720. doi: 10.1083/jcb.109.6.2703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chen Y, Balthasar JP. Evaluation of a catenary PBPK model for predicting the in vivo disposition of mAbs engineered for high-affinity binding to FcRn. AAPS J. 2012;14:850–859. doi: 10.1208/s12248-012-9395-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sarin H. Physiologic upper limits of pore size of different blood capillary types and another perspective on the dual pore theory of microvascular permeability. J Angiogenes Res. 2010;2:14. doi: 10.1186/2040-2384-2-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Warren MF. The lymphatic system. Annul Rev Physiol. 1940;2:109–124. [Google Scholar]
- 22.Wiig H, Tenstad O. Interstitial exclusion of positively and negatively charged IgG in rat skin and muscle. Am J Physiol Heart Circ Physiol. 2001;280:H1505–H1512. doi: 10.1152/ajpheart.2001.280.4.H1505. [DOI] [PubMed] [Google Scholar]
- 23.Wiig H, Kaysen GA, al-Bander HA, De Carlo M, Sibley L, Renkin EM. Interstitial exclusion of IgG in rat tissues estimated by continuous infusion. Am J Physiol. 1994;266:H212–H219. doi: 10.1152/ajpheart.1994.266.1.H212. [DOI] [PubMed] [Google Scholar]
- 24.Lindena J, Kupper W, Trautschold I. Catalytic enzyme activity concentration in thoracic duct, liver, and intestinal lymph of the dog the rabbit, the rat and the mouse Approach to a quantitative diagnostic enzymology, II Communication. J Clin Chem Clin Biochem. 1986;24:19–33. doi: 10.1515/cclm.1986.24.1.19. [DOI] [PubMed] [Google Scholar]
- 25.Stucker O, Pons-himbert C, Laemmel E. Towards a better understanding of lymph circulation. Phlebolymphology. 2008;15:31–36. [Google Scholar]
- 26.Abuqayyas L, Balthasar JP. Application of knockout mouse models to investigate the influence of FcgammaR on the tissue distribution and elimination of 8C2, a murine IgG1 monoclonal antibody. Int J Pharm. 2012;439:8–16. doi: 10.1016/j.ijpharm.2012.09.042. [DOI] [PubMed] [Google Scholar]
- 27.Oberneder R, Weckermann D, Ebner B, Quadt C, Kirchinger P, Raum T, Locher M, Prang N, Baeuerle PA, Leo E. A phase I study with adecatumumab, a human antibody directed against epithelial cell adhesion molecule, in hormone refractory prostate cancer patients. Eur J Cancer. 2006;42:2530–2538. doi: 10.1016/j.ejca.2006.05.029. [DOI] [PubMed] [Google Scholar]
- 28.Smith DA, Minthorn EA, Beerahee M. Pharmacokinetics and pharmacodynamics of mepolizumab, an anti-interleukin-5 monoclonal antibody. Clin Pharmacokinet. 2011;50:215–227. doi: 10.2165/11584340-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 29.Cavelti-Weder C, Babians-Brunner A, Keller C, Stahel MA, Kurz-Levin M, Zayed H, Solinger AM, Mandrup-Poulsen T, Dinarello CA, Donath MY. Effects of gevokizumab on glycemia and inflammatory markers in type 2 diabetes. Diabetes Care. 2012;35:1654–1662. doi: 10.2337/dc11-2219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Curtin F, Lang AB, Perron H, Laumonier M, Vidal V, Porchet HC, Hartung HP. GNbAC1, a humanized monoclonal antibody against the envelope protein of Multiple Sclerosis-associated endogenous retrovirus: a first-in-humans randomized clinical study. Clin Ther. 2012;34:2268–2278. doi: 10.1016/j.clinthera.2012.11.006. [DOI] [PubMed] [Google Scholar]
- 31.White B, Leon F, White W, Robbie G. Two first-in-human, open-label, phase I dose-escalation safety trials of MEDI-528, a monoclonal antibody against interleukin-9, in healthy adult volunteers. Clin Ther. 2009;31:728–740. doi: 10.1016/j.clinthera.2009.04.019. [DOI] [PubMed] [Google Scholar]
- 32.Hetherington S, Texter M, Wenzel E, Patti JM, Reynolds L, Shamp T, Swan S. Phase I dose escalation study to evaluate the safety and pharmacokinetic profile of tefibazumab in subjects with end-stage renal disease requiring hemodialysis. Antimicrob Agents Chemother. 2006;50:3499–3500. doi: 10.1128/AAC.00407-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Subramanian GM, Cronin PW, Poley G, Weinstein A, Stoughton SM, Zhong J, Ou Y, Zmuda JF, Osborn BL, Freimuth WW. A phase 1 study of PAmAb, a fully human monoclonal antibody against Bacillus anthracis protective antigen, in healthy volunteers. Clin Infect Dis. 2005;41:12–20. doi: 10.1086/430708. [DOI] [PubMed] [Google Scholar]
- 34.Camidge DR, Herbst RS, Gordon MS, Eckhardt SG, Kurzrock R, Durbin B, Ing J, Tohnya TM, Sager J, Ashkenazi A, et al. A phase I safety and pharmacokinetic study of the death receptor 5 agonistic antibody PRO95780 in patients with advanced malignancies. Clin Cancer Res. 2010;16:1256–1263. doi: 10.1158/1078-0432.CCR-09-1267. [DOI] [PubMed] [Google Scholar]
- 35.Puchalski T, Prabhakar U, Jiao Q, Berns B, Davis HM. Pharmacokinetic and pharmacodynamic modeling of an anti-interleukin-6 chimeric monoclonal antibody (siltuximab) in patients with metastatic renal cell carcinoma. Clin Cancer Res. 2010;16:1652–1661. doi: 10.1158/1078-0432.CCR-09-2581. [DOI] [PubMed] [Google Scholar]
- 36.Carpenter PA, Appelbaum FR, Corey L, Deeg HJ, Doney K, Gooley T, Krueger J, Martin P, Pavlovic S, Sanders J, et al. A humanized non-FcR-binding anti-CD3 antibody, visilizumab, for treatment of steroid-refractory acute graft-versus-host disease. Blood. 2002;99:2712–2719. doi: 10.1182/blood.v99.8.2712. [DOI] [PubMed] [Google Scholar]
- 37.D’Argenio DZ, Schumitzky A. ADAPT V User’s Guide: Pharmacokinetic/Pharmacodynamic System Analysis Software, Biomedical Simulations Resource. Los Angeles, CA: 2009. [Google Scholar]
- 38.ICRP Publication 89. Basic anatomical and physiological data for use in radiological protection: reference values A report of age- and gender-related differences in the anatomical and physiological characteristics of reference individuals. ICRP Publication 89 Ann ICRP. 2002;32(3–4):5–265. [PubMed] [Google Scholar]
- 39.Urva SR, Yang VC, Balthasar JP. Physiologically based pharmacokinetic model for T84.66: a monoclonal anti-CEA antibody. J Pharm Sci. 2010;99:1582–1600. doi: 10.1002/jps.21918. [DOI] [PubMed] [Google Scholar]
- 40.Abuqayyas L, Balthasar JP. Application of PBPK modeling to predict monoclonal antibody disposition in plasma and tissues in mouse models of human colorectal cancer. J Pharmacokinet Pharmacodyn. 2012;39:683–710. doi: 10.1007/s10928-012-9279-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hart TK, Cook RM, Zia-Amirhosseini P, Minthorn E, Sellers TS, Maleeff BE, Eustis S, Schwartz LW, Tsui P, Appelbaum ER, et al. Preclinical efficacy and safety of mepolizumab (SB-240563), a humanized monoclonal antibody to IL-5, in cynomolgus monkeys. J Allergy Clin Immunol. 2001;108:250–257. doi: 10.1067/mai.2001.116576. [DOI] [PubMed] [Google Scholar]
- 42.Choy EH, Connolly DJ, Rapson N, Jeal S, Brown JC, Kingsley GH, Panayi GS, Johnston JM. Pharmacokinetic, pharmacodynamic and clinical effects of a humanized IgG1 anti-CD4 monoclonal antibody in the peripheral blood and synovial fluid of rheumatoid arthritis patients. Rheumatology (Oxford) 2000;39:1139–1146. doi: 10.1093/rheumatology/39.10.1139. [DOI] [PubMed] [Google Scholar]
- 43.Tabrizi M, Bornstein GG, Suria H. Biodistribution mechanisms of therapeutic monoclonal antibodies in health and disease. AAPS J. 2010;12:33–43. doi: 10.1208/s12248-009-9157-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wiig H, Swartz MA. Interstitial fluid and lymph formation and transport: physiological regulation and roles in inflammation and cancer. Physiol Rev. 2012;92:1005–1060. doi: 10.1152/physrev.00037.2011. [DOI] [PubMed] [Google Scholar]
- 45.Boswell CA, Tesar DB, Mukhyala K, Theil FP, Fielder PJ, Khawli LA. Effects of charge on antibody tissue distribution and pharmacokinetics. Bioconjug Chem. 2010;21:2153–2163. doi: 10.1021/bc100261d. [DOI] [PubMed] [Google Scholar]
- 46.Tabrizi MA, Tseng CM, Roskos LK. Elimination mechanisms of therapeutic monoclonal antibodies. Drug Discov Today. 2006;11:81–88. doi: 10.1016/S1359-6446(05)03638-X. [DOI] [PubMed] [Google Scholar]
- 47.Davies PF, Ross R. Mediation of pinocytosis in cultured arterial smooth muscle and endothelial cells by platelet-derived growth factor. J Cell Biol. 1978;79:663–671. doi: 10.1083/jcb.79.3.663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Bordon Y. Antibody responses: FcRn-not just for the kids. Nat Rev Immunol. 2011;11:234–235. doi: 10.1038/nri2967. [DOI] [PubMed] [Google Scholar]
- 49.Xiao JJ. Pharmacokinetic models for FcRn-mediated IgG disposition. J Biomed Biotechnol. 2012;2012:282989. doi: 10.1155/2012/282989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jin F, Balthasar JP. Mechanisms of intravenous immunoglobulin action in immune thrombocytopenic purpura. Hum Immunol. 2005;66:403–410. doi: 10.1016/j.humimm.2005.01.029. [DOI] [PubMed] [Google Scholar]
- 51.Havas E, Parviainen T, Vuorela J, Toivanen J, Nikula T, Vihko V. Lymph flow dynamics in exercising human skeletal muscle as detected by scintography. J Physiol. 1997;504(Pt 1):233–239. doi: 10.1111/j.1469-7793.1997.233bf.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Aukland K. Distribution of body fluids: local mechanisms guarding interstitial fluid volume. J Physiol (Paris) 1984;79:395–400. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.