Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Nov 21;3:3291. doi: 10.1038/srep03291

Experimental demonstration of surface and bulk plasmon polaritons in hypergratings

Kandammathe Valiyaveedu Sreekanth 1, Antonio De Luca 2, Giuseppe Strangi 1,2,a
PMCID: PMC3836085  PMID: 24256947

Abstract

Hyperbolic metamaterials (HMMs) represent a novel class of fascinating anisotropic plasmonic materials, supporting highly confined bulk plasmon polaritons in addition to the surface plasmon polaritons. However, it is very challenging to tailor and excite those modes at optical frequencies using prism coupling technique because of the intrinsic difficulties to engineer non-traditional optical properties using artificial nanostructures and the unavailability of high refractive index prisms for matching the momentum between the incident light and the guided modes. Here, we experimentally demonstrate the excitation of both surface and bulk plasmon polaritons in a HMM through a grating coupling technique of surface plasmon excitation that makes use a hypergrating, which is a combined structure of metallic diffraction grating and HMM. Initially, we propose an optical hyperbolic metamaterial based on Au/TiO2 multilayers and confirm the hyperbolic dispersion, and the presence of high-k modes in the fabricated HMM. Reflection measurements as a function of incident angle and excitation wavelength show the existence of both surface and bulk plasmon polaritons inside the hypergrating. The proposed configuration is expected to find potential applications in bio-chemical sensors, integrated optics and optical sub-wavelength imaging.

In recent years, metamaterials research has received considerable attention among scientific community because of the fascinating scientific aspects and their important applications such as negative refraction, optical antennas, optical cloaking, super resolution imaging, ultra compact optical circuits, plasmonic nanolasers, etc1,2,3,4,5,6,7,8,9,10. Among optical metamaterials, hyperbolic metamaterials (HMMs) have emerged as one of the most important topic at optical frequencies and attracted great deal of attention due to their striking electromagnetic features accompanied by ease of nanofabrication and bulk three dimensional non-resonant responses with deep sub-wavelength unit cells11,12,13,14. A HMM is a non-magnetic extremely anisotropic artificial medium, that cannot be found in nature at optical frequencies having an open hyperboloid iso-frequency surface15,16,17,18,19. The interesting properties of hyperbolic metamaterials promise a large variety of potential applications such as negative refraction, spontaneous emission enhancement, biosensing, and nanoscale light confinement13,20,21,22,23,24,25,26,27,28.

Being characterized by hyperbolic dispersion, HMMs support surface plasmon polaritons (SPPs) as well as highly confined bulk plasmon polaritons (BPPs)29. A periodic metal/dielectric stack (HMM) supports the bulk plasmon modes, which are the entire family gap plasmon modes of multilayer29. BPPs are propagating waves inside the multilayer with an exponentially decay outside. The theoretical and numerical analyses of these modes in a multilayer have been previously investigated29,30,31,32,33,34. However, the experimental verification of their existence in a multilayer is extremely challenging because of the large optical loss due to very high modal indices and deep sub-wavelength confinement. Recently, Avrutsky et al. have reported the excitation of bulk plasmon modes in a multilayer made of silica/gold layers at infrared frequency using prism coupling technique29. However, it is very difficult to excite bulk plasmon modes at optical frequencies using a prism coupling technique because of the unavailability of high refractive index prisms for matching the momentum between the incident light and the guided modes. Here, we propose and fabricate a novel hypergrating configuration to design optical HMMs and experimentally demonstrate that it is possible to excite SPP and BPP modes at optical frequencies based on a grating coupling technique of surface plasmon excitation. Nanofabrication and nanophotonics strongly interplayed during the design and fabrication processes to create the artificial metal-dielectric superlattice with subwavelength layer thickness (almost λ/20), and to invent a proper hypergrating to couple and simultaneously probe SPP and BPP modes. In this context, hypergrating refers as a combined structure of metallic diffraction grating and HMM. Such types of structures were previously proposed for far-field sub-wavelength imaging35,36, but their experimental verification has not been reported hitherto. In the present work, we initially fabricate a HMM based on Au/TiO2 multilayers to experimentally confirm the hyperbolic dispersion and the presence of high-k modes inside the HMM. Then SPPs and BPPs are excited and probed up through the grating coupling technique, by fabricating a properly designed one-dimensional metallic diffraction grating on top of the HMM. Our proposed hypergrating configuration demonstrates an extraordinary potential to open new routes towards a wide range of breakthrough applications including bio-chemical sensing and optical sub-wavelength resolution imaging.

Results

Design and fabrication of the hypergrating

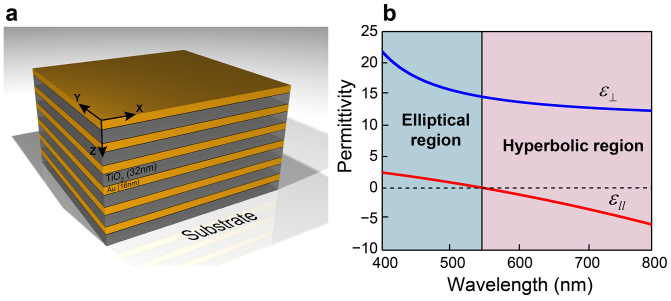
The schematic of the fabricated hyperbolic metamaterial structure is shown in Fig. 1(a), which consists of 12 alternating layers of gold (Au) and titanium dioxide (TiO2) thin films. The proposed HMM was fabricated by sequential deposition of TiO2 and Au on a glass substrate (see Methods). The measured thicknesses are 32 nm and 16 nm for TiO2 and Au, respectively. Hence the calculated fill fraction of metal is 33%. Since the fabricated HMM belongs to effective medium approximations, we used effective medium theory (see Supplementary information) to calculate the dielectric permittivity of the entire structure. Then, we performed spectroscopic ellipsometry measurements to confirm the dielectric tensor component (εll) in the parallel direction (XY plane). The simulated results are shown in Fig. 1(b), which show that the fabricated structure is a type II HMM with dielectric permittivity tensor components, εll(εx = εy) < 0 and ε⊥(εz) > 0, confirming the designed hyperbolic dispersion at optical frequencies, above 548 nm wavelength.

Figure 1. Characterization of hyperbolic metamaterial.

Figure 1

Open in a new tab

(a) Schematic diagram of fabricated hyperbolic metamaterial, which consists of 6 bilayers of Au/TiO2, (b) Real parts of effective permittivity of HMM determined with effective media theory. The permittivity tensor component in the parallel direction (XY plane) is determined and fitted using spectroscopic ellipsometry.

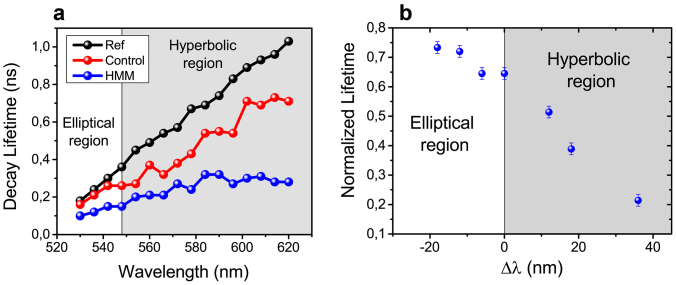
To evidence the existence of high-k modes in the fabricated HMM, we performed fluorescence lifetime measurements as a function of emission wavelengths using ultra-fast time correlated single photon counting (TCSPC) set-up (see Methods). Short-living excitonic states of the chromophores placed in close proximity to the metal-dielectric multilayers and measured in the hyperbolic band, would represent a clear signature of the presence of high-k modes. The studied HMM structure consists of a DCM dye (0.3% by wt. in ethanol solution) dissolved polymer (PMMA) layer of 100 nm thickness on top of the Au/TiO2 multilayer, separated by a TiO2 spacer layer of 10 nm thickness (see Supplementary Fig. S1). The maximum emission wavelength of DCM dye dissolved PMMA is observed at 620 nm for an excitation wavelength of 450 nm (see Supplementary Fig. S3). The fluorescence lifetime measurements of three samples such as reference sample (DCM on a TiO2/glass substrate), control sample (DCM on a 1bilayer of Au/TiO2) and HMM (DCM on the HMM) were performed and the results are shown in Fig. 2(a) (also see Supplementary Fig. S4). It is evident from Fig. 2(a) that there is a large variation in spontaneous emission lifetime of DCM onto the HMM compared to reference sample and control sample. This unusual behaviour is attributed to the existence of high-k modes as well as non-radiative and SPP modes present in the HMM12. Also, dye on reference sample and control sample show an increase in lifetimes with emission wavelengths; however lifetime of DCM onto HMM is almost constant in the hyperbolic region of the emission spectra. The coupling of the high-k metamaterial states is responsible for the observed shortest life times of HMM12. To further evidence that the high-k modes are responsible for the reduction of lifetime in the hyperbolic region, we calculated the normalized lifetime of dye on HMM with respect to reference sample. As shown in Fig. 2(b), a considerable reduction in normalized lifetime is observed in the hyperbolic region, i.e. when the wavelength crosses the transition wavelength. Note that in Fig. 2(b), the emission wavelengths are normalized with respect to transition wavelength (548 nm). We also verified the coupling of dye emission into the metamaterial states using steady-state photoluminescence measurements, observing a strong quenching in the emission in the case of HMM (see Supplementary Fig. S5). From the above observed properties, we confirmed that the fabricated Au/TiO2 multilayer is an optical hyperbolic metamaterial.

Figure 2. Photoluminescence measurements of hyperbolic metamaterial.

Figure 2

Open in a new tab

(a) Experimentally obtained spontaneous emission lifetimes of the DCM dye as a function of emission wavelengths on HMM, control and reference sample and (b) Lifetime of dye on HMM normalized with respect to reference sample. The emission wavelengths are normalized with respect to the transition wavelength (548 nm) with negative and positive regions respectively represent the elliptical and hyperbolic dispersion.

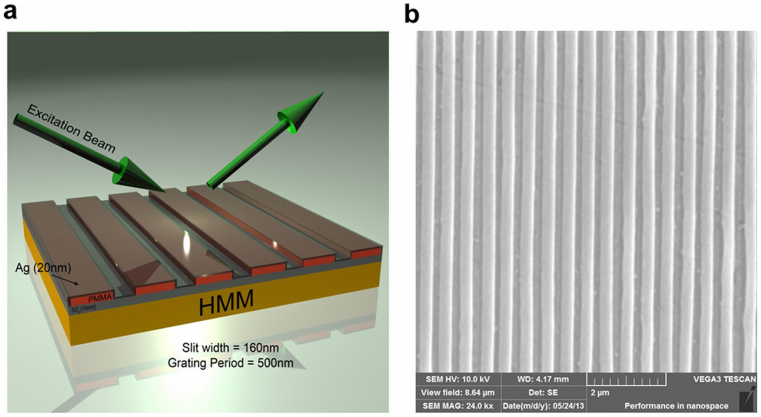
In order to excite both surface and bulk plasmon modes inside the HMM, we designed and fabricated a hypergrating structure as shown in Fig. 3(a). Hypergrating is a combined structure of one-dimensional (1D) metallic diffraction grating and HMM. We used Electron- beam lithography to pattern 1D grating lines on top of the HMM. Then we directly deposited a silver (Ag) layer of 20 nm thickness on the PMMA grating (see Methods). Ag has been selected as metal, because it is well known that it has a lower optical loss level compared to Au and hence it has higher plasmonic coupling efficiency. Note that there are no problems existing in evaporating Ag directly onto photoresist and we ensured that the over layer contamination is negligible. The SEM image of as prepared grating lines is shown in Fig. 3(b). From the image, it is clear that the Ag is uniformly distributed on the sample. Note that the total area successfully patterned on the HMM is around 5 mm × 5 mm. The fabricated gratings have an average period of 500 nm, average slit width of 160 nm and height around 120 nm. In order to avoid the direct contact of grating with HMM, a TiO2 spacer layer of 10 nm thickness is deposited between them.

Figure 3. Hypergrating geometry.

Figure 3

Open in a new tab

(a) Schematic diagram of fabricated hypergrating structure in reflection geometry and (b) SEM image of fabricated one-dimensional grating lines on top of the HMM with an average period of 500 nm and average slit width of 160 nm.

Excitation of surface and bulk plasmon polaritons

According to the grating coupling technique of surface plasmon excitation, the surface plasmon modes can be excited when the wavevector of the grating diffraction orders are greater than that of the incident light. Under this condition, diffraction orders are no longer propagating waves, but evanescent field and the enhanced wavevector of evanescent field is responsible for the coupling of incident light to the surface plasmon modes according to the coupling condition given by 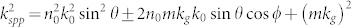Inline graphic. Being θ the incident grazing angle, ϕ is the azimuthal angle (the angle between the plane of incidence and the grating wavevector), n0 is the refractive index of incident medium, k0 = 2π/λ is the vacuum wavevector, m is the grating diffraction order and kg = 2π/Λ is the grating wavevector, with Λ the grating period. When ϕ = 0, kspp = n0k0 sinθ ± mkg. In all our experiments, the polarization of the beam is set to be p-polarization (TM) and ϕ = 0.

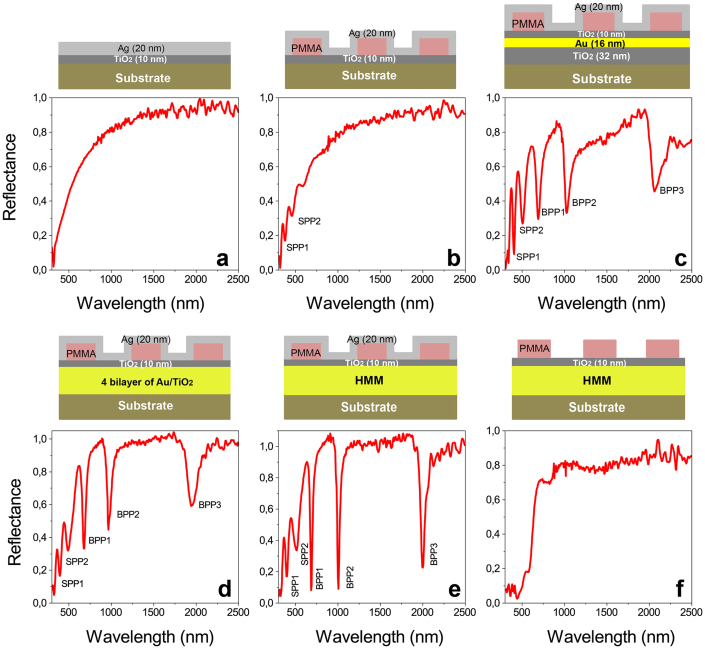
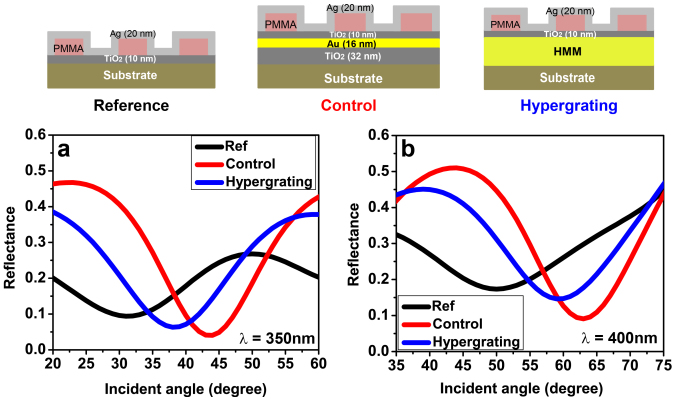
In order to strongly evidence our findings, six different samples have been fabricated and analyzed (see Supplementary Fig. S2). The reflectance spectra of these six samples as a function of excitation wavelengths are shown in Fig. 4. Here the incident grazing angle is set to be 50°. In order to compare the results, we first analyzed the reflectance spectrum of a uniform Ag layer (20 nm) on a TiO2/glass substrate (Fig. 4(a)) by using variable angle spectroscopic ellipsometry. As well known, no surface plasmon excitation is possible for this sample because there is no coupling. Then we studied the reflectance spectrum of a reference sample (Ag grating on a TiO2/glass substrate). Two reflectance minima are observed at visible wavelengths (from 350 nm to 450 nm), which shows the existence of SPPs in the sample (Fig. 4(b)). The reflectance spectrum of a control sample (Ag grating on a 1 bilayer of Au/TiO2) is measured and shown in Fig. 4(c). In contrast to Fig. 4(b), the control sample shows three extra reflectance minima at wavelengths such as 700 nm, 1000 nm and 2000 nm in addition to other two reflectance minima of SPP. These minima at higher wavelengths show the existence of gap plasmon (or bulk plasmon) modes in the control sample. Further, we studied the reflectance spectrum of another sample which consists of Ag grating on a 4 bilayers of Au/TiO2 and observed almost same behavior as that of control sample (Fig. 4(d)). However, both SPPs and bulk plasmon bands are slightly modified. Figure 4 (e) shows the reflectance spectrum of a hypergrating. According to Fig. 4(e), the reflectance minima at wavelength such as 700 nm, 1000 nm and 2000 nm are very narrow and deeper as compared to Fig. 4(c) & 4(d). This deepest narrow reflectance curves represent the existence of highly confined bulk plasmon polaritons (super modes) in the hypergrating. The reflectance minima for bulk plasmon modes are slightly shifted when the number of bilayers is increased from 1 to 6 and it is due to the coupling of individual gap plasmon modes. In order to further confirm the results, we analyzed the reflectance spectrum of a hypergrating without Ag layer on top of the grating and result is shown in Fig. 4(f). It is evident from the figure that no reflectance minima are obtained for the sample because there is no surface plasmon excitation, similar to Fig. 4(a). Moreover, transmission measurements of these samples at normal incidence are performed (see Supplementary Fig. S6). Also, reflection and transmission measurements of multilayer samples are performed (see Supplementary Fig. S7). By comparing these results with hypergrating results (Fig. 4(e)), it is clearly confirmed the existence of both surface modes and bulk plasmon supermodes in the fabricated hypergrating. Since both surface and bulk plasmon mode excitation depends on incident angle, we measured the reflectance of hypergrating for different angle of incidence (see Supplementary Fig. S8) by exploiting the very high sensitivity of the spectroscopic ellipsometer. We observed that there is a blue shift in reflectance minima for both surface and bulk plasmon modes when the incident angle is increased. This is attributed to the variation in modal indices (effective indices) of modes with incident angles37. However, the shift decreases when the excitation wavelengths decrease and the reflectance dip became deeper and narrow for higher incident angles. In order to validate the experimental results with theory, the dispersion relations of both SPP and BPP modes are investigated (see Supplementary information). The dispersion plot of SPP and BPP modes are shown in Fig. S10. It is clear from the figure that dispersions of both modes are well beyond the air light line and the wavevector of SPP modes are higher at shorter wavelengths (below λ = 440 nm). However, the wavevector of BPP modes are higher than that of SPP modes at higher wavelengths. Hence, it is confirmed from the Fig. 4 that the experimentally observed reflectance minima at shorter wavelengths (350 to 450 nm) are due to SPP modes and at higher wavelengths (700 nm, 1000 nm and 2000 nm) are due to BPP modes.

Figure 4. Reflectance spectra as a function of excitation wavelengths.

Figure 4

Open in a new tab

Studied structure is shown above each graph: (a) Uniform Ag layer of 20 nm thickness on a TiO2/glass substrate, (b) Reference sample (Ag grating on a TiO2/glass substrate), (c) Control sample (Ag grating on a 1 bilayer of Au/TiO2), (d) Ag grating on a 4 bilayers of Au/TiO2, (e) Hypergrating (Ag grating on a 6 bilayers of Au/TiO2), and (f) hypergrating without Ag layer on top of the grating. (a)–(f) Incident grazing angle is taken to be 50°. In figures (b)–(e), SPP and BPP respectively represent the surface plasmon polaritons and bulk plasmon polaritons.

As mentioned before, bulk plasmon modes represent the entire family gap plasmon modes of a multilayer. More specifically, gap plasmon modes are the modes with symmetric field distribution across the dielectric layer surrounded by metals and large modal indices is possible by decreasing the dielectric layer thickness. The large modal indices represent the strong mode confinement and shorter propagation length. While bulk plasmon modes provide only short propagation length, it can provide strong mode confinement at nanoscale. The multilayer also supports surface plasmon modes at each metal/dielectric interface. Both modes can be experimentally probed by studying the reflectance spectra as a function of incident angle at a particular wavelength. The SPP excitation of samples such as reference, control and hypergrating is shown in Fig. 5. Here, the coupling angle (resonance angle) of all samples is increased when the wavelength of the excitation light is increased from 350 nm to 400 nm. According to the grating coupling technique, the modal index of the mode is given as, nmod al = ((λ/Λ) + n0 sinθ). Hence the experimentally calculated modal indices of the hypergrating for the wavelengths 350 nm and 400 nm are 1.315 and 1.66, respectively. Also, the theoretically calculated modal indices of the SPP modes for the wavelength region 300 nm to 400 nm are shown in Fig. S11a (see Supplementary information). It is evident from the figure that the SPP modal index increases with increasing wavelength for shorter wavelength region. It shows that the experimental results are well correlated with the theoretical results. In addition, the control and hypergrating samples show deeper, and narrow reflection minima as compared to reference sample because a multilayer structure also supports various plasmonic modes such as long- and short-range surface plasmons at each metal/dielectric interfaces29.

Figure 5. Excitation of surface plasmon polaritons for hypergrating, control sample and reference sample.

Figure 5

Open in a new tab

Excitation wavelength (a) λ = 350 nm, and (b) λ = 400 nm. The coupling angle of all samples increase with an increase of wavelength.

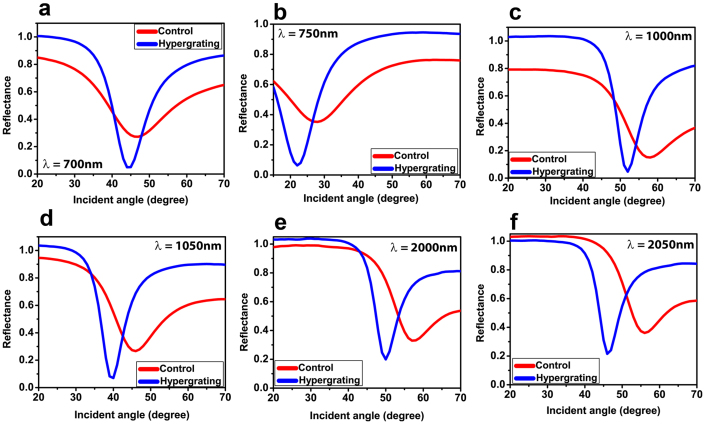
The excitation of bulk plasmon modes at different excitation wavelengths are shown in Fig. 6. We could not observe any reflectance minima for reference sample because there is no plasmon bands present at these wavelengths (Fig. 4(b)). We investigated the bulk plasmon mode excitation at three bulk plasmon bands such as 650 nm to750 nm, 1000 nm to 1100 nm and 2000 nm to 2100 nm. As shown in Fig. 6, very narrow and deep reflectance minima are obtained for hypergrating as compared to control sample. This shows the excitation of bulk plasmon modes in the hypergrating structure. The shift in coupling angle from control to hypergrating is higher at higher wavelengths. This large shift in coupling angle could be due to the strong mode confinement of bulk modes at higher wavelengths. Also, the decrease in resonance angle is observed when the excitation wavelength is increased in each bulk plasmon bands, which shows the decrease in modal indices of bulk modes with an increase of excitation wavelength (see Supplementary Fig. S9). The modal indices of BPP modes of three bulk plasmon bands are calculated and tabulated in Table 2 (see Supplementary Information). Then the modal indices of BPP modes are theoretically calculated and shown in Fig. S11b. From the theoretical and experimental data, it is confirmed that the modal index of BPP modes are decreasing with increasing wavelength for shorter wavelength band (650 nm to 750 nm and 1000 nm to 1100 nm). However, the modal index values are almost constant at higher wavelength band (2000 nm to 2100 nm). In particular, we obtained very large coupling angle shift for visible wavelength band (650 nm to 750 nm) as compared to higher wavelength band (2000 nm to 2100 nm). This large shift is due to the large modal index variation of BPP modes at shorter wavelength region. From the modal index analysis of BPP modes, it is found that the modal index of BPP modes increases when the wavelength range of the BPP band is increased from visible to near-infrared. Therefore, the modes at first BPP band (650 nm to 700 nm) represent the fundamental modes and modes at other two bands represent the higher order modes (i. e 1000 nm to 1100 nm is 1st order modes and 2000 nm to 2100 nm is 2nd order modes).

Figure 6. Excitation of bulk plasmon polaritons at three bulk plasmon bands for hypergrating and control sample.

Figure 6

Open in a new tab

Excitation wavelength (a) λ = 700 nm, (b) λ = 750 nm, (c) λ = 1000 nm, (d) λ = 1050 nm, (e) λ = 2000 nm and (f) λ = 2050 nm. There is a decrease in coupling angle when the excitation wavelength is increased in all considered plasmon bands.

Discussion

We designed, fabricated and characterized an optical hypergrating for the excitation of both surface and bulk plasmon modes in a hyperbolic metamaterial. Nanofabrication and nanophotonic techniques have been sinergically combined to create the designed metal-dielectric multilayer lattice coupled with a subwavelength silver grating to excite and probe SPP and BPP modes. The excitation of those tailored modes is experimentally demonstrated in a wide wavelength region from visible to near infrared using p-polarized light. The experimental results are then validated with theoretical results. HMMs are considered to be among the most promising optical metamaterials, since they represent a very advanced quantum nanophotonic system having unique opto-plasmonic features. Moreover, our results can be expected to find a multitude of applications from imaging and sensing to quantum optics. Recently, nanograting based SPR bio-chemical sensors have received an increasing attention due their advantages to effect the miniaturization and to make the size of the chips even smaller for commercial applications including antigen-antibody, protein, and chemicals detection38. The sensitivity of such sensors can be remarkably improved by using a hypergrating based sensor configuration. The proposed configuration can also be expected to find important applications in optical sub-wavelength resolution imaging in cancer research.

Methods

Sample preparation

HMM fabrication

Hyperbolic metamaterials were realized by sequential deposition of TiO2 and Au layers on a glass substrate (Micro slides from Corning) using RF sputtering technique (TiO2 target from Stanford Materials Corporation) and thermal evaporation of Au pellets (from Kurt J. Lesker Company), respectively. Variable Angle Spectroscopic Ellipsometry (J. A. Woollam Co., Inc, V-VASE) was used to measure the thicknesses of both layers. DCM dye (Mutagenic from Exciton) was initially dissolved in ethanol (0.3% by wt. in ethanol solution) and then the solution was mixed with PMMA resist (950 PMMA C2 Resist from MICROCHEM). As prepared DCM + PMMA solution was spin coated on the HMM sample at 5000 rpm, in order to get a thickness of around 100 nm. The thickness was measured using a Stylus Profilometer (KLA-Tencor P-6).

Hypergrating fabrication

One-dimensional gratings on top of the HMM was fabricated using Electron-beam lithography (Tescan Vega). Initially, MMA resist (8.5 MMA EL 11 from MICROCHEM) was spin coated on the sample at 4000 rpm and baked at 180°C for 5 min. After some time, PMMA resist (950 PMMA C2 Resist from MICROCHEM) was spin coated at 5000 rpm and baked at 180°C for 8 min. As prepared samples were patterned using e-beam lithography with dosage 150 μC/cm2 and beam intensity 6. The exposed samples were developed using MIBK: IPA solution for 90 s and IPA for 30 s. The developed samples were imaged using scanning electron microscope (SEM by Tescan Vega), confirming that the grating lines were exactly fitting the design. After that an Ag layer of 20 nm thickness was deposited directly on top of the sample using thermal evaporation of Ag pellets (from Kurt J. Lesker Company). As prepared samples were again imaged using SEM to see the uniformity of Ag layer on the gratings.

Experiments

Ellipsometry measurements

The effective permittivities of the samples were measured using a J. A. Woollam Co., Inc, V-VASE Ellipsometer and then the results were fitted using WVASE32 software.

Reflectivity and transmission measurements

The reflectivity spectra as a function of incident angle and excitation wavelengths were acquired using a J.A. Woollam Co. Inc V-VASE instrument with an angular resolution of 1° and wavelength spectroscopic resolution of 1 nm. The transmission measurements were performed using both J.A. Woollam Co. Inc V-VASE instrument and UV-Vis Spectrophotometer (Cary Series).

Lifetime and steady state photoluminescence measurements

Ultrafast optical set up has been used to measure the lifetimes of the samples. The optical set up consists of a Ti: Sapphire tunable femtosecond laser (Chameleon Ultra II from Coherent), Pulse Picker (by Coherent), Second Harmonic Generator (by Coherent), and a spectrofluorometer for time-correlated single photon counting (TCSPC) instrument (by Edinburgh instruments). The time resolution of the TCSPC instrument is ≤5 ps. In the experiments, the DCM dye was excited using a pulsed laser at 450 nm with a pulse width of about 140 fs and a repetition rate of 4 MHz. Here the emission wavelengths were varied using a monochromator that belongs to the TCSPC instrument. The same fluorometer was used to measure the steady state photoluminescence of the samples. The detection method was based on a reflection geometry in which dyes were excited using a mercury lamp and the emitted signals were detected using a last generation multichannel photomultiplier tube (MC-PMT).

Author Contributions

K.V.S. and G.S. conceived and designed the research. K.V.S. fabricated the samples. K.V.S. and A.D.L. performed the experiments and analyzed the data. K.V.S. carried out the numerical and theoretical simulations. All authors discussed the results and contributed in preparing the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep03291-s1.pdf (1.2MB, pdf)

Acknowledgments

We acknowledge support of the Ohio Third Frontier Project “Research Cluster on Surfaces in Advanced Materials (RC-SAM) at Case Western Reserve University”.

References

  1. Liu N. et al. Three-dimensional photonic metamaterials at optical frequencies. Nat. Mater. 7, 31–37 (2008). [DOI] [PubMed] [Google Scholar]
  2. Pendry J. B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 85, 3966–3969 (2000). [DOI] [PubMed] [Google Scholar]
  3. Shelby R. A., Smith D. R. & Schultz S. Experimental verification of a negative index of refraction. Science 292, 77–79 (2001). [DOI] [PubMed] [Google Scholar]
  4. Xiao S. et al. Loss-free and active optical negative-index metamaterials. Nature 466, 735–738 (2010). [DOI] [PubMed] [Google Scholar]
  5. Valentine J. et al. Three dimensional optical metamaterials with a negative refractive index. Nature 455, 376–379 (2008). [DOI] [PubMed] [Google Scholar]
  6. Novotny L. & van Hulst N. Antennas for light. Nat. Photon. 5, 83–90 (2011). [Google Scholar]
  7. Cai W., Chettiar U. K., Kildishev A. V. & Shalaev V. M. Optical cloaking with metamaterials. Nat. Photon. 1, 224–227 (2007). [Google Scholar]
  8. Lu D. & Liu Z. Hyperlenses and metalenses for far-field super-resolution imaging. Nat. Commun. 3, 1205 (2012). [DOI] [PubMed] [Google Scholar]
  9. Juan M. L., Righini M. & Quidant R. Plasmon nano-optical tweezers. Nat. Photon. 5, 349–356 (2011). [Google Scholar]
  10. Liu Z. et al. Far-Field Optical Hyperlens Magnifying Sub-Diffraction-Limited Objects. Science 315, 1686 (2007). [DOI] [PubMed] [Google Scholar]
  11. Hu H., Ji D., Zeng X., Liu K. & Gan Q. Rainbow trapping in hyperbolic metamaterial waveguide. Sci. Rep. 3, 1249; 10.1038/srep01249 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Krishnamoorthy H. N. S., Jacob Z., Narimanov E., Kretzschmar I. & Menon V. M. Topological transitions in metamaterials. Science 336, 205–209 (2012). [DOI] [PubMed] [Google Scholar]
  13. Hoffman A. J. et al. Negative refraction in semiconductor metamaterials. Nat. Mater. 6, 946–950 (2007). [DOI] [PubMed] [Google Scholar]
  14. Cortes C. L., Newman W., Molesky S. & Jacob Z. Quantum nanophotonics using hyperbolic metamaterials. J. Opt. 14, 063001 (2012). [Google Scholar]
  15. Smith D. R., Kolinko P. & Schurig D. Negative refraction in indefinite media. J. Opt. Soc. Am. B 21, 1032–1043 (2004). [Google Scholar]
  16. Noginov M. A. et al. Bulk photonic metamaterial with hyperbolic dispersion. Appl. Phys. Lett. 94, 151105 (2009). [Google Scholar]
  17. Biehs S. A. & Tschikin M. Hyperbolic metamaterials as an analog of a blackbody in the near field. Phys. Rev. Lett. 109, 104301 (2012). [DOI] [PubMed] [Google Scholar]
  18. Smith D. R. & Schurig D. Electromagnetic wave propagation in media with indefinite permittivity and permeability tensors. Phys. Rev. Lett. 90, 077405 (2003). [DOI] [PubMed] [Google Scholar]
  19. Smolyaninov I. I. & Narimanov E. E. Metric signature transitions in optical metamaterials. Phys. Rev. Lett. 105, 067402 (2010). [DOI] [PubMed] [Google Scholar]
  20. Jacob Z., Smolyaninov I. I. & Narimanov E. E. Broadband Purcell effect: Radiative decay engineering with metamaterials. Appl. Phys. Lett. 100, 181105 (2012). [Google Scholar]
  21. Govyadinov A. A. & Podolskiy V. A. Metamaterial photonic funnels for subdiffraction light compression and propagation. Phys. Rev. B 73, 155108 (2006). [Google Scholar]
  22. Kim J. et al. Improving the radiative decay rate for dye molecules with hyperbolic metamaterials. Opt. Exp. 20, 8100–8116 (2012). [DOI] [PubMed] [Google Scholar]
  23. Zhang S. et al. Negative refractive index in chiral metamaterials. Phys. Rev. Lett. 102, 023901 (2009). [DOI] [PubMed] [Google Scholar]
  24. Shalaginov M. Y. et al. Broadband enhancement of spontaneous emission from nitrogen-vacancy centers in nanodiamonds by hyperbolic metamaterials. Appl. Phys. Lett. 102, 173114 (2013). [Google Scholar]
  25. Tumkur T. U., Gu L., Kitur J. K., Narimanov E. E. & Noginov M. A. Control of absorption with hyperbolic metamaterials. Appl. Phys. Lett. 100, 161103 (2012). [Google Scholar]
  26. Kabashin A. V. et al. Plasmonic nanorod metamaterials for biosensing. Nat. Mater. 8, 867–71 (2009). [DOI] [PubMed] [Google Scholar]
  27. Hess O. et al. Active nanoplasmonic metamaterials. Nat. Mater. 11, 573–584 (2012). [DOI] [PubMed] [Google Scholar]
  28. Yang X., Yao J., Rho J., Yin X. & Zhang X. Experimental realization of three-dimensional indefinite cavities at the nanoscale with anomalous scaling laws. Nat. Photon. 6, 450–454 (2012). [Google Scholar]
  29. Avrutsky I., Salakhutdinov I., Elser J. & Podolskiy V. Highly confined optical modes in nanoscale metal-dielectric multilayers. Phys. Rev. B 75, 241402(R) (2007). [Google Scholar]
  30. Tanaka K. & Tanaka M. Simulations of nanometric optical circuits based on surface plasmon polariton gap waveguide. Appl. Phys. Lett. 82, 1158 (2003). [DOI] [PubMed] [Google Scholar]
  31. Alu A. & Engheta N. Optical nanotransmission lines: synthesis of planar left-handed metamaterials in the infrared and visible regimes. J. Opt. Soc. Am. B 23, 571–583 (2006). [Google Scholar]
  32. Avrutsky I., Soref R. & Buchwald W. Sub-wavelength plasmonic modes in a conductor-gap-dielectric system with a nanoscale gap. Opt. Exp. 18, 348–363 (2010). [DOI] [PubMed] [Google Scholar]
  33. Pile D. F. P. et al. Numerical analysis of coupled wedge plasmons in a structure of two metal wedges separated by a gap. J. Appl. Phys. 100, 013101 (2006). [Google Scholar]
  34. Chen J., Wang P., Zhang Z. M., Lu Y. & Ming H. Coupling between gap plasmon polariton and magnetic polariton in a metallic-dielectric multilayer structure. Phys. Rev. E 84, 026603 (2011). [DOI] [PubMed] [Google Scholar]
  35. Thongrattanasiri S. & Podolskiy V. A. Hypergratings: nanophotonics in planar anisotropic metamaterials. Opt. Lett. 34, 890–892 (2009). [DOI] [PubMed] [Google Scholar]
  36. Ni X. et al. Loss-compensated and active hyperbolic metamaterials. Opt. Exp. 19, 25242–25254 (2011). [DOI] [PubMed] [Google Scholar]
  37. Fan X., Wang G. P., Lee J. C. W. & Chan C. T. All-angle broadband negative refraction of metal waveguide arrays in the visible range: Theoretical analysis and numerical demonstration. Phys. Rev. Lett. 97, 073901 (2006). [DOI] [PubMed] [Google Scholar]
  38. Homola J. et al. Surface plasmon resonance sensors: review. Sensors and Actuators B: Chemical 54, 3–15 (1999). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep03291-s1.pdf (1.2MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES