Retinocollicular mapping explained?

Abstract

We review and comment on Grimbert & Cang’s (2012) model of the development of topographically ordered maps from the retina to the superior colliculus. This model posits a phase in which arbours are created in zones permitted by Eph and ephrin signalling, followed by a phase in which activity-dependent synaptic plasticity refines the map. We show that it is not possible to generate the arborization probability functions used in Grimbert & Cang’s simulations using gradients of Ephs and ephrins and the interaction mechanism that Grimbert & Cang propose in their results. Furthermore, the arborization probabilities we do generate are far less sharp than we imagine truly “permissive” ones would be. It remains to be seen if maps can be generated from the non-permissive arborization probabilities generated from gradients.

Commentary

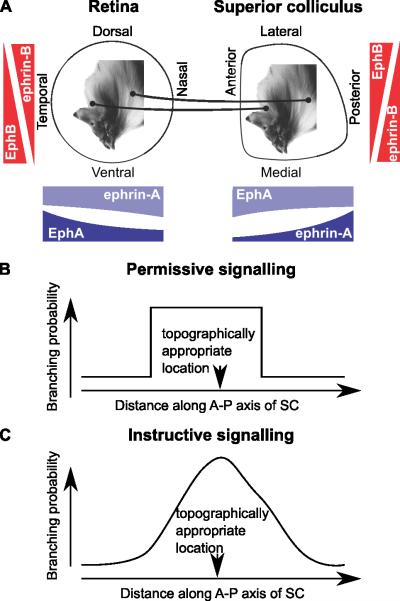
The extensive experimental and theoretical investigation of the development of topographically ordered maps from the retina to its targets (Figure 1A) has led to two important theories of map development: molecular signalling and activity-dependent synaptic plasticity (Goodhill & Xu, 2005). In theories of molecular signalling, retinal ganglion cell (RGC) growth cones bear receptors in different densities depending on the location of the RGC soma in the retina, and these receptors are activated by ligands expressed in cells in the superior colliculus (SC) at levels depending on their location. This confers on each RGC a preferred location in the SC, which, depending on the pattern of receptor and ligand expression, is not necessarily its correct topographical position. Activity-dependent synaptic plasticity of RGC-SC synapses along with correlated activity in the retina can also, in theory, lead to map formation, though extra cues are needed to ensure the orientation of the map is correct (Willshaw & von der Malsburg, 1976). In both theories other mechanisms, such as competition, may be required for a normal topographic map to form.

Figure 1. Retinocollicular mapping and permissive versus instructive molecular signalling.

A, Schematic diagram of retinocollicular mapping and forward and reverse gradients. Along the nasotemporal and anterior-posterior axes, the forward signalling system is made up of EphA in retina and ephrin-A in the superior colliculus (SC) and the reverse system comprises ephrin-A in the retina and EphA in the SC. The size of gradients is proportional to those used in the simulations shown in Figure 2. Along the retinal dorsoventral axis and the mediolateral axis of the SC EphB and ephrin-B make up the forward and reverse system; they are not modelled explicitly in Grimbert & Cang (2012), so the the gradients shown are purely schematic. B, Permissive cues restrict the region in which an axon can arborize, but do not favour any position within the permitted region. C, Instructive cues give the maximum arborization probability at the topographically appropriate location.

There is experimental evidence that both molecular signalling and activity-dependent synaptic plasticity are involved in map formation. In support of molecular signalling, the Eph and ephrin families of molecules are expressed in gradients along the axes of the retina and colliculus, and their disruption genetically leads to disrupted maps (Feldheim & O’Leary, 2010; Cang & Feldheim, 2013). In support of activity-dependent synaptic plasticity, correlated activity exists in the retina in the form of retinal waves, and its disruption leads to impaired map precision (Torborg & Feller, 2005). Thus the two theories are complementary and the questions centre around the exact form and role of each mechanism and how they interact.

Grimbert & Cang (2012) use a computational model to address the roles of activity-dependent synaptic plasticity and molecular signalling in the development of topographically ordered maps from the retina to the SC. In contrast to previous models where molecular signalling and activity act simultaneously (Whitelaw & Cowan, 1981; Fraser & Perkel, 1990; Triplett et al., 2011), in Grimbert & Cang’s model molecular signalling and activity act in two phases, similarly to Godfrey et al. (2009). (i) In the arborization phase, RGC arbors, represented as points, are placed on the SC according to a probability distribution determined by molecular signalling, assumed to be mediated by gradients of Ephs and ephrins. Grimbert & Cang explore the hypothesis that molecular signalling imparts permissive rather than instructive information. Permissive signalling restricts the space in the SC within which RGC axons are permitted to arborize, but within the allowed space axons have little or no preference for any one location (Figure 1B). In contrast, an instructive mechanism gives each RGC a preferred location in the SC that coincides with its topographically appropriate location in the final map (Figure 1C). After the arbors have been placed, those in the least favourable locations are pruned. (ii) In the dynamic phase, the arbors move around under the influence of spatially correlated neural activity and competition. The development of wild type (WT) maps is simulated in this model and, by manipulating the probability distribution representing molecular signalling information, the model can also produce maps resembling those found in the Isl2-EphA3 knock-in phenotype (Brown et al., 2000), the EphA7 KO phenotype (Rashid et al., 2005) and the p75NTR KO phenotype (Lim et al., 2008).

Grimbert & Cang focus on the nasotemporal to anterior-posterior projection; for dorsoventral to mediolateral mapping, they assume that axons enter the SC at approximately the correct mediolateral position. They model the forward and reverse signalling pathways by means of two arborization probability functions (Figure 2A,B) that, when multiplied together (Figure 2C), permit growth of each RGC in a region around its topographically appropriate location. However, Grimbert & Cang face the challenge of showing how known gradients of Ephs and ephrins can lead to this permissive signal. In the Results, they make the reasonable assumption that “permission to arborize is inversely proportional to both receptor and ligand concentrations”. Because measured concentration gradients are approximated by a constant plus an exponential (Reber et al., 2004), they deduce correctly that each arborization probability function should have a sigmoidal dependence on distance along the anterior-posterior axis. However, when we computed a probability to arborize that is inversely proportional to the gradients measured by Reber et al. (2004) we found that the dependence of the arborization probability on distance along the nasotemporal axis (Figure 2H) is far less sharp than in the functions used by Grimbert & Cang (Figure 2D). This problem might be alleviated by invoking cooperative binding between Ephs and ephrins which would sharpen the resulting probability distributions.

Figure 2. Arborization probabilities of axons from the retinal nasotemporal axis along the anterior-posterior axis of the SC.

A–D, The arborization probabilities plotted from equations in the Methods section of Grimbert & Cang (2012) and displayed in their Figure 2A–C. A, The forward arborization probability P_F, which restricts arborizations from temporal axons in the posterior SC. B, the reverse arborization probability P_R. C, the combined arborization probability P_A, which is the product of P_F and P_R. Note that each axon is permitted to arborize in a region around its topographically appropriate location. The filled and open circles indicate the locations in the SC of arborizations from nasal and temporal axons generated by sampling from P_A. There are seven points in total; in Grimbert & Cang’s simulations the arborizations with the four lowest values of P_A (open circles) would be pruned leaving the three arborizations with the highest values of P_A (filled circles). D, A nasotemporal slice of the forward arborization probability in A. E–H, Arborization probabilities computed by substituting plausible but unmatched gradients into the prescription in the Results section of Grimbert & Cang (2012). E, The forward arborization probability P_F= 1/R_F L_F, where R_F is the concentration of EphA receptor borne by an arbor and L_F is the concentration of ephrin-A ligand it encounters at a location in the SC. Gradients are R_F( x )= (1 .05+ 0. 26 exp( 2.3 x ))/1.05, where x= 0 is nasal and x= 1 is temporal (Reber et al., 2004), and L_F( y )= exp(2. 1( y− 1)), where y= 0 is anterior and y= 1 is posterior. F, the reverse arborization probability P_R and the concentrations R_R and L_R of ephrin-A and EphA are related similarly, with gradients R_R( x )= 1+ 1.7 exp(− x) and L_R( y )= 1+ 0.6 exp (− 2.6 y ) . G, the arborization probability computed from the product of P_F and P_R (E, F) and arborizations generated from the probability distribution as described in C. H, A nasotemporal slice of the plausible forward arborization probability, which is equal to 1/ R_F( x) . Code to reproduce this figure is available in the Supplemental Information.

Grimbert & Cang criticise, rightly in our view, the notion that gradients in the forward and reverse pathways need to be precisely matched to give an instructive mechanism in which each axon prefers to connect to its topographically appropriate location (Gierer, 1983; Yates et al., 2004). However the parameters of their arborization probability functions are such that the permitted area of any RGC is centred on its final location, which is analogous to having matching gradients.

To explore this, we put deliberately unmatched but plausible gradients into Grimbert & Cang’s prescription for the branching probabilities (Figure 2E,F). This resulted in a probability map (Figure 2G) that did not have a stripe along the correct map, and is akin to a Type II affinity mechanism (Prestige & Willshaw, 1975) which requires additional mechanisms for a map to form. Furthermore, the linear contours evident in their forward and reverse signalling functions (Figure 2A,B) are not found in the plots created by the product of inverse gradients (Figure 2E,F); it can be verified that the curved contours observed are a mathematical property of a product of sigmoids. It remains to be shown whether the second phase of development would be able to form a WT map from this starting point. With the branching probabilities formed by the product of the inverse gradients, for any location along the nasotemporal axis, the probability will be a scaled version of the same function along the anterior-posterior axis. Given Grimbert & Cang’s strategy for resampling rejected positions on the anterior-posterior axis, the scaled versions of the probability distribution should all give the same final distribution of positions, regardless of the RGC position. This is illustrated in Figure 2G, which shows, for one nasal and one temporal axon, arbor locations along the anterior-posterior axis generated by sampling randomly from the arborization distribution. The distributions overlap considerably along the anterior-posterior axis, in contrast to the distribution of points chosen using Grimbert & Cang’s arborization probability (Figure 2C).

In the dynamic phase, the molecular signalling is inactive and the arbor points move solely under the influence of correlated activity and competition. The correlated activity moves arbors towards the mean locations of arbors emanating from nearby locations on the retina. The competition causes arbors in areas of the SC with higher densities of arbors to move to areas containing lower densities (Fraser & Perkel, 1990; Simpson & Goodhill, 2011), which tends to smooth out the distribution over the colliculus. As demonstrated in the ephrin-A triple knock-out (TKO) simulations (Figure 6 in Grimbert & Cang), in which molecular signalling along the nasotemporal axis is abolished, the net effect of activity and competition is to create local order without global order. This type of order is obtained when chemical cues are removed in previous models with correlated activity and synaptic plasticity (Willshaw & von der Malsburg, 1976). In the WT simulations (Figure 4 in Grimbert & Cang), the activity and competition serve to refine the coarse mapping created by the gradients.

Grimbert & Cang go on to apply the model to the Isl2-EphA3 knock-in phenotypes (Brown et al., 2000). To do this, they modify the shape of the probability maps. In contrast to other models (Willshaw, 2006; Tsigankov & Koulakov, 2010), the new probability maps are not derived from the levels of EphA borne by the WT and Isl2 cells, but are “chosen for their simple convex shape”. With these modified probability maps, the authors get the model to produce double maps.

Leaving aside the justification for the changes in the branching probability distributions, the model makes an interesting prediction. Retrograde tracing with injections in the centre of the SC (Brown et al., 2000) show that nasal axons projecting there express Isl2-EphA3, but temporal ones do not. Grimbert & Cang’s model and other models are consistent with this finding. However, Grimbert & Cang’s model predicts that anterior injections will label both Isl2-EphA3⁺ and Isl2-EphA3⁻ RGCs. Other models (Tsigankov & Koulakov, 2010; Willshaw, 2006) predict otherwise. Brown et al. (2000) did not report anterior injections and so this prediction is yet to be tested.

The EphA7 knock-out (Rashid et al., 2005) is modelled by complete removal of the reverse signalling pathway. This is a stronger manipulation than in the phenotype, where there is still a gradient of EphA4 in the SC. Nevertheless, activity and competition are shown to be able to bunch together neurons at the anterior edge of the SC, in line with experimental results. It would be interesting to explore this mechanism in other models.

In order for Grimbert & Cang to reproduce the p75NTR KO phenotype, they reduce the inhibitory effect of the reverse signalling and also weaken the competition by 30%. The reduction in reverse signalling allows nasal axons to branch in inappropriate (anterior) parts of the SC. Were the competition to be at full strength, the map would be more ordered than the phenotype; the effect of weakening the competition is to reduce its ability to create order.

In summary, Grimbert & Cang argue that molecular signalling provides permissive rather than instructive cues and in their model, activity and competition can refine a crude initial map. They reason that models should not depend on precise matching of parameters, but their explanation of how molecular signalling gives rise to permissive cues that can be refined by activity does seem to depend on matching of parameter values. Their model proposes “an alternative to the usual view that retinotopic order is shaped through chemoaffinity while activity-dependent processes only serve to refine the map”. However in the WT, each RGC’s permissive region is centred on its topographically appropriate location; thus activity only needs to refine the projection. To offer a true alternative, and demonstrate how activity can remodel the map deeply, they need to apply their competition and activity mechanism to probability maps produced by non-matched chemical gradients which have not shaped the topography so strongly. In its favour, their model is applied to a wide range of experimental maps and provides a novel prediction that can be tested in Isl2-EphA3 mice.