Reorientation patterns in central-place foraging: internal clocks and klinokinesis

Abstract

We study central-place foraging patterns of Aphaenogaster senilis ants at a population level by video framing individual ant trajectories in a circular arena with a nest connected to its centre. The ants naturally leave and enter the nest and forage generating non-trivial movement patterns around the nest. Our data analysis indicated that the trajectories observed can be classified into two strategies: the risk-averse strategy, which involves wandering around the nest without departing far from it and the risk-prone strategy, which involves long exploration paths with periodic returns to the central region, nearby the nest. We found that both risk-prone and risk-averse strategies exhibit qualitatively the same reorientation patterns, with the time between consecutive reorientations covering a wide range of scales, and fitting a stretched exponential function. Nevertheless, differences in the temporal scales and the time variability of such reorientation events differ, together with other aspects of motion, such as average speed and turns. Our results give experimental evidence that the internal mechanisms driving reorientations in ants tend to favour frequently long relocations, as theory predicts for efficient exploration in patchy landscapes, but ants engaged in central-place foraging can modulate such behaviour to control distances from the nest. Previous works on the species support the idea that risk-prone and risk-averse strategies may reflect actual differences between individuals age and experience; these factors (age and experience) should be then relevant in modulating the internal reorientation clocks. To support the validity of our findings, we develop a random-walk model combining stretched exponential reorientation clocks with klinokinesis that fits the time length and the travelled distance distributions of the observed trajectories.

1. Introduction

Over the last years, interdisciplinary interest has grown in understanding the drivers of random (non-informed) search efficiency [1,2]. This is in part because random searches, albeit being an idealized process, can be empirically approached and represent a great opportunity to study the links between elementary aspects of animal sensory–motor mechanisms and movement patterns. In a pure random search, the organisms are assumed to look for targets without any prior knowledge (or just minimal) about their possible location, so the only way in which the target detection rate can be effectively enhanced is by avoiding ineffective or recurrent trajectories. This can be done either by introducing some level of systematicity in the process, e.g. by consciously avoiding already visited places, or by performing random search patterns which statistically operate in a similar fashion without requiring such explicit consciousness. Most theoretical works in this field have focused on the case where systematic components are precluded, so search trajectories can be adequately described through random walks or similar approaches. In such situations, an adequate balance between intensive search (in order to exhaustively explore particular areas) and relocation towards new unexplored areas represents the most convenient strategy to increase encounter rates, providing a justification for the intermittent (e.g. run and tumble) patterns of motion found in nature [3,4].

How information use, together with the internal states of organisms, can ultimately regulate the preferential use of intensive or extensive search is still an elusive question in ecology and psychology. The term reorientation clock [5–7] has been coined to suggest the existence of internal complex behavioural phenomena capable of adjusting the dynamics of the collection of times and positions at which reorientations do occur [5,8]. In particular, the existence of fractal clocks (i.e. multi-scale relocations separating consecutive reorientation events) could improve random search efficiency in heterogeneous landscapes [5,9–11], in consonance with the well-known Lévy flight foraging hypothesis [12,13]. This has been partially supported by observations where individuals tend to show a larger proportion of long reorientation interevents when resources are scarce and unpredictable compared with when resources are readily available (see [3,13,14]).

Though a large number of works have already explored the aforementioned points, very few of them have focused on the combined effects of random exploration and the presence of atractor points. Mechanistic home range models are considered convenient mathematical tools to interpret the paths of central-place foragers, where the random component of explorative movement is constrained or combined with other effects, e.g. landscape heterogeneities, presence of conspecifics or predators. This prevents the individuals from departing excessively from a central position [15]. A comprehensive review on these mechanistic approaches has been published recently [16]; models within this category include classical focal point attraction models [17,18] and those based on reaction–advection equations [19,20], intermittent motion [21–23] or reinforced random walks [24–28]. It is also important to mention the works on klinokinesis initiated in the late 1980s by Benhamou & Bovet [29–31], where they studied central-place foraging and home range emergence through the idea that animals adjust their sinuosity (defined as a measure of the ‘amount of turning’) as a function of their direction of motion. These authors have also discussed how such a kinesis mechanism could be distinguished from taxis or other directional behavioural phenomena [32,33].

The exploration of new or unfamiliar landscapes by ants represents an archetypal case where random search and central-place foraging must be taken together to understand the emerging dynamics of motion. Ant colonies, however, can be rarely studied in such terms because most searches in field conditions should be considered informed searches. Site or direction fidelity, guided by visual landmarks or other navigational cues, as well as cooperative behaviour driven by chemicals tend to dominate in ants. Those species which do not rely on cooperative strategies (e.g. in pheromone trails) for foraging, like several desert ants of the genera Cataglyphis [34,35], usually have very good navigational skills. It is thus difficult to get rid of both navigational skills and cooperative strategies in ants to study pure random exploration of space. As an interesting alternative, a recent work [36] with the desert ant Melophorus bagoti, has studied search patterns of individuals in field conditions by training individuals to a feeder over a period of several days and then putting them to test by removing the feeder and studying the corresponding trajectories. The probability distribution of reorientation interevents followed an exponential distribution, contrary to the results of other experiments for the same species where Lévy flights were observed [37,38]. While the differences between those cases remain unclear, it is suggested [36] that the use of path integration could be more intense under some situations than others, then preventing random search features from being dominant.

Then, pure random searches in ant colonies can only be systematically studied under laboratory conditions. In this work, we provide the results of experiments carried out with Aphaenogaster senilis ants. The ants were allowed to leave their nest and explore freely a circular homogeneous arena in order to look for a small feeder randomly placed in it. Visual landmarks and external cues were removed as much as possible in order to prevent the ants from exhibiting any directional preference or site fidelity. Then the conditions under which the experiments were conducted should make it possible to get approximately random search trajectories and the corresponding analysis should shed some light on how the internal states of the ants drive decision-making in such contexts.

2. Material and methods

2.1. Experiments

Aphaenogaster senilis is a western Mediterranean species [39] foraging from early spring until mid-autumn and at temperatures from 15°C to 30°C [40]. Their foraging distances lie in the range 0.3–6.3 m (mean: 1.68 m) [41,42]. A bimodal behavioural profile has been reported before [43], with older individuals engaged in foraging while younger workers do nest maintenance tasks, in agreement with the German categorization of Aussendiensttiere and Innendiensttiere.

A complete society (queen, brood and workers) of A. senilis was collected by excavation at the Universitat Autonoma de Barcelona campus and maintained in an artificial nest. Two groups of approximately 150 workers each were separated from the colony and housed in artificial nests together with abundant larvae in order to stimulate them for foraging. Such small groups were used in the experiments to reduce the number of foragers in the trials, and so the effects from antennae contact and chemical communication.

During the one month experimental period, every group of workers was allowed once a day to explore for 40 min a circular arena of 1 m radius (figure 1). The arena had a white uniform surface to facilitate video tracking, and it was bounded by plastic walls 5 cm high which were periodically greased with fine natural oil in order to prevent ants from escaping. The whole arena (from the sides and from above) was surrounded by a thick and dark curtain which prevented any outer source of light from being perceived within. The only source of light in the arena was then that provided by a group of eight fluorescent tubes forming a regular octagon, situated 1 m above the centre of the arena. In summary, the whole setting was prepared and designed to be symmetric if seen from the centre of the arena, so no directional landmarks existed (note that a very similar setting has been recently used to study pheromone trail formation in Argentine ants [44]).

Figure 1.

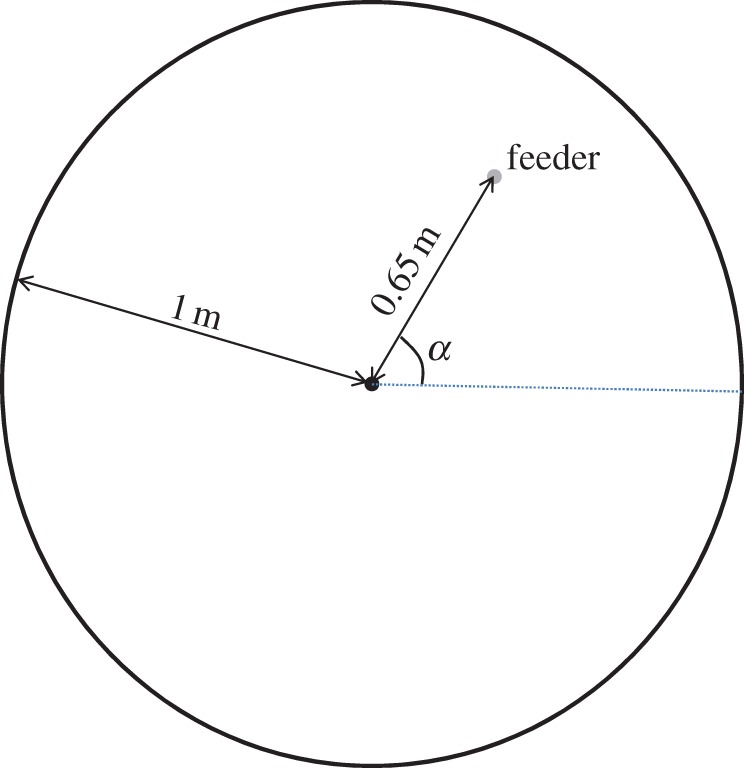
Scheme of the experimental setting used. (Online version in colour.)

All the trials were carried out during the spring 2012 in a dark room at an approximately constant temperature (about 25°C). The ants were allowed to leave the nest through a plastic tube (of approx. 1 cm diameter and 10 cm long) connected to the centre of the the arena from below. A small feeder was previously placed in the arena at a distance of 65 cm from the centre, while the exact angular direction α from the centre (figure 1) was randomly changed from one day to the next by using a standard random generator. Several food items (pieces of cookies and/or fresh mealworms) were offered each day to the ants. The items were small enough to allow a single individual to carry them out to the nest, while the total quantities of food offered each day to the ants were estimated to satisfy the nutritional requirements for the groups while keeping them stimulated for foraging. After each trial, the arena was thoroughly washed with water and ethanol to remove any traces of pheromones (which for A. senilis consist mostly of hydrocarbons and alkaloids [45,46]).

2.2. Data acquisition and analysis

For one week, the trials were used as a training period to let the ants get familiarized with the arena and the corresponding search task. Accordingly, these data were not used in our analysis. All the experiments, including the training period, were captured with a wide-lens digital video camera above the centre of the arena. The films obtained with this setting had a 1024 × 1280 resolution and a frequency of 15 frames per second (FPS).

We determined the first-detection time of each trial, i.e. the time lapsing from the start of the trial up to the instant at when any of the ants first finds the feeder. Given that A. senilis uses group recruitment for foraging [46,47]) all subsequent trajectories were discarded to prevent any effects from recruitment chemical signals. Note also that we cannot completely dismiss the possibility that, prior to the first-detection time, chemicals related to nest recognition are already present in the arena. The use of such recognition signals for A. senilis, however, has not been documented before in the literature.

Standard analysis [44,48] was used to extract the ant trajectories from the video frames. Each frame was converted into a binary map, and the position of the ant was then determined as the centre of mass of adjacent positive pixels. The encounter between two ants (so the regions they occupy are adjacent to each other or overlap) was solved by assuming [49] that after the encounter the two individuals tend to go on moving approximately in the same direction they had prior to it. Encounters among three or more ants were very rare, but in such a case they were treated in an analogous way.

A total of 36 films were analysed and three of them were discarded because of problems with the light or the camera. From the others, we obtained 2692 complete trajectories prior to first-detection (a trajectory is said to be complete if the ant starts moving outwards from an imaginary circle of radius 5 cm centred at the arena, and eventually comes back to it). To compute instantaneous speeds and turning angles, we reduced at practice the frame frequency to 5 FPS. We computed the instantaneous speed as the distance covered by the ant from one frame to the next, and the direction of motion as the angle between the corresponding displacement and the horizontal axis. Turning angles were then identified as the changes in the direction of motion from one frame to the next, and reorientations were defined as those turning angles that were larger than 1 radian. To justify this last criterion, we first computed the turning angle distribution which showed a decaying trend relating turn magnitudes with their probabilities, except for the large turn values whose probability remained small and constant regardless of the turn magnitudes (uniform distribution). We used a sequential pointwise model comparison based on Akaike information criteria (AIC) weights [5,14], comparing a negative exponential with a uniform distribution to determine the turning value at which the crossover between the two distributions or regime takes place. A uniform tail regime at the tail of the turning angle distribution may indicate the existence of reorientation behaviour that should be clearly distinguished from the more common, smaller turns owing to scanning [5]. We also tried to use threshold values values between 0.5 and 1.5 radians to define reorientations and our results did not change significantly.

3. Results

The times at which first-detection occurred varied considerably from one trial to another, with an average time of 4.66 min (s.d. = 2.63 min, with a minimum of 1.32 min and a maximum of 10.17 min). We did not observe any significant trend throughout the days, which seems to suggest that the experimental conditions did not change appreciably with time and that learning processes are non-existent or ineffectual. If anything, we observed a slight decrease in the mean time to first-detection together with a slight increase in the mean number of ants that left the nest throughout the first minutes of the trials (figure 2). All this together could indicate that during the 30 days over which the experiments were performed some juvenile ants probably became more experienced, and so joined the foraging tasks.

Figure 2.

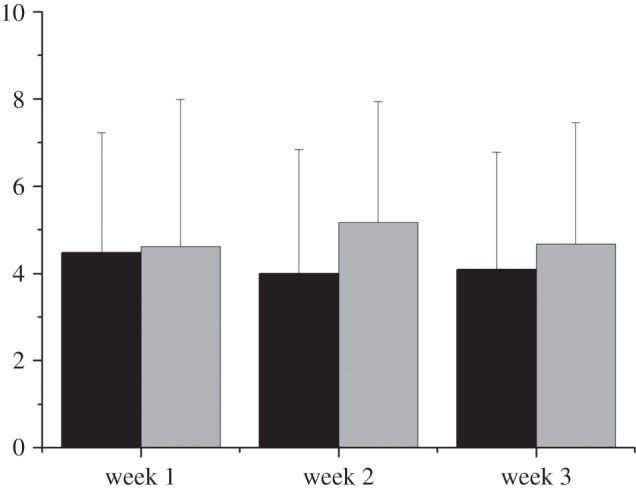
Mean time required by the ants to find for the first time the feeder (black bars) (ANOVA: F_2,20 = 0.031, p < 0.05) and mean number of ants present in the arena during the first 3 min of the trial (grey bars) (ANOVA: F_2,20 = 0.038, p < 0.05) throughout the three weeks during which the experiments were performed.

3.1. Bimodal population behaviour

From visual inspection, it can be inferred (see the electronic supplementary material) that ants in the arena exhibited two different patterns of motion. Most of the ants just meandered around the nest entrance without departing far from it (no more than 20–25 cm), doing seemingly circular paths around the centre for a while, and then coming back to it; we call this a risk-averse strategy. On the other hand, a few workers (presumably those experienced in foraging) were observed to cover larger distances, often reaching the walls of the arena in less than 1 min (in the following, this will be referred as a risk-prone strategy). Risk-prone trajectories, however, did not always depart from the nest but were observed to go back-and-forth to it, so that the ants reached and explored regions relatively close to the entrance but not necessarily going back to the nest.

To verify that this behaviour is not just a visual artefact, we computed, for each trajectory, the mean Euclidean distance to the centre of the arena, i.e. The frequency distribution of clearly illustrates the bimodal population behaviour. Figure 3 shows that the frequency distribution decays initially very fast (in a seemingly exponential way) but a change of tendency, denoting bimodality, occurs at values around 20–25 cm. We used a bilinear regression fit [50,51] to accurately estimate the crossover point between the two slopes (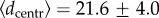 cm, with 95% CI).

Figure 3.

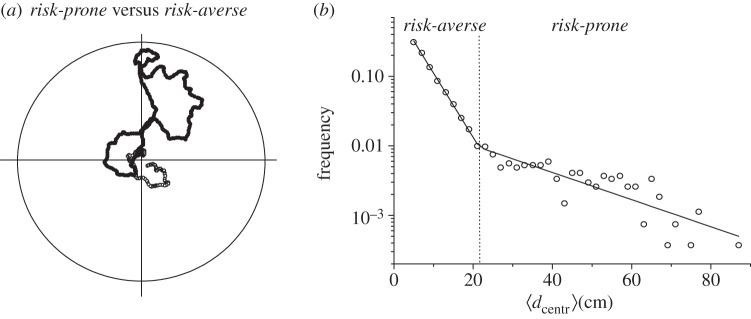
(a) Example of a risk-averse (open circles) and a risk-prone (full circles) trajectory. (b) Frequency distribution of the mean distance of each trajectory to the centre of the arena. A biexponential fit (solid line) allows us to distinguish the regions of risk-averse and risk-prone trajectories ().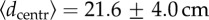

We stress that the nomenclature of risk-averse and risk-prone is used throughout the work to designate trajectories and/or strategies, but not individuals. As ants were not marked in our experiments, we cannot determine whether the two strategies observed corresponded to fixed personalities or behavioural plasticity, the latter reflecting different group requirements and/or environmental conditions.

We next tested whether the distinction between risk-prone and risk-averse strategies also involved changes in the patterns of motion and not only in the exploration distances covered by the individuals. We thus studied the speed and turning angle distributions of both types of trajectories. Note that risk-averse trajectories were much more frequent in number (they represent approx. 90% of the trajectories) but because risk-prone trajectories were on average six to eight times longer than that of the risk-averse the statistical significance of both types is practically the same.

The distribution of turning angles decayed initially rather fast (see Gaussian and exponential fits in figure 4 as a guide) but showed a seemingly uniform distribution for large angles (figure 4, inset). This behaviour is a clear signature that identifiable reorientation behaviour (different from scanning orientations [5,12,52]) exists. After these reorientation events, new directions of motion are uniformly distributed and directional persistence is lost [5]. Reorientations were slightly more frequent in the risk-averse strategy and, as a consequence, we also observed differences in turn angles, being the mean turn angle for the risk-averse strategy (0.46 rad) larger than that for the risk-prone strategy (0.41 rad). We also observed differences in the speed distributions (figure 4b), with a larger mean speed for the risk-prone strategy compared with the risk-averse strategy (34 versus 30 mm s⁻¹, respectively). The statistical significance of these results was tested by carrying out Kruskal–Wallis H tests, which provided clear evidence that the mean values for turning angles and speeds are statistically different in risk-prone and risk-averse trajectories (turning angles: H = 305.6, p < 0.001; speed: H = 6645.3, p < 0.001).

Figure 4.

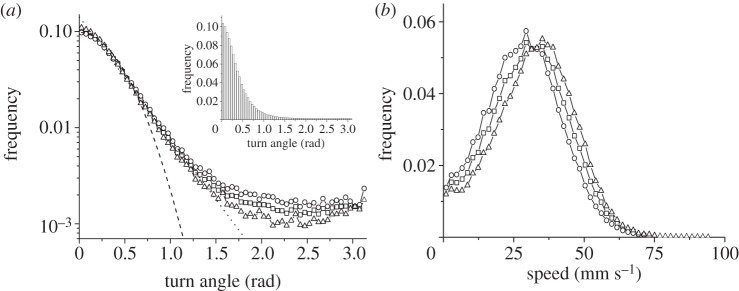
Frequency distribution of (a) turn angles and (b) instantaneous speeds for risk-prone and risk-averse trajectories compared to the overall behavior. Gaussian and exponential fits (dashed and dotted lines, respectively) of the turn angle distribution are shown for the overall behaviour. Inset: frequency distribution in normal scale emphasizing the emergence of a uniform distribution for large turning angles. Squares, all trajectories; triangles, risk-prone; circles, risk-averse trajectories.

All in all, our results suggest that risk-averse and risk-prone strategies involved different patterns of motion and that those individuals more actively engaged in search tasks do really behave accordingly showing a more efficient exploration pattern with larger mean speeds and less reorientations, thus, reducing space-use overlap.

3.2. Reorientation patterns

Mean speed and turning angles showed in the experiments a clear negative correlation (figure 5). Reorientations are thus evidently related to instants of low speed, providing some evidence that the motion patterns of ants are intermittent, similar to other species of insects [3]. Ants will thus slow down the movement from time to time, breaking directional persistence and generating new directions of motion.

Figure 5.

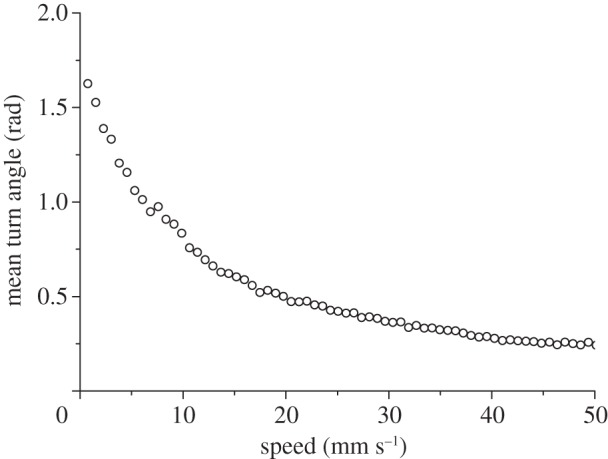
Mean turn angle as a function of the instantaneous speed averaged over all the trajectories.

We assessed whether the interevent statistics for reorientations also differed for risk-prone and risk-averse strategies. Figure 6a shows the cumulative probability distribution of time lapsing between consecutive reorientations pooling all the trajectories. Figure 6b, on its turn, shows the comparison between reorientation interevent distributions for risk-prone and risk-averse strategies. Likelihood methods were used to determine the fit of these distributions to exponential, stretched exponential and power-law functions. While the fits were based on the probability density function, figure 6 shows the results in terms of the corresponding cumulative distributions (e.g. [53]). In all the cases, the best fit was clearly obtained for a stretched exponential 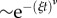with an exponent ν close to 0.4 (see the details in the figure caption). Power-law-like signatures, however, can be observed from a visual inspection of the results (see, for example, the inset in figure 6b, where the frequency distribution and not the cumulative is observed), which suggests in any case clear evidence of heavy-tailed distributions. Although the fittings carried out yield slightly different values of the parameters ξ and ν for the risk-prone and the risk-averse strategies, the emergence of stretched exponential functions in all the cases suggests that the internal mechanisms driving decision-making should be the same for the ants engaged in any of the two strategies. Of note is that risk-averse and risk-prone strategies (figure 6b) lead to relatively similar values for the exponent ν. Differences only appeared on the characteristic timescale of reorientations, the risk-prone strategy showing larger characteristic reorientation scales than the risk-averse strategy (λ⁻¹ = 3.5 s for risk-averse versus λ⁻¹ = 10 s for risk-prone). These mechanisms should then have a genetic or physiological basis but possibly modulated through learning or age.

Figure 6.

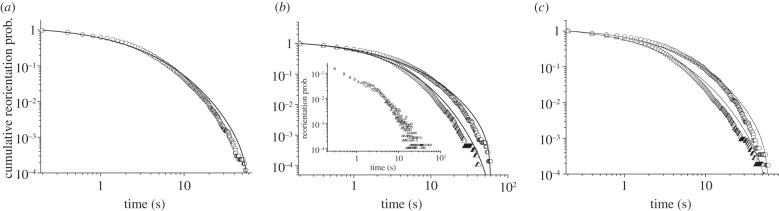
Cumulative probability of the time between consecutive reorientations, showing the explicit comparison between the whole set of trajectories (a), risk-prone (circles) versus risk-averse (triangles) strategies (b) and the reorientations close to the centre versus those far away from it (c) (triangles, d_centr < 25 cm; circles, d_centr > 25 cm). Solid lines indicate for each case the fit to a stretched exponential 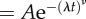obtained through likelihood methods (overall: λ = 0.144 s⁻¹, ν = 0.408; risk-averse: λ = 0.288 s⁻¹, ν = 0.485; risk-prone: λ = 0.100 s⁻¹, ν = 0.372; d_centr < 25 cm: λ = 0.149 s⁻¹, ν = 0.426; d_centr > 25 cm: λ = 0.276 s⁻¹, ν = 0.434). The inset shows the probability distribution in a log–log scale to stress the similarity between internal clocks for risk-prone and risk-averse strategies.

We finally checked that the reorientation statistics observed in the experiment only emerges as the result of random exploration and not from the information exchange through encounters between conspecifics. As these encounters are more frequent as the distance to the centre of the arena decreases, we also compared the reorientation patterns occurring at small (d_centr < 25 cm) and large distances (d_centr > 25 cm) to the centre, independently of whether the reorientations corresponded to risk-prone or risk-averse strategies. The results (figure 6c) confirm that the stretched exponential distribution emerges always independently whether reorientations occur close to the centre or not. This seems to prove the independence of that behaviour from possible communication fluxes through antennae contact, so the observed behaviour should be attributed to internal decision-making mechanisms used by the ants.

Figure 6c, on the other hand, may suggest that the main factor driving the reorientation patterns observed is distance, rather than the specific strategy followed by the ants. That possibility has also been tested by comparing both risk-averse and risk-prone trajectories for d_centr < 25 cm and d_centr > 25 cm (see electronic supplementary material). Differences in the timescale between the two strategies persist in both distance regimes, suggesting that distance while obviously it may play a role in the process (because crowding effects, although small in our experimental setting, do exist in the region close to the nest) it is not a critical factor.

3.3. The nest as a central point of attraction

In risk-averse strategies, ants never departed very far from the centre, and the risk-prone strategy involved frequent back-and-forth movements to/from the vicinity of the centre. All this indicated that the centre acted as a focal point of attraction as expected in a context of central-place foraging. To investigate these phenomena in more detail, we adopt here the ideas by Bovet & Benhamou [29,30,32]. Accordingly, the sinuosity of the trajectory (if not the whole pattern of motion) would depend on whether the ant is moving towards the point of attraction or else it is departing from it. To examine this, we defined the deviation angle β as the difference between the direction of motion of the ant and the direction pointing from the centre to the ant's position (i.e. β = 0 corresponds to a trajectory departing from the centre in radial direction and β = π corresponds to a trajectory pointing to it).

Figure 7 shows the effects of the deviation angle β on the ants movement, considering separately risk-prone and risk-averse strategies. In summary, the frequency distribution of the parameter β (figure 7a) indicated that instantaneous movements departing from the centre were much more frequent than those coming back to it, but instead the latter movements were done on average at a faster speed (figure 7b). This picture suggests that exploration paths from the nest outwards were more sinuous whereas returns to the nest were much straighter.

Figure 7.

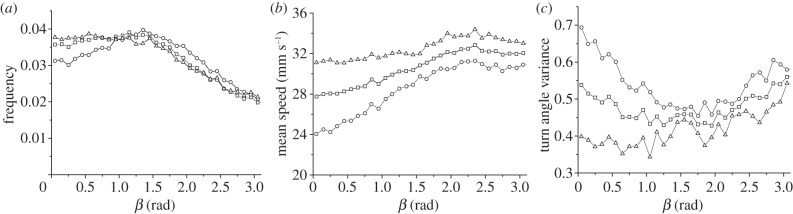
Effect of the deviation angle β on the experimental motion of ants. (a) Frequency distribution of β, (b) mean speed and (c) standard deviation of the turn angles as a function of β. (a–c) Squares, all trajectories; triangles, risk-prone; circles, risk-averse trajectories.

Finally, we analysed the variance of the turn angles (figure 7c), which is the most adequate way to measure the sinuosity of the trajectory. When the ants were departing from the centre (i.e. for β small) the sinuosity of the trajectory increased, as expected in a klinokinetic process, indicating that the centre acted as a point of attraction making the ants increase their turning rates in order to prevent them from moving away too much. However, the same effect emerged when ant trajectories were pointing towards the centre (so β was close to π in radians), so the centre of the arena can also act sometimes as a repeller. While both effects were present in the two strategies, the attractive role of the centre was stronger in the risk-averse strategy, whereas the negative attraction (or repulsion) effect was dominant in the risk-prone strategy. A clear interpretation of the latter remains elusive. One possibility is that this ‘repulsion’ effect reflects a tendency of ants to avoid coming back to the central region while engaged in exploration tasks, so in that case departures from the centre may be intentional. Alternatively, it could be a signature of a zigzag or some other kind of meandered trajectory used by ants to find the nest in their way back (in analogy with similar strategies reported in other organisms, as birds [54] or amoeba [55]). In fact, we have detected that turning angles exhibit negative correlations for a time window of 0.5–2 s (see the electronic supplementary material, figure S2), which is compatible with the existence of a zigzag motion in ants. Visual inspection of the video recordings, however, did not seem to confirm the idea that zigzag is used by the ants, so these results might be influenced by the existence of relatively frequent encounters close to the nest or by the tendency of ants to try following straight paths (which could lead to small zigzag-like corrections), etc. After careful analysis, we have found that our datasets do not allow us to provide evidence of which is the specific mechanism driving negative correlations in turn angles.

3.4. A random-walk model

We have developed a comprehensive mechanistic model which reproduces the basic properties of the observed trajectories (figure 8). Each individual performs autonomous and stochastic decision-making regarding reorientation events. Specifically, consecutive reorientations are assumed to be separated by random times extracted from a stretched exponential distribution with exponent 0.4, according to our findings in the Results section. Every time a reorientation occurs, a new direction of motion is randomly chosen from a uniform distribution (in analogy with the Lévy-modulated correlated walks used in [5,56]). Also, the individuals are given the possibility to switch between homing and exploring behavioural modes.

Figure 8.

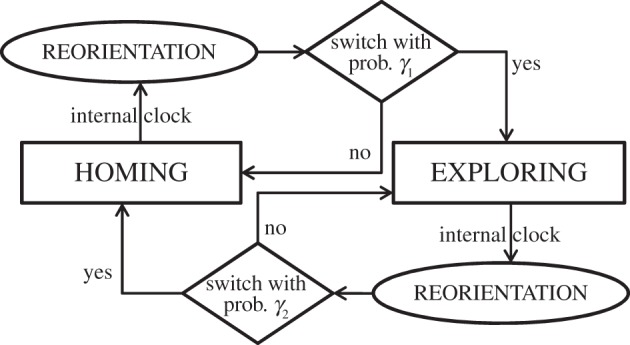
Main algorithm of the random-walk model for central-place foraging in A. senilis ants.

Homing behaviour, from an ecological perspective, involves movement and sensory–motor mechanisms that return animals to their home sites. The navigational mechanisms, the sensors and the memory used by animals while homing are often quantitatively and qualitatively different from the ones used in exploratory modes where local scanning mechanisms, and memory or expectation into a less extent, may drive the whole movement [57,58].

The switching dynamics between homing and exploring is assumed to occur only at reorientation event times; the underlying idea is that reorientation behaviour does not only serve to break down the directional persistence, but it can also provide a strategic pause for internally processing information, and subsequently make decisions about whether to keep on exploring or not. For the sake of simplicity, the switch between these two modes is assumed to be driven by a Markov process, with a constant probability γ₁ of switching from exploring to homing and a probability γ₂ of switching from homing to exploring.

The general pattern of motion followed by the individuals when exploring or homing consists of a two-dimensional random-walk model. Between two consecutive time steps (time step is taken as 0.2 s in accordance with the separation between consecutive frames in our experimental data), the individual moves from one place to another with given values for the speed and the direction of motion. The values of the speed at each move are taken from a Gaussian distribution centred at v = 32 cm s⁻¹ and with a standard deviation of 20 cm s⁻¹ (these values are obtained from a Gaussian fit of the data in figure 4). Likewise, turning angles also follow a Gaussian distribution with vanishing mean. The variance of this Gaussian distribution, however, is not constant but it is assumed to depend on the deviation angle β defined above, in accordance with the klinokinetic models by Benhamou & Bovet [30,32]. In the cited works, it was argued that a reasonable dependence for σ(β) was typically σ(β) = k[1 − fcos(β)], where k is a positive constant and f is called the klinokinetic factor. In our case, however, we have checked that such a cosine dependence is not compatible with the results from figure 7. Actually, several dependences were tested before we found a satisfactory dependence from which a good fitting is obtained. So, we rather adopt here a klinokinetic model with a dependence of the type

3.1

and

3.2

which fits well with the behaviour observed in figure 7c. This specific distinction is the only explicit difference made in our model between homing and exploring modes. Note, however, that we could have also considered different speeds or patterns of motion for the two modes. While this would be desirable for the sake of realism, we have checked numerically that this level of detail was not necessary to reach a good agreement between the model and the data, so we have decided to obviate it here to keep the model as simple as possible.

To verify that this random-walk approach can really reproduce the experimental ant trajectories, we use the model to fit the probability distributions of time durations and lengths of the complete trajectories of the ants. According to our discussion above, it was necessary to consider explicitly two kinds of strategies in the model: risk-averse and risk-prone. The only difference between them in the model is on the amount of time spent by each one in the homing or in the exploring mode. We assumed then γ₁ = 0 for risk-averse trajectories (so they spend all of the time in the homing mode) whereas γ₁ > γ₂ > 0 was used for risk-prone trajectories (which means that most of the time these remain in the exploring mode, whereas periods of homing are also possible). The specific values obtained from our fitting analysis for γ₁, γ₂ and the other parameters in the model are provided in figure 9 (see caption). The good agreement observed there for the duration and length distribution of the trajectories confirms that the scheme provided in figure 8 provides a convenient description of the system.

Figure 9.

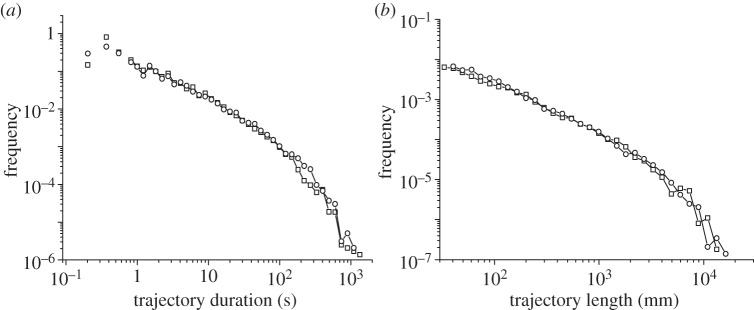
(a) Direct comparison between the frequency distribution of the trajectory durations and (b) lengths obtained from experiments and those obtained from the random-walk approach proposed here. The fit has been obtained by using a standard deviation of 0.17 rad⁻¹ for turn angles, with f₁ = 0.9, f₂ = 0.7. For the switching we used γ₁ = 0.1 s⁻¹, γ₂ = 0.3 s⁻¹ for the risk-prone strategy (risk-averse trajectories are assumed to stay permanently in the ‘homing’ mode), with a 90% of risk-averse trajectories and a 10% to risk-prone (in accordance with our observations). (a,b) Squares, experimental; circles, simulated.

Furthermore, the fitting exercise carried out in the lines above not only confirms the goodness of our approach but also provides useful biological information about the details of the foraging process. We have already mentioned above, for instance, that several dependences were discarded for our klinokinetic function before a satisfactory fitting was reached. Also, it was checked that the heavy tail of the stretched exponential used for times between reorientations was essential for that purpose, too. We carried out several tests with different functions for the distribution of those times and only those with these heavy tails (e.g. power-laws) fitted easily the experimental results without the use of unrealistic parameters.

4. Discussion

Our work emphasizes the existence of two essential ingredients to understand the experimental trajectories of A. senilis ants in an experimental set-up designed to observe central-place foraging with both minimal environmental signals and conspecific information transference. First, one must distinguish two types of behavioural strategies, risk-averse and risk-prone, that we hypothesize should approximately correspond to juveniles and experienced foragers, in accordance with previous observations [43]. Our data are even able to quantify such a distinction by means of the average Euclidean distance of a trajectory to the nest (figure 4), so finding a characteristic distance (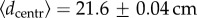) that delimits the influence region of risk-averse strategies. We could not identify individuals to determine whether they always ‘play’ the same strategy or else they show behavioural plasticity, but this could be done by colour marking the ants (forthcoming experiments will certainly account for the individual identification of ants).

Second, one must take into account the behaviour with respect to the central nest. Whereas the risk-averse strategy shows a continuous tendency to stay close to the centre of attraction, the risk-prone strategy involves the switching, from time to time, between this attracting mode (termed here as homing behaviour) and an exploring mode where the preferential tendency is to move away from the centre. In the risk-prone strategy, we hypothesize that the use of periodic returns by explorers to the central region could be related to potential information exchanges with other individuals. Of course, we must admit that this scheme (condensed into the random-walk model in figure 8) is probably not the only one able to fit the observed trajectories, but we claim that it is relatively simple and provides a reasonable description of both a random search summed to a central-place attraction in ants.

We have also focused on what kind of mechanisms ants use to reorient in space. For a search with complete information about the target location, reorientation behaviour becomes inefficient and a ballistic-like motion towards the target should be expected. However, when information is not available and there is not a specific will to leave the area, a run-and-tumble strategy may be efficient. In particular, the use of heavy-tailed distributions (such as stretched exponentials) as internal reorientation clocks is in agreement with the idea that frequently long relocations do provide functional advantages for organisms during random exploration of space [5,59] and it is not in conflict with the presence of klinokinetic effects owing to central-place foraging [29–31].

Owing to the symmetry and homogeneity properties of our arena, we have been able to infer klinokinetic behaviour by quantifying the most essential characteristics of motion (e.g. speed or turning angles) as a function of the deviation angle β. In particular, we have shown how individuals behave as long as they depart from or approach the nest. As expected for a central-place (or home range) foraging scheme, we have found a tendency to perform larger turning angles when departing from the centre, but additional (non-trivial) effects have been detected too. For instance, we have observed that returns to the nest are straighter and faster compared with departures from the centre. Also, we have found that the behaviour of turning angles when ants are engaged in larger scale exploration tasks (this is, in the risk-prone strategy) exhibits different klinokinetic dynamics. To our knowledge, this is one of the first works where such an experimental study of klinokinesis has been systematically conducted. These fingings are illustrative of the utility of high-resolution, large-scale tracking experiments under controlled environments in order to capture the main drivers of movement patterns which would be much more difficult to identify under field conditions.

Funding statement

This research has been partially supported by grants no. FIS 2012-32334 (V.M., D.C.), SGR 2009-00164 (V.M., D.C.). F.B. acknowledges the support of the Ministerio de Economía y Competitividad (grant nos. 2009-04133 and BFU2010-22337) and the Human Frontier Science Program (grant no. RGY0084/2011).