Abstract
This is Part II of a series of three papers which jointly address the combustion chemistry of furan and its alkylated derivatives 2-methylfuran (MF) and 2,5-dimethylfuran (DMF) under premixed low-pressure flame conditions. Some of them are considered to be promising biofuels. With furan as a common basis studied in Part I of this series, the present paper addresses two laminar premixed low-pressure (20 and 40 mbar) flat argon-diluted (50%) flames of MF which were studied with electron-ionization molecular-beam mass spectrometry (EI-MBMS) and gas chromatography (GC) for equivalence ratios φ=1.0 and 1.7, identical conditions to those for the previously reported furan flames. Mole fractions of reactants, products as well as stable and reactive intermediates were measured as a function of the distance above the burner. Kinetic modeling was performed using a comprehensive reaction mechanism for all three fuels given in Part I and described in the three parts of this series. A comparison of the experimental results and the simulation shows reasonable agreement, as also seen for the furan flames in Part I before. This set of experiments is thus considered to be a valuable additional basis for the validation of the model. The main reaction pathways of MF consumption have been derived from reaction flow analyses, and differences to furan combustion chemistry under the same conditions are discussed.
Keywords: 2-methylfuran, low-pressure flame, model, reaction mechanism, reaction flow analysis, molecular-beam mass spectrometry, gas chromatography
1. Introduction
As traditional fossil fuels are considered to be largely responsible for causing important degradation of air quality and for impacting global climate, there is an increasing interest to shift from petroleum-based fuels to biofuels [1].
The potential of using 2-methylfuran (MF) as biofuel in engines has been demonstrated [2,3]. In fact, MF has several advantages over smaller alcohols, such as ethanol. It has a high energy density (ca. 29 MJ/L, compared to ca. 21 MJ/L for ethanol and 27 MJ/L for 1-butanol), close to that of gasoline (ca. 32MJ/L). MF could also be produced from non-edible biomass [4-6]. Before using MF as a fuel, the fundamental understanding of its combustion chemistry is desirable. Particularly since oxygenated fuels are known to produce several carbonyl compounds as potential pollutants, little information is as yet available regarding undesired and potentially harmful products. The pyrolysis of 2-methylfuran was investigated in two earlier publications [7,8]. Grela et al. [7] studied the very low-pressure (1 mTorr) pyrolysis of furan, MF and 2,5-dimethylfuran (DMF) in the temperature range 1050-1270 K. The reactant molecules were heated in a steady flow reactor and the products were analyzed by an online mass spectrometer. Lifshitz et al. [8] studied the decomposition of MF behind reflected shock waves in a pressurized driver single-pulse shock tube between 1100 and 1400 K. Identified stable species were MF, CO, CH4, C2H4, C2H6, C2H2, C3H6, allene, propyne, 1,3-butadiene, 1,2-butadiene, 1-butyne, 2-butyne, C4H4, C4H2, furan, CH2CO, and C6H6.
Besides experimental investigations, the thermal decomposition kinetics of furans has also been studied theoretically by quantum chemical methods to determine the enthalpies of formation and bond dissociation energies [9], and also to calculate energetics and kinetics of a range of unimolecular decomposition pathways [10].
Most recently, a chemical kinetic mechanism was proposed by Somers et al. [11] for the ignition of MF in a shock tube at atmospheric pressure for a limited range of conditions (φ=0.5-2.0, T~1200-1800 K). They also determined laminar burning velocities using the heat-flux method for mixtures of MF in air at equivalence ratios of 0.55 to 1.65, initial temperatures of 298 to 398 K, and atmospheric pressure. Their detailed chemical kinetic mechanism consists of 2059 reactions and 391 species. Also Wei et al. [12] have investigated the combustion of MF in lean and fuel-rich low-pressure premixed flames using tunable synchrotron vacuum ultraviolet photoionization and molecular-beam mass spectrometry, but concentration profiles were not reported.
As part of continuing efforts to improve the knowledge on the combustion chemistry of renewable fuels, Part II of this series, which started with furan combustion in Part I [13], focuses on low-pressure premixed MF/oxygen/argon flames. Stable and radical intermediate species were detected and quantified with two independent techniques: electron-ionization molecular-beam mass spectrometry (EI-MBMS) in Bielefeld complemented by gas chromatography (GC) in Nancy to identify some isomers. Following the analysis of furan flames burnt under identical conditions, results of the simulation of the MF flames analyzed here are given using the same model as reported in Part I [13].
2. Experimental results
In line with the setup and procedures in Part I [13], laminar flat flames of MF have been stabilized on two burners of slightly different diameters (64 vs. 60 mm diameter) in Bielefeld and Nancy, respectively. A complete description of the experimental setups used in this study has been given in [13-16] and will therefore not be repeated here.
The gases were regulated by calibrated mass-flow controllers with an error of less <5% since gas conversion factors were applied. In Bielefeld, the liquid MF fuel was metered by a syringe pump, evaporated at 373 K, and added to the gas stream. In Nancy, the liquid fuel flow rate was controlled by using a liquid mass-flow controller, mixed with argon and then evaporated by passing it through a CEM (Controlled Evaporator and Mixer). The temperature of this CEM was set at 373 K. The experimental conditions are presented in Table 1. As in Part I [13], EI-MBMS and online GC were used for the analysis of the reaction products. Analyses, evaluation data, and errors related to the measurements and the determination of calibration factors were extensively discussed previously [13].
Table 1.
Flow conditions for methylfuran (MF) flames; SLM: Standard liter per minute.
| φ | Burner diameter (mm) |
Gas flow (SLM) | Pressure (mbar) |
C/O ratio |
Dilution | Flow velocity at T=333 K# (cm s−1) |
|||
|---|---|---|---|---|---|---|---|---|---|
| MF | O2 | Ar | |||||||
| Bielefeld | 1.0 | 64 | 0.33 | 1.95 | 2.28 | 20 | 0.39 | 50% | 146 |
| 1.7 | 64 | 0.50 | 1.78 | 2.28 | 40 | 0.62 | 50% | 73 | |
| Nancy | 1.7 | 60 | 0.44 | 1.56 | 2.00 | 40 | 0.62 | 50% | 73 |
The flow velocity is referred to the temperature of the burner surface (cooling water).
The present work could be considered as the first analysis of MF combustion in laminar premixed low-pressure flames with mole fraction profiles provided. Note that in the literature, only Wei et al. [12] studied MF combustion in laminar premixed low-pressure flames, without reporting species profiles, however.
The quantitative results for both equivalence ratios (φ=1.0 and 1.7) are summarized in Table 2 (EI-MBMS experiments) and the isomers of intermediate species are presented in Table 3 (GC analysis). Figures 1-6 and S1-S5 in the Supplemental Material present the EI-MBMS mole fraction profiles of chemical species (major, stable, radical and intermediate) as a function of distance to the burner h. The reaction zone peaks at ~2-4 mm above the burner. GC measurements (Table 3 and Figs. 7 and 8) allowed the identification of isomers which were not distinguishable in the EI-MBMS experiments. Note that in the GC experiments, the flame is closer to the burner because the conditions for the two setups are not exactly identical (especially the size of sampling probes); thus the temperature profiles are different and the species profiles obtained by GC and MBMS are shifted (as shown in Figs. 7 and 8). Nevertheless, the sums of maximum mole fractions of isomers measured by GC are in good agreement with the sums detected by MBMS, within the experimental uncertainty, as shown in Table 3. Temperature was derived from the pressure in the first pumping stage of EI-MBMS by a procedure described in Part I [13] and calibrated at a height of h=25 mm above the burner from CO/CO2 absorption measurements with a quantum cascade laser using tomographic reconstruction [13]. The temperature profile obtained this way traces the fate of a gas sample withdrawn by the probe and is therefore called “perturbed” temperature profile here.
Table 2.
Intermediate species identification with EI-MBMS in methylfuran experiments. M: nominal mass, E: electron energy, IP: ionization threshold, h: position of maximum, xmax: peak mole fraction, φ: equivalence ratio. Calibration methods: RICS (of reference species in parenthesis), convolution (of energy distribution and ionization cross section) or direct (cold gas calibration).
| Species | M | E (eV) | IP (eV) | Calibrated as | Calibration method |
Ref. | φ = 1.0 | φ= 1.7 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| h (mm) | xmax | h (mm) | xmax | |||||||
| CH3 | 15 | 10.5 | 9.84 | Methyl | RICS (CH4) | [22] | 3.0 | 1.92E-03 | 2.5 | 1.53E-03 |
| CH4 | 16 | 12.0 | 12.61 | Methane | Direct | [23] | 3.5 | 3.05E-03 | 3.5 | 4.26E-03 |
| C2H2 | 26 | 12.0 | 11.40 | Acetylene | Direct | [24] | 3.7 | 1.59E-02 | 3.5 | 3.34E-02 |
| C2H3 | 27 | 10.5 | 8.25 | Vinyl | RICS (C2H4) | [25] | 3.0 | 7.98E-06 | 2.0 | 5.95E-06 |
| C2H4 | 28 | 11.25 | 10.51 | Ethene | Direct | [26] | 3.2 | 6.21E-03 | 3.0 | 8.04E-03 |
| C2H5 | 29 | 10.5 | 8.12 | Ethyl | RICS (C4H6) | [25] | 2.7 | 4.10E-05 | 2.5 | 2.52E-05 |
| HCO | 29 | 10.5 | 8.12 | Formyl | Convolution | [25] | 3.0 | 4.46E-05 | 2.0 | 2.97E-05 |
| C2H6 | 30 | 12.0 | 11.52 | Ethane | Direct | [26] | 2.5 | 2.37E-03 | 2.5 | 2.55E-03 |
| CH2O | 30 | 11.25 | 10.88 | Formaldehyde | Convolution | [25] | 2.7 | 3.98E-03 | 3.0 | 3.30E-03 |
| CH4O | 32 | 11.25 | 10.23 | Methanol | Direct | [26] | 1.2 | 2.23E-04 | 1.5 | 1.39E-04 |
| C3H3 | 39 | 10.5 | 8.67 | Propargyl | RICS (C3H6) | [25] | 3.0 | 1.82E-04 | 2.5 | 2.48E-04 |
| C3H4 | 40 | 11.25 | 10.36 | Propyne | RICS (C3H6) | [25] | 3.2 | 2.95E-03 | 3.0 | 4.76E-03 |
| C3H5 | 41 | 10.5 | 8.13 | Allyl | RICS (C3H6) | [25] | 3.0 | 3.05E-04 | 2.5 | 1.90E-04 |
| C2H2O | 42 | 10.5 | 9.62 | Ketene | Convolution | RICS (C2H6O) | 3.2 | 6.37E-04 | 3.0 | 5.51E-04 |
| C3H6 | 42 | 10.5 | 9.73 | Propene | Direct | [26] | 2.7 | 1.83E-03 | 2.0 | 1.13E-03 |
| C2H4O | 44 | 11.25 | 10.23 | Acetaldehyde | Direct | [24] | 3.0 | 1.04E-03 | 3.0 | 6.08E-04 |
| C2H6O | 46 | 11.25 | 10.02 | Dimethylether | Direct | [24] | 2.0 | 3.40E-05 | 2.0 | 2.56E-05 |
| C4H2 | 50 | 11.25 | 10.17 | 1,3-Butadiyne | Convolution | [25] | 4.0 | 5.09E-04 | 3.5 | 2.15E-03 |
| C4H4 | 52 | 10.5 | 9.58 | 1-Butene-3-yne | Convolution | [25] | 3.5 | 1.50E-03 | 3.0 | 2.16E-03 |
| C4H5 | 53 | 10.5 | 7.97 | But-2-yn-1-yl | Convolution | RICS (C4H6) | 3.0 | 3.07E-05 | 2.0 | 3.83E-05 |
| C4H6 | 54 | 10.5 | 9.07 | 1,3-Butadiene | Convolution | [25] | 3.0 | 2.23E-03 | 2.5 | 2.02E-03 |
| C4H7 | 55 | 10.5 | 7.40 | But-3-en-1-yl | RICS (1-C4H8) | [25] | 2.5 | 1.71E-04 | 2.0 | 1.46E-04 |
| C4H8 | 56 | 10.5 | 9.55 | 1-Butene | Direct | [26] | 2.5 | 1.12E-03 | 2.0 | 8.62E-04 |
| C3H4O | 56 | 11.25 | 10.11 | Acrolein | RICS (C3H6O) | [24] | 2.7 | 1.96E-03 | 2.5 | 1.37E-03 |
| C3H6O | 58 | 10.5 | 9.96 | Propanal | Direct | [24] | 2.5 | 3.54E-04 | 2.0 | 1.75E-04 |
| C5H4 | 64 | 10.5 | 9.50 | 1,3-Pentadiyne | RICS (C5H8) | [24] | 3.7 | 2.25E-05 | 3.0 | 5.79E-05 |
| C5H6 | 66 | 10.5 | 8.57 | 1,3-Cyclopentadiene | RICS (C5H8) | [24] | 3.2 | 1.58E-04 | 2.5 | 2.02E-04 |
| C5H7 | 67 | 10.5 | 7.54 | 3-Cyclopentenyl | Convolution | RICS (C5H8) | 2.5 | 2.16E-06 | 2.0 | 2.23E-06 |
| C4H4O | 68 | 10.5 | 8.88 | Furan | Direct | [24] | 3.0 | 3.08E-03 | 2.0 | 3.10E-03 |
| C5H8 | 68 | 10.5 | 8.59 | 1,3-Pentadiene | Direct | [24] | 2.7 | 5.78E-05 | 2.0 | 6.88E-05 |
| C4H6O | 70 | 10.5 | 9.65 | 2-Butenone | Convolution | RICS (butanal) | 2.7 | 3.95E-04 | 2.0 | 2.41E-05 |
| C5H10 | 70 | 10.5 | 9.04 | 2-Pentene | RICS (C5H8) | [24] | 2.2 | 1.10E-04 | 2.0 | 1.24E-04 |
| C4H8O | 72 | 10.5 | 9.71 | Isobutanal | Convolution | RICS (butanal) | 2.2 | 1.14E-04 | 2.0 | 4.21E-05 |
| C6H2 | 74 | 10.5 | 9.50 | Triacetylene | Convolution | [25] | 4.0 | 1.22E-05 | 3.0 | 6.09E-05 |
| C6H4 | 76 | 10.5 | 9.03 | Benzyne | Convolution | RICS (C6H2) | 3.7 | 9.19E-06 | 3.0 | 2.95E-05 |
| C6H6 | 78 | 10.5 | 9.24 | Benzene | Direct | [25] | 3.5 | 1.41E-04 | 3.0 | 2.75E-04 |
| C5H4O | 80 | 10.5 | 8.12 | Allenylketene | Convolution | RICS (butanal) | 3.0 | 5.54E-06 | 2.5 | 5.49E-06 |
| C6H8 | 80 | 10.5 | 8.82 | 1,4-Cyclohexadiene | Convolution | RICS (C6H6) | 2.7 | 2.97E-05 | 2.0 | 4.28E-05 |
| C5H5O | 81 | 10.5 | 7.05 | 2-Furanylmethyl | Convolution | RICS (furan) | 2.5 | 8.22E-05 | 2.0 | 9.74E-05 |
| C5H8O | 84 | 10.5 | 9.39 | 3-Pentene-2-one | Convolution | RICS (acetone) | 2.0 | 5.16E-04 | 1.5 | 2.41E-04 |
| C7H8 | 92 | 10.5 | 8.82 | Toluene | Convolution | RICS (C6H6) | 3.2 | 2.46E-05 | 2.5 | 4.24E-05 |
| C6H6O | 94 | 10.5 | 8.49 | Phenol | Convolution | RICS (C6H6) | 3.0 | 4.16E-05 | 3.0 | 3.65E-05 |
| C5H4O2 | 96 | 10.5 | 9.22 | Furfural | Convolution | RICS (furan) | 2.5 | 6.69E-05 | 2.0 | 6.25E-05 |
| C6H8O | 96 | 10.5 | 8.45 | 2-Ethylfuran | Convolution | RICS (furan) | 2.5 | 2.59E-04 | 2.0 | 2.85E-04 |
Table 3.
Comparison of maximum mole fractions (GC/MBMS/Model) for some intermediates in the MF/O2/Ar flame, φ=1.7.
| Formula | Species | xmax (GC) | xmax (Model) | xmax (MBMS) |
|---|---|---|---|---|
| C2H2 | Acetylene | 2.50E-02 | 3.14E-02 | 3.34E-02 |
| C2H6 | Ethane | 3.16E-03 | 2.85E-03 | 2.55E-03 |
| C3H4 | Propyne | 2.73E-03 | 0.65E-03 | 4.76E-03 |
| Allene | 1.07E-03 | 0.29E-03 | ||
| C3H6 | Propene | 1.44E-03 | 1.44E-03 | 1.13E-03 |
| C4H4 | 1-Butene-3-yne | 4.20E-03 | 1.82E-03 | 2.16E-03 |
| C4H6 | 1,3-Butadiene | 3.36E-03 | 1.81E-03 | 2.02E-03 |
| 1,2-Butadiene | 2.39E-04 | 0.81E-04 | ||
| 2-Butyne | 2.43E-04 | 0.33E-04 | ||
| C4H8 | 1-Butene | 4.28E-04 | 3.68E-04 | 8.62E-04 |
| 2-Butene | 1.19E-04 | 1.56E-04 | ||
| C5H6 | 1,3-Cyclop entadiene | 2.77E-04 | 1.17E-05 | 2.02E-04 |
| 1-Pentene-3-yne | 4.29E-05 | a | ||
| C5H8 | 1,3-Pentadiene | 8.80E-05 | 2.70E-05 | 6.88E-05 |
| Isoprene | 8.92E-05 | 2.75E-05 | ||
| 2-Pentyne | 1.67E-05 | 1.00E-07 | ||
| C5H10 | 2-Pentene | 1.69E-04 | 1.45E-04 | 1.24E-04 |
| 3-Methyl-1-butene | 0.86E-04 | |||
| 1-Pentene | 0.08E-04 | 1.10E-04 | ||
| C6H6 | Benzene | 3.93E-04 | 0.78E-04 | 2.75E-04 |
| C7H8 | Toluene | 6.01E-05 | 3.71E-05 | 4.24E-05 |
| C2H4O | Acetaldehyde | 8.73E-04 | 5.00E-04 | 6.08E-04 |
| Ethylene oxide | 3.81E-06 | 2.39E-04 | ||
| C2H6O | Dimethylether | 3.79E-05 | 6.22E-05 | 2.56E-05 |
| Ethanol | b | a | ||
| C3H6O | Propanal | 1.48E-04 | 6.62E-04 | 1.75E-04 |
| Acetone (impurity~7E-04) | 1.13E-04 | 3.74E-06 | ||
| C4H4O | Furan | c | 7.89E-03 | 3.10E-03 |
|
C4H6O |
2-Butenone | 3.25E-04 | a | 2.41E-04 |
| 2-Butenal | 6.87E-05 | a | ||
| Isobutenal | 2.09E-05 | a | ||
| 2,3-Dihydrofuran | 3.01E-06 | 1.17E-04 | ||
| C4H8O | Isobutanal | 1.58E-05 | a | 4.21E-05 |
| 2-Butanone | 5.22E-06 | a | ||
| C5H8O | 3-Penten-2-one | 2.07E-05 | a | 2.41E-04 |
| C6H8O | 2-Ethylfuran | 2.16E-04 | a | 2.85E-04 |
| 2,5-DMF | 1.37E-05 | 0.73E-05 | ||
| 2,4-DMF | 1.05E-05 | a | ||
| C5H4O2 | Furfural | 2.67E-05 | a | 6.25E-05 |
not available
not detected
identified, but not quantified
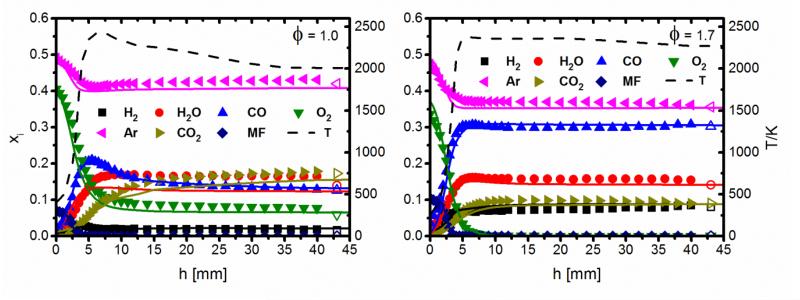
Figure 1. Main species mole fraction xi and temperature T profiles as a function of height above burner h.
Symbols: experiment (EI-MBMS), lines: model results. Equilibrium values (open symbols) are indicated at h=43 mm. Perturbed temperature profiles were calibrated by QCL absorption at 25.0 mm; they were used as input parameters for the numerical simulation without any changes.
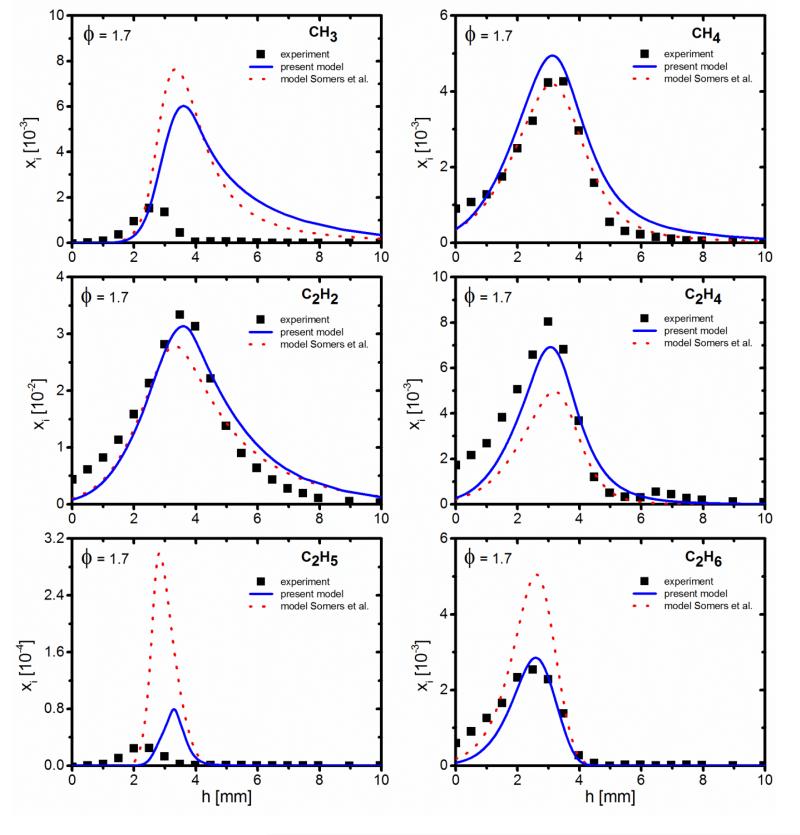
Figure 2. Mole fraction profiles of selected C1 and C2 species for φ=1.7.
Symbols: experiment (EI-MBMS), lines: simulation; solid lines: present model, dotted lines: model of Somers et al. [11]. Mole fraction profiles for φ=1.0 can be found in the Supplemental Material.
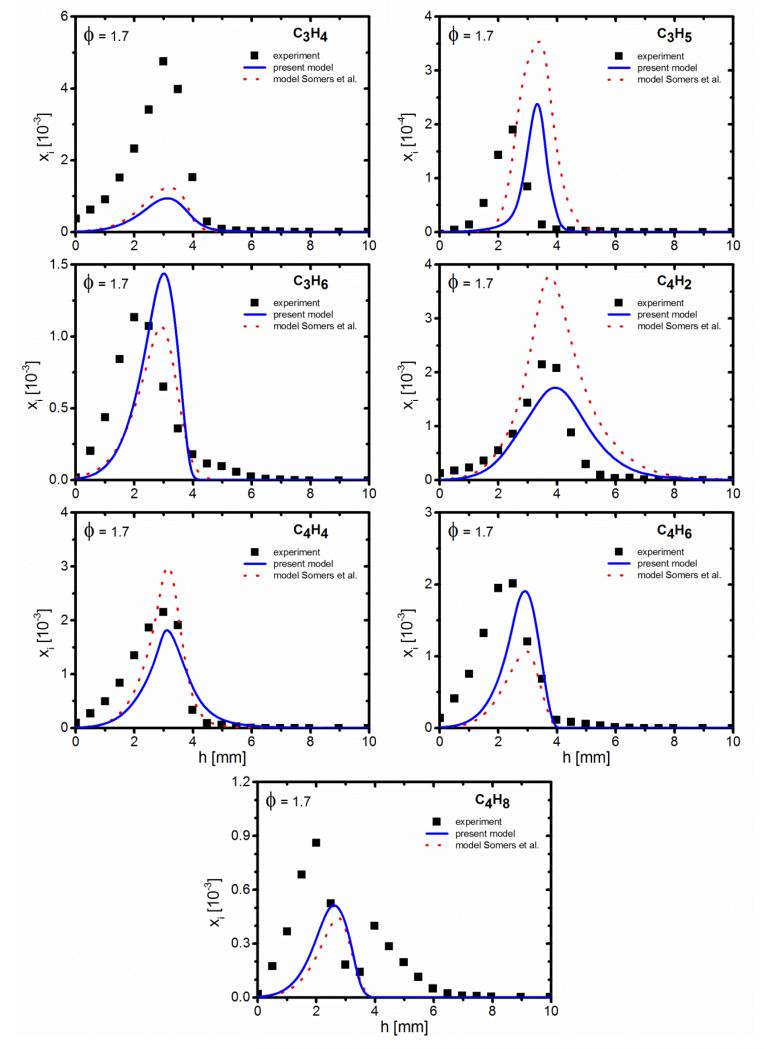
Figure 3. Mole fraction profiles of selected C3 and C4 species for φ=1.7.
Symbols: experiment (EI-MBMS); lines: simulation; solid lines: present model, dotted lines: model of Somers et al. [11]. Mole fraction profiles for φ=1.0 can be found in the Supplemental Material.
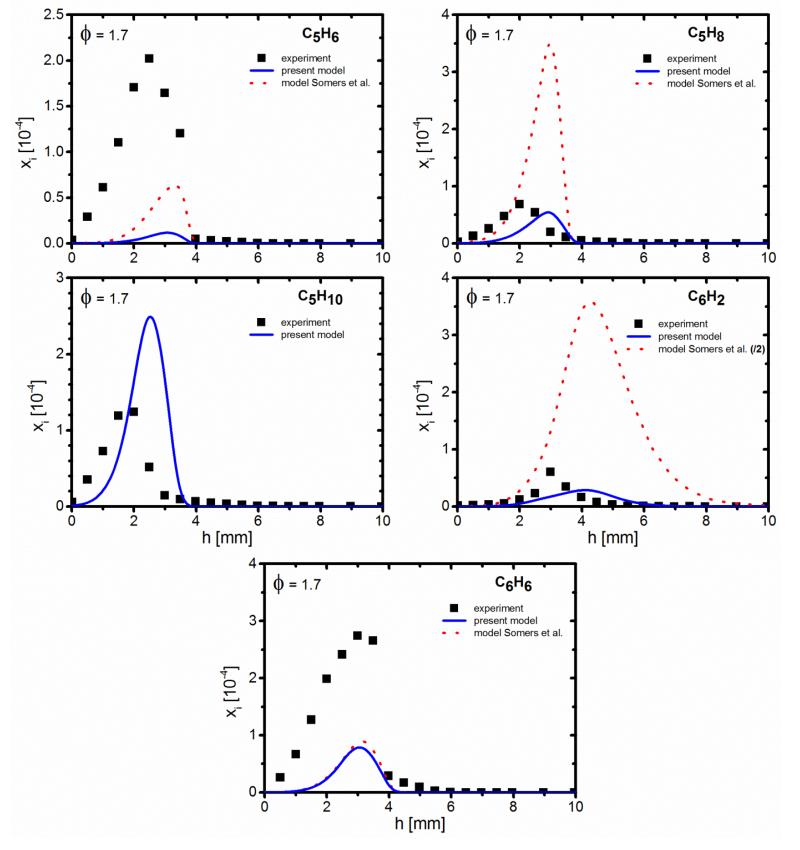
Figure 4. Mole fraction profiles of selected C5 and C6 species for φ=1.7.
Symbols: experiment (EI-MBMS); lines: simulation; solid lines: present model, dotted lines: model of Somers et al. [11], except for C5H10 (simulation data were not available). Mole fraction profiles for φ=1.0 can be found in the Supplemental Material.
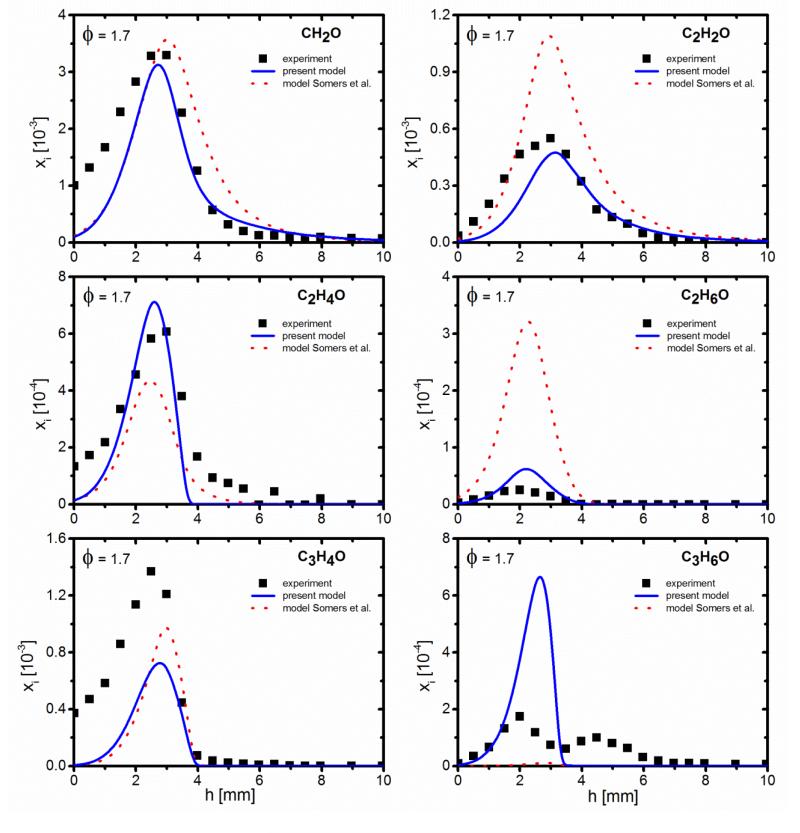
Figure 5. Mole fraction profiles of selected C1-C3 oxygenated species for φ=1.7.
Symbols: experiment (EI-MBMS); lines: simulation; solid lines: present model, dotted lines: model of Somers et al. [11]. Mole fraction profiles for φ=1.0 can be found in the Supplemental Material.
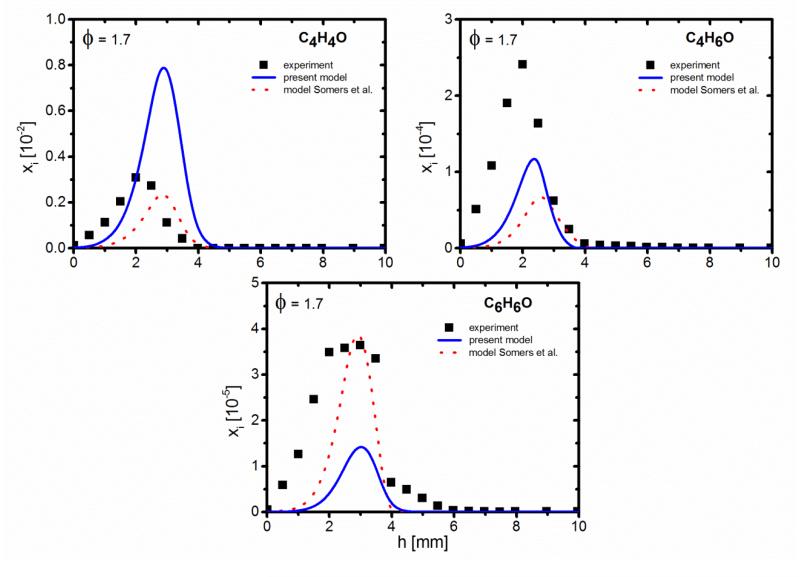
Figure 6. Mole fraction profiles of selected C4-C6 oxygenated species for φ=1.7.
Symbols: experiment (EI-MBMS); lines: simulation; solid lines: present model, dotted lines: model of Somers et al. [11]. Mole fraction profiles for φ=1.0 can be found in the Supplemental Material.
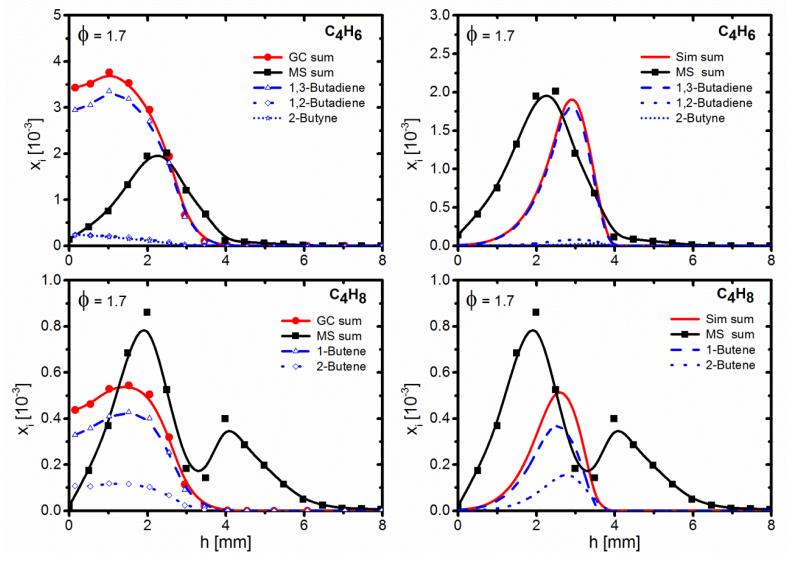
Figure 7. C4H6 isomers (1,3-butadiene, 1,2-butadiene, and 2-butyne) and C4H8 isomers (1-butene and 2-butene).
Left: mole fraction profiles (sums of C4H6 and C4H8) obtained in the MBMS experiment and results of the GC analysis. Right: respective model prediction and MBMS experiment results.
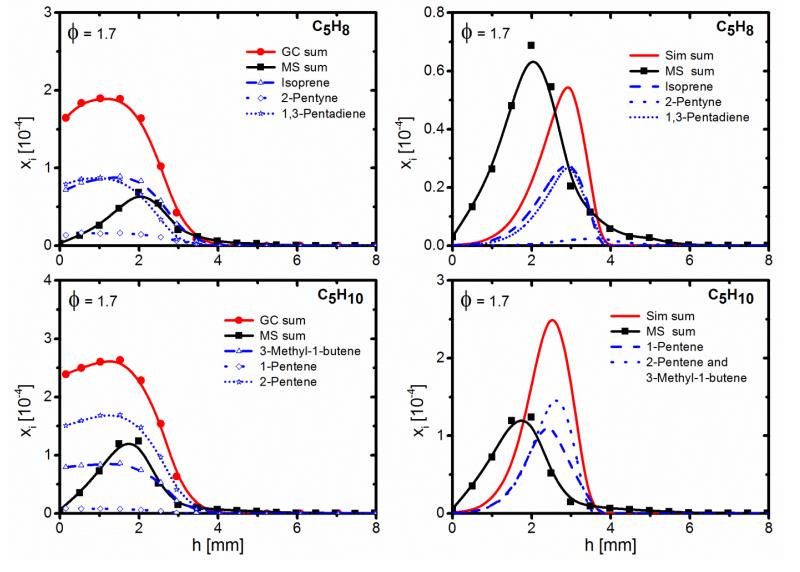
Figure 8. C5H8 isomers (isoprene, 2-pentyne, and 1,3-pentadiene) and C5H10 isomers (1-pentene, 3-methyl-1-butene and 2-pentene).
Left: mole fraction profiles (sums of C5H8 and C5H10) obtained in the MBMS experiment and results of the GC analysis. Right: respective model prediction and MBMS experiment results.
Figure 1 shows the major species profiles (MF, O2, Ar, CO, CO2, H2O, and H2) from the EI-MBMS measurements including the temperature profile in both MF flames (φ=1.0 and 1.7). The open symbols at 43 mm are equilibrium values calculated from Gaseq [17] for the experimental flame temperatures. The trends of these major species profiles are generally similar to those seen in the furan flames in Part I [13] and their mole fractions at h=40 mm are very close to equilibrium. As expected, the mole fraction of CO2 formed in the stoichiometric flame is larger than that in the fuel-rich flame, with the opposite trend noted for CO and H2. Also, the CO profile exhibits a maximum in the φ=1.0 flame, while remaining constant along the post-flame region in the fuel-rich flame.
Figure 2 and S1 display the mole fraction profiles of C1-C2 hydrocarbon intermediates, from the EI-MBMS measurements, including CH3 (methyl radical), CH4 (methane), C2H2 (acetylene), C2H4 (ethene or ethylene), C2H5 (ethyl radical), and C2H6 (ethane). Acetylene is the most abundant one of all intermediates in the MF flames with maximum mole fractions of 3.3×10−2 and 1.6×10−2 in the fuel-rich and the stoichiometric flame, respectively. The observation that the peak mole fraction of C2H2 is approximately doubles with increasing equivalence ratio from 1.0 to 1.7 (see Table 2) is also true for the furan flames in Part I [13] and the DMF flames in Part III [18]. Acetylene is considered to be the most representative soot precursor in a variety of hydrocarbon fuel flames because it contributes to the formation of benzene and aromatic rings, the first step toward the production of soot. CH4, C2H4, and C2H6 reach their maxima at 2.5-3.5 mm above the burner, with mole fractions of 4.3×10−3, 8.0×10−3, and 2.6×10−3 (φ=1.7), respectively.
Figures 3 and S2 present the profiles of C3-C4 hydrocarbon intermediates from the EI-MBMS measurement, including C3H4 (sum of allene and propyne), allyl radical (C3H5), propene (C3H6), C4H2 (1,3-butadiyne), C4H4 (1-butene-3-yne), C4H6 (sum of 1,3-butadiene, 1,2-butadiene, and 2-butyne), and C4H8 (sum of 1-butene and 2-butene). With the equivalence ratio increasing from 1.0 to 1.7, the maximum mole fractions of C3H4 and C4H4 are enhanced by about a factor of 1.5, while that of C4H2 is multiplied by about a factor of 4. C3H4 is the most abundant one of the C3 species with maximum mole fractions of 3.0×10−3 and 4.8×10−3 in the stoichiometric and the fuel-rich flame, respectively. The mole fractions of C4H2, C4H4, and C4H6 are quite similar in the fuel-rich flame, with a maximum of up to 2.0×10−3 (Fig. 3), while in the stoichiometric flame the most abundant C4 species is C4H6 (Fig. S2) with a maximum mole fraction of 2.2×10−3. From the GC analysis, C3H4 and C4H6 are predominantly propyne and 1,3-butadiene, respectively, and C4H8 is for a large part 1-butene (Table 3 and Fig. 7). The second peak seen in the MBMS measurements for C4H8 (Figs. 3 and 7) as well as for C3H6O (Fig. 5) is probably an experimental artefact.
Figures 4 and S3 show the mole fraction profiles of C5 and C6 compounds from the EI-MBMS measurement, including C5H6 (sum of 1,3-cyclopentadiene and 1-pentene-3-yne), C5H8 (sum of 1,3-pentadiene, isoprene, and 2-pentyne), C5H10 (sum of 2-pentene, 3-methyl-1-butene, and 1-pentene), C6H2 (1,3,5-hexatriyne), and C6H6 (benzene). The mole fraction of C5H6 is the largest one (maximum mole fraction of 2.0×10−4 in the fuel-rich flame) of the C5 intermediates. C6H6 is the most abundant one of the selected C6 intermediates. The GC analysis (Table 3) shows that 1,3-cyclopentadiene contributes for an important part (>80 %) to the two C5H6 isomers. Among C5H8 isomers, the maximum mole fractions of 1,3-pentadiene and isoprene are quite similar (~9.0×10−5) and are much larger than that of 2-pentyne (~1.7×10−5, see Table 3 and Fig. 8). For the three C5H10 isomers, the contribution of 2-pentene is about 64%, of 3-methyl-1-butene is about 33%, and of 1-pentene is about 3% (Table 3 and Fig. 8). For C6H6, only benzene is detected, fulvene is not seen. Note that Wei et al. [12] have detected 1,3-cyclopentadiene, 1-pentene-3-yne, 2-pentene, and benzene as well in their MF flames using photoionization MBMS.
Figures 5, 6, S4, and S5 present the mole fraction profiles of selected oxygenated intermediates from the EI-MBMS measurement. These figures show that CH2O (formaldehyde), toxic and cancerogenic, is measured with the largest mole fraction (maximum of 3.3×10−3 at h=3.0 mm for φ=1.7 and of 4.0×10−3 at h=2.7 mm for φ=1.0). For the oxygenated intermediates from C2 to C6, C4H4O (furan) is the most abundant one, with maximum mole fractions of up to 3.1×10−3 (φ=1.7, Fig. 6) and, similarly, 3.1×10−3 (φ=1.0, Fig. S5). Note that furan has not been observed in the measurement of Wei et al. [12], while in the present work furan was well identified by GC/MS. From the GC analysis (Table 3), acetaldehyde contributes for a very important part (~99%) to the C2H4O isomers. From the EI-MBMS experiment, the mole fraction profiles of C2H4O (Figs. 5 and S4) reach their maximum near 3 mm above the burner, with maximum values of 6.1×10−4 (φ=1.7) and 1.0×10−3 (φ=1.0). Propenal (acrolein, C3H4O) is also measured with a large mole fraction of up to 2.0×10−3 in the stoichiometric flame (Fig. S4). C3H6O is detected with a lower mole fraction of up to 3.5×10−4 (φ=1.0). The GC analysis (Table 3) shows that propanal is the most abundant one of the two isomers of C3H6O (propanal and acetone). C4H6O includes four isomers, namely 2-butenone, 2-butenal, isobutenal, and 2,3-dihydrofuran, with 2-butenone being the predominant one (maximum mole fraction of ~3.3×10−4). This observation is similar to that for DMF flames [18], but different to that in furan flames [13], where 2-butenal was detected with the largest mole fraction. Isobutanal is the most abundant compound of two C4H8O isomers (isobutanal and 2-butanone). C6H8O is to a large part 2-ethylfuran (~90%), while 2,5-dimethylfuran and 2,4-dimethylfuran are detected with somewhat lower contribution. Furfural (C5H4O2) is measured in the MF flames, but was not detected in the furan flames (Part I [13]) and the DMF flames (Part III [18]). Note that Wei et al. [12] have also detected 2-butenone (or 3-buten-2-one), 2-butanone, 2-ethylfuran, and 2,5-dimethylfuran in their MF flames.
Regarding selected aromatic species (benzene, toluene, and phenol), benzene is the most abundant one with maximum mole fractions of 1.4×10−4 (φ=1.0) and 2.8×10−4 (φ=1.7), a factor of 2 larger than detected in the furan flames in Part I [13]. Toluene and phenol were measured with a smaller mole fraction, in the range of 2.5×10−5-4.0×10−5. Two other aromatic compounds detected by GC are styrene (C8H8) and ethyl benzene (C8H10), with a mole fraction of ~2.0×10−5. As a first approximation, other species with a nominal mass m/z>96 were ignored in the EI-MBMS measurement, because their signals were quite small.
3. Kinetic modeling
The PREMIX computer code from the CHEMKIN package [19] was used for the kinetic modeling to simulate the combustion of MF. It computes species concentrations from the balance between the net rate of production of each species by chemical reactions and the difference between the input and output flow rates of species. The detailed kinetic mechanism, presented in Part I [13], was used. It is based on the combustion mechanism proposed previously for DMF [20], which is built up following hierarchical construction principles. Only the MF sub-mechanism is described and discussed in this paper.
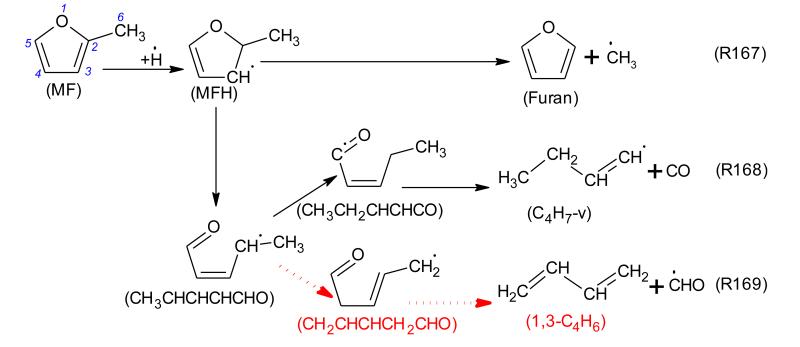
The sub-mechanism of MF is based on analogies with DMF and furan reactions. Low-pressure coefficients were used in the case of pressure-dependent rate coefficients. It is important to note that the high-pressure rate coefficients of Sirjean et al. [20] need to be used for simulation of data under high-pressure conditions. It includes unimolecular initiations, H-atom abstractions, H-atom additions to double bonds, and the subsequent decomposition of the created radicals. In the present work, the most important modification of the MF oxidation sub-mechanism described previously [20] is the addition of an H-atom addition reaction on carbon C2 (the carbon atom bearing the methyl group), yielding 1,3-butadiene (1,3-C4H6) and the CHO radical (dashed arrow in Fig. 9). Figure 9 shows that H-additions at C2 of MF lead to the formation of the resonance-stabilized 2-methyl-2,3-dihydrofuran-3-yl (MFH; C5H7O) which decomposes then to: (i) furan and the CH3 radical by ipso-addition (R167), (ii) the but-1-en-1-yl radical (C4H7-v, CH3–CH2–CH=CH) and CO (R168), and (iii) 1,3-butadiene (1,3-C4H6) and the CHO radical (R169) through ring opening and several steps of internal H-atom transfer. The first two reactions (R167 and R168) have been considered by Sirjean et al. [20], while the latter (R169) has been considered in the present study and has been added to the MF sub-mechanism. A new set of rate coefficients was applied for these H-atom addition reactions (reactions R167-R169). Their rate coefficients are presented in Table 4 and were estimated by analogy with the reactions of DMF at low pressure. The pre-exponential factors of reactions R168 and R169 were obtained using the following procedure: the sum was taken equal to the pre-exponential factor of the reaction DMF+H=CH3CO+1,3-C4H6, while the branching ratio was set equal to that in the mechanism of Somers et al. [11] at low pressure and high temperature.
Figure 9. H-atom additions at C2 position in MF: solid arrows (R167 and R168) have been considered in the mechanism of Sirjean et al. [20]; dashed arrow (R169) has been added in the present study. Rate coefficients of reactions R167, R168, and R169 are given in Table 4.
Table 4.
Rate coefficients of H-atom additions in the format A × Tn × exp(−E/RT). (k units: cm3, mol, s−1, kcal).
| No. | Reactions | A | n | E | Footnote |
|---|---|---|---|---|---|
| R167 | MF + H = furan + CH3 | 5.82E+19 | −1.61 | 9.7 | a |
| R168 | MF + H = CO + C4H7-v | 1.19E+32 | −5.24 | 17.0 | a,b |
| R169 | MF + H = CHO + 1,3-C4H6 | 1.49E+31 | −5.24 | 17.0 | a,b |
Analogy with the reactions of DMF at low pressure.
Sum of pre-exponential factors of reactions R168 and R169 was taken equal to the pre-exponential factor of the reaction DMF+H=CH3CO+1,3-C4H6, while their ratio was set equal to that in the mechanism of Somers et al. [11] at low pressure and high temperature.
The model used for flame simulations in this study consists of 305 species and 1472 reactions. The mechanism, thermodynamic and transport data are available in CHEMKIN format in the Supplemental Material of Part I [13].
4. Discussion
4. 1 Comparison between experimental and simulated results
Simulations have been performed using the PREMIX software from CHEMKIN [19]. Perturbed temperature profiles from the experiment were used as input parameters without any shift between measurement and computation. Figure 1 displays the comparison between experimental and modeling results for the major species (MF, O2, Ar, CO, CO2, H2, and H2O) for both equivalence ratios (φ=1.0 and 1.7). The model satisfactorily reproduces the consumption of reactants (MF and O2), the formation of main products (CO2, CO, H2O, and H2), and the diluent (Ar) profile, both with regard to the profile shape and the mole fraction values. Note that a small discrepancy (~20%) between prediction and experiment was observed beyond 5 mm for the H2O profile in the stoichiometric flame which is, however, within the experimental error range.
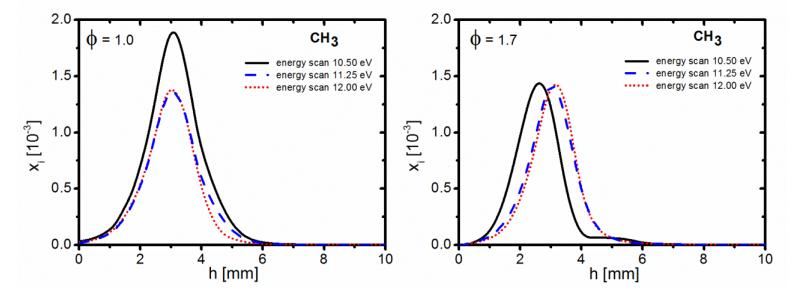
Intermediate species and the respective model predictions will be discussed for both equivalence ratios (φ=1.0 and 1.7); results for the fuel-rich flame are presented in Figs. 2-6. Analogous figures for the stoichiometric conditions can be found in the Supplemental Material. Figures 7 and 8 present results from EI-MBMS in comparison with GC measurements and simulation results. In general, quite good agreement between experimental and simulation results is observed for all intermediate species, concerning both the positions and shapes of the concentration profiles as well as their maximum values. Note that in the fuel-rich flame, small discrepancies between predictions and experiments were observed for the peak location of the profile for a number of species, including CH3, C2H5, C3H5, C3H6, C4H6, C4H8, C5H6, C5H8, C5H10, C6H2, C3H6O, C4H4O, and C6H6O. For all these species, the energy scan at 10.5 eV has been used to minimize fragmentation (see Table 2). This disagreement is potentially owed to small experimental changes between runs. Since it approximately corresponds to the experimental uncertainty of <0.5 mm in determining the absolute position, the evaluation here has placed more emphasis on potential fragmentation interferences. Indeed, for this energy, the peak location of these species is slightly closer to the burner than at 11.25 and 12 eV, while all scans at different energies peak at the same position in the stoichiometric flame (see the CH3 profile in Fig. 10 as an example).
Figure 10. Mole fraction profiles of CH3 from the EI-MBMS measurement for three energy scans at 10.5, 11.25, and 12eV in the two MF flames (φ=1.0 and 1.7).
The model tends to overpredict the maximum mole fractions of the radicals CH3 in both flames and of the radical C2H5 in the fuel-rich flame (Fig. 2). Note that CH4 and C2H6 are directly formed from CH3 radicals. C2H6 is then consumed mainly by H-abstraction to form the C2H5 radical. The mole fractions of CH4 and C2H6 for both equivalence ratios are well predicted by the model, indicating a rather correct simulation of CH3 amounts by the model. The uncertainty in the RICS calibration for radicals such as CH3 and C2H5 can be as much as a factor of 4. Therefore, the agreement is still within the expected experimental uncertainties for these two radicals.
The formation of C3H4, sum of allene (H2C=C=CH2; aC3H4) and propyne (HC≡C–CH3; pC3H4), is underpredicted by the model by a factor of 4-5. This underprediction has also been found in the furan simulation [13]. In EI-MBMS, C3H4 is calibrated as propyne, since this species is the most abundant one of the two isomers of C3H4 detected by GC (see Table 3). An agreement between EI-MBMS and GC measurements is observed for the maximum mole fraction of C3H4 within the experimental error range. A good agreement of the propyne/allene ratio in the GC measurement (~2.6) and the simulation (~2.2) is found. However, the individual pC3H4 and aC3H4 mole fractions are underpredicted by the model. According to the rate of production (ROP) analysis, pC3H4 is mainly formed through the following reaction pathway (rp1):
 |
(rp1) |
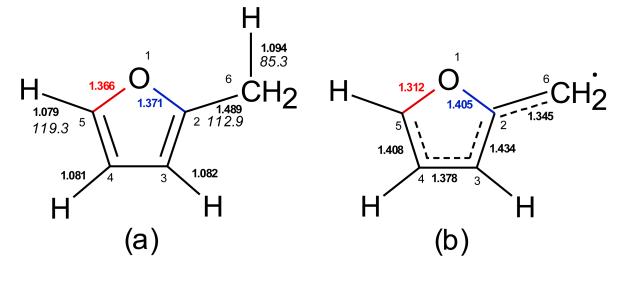
This reaction pathway shows that pC3H4 can be formed from the 2-methylfuran-5-yl radical (M5F-2yl) via the formation of the CH3CCHCHCO radical (reactions R170 and R171). The M5F-2yl radical is produced directly from MF by H-abstractions from the C-atom in position 5 (see the definition of the carbon position in the structure of MF in Fig. 11a). As presented in Ref. [20], the rate coefficients of the reactions R160-R163, R170, and R171 have been estimated by analogy with furan. Uncertainties in the rate coefficients of these reactions could explain a lack of propyne formation, leading also to an underestimated allene formation.
Figure 11. Structure of (a) MF and (b) 2-furylmethyl radical.
Bold numbers: bond length (in Å) [12]; italic numbers: calculated bond dissociation energy (in kcal·mol−1) from the thermochemical data of molecules and radicals calculated theoretically at the CBS-QB3 level of theory [20]; numbers near the atoms are the atom labels.
The overall performance of the model for the C4 species is better for MF than for furan under stoichiometric conditions. For the fuel-rich case, the agreement between model and experiment is significantly better for C4H6, while the predictions for other C4 species are of similar quality for both fuels. From the GC analysis, C4H6 is predominantly 1,3-butadiene, and C4H8 is to a large part 1-butene, as shown in Table 3 and Fig. 7. While the mole fractions of these isomers are slightly different for the two stoichiometries, trends are quite similar, also to those noted for the furan fuel under the same conditions. As discussed in Section 2, the flame is closer to the burner in the GC experiment and the conditions for the two setups are not exactly identical (especially the size of sampling probes); thus the temperature profiles are different and the species profiles obtained by GC and MBMS are shifted. For C4H6 and C4H8, the sums of all isomers measured by GC are, within the experimental uncertainty, in good agreement with the sums detected by MBMS. The different isomers are also quite well represented by the model regarding their relative importance (Fig. 7 and Table 3).
The formation of C5H6 is underpredicted in both flames. A good agreement between EI-MBMS and GC measurements (see Table 3) is observed for the maximum mole fraction of C5H6. The ROP analysis indicates that most of 1,3-C5H6 is formed directly from the phenoxy radical (C6H5O#) or via the formation of the cyclopentadienyl radical (C5H5#). Underestimating the formation of the C6H5O# radical has a consequence of too low 1,3-C5H6 as well as phenol (C6H6O) formation, a trend that will be discussed below.
C5H8 peak mole fractions differ by about a factor of 2.5 between MBMS and GC measurements, as demonstrated in Fig. 8. The isomer composition shows that two compounds contribute predominantly to the total mole fraction, namely isoprene and 1,3-pentadiene; 2-pentyne is detected with somewhat lesser contribution. While the sum of isomers agrees well between MBMS and the simulation, only two isomers, namely 1,3-pentadiene and isoprene, show up as being important for the model, with no significant contribution from 2-pentyne.
The model overpredicts the formation of C5H10 by about a factor of 1.4 and 2 for the stoichiometric and the fuel-rich flame, respectively. In EI-MBMS, C5H10 is calibrated as 2-pentene, the most abundant one of the three isomers of C5H10 detected by GC (see Fig. 8 and Table 3). The maximum mole fraction of C5H10 quantified by EI-MBMS is about a factor of 2 lower than that measured by GC. This could be associated to the uncertainty in the EI-MBMS calibration for C5H10 (RICS method from isoprene) and may still be considered as reasonable within the error limits. The isomer composition evident from Fig. 8 is similar between the GC experiment and the model, with 2-pentene as the most important species. Note that 3-methyl-1-butene is clearly identified with the GC experiment while in the model the sum of 2-pentene and 3-methyl-1-butene is considered, because the combination of the resonance-stabilized but-1-en-1-yl radical with the methyl radical can give both isomers.
For oxygenated intermediates (Figs. 5-6 and S4-S5), the mole fraction profiles of CH2O, C2H2O, C2H4O, C2H6O, and C3H4O are well predicted by the present model within the error limits of experimental values. The model reasonably predicts the formation of C3H6O and C4H4O in the stoichiometric flame, but tends to overpredict them in the fuel-rich flame. Phenol (C6H6O) is underpredicted by the model in both flames, see Figs. 6 and S5. The most important formation reaction for C6H6O is the combination of an H-atom and the phenoxy radical (C6H5O#). Thus, a possibly too inefficient formation of the C6H5O# radical leads to an insufficient C6H6O formation, as well as to a too insignificant 1,3-C5H6 formation (Figs. 4 and S3) as mentioned before.
For comparison of the simulation with the present model, the detailed kinetic mechanism of Somers et al. [11] has also been used and the respective results have been included in Figs. 2-6 and S1-S5 in the Supplemental Material (dotted lines). Their mechanism consists of 391 species and 2059 reactions and has been validated against experimental ignition delay times and laminar burning velocities. This simulation was performed using the CHEMKIN-PRO package [21]. Overall, this mechanism also predicts the formation of intermediates in the flames studied here quite well. Similar results with both mechanisms are seen for CH3, CH4, C2H2, C2H4, C3H4, C4H8, C6H6, CH2O, C3H4O, and C4H6O. Similar trends showing some disagreement between experiment and model for C3H4, C5H6 and C6H6 profiles are also observed with the mechanism of Somers et al. [11]. Larger discrepancies between the simulations with the model of Somers et al. and those using the present model are found for the following intermediates:
C2H5, C2H6, C3H5, C4H2, C5H8, C6H2, C2H2O, C2H6O, and C6H6O: their mole fractions calculated by the model of Somers et al. [11] are larger than those using the present model. For these species, the model of Somers et al. predicts well the formation of C2H6, C3H5, and C2H2O (in the stoichiometric flame), and C6H6O (in both flames), while it overpredicts the formation of C2H5 and C2H6 (only in the fuel-rich flame), and C4H2, C5H8, C6H2, and C2H6O (in both flames).
C4H6 (in the fuel-rich flame), C4H8 (in the stoichiometric flame), and furan (C4H4O): their mole fractions calculated by the model of Somers et al. [11] are somewhat lower than those from the present model. For these species, their model predicts well the formation of C4H4O in the fuel-rich flame, while it underpredicts the formation of C4H6 in the fuel-rich flame, C4H8 and C4H4O in the stoichiometric flame.
C5H10: this species is not included in the model of Somers et al. [11], but the present model predicts the formation of this species reasonably well.
It should be stressed that such differences in results for individual species in a given flame situation may be interesting and could be analyzed separately in further detail; the main focus here, however, is to examine the overall performance of a comprehensive model versus systematic experiments in six flames of three fuels. We will thus concentrate on a reaction pathway analysis for MF combustion in the following.
4.2. Reaction pathways of MF combustion
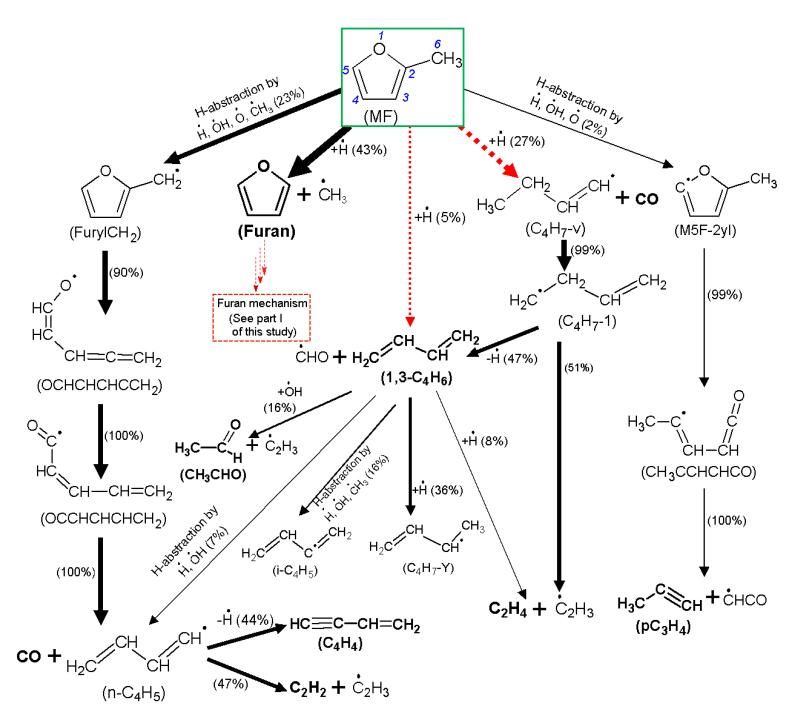
For a more detailed analysis of the MF combustion chemistry, the main pathways of MF consumption under flame conditions are inspected using a reaction flow analysis with the present model. The structure and nomenclature of selected species relevant to the following discussion in this section are shown in Table 5. Figure 12 displays the simulated main consumption paths of MF in the fuel-rich flame (φ=1.7) at a distance of 2.97 mm from the burner, corresponding to a temperature of 1197 K and 80% conversion of MF. A sufficient conversion has been chosen so that the major ways of consumption of the primary products can be observed.
Table 5.
Structure and nomenclature of some species involved in the detailed mechanism of the MF oxidation.
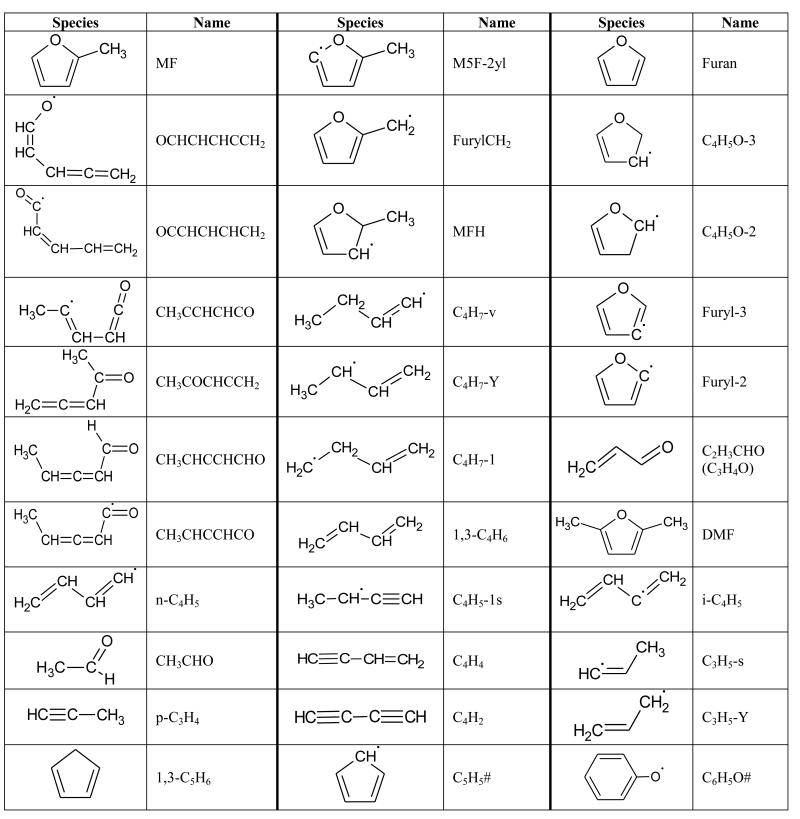
|
Figure 12. Reaction flow analysis for the consumption of MF in the fuel-rich MF flame (φ=1.7) for a distance of 2.97 mm from the burner, corresponding to a simulated temperature of 1197 K and 80% conversion of MF.
The size of the arrows is proportional to the relative rates of consumption of a given species. Dashed arrows: reaction pathways which have been added or revised in the present study (see Section 3).
Under these conditions, an important part of MF is consumed by ipso-addition yielding furan (C4H4O) and the CH3 radical (~43%). About 32% of MF is consumed by two other pathways through H-addition at the C2 position of MF, yielding the but-1-en-1-yl radical (C4H7-v, CH3–CH2–CH=CH) and CO (~27%) or 1,3-butadiene (1,3-C4H6) and the CHO radical (~5%). In the MF molecule, the bond energy of the C6-H bond (of the methyl group) is much lower than that of the C-H bond in the furan ring and that of the C2-C6 bond, as shown in Fig. 11a. By H-abstractions from the methyl group of MF, about 23% of MF is consumed to form the resonance-stabilized 2-furylmethyl radical (furylCH2), the structure of which is presented in Fig. 11b. H-abstraction from the C5 position of MF is a minor channel of consumption (only 2%) to yield the 2-methylfuran-5-yl radical (M5F-2yl).
Subsequently, furan produced by the ipso-addition reacts via several pathways, as shown in Part I [13]: (i) H-addition at the C2 position of furan to give the dihydrofuryl-3 radical (C4H5O-3), (ii) OH-addition at the C═C double bond forming propenal (acrolein, C3H4O) and the CHO radical, (iii) H-abstractions forming two types of furyl radicals, and (iv) H-addition to furan yielding the dihydrofuryl-2 radical (C4H5O-2). Furan is an important primary product in the MF decomposition. Thus, the revision of the furan sub-mechanism [13] also plays an important role in the MF simulation.
The C4H7-v radical is consumed mainly by isomerization (99%) yielding the but-3-en-1-yl radical (C4H7-1, CH2=CH–CH2–CH2) which decomposes then into C2H4 and the C2H3 radical by β-scission of the C-C bond (51%) or to 1,3-C4H6 and an H-atom by β-scission of the C-H bond (47%). Note that more than 80% of C2H4 is formed from this decomposition pathway. In the MF flame, the formation of C2H4 via furan formation is a minor contribution for its total amount. This explains why C2H4 formation is well predicted in the case of MF, while it was significantly underestimated in the furan work [13]. 1,3-C4H6 is also formed directly from MF by the second channel of H-addition on the C2 position of MF. 1,3-C4H6 is consumed subsequently by several reactions including (i) H-addition at the C═C double bond to yield the but-1-en-3-yl radical (C4H7-Y, CH3–CH–CH=CH2), (ii) OH-addition at the C═C double bond followed by β-scission of the C-C bond, with acetaldehyde (CH3CHO) and the C2H3 radical as the products, (iii) H-abstractions to form butadien-1-yl (n-C4H5) or butadien-2-yl (i-C4H5). As presented above, profiles of C2H4 (Fig. 2), C4H6 (mostly 1,3-C4H6) (Figs. 3, 7, and S2), and C2H4O (mostly CH3CHO) (Figs. 5 and S4) are quite well reproduced by the present model.
The resonance-stabilized furylCH2 radical obtained by H-abstractions isomerizes to form the OCHCHCHCCH2 radical followed by the formation of the OCCHCHCHCH2 radical which then decomposes into the n-C4H5 radical and CO by α-scission of the C-C bond. The n-C4H5 radical reacts by β-scission of the C-H bond to yield 1-butene-3-yne (vinylacetylene, C4H4) and an H-atom or by β-scission of the C-C bond to form acetylene (C2H2) and the C2H3 radical. About 38% of the C2H2 formation results from this reaction pathway and about 45% from the reactions sC3H5=C2H2+CH3 and C2H3+H=C2H2+H2. C2H2, which is detected with the largest mole fraction of all intermediates, is well predicted by the present model, as shown in Figs. 2 and S1.
The 2-methylfuran-5-yl radical (M5F-2yl) is consumed (99%) by isomerization yielding the CH3CCHCHCO radical which entirely decomposes into propyne (pC3H4) and the CHCO radical.
Some further reaction pathways, not included in Fig. 12, also merit a brief discussion. Combination reactions of the C2H3 and CH3 radicals or of the allyl radical (C3H5-Y) and an H-atom contribute significantly to the formation of propene (C3H6). 1,3-Butadiyne (C4H2) is mainly yielded by the reaction C2H2+C2H=C4H2+H and mainly consumed by the reaction with OH to yield CHO and C3H2 (C4H2+OH=CHO+C3H2). About 65% of 1-butene (1-C4H8), which is the most abundant one of the two isomers of C4H8 detected by GC (see Table 3), results from the combination reaction of allyl and methyl radicals (C3H5-Y+CH3=1-C4H8), and about 30% from the reaction of C4H7-Y with an H-atom (C4H7-Y+H=C4H8). As shown in Fig. 12, the C4H7-Y radical is obtained by the direct decomposition of MF. An important part of 1,3-pentadiene (1,3-C5H8) or of isoprene (i-C5H8), which are two abundant compounds of the three isomers of C5H8 detected by GC (see Table 3 and Fig. 8), is formed from the combination reaction of CH3 and n-C4H5 radicals or of CH3 and i-C4H5 radicals, respectively. As seen in Fig. 12, the n-C4H5 and i-C4H5 radicals appear in the direct decomposition of MF. C6H2 is formed from the reaction of C4H2 and the C2H radical. Formaldehyde (CH2O) is formed by several reactions in flames. However, a large part (~40%) comes from the reaction of O2 with C2H3 radical, which is formed directly from the fuel especially via the revised H-addition pathways (Fig. 12). Ketene (C2H2O) which is remarkably well predicted, similarly to results in [13], is produced through the following four reactions: CH2CHO(+M)=C2H2O+H(+M), C3H6+O=C2H2O+H+CH3, C3H3+O2=C2H2O+CHO, and i-C4H3+O2=C2H2O+CHCO. Dimethylether (C2H6O) is formed from the combination of CH3O and CH3 radicals and mainly consumed by H-abstractions. About 55% of acrolein (C3H4O) is yielded by OH-addition to the C═C double bond of furan (furan+OH=C3H4O+CHO) and about 40% results from the reaction of the n-C4H5 radical with O2 (n-C4H5+O2=C3H4O+CHO). As presented in Fig. 12, furan and the n-C4H5 radical are formed directly from MF. The simulated acrolein profile in MF flames is lower by a factor of 2 compared to experimental mole fractions (Fig. 5). Note that the addition of OH to MF could lead to the formation of oxygenated products, with acrolein being one of the potential products. Remember that OH-additions on DMF and furan are included in the sub-mechanism based on the work of Sirjean et al. [20] and Tian et al. [27]. Because of their symmetry, DMF and furan feature only one single resonance-stabilized adduct, which was assumed to yield one major exit channel in these previous studies. The asymmetry of the MF molecule would lead to two resonance-stabilized adducts that can further decompose into smaller fragments. Therefore, the overall OH-addition process requires estimating the branching ratio of this process, which is beyond the scope of this work. We attempted to determine the influence of this process on MF conversion by adding the reaction MF+OH=>acrolein+CH3CO by analogy with the equivalent reaction for furan (the simulated results using the model with this OH-addition to MF are not presented in this paper). This reaction would constitute an upper limit case where the branching fraction is 1 for the acrolein production channel. For the simulation conditions of Fig. 12, we observed that MF consumption by OH-addition was less than 5%. All species profiles remained almost unchanged except for the acrolein simulated mole fraction that was multiplied by a factor of 4, therefore overestimating the experimental profile by a factor of 2. This result is consistent with complex pressure- and temperature-dependent branching ratios for the MF+OH process and was neglected here to avoid additional complexity and uncertainty in the model.
Propanal and acetone (C3H6O) are mainly formed by the reactions CH3+CH2CHO and CH3+CH3CO, respectively, and then mainly consumed by H-abstractions.
In the stoichiometric MF flame, the same reactions are involved in the consumption of MF with some differences in their respective importance. Particularly, when the equivalence ratio decreases, the importance of reactions involving oxygenated radicals such as OH radicals or O-atoms is slightly enhanced, while that of reactions involving non-oxygenated radicals such as H-atoms or CH3 radicals is reduced. The reaction flow analysis for the consumption of MF in the stoichiometric MF flame (φ=1.0, at h=3.0 mm, corresponding to a temperature of 1210 K and 85% conversion of MF) is given in Fig. S6 in the Supplemental Material. This analysis shows that two important pathways of MF consumption are ipso-addition (~36%) and H-abstractions from the methyl group of MF (35%). Two other H-additions contribute with ~26% to the fuel consumption. H-abstraction from the C5 position of MF is always a minor channel of the fuel consumption (~3%).
Thanks to the reaction pathway analysis, it can be noted that the added and revised H-addition pathways played an important role in fuel consumption and species formation. Indeed, the simulated mole fraction profile of a number of intermediates was improved with the present revised model, compared to the computed results using the model before modifications (not shown in the figures of this paper). Specifically, (i) by competition with the new H-addition pathway in the fuel consumption channels, the formation of furan (C4H4O) and CH3 radicals through ipso-addition decreases, which leads then to a decrease of the mole fraction of C2H6 (C2H6=CH3+CH3) by a factor of ~1.6; (ii) the mole fraction of C4H6 increases by a factor of 7.5, and those of C2H4, C4H8, C5H8, CH2O, C2H4O, and C3H6O increase by factors of ~1.5-2. The formation of these species was already discussed above, where a strong link between the added reactions and the formation of these species was shown.
5. Summary and conclusion
The combustion of 2-methylfuran has been investigated in detail under stoichiometric and fuel-rich premixed low-pressure flame conditions. From a combination of EI-MBMS and GC, a large number of combustion products was identified and quantified. Mole fraction profiles of about 60 species were measured. A detailed kinetic model consisting of 305 species and 1472 reactions was developed, based on that of Sirjean et al. [20]. This single mechanism, previously used to predict the structure of furan flames [13], was also employed for 2-methylfuran combustion in this work. Good general agreement between experimental and modeling results for the major combustion products as well as for many intermediate species was observed. This quite satisfactory agreement refers to most profile shapes as well as to the majority of quantitative mole fraction results within experimental uncertainty. The proposed kinetic model was used to delineate the main routes of 2-methylfuran consumption, and the importance of the furan sub-mechanism in MF combustion emphasizes the adopted strategy to simulate both fuels with a single reaction mechanism.
For comparison purposes, simulations with the model of Somers et al. [11] were also presented and some differences were noted. These can be linked to the use of different sub-mechanisms of MF oxidation and of different reaction bases for the species higher than C2. Overall, a better agreement is obtained with our mechanism as it can be seen in the MF flames of both stoichiometries.
Supplementary Material
Acknowledgments
CT and DL thank the Alexander von Humboldt foundation for their research fellowships. The authors thank Patrick Nau, Julia Koppmann, and Alexander Lackner for their assistance with the temperature measurements and Regine Schröder for her assistance in preparing the manuscript. LST and DF were in part supported under the STSM program of COST Action CM 0901. The LRGP group was supported by the European Commission (“Clean ICE” ERC Advanced Research Grant) and was also granted access to the HPC resources of CINES under the allocation C2013086686 made by GENCI (Grand Equipement National de Calcul Intensif).
Footnotes
Supplemental Material is available
References
- [1].Kohse-Höinghaus K, Oßwald P, Cool TA, Kasper T, Hansen N, Qi F, Westbrook CK, Westmoreland PR. Angew. Chem. Int. Ed. 2010;49:3572–3597. doi: 10.1002/anie.200905335. [DOI] [PubMed] [Google Scholar]
- [2].Wang C, Xu H, Daniel R, Ghafourian A, Herreros JM, Shuai S, Ma X. Fuel. 2013;103:200–211. [Google Scholar]
- [3].Thewes M, Muether M, Pischinger S, Budde M, Brunn A, Sehr A, Adomeit P, Klankermayer J. Energy Fuels. 2011;25:5549–5561. [Google Scholar]
- [4].Román-Leshkov Y, Barrett CJ, Liu ZY, Dumesic JA. Nature. 2007;447:982–986. doi: 10.1038/nature05923. [DOI] [PubMed] [Google Scholar]
- [5].Tran L-S, Sirjean B, Glaude P-A, Fournet R, Battin-Leclerc F. Energy. 2012;43:4–18. doi: 10.1016/j.energy.2011.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Lange J-P, van der Heide E, van Buijtenen J, Price R. ChemSusChem. 2012;5:150–166. doi: 10.1002/cssc.201100648. [DOI] [PubMed] [Google Scholar]
- [7].Grela MA, Amorebieta VT, Colussi AJ. J. Phys. Chem. 1985;89:38–41. [Google Scholar]
- [8].Lifshitz A, Tamburu C, Shashua R. J. Phys. Chem. A. 1997;101:1018–1029. [Google Scholar]
- [9].Simmie JM, Curran HJ. J. Phys. Chem. A. 2009;113:5128–5137. doi: 10.1021/jp810315n. [DOI] [PubMed] [Google Scholar]
- [10].Simmie JM, Metcalfe WK. J. Phys. Chem. A. 2011;115:8877–8888. doi: 10.1021/jp2039477. [DOI] [PubMed] [Google Scholar]
- [11].Somers KP, Simmie JM, Gillespie F, Burke U, Connolly J, Metcalfe WK, Battin-Leclerc F, Dirrenberger P, Herbinet O, Glaude P-A, Curran HJ. Proc. Combust. Inst. 2013;34:225–232. doi: 10.1016/j.proci.2012.06.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Wei L, Li Z, Tong L, Wang Z, Jin H, Yao M, Zheng Z, Wang C, Xu H. Energy Fuels. 2012;26:6651–6660. [Google Scholar]
- [13].Liu D, Togbe C, Tran L-S, Felsmann D, Oßwald P, Nau P, Koppmann J, Lackner A, Glaude P-A, Sirjean B, Fournet R, Battin-Leclerc F, Kohse-Höinghaus K. Combust. Flame. Submitted for publication 2013. [Google Scholar]
- [14].Oßwald P, Güldenberg H, Kohse-Höinghaus K, Yang B, Yuan T, Qi F. Combust. Flame. 2011;158:2–15. [Google Scholar]
- [15].Oßwald P, Kohse-Höinghaus K, Struckmeier U, Zeuch T, Seidel L, Leon L, Mauss F. Z. Phys. Chem. 2011;225:1029–1054. [Google Scholar]
- [16].Pousse E, Glaude PA, Fournet R, Battin-Leclerc F. Combust. Flame. 2009;156:954–974. [Google Scholar]
- [17].Morley C. Gaseq v0.63, Program for thermodynamic gas equation. 1999
- [18].Togbé C, Tran L-S, Liu D, Felsmann D, Oßwald P, Glaude P-A, Sirjean B, Fournet R, Battin-Leclerc F, Kohse-Höinghaus K. Combust. Flame. Submitted for publication 2013. [Google Scholar]
- [19].Kee RJ, Rupley FM, Miller JA. CHEMKIN II: A Fortran Chemical Kinetics Package for the Analysis of Gas-Phase Chemical Kinetics. Sandia National Laboratories; 1989. [Google Scholar]
- [20].Sirjean B, Fournet R, Glaude P-A, Battin-Leclerc F, Wang W, Oehlschlaeger MA. Journal of Physical Chemistry A. 2013;117:1371–1392. doi: 10.1021/jp308901q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].CHEMKIN-PRO. Vol. 716. Reaction Design Inc.; San Diego, CA: 2010. [Google Scholar]
- [22].Joshipura KN, Vinodkumar M, Patel UM. J. Phys. B: At. Mol. Opt. Phys. 2001;34:509–519. [Google Scholar]
- [23].Orient OJ, Srivastava SK. J. Phys. B: At. Mol. Opt. Phys. 1987;20:3923–3936. [Google Scholar]
- [24].Fitch WL, Sauter AD. Anal. Chem. 1983;55:832–835. [Google Scholar]
- [25].Kim Y-K, Irikura KK, Rudd ME, Ali MA, Stone PM, Coursey JS, Dragoset RA, Kishore AR, Olsen KJ, Sansonetti AM, Wiersma GG, Zucker DS, Zucker MA. Electron-Impact Cross Sections for Ionization and Excitation. http://physics.nist.gov/PhysRefData/Ionization/Xsection.html. [Google Scholar]
- [26].Nishimura H, Tawara H. J. Phys. B: At. Mol. Opt. Phys. 1994;27:2063–2074. [Google Scholar]
- [27].Tian Z, Yuan T, Fournet R, Glaude P-A, Sirjean B, Battin-Leclerc F, Zhang K, Qi F. Combust. Flame. 2011;158:756–773. doi: 10.1016/j.combustflame.2010.12.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.