Effects of Zn²⁺ Binding on the Structural and Dynamic Properties of Amyloid Β Peptide Associated with Alzheimer’s Disease: Asp¹ or Glu¹¹?

Abstract

Extensive experimental and computational studies have suggested that multiple Zn²⁺ binding modes in amyloid β (Aβ) peptides could exist simultaneously. However, consistent results have not been obtained for the effects of Zn²⁺ binding on Aβ structure, dynamics, and kinetics in particular. Some key questions such as why it is so difficult to distinguish the polymorphic states of metal ions binding to Aβ and what the underlying rationale is, necessitate elucidation. In this work, two 3N1O Zn²⁺ binding modes were constructed with three histidines (His⁶, His¹³, and His¹⁴), and Asp¹/Glu¹¹ of Aβ40 coordinated to Zn²⁺. Results from molecular dynamics simulations reveal that the conformational ensembles of different Zn²⁺-Aβ40 complexes are nonoverlapping. The formation of turn structure and, especially, the salt bridge between Glu²²/Asp²³ and Lys²⁸ is dependent on specific Zn²⁺ binding mode. Agreement with available NMR observations of secondary and tertiary structures could be better achieved if the two simulation results are considered together. The free energy landscape constructed by combining both conformations of Aβ40 indicates that transitions between distinct Aβ40 conformations thar are ready for Zn²⁺ binding could be possible in aqueous solution. Markov state model analyses reveal the complex network of conformational space of Aβ40 modeulated by Zn²⁺ binding, suggesting various misfolding pathways. The binding free energies evaluated using a combination of quantum mechanics calculations and the MM/3D-RISM method suggest that Glu¹¹ is the preferred oxygen ligand of Zn²⁺. However, such preference is dependent on the relative populations of different conformations with specific Zn²⁺ binding modes, and therefore could be shifted when experimental or simulation conditions are altered.

Both amyloid β (Aβ) peptides and biological metal ions have been suggested to be associated with the pathogenesis of Alzheimer’s disease (AD).¹⁻¹⁵ Aβ40 and Aβ42 peptides are the primary species in the structure of the senile plaques found in the brain tissues of AD patients.⁴⁻⁶ Metal ions like Zn²⁺ and Cu²⁺ have also been found in the vicinity of the plaques, and have been suggested to be able to modulate the aggregation of Aβ peptides in in vitro experiments.^{10,11,16−18} The N-terminal region of 1–16 amino acids (Aβ16) has been identified as the minimal metal binding site of Aβ.¹⁹⁻²¹ However, the exact coordination sphere seems to indicate a polymorphic property of metal binding in various experimental conditions.^7−9,22 For example, solution NMR studies on the N-acetylated and C-amidated Aβ16 (PDB ID: 1ZE9) suggest that the Zn²⁺ binding sites include His⁶, Glu¹¹, His¹³, and His¹⁴.^19,20 Besides Glu¹¹, recent NMR studies on Aβ28, Aβ40, and Aβ42 also imply that Asp¹ is involved in the oxygen coordination of Zn²⁺.^7,9,23−25 Other possible oxygen ligands include Glu³, Asp⁷, and H₂O. Several experiments demonstrate that Arg⁵ and Tyr¹⁰ are unlikely to be oxygen ligands of Zn²⁺.^7−9,23

Recent NMR studies on the effects of Zn²⁺ binding on the structural and dynamic properties of Aβ40/Aβ42 in monomeric form suggested that three histidines (His⁶, His¹³, and His¹⁴) are the nitrogen coordinate sites of Zn²⁺.^{23,24,26−28} A second but weaker binding site possibly involving residues Asp²³ and Lys²⁸ (Asp²³, Val²⁴, Asn²⁶, and Lys²⁸) has been proposed based on high-resolution NMR data.²⁴ Another recent solid state NMR study with Aβ42 fibrils grown in physiological buffers also suggested that the binding of Zn²⁺ affects both N-terminus and the formation of the salt-bridge between Asp²³ and Lys²⁸.²⁸ Complementary to experiments, computational studies provide valuable structural insights about the binding of Zn²⁺ on Aβ monomers and oligomers.²⁹⁻³³ Molecular dynamics (MD) simulations, especially replica-exchange MD (REMD) simulations, have been applied to explore the conformational distribution of Zn²⁺-bound Aβ40 monomer and oligomers.³¹⁻³³ The polymorphic populations of Zn²⁺-bound monomers and oligomers have emerged from the above MD simulations. In addition, ab initio MD simulations have been performed to investigate the Aβ aggregation mechanism induced by Zn²⁺.²⁹ Although these theoretical studies give deep insights into understanding of the metal–Aβ interactions, some key questions, such as the effects of different Zn²⁺ binding modes on the structural, dynamic, and kinetic properties of Aβ, the relative binding affinity of various Zn²⁺ binding modes, and the possible rationale for such affinity difference, still remain elusive.

In this work, two Zn²⁺-bound Aβ40 peptides were constructed. In addition to three histidines, either Asp¹ or Glu¹¹ was considered as the oxygen coordination ligand. Extensive REMD simulations were carried out to sample their conformational spaces,^34,35 while quantum mechanical (QM) calculations were performed to compare the relative binding free energies of the two Zn²⁺ binding modes. Results from REMD simulations show that two Zn²⁺-Aβ40 systems display quite distinct structural properties. Dihedral principal component analyses, as well as Markov state models, provide molecular thermodynamic and kinetic pictures for two systems. Their preparation free energies that are required for the binding of Zn²⁺ overlap to a large extent. QM calculations suggest that Glu¹¹ is the preferred oxygen ligand coordinated to Zn²⁺. However, such preference could be shifted when the preparation energy is added to the overall binding free energy.

Results and Discussion

Cluster Analysis of the Conformational Spaces of Zn²⁺-Aβ40 Peptides

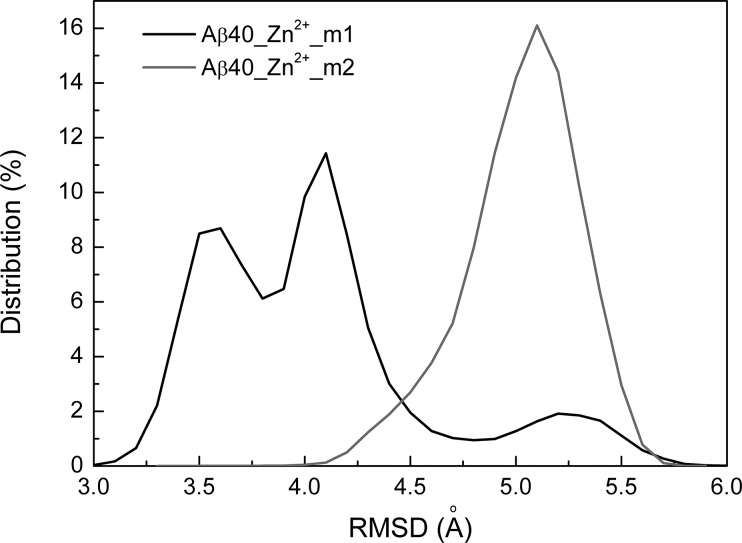
First, it is interesting to investigate the effects of the hydrophobic region Aβ(17–40) on the Zn²⁺ binding conformations of Aβ16. The backbone root-mean-square deviations (RMSDs) of the N-terminal region (Aβ16) with respect to the NMR structure (PDB ID: 1ZE9)^20,36 were calculated and shown in Figure 1. The RMSD distribution histogram shows that Aβ16 samples more conformations with two peaks located at different positions when Glu¹¹ is coordinated to Zn²⁺ (Zn²⁺-Aβ40_m1), indicating different effects of the C-terminal region of Aβ(17–40) conformations on the dynamics of Aβ16.

Figure 1.

Distribution of the backbone RMSD of the N-terminal region of Aβ16.

The main structural features of each Zn²⁺-Aβ40 peptide could be captured by a few representative structures selected from its conformational space. Cluster analysis provides a convenient tool to separate the conformational ensemble into clusters with similar geometry. The method proposed by Daura et al.³⁷ was applied here, using a cutoff of 3 Å with regard to backbone atoms of Aβ40. A total of 176 and 184 clusters were obtained for Zn²⁺-Aβ40_m1 and Zn²⁺-Aβ40_m2, respectively. However, the top five larger clusters contain about 80.2% and 82.6% of all conformations for the two systems, respectively. The central structures of these most populated clusters are shown in Figure 2. Apparently, the conformational ensemble of Zn²⁺-Aβ40_m1 was dominated by one cluster (57.8%). In contrast, the ensemble of Zn²⁺-Aβ40_m2 seems more heterogeneous, and three primary clusters cover 30.0%, 23.1%, and 20.7% of all conformations, respectively. The above results indicate that when the movement of Glu¹¹ was constrained by coordinating to Zn²⁺, the overall plasticity of Aβ40 decreased significantly. However, in the case where Asp¹ acted as the oxygen ligand, Aβ40 is still flexible enough to result in more small clusters (184 versus 176). Furthermore, if the two ensembles of Aβ40 conformations were mixed and the same clustering method was applied, a total of 360 clusters were obtained. Thus, there is no overlap between the two ensembles, excluding the possibility that Asp¹ and Glu¹¹ could be coordinated to Zn²⁺ simultaneously.

Figure 2.

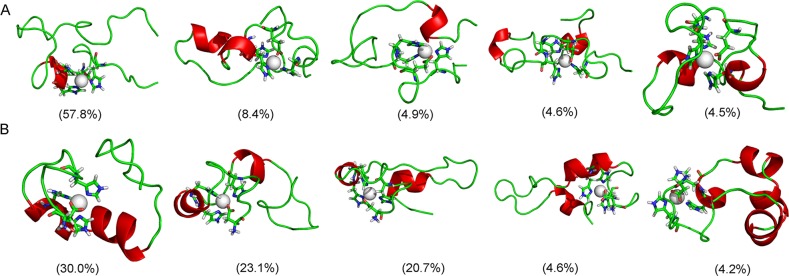
Representative conformations for the most populated cluster in Zn²⁺-Aβ40_m1 (A) and Zn²⁺-Aβ40_m2 (B).

Secondary Structure Analysis

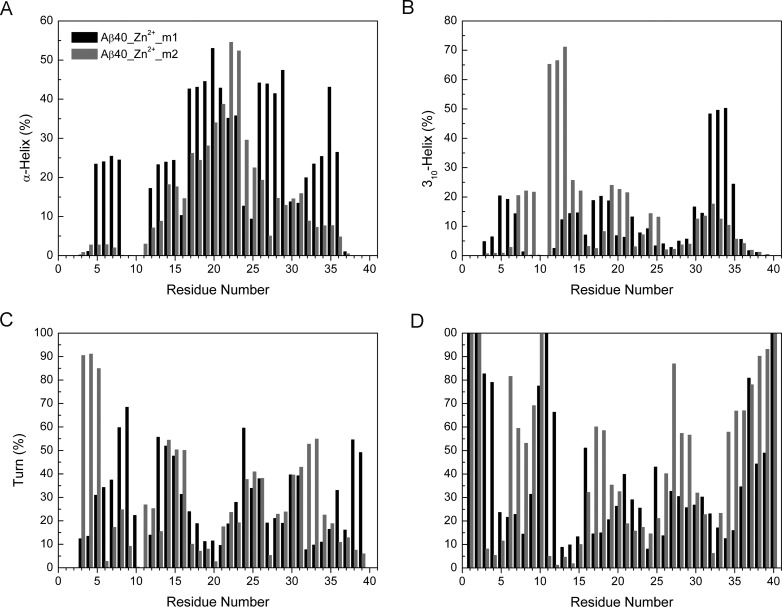
The secondary structures of Zn²⁺-bound Aβ40 were then calculated and compared using DSSP program (Figure 3).³⁸ For Zn²⁺-Aβ40_m1, residues at N- and C- termini are unstructured coil with more than 40% probability. Abundant helix (α-helix+3₁₀-helix) structures were observed in center hydrophobic core (CHC) 17–21 (∼42–71%), residues 26–29(∼44–53%), and residues 32–35 (∼65–73%). Such results were consistent with our previous REMD simulations where both termini of Aβ40 were capped.³³ However, these observations may overestimate the helix contents in Zn²⁺-bound Aβ40 due to the force field used and DSSP program as discussed in the literatures.^{30,31,39−41} Because we are only interested in the relative values, these limitations would have little effect on our results and discussions. Notable turn structures form in regions 7–9 and 13–15, with probabilities varying from 43 to 58%. Residues 16 and 30 are more likely to display β strand with negligible probabilities (<15%) (Figure S1, Supporting Information).

Figure 3.

Content of secondary structures for two Zn²⁺-Aβ40 systems.

Compared to Zn²⁺-Aβ40_m1, the C-terminus of Zn²⁺-Aβ40_m2 (residues 34–40) adopts random coil structure more frequently, implying it is more dynamic. Residues 11–15 and 19–25 display pronounced helix structures, with probabilities varying from 50 to 83% and 38 to 50%, respectively. A very stable turn structure occurs in a region 3–5, with 82–91% probability.

Consistent results have not been obtained from various experimental studies of the effects of Zn²⁺ binding on the secondary structures of Aβ40. Based on high-resolution NMR studies of the Zn²⁺ binding to Aβ40 at 286 K and physiological pH, regions 2–5 and 7–12 could possibly display turn structures.²⁴ Interestingly, our simulation results show that the region 2–5 exists as turn structure when Asp¹ is the oxygen ligand of Zn²⁺ (Zn²⁺-Aβ40_m2), whereas the region 7–12 prefers turn structure when Glu¹¹ is the oxygen ligand of Zn²⁺ (Zn²⁺-Aβ40_m1). Recent NMR studies performed at 278 K and pH 7.2 suggested that a turn like structure could be induced at a region 24–28 and stabilized by the salt bridge between Asp²³ and Lys²⁸.²³ In contrast, according to the solid-state NMR studies of Zn²⁺ binding to Aβ42 fibrils carried out at room temperature and pH 7.4, major structural changes happened in the N-terminus and the loop region (residues 23–31).²⁸ In particular, the salt bridge formed between Asp²³ and Lys²⁸ was found broken²⁸ (see discussion below). With regard to this work, either helix or random coil structure was identified from our simulations, depending on whether Asp¹ or Glu¹¹ is the oxygen ligand of Zn²⁺.

Tertiary Structure Analysis

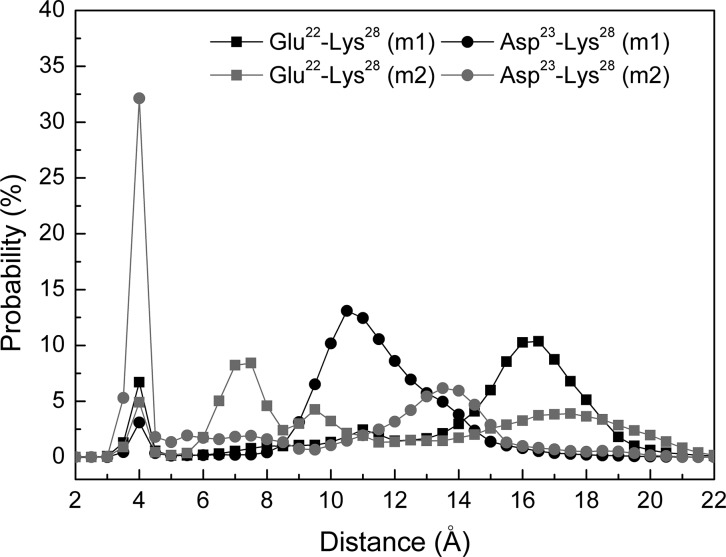
The tertiary structure analysis was performed by calculating the contact frequencies among all residues (Figure 4). We consider two amino acids are in contact if the center of mass between these two residues is within 6.5 Å. As expected, Zn²⁺ binding residues and residues flanking these amino acids are in contact. Especially, in Zn²⁺-Aβ40_m1, residues at the N-terminus (1–5) contact with C-terminal residues including Gly³³, Leu³⁴, Gly³⁷, and Val³⁸ with ∼20% probability. Two Zn²⁺ binding residue (His¹³ and His¹⁴) also contact with C-terminal residues like Ile³², Gly³³, and Val⁴⁰ with probabilities varying from 55% to 74%. The above two cooperative interactions may result in a higher turn content in the linking region 7–9. In the case of Zn²⁺-Aβ40_m2, the N-terminus contacts the C-terminus of Aβ40 more frequently than in the context of Zn²⁺-Aβ40_m1. In addition, several central residues (such as Phe¹⁹, Phe²⁰, Asp²³, and Val²⁴) contact the C-terminal residues (Gly³⁷, Gly³⁸, and Val³⁹) with ∼20% to 30% probabilities, which can be attributed to the flexible C-terminus of Aβ40. Moreover, a closer examination of the contacts between Glu²² or Asp²³ and Lys²⁸ in terms of the distance between the anionic and cationic residues suggests that a salt bridge formed between Asp²³ and Lys²⁸ occurs most frequently in the system Zn²⁺-Aβ40_m2 (Figure 5). On the other hand, the salt bridge formed between Glu²² and Lys²⁸ is more frequent than it does between Asp²³ and Lys²⁸ in the system Zn²⁺-Aβ40_m1. Although Glu²² and Asp²³ are neighboring residues, they seem to be competitors for the formation of salt bridge with Lys²⁸. This phenomenon has also been observed for Zn²⁺-free Aβ40 previously.³¹ If we assume two Zn²⁺ binding modes coexist, it is not surprising to speculate that the formation of the salt bridge between Asp²³ and Lys²⁸ of Aβ40 could be either discernible or not, depending on which one is the most populated species under specific conditions. Because of the difficulties in the characterization of the polymorphic states of Zn²⁺ binding with Aβ peptides, fully consistent results obtained from experiments and simulations are not expected. Even so, our results demonstrate that using the results obtained from two independent simulations can provide better rationale for the observations from various experiments.

Figure 4.

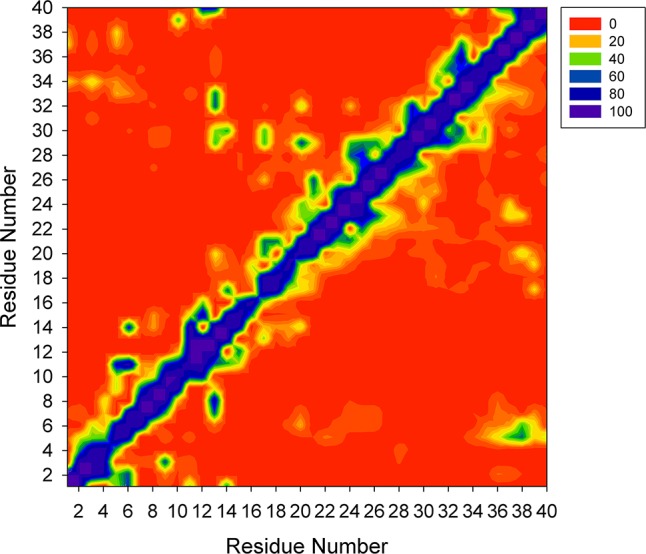
Contact maps for two Zn²⁺-Aβ40 systems. The contact map of Zn²⁺-Aβ40_m1 is shown in the upper half panel, and the contact map of Zn²⁺-Aβ40_m2 is shown in the lower half panel.

Figure 5.

Distance distributions between C^δ of Glu²² and N^ξ of Lys²⁸ and between C^γ of Asp²³ and N^ξ of Lys²⁸.

Free Energy Surfaces

The two-dimensional free energy surfaces of Zn²⁺-bound Aβ40 peptides were constructed using dihedral principle component analysis (dPCA), which has been shown to be able to separate internal and overall motions of a protein and thus can characterize more complex features of the free energy landscape (FEL) of disordered proteins.⁴²⁻⁴⁴ Figure 6 shows that, for each system, the global energy minimum is separated from the other part by high energy barriers, which is more significant for system Zn²⁺-Aβ40_m2 (Figure 6B). Multiple local minima with comparable energies were identified to be separated by shallow energy barriers for each FEL. Conformational conversions within basins seem much easier for system Zn²⁺-Aβ40_m2 because each basin covers larger area in the surface (Figure 6B). These findings are consistent with the clustering results that the conformational space of Zn²⁺-Aβ40_m1 is dominated by one cluster whereas several comparable clusters exist in the ensemble of Zn²⁺-Aβ40_m2 conformations. Assuming two zinc binding modes are equally populated and combining the two trajectories of Aβ40, we constructed a third FEL as shown in Figure 6C. Similar to individual FEL, this surface is divided into two parts. According to their relative conformational energies (see discussion below), the global minimum corresponds to the lowest basin of Zn²⁺-Aβ40_m1. Of note, the other part of this surface is not so rugged as compared to individual FEL, suggesting that various Aβ40 conformations that are ready for Zn²⁺ binding can exist in aqueous solution simultaneously and conformational transitions may occur easily. However, such free energy scenario is not static but largely dependent on the relative populations of different Zn²⁺-bound Aβ40. From a statistical point of view (see discussion below), the average energy barrier needs to be crossed is ∼123 kcal/mol, indicating that conformational conversions between the two states might be difficult.

Figure 6.

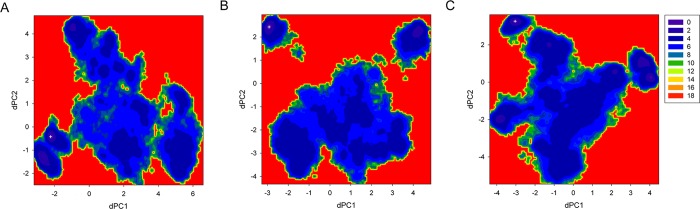
Conformational free energy surfaces for Zn²⁺-Aβ40 systems. Each was constructed by projecting its conformations onto the first two dihedral principle components (dPC1 and dPC2). The free energy values (in kcal/mol) were obtained by ΔG = −k_BT[ln(P_i ) – ln(P_max)], where P_i and P_max are the probability distributions calculated from a histogram of individual REMD simulation trajectory. ln(P_i) – ln(P_max) was used to ensure ΔG = 0 for the lowest free energy points (denoted as a cross symbol).

Markov State Model Analyses

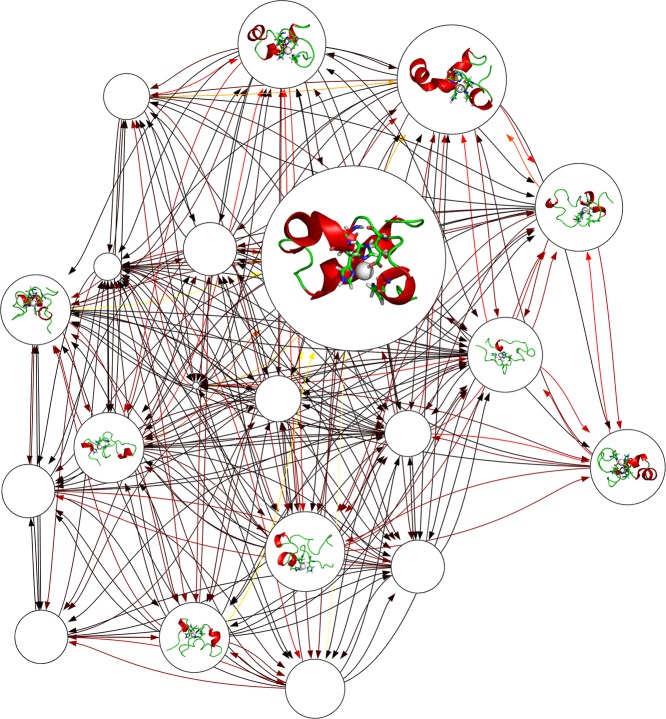
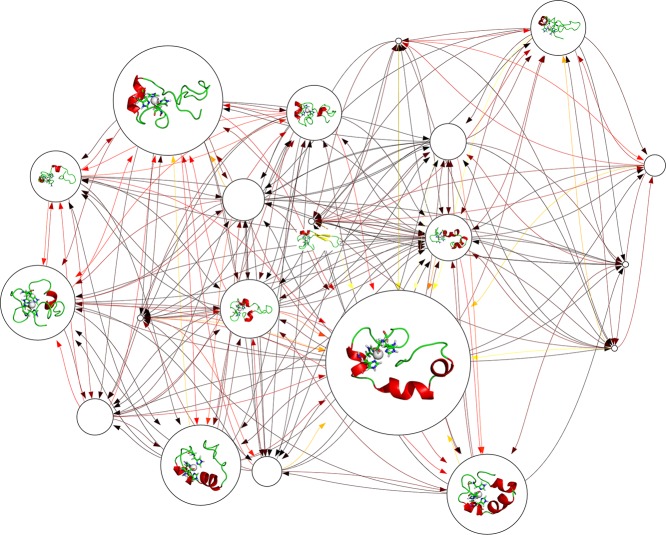
The independent conformational states were further characterized by construction of Markov state models (MSM),⁴⁵⁻⁴⁷ which assume that the structural similarity implies a kinetic similarity, and conformations can interconvert rapidly within the same state. Network graphs containing 20 microstates are shown in Figures 7 and 8 for Zn²⁺-Aβ40_m1 and Zn²⁺-Aβ40_m2, respectively. Both networks display busy transitions from one states to another, with the most populated microstates serve as kinetic hubs whereas the less populated states are more likely to be metastable intermediates. In particular, conformations with β-strands are identified in the network of Zn²⁺-Aβ40_m2 (Figure 8), but their role in the whole transition network may not so significant because various alternative pathways that do not involve these states are available. The mean first passage times (MFPTs), which quantitatively estimate the average time needed to walk from all the other states to a give state, are calculated and compared for two Zn²⁺ binding modes (Figure S3, Supporting Information). In general, the MFPTs increase as the populations of microstates decrease, suggesting a simple population-dependent transition network for Zn²⁺-bound Aβ40. As intrinsically disordered proteins, there is no such native state that may act as kinetic hubs⁴⁸ or traps;⁴⁹ the role of each state in the kinetic network relies on its relative population and thus can be easily changed. In addition, both state populations (Figure S2, Supporting Information) and MFPTs (Figure S3, Supporting Information) of two systems are very close to each other, indicating that it is rather difficult to distinguish the kinetic behavior of different Zn²⁺-bound Aβ40.

Figure 7.

Markov state model constructed for Zn²⁺-Aβ40_m1. In the network graph, the node size is proportional to its corresponding equilibrium populations. Transition probabilities between microstates are colored according to their hot degrees; that is, darker color indicates larger transition probability. Representative conformations are shown for the top 10 microstates only. The Zn²⁺ binding sites including three His and one Glu residues are displayed as sticks, while Zn²⁺ is displayed as white van der Waals spheres.

Figure 8.

Markov state model constructed for Zn²⁺-Aβ40_m2. The representations are the same as shown in Figure 7.

Binding Free Energies

The calculated binding free energies of the two system are summarized in Tables 1 and 2. The Zn²⁺ binding free energies of the two model structures (Figure 9) are very close to each other in gas phase and in aqueous solution, suggesting there is no significant preference of Zn²⁺ for anionic Asp¹ or Glu¹¹. Previous studies of Cu²⁺ binding to Aβ40/Aβ42 peptides also found that Asp and Glu are comparably favorable ligands of Cu²⁺.⁵⁰ To fully assess the capability of Zn²⁺ binding, the free energy change for the conformations of Aβ40 that are ready for Zn²⁺ binding is required. This preparation energy was first evaluated using the MM/GBSA method which has been shown to give satisfactory performance and efficiency.⁵¹ Because only the relative values are important, the conformational energy of free Aβ40 was taken as a reference and was not calculated. Adding the binding free energy from QM calculations and the preparation energy of Aβ40 gives the final Zn²⁺ binding free energy (Table 1). Compared to Glu¹¹, Asp¹ is a more favored Zn²⁺ ligand, with a relatively lower binding energy of 4.89 kcal/mol. Not surprisingly, the difference of enthalpy (8.73 kcal/mol) in the preparation energy is the predominant contribution, which can be further attributed to the solvation free energy (Table 2). As a result, different Zn²⁺ binding modes greatly influence the solvation property of Aβ40. Although entropy calculated using normal-mode analysis has been applied to Aβ and α-synuclein monomers,⁵²⁻⁵⁵ our results indicate that Aβ40 has almost the same entropy upon different Zn²⁺ binding modes may suggest that it is not an appropriate approach to characterize intrinsically disordered proteins (IDPs) like Aβ.⁵⁶

Table 1. Binding Free Energies (in kcal/mol) for Zn²⁺-Bound Aβ40 Systems in Terms of the MM/3D-RISM Theory^a.

systems	ΔGbinding (QM,gas)	ΔGsolv (QM)	ΔGprep	ΔGbinding
Zn2+-Aβ40_m1	–530.64	442.28	–2888.69 – Gref	–2977.05 – Gref
Zn2+-Aβ40_m2	–529.20	444.68	–2765.23 – Gref	–2849.75 – Gref
ΔΔGbinding = ΔGbinding(m1) – ΔGbinding(m2) = −127.30

^aΔG_binding (QM,gas) is the binding energy calculated in gas phase based on QM model structures. ΔG_solv (QM) is the solvation free energy of QM model structures. ΔG_binding (QM) is the binding free energy of QM model structures. ΔG_prep is the preparation energy calculated using the MM/3D-RISM method. G_ref is the free energy of the reference system (Zn²⁺-free Aβ40). ΔG_binding is the total free energy of Zn²⁺ binding to Aβ40.

Table 2. Energy Components Used for the Calculation of Preparation Energy of Aβ40 Based on the MM/GBSA and MM/3D-RISM Methods.

system	Zn2+-Aβ40_m1	Zn2+-Aβ40_m2
MM/GBSA method (energy unit: kcal/mol)
⟨Sol.⟩	–751.29 (4.48)	–703.67 (14.73)
⟨H⟩	–853.65 (1.81)	–863.25 (2.80)
⟨TS⟩	443.72 (0.06)	442.85 (0.07)
⟨Gprep⟩	–1297.37 (1.87)	–1306.10 (2.86)
MM/3D-RISM method
⟨Sol.⟩	23.33 (1.69)	85.27 (14.49)
⟨H⟩	–2151.46 (1.91)	–2142.43 (6.21)
⟨TS⟩	737.23 (26.25)	622.80 (10.34)
⟨Gprep⟩	–2888.69 (2.23)	–2765.23 (6.33)

Figure 9.

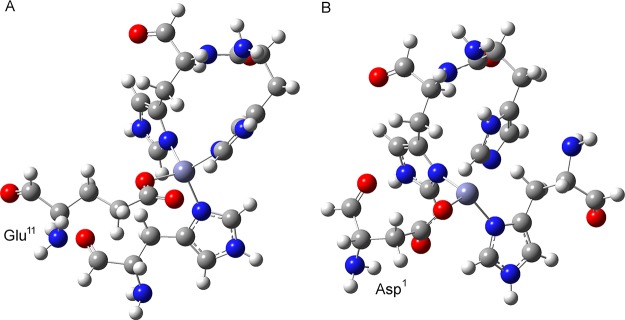
Small model structures used for quantum mechanical calculation of Zn²⁺ binding free energy when Glu¹¹ (A) or Asp¹ (B) is coordinated to Zn²⁺.

In contrast, results based on the MM/3D-RISM method indicate that Glu¹¹ is more preferred oxygen ligand (Table 1), and the major contributions arise from the favorable enthalpy (including solvation free energy) and the entropy (Table 2). Moreover, the finding that the distribution of enthalpy can be well approximated by the Gaussian function (Figure S6, Supporting Information) is in agreement with previous studies of conformational entropy of Aβ42 and its mutants.^57,58 The entropy of Aβ42 has been estimated to be 859.6 kcal/mol based on the 3D-RISM calculations,⁵⁷ thus, the entropy loss of Aβ40 (assumed the same as Aβ42, and taken as a reference) is much significant in the case where Asp¹ is coordinated to Zn²⁺ (Table 2).

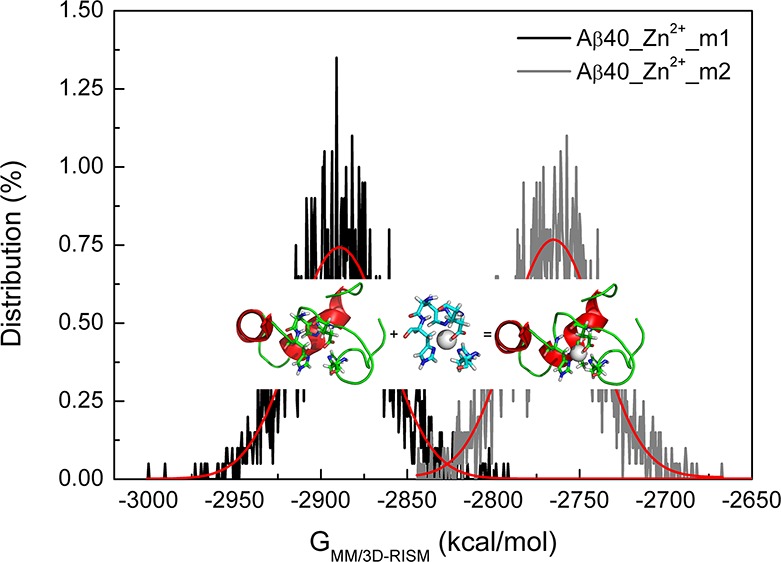
Do the above results mean that we can clearly distinguish Zn²⁺ binding modes between Asp¹ and Glu¹¹ under the same conditions? Note that all the values obtained from the MM/3D-RISM calculations are block averaged. A Gaussian distribution is expected for the preparation energy of each system (Figure 10 and Supporting Information Figure S6). Of importance, in the whole energy range, the two sets of energy values overlap to some extents, suggesting the existence of Asp¹ coordinated to Zn²⁺ cannot be excluded entirely. Overall, the different conformations of Aβ40 with different Zn²⁺ binding modes support the proposed concept of polymorphism in metal ions binding to Aβ peptides. Assuming the same population of conformations of Aβ40 (∼1%), the decrease of binding free energy (−127.30 kcal/mol) when Glu¹¹ binds to Zn²⁺ relative to Asp¹ implies an incredible increase of the binding affinity (∼10⁹⁹). However, in the range of overlapped energy (−2850 to −2800 kcal/mol for example), the relative population of Zn²⁺-Aβ40 conformations with the same preparation energy determines which binding mode is preferred.

Figure 10.

Distribution of the preparation free energies for Zn²⁺-Aβ40 systems. Red curves denote the fit by the Gaussian function.

Previous studies of interactions of small molecules with Aβ have suggested that multiple binding modes with different affinities are possible.⁵⁹⁻⁶¹ Here, we show the same polymorphic property of binding of Zn²⁺ with disordered Aβ. The binding of metal ions to Aβ is very sensitive to environmental conditions such as temperature, ionic strength, peptide concentrations, and pH in particular,^22,62,63 resulting in heterogeneous distribution of binding conformations.^7,8,64 In addition, the binding mode is also dependent on the length of Aβ peptide.²² Note that the fragment of 1–16 of Aβ (Aβ16) has been considered as the metal binding domain.^20,21,68 If Aβ16 was protected with N-terminus acetylated and C-terminus amidated, Glu¹¹ has been identified as the only oxygen coordination of Zn²⁺, and the Zn²⁺-Aβ16 complex is soluble and stable. In contrast, the unprotected Aβ16 aggregated immediately upon addition of Zn²⁺ in physiological conditions.²¹ Our solvation free energy results based on the MM/3D-RISM also show that the Zn²⁺-Aβ40 complex is less soluble and consequently more prone to aggregate to form toxic oligomers when Asp¹ is involved in the binding of Zn²⁺ (Table 2). Besides the polymorphic Zn²⁺-Aβ40 conformations, the interplay of different Zn²⁺ binding modes may further alter the conformations of Aβ40 and regulate their population shifts. As a result, the Zn²⁺ binding mode of Aβ40 is not just a problem with respect to Asp¹ or Glu¹¹, but greatly influenced by environmental variability.

Conclusions

In order to understand how the interactions of metal ions with Aβ influence the structural, thermodynamic, and kinetic properties of Aβ, a combination of REMD simulations, dihedral PCA, Markov state model, and QM calculations was applied to investigate the polymorphic states of Zn²⁺-bound Aβ40 peptides. In particular, the binding preference of two different Zn²⁺ binding modes, that is, Asp¹ or Glu¹¹, binds to Zn²⁺, was examined. Our results show that there is no overlap between conformational ensemble of Aβ40 with different residues (Asp¹ or Glu¹¹) coordinated to Zn²⁺. Using results obtained from two independent simulations, the formation of turn structure in the regions 3–5, 7–9, and 13–15 are consistent with available observations from various NMR studies. Notable, the formation of the salt bridge between Asp²³ and Lys²⁸ is more frequent when Asp¹ is coordinated to Zn²⁺, whereas this salt bridge seems to be disrupted when Glu¹¹ is coordinated to Zn²⁺ because the interactions of Glu²² with Lys²⁸ are more competitive. These findings provide new insights into understanding the polymorphic properties of Aβ structures that coordinate with metal ions.

The binding preference of Zn²⁺ to Asp¹ and Glu¹¹ seems to be negligible according to our QM calculations of simplified model structures. However, Glu¹¹ is found as a more favorable Zn²⁺ binding site in the framework of Aβ40 in terms of the more accurate MM/3D-RISM calculations, which is primarily attributed to the favorable enthalpy and entropy when Zn²⁺ binds to Glu¹¹. Although the energy barrier is difficult to cross in the conformational transitions between different Zn²⁺-bound Aβ40, the overlap of the preparation free energies in a wide range indicates the co-occurrence of polymorphic Zn²⁺ binding modes under the same experimental conditions. The interplay between different binding modes further complicates their relative populations. The kinetic networks show the presence of numerous hub-like microstates that help to create diverse misfolding pathways. Strategies like chemical protection and mutation might not be useful to unambiguously probe the metal binding sites in Aβ peptides as have already been discussed.⁶⁵

Methods

REMD Simulations

Because experimental structures of full-length Zn²⁺-bound Aβ40 peptides are not available, the Zn²⁺-Aβ40 complex was usually constructed by linking experimental structures of Zn²⁺-Aβ16 (PDB ID: 1ZE9)^20,36 with C-terminal region of Aβ(17–40) extracted from Aβ fibril structure (PDB ID: 2BEG).³¹⁻³³ Different from our previous studies,^33,60 both N and C termini of Zn²⁺-Aβ16 were unprotected. In this work, two 3N1O Zn²⁺ binding modes were considered, that is, [His⁶, Glu¹¹, His¹³, His¹⁴] (referred to as Zn²⁺-Aβ40_m1), and [Asp¹, His⁶, His¹³, His¹⁴] (referred to as Zn²⁺-Aβ40_m2). The same force field parameters as used previously were applied in this work.^33,60 Briefly, the peptide was represented by Amber ff99SB force fields,⁶⁶ with the Zn²⁺ binding sites modeled by Amber force field parameters derived from QM calculations.^33,60,67 The modified generalized Born model (Onufriev–Bashford–Case model) was used to implicitly account for the solvent effects.⁶⁸ All REMD simulations were performed using Amber 12 software.⁶⁹

MD simulations (including REMD simulations in particular) have become one of the most popular methods to explore the conformational spaces of intrinsically disordered proteins like Aβ peptides in various length and their interactoins with small molecules.^{31−33,36,41−44,70−80} In REMD simulations, N independent replicas are simulated at N different temperatures in parallel. At a specific time interval, the neighboring replicas attempt to exchange with an acceptance rate determined by the Metropolis criteria. Consistent with our previous studies,^33,60 the temperature ranges from 280 to 400 K, and 16 replicas for each Zn²⁺-Aβ40 system were used. The average acceptance rates are about 53% and 52% for Zn²⁺-Aβ40_m1 and Zn²⁺-Aβ40_m2, respectively, in line with previous REMD simulations of Aβ monomers and oligomers with acceptance rates vary from 40% to 67%.⁴⁵⁻⁴⁸ Convergence of the REMD simulations was checked by the calculation of the cumulative helix content.^33,60,81 It was found that each 250 ns REMD simulation reaches convergence after 100 ns (Figure S4, Supporting Information). Therefore, only the last 100 ns trajectories simulated at 280 K (experimental relevant temperature) were used for data analysis.

Direct comparisons with NMR observables such as chemical shifts, scalar coupling constants, and relaxation data are not feasible because rather limited NMR data of Zn²⁺-bound Aβ is available. In our recent studies of Zn²⁺-bound Aβ peptides,⁸² we attempted to reproduce the NMR ¹⁵N relaxation parameters including the longitudinal relaxation rates R₁, transverse relaxation rates R₂, and nuclear Overhauser effect rates (NOEs) using REMD simulation trajectories obtained at high temperature (408 K). In order to correct for the effect of elevated temperature, the time axis needs to be rescaled by optimizing a scaling factor that maximizes the agreement between simulated and experimentally determined relaxation data. Here, the same protocol was applied to compare the internal dynamics of different Zn²⁺ binding modes. It was found that using the same scaling factor (α = 260), Zn²⁺-Aβ40_m1 and Zn²⁺-Aβ40_m2 display similar trend for these relaxation data (Figure S5, Supporting Information). However, the significant discrepancy of NOE values between experiment and Zn²⁺-Aβ40_m2 may imply that different scaling factors are required to optimize the match between experimental and simulated relaxation data. As a result, the involvement of Asp¹ or Glu¹¹ in the binding of Zn²⁺ may affect the overall dynamics of Aβ in solution differently.

Markov State Model

The same protocol as applied in our recent work⁸³ was used to build a coarse grained MSM for each Zn²⁺-Aβ40 system. Briefly, Ward’s algorithm was first applied to cluster conformations of each ensemble into small states named microstates based on the backbone dihedral angles. Then the transition probability matrix was calculated to determine the implied time scales that corresponds to the time scale required for transition between different microstates. The Perron cluster cluster analysis (PCCA) algorithm was used to group kinetically related microstates into different macrostates. MSMBuilder2⁸⁴ and MSMExplorer⁸⁵ were used to construct and visualize MSMs.

Free Energy of Zn²⁺-Bound Aβ40

The preparation energy of Aβ40 is defined as the free energy difference between Zn²⁺-free conformations and conformations that are required for Zn²⁺ binding. Since the energy of Zn²⁺-free Aβ40 conformations was just taken as a reference, and we were concerned about the relative free energy, REMD simulations were not performed on Aβ40 peptide. The free energy of the conformations that are ready for Zn²⁺ binding is obtained using the conformational ensemble of Zn²⁺-bound Aβ40 after removing Zn²⁺. The MM/GBSA method was applied to estimated the preparation free energy as⁸⁶

where E_MM is the internal energy (a sum of electrostatic E_elec and van der Waals E_vdw interaction energies). The solvation free energy G_solv includes the electrostatic contribution and the nonpolar part that is proportional to the solvent accessible surface area of Zn²⁺-Aβ40. The entropy S was calculated using normal-mode analysis on trajectories obtained from REMD simulations. Each energy term was calculated using the block average method. That is, the 100 ns trajectory was divided into five 20 ns parts and the standard deviations were calculated.

Because of the drawback of the implicit model used to calculate the solvation free energy in the MM/GBSA method, the three-dimensional reference interaction site model (3D-RISM) was also applied to calculate the solvation free energy.⁸⁷ This alternative approach is based on the integral-equation theory of liquids and is able to account for both polar and nonpolar features of the solvation structure.^88,89 In this work, the KH closure approximation proposed by Kovalenko and Hirata was used to calculate the solvation free energy.⁹⁰ In particular, a new method of computing the conformational entropy of IDPs like amyloid peptides has recently been derived from the 3D-RISM theory.^57,58

where H is the enthalpy obtained from the 3D-RISM calculation and ⟨...⟩ denotes the average. In this work, the value of H was obtained by combining the protein internal energy (E_MM) and the solvation free energy from the 3D-RISM calculations.

QM Calculations

Due to the size limitation for QM calculations, only a small model structure (Figure 9) containing the Zn²⁺ coordination sphere was used here. Note that His¹³ and His¹⁴ are linked together to accurately model adjacent hisditine residues in Aβ40. All QM calculations were carried out by DFT calculations implemented in Gaussian 09.⁹¹ The model structure was first optimized with B3LPY/6-31+G* basis set. Then frequency analysis was performed in order to verify that the optimized structure was at a stationary point of the potential energy surface. Finally, thermodynamic values such as zero-point energies, enthalpies, entropies, and Gibbs free energies were obtained. Solvation free energies were calculated by applying the self-consistent reaction field polarizable continuum model, as implemented in Gaussian 09 (with keywords scrf=cpcm).⁹¹ Previous studies on the binding of Cu²⁺ to Aβ40 suggested that the whole entropy of each Zn²⁺ ligand can be reasonably approximated using only the vibrational entropy of each ligand.⁵⁰ Therefore, entropy contributions from translational and rotational components were neglected in our calculations. For metal ions, the semiempirical Sackur-Tetrode equation has been used to calculate the translational entropy of Cu²⁺, and the reported experimental solvation energy of Cu²⁺ was introduced as well.⁵⁰ Since we are interested in the relative energy, both the translational entropy and solvation energy of Zn²⁺ were obtained from QM calculations.

The overall Zn²⁺ binding free energy was calculated as

and ΔG_binding (gas, QM) was calculated as

where G_model, G_His-His, G_Asp/Glu, and G_His are the free energies of the small model structure, His-His, Asp/Glu, and His fragments, respectively. ΔG_solv (QM) is the QM solvation energy, and ΔG_prep is the preparation energy relative to Zn²⁺-free Aβ40.

Supporting Information Available

β-Strand contents (Figure S1), populations of microstates (Figure S2), MFPTs (Figure S3), convergence test of REMD simulations (Figure S4), comparison of NMR observables (Figure S5), energy components for binding free energy calculations (Table S1), and distribution of preparation energy calculated by MM/3D-RISM theory (Figure S6). This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

L.X. and X.W. performed research and analyzed data; L.X., X.W. and X.W. wrote the paper.

This work was supported by the Major State Basic Research Development Program (2009CB918501). L.X. is thankful for financial support from the Fundamental Research Funds for the Central Universities (Grant No. DUT12LK38).

The authors declare no competing financial interest.