Abstract
We report evidence that adenylate kinase (AK) from Escherichia coli can be activated by the direct binding of a magnesium ion to the enzyme, in addition to ATP-complexed Mg2+. By systematically varying the concentrations of AMP, ATP, and magnesium in kinetic experiments, we found that the apparent substrate inhibition of AK, formerly attributed to AMP, was suppressed at low magnesium concentrations and enhanced at high magnesium concentrations. This previously unreported magnesium dependence can be accounted for by a modified random bi-bi model in which Mg2+ can bind to AK directly prior to AMP binding. A new kinetic model is proposed to replace the conventional random bi-bi mechanism with substrate inhibition and is able to describe the kinetic data over a physiologically relevant range of magnesium concentrations. According to this model, the magnesium-activated AK exhibits a 23- ± 3-fold increase in its forward reaction rate compared with the unactivated form. The findings imply that Mg2+ could be an important affecter in the energy signaling network in cells.
Adenylate kinase (AK)2 is a ∼24-kDa enzyme involved in cellular metabolism that catalyzes the reversible phosphoryl transfer reaction (1) as in Reaction 1.
| REACTION 1 |
It is recognized to play an important role in cellular energetic signaling networks (2, 3). A deficiency in human AK function may lead to such illness as hemolytic anemia (4–8) and coronary artery disease (9); the latter is thought to be caused by a disruption of the AMP signaling network of AK (10). The ubiquity of AK makes it an ideal candidate for investigating evolutionary divergence and natural adaptation at a molecular level (11, 12). Indeed, extensive structure-function studies have been carried out for AK (reviewed in Ref. 13). Both structural and biophysical studies have suggested that large-amplitude conformational changes in AK are important for catalysis (14–19). More recently, the functional roles of conformational dynamics have been investigated using NMR (20–22), computer simulations (23–27), and single-molecule spectroscopy (28). Given the critical role of AK in regulating cellular energy networks and its use as a model system for understanding the functional roles of conformational changes in enzymes, it is imperative that the enzymatic mechanism of AK be thoroughly characterized and understood.
The enzymatic reaction of adenylate kinase has been shown to follow a random bi-bi mechanism using isotope exchange experiments (29). Isoforms of adenylate kinases characterized from a wide range of species have a high degree of sequence, structure, and functional conservation. Although all AKs appear to follow the same random bi-bi mechanistic framework (15, 29–33), a detailed kinetic analysis reveals interesting variations among different isoforms. For example, one of the most puzzling discrepancies is the change in turnover rates with increasing AMP concentration between rabbit muscle AK and Escherichia coli AK. Although the reactivity of rabbit muscle AK is slightly inhibited at higher AMP concentrations (29, 32), E. coli AK exhibits its maximum turnover rate around 0.2 mm AMP followed by a steep drop, which plateaus at still higher AMP concentrations (33–35). This observation has been traditionally attributed to greater substrate inhibition by AMP in E. coli AK compared with the rabbit isoform; yet, the issue of whether the reaction involves competitive or non-competitive inhibition by AMP at the ATP binding site remains unresolved (15, 33, 35–37).
Here, we report a comprehensive kinetic study of the forward reaction of AK, exploring concentrations of nucleotides and Mg2+ that are comparable to those inside E. coli cells, [Mg2+] ∼ 1–2 mm (38) and [ATP] up to 3 mm (39). We discovered a previously unreported phenomenon: an increase in the forward reaction rate of AK with increasing Mg2+ concentrations, where the stoichiometry of Mg2+ to the enzyme is greater than one. The new observation leads us to propose an Mg2+-activation mechanism augmenting the commonly accepted random bi-bi model for E. coli AK. Our model can fully explain AK’s observed kinetic behavior involving AMP, ATP, and Mg2+ as substrates, out-performing the previous model requiring AMP inhibition. The new Mg2+-activation model also explains the discrepancies in AMP inhibition behavior and currently available E. coli AK kinetic data. Given the central role of AK in energy regulation and our new experimental evidence, it is possible that Mg2+ and its regulation may participate in respiratory network through AK (40–42), an exciting future research direction.
EXPERIMENTAL PROCEDURES
Sources—AMP, ADP, ATP, pyruvate kinase (PK), lactate dehydrogenase, bovine serum albumen (BSA), phosphoenolpyruvate (PEP), dithiothreitol, and EGTA were purchased from Sigma-Aldrich and used without further purification. Unless specified, other reagents were also from Sigma. Nicotinamide adenine dinucleotide disodium salt (NADH) was from Indofine Chemical Co.
Purification of AK—The wild-type E. coli AK gene from the K-12 strain was a generous gift from Prof. Michael Glaser’s group. The wild-type adenylate kinase was purified in a manner similar to that described earlier (28). The protein was first purified with an Affi-Gel® Blue Gel column (100–200 mesh, Bio-Rad). Further purification was performed with a Q-Sepharose anion exchange column (Amersham Biosciences) and a 1-m S-200 gel-filtration column (Amersham Biosciences).
Forward Activity Assay of Adenylate Kinase—All of the work was done with the assay buffer: 100 mm Tris (pH by acetic acid), pH 7.5, 100 mm KCl, 0.05 mg/ml (0.75 μm) BSA, and 0.6 mm TCEP. The production of ADP was monitored with the coupling enzymes PK and lactate dehydrogenase. Each ADP produced caused the oxidation of one NADH to NAD+ and was detected by the absorbance change at 340 nm (29). The coupling reagent concentrations used were: 4 mm PEP and 0.25 mm NADH with 1.5 unit of PK and 2 units of lactate dehydrogenase per 100-μl reaction. The concentration of AK in each reaction was 0.89 nm. The forward reaction rates of AK were assayed at AMP and ATP concentrations between 0 to 3 mm, and magnesium acetate (MgOAc2) concentrations from 0 to 1.5 mm. All the measurements were carried out in 96-well plates and read with a microplate reader (Molecular Devices SpectraMax M5) at room temperature (24 °C). All of the rates reported in this work are initial reaction rates. Each experiment was repeated at least three times and averaged to determine error bars. All error bars are reported to one standard deviation. Although PK is known to utilize Mg2+ as a cofactor, the amount of PK in each reaction is at least two orders of magnitudes lower than the lowest Mg2+ concentration used (43). Therefore, PK should have negligible effect on the Mg2+ concentration in each reaction. To ensure that BSA does not affect reactivity readout, a control experiment was done where AK reactivity was assayed while systematically varying BSA concentrations between 0 and 1 mg/ml (15 μm). The results showed that BSA does not affect AK reactivity, which in turn indicates that BSA does not affect the Mg2+ concentration in the solution (see supplemental materials).
Magnesium Binding Assay of AK—To directly measure the binding affinity of E. coli AK to Mg2+, we chose mag-fluo-4 from Invitrogen as an indicator for Mg2+ concentration. The indicator is non-fluorescent in its uncomplexed form, but strongly fluorescent at ∼517 nm when complexed to Mg2+ (Kd = 4.7 mm) and Ca2+ (Kd = 22 μm; binding constants provided by the vendor). The buffer prepared for this binding assay contained 100 mm Tris/HCl, pH 7.5, 100 mm KCl, 1 mm dithiothreitol, and 20 μm EGTA. We used the reducing agent dithiothreitol in place of TCEP in this experiment to eliminate any undesirable Mg2+ binding competition by TCEP. EGTA was necessary to remove trace amounts of calcium ions, which severely interfere with the fluorescence readout of mag-fluo-4. The experiments were performed in the same plate reader in 384-well plates at room temperature (24 °C). Each well contained 2 mm Mg2+ and 20 μm mag-fluo-4 indicator. The concentration of AK was assayed between 0 and 1.5 mm. Each experiment was blanked at the same protein concentration but zero Mg2+, and all the measurements were repeated at least three times and averaged to determine error bars. The binding constant was calculated by fitting the titration curve to the numerical solution of coupled equations: AK + Mg2+ ↔ AK·Mg2+, Kd = [AK][Mg2+]/[AK·Mg2+] and Ind + Mg2+ ↔ Ind·Mg2+, Kd = [Ind][Mg2+]/[Ind·Mg2+], where Ind denotes the indicator, and Kd for the indicator is 4.7 mm.
A series of control experiments on BSA, PEP, and TCEP were carried out in similar fashion to ensure that none of these reagents bind Mg2+ strongly enough to interfere with the AK kinetic assay. The Mg2+ binding assay for BSA was done in the same condition as AK, but the concentration of BSA was varied between 0 and 2.9 mm. The Kd measurements for PEP and TCEP were done in a buffer containing 100 mm KCl, 100 mm Tris/HCl, pH 7.5, 20 μm EGTA, and 0.01% Tween 20. The surfactant Tween 20 was necessary to minimize scattered light during top read fluorescence measurements in the absence of BSA.
Analytical Procedures—Data analysis and multiparameter, global chi-squared fitting was done in Matlab (Mathworks, Inc.) with fminuit (44). Error bars for each fit parameter were obtained by a 100-iteration Monte Carlo simulation of the original data set; all errors are reported to one standard deviation. Mass balance of Mg2+ ions was achieved numerically by using Kd values measured in this work (PEP, TCEP, and BSA), determined from literature (ATP) or fit as a model parameter (AK).
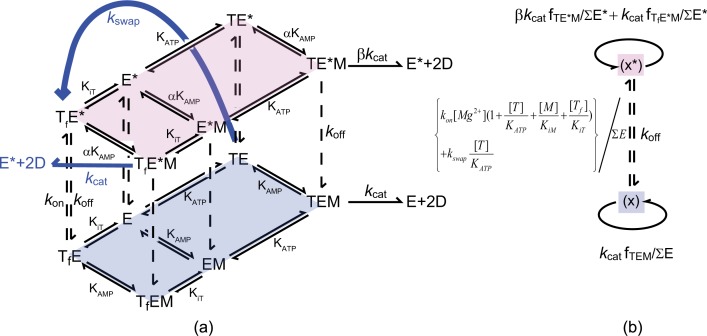
Magnesium Ion-activated Random bi-bi Mechanism for the Forward Reaction—To illustrate magnesium ion activation of AK, we propose a model with two different forms of the enzyme with distinct catalytic rates, the original unactivated enzyme (E) and the Mg2+-activated form (E*). Note that this is different from the iso-random bi-bi mechanism proposed earlier for rabbit muscle AK (32). In that work, the two putative enzyme forms were attributed to two different conformations of AK, in which each form follows its own random bi-bi mechanism with distinct dissociation constants and catalytic rates. In the present work, the relative population of the activated enzyme, E*, is determined by the Mg2+ affinity of unactivated enzyme. Judging from the sigmoidal shape of initial rate curves with increasing AMP concentrations, we propose that Mg2+ can only bind to the enzyme prior to AMP binding, but may dissociate from all the activated E* species. Therefore, the Mg2+ affinity cannot be described by a simple dissociation constant between activated and unactivated species. We employ a hybrid rapid equilibrium and steady-state approximation to describe this ordered binding (45, 46).
Fig. 1 shows a sketch of our model. The following convention has been used: E is AK without ligand, TE is Mg2+·ATP-bound AK, EM is AMP-bound AK, and an asterisk indicates an additional Mg2+ bound directly to the enzyme complex. In this convention, the TE* complex has two Mg2+ ions, one associated with ATP and the other bound directly to the enzyme. We use KATP and KAMP to denote the dissociation constants of Mg2+·ATP and AMP binding to the enzyme. Similarly, KiT and KiM are the dissociation constants for inhibitory species with a free ATP (ATP molecule without a Mg2+ bound, denoted as Tf) or an AMP bound to the Mg2+·ATP site.
FIGURE 1.
a, the proposed Mg2+-activation model. The forward AK reactions of the unactivated enzyme (E) and its Mg2+ activated counterpart (E*) each follow a random bi-bi model, illustrated by the diamond shapes and assumed to be in rapid equilibrium. The conversion between E and E* (vertical dashed lines) is treated with the steady-state approximation. In the activated form (the upper tier), the dissociation constants KAMP and the catalytic rate kcat are increased by a factor of α and β, respectively (E = AK enzyme, E* = AK·Mg2+, T = ATP·Mg2+, M = AMP, and D = ADP. Tf denotes ATP without Mg2+that has been bound to the enzyme). The blue arrows denote the second order correction to our proposed model. b, a reduction of the model in a according to the hybrid rapid equilibrium and steady-state assumption used to model the kinetic data.
The upper tier of the model in Fig. 1 represents all the activated enzyme·substrate complexes, and the lower tier represents all the enzyme species in their unactivated form. In the Mg2+-activated random bi-bi scheme, we assume that the dissociation constant for AMP, KAMP, and the catalytic rate, kcat, are enhanced by a factor of α and β, respectively, compared with their unactivated counterparts. The dissociation constant for ATP and E* is assumed to be the same as KATP. The vertical dashed lines linking the two tiers represent the binding and dissociation of Mg2+ to the enzyme. We assume all the upward dashed arrows have the same rate, kon × [Mg2+], and the downward arrows have the rate constant, koff. We further assume the species within each tier are in rapid equilibrium, but we treat the vertical dashed arrows with the steady-state approximation.
The central cube, consisting of E, TE, EM, TEM, and their activated counterparts, expresses the forward reaction rate in a simplified manner. In reality, additional factors must be considered, such as inhibition by free ATP and AMP binding to the Mg2+·ATP binding site. To achieve the goal of a robust fitting from limited experimental parameters (systematically varied ATP, AMP, and Mg2+ concentrations), we performed our experiments around the physiological Mg2+ concentrations where the activation by Mg2+ is the most prominent. In this regime, the inhibition of free ATP, denoted Tf, is non-negligible. For presentation clarity, we have omitted the AMP inhibition component of Fig. 1, which would be schematically identical to the free ATP inhibition depicted. As further elaborated in the discussion section, the AMP inhibition plays a much lesser role than the sequential binding of the activator Mg2+, and therefore can be neglected. Although capable of describing the AMP dependence of one kinetic trace at a single fixed ATP concentration, this mechanism cannot fully capture the fine features of the kinetic experiments when more than one ATP concentration is considered.
As a second-order correction, we propose the addition of two extra reaction pathways to the model (plotted in blue in Fig. 1). First, it was assumed that the magnesium ion from the Mg2+·ATP complex of species TE can be transferred to the enzyme. In other words, TE can turn into TfE* with a rate constant kswap. Furthermore, we assumed that, after acquiring an AMP molecule, the species TfE*M can also produce two ADPs at the original catalytic rate constant kcat. The justifications and ramifications of this second order correction will be discussed in further detail later. Our experimental conditions have an ionic strength of 180 mm, which leads to a dissociation constant of Kd = 152 μm between Mg2+ and ATP in solution (47). In all of our models, the dissociation constant of Mg2+ and ATP from Ref. 47 was used; however, the choice of dissociation constant from different literature sources does not significantly affect the fitting results beyond error bars.
Fig. 1b is a reduction of Fig. 1a under the hybrid rapid equilibrium and steady-state approach. Here, the relative population of the unactivated AK species is represented by ∑E, and the Mg2+-activated populations with ∑E*. ∑E and ∑E* can be expressed as follows.
| (Eq. 1) |
| (Eq. 2) |
The relative populations of the unactivated (X), and activated species (X*), are determined according to the following steady-state approximation.
| (Eq. 3) |
| (Eq. 4) |
The last term in Equation 4 represents the second order correction, which allows the bound Mg2+·ATP to lose its Mg2+ directly to AK. The fractions of product producing species can be written as in Equations 5–7.
| (Eq. 5) |
| (Eq. 6) |
| (Eq. 7) |
The initial rate can be written as,
| (Eq. 8) |
where [Etot] denotes the total enzyme concentration. Inserting Equations 1–7 into Equation 8, we arrive at Equation 9.
In Equation 9, the Mg2+ association and dissociation rates, kon and koff, always appear as a ratio. In the results section, we will only report this ratio, because we cannot resolve rates independently from the fitting. This ratio, koff/kon, can be interpreted as an effective dissociation constant and corresponds to the Kd measured in the direct binding assay, although the amount of enzymes that bind Mg2+ under reactive conditions also depends on the AMP concentration and the Mg2+ swapping rate constant, kswap. For convenience in the fitting, we define the factor κ to have the relationship kswap = κkon. Here, the factor κ has units of millmolar, because kswap and kon carry different units. This proposed model, while highly simplified due to limited set of fitting parameters, illustrates the kind of mechanistic features needed to fully describe the observed kinetics.
RESULTS AND DISCUSSION
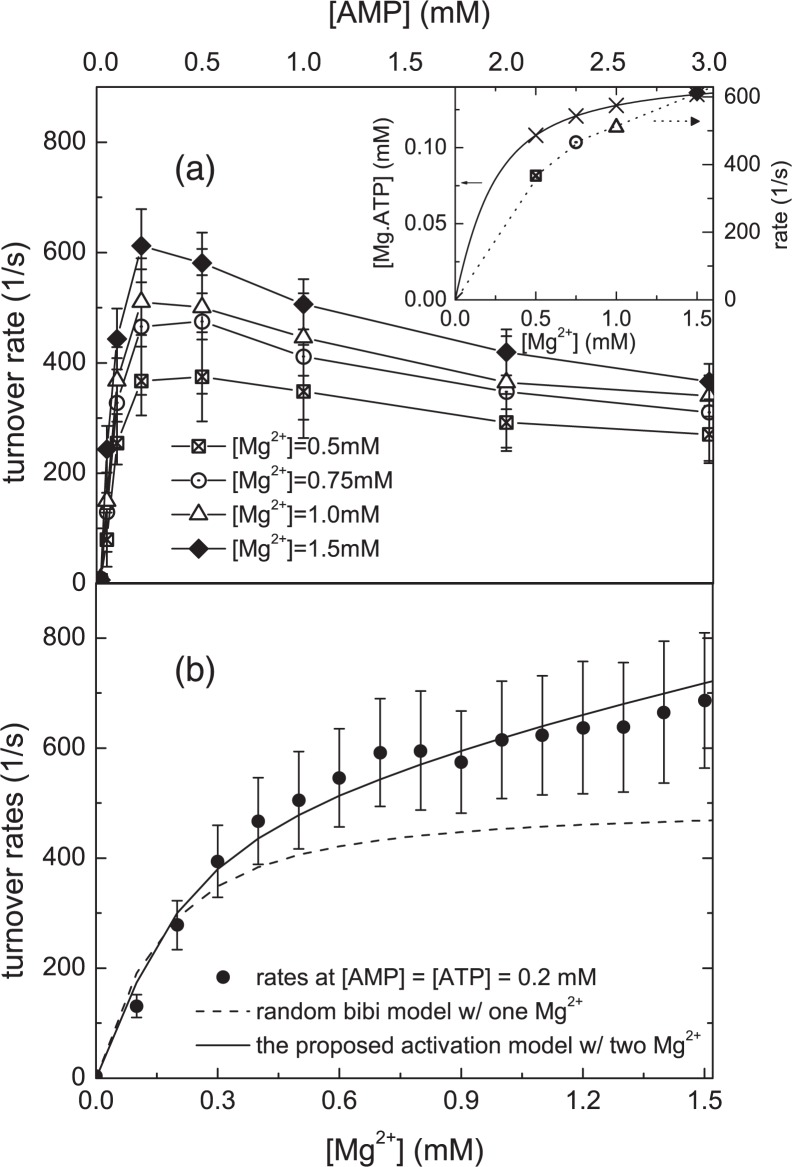
In Fig. 2a, we have plotted initial rate versus [AMP] curves with [ATP] = 0.15 mm at various Mg2+ concentrations. From the dissociation constant for Mg2+·ATP, we can estimate the Mg2+-bound ATP concentration at each Mg2+ concentration. The result is plotted in the inset of Fig. 2a assuming the Mg2+·ATP dissociation constant from Ref. 47 (data plotted in crosses). In the inset, we have also plotted the representative initial rates at 0.2 mm AMP and 0.15 mm ATP. From the inset we can see that the increase of initial rate is much greater than
| (Eq. 9) |
the increase of total [Mg2+·ATP]. The results indicate that the increase in the concentration of Mg2+·ATP is not the sole contribution to the Mg2+ dependence of the reaction rates in Fig. 2a. This observation clearly shows that Mg2+ enhances the forward reaction rate. Armed with the knowledge that AK is activated by Mg2+, we next investigate the stoichiometry of the Mg2+ ions. The monophosphate kinase family to which AK belongs is capable of binding to more than one divalent metal ion, as demonstrated by x-ray crystallography (12, 48–51). More broadly, the reactivity of protein kinases are also known to be tuned by a second Mg2+ ion in addition to the ATP-complexed Mg2+ ion (52), also supported by x-ray crystallography (53–55). For protein kinases, the effective stoichiometry of catalytically important Mg2+ binding has been determined by kinetic studies (52). Similarly, to investigate AK’s Mg2+ dependence, we have performed kinetic experiments systematically varying the Mg2+ concentration while keeping [ATP] = [AMP] = 0.2 mm. The experimental results are displayed in Fig. 2b. The dashed line is the best fit from a model in which Mg2+ is only complexed to ATP (a stoichiometry of one, details in supplemental materials). Fig. 2b clearly shows that the model with a single Mg2+ ion starts to level out as magnesium concentrations exceed that of ATP. This is in sharp contrast to the experimental data, which show the reaction rate continues to rise beyond [Mg2+] = 0.2 mm throughout the entire [Mg2+] range. By contrast the newly proposed Mg2+ activation model, with a stoichiometry of two magnesium ions, the simplest model that accounts for an effective magnesium stoichiometry greater than one, correctly reproduces the experimentally observed Mg2+ dependence. The result shows that more than one magnesium ion participates in catalysis and that additional Mg2+ enhances the reaction rate.
FIGURE 2.
Initial rates versus [AMP]. a, the rates at [ATP] = 0.15 mm for four different total Mg2+ concentrations. An increase in initial rate at higher [Mg2+] is seen from this comparison. Inset: an estimate of the Mg2+·ATP complex concentrations at the assay conditions in a. Using dissociation constants of Mg2+·ATP from Ref. 47, the concentrations of Mg2+·ATP complex are plotted in crosses. Initial rates from a at [AMP] = 0.2 mm are also plotted for comparison. The scale of these rates is at the right-hand side. These data suggest that the observed Mg2+ activation is not solely due to an increase in the available pool of Mg2+·ATP. b, the same assay is done at [ATP] = [AMP] = 0.2 mm as a function of [Mg2+]. The conventional random bi-bi mechanism (dashed curve) with a stoichiometry of one magnesium (bound to ATP) predicts a Mg2+ rate curve, which plateaus when the Mg2+ concentration is similar to the ATP concentration, in contrast to the real data. On the other hand, the proposed Mg2+activation model with a stoichiometry of two Mg2+ ions (solid line) exhibits excellent agreement with data. Combining the findings of a and b, the data indicate that AK is catalytically activated by Mg2+ ions.
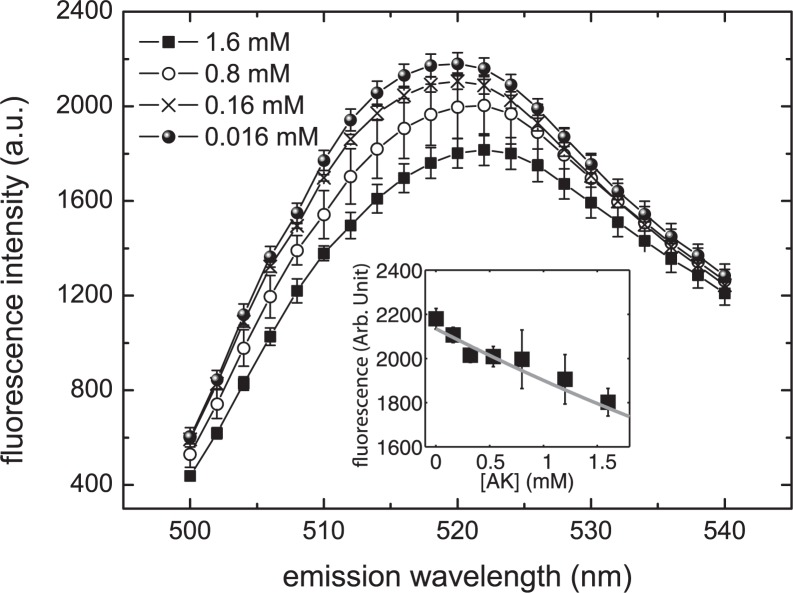
We next determine whether magnesium ions can bind directly to AK. A magnesium binding assay was carried out for this purpose and the results are plotted in Fig. 3. It is clear that the fluorescence level of the indicator, mag-fluo-4, changes with protein concentration. These data strongly support the hypothesis that magnesium ions bind directly to AK. From the reduction of fluorescent intensity with increasing AK concentration, we determine the dissociation constant of Mg2+·AK to be 4.0 ± 1.5 mm (data and fit shown in the inset of Fig. 3). The same assay was performed on other reagents used in the kinetic assay to determine their respective affinities for magnesium. The Kd for magnesium ion with TCEP and PEP were determined to be 39.1 ± 4.9 mm and 20.7 ± 1.2 mm, respectively (see supplemental materials for data and fit). These Mg2+ binding affinities are almost an order of magnitude weaker than AK, so the effects of TCEP and PEP competing for Mg2+ with AK should be negligible. The Kd of BSA was determined to be 0.91 ± 0.15 mm. Note that, in this work, we assume the stoichiometry of Mg2+ binding for all of the reagents to be one to one. Under the situation that BSA binds to more than one Mg2+, the Kd reported would be an underestimation. Because we use 0.05 mg/ml (0.75 μm) BSA in our reaction, the BSA would not bind >0.9 μm of Mg2+, which would result in a negligible reduction of the amount of Mg2+ in the reaction.
FIGURE 3.
The fluorescence spectra from the AK Mg2+ binding assay. The monotonic reduction of fluorescence intensity with increasing AK concentration is a clear indication of direct magnesium ion binding to AK. In the inset we have plotted the fluorescence intensity (at 520 nm) of the indicator versus AK concentration. We then fit the data to a curve by numerically solving the mass balance equations between the free Mg2+, Mg2+·indicator complex (known Kd = 4.7 mm), and Mg2+·enzyme complex (the unknown). The Kd value for E* was found to be 4.0 ± 1.5 mm.
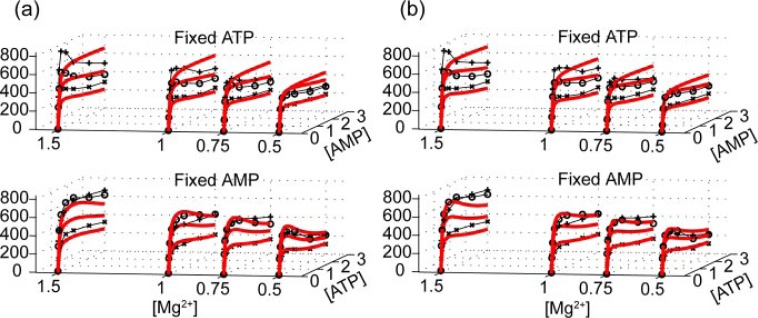
Having established that Mg2+ can directly bind to E. coli AK and that direct interaction between Mg2+ and AK elevates its reactivity, we next study the mechanistic roles of the additional Mg2+. The kinetic data for the forward reaction at four Mg2+ concentrations is shown in Fig. 4a. A multiparameter global fit, which includes all Mg2+ concentrations, using the conventional random bi-bi model with competitive AMP and free ATP inhibition is plotted in the red lines (χ̃2 = 1.7). This model is unable to reproduce the characteristic sigmoidal shape seen at higher Mg2+ concentrations. If one fits each magnesium concentration individually, the kcat predicted by the conventional model would be magnesium-dependent. This can be illustrated by considering the magnesium dependence of the initial rates when the concentrations of AMP and ATP are the same, as seen in Fig. 2a. If we try to address the Mg2+ activation by building a two-tier random bi-bi model, with the upper and lower tiers representing an activated and unactivated AK, respectively, we arrive at a global fitting as shown in Fig. 4b (χ̃2 = 1.5, see supplemental materials for the details of this model). The fits shown in Fig. 4b are not too different from Fig. 4a and are still unable to capture the unique Mg2+-dependent features evident in the data (note the regions at both high and low AMP concentrations). The behavior of the entire series of curves argues against the model of AMP inhibition as a major contribution to the sigmoidal curves and suggests the need for a new model to explain the observed Mg2+ and AMP dependence of the rates.
FIGURE 4.
Global fitting of the original random bi-bi model including AMP and free ATP inhibition. From the figure we can see that the conventionally accepted model (a) cannot generate a fit if we perform a global fitting of multiparameters. Even when we modify the model to include Mg2+ activation at rapid equilibrium, the fitting results stay more or less unchanged (b). See supplemental materials for detailed model definitions and equations.
The standard random bi-bi with Mg2+-activation model failed to capture the steep drop of rates with increasing AMP concentrations. Because the AMP inhibition is already taken into account in this model, there must be additional effects that contribute to the depression of the rates. These results led us to propose a new model in which the increase of AMP will hinder the Mg2+ activation. One explanation is that the binding of AMP hinders Mg2+ activation, such that activation can only be achieved by a sequential binding of Mg2+ followed by AMP.
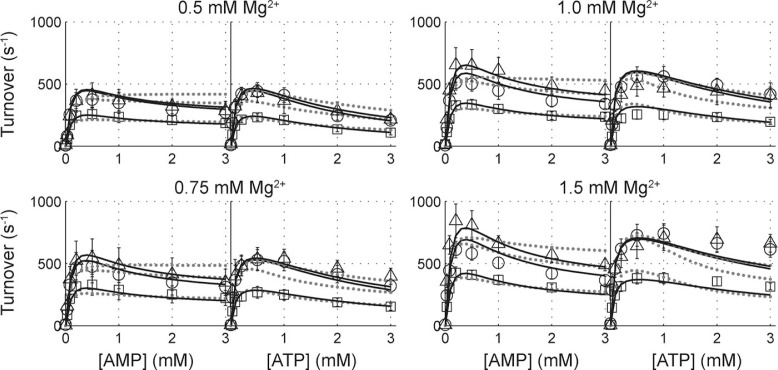
The newly proposed Mg2+-activation modified random bi-bi model can be globally fit to the forward assay data, as shown in Fig. 5. The fitting results are summarized in Table 1. The fitting results reported in Table 1 were obtained by fixing the Kd (i.e. koff/kon in the model) to the measured value of 4.0 mm (see supplemental materials for results with koff/kon as a free parameter). This model predicts a KiM (dissociation constant for inhibitory AMP), which is more than two orders of magnitude larger than substrate dissociation constants KAMP or KATP, indicating that the effects from AMP inhibition are very weak. Therefore, we have removed competitive inhibition by AMP from the model (fitting results with AMP inhibition considered are reported in the supplemental materials). This result further substantiates our proposal that the sigmoidal rate versus [AMP] curve is not caused by AMP inhibition. Instead, it can be accounted for by the requirement for a sequential binding of the activator Mg2+ followed by AMP. We first fit our data with the model described in Fig. 1 without the second order corrections, illustrated by black lines in Fig. 1a. Without the second order correction, this model can generate a satisfactory fit to the data (dashed lines in Fig. 5, χ̃2 = 1.36). The major discrepancy, however, comes from experiments at high Mg2+ and ATP concentrations, where the model predicts a more significant inhibition than was observed experimentally. In this regime, the Mg2+·ATP concentration is relatively high compared with the low [Mg2+] conditions. To explain this discrepancy, an alternate channel to mitigate inhibition at higher ATP and Mg2+ concentrations is required. Therefore, as a second order correction, we hypothesize that, once Mg2+· ATP is bound to AK, the magnesium ion can occasionally be transferred to AK’s Mg2+ binding site. The TfE*M complex (the Mg2+- bound AK complexed with a free ATP and AMP) can, in turn, produce ADP. If we include the effects of the second order correction (blue lines in Fig. 1), we obtain a very satisfactory fit, solid lines in Fig. 5 (χ̃2 = 0.71). These results indicate that in the Mg2+-activated “super-enzyme,” E*, works 23 ± 3-fold faster than the unactivated form. The AMP binding affinity of the Mg2+-activated enzyme is 1.4 ± 0.1 times weaker, and this small change in nucleotide affinity can possibly be attributed to a reconfiguration of AK’s active site upon the addition of the activating magnesium ion.
FIGURE 5.
Kinetic analysis of E. coli adenylate kinase forward reaction at varying Mg2+ concentrations. In each panel, data points for fixed substrate concentrations of 1, 0.15, and 0.05 mm are plotted in open triangles, circles, and squares, respectively. Dotted lines show the fit of data to our newly proposed, magnesium activated random bi-bi model with competitive AMP and free ATP inhibition. With the implementation of our second order correction, we obtain an improved fitting, as demonstrated by the bold, dark lines.
TABLE 1.
Parameters generated from a global fitting of the magnesium activation model (Equation 9) to the AK forward assay data presented in Fig. 5.
| Parameter | Mg2+ activation model | Model with second order correction |
|---|---|---|
| kcat (s−1) | 605 ± 22 | 319 ± 28 |
| KAMP (mm) | 0.070 ± 0.005 | 0.207 ± 0.017 |
| KATP (mm) | 0.088 ± 0.006 | 0.049 ± 0.003 |
| KiT (mm) | 0.60 ± 0.12 | 0.28 ± 0.04 |
| koff/kon (mm) | 4.0 ± 1.5 (fixed) | 4.0 ± 1.5 (fixed) |
| κ ≡ ks/kon (mm) | NAa | 1.9 ± 0.3 |
| α | 8.6 ± 1.4 | 1.34 ± 0.13 |
| β | 52.6 ± 6.4 | 23.2 ± 3.0 |
| χ̃2 | 1.36 | 0.71 |
NA, not applicable.
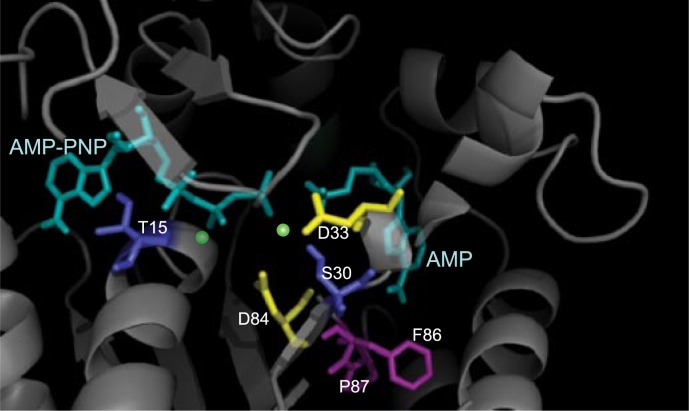
Although the main goals of this report were to report the AK unexpected magnesium-dependent activity and investigate its mechanistic origin, it is nevertheless instructive to consider possible physical origins for the observation. It is common for divalent metal ions to bind to enzymes and, in turn, facilitate catalytic reactions. A number of proteins are known to directly bind Mg2+ (56–60). The crystal structures of E. coli AKs with substrates (AMP, ATP analog, and Mg2+) were done with a resolution of ∼2 Å (15). However, that work was unable to resolve the precise location of any Mg2+ ions, even though the experimental resolution was sufficient for detection of Mg2+ ions. This is consistent with the low binding affinity (∼4 mm) measured in this work. The lack of Mg2+-bound crystal structure leaves room for speculating its possible binding site in AK. Earlier studies on the E. coli AK “AMP inhibition” can provide some clues. In the works by Gilles et al. (36), and by Liang et al. (35), the turnover rates of wild-type E. coli AK have been compared with those from mutants Pro-87 → Ser and Phe-86 → Trp, respectively. It is clear from the data shown that the “AMP inhibition” behavior was entirely eliminated by introducing a mutation on residues 86 or 87. If we interpret the same data, not from the AMP inhibition point of view, but under the Mg2+-activation model, the mutations can be viewed as abolishing the Mg2+ ion binding capability, presumably at a site nearby or allosterically linked to residues 86 and 87. In fact, from available crystal structures (Fig. 6), residues 86 and 87 (in magenta) are directly beneath the AMP binding site. This interpretation therefore provides a tantalizing physical picture for our model in which AMP binding frustrates direct Mg2+ binding to AK. In search of the likely Mg2+ binding sites, we compared an E. coli AK structure (1ANK (61)) to UMP kinase from Pyrococcus furiosus (2BMU (51)), in which the substrates with two Mg2+ were resolved and discussed. From a detailed comparison of the two structures, we can single out the possible Mg2+ binding residues. In Fig. 6, Asp-33, Asp-84 (both drawn in yellow), Ser-30 (in deep blue), and the γ phosphate group may form one of the divalent metal ion sites. The other possible site resides in between Thr-15, β-phosphate group, and shares Asp-84 with the first site. The proposed Mg2+ sites are marked in green in Fig. 6. Asp-84 is very close to the two residues, Phe-86 and Pro-87, which were previously shown to abolish the sigmoidal AMP inhibition behavior discussed above (34, 35). This physical picture is also consistent with the proposed second-order correction to the model where Mg2+ can exchange binding sites in the highly flexible interior of the enzyme (cf. the pathway indicated by the blue line in Fig. 1).
FIGURE 6.
A close-up crystal structure of E. coli AK ligand binding sites (1ANK (61)). The substrates AMP-PNP and AMP are drawn in cyan. Residues Asp-33 and Asp-84 (yellow) as well as residues Ser-33 and Thr-15 (deep blue) are potential magnesium binding residues. The postulated magnesium ion binding locations, (green dots) are in between these residues and the β- and γ-phosphate groups of AMP-PNP. Residues Phe-86 and Pro-87 (magenta) have been shown to interfere with the “AMP inhibition behavior” (35, 36) and are located near the AMP binding site.
The demonstration of the Mg2+-dependent mechanism of AKs raises an obvious question: What is the biological role of Mg2+-activation in adenylate kinase? To discuss this question, we consider the primary biochemical function of AK, to rapidly equilibrate ATP·Mg, AMP, ADP·Mg, and ADP. The [ATP]/[ADP] ratio in its general form has long been recognized as an important parameter in energy regulation in cells (62, 63). In bacteria, for instance, imbalances in the [ATP]/[ADP] ratio have been associated with changes in its DNA super-coiling state (64–66) and also with its carbon source intake efficiency (67). More generally, the energy state when [Mg2+] is constant is expected to be regulated by molecular sensing of [ATP·Mg]/[ADP·Mg], where the magnesium-bound nucleotides serve as substrates for various sensing cascades, or by sensing [ATP]free/[ADP]free, where the unbound nucleotides may act as inhibitors in the energy regulatory network (41). These ratios, however, are mediated by Mg2+ concentration through the association between Mg2+ and ATP or ADP. Indeed, the possible roles of Mg2+ in energy homeostasis have been pointed out by Blair almost four decades ago (68). Because magnesium is required in many biochemical processes and is generally well regulated (69), Blair further hypothesized that the regulatory role that magnesium ion play through AK is during the transient response of a cell’s energy state (68).
The foregoing discussions and the findings in the present work therefore frame a hypothesis that AK serves as a coupling enzyme between the Mg2+ regulatory network and bioenergy homeostasis where the Mg2+-activated mechanism helps to cope with transient increase in Mg2+ concentration, for example, by hormonal stimuli in mammalian cells (70). Therefore, our findings raise the possibility of further investigations of the regulatory roles of AK by examining the transient coupling between Mg2+ and energy regulation networks (71).
In conclusion, we have discovered that the E. coli adenylate kinase forward enzymatic reaction can be activated by direct binding a Mg2+ ion, prior to AMP binding. When globally fit to AK kinetic data over a range of substrate concentrations, including various Mg2+ concentrations, this newly proposed model generates a satisfactory fit. This finding may have implications of the role of AK in the magnesium-regulated energy homeostasis network.
Acknowledgments
We thank Jason Brokaw, Jhih-Wei Chu, Jamie Cate, and Jack Kirsch for fruitful discussions. We also thank Rachel Brem for generously granting us access to a microplate reader.
Footnotes
The work was supported by the National Science Foundation and by the A. P. Sloan Foundation. The costs of publication of this article were defrayed in part by the payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. Section 1734 solely to indicate this fact.
The abbreviations used are: AK, adenylate kinase; PK, pyruvate kinase; BSA, bovine serum albumen; PEP, phosphoenolpyruvate; AMP-PNP, adenosine 5′-(β,γ-imino)triphosphate; TCEP, tris(2-carboxyethyl)phosphine hydrochloride.
Supplemental material: http://www.jbc.org/content/suppl/2008/11/25/M803658200.DC1.html
The on-line version of this article (available at http://www.jbc.org) contains supplemental Text, Figs. S1–S14, Tables S1–S5, and an additional reference.
REFERENCES
- 1.Noda L. Adenylate Kinase. 3d Ed. Academic Press; New York: 1970. [Google Scholar]
- 2.Dzeja PP, Terzic A. J Exp Biol. 2003;206:2039–2047. doi: 10.1242/jeb.00426. [DOI] [PubMed] [Google Scholar]
- 3.Saks V, Dzeja P, Schlattner U, Vendelin M, Terzic A, Wallimann T. J. Physiol (London) 2006;571:253–273. doi: 10.1113/jphysiol.2005.101444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bianchi P, Zappa M, Bredi E, Vercellati C, Pelissero G, Barraco F, Zanella A. Br J Haematol. 1999;105:75–79. [PubMed] [Google Scholar]
- 5.Corrons JLV, Garcia E, Tusell JJ, Varughese KI, West C, Beutler E. Blood. 2003;102:353–356. doi: 10.1182/blood-2002-07-2288. [DOI] [PubMed] [Google Scholar]
- 6.Lachant NA, Zerez CR, Barredo J, Lee DW, Savely SM, Tanaka KR. Blood. 1991;77:2774–2784. [PubMed] [Google Scholar]
- 7.Matsuura S, Igarashi M, Tanizawa Y, Yamada M, Kishi F, Kajii T, Fujii H, Miwa S, Sakurai M, Nakazawa A. J Biol Chem. 1989;264:10148–10155. [PubMed] [Google Scholar]
- 8.Qualtieri A, Pedace V, Bisconte MG, Bria M, Gulino B, Andreoli V, Brancati C. Br J Haematol. 1997;99:770–776. doi: 10.1046/j.1365-2141.1997.4953299.x. [DOI] [PubMed] [Google Scholar]
- 9.Pucar D, Janssen E, Dzeja PP, Juranic N, Macura S, Wieringa B, Terzic A. J Biol Chem. 2000;275:41424–41429. doi: 10.1074/jbc.M007903200. [DOI] [PubMed] [Google Scholar]
- 10.Dzeja PP, Bast P, Pucar D, Wieringa B, Terzic A. J Biol Chem. 2007;282:31366–31372. doi: 10.1074/jbc.M705268200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fukami-Kobayashi K, Nosaka M, Nakazawa A, Go M. FEBS Lett. 1996;385:214–220. doi: 10.1016/0014-5793(96)00367-5. [DOI] [PubMed] [Google Scholar]
- 12.Counago R, Chen S, Shamoo Y. Mol. Cell. 2006;22:441–449. doi: 10.1016/j.molcel.2006.04.012. [DOI] [PubMed] [Google Scholar]
- 13.Yan HG, Tsai MD. In: Advances in Enzymology and Related Areas of Molecular Biology. Purich DL, editor. Wiley; New York: 1999. pp. 103–134. [Google Scholar]
- 14.Vonrhein C, Schlauderer GJ, Schulz GE. Structure. 1995;3:483–490. doi: 10.1016/s0969-2126(01)00181-2. [DOI] [PubMed] [Google Scholar]
- 15.Bilderback T, Fulmer T, Mantulin WW, Glaser M. Biochemistry. 1996;35:6100–6106. doi: 10.1021/bi951833i. [DOI] [PubMed] [Google Scholar]
- 16.Elamrani S, Berry MB, Phillips GN, McCammon JA. Proteins. 1996;25:79–88. doi: 10.1002/(SICI)1097-0134(199605)25:1<79::AID-PROT6>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- 17.Sinev MA, Sineva EV, Ittah V, Haas E. Biochemistry. 1996;35:6425–6437. doi: 10.1021/bi952687j. [DOI] [PubMed] [Google Scholar]
- 18.Shapiro YE, Sinev MA, Sineva EV, Tugarinov V, Meirovitch E. Biochemistry. 2000;39:6634–6644. doi: 10.1021/bi992076h. [DOI] [PubMed] [Google Scholar]
- 19.Shapiro YE, Kahana E, Tugarinov V, Liang ZC, Freed JH, Meirovitch E. Biochemistry. 2002;41:6271–6281. doi: 10.1021/bi012132q. [DOI] [PubMed] [Google Scholar]
- 20.Wolf-Watz M, Thai V, Henzler-Wildman K, Hadjipavlou G, Eisenmesser EZ, Kern D. Nat Struct Mol Biol. 2004;11:945–949. doi: 10.1038/nsmb821. [DOI] [PubMed] [Google Scholar]
- 21.Henzler-Wildman KA, Thai V, Lei M, Ott M, Wolf-Watz M, Fenn T, Pozharski E, Wilson MA, Petsko GA, Karplus M, Hubner CG, Kern D. Nature. 2007;450:838–844. doi: 10.1038/nature06410. [DOI] [PubMed] [Google Scholar]
- 22.Aden J, Wolf-Watz M. J Am Chem Soc. 2007;129:14003–14012. doi: 10.1021/ja075055g. [DOI] [PubMed] [Google Scholar]
- 23.Miyashita O, Onuchic JN, Wolynes PG. Proc Natl Acad Sci U S A. 2003;100:12570–12575. doi: 10.1073/pnas.2135471100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Temiz NA, Meirovitch E, Bahar I. Proteins-Struct Funct Bioinform. 2004;57:468–480. doi: 10.1002/prot.20226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Arora K, Brooks CL. Proc Natl Acad Sci U S A. 2007;104:18496–18501. doi: 10.1073/pnas.0706443104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chu JW, Voth GA. Biophys J. 2007;93:3860–3871. doi: 10.1529/biophysj.107.112060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lu Q, Wang J. J Am Chem Soc. 2008;130:4772–4783. doi: 10.1021/ja0780481. [DOI] [PubMed] [Google Scholar]
- 28.Hanson JA, Duderstadt K, Watkins LP, Bhattacharyya S, Brokaw J, Chu JW, Yang H. Proc Natl Acad Sci U S A. 2007;104:18055–18060. doi: 10.1073/pnas.0708600104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rhoads DG, Lowenste JM. J Biol Chem. 1968;243:3963–3972. [PubMed] [Google Scholar]
- 30.Hibino T. J Biol Chem. 2005;280:30671–30680. doi: 10.1074/jbc.M412601200. [DOI] [PubMed] [Google Scholar]
- 31.Munier-Lehmann H, Burlacu-Miron S, Craescu CT, Mantsch HH, Schultz CP. Proteins. 1999;36:238–248. [PubMed] [Google Scholar]
- 32.Sheng XR, Li X, Pan XM. J Biol Chem. 1999;274:22238–22242. doi: 10.1074/jbc.274.32.22238. [DOI] [PubMed] [Google Scholar]
- 33.Sinev MA, Sineva EV, Ittah V, Haas E. FEBS Lett. 1996;397:273–276. doi: 10.1016/s0014-5793(96)01195-7. [DOI] [PubMed] [Google Scholar]
- 34.Gilles AM, Saintgirons I, Monnot M, Fermandjian S, Michelson S, Barzu O. Proc Natl Acad Sci U S A. 1986;83:5798–5802. doi: 10.1073/pnas.83.16.5798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Liang P, Phillips GN, Glaser M. Proteins. 1991;9:28–36. doi: 10.1002/prot.340090105. [DOI] [PubMed] [Google Scholar]
- 36.Gilles AM, Marliere P, Rose T, Sarfati R, Longin R, Meier A, Fermandjian S, Monnot M, Cohen GN, Barzu O. J Biol Chem. 1988;263:8204–8209. [PubMed] [Google Scholar]
- 37.Reinstein J, Vetter IR, Schlichting I, Rosch P, Wittinghofer A, Goody RS. Biochemistry. 1990;29:7440–7450. doi: 10.1021/bi00484a013. [DOI] [PubMed] [Google Scholar]
- 38.Alatossava T, Jutte H, Kuhn A, Kellenberger E. J Bacteriol. 1985;162:413–419. doi: 10.1128/jb.162.1.413-419.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lasko DR, Wang DIC. Biotechnol Bioeng. 1996;52:364–372. doi: 10.1002/(SICI)1097-0290(19961105)52:3<364::AID-BIT2>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
- 40.Leyssens A, Nowicky AV, Patterson L, Crompton M, Duchen MR. J. Physiol (London) 1996;496:111–128. doi: 10.1113/jphysiol.1996.sp021669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Igamberdiev AU, Kleczkowski LA. J Exp Bot. 2006;57:2133–2141. doi: 10.1093/jxb/erl006. [DOI] [PubMed] [Google Scholar]
- 42.Igamberdiev AU, Kleczkowski LA. Biochem J. 2001;360:225–231. doi: 10.1042/0264-6021:3600225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ainswort S, Macfarla N. Biochem J. 1973;131:223–236. doi: 10.1042/bj1310223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.James F, Roos M. Comput Phys Commun. 1975;10:343–367. [Google Scholar]
- 45.Huang CY. Methods Enzymol. 1979;63:54–84. doi: 10.1016/0076-6879(79)63006-9. [DOI] [PubMed] [Google Scholar]
- 46.Segel IH. In: Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady State Enzyme Systems. Wiley Classics Library, editor. Wiley; New York: 1993. pp. 503–523. [Google Scholar]
- 47.Zhang WQ, Truttmann AC, Luthi D, McGuigan JAS. Anal Biochem. 1997;251:246–250. doi: 10.1006/abio.1997.2238. [DOI] [PubMed] [Google Scholar]
- 48.Berry MB, Phillips GN. Proteins. 1998;32:276–288. doi: 10.1002/(sici)1097-0134(19980815)32:3<276::aid-prot3>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 49.Ostermann N, Schlichting I, Brundiers R, Konrad M, Reinstein J, Veit T, Goody RS, Lavie A. Structure. 2000;8:629–642. doi: 10.1016/s0969-2126(00)00149-0. [DOI] [PubMed] [Google Scholar]
- 50.Bae E, Phillips GN. J Biol Chem. 2004;279:28202–28208. doi: 10.1074/jbc.M401865200. [DOI] [PubMed] [Google Scholar]
- 51.Marco-Marin C, Gil-Ortiz F, Rubio V. J Mol Biol. 2005;352:438–454. doi: 10.1016/j.jmb.2005.07.045. [DOI] [PubMed] [Google Scholar]
- 52.Adams JA. Chem Rev. 2001;101:2271–2290. doi: 10.1021/cr000230w. [DOI] [PubMed] [Google Scholar]
- 53.Hubbard SR. EMBO J. 1997;16:5572–5581. doi: 10.1093/emboj/16.18.5572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Niefind K, Putter M, Guerra B, Issinger OG, Schomburg D. Nat Struct Biol. 1999;6:1100–1103. doi: 10.1038/70033. [DOI] [PubMed] [Google Scholar]
- 55.Yde CW, Ermakova I, Issinger OG, Niefind K. J Mol Biol. 2005;347:399–414. doi: 10.1016/j.jmb.2005.01.003. [DOI] [PubMed] [Google Scholar]
- 56.Milne JA, Cook RA. Biochemistry. 1979;18:3604–3610. doi: 10.1021/bi00583a026. [DOI] [PubMed] [Google Scholar]
- 57.Thomas AP, Diggle TA, Denton RM. Biochem J. 1986;238:83–91. doi: 10.1042/bj2380083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Younis HM, Weber G, Boyer JS. Biochemistry. 1983;22:2505–2512. [Google Scholar]
- 59.Reid JD, Hunter CN. J Biol Chem. 2004;279:26893–26899. doi: 10.1074/jbc.M400958200. [DOI] [PubMed] [Google Scholar]
- 60.Shi JY, Krishnamoorthy G, Yang YW, Hu L, Chaturvedi N, Harilal D, Qin J, Cui JM. Nature. 2002;418:876–880. doi: 10.1038/nature00941. [DOI] [PubMed] [Google Scholar]
- 61.Berry MB, Meador B, Bilderback T, Liang P, Glaser M, Phillips GN. Proteins. 1994;19:183–198. doi: 10.1002/prot.340190304. [DOI] [PubMed] [Google Scholar]
- 62.Atkinson DE. Biochemistry. 1968;7:4030–4034. doi: 10.1021/bi00851a033. [DOI] [PubMed] [Google Scholar]
- 63.Pradet A, Raymond P. Annu Rev Plant Physiol Plant Mol Biol. 1983;34:199–224. [Google Scholar]
- 64.van Workum M, van Dooren SJM, Oldenburg N, Molenaar D, Jensen PR, Snoep JL, Westerhoff HV. Mol Microbiol. 1996;20:351–360. doi: 10.1111/j.1365-2958.1996.tb02622.x. [DOI] [PubMed] [Google Scholar]
- 65.Jensen PR, Loman L, Petra B, Vanderweijden C, Westerhoff HV. J Bacteriol. 1995;177:3420–3426. doi: 10.1128/jb.177.12.3420-3426.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Hsieh LS, Rouviereyaniv J, Drlica K. J Bacteriol. 1991;173:3914–3917. doi: 10.1128/jb.173.12.3914-3917.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Koebmann BJ, Westerhoff HV, Snoep JL, Nilsson D, Jensen PR. J Bacteriol. 2002;184:3909–3916. doi: 10.1128/JB.184.14.3909-3916.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Blair JM. Eur J Biochem. 1970;13:384–390. doi: 10.1111/j.1432-1033.1970.tb00940.x. [DOI] [PubMed] [Google Scholar]
- 69.Romani A. Arch Biochem Biophys. 2007;458:90–102. doi: 10.1016/j.abb.2006.07.012. [DOI] [PubMed] [Google Scholar]
- 70.Touyz RM, Schiffrin EL. J Biol Chem. 1996;271:24353–24358. doi: 10.1074/jbc.271.40.24353. [DOI] [PubMed] [Google Scholar]
- 71.Carrasco AJ, Dzeja PP, Alekseev AE, Pucar D, Zingman LV, Abraham MR, Hodgson D, Bienengraeber M, Puceat M, Janssen E, Wieringa B, Terzic A. Proc Natl Acad Soc U S A. 2001;98:7623–7628. doi: 10.1073/pnas.121038198. [DOI] [PMC free article] [PubMed] [Google Scholar]