Estimating trends in the total fertility rate with uncertainty using imperfect data: Examples from West Africa

Abstract

Background

Estimating the total fertility rate is challenging for many developing countries because of limited data and varying data quality. A standardized, reproducible approach to produce estimates that include an uncertainty assessment is desired.

Methods

We develop a method to estimate and assess uncertainty in the total fertility rate over time, based on multiple imperfect observations from different data sources, including surveys and censuses. We take account of measurement error in observations by decomposing it into bias and variance, and assess both by linear regression on a variety of data quality covariates. We estimate the total fertility rate using a local smoother, and assess uncertainty using the weighted likelihood bootstrap.

Results

We apply our method to data from seven countries in West Africa and construct estimates and uncertainty intervals for the total fertility rate. Based on cross-validation exercises, we find that accounting for differences in data quality between observations gives better calibrated confidence intervals and reduces bias.

Conclusions

When working with multiple imperfect observations from different data sources to estimate the total fertility rate, or demographic indicators in general, potential biases and differences in error variance should be taken into account to improve the estimates and their uncertainty assessment.

1. Introduction

In this article we describe a new method to estimate the total fertility rate (TFR) over time from multiple sources of imperfect data. The procedure is automated and therefore reproducible, and it takes account of data quality by characterizing bias and measurement error separately. We illustrate the method using fertility data from seven countries in West Africa whose fertility data are of widely varying quality and coverage. We assess it using cross-validation and show that it is reasonably well calibrated.

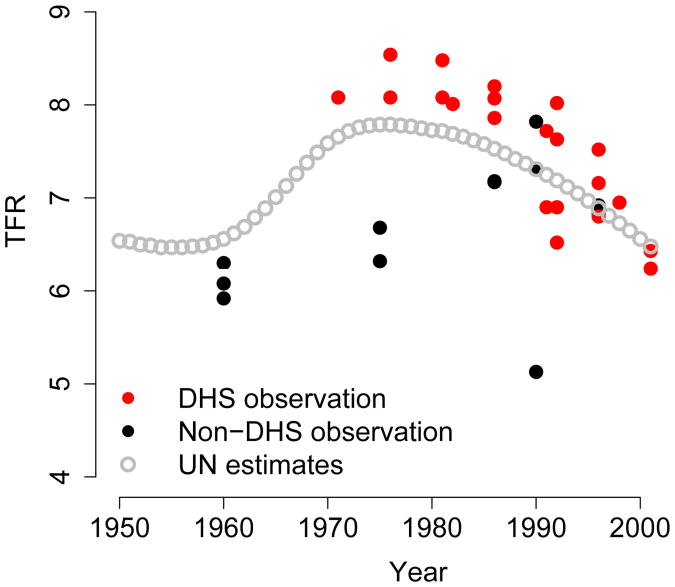
Estimating demographic indicators is challenging for many developing countries because of limited data and varying data quality. This is illustrated in Figure 1 for Burkina Faso in West Africa. The black and red dots are nationally representative observations of the total fertility rate in Burkina Faso constructed using age-specific fertility rates. For the period from 1950 until the mid 1970s, there are very few observations for the TFR. After 1970 the number of observations increases, but they vary a great deal because of issues with data quality, e.g. observations are biased because of the collection process, or measured with large errors.

Figure 1. Observations of the TFR in Burkina Faso, and UN estimates.

The United Nations (UN) Population Division produces estimates of the TFR from 1950 up to the most recent five-year period, for all countries in the world. Here we use the 2006 estimates (United Nations, Department of Economic and Social Affairs, Population Division 2007). UN analysts estimate the fertility rates in a labor-intensive, iterative fashion: initially, age-specific fertility rates are estimated based on all available nationally representative data combined with expert knowledge of the reliability of the different subsets of observations (e.g. known issues with a particular survey or census, or general knowledge of undercounts or overcounts of particular retrospective estimates of fertility rates). The initial fertility estimates are combined with estimates of mortality and migration to derive estimates of population counts. The population count estimates are then compared to bias-adjusted census counts. If estimated and observed population counts differ substantially, the estimates of the three input components of the population counts are reconsidered. Uncertainty in these input components allows for adjustments of the initial input values until population estimates and observations are in agreement. The UN estimates for Burkina Faso are shown in Figure 1.

The UN estimates of the TFR are generally considered to be of good quality and are widely used. The observations from Demographic and Health Surveys (DHS), shown in red in Figure 1, are also considered to be of good quality and widely used. Figure 1 shows that when examining the TFR in Burkina Faso, different conclusions about its level and trend can be drawn depending on whether the UN estimates or the DHS estimates are being used. The DHS observations are estimates from nationally representative surveys and as such are subject to sampling and other errors. The UN estimates use a wide variety of available information including what is known about other demographic indicators. However, the UN estimates have the drawback of being hard to reproduce because they are not produced in an automated way, and of having no associated statements of uncertainty.

There are no standardized, reproducible methods for estimating trends in fertility rates in developing countries based on different data sources that assess the uncertainty of the estimates. Much of the literature on fertility estimation methods focuses on the development of indirect estimation techniques (Brass 1964; Brass et al. 1968; Trussell 1975; United Nations 1983; Brass 1996; Feeney 1998). These techniques deal with bias caused by recall lapse errors, omissions of births (especially soon after birth), and misinterpretation of the reference period in retrospective estimates of fertility rates (Som 1973; Potter 1977; Becker and Mahmud 1984; Pullum and Stokes 1997) by reconciling information from recent fertility (in the last year or years) with lifetime fertility. Recent fertility is adjusted rather than the full retrospective birth histories stretching back 25 years.

These methods typically rely on just one source of data, and the assumptions they require can affect their accuracy (Moultrie and Dorrington 2008). The indirect methods address a particular type of bias but do not confront differences in the variance of the measurement error. More recently, Schoumaker (2010, 2011) attempted to improve reconstructed fertility trends by analyzing birth histories for multiple DHS simultaneously, and showed the challenges in reconciling differences in levels and trends between surveys within the same country, especially for the earliest and latest observation periods from one survey. The drawbacks of this kind of approach are that they can only be applied to countries with multiple birth history surveys, and that other data sources, including adjusted fertility from indirect methods, cannot easily be taken into account.

Here we introduce a new, automated, reproducible method for estimating trends in the TFR, with measures of uncertainty for countries with limited data from multiple sources of varying quality. We assess the quality of our method using cross-validation by excluding subsets of the data, and evaluating how well we can predict both the excluded data and the errors in the predictions, using the remaining data. We apply our method to data from seven countries in West Africa which have experienced among the highest fertility rates in the world in recent years. We compare our findings to the results from a method that is similar except that it does not weight the observations, and so does not take into account data quality.

2. Data

The data we use to illustrate and test our method come from seven countries in West Africa that represent the type of situation for which this method has been developed. Data on fertility in these countries come from multiple sources of uneven quality; the problems include limited coverage through time, bias, and measurement error. Moreover countries like these, with similar data problems, are likely to be those with high fertility, and therefore important for understanding the population dynamics of their regions.

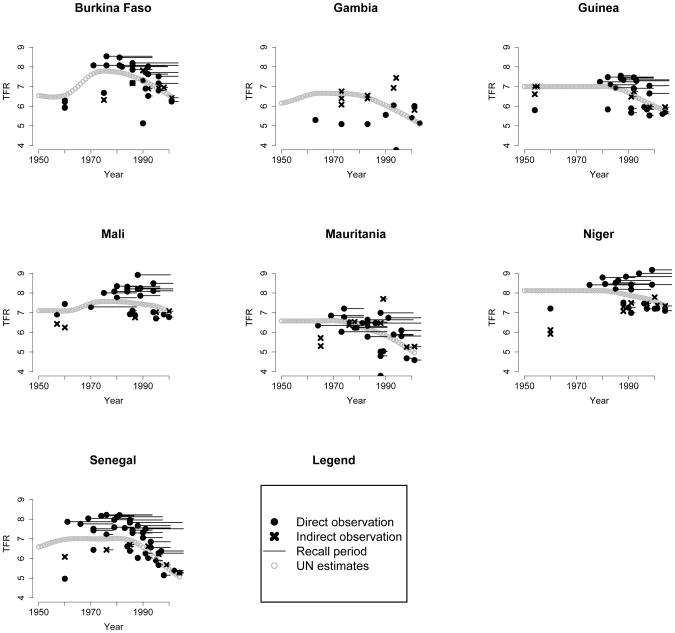
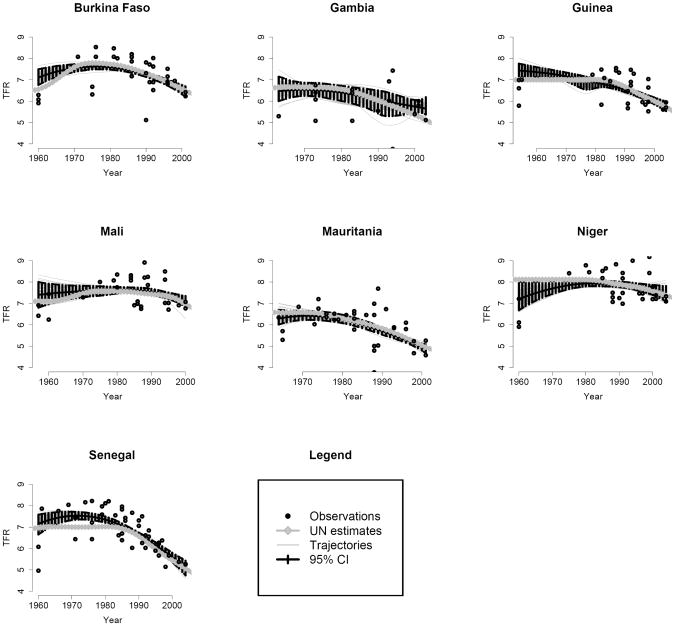
The data set consists of nationally representative observations of the TFR for Burkina Faso, Gambia, Guinea, Mali, Mauritania, Niger and Senegal. All the observations were collected retrospectively by either asking women about their births in a restricted period (e.g. the number of births in the last year before the survey/census) or for their complete birth histories (birth of their first child, second child, etc.). Figure 2 shows the observations in each of the seven countries. For each observation the recall period is displayed by a horizontal line that joins the midpoint of the observation period to the year of data collection. The UN estimates are shown in grey (United Nations, Department of Economic and Social Affairs, Population Division 2007).

Figure 2.

Direct observations (dots) and indirect observations (crosses) for different data sources. The black horizontal lines extend from the midpoint of the observation period to the year of data collection. The UN estimates are plotted as grey circles.

The observations are from sources that fall into three groups: censuses, Demographic and Health Surveys (DHS) and non-DHS surveys – the World Fertility Surveys and other surveys. Censuses and non-DHS surveys generally collect only lifetime fertility and/or recent fertility (in the past year). The retrospective estimates of the TFR produced by the DHS are based on complete birth histories of all women who participated in the survey, typically aged 15-49. The birth history data are tabulated by period. For example, based on the DHS in Burkina Faso in 2003, age-specific fertility rates were obtained for periods 0-4 years, 5-9 years, 10-14 years, 15-19 years and 20-24 years before the survey, and the TFR was calculated for each period from the age-specific fertility rates. For the periods in which no estimates of the age-specific fertility in older age groups were available (because women aged 50 and over were not interviewed), the outcomes for the older age groups were extrapolated from the outcomes in the younger age groups in that period, and from the observed age pattern of fertility in the most recent period.

Table 1 summarizes the observations based on their data quality covariates. For each observation four data quality covariates are available: source, period before survey (PBS), direct/indirect estimation method, and time span. Source is either Census, DHS or other survey. Period before survey is the midpoint of the period before the survey to which the retrospective estimate refers. Time span is the length of the observation period in years. The data quality covariate “Direct” in Table 1 divides the data set into direct and indirect estimates. Direct estimates are observations based on the reported number of births in a given period, as described above. Indirect estimates are for the most recent period before a survey or census, and they are constructed using indirect estimation methods that correct for recall lapse biases in retrospective observations of fertility (Som 1973; Potter 1977; Becker and Mahmud 1984; Pullum and Stokes 1997).

Table 1.

Summary of fertility data for seven countries in West Africa. The number of observations for each observed combination of data quality covariates: Source, Period Before Survey (PBS—based on the midpoint of the period before the survey to which the retrospective estimate refers), Direct (specifying whether the observation is a direct or an indirect estimate) and Time span (the number of years included in the observation).

Combination	Source	PBS	Direct	Time span	# Obs.
1	Census	0-1 Year	No	1 Year	18
2			Yes	1 Year	20
3	Survey	0-1 Year	No	1 Year	12
4			Yes	1 Year	12
5		1-5 Years	No	3 Years	1
6	DHS	1-5 Years	No	3 Years	15
7			No	4-5 Years	7
8			Yes	3 Years	13
9			Yes	4-5 Years	23
10			Yes	5+ Years	1
11		5-10 Years	Yes	4-5 Years	23
12			Yes	5+ Years	22
13		10+ Years	Yes	4-5 Years	50

The indirect techniques rely on the use of the P/F ratio (Brass 1964, Brass et al 1968), which compares cumulative cohort fertility to cumulative period fertility. The assumptions underlying this method are that fertility and its age distribution are constant over time, and that the fertility of non-surviving women is equal to the fertility of surviving women (whose number of children is reported). Under these assumptions cohort and period fertility are equal, and deviations from equality are used to adjust the observed fertility rates. Several variations of the P/F ratio are used to relax these assumptions (Trussell 1975; United Nations 1983; Feeney 1998). However, because of the problems with the indirect estimation techniques (Moultrie and Dorrington 2008), indirect estimates can be biased, too. Therefore, direct estimates (including unadjusted estimates for longer retrospective periods) as well as indirect estimates are taken into account and analyzed simultaneously.

3. Methods

Our method has four parts. First, the bias for each TFR observation is estimated by regression on the data quality covariates and subtracted from the observation. Second, the measurement error variance is estimated, also by regression on data quality covariates. Third, the TFR trajectory for each country is estimated by weighted local smoothing of the bias-adjusted observations, with the weights being the reciprocals of the estimated measurement error variances. Fourth, we assess the uncertainty of our TFR estimates using the weighted likelihood bootstrap. We compare the four-step method with one that omits the first two steps, in order to evaluate the effects of accounting for data quality.

3.1 Modeling data quality

Some observations of the TFR are better than others, depending on the quality of the underlying data. We decompose data quality into two components: bias and measurement error variance. Bias refers to systematic over- or underestimation of the TFR resulting from problems such as an unrepresentative sample or missing data. Measurement errors occur randomly during the data collection process and include sampling and non-sampling errors. Sampling errors occur if the observation is based on a subset of the population, and non-sampling errors are errors that are made during data collection and/or input. Unlike sampling errors, non-sampling errors have many different sources and are often hard to detect or control, and for many estimates of fertility rates non-sampling errors are bigger than sampling errors (United Nations 1982).

Previous work on the quality of demographic estimates typically has not distinguished between bias and measurement error variance. We emphasize the importance of doing so because they can be adjusted for separately and can point in opposite directions. Some observations may have large biases but small measurement errors while others may be unbiased but less precise. Therefore it is important to account for bias and measurement error variance separately. We correct bias by adjusting the observations, and we account for differences in measurement error variance (heteroskedasticity) by weighting the observations. A biased observation with small measurement error variance is adjusted and then assigned a high weight. An unbiased observation with large measurement error variance is not adjusted, but gets a low weight.

Our probability model for observation y_cts is:

$$y_{\mathit{\text{cts}}}|f_{\mathit{\text{ct}}}\sim N\left(f_{\mathit{\text{ct}}}+{\delta }_{\mathit{\text{cts}}},{\sigma }_{\mathit{\text{cts}}}^2\right)\left(c=1,\dots ,7;t=1,\dots ,T_c;s=1,\dots ,n_{\mathit{\text{ct}}}\right),$$

where y_cts is the s-th estimate of the TFR for country c in year t, f_ct is the unobserved true TFR in year t for country c, δ_cts is the bias of observation y_cts, and ${\mathit{\sigma }}_{\mathit{\text{cts}}}^2$ is the observation-specific error variance. We use data quality covariates to assess the bias and error variance of each TFR estimate, an extension of work on differences in error variance in child mortality rates by Hill et al. (1998) and the Interagency group for child mortality estimation (UNICEF, WHO, World Bank and UNPD, 2007). We use linear regression to estimate how bias and error variance depend on data quality covariates using the combined observations from the seven countries in West Africa.

3.2 Estimating bias

Bias is estimated as a function of the data quality covariates using linear regression. The advantage of this approach compared to indirect estimation methods is that no assumptions are made about the age structure of the fertility rates or the trends in fertility over time. Multiple data sources are modeled and adjusted simultaneously, and bias is estimated based on what has been observed in the seven countries in West Africa.

In order to identify bias we need an unbiased reference to which we can compare the observations. This reference must be a series of TFR values that covers the period of time for which there are data for the country, and must contain values whose errors are equally likely to over- or understate the TFR. In this sense the reference is ‘fair’ and should upon averaging provide a reasonable notion of any systematic errors (i.e. bias) in the observations. It is not necessary for the reference to be accurate or precise, just that its errors – however big they may be – not be systematically in one direction or the other.

Among the options we have – DHS, non-DHS surveys, censuses and the UN estimates – we chose the UN estimates as our unbiased reference. The UN estimates are the result of a cumulative process (continuous revision) of triangulation and validation using many types of data in addition to fertility data (i.e. population counts, age structures and mortality data) and are based on all available fertility data regardless of source. Uniquely among the possible choices, the UN estimates cover the full period of observation for each country. Finally, the UN estimates benefit from the accumulated expertise and knowledge of the UN Population Division's analysts. In contrast, the other sources of data all have limitations that make them less suitable as the reference; either they are not available or do not cover the whole period for each country (e.g. no DHS has ever been conducted in Gambia), or they might be biased or flawed in one sense or another. For example, a pooled analysis of birth histories by Schoumaker (2010, 2011) showed substantial inconsistencies between consecutive DHS within countries, and frequent omissions and displacements of births over the three years preceding the survey leading to large underestimates in fertility levels, often by as much as 15%.

At first glance this seems contradictory; if the existing UN estimates are unbiased why not just use them? Recall that our purpose is to develop an automated method as good as or better than the UN's current highly labor-intensive procedure that could eventually replace it, subject to inspection and revision by the analysts. In doing this it makes sense to make use of the extensive work and expert knowledge of UN analysts in the past. We do not assume that the UN estimates are correct, rather just that their errors are not consistently either too high or too low on average. This provides a fair reference to begin the process of characterizing bias. In this context, the UN estimates are used only as initial baseline estimates in the multi-step process of modeling data quality, and to incorporate expert knowledge.

Based on these considerations, we assume the UN TFR estimates are unbiased so that E[u_ct] = f_ct, where u_ct denotes the UN estimate for country c, year t. Given this, the bias δ_cts of observation y_cts is the expected value of the difference d_cts = y_cts − u_ct between the observation and the UN estimate so that E[d_cts] = δ_cts. We estimate the biases δ_cts by regressing d_cts on the data quality covariates using the model

$$E\left[d_{\mathit{\text{cts}}}\right]={\mathit{\text{x}}}_{\mathit{\text{cts}}}\mathit{\beta },$$

where the row x_cts of the design matrix X contains the data quality covariates. Thus the biases δ_cts can be estimated from the relationship δ_cts = x_ctsβ using least-squares estimation.

The next question is which predictors to include in the bias regression model. There are four data quality covariates, and each is a categorical variable that can take several values. We code these as dummy variables and consider the possibility of including or excluding each of them. Dummy variables for the individual DHS (each of which generates multiple observations) as well as the observation year, year of data collection and the level of the TFR (as given by the UN estimates) are also candidates to put into the model. To select the best model, we use a Bayesian variable selection approach (Raftery 1995). Specifically, we consider all candidate models based on possible subsets of predictors and choose the one model with the smallest value of the Bayesian Information Criterion (BIC). The BIC is a model selection criterion that combines a negative measure of model fit with a penalty term for the number of predictor variables in the candidate model. This procedure is carried out using the bicreg function in the BMA package of the statistical language R (Raftery, Painter, and Volinsky 2005), available at http://cran.rproject.org/web/packages/BMA.

The estimated biases δˆ_cts are then subtracted from the observations to get the bias-adjusted observations

$$\begin{array}{c}{z}_{\mathit{\text{cts}}}=y_{\mathit{\text{cts}}}-{\hat{\delta }}_{\mathit{\text{cts}}}\sim N\left(f_{\mathit{\text{ct}}},{\rho }_{\mathit{\text{cts}}}^2\right),\end{array}$$ (1)

where ${\mathit{\rho }}_{\mathit{\text{cts}}}^2$ is the observation-specific error variance of the bias-adjusted observation.

3.3 Estimating measurement error variance

A similar approach is used for estimating the measurement error variances, i.e. heteroskedasticity, the values of ${\mathit{\rho }}_{\mathit{\text{cts}}}^2$ in Eq. (1). We assume that the absolute differences between the UN estimates and the bias-adjusted observations z_cts are proportional to the absolute differences between bias-adjusted observations and the true TFR (see Appendix for a more detailed discussion of this approach), so that

$$E|z_{\mathit{\text{cts}}}-u_{\mathit{\text{ct}}}|\propto E|z_{\mathit{\text{cts}}}-f_{\mathit{\text{ct}}}|.$$

It follows from Eq. (1) that $E|z_{\mathit{\text{cts}}}-f_{\mathit{\text{ct}}}|=\sqrt{\frac{2}{\pi }}{\rho }_{\mathit{\text{cts}}},$ and so

$$E|z_{\mathit{\text{cts}}}-u_{\mathit{\text{ct}}}|\propto {\rho }_{\mathit{\text{cts}}}.$$

We can therefore estimate the association between the data quality covariates and the relative differences in ρ_cts between observations using the regression model

$${\rho }_{\mathit{\text{cts}}}\propto E|z_{\mathit{\text{cts}}}-u_{\mathit{\text{ct}}}|={\mathit{\text{w}}}_{\mathit{\text{cts}}}\mathbf{\lambda },$$

where the row w_cts of the design matrix W contains the data quality covariates that are predictive of the measurement error variance, and λ is the vector of regression coefficients, such that ρ_cts ∝ w_ctsλ. Variable selection is done in the same way as for the bias regression, and the vector of regression coefficients λ is estimated using least-squares estimation.

Note that this approach does not guarantee positive estimates of the standard deviation. However, in our experience negative estimates do not occur, and the resulting regression model performs well. It would be possible to guarantee that negative estimates would never occur by applying regression to the logarithms of the absolute errors rather than the absolute errors themselves. We use the absolute residuals as the response variable (rather than the squared residuals) because the results of the analysis with absolute residuals are less sensitive to outliers.

3.4 Estimating TFR trajectories and their uncertainty

To estimate the annual country-specific TFR, we apply a local smoother (Cleveland and Devlin 1988; Cleveland, Grosse, and Shyu 1991; Loader 1999) to the bias-adjusted TFR estimates weighted by the reciprocals of their estimated error variances. In this procedure, the TFR f_ct* in year t* is estimated by fitting a quadratic polynomial to a set of bias-adjusted observations of the TFR that are closest to year t*. The number of observations in the set is determined by the smoothing parameter α of the local smoother. For α > 1, all observations within a country are used, while for α < 1, a proportion α of all observations is used. The observations within the set are weighted using a tricube weighting function such that data points that are further away from year t* get a smaller “distance weight”. The smoothing parameter α is estimated by cross-validation based on the data sets for all countries combined; α is chosen to minimize the overall mean squared error when leaving out observations one at the time. We use the R function locfit (Loader 1999) to fit the local smoother to the bias-adjusted TFR observations, taking into account the differences in error variance between observations.

We assess uncertainty in the TFR trajectories using the weighted likelihood bootstrap (Newton and Raftery 1994). This is similar to the standard bootstrap (Efron 1979) except that where the standard bootstrap resamples data points, the weighted likelihood bootstrap gives a positive weight to every data point. The weights are sampled from a Dirichlet distribution. The weighted likelihood bootstrap works better in our case, because the fit of the local smoother to resampled bootstrapped data breaks down if few or no data points at the end points of the observation period are resampled. In the weighted likelihood bootstrap, no data points are left out and so this problem does not arise.

To sample B bootstrap replicates from our data, the weighted likelihood bootstrap works as follows. For b = 1, …, B we cycle through the following steps:

1. For each country c, sample bootstrap weights $p_{\mathit{\text{cts}}}^{\left(b\right)}$ for observation y_cts from the distribution

   $$\left(p_1,\dots ,p_m\right)\sim {\text{Dirichlet}}_m\left(1,\dots ,1\right),$$

   where $m={\sum }_{t=1}^{T_c}{n}_{\mathit{\text{ct}}}$ is the total number of observations in country c. The Dirichlet_m(1,…,1) distribution is uniform in the sense that it gives equal probability to all values of the vector (p₁,…,p_m) such that p₁ + … + p_m = 1, and all p_i′s are positive.

2. Estimate the biases ${\delta }_{\mathit{\text{cts}}}^{\left(b\right)}$ using weighted regression, based on the data set of all countries and

   $$y_{\mathit{\text{cts}}}\sim N\left(f_{\mathit{\text{ct}}}+{\delta }_{\mathit{\text{cts}}},\frac{{\sigma }^2}{p_{\mathit{\text{cts}}}^{\left(b\right)}}\right),$$

   where σ² is the error variance for all observations combined. The bias-adjusted observations are given by $z_{\mathit{\text{cts}}}^{\left(b\right)}=y_{\mathit{\text{cts}}}-{\hat{\delta }}_{\mathit{\text{cts}}}^{\left(b\right)}.$

3. Estimate the differences in error variance ${\rho }_{\mathit{\text{cts}}}^{\left(b\right)}$ using weighted regression, based on the data set of all countries and

   $$z_{\mathit{\text{cts}}}^{\left(b\right)}\sim N\left(f_{\mathit{\text{ct}}},\frac{{\rho }_{\mathit{\text{cts}}}^{2\left(b\right)}}{p_{\mathit{\text{cts}}}^{\left(b\right)}}\right).$$

4. Estimate the TFR by fitting the local smoother to the bias-adjusted observations $z_{\mathit{\text{cts}}}^{\left(b\right)}$, taking into account the differences in error variance ${\rho }_{\mathit{\text{cts}}}^{\left(b\right)}$ and the bootstrap weights $p_{\mathit{\text{cts}}}^{\left(b\right)}$. The distance weights and the local neighborhoods in the local smoother vary by bootstrap replicate too, because the smoothing parameter α is re-estimated within each bootstrap replicate.

3.5 Model validation

We validated the method using cross-validation in which some observations are excluded while the method is applied to the remaining observations. We then assess how well the resulting predictive distributions agree with the excluded observations. More precisely, we assess whether the predictive distributions are calibrated, meaning that the prediction intervals contain the truth the right proportion of the time. We use the following measures of calibration: (a) the proportion of excluded observations that fall outside their prediction intervals, (b) the average bias of the estimated TFR compared to the excluded observations, (c) the standardized absolute prediction error, and (d) the probability integral transform histogram of the excluded observations.

The prediction intervals for the left-out observations y_cts are based on

$$y_{\mathit{\text{cts}}}\sim N\left({\stackrel{\sim }{f}}_{\mathit{\text{ct}}}+{\stackrel{\sim }{\delta }}_{\mathit{\text{cts}}},{\stackrel{\sim }{\nu }}_{\mathit{\text{cts}}}^2\right).$$ (2)

In Eq. (2), f̃_ct is the median TFR (which gives a more robust estimate of the TFR level when outliers are present than does the mean), δ̃_cts is the estimated bias and ${\stackrel{\sim }{\mathit{\nu }}}_{\mathit{\text{cts}}}^2$ is the estimated total variance, all estimated from the training data set and the data quality covariates of observation y_cts. The predictive variance of the observations is

$${\stackrel{\sim }{\nu }}_{\mathit{\text{cts}}}^2=\text{Var}\left({\stackrel{\sim }{f}}_{\mathit{\text{ct}}}\right)+{\stackrel{\sim }{\rho }}_{\mathit{\text{cts}}}^2,$$

where the variance of the TFR Var(f̃_ct) and the observation-specific error variance ${\stackrel{\sim }{\mathit{\rho }}}_{\mathit{\text{cts}}}^2$ are estimated from the training data set.

With respect to the estimated TFR, the bias in the set of excluded observations is estimated by the mean of the differences between a bias-adjusted excluded observation and the estimated TFR. The standardized absolute prediction error (SAPE) for observation y_cts is defined by:

$${\text{SAPE}}_{\mathit{\text{cts}}}=\sqrt{\frac{\pi }{2}}\frac{\left|y_{\mathit{\text{cts}}}-{\stackrel{\sim }{\delta }}_{\mathit{\text{cts}}}-{\stackrel{\sim }{f}}_{\mathit{\text{ct}}}\right|}{{\stackrel{\sim }{\nu }}_{\mathit{\text{cts}}}}.$$

If our modeling assumptions hold, the mean expected SAPE is equal to 1 because $E\left|y_{\mathit{\text{cts}}}-{\stackrel{\sim }{\delta }}_{\mathit{\text{cts}}}-{\stackrel{\sim }{f}}_{\mathit{\text{ct}}}\right|=\sqrt{2/\pi }{\stackrel{\sim }{\nu }}_{\mathit{\text{cts}}}$. A larger value of the mean SAPE indicates that the left-out observations are more spread out than expected, while a smaller value says they are less spread out.

Our last calibration criterion is the probability integral transform (PIT) histogram. The probability integral transform for the excluded observation y_cts is

$${\text{PIT}}_{\mathit{\text{cts}}}=\Phi \left(\frac{y_{\mathit{\text{cts}}}-{\stackrel{\sim }{\delta }}_{\mathit{\text{cts}}}-{\stackrel{\sim }{f}}_{\mathit{\text{ct}}}}{{\stackrel{\sim }{\nu }}_{\mathit{\text{cts}}}}\right),$$

where Φ(·) is the cumulative distribution function of the standard normal distribution. From Eq. (2) it follows that the PIT values should be approximately uniformly distributed between 0 and 1 if our model is valid. Calibration is assessed using the histogram of the PIT values of the excluded observations, which should be approximately uniform. For a histogram with H bins, each bin with width 1/H should contain about a proportion 1/H of the PIT values and thus have height 1. The summary criterion for model comparison in terms of PIT values is given by the area of the PIT histogram that is located above one, as this represents the deviation from uniformity of the PIT values (Berrocal, Raftery, and Gneiting 2007). We call this the “PIT area”. If the TFR estimates are unbiased, a smaller value of the PIT area means a better calibrated model. For more complete details of our method, see Alkema (2008).

4. Results

4.1 Bias regression

The covariates selected for the bias regression model are: the recall period of the observation, its estimation method and the observation year. The results for the complete data set are given in Table 2. A positive coefficient represents a positive bias of observations with that covariate, indicating that the observations are on average higher than the UN estimate. For the seven countries in West Africa, retrospective estimates that refer to periods more than 5 years in the past have a positive bias of more than one child, compared to recall periods of less than 5 years (where positive estimates indicate that the observation was higher than the UN estimate). The regression coefficient is 1.07 children, if the midpoint of the period before the survey is between 5 and 10 years (PBS 5–10) and 1.30 children if the period is more than 10 years (PBS 10+). The regression coefficients for PBS 5-10 and PBS 10+ are not significantly different when taking into account their standard errors.

Table 2.

Estimated coefficients in the bias regression model (standard errors and t-values are corrected for heteroskedasticity using the heteroskedasticity consistent (HC3) estimator by MacKinnon and White (1985). Heteroskedasticity and autocorrelation consistent estimates are not reported but were of the same order of magnitude)

	Coefficient	Std. Error	t-value
Intercept	−0.74	0.15	−4.8
PBS 5 - 10 Years	1.07	0.09	12.4
PBS 10+ Years	1.30	0.10	13.3
Direct	−0.45	0.11	−4.0
Year - 1954	0.02	0.004	5.1

Compared to indirect estimates, direct observations have a negative bias of almost half a child. Bias is positively associated with the observation year: the longer ago the observation, the more negative its bias. The first observation was in 1954, and in that year the bias started with a large negative value of −0.74 for indirect estimates with recall period less than 5 years, and the bias became less negative at the rate of 0.02 children per year.

The estimated bias for each outcome category and different years are given in Table 3. Note that the first observation with a recall period of more than 5 years is in 1961. The most recent estimate with a period before survey of more than 10 years is in 1994, and likewise in 1999 for a retrospective period between 5 and 10 years. The bias is essentially zero for indirect estimates in 1994 with a recall period of less than 5 years.

Table 3. Estimated biases for different observation years and outcome categories (using unrounded estimates of the regression coefficients from Table 1).

		Period Before Survey
Obs. year	Direct	< 5 Years	5 - 10 Years	10+ Years
1954	Yes	−1.19
	No	−0.74
1961	Yes	−1.06	0.01	0.24
	No	−0.61
1970	Yes	−0.89	0.18	0.40
	No	−0.44
1980	Yes	−0.70	0.37	0.59
	No	−0.25
1994	Yes	−0.44	0.63	0.85
	No	0.01
1999	Yes	−0.35	0.73
	No	0.11
2004	Yes	−0.25
	No	0.20

The bias regression model estimates confirm known problems with TFR observations mentioned in the literature, such as shifting of births, recall bias, age misreporting and other data reporting issues in retrospective fertility estimates (Ewbank 1981; Machiyama 2010; Pullum 2006; United Nations 1982). Shifting births back in time can explain the negative bias of direct estimates in the most recent five year period before the survey. The shifting back of births often occurs across a boundary five years before a survey because the structure of the survey instrument requires the interviewer to ask additional questions about children born within five years of the survey date. This effect leads to an underestimate in the direct estimate of the TFR for the preceding five year period.

Bias also increases with the recall period of the observation, as can be seen by reading the table from left to right. The positive bias of observations with longer recall periods is surprising at first sight, but is in line with the data in Figure 2, in which almost all observations with long recall periods (long horizontal lines) were higher than the UN estimates. There are three possible explanations for the positive bias of observations with longer recall periods. The first is back-shifting of births; back-shifting births will increase the observations for the second most recent period before the survey. Second, differences in survival rates could partly explain the positive bias of retrospective estimates because the estimates are based on the birth histories of the women who survived until the year of the survey. Thus a positive correlation between fertility and female survival results in overestimation of the total fertility rate. This effect might be compounded by a potential adoption effect, in which adopted children or step-children are reported as biological children, especially in Sahelian countries with a high proportion of polygamous unions.

Lastly, some of the positive bias of retrospective estimates seem to be due to overestimates of the age-specific fertility rates in the older age groups. As explained in Section 2, the TFR is based on the age-specific fertility rates in each period. The age-specific rates for the unobserved older age groups in observations with a long recall period are extrapolated from the observed fertility outcomes in younger age groups in that period and the age patterns in the most recent period. However, if age patterns are changing over time, i.e. if fertility is declining more slowly in the younger age groups, then this extrapolation technique will give overestimates in the older age groups in the past.

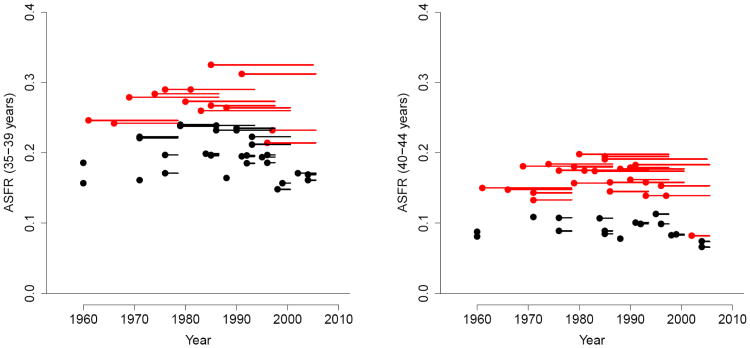
Figure 3 shows the age-specific fertility rates in age groups 35-39 and 40-44 in Senegal. The observations plotted in black are observed age-specific fertility rates, while the red dots represent rates based on the extrapolation method. The extrapolated estimates tend to be much higher than the observed rates, causing positive bias in the TFR. The bias regression gives the average bias for TFRs based on longer recall periods for all seven countries. Note that our method corrected this bias without knowing in advance that it existed or what caused it.

Figure 3.

Illustration of positive biases in observations with longer recall periods in Senegal: Age-specific fertility rates for (a) 35-39 and (b) 40-44 year age groups with observed rates in black, extrapolated rates in red, and the recall period from the midpoint of the observation to the survey year given by the horizontal line

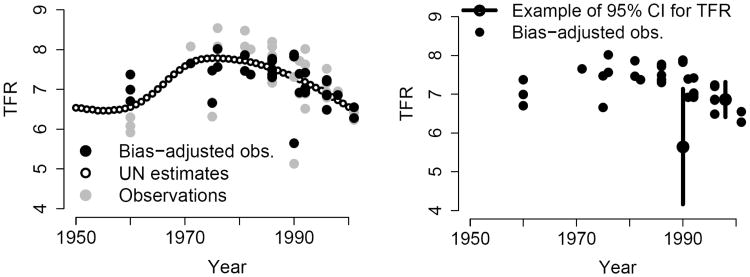
Figure 4(a) shows the outcomes of the bias regression model for the TFR in Burkina Faso. The observations in Burkina Faso are plotted with grey dots and the UN estimates are given by the black circles. The black dots are the bias-adjusted observations when all the observations in the data are used in the bias regression model. The bias-adjusted observations show a more coherent trend than the uncorrected observations.

Figure 4.

Illustration of bias adjustment and difference in error variance for Burkina Faso: (a) UN estimates (black circles) and observations y_cts (grey dots) with the bias-adjusted observations y_cts − δˆ_cts (black dots), (b) Bias-adjusted observations (black dots) with the 95% confidence interval for the TFR based on a single observation, [y_cts − δˆ_cts − 2ρˆ_cts, y_cts − δˆ_cts + 2ρˆ_cts], shown for two observations (vertical black lines)

4.2 Error variance regression

The best-fitting error variance regression model includes the following variables: collection year after 1995, recall period up to one year and DHS in Mauritania in 1990. The estimated measurement standard deviations ρˆ_cts for the different outcome categories are given in Table 4. The indicator for data collection year is included because residual plots show that the error variance is higher for observations that were collected before the mid 1990s, indicating that data quality improved after 1995. If an observation was based on one year of data before the survey was collected, its error variance increased. This effect might be explained by differences in error variance by source: all observations within one year before the survey are from censuses and other surveys, not from DHSs. The DHS in Mauritania in 1990 had higher error variance than the other DHS (see Discussion).

Table 4. Results of error variance regression: estimated measurement standard deviations, ρˆ_cts for different outcome categories.

	Observations from DHS Mauritania (1990)
	No		Yes
Category	No. obs.	ρˆcts	No. obs.	ρˆcts
PBS >1, Before 1995	104	0.42	9	0.85
PBS 0-1, Before 1995	51	0.74	0	-
PBS >1, After 1995	42	0.23	0	-
PBS 0-1, After 1995	11	0.55	0	-

The larger the standard deviation of an observation within a certain category, the less informative that observation is about the TFR and the wider the confidence interval for the TFR based on that observation alone. The confidence intervals for the TFR based on the estimated standard deviations are given for two observations in Burkina Faso in Figure 4(b), with recall periods of less than one year, and 1-5 years respectively. The comparison illustrates the fact that the bias-adjusted observation that is farther away from the general trend (with a recall period of less than one year) has a larger estimated error variance, as expected.

These results underscore the importance of distinguishing between bias and variance. For example, we find that direct estimates made in 1999 on the basis of retrospective data (PBS > 5 years) have large bias but low variance, so our method adds a bias adjustment to these estimates but then gives the adjusted estimates higher weights. In contrast, indirect estimates with short recall periods made before 1995 had little or no bias, but larger variance. Our method does not adjust these estimates at all, but gives them smaller weights.

4.3 TFR estimates

The TFR estimates and their uncertainties for each country are shown in Figure 5. The grey lines in the plots are a random sample of TFR trajectories produced by the local smoother fits in the weighted likelihood bootstrap. The solid black line is the TFR estimate from our method and the dashed lines show the annual 95% confidence intervals (based on the 2.5% and 97.5% percentiles of the sample of TFR trajectories). The UN estimates are plotted on the same figure as a solid grey line with squares.

Figure 5.

Median estimates and confidence intervals for the TFR. The annual median estimates are shown by the solid line and the annual 95% confidence intervals (CI) by vertical lines. The grey lines are a random sample of TFR trajectories produced by the local smoother fits in the weighted likelihood bootstrap. The observations are displayed as black dots and the UN estimates by the grey line with squares

In general the UN estimates are within or close to our 95% confidence intervals except for lower UN estimates in Senegal from 1970 through the mid 1990s. We estimate a larger increase in fertility in the 1960s than the UN for Niger and Senegal and a smaller increase for Burkina Faso. For the Gambia, the UN estimates show a steeper decline during the second half of the observation period. The results illustrate the fact that our estimates are not the same as the UN estimates, even though our method assumes the UN estimates to be unbiased. The average difference between the UN estimates and ours is zero — our definition of unbiased.

For all countries except the Gambia, the median width of the 95% confidence intervals is about 0.35 children. The confidence intervals for the TFR are wider for the years before the mid 1970s than afterwards. The Gambia has the most uncertainty about past levels of the TFR because of the scarcity of data, particularly the absence of a DHS, and the extent to which the observations vary. For the Gambia the median width of the 95% confidence intervals is 0.74 children, about twice as wide as for the other countries. The confidence intervals are narrowest around 2000 and in the mid 1970s because these were periods with more observations.

4.4 Method validation and comparison

Our method takes account of the differences in data quality between data sources, but one can ask whether this actually improves the estimates. We assess this by comparing our method with a method that is the same except that it does not adjust or weight the observations for data quality. We will refer to the method that takes account of bias and difference in measurement errors as the corrected method, and to the method that treats all observations equally as the uncorrected method.

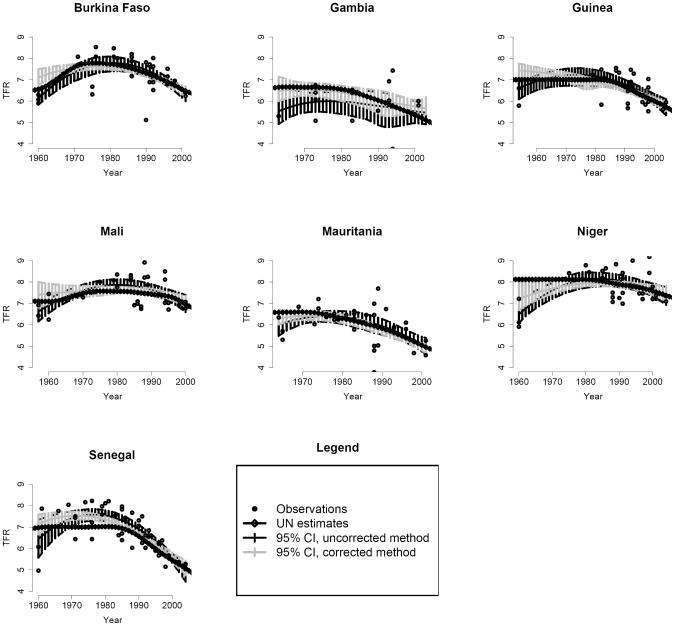
Figure 6 shows the confidence intervals for the TFR for both methods in the seven countries in West Africa. The two methods differ most at the start of the observation period, with the uncorrected method giving lower estimates than the corrected method. For most countries the uncorrected method peaks in the mid 1980s at a TFR that is higher than the estimate from the corrected method. In the Gambia, the only country without a DHS, the uncorrected method gives lower estimates than the corrected method for all years. The confidence intervals are generally much narrower for the corrected method — on average 40% narrower. In most cases the UN estimates are inside the 95% confidence intervals of both methods.

Figure 6.

95% Confidence intervals for the TFR for the corrected method (grey) and the uncorrected method (black). The solid line shows the annual median estimates and the 95% confidence intervals are plotted with dashed lines. The observations are displayed as black dots and the UN estimates by the grey line with squares.

To validate the methods, we left out different subsets of the observations, implemented the methods without them, and then compared the resulting predictive distributions with the observations themselves. The subsets excluded for this cross-validation exercise were: (i) random subsets of observations (10 different subsets of 50 observations each) and (ii) one DHS at a time (there were 22 DHS in all). Leaving out one survey at a time and then examining the way the excluded observations fit into the uncertainty assessment is the most realistic scenario in terms of adding “new” observations to the data set that are independent of the observations that are already in the data set. We did this for both methods.

The results are summarized for the two excluded categories in Table 5. The average bias was 0.03 children or less for both categories for the corrected method and larger for the uncorrected method, reaching 0.21 children for the excluded DHSs. Uncertainty is slightly underestimated in the corrected method, as shown by the standardized absolute prediction error (SAPE) which is larger than one for both outcomes, and by the proportions of observations that fall outside the prediction intervals.

Table 5.

Validation results for the corrected and uncorrected methods: Bias (the average difference between excluded observations and the median TFR estimate), SAPE (the standardized absolute prediction error), PIT area (the area above one in the PIT histogram), and the proportion of excluded observations that fall outside their 80% and 95% prediction intervals

Proportion of observation
Excluding	Method	Bias	SAPE	PIT area	<80	>80	<95	>95
50 Observations	Corrected	−0.02	1.06	0.05	0.08	0.11	0.04	0.04
	Uncorrected	−0.06	1.00	0.11	0.12	0.04	0.03	0.01
DHS	Corrected	0.03	1.23	0.14	0.14	0.13	0.04	0.07
	Uncorrected	0.21	1.08	0.19	0.07	0.14	0.01	0.04

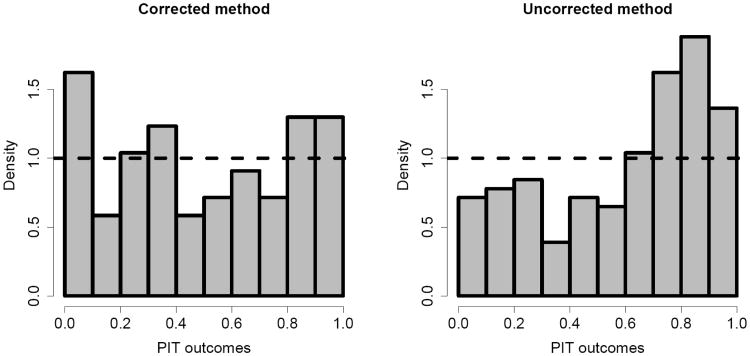
The PIT histograms in Figure 7 do not show any systematic lack of calibration for the corrected method, but they clearly indicate the bias in the uncorrected method. This is confirmed by the better values of the PIT area for the corrected method compared to the uncorrected method. Overall we conclude that our corrected method is reasonably well calibrated, and that accounting for data quality is worthwhile in that it removes the systematic bias in the uncorrected method and reduces the width of the confidence intervals, while yielding calibrated uncertainty statements.

Figure 7. Histograms of the outcomes of the probability integral transforms for the excluded observations when leaving out one DHS at a time for the corrected and the uncorrected method.

5. Discussion

We have proposed a new approach for estimating the TFR over time from multiple data sources of varying quality, and we have applied it to seven West African countries. Our approach consists of four steps: bias adjustment, estimation of measurement error variance, local smoothing of the bias-adjusted values with weights based on the error variance, and uncertainty assessment using the weighted likelihood bootstrap. We evaluated the results by cross-validation and found our method to be reasonably well calibrated. Comparison to a similar method that excludes the first two steps shows that taking account of data quality removes bias and reduces the average width of the confidence intervals.

We have focused here on the estimation of period TFR rather than cohort TFR because that is what the UN has published for many years. This is because most data are collected cross-sectionally and so lend themselves to the estimation of period TFRs. To reconstruct a full cohort history one needs full birth histories, which are often unavailable for the whole time period since 1950, and, if they are available, they are truncated for older women and incomplete for younger ones. Moreover, there is a greater focus on recent fertility and especially its pace of decline, because the UN uses its period TFR estimates as a basis for the projection of future population size, by breaking down the projected TFR in each period into age-specific fertility rates for that period. For this purpose, period TFRs are more appropriate than cohort TFRs, even if the latter were available.

Our method has been developed for an aggregate rate (the TFR) while often age-specific rates are needed. The method could be applied directly to age-specific fertility rates, but this has the disadvantage that adherence to overall patterns is not guaranteed. A possible alternative would be to use our present method in combination with age-specific fertility schedules.

There are several limitations to our study. The main drawback of our estimation method is that it requires an “unbiased” data source in order to predict bias and measurement error variance. This data source does not have to be perfect or even of high quality, but it is required to have no systematic tendency to substantially over- or underestimate the TFR. We used the existing UN estimates for this purpose. We did this because the UN estimates are the only source of data that cover the entire period of observation for each country, and because they are the result of a continuous process of refinement that uses other types of data, including exogenous information about the proximate determinants of fertility (Bongaarts and Potter 1983) to validate the estimates. Another possibility would be to use the DHS data with short recall periods as the unbiased data source. A problem with this is, however, that some DHS could be flawed, and that the DHS do not cover the entire time period required in each country.

Given that we used the UN estimates as an unbiased data source, what would be the consequence of potential biases in the UN estimates on our TFR estimates? If the UN estimates were consistently biased upwards in all countries, or consistently biased downwards in all countries, the estimated bias corrections for the observations would be incorrect, and so the estimated TFR would be incorrect-biased in the same direction as the UN estimates. Given the approach that the UN uses to estimate the TFR, we feel that this is unlikely.

In our error variance regression analysis, we assumed that the absolute differences between the bias-adjusted observations and the UN estimates are, on average, proportional to the differences between the true TFR and the bias-adjusted observations in the error variance regression. If this assumption does not hold, the estimates of the differences in the measurement error variances ( ${\mathit{\rho }}_{\mathit{\text{cts}}}^2$) would be biased. We think our assumption is reasonable because we expect the errors in the UN estimates to be small compared to the data errors (see Appendix).

Despite the limitations of our study, our validation exercise shows that our confidence intervals are reasonably well calibrated. This finding indicates that either our assumptions were reasonable, or that violations of our modeling assumptions were in opposite directions and cancelled each other out.

Because our method is automated, the results need to be carefully reviewed. This process can lead to new insights or extract implicit “expert information”, as we found for the positive biases in the observations with longer recall periods, as illustrated in Figure 3. An expanded dataset, covering more countries and more data sources, could enrich this analysis and provide new insights on some of the biases. The modeling approach could be improved by taking into account additional fieldwork covariates, such as interviewer and supervisor effects, time and duration of interview, background characteristics of interviewers (Johnson et al. 2009), length of training of interviewers, ratios of respondents/interviewers, interviewers/supervisors and sample size/duration of fieldwork, as well as logistic problems and budget cost. Note however, that while many of these covariates can be obtained for DHS, they are often unavailable for other data sources.

Other approaches to estimate the TFR in developing countries with imperfect data could be considered, such as the Multiple-Indicator Multiple-Cause method (Bollen 1989). More generally, a different (e.g. parametric) function could have been chosen to model the TFR over time, and biases and differences in error variance could have been estimated simultaneously while estimating the trend in the TFR in each country. This is an area for future research. While such an approach sounds promising for overcoming some of the limitations of our proposed method, it would be difficult to use in the countries under consideration in this article. First, it is not clear how to decide on an appropriate functional form to describe changes in the TFR over time. More importantly, it is not possible to estimate biases in observations without specifying, a priori, which set of observations are to be treated as unbiased. Our method overcomes these difficulties by using a local smoother to model the TFR, and by using the UN estimates only as an initial estimate. Moreover, as explained above, in our current approach we were able to extract implicit “expert information” from the UN estimates, which would not be trivial in a standard framework.

Our method for fertility could be adapted to simultaneously account for bias and differences in measurement error variance in the estimation of mortality rates. Current attempts to do this fall short in various ways. Rajaratnam et al. (2010) use Gaussian process regression to estimate child mortality for all countries of the world. In their approach, data quality is taken into account by estimating average biases in observations from vital registration systems, and by estimating sampling and non-sampling variability for different sources. This approach neither allows for bias in observations from other sources nor acknowledges differences in bias or non-sampling variability between observations from the same source. In past estimates of under-five mortality by the Interagency Group for Child Mortality Estimation (UNICEF, WHO, World Bank and UNPD, 2007) and Hill et al. (1998) data quality was taken into account by assigning a weight to each observation which depended on its data quality covariates (e.g. data collection processes) and expert judgment, but this approach did not adjust for bias in the different data sources. We hope future work will explore the possibility of adapting and applying our method to mortality estimation techniques.

Appendix.

Our probability model for observation y_cts is:

$$y_{\mathit{\text{cts}}}|f_{\mathit{\text{ct}}}\sim N\left(f_{\mathit{\text{ct}}}+{\delta }_{\mathit{\text{cts}}},{\sigma }_{\mathit{\text{cts}}}^2\right)\left(c=1,\dots ,7;t=1,\dots ,T_c;s=1,\dots ,n_{\mathit{\text{ct}}}\right),$$ (3)

where y_cts is the s-th estimate of the TFR for country c in year t, f_ct is the unobserved true TFR in year t for country c, δ_cts is the bias of observation y_cts, and ${\mathit{\sigma }}_{\mathit{\text{cts}}}^2$ is the observation-specific error variance. The corresponding model, written in matrix notation, is given by:

$$\mathit{\text{y}}|\mathit{\text{f}}\sim N\left(\mathit{\text{f}}+\delta ,\mathbf{\Lambda }\right),$$

or similarly,

$$\mathit{\text{y}}=\mathit{\text{f}}+\mathit{\delta }+\mathit{\varepsilon },$$

$$\mathit{\varepsilon }\sim N\left(0,\mathbf{\Lambda }\right),$$

where y is the vector of observations y_cts, f the corresponding vector of true values of the TFR, δ the vector of corresponding biases, Λ a matrix with corresponding ${\sigma }_{c,t,s}^2$ on the diagonal, and ɛ the vector of measurement errors.

Let u be a vector of UN estimates, where the ith entry corresponds to the ith observation in vector y. We assume that

$$\mathit{\text{u}}|\mathit{\text{f}}\sim N\left(\mathit{\text{f}},\mathbf{\Gamma }\right),$$

or similarly

$$\mathit{\text{u}}=\mathit{\text{f}}+\mathit{\eta },$$

$$\mathit{\eta }\sim N\left(\mathbf{0},\mathbf{\Gamma }\right),$$

where the errors in the UN estimates are denoted by vector η with covariance matrix Γ.

The difference between the observations and UN estimates is given by:

$$\mathit{\text{d}}=\mathit{\text{y}}-\mathit{\text{u}}=\mathit{\delta }+\mathit{\varepsilon }-\mathit{\eta },$$

and we assume

$$E\left[d_{\mathit{\text{cts}}}\right]={\mathit{\text{x}}}_{\mathit{\text{cts}}}\mathit{\beta },$$

such that

$$\mathit{\text{d}}\sim N\left(\mathit{\text{X}}\mathit{\beta },\mathit{\prod }\right),$$ (4)

where each row in design matrix X corresponds to the data quality covariates of observation y_cts and covariance matrix ∏ is given by

$$\mathbf{\prod }=\mathbf{\Lambda }+\mathbf{\Gamma }-2\text{Cov}\left(\mathit{\varepsilon },\mathit{\eta }\right).$$

β is estimated using least-squares estimation, and estimates of its standard errors are corrected for heteroskedasticity using the heteroskedasticity consistent (HC3) estimator by MacKinnon and White (1985). Standard errors of the βˆ's based on various corrections for autocorrelation (off-diagonal elements in ∏) were of similar magnitude.

The least-squares estimate for d is given by dˆ = Hd, where H = X(X′X)⁻¹ X′ and

$$\left(\mathit{\text{d}}-\widehat{\mathit{\text{d}}}\right)\sim N\left(\mathbf{0},\left(\mathit{\text{I}}-\mathit{\text{H}}\right)\mathbf{\prod }\left(\mathit{\text{I}}-\mathit{\text{H}}\right)\right).$$

The estimated biases dˆ are subtracted from the observations to get the bias-adjusted observations z_c,ts. In vector notation:

$$\begin{array}{c}\mathit{\text{z}}=\mathit{\text{y}}-\widehat{\mathit{\text{d}}},\\ =\left(\mathit{\text{y}}-\mathit{\text{d}}\right)+\left(\mathit{\text{d}}-\widehat{\mathit{\text{d}}}\right),\\ =\mathit{\text{u}}+\left(\mathit{\text{d}}-\widehat{\mathit{\text{d}}}\right),\\ =\mathit{\text{f}}+\mathit{\eta }+\left(\mathit{\text{d}}-\widehat{\mathit{\text{d}}}\right),\end{array}$$

such that

$$\mathit{\text{z}}-\mathit{\text{u}}\sim N\left(\mathbf{0},\left(\mathit{\text{I}}-\mathit{\text{H}}\right)\prod \left(\mathit{\text{I}}-\mathit{\text{H}}\right)\right),$$ (5)

$$\mathit{\text{z}}-\mathit{\text{f}}\sim N\left(\mathbf{0},\left(\mathit{\text{I}}-\mathit{\text{H}}\right)\prod \left(\mathit{\text{I}}-\mathit{\text{H}}\right)+\mathbf{\Gamma }+2\text{Cov}\left(\mathit{\eta },\mathit{\text{d}}-\widehat{\mathit{\text{d}}}\right)\right).$$ (6)

To estimate the variance of z, we assume that the absolute differences between the UN estimates and the bias-adjusted observations z_cts are proportional to the absolute differences between bias-adjusted observations and the true TFR, or, equivalently, that the standard deviation of (z_i − u_i) is proportional to the standard deviation of z_i and thus (z_i − f_i), for bias-adjusted observation i = 1,…I. Biases from violating this assumption are expected to be small if the errors in the UN estimates (η) and their covariance matrix Γ are small compared to the data errors. Alternative approaches to estimating the variance of z could be considered but would require additional assumptions about Γ and the correlation between η and ɛ, as well as a more involved estimation procedure.