Lead Optimization Mapper: Automating free energy calculations for lead optimization

Abstract

Alchemical free energy calculations hold increasing promise as an aid to drug discovery efforts. However, applications of these techniques in discovery projects have been relatively few, partly because of the difficulty of planning and setting up calculations. Here, we introduce Lead Optimization Mapper, LOMAP, an automated algorithm to plan efficient relative free energy calculations between potential ligands within a substantial library of perhaps hundreds of compounds. In this approach, ligands are first grouped by structural similarity primarily based on the size of a (loosely defined) maximal common substructure, and then calculations are planned within and between sets of structurally related compounds. An emphasis is placed on ensuring that relative free energies can be obtained between any pair of compounds without combining the results of too many different relative free energy calculations (to avoid accumulation of error) and by providing some redundancy to allow for the possibility of error and consistency checking and provide some insight into when results can be expected to be unreliable. The algorithm is discussed in detail and a Python implementation, based on both Schrödinger's and OpenEye's APIs, has been made available freely under the BSD license.

1 Introduction

A good deal of early-stage drug discovery focuses on finding small molecules with suitable affinity for a target binding site in a receptor, while simultaneously having good physical and pharmacological properties to make orally available drugs[17, 49, 31]. The very earliest stages of the process involve finding hits, small molecules which bind to the target receptor relatively weakly. Then, these hits need to be turned into leads – molecules which have suitable properties to potentially become drugs while also having sufficient affinity for the target receptor [17, 31].

Ideally, computational methods could play a role in guiding early stage drug discovery, which has traditionally been slow and time-consuming, filled with trial and error. Even the process of finding molecules which bind with sufficient affinity to the target compound can be slow and involve synthesizing hundreds of molecules [49, 64] resulting in substantial costs, both in terms of material and in time spent[17, 58]. However, developing computational tools with sufficient accuracy to reliably guide this discovery and optimization process has proven challenging [11, 64]. Some of the most popular methods, such as docking, while seeing widespread use, do not reliably yield any correlation between predicted binding strength and experimental data [64]. The path to improve these methods has often been unclear, in part because of the number of approximations made. So, while computational methods are used in early stage drug discovery, in most discovery projects they do not play a key role in guiding the process [16, 64, 46, 47]. More quantitative methods could have a more dramatic impact on the early stage discovery process.

Some methods promise higher accuracy, and thus the potential for more of a role in guiding early stage drug discovery. More rigorous methods for binding affinity prediction are available, such as alchemical binding free energy techniques. These compute binding free energies, or differences in binding free energies, from molecular simulations using techniques based on perturbations [12, 33, 18, 54]. These techniques can be used to compute both absolute binding free energies (ABFE) [8, 39, 13] or, more commonly, relative binding free energies (RBFE) between related inhibitors 59, 12, 33, 11]. While in a number of cases these techniques show considerable promise, a key obstacle hampering their more widespread use has been the difficulty of setting up and performing these calculations, which typically requires considerable expert intervention [9, 10]. So, while more rigorous methods are available, they, too, do not typically help guide drug discovery[11].

Here, our focus is on automating setup of alchemical relative free energy calculations, allowing their application to large numbers of molecules with relatively little human intervention in a discovery-type setting. We had previously worked only on small numbers of molecules, and the overhead involved in setup was not a huge concern. However, an abrupt collision with the realities faced every day by modelers in the pharmaceutical industry helped us realize we need to do better, as we sought to use free energy calculations to screen a modest library of potential inhibitors. Essentially, our problem (not unlike that facing many early stage drug discovery projects) was this: Given a set of knowns, and a library of tens to a few hundred potential other molecules of interest (some related to knowns, some not related), predict which of this library might be best to follow up on experimentally. The relevance of this task to drug discovery motivated the present development of an automated setup tool for alchemical free energy calculations. The importance of this problem has also similarly motivated a recent tool for automated setup of endpoint free energy calculations[22].

In planning calculations of binding free energies for these compounds, we chose to compute RBFE, comparing binding strengths of related compounds, rather than computing ABFE for individual compounds. Several reasons motivated this choice. First, RBFE calculations between related compounds are often considered more efficient than ABFE calculations since they involve insertion and deletion of relatively few atoms, historically one of the most computationally expensive steps [1, 68, 60]. Also, any protein motions or conformational changes that happen on binding but are common to all ligands do not necessarily need to be sampled, as can be seen from decomposing the thermodynamic cycle for binding into a conformational change step and a binding step[36, 40]. Second, many molecules in our initial set were charged, and free energy calculations involving changes in the system net charge, as we would be doing in ABFE calculations, pose technical challenges that are not yet well understood for systems more complicated than individual ions in water [26, 27, 23, 24]. Preserving the net charge of the system by doing relative free energy calculations between molecules sharing the same net charge bypasses these problems.

It is worth noting that RBFE calculations do have one major limitation, in that they do require knowledge of the likely binding mode of the compounds of interest. Such knowledge will often be available in structure-based drug design projects, especially at the lead optimization phase, but it is worth noting this requirement. This challenge is not unique to RBFE calculations, though – the same issue also confronts most other techniques, including ABFE calculations, which also must either take the likely binding mode as input, or at least sample it adequately in the resulting simulations. However, in cases where there is substantial uncertainty as to the compound's likely binding mode and multiple possibilities are available, ABFE calculations may actually be preferable to RBFE calculations as multiple binding modes can be difficult to handle within the RBFE framework [40]. Overall, though, it is generally thought that RBFE calculations are easier and more efficient than ABFE calculations.

While RBFE calculations avoid some problems with ABFE calculations, they do require a planning step that is not needed for ABFE calculations: For a possible 50 compound lead series, which of 50 × 49/2 = 1225 possible relative free energy calculations should we actually do? Each relative free energy calculation compares binding of a pair of inhibitors, so we need an automated way to decide which pairs of inhibitors we ought to plan relative calculations between. Rather than doing 1225 RBFE calculations, we ought to be able to span the entire library with just over 50 relative calculations, yielding relative free energies for all of the molecules. Hence, our main focus here is development of a tool which can automatically plan RBFE calculations spanning a library of compounds.

2 LOMAP Method

2.1 Design goals

What criteria make for a good relative free energy calculation? That is, for a library of n compounds, with n × (n – 1)/2 possible relative free energy calculations, which calculations can we expect to actually work reasonably well? Some choices are clearly bad. For example, if two molecules share absolutely no atoms in common, computing an RBFE between the two requires subtraction of two ABFE calculations. Beyond this obvious consideration, we specified a number of other design goals. These are broadly based on efficiency considerations identified in the literature, and also focus to some extent on minimizing error accumulation and building in ways to identify calculations which may be wrong due to poor convergence.

2.1.1 Goal 1: Compounds being compared should be as similar as possible, minimizing atomic deletions and insertions

Generally, we would prefer the compounds being compared to be as chemically similar as possible, maximizing the likelihood that they have the same or similar binding modes and minimizing the number of atomic deletions and insertions required [1, 68, 60, 3, 25]. For example, changes in atomic partial charge and atom type can be typically done using molecular dynamics simulations involving relatively few intermediates (λ values) spanning between the two end states, perhaps even as few as 5-11[29, 33, 30, 62]. Insertions of individual atoms can also be done in a relatively straightforward way[25, 60, 3] but deletions or insertions of entire functional groups may require as much as 2-3 times as many simulations[56, 57, 38, 1, 68, 60] because of the need to spread out deletions/insertions across multiple simulations. Additionally, these larger chemical changes typically lead to larger free energies, and hence the chance of larger errors. So, a major goal is to plan relative calculations between the most similar molecules, minimizing the number of atomic deletions and insertions.

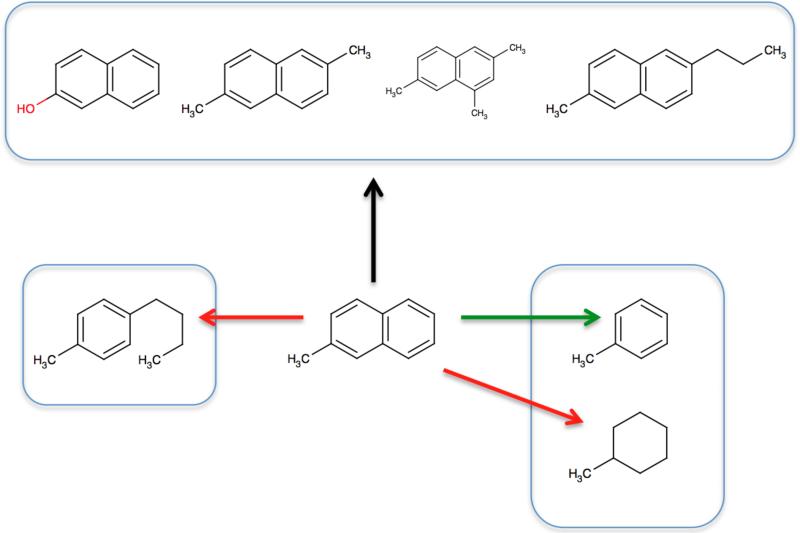
It is worth noting, however, that from the standpoint of classical fixed-charge simulations, “similar” means something slightly different than it typically does in drug discovery. Specifically, in simulations, atom type changes are quite straightforward, and need not be avoided. For example, changing benzene into chlorobenzene is easy – no atoms are deleted or inserted, and there is only a modification of the atomic partial charges and minor changes to some Lennard-Jones parameters. Similarly, changing a nitrogen-containing heterocycle into a sulfur-containing one is straightforward as long as the pattern of connected atoms is the same. So we are willing to grant considerable chemical leeway when deciding which molecules are “similar”. Figure 1 shows an example of a variety of favorable transformations beginning from 2-methylnaphthalene.

Fig. 1.

Favorable mutations of 2-methylnaphthalene, based on our design goals. Black and green arrows show allowed transformations from 2-methylnaphthalene. Red arrows show transformations which are not allowed. Transformations marked by the black arrow are considered the most favorable, and similarity (and hence favorability) decreases from left to right, based on design Goal 1. Mutation from 2-methylnaphthalene to 1-butyl-4-methylbenzene is prohibited (red arrow to left) because it would involve breaking a ring in a bi-cycle (Goal 4). Mutation to toluene (green arrow) is allowed only under the “loose” scoring scheme, and only if necessary to span the set (Section 2.2.4), while mutation to methylcyclohexane is prohibited (red arrow to right) because it involves breaking a ring in a bi-cycle and leaving a flexible ring behind (design Goal 4).

2.1.2 Goal 2: Rings should be preserved as much as possible

The larger the functional group being deleted, the larger the potential problems with insertion/deletion, so we prefer to avoid deletion and insertion of ring systems as much as possible (though this is to be preferred over breaking or forming rings[53], as noted below). Additionally, deletion of large bulky functional groups such as rings may provide a molecule with substantially more room in a binding site, reducing the likelihood that it will remain in the expected binding mode, and increasing the potential for problems adequately sampling potential binding modes [40]. Hence, we choose to try and retain ring systems as much as possible.

2.1.3 Goal 3: Ligands being compared must share the same net charge

As noted above, for technical reasons, relative free energy calculations involving changes of the net charge of a system are to be expected to be unreliable. Specifically, changing one charged ligand into a ligand of a different charge in the binding site leads to a contribution to the free energy due to the change in charge and its interaction with the surrounding solvent dielectric, periodic copies of the system, and other factors [26, 27, 23, 24]. This would cancel out if these contributions were the same in solvent, but in general they are not, partly due to differences in system size and composition in the two environments. Therefore, we choose to plan relative calculations only between subsets of ligands of the same net charge. To allow estimation of the affinity of all compounds, selected compounds of known affinity could be included in each subset, if such compounds are available (see Section 2.2.4). In our view, RBFE calculations for chemical modifications which change the net charge (such as addition of a carboxylic acid) must wait for algorithmic developments.

2.1.4 Goal 4: Portions of multi-ring systems can only be deleted if rings are planar, and this should be avoided when possible

Alchemical free energy calculations rely on a thermodynamic cycle, which must properly close to yield relative free energies. When deleting atoms, we leave behind so-called “dummy atoms” which still have bonds to the remainder of the molecule but do not interact with the system in any other way[53]. For our thermodynamic cycle to close, the contribution of these dummy atoms to the free energy of the system must be independent of the molecular environment. For example, if we delete a methyl group in a binding site and in solution, the free energy of the dummy methyl group must be the same in both environments. This criterion is met for methyl groups, because a dummy methyl group, in our simulations, is a simple set of masses and springs (and potentially torsions) with an energy that does not depend on the environment. Thus, any free energy contributions from the dummy atoms in the binding site rigorously cancel with contributions from the dummy atoms in solution, the other side of the thermodynamic cycle. Thus, the bonded terms of dummy atoms make no contribution to the relative free energy[5, 4].

In general, dummy atoms do not contribute to the relative free energy for all transformations of groups of atoms into dummy atoms except when the geometry is modified due to the influence of external forces [5, 4]. That is, cancellation will occur for any simple deletion of singly-connected groups of atoms. However, bonded terms can in some cases contribute to relative free energies under the influence of external forces[5, 4]. The main scenario in which this can be expected to happen is for deletion of multiply connected groups. For example, for mutation of cyclohexane into butane, dummy carbon atoms left behind from cyclohexane can affect the free energy in at least two ways. First, since the dummy atoms are still bonded to the butane atoms, they can affect the conformation of butane, altering which states are preferred. Second, the free energy of the system of dummy atoms (masses and springs) depends on the conformation of butane. If the preferred conformation of butane is different in complex versus in solvent (such as due to contacts with the receptor), the free energy of the dummy atoms will be different, producing a thermodynamic cycle which does not properly close due to free energy contributions from these bonded terms. This has the potential to happen whenever portions of rings (partial loops of atoms) are being deleted. Practical complexities such as the necessity to break or form bonds when opening or closing rings also make these cases difficult, as discussed elsewhere[5, 4].

So, we can avoid any contributions from the bonded terms of dummy atoms by avoiding breaking or forming rings, but in some cases this may be necessary, as we explain below. If ring breaking or forming is necessary, any contributions from dummy atoms will be small whenever the conformation of the molecule, with its dummy atoms, is essentially the same in water versus in complex, which will happen when the portion of the molecule being left behind is rigid. For example, for a naphthalene to benzene transformation or similar (Figure 1), benzene is quite rigid, and has a very limited range of motion regardless of environment. It is unlikely that a binding site could alter the conformation of benzene enough in order to induce a significant change in the bonded energies of the naphthalene dummy atoms left behind. In such cases, there may still be a small contribution of bonded terms to the overall relative free energy (that is, the thermodynamic cycle may not quite close formally) but we believe the effect will be quite small. In contrast, a naphthalene to cyclohexane transformation is much more risky, because the ring behind left behind now becomes flexible (cyclohexane) and its bond lengths will change appreciably, substantially affecting the bonded energies of the dummy atoms left behind from the additional ring system.

Here, then, our goal is to avoid inserting or deleting any partial rings as by so doing we can avoid introducing any errors due to bonded contributions to relative free energies. However, making this an absolute rule proves to be a bad idea. For example, if the set of molecules contains one group consisting of benzene derivatives (potentially with R-groups attached in various places) and another group based on the naphthalene scaffold, with two aromatic rings (again potentially with R groups) linked together. If we abide by the rule of never inserting or deleting partial rings, we will end up with two disconnected groups of molecules and no way to compare their binding affinities. We propose that in such cases, where rigid rings are being retained in a proposed partial ring deletion, it is acceptable to delete the partial ring in question and assume that bonded contributions to the free energy cancel (green arrow, Figure 1). So, our goal is to prefer relative free energy calculations which preserve rings or avoid deleting partial rings, but when absolutely necessary, we will tolerate deletion of partial rings as long as the components being left behind are essentially rigid.

2.1.5 Goal 5: Every molecule must be part of at least one closed thermodynamic cycle

Free energy calculations can yield accurate free energies, or results which are wildly wrong[8, 69, 14]. When the latter situation occurs, the source of error can be difficult to discern. Assuming the system being modeled is representative of experimental conditions, there are two main sources of error – poor convergence (i.e. the free energies would have been correct if only enough simulation were done) or force field inadequacies (i.e. additional simulation would have kept computed free energies the same and only reduced the uncertainty). One way to check for convergence problems is to add some redundancy into relative free energy calculations, introducing additional calculations between some molecules and hence adding some cycles – closed paths around which relative free energies must formally sum to zero. The difference from zero is called the cycle closure error. This has been done in some relative free energy calculations in the past (for example references [6, 19, 14, 61, 34, 44, 48, 63]) and provides a lower bound on the amount of convergence error in the calculations. The literature suggests that this can be a useful lower bound, in the sense that sometimes the cycle closure error is extremely large, as much as several kcal/mol [6, 19, 14, 61, 34]. One frequently requested feature from modelers in industry is the ability to know when calculations are expected to fail, and this provides at least some information in that regard.

Overall, then, in order to provide some level of consistency checking and detection of convergence errors, we require every molecule be part of at least one closed thermodynamic cycle.

2.1.6 Goal 6: The set of planned calculations should be spanned by relatively few calculations

When computing relative free energies across a large set of molecules, we may need to combine results of multiple calculations, leading to an accumulation of statistical error. To prevent these errors from becoming too large, we want to be able to get between any two molecules with no more than a certain maximum number of calculations.

2.2 Algorithm

Our main goal, then, is to construct a undirected graph where each node (or vertex) is a compound of interest and each edge (or arc) a relative free energy computation for the two flanking compounds. The edges should be assigned in a way to accomplish our design goals mentioned above. Effective free energy computation typically requires that the two molecules be sufficiently similar. So the edges (planned calculations) will depend heavily on the computed similarities between molecules. In the following, we introduce our definition of the similarity concept.

2.2.1 We want a similarity measurement to assess ease of computation

Intuitively speaking, similarity refers to the “likeness” of two molecules and is one of the factors that strongly influences the success of relative free energy calculations. For this reason, similarity is a pivotal concept in our algorithm, and we define it as a scalar quantity measuring the feasibility of a specific calculation. The higher the similarity, the more feasible the calculation is. To measure similarity, we seek scores spanning a known range, with the minimum representing total dissimilarity, and the maximum representing identity. We choose the range [0, 1] to denote the similarity score. This choice of the range is somewhat arbitrary but has several advantages described below.

This definition of similarity relates directly to how we construct the graph of planned calculations. When the similarity between two compounds is high, we should have a higher likelihood of connecting them by an edge. Often, the term “similarity” in the literature refers to a simple measurement of chemical similarity. Here, however, we move past simple chemical similarity and define similarity scores which ensure our design goals will be met. Thus, we are more concerned with assessing the computational difficulty of particular transformations than rigorously scoring chemical similarity. That is, we are more interested in scoring computability. To appreciate this, consider a possible transformation between methane and ethane, and another transformation between benzene and toluene. Chemically, benzene and toluene are more similar, but in (in the absence of other sampling considerations) RBFE calculations between both pairs are expected to require roughly the same amount of computational resources because the mutation is identical for both pairs (hydrogen to methyl). Thus, to measure computability, similarity scores should be very close (if not identical) for methane-to-ethane versus benzene-to-toluene transformations.

To score efficiency of transformations based on a chemical similarity metric requires one major assumption – that the most important contribution to a transformation's difficulty is the magnitude of the transformation itself. This will certainly not always be the case. For example, in a hypothetical receptor, one extremely small chemical modification (introduction of a methyl at a particular location, for example) might introduce a dramatic binding mode change or a new receptor conformation, posing substantial computational challenges, while a much more dramatic modification (introducing a phenyl group elsewhere in the molecule, for example) might do very little to the binding mode and receptor conformation and be computationally straightforward. However, in the limit of adequate binding mode and receptor sampling, transformation difficulty is an important metric. Even when facing potential problems in binding mode and receptor sampling, if we lack information on when to expect these effects, we should still be best served by focusing on the difficulty of particular transformations.

2.2.2 Our similarity measurement starts with the size of the maximum common substructure

A common theme of Goals 1-2 above (Section 2.1) is the desire to minimize the number of atomic insertions and deletions, which we can build in to our similarity scores by using the size of the maximum common substructure (MCS) as the foundation for scoring. An MCS search determines the largest common substructure shared by two molecules. Once this is known, the number of atomic deletions or insertions is immediately apparent, as is the change in any ring systems.

Here, we can make an MCS search better suit our needs by modifying it slightly. Specifically, we treat all heavy atoms as equivalent in the search, since as noted in Goal 1 (Section 2.1) , changes in atom types are straightforward. Thus our search focuses on molecular topologies rather than atom types. We also adjust the search to prefer substructure matches which preserve ring systems as much as possible (Goal 2). The resulting modified MCS search forms the foundation for our similarity scores.

Initial similarity scores are calculated based on the size of the MCS using the expression

$$S=\exp [-\beta \times (N_A+N_B-2N_{MCS})]$$ (1)

where β is an arbitrary constant value, and N_A, N_B, and N_MCS are the number of heavy atoms of the two input molecules and of the MCS, respectively. Thus the term N_A + N_B − 2N_MCS is the total number of atoms inserted or deleted in the transformation. We use an exponential both to ensure that scores range between 0 and 1, and to strongly favor small structural changes.

2.2.3 We construct similarity scores based on the modified MCS search, and fold in other scoring rules

We want similarity score calculations to be easy to automate and extend. As noted, the MCS similarity provides the foundation for our scores, but we still have several other goals (Section 2.1) to achieve. The easiest way to do this is by modifying our similarity score to include these aspects as well. Specifically, we need to also ensure that compounds being compared share the same net charge, and avoid broken or partial ring systems in our transformations. To include these factors in similarity scores, we built a simple rule engine, which provides a mechanism to combine multiple requirements (rules) or scores into a total. A rule here represents a regulation for similarity calculation, and its application involves taking in a pair of input molecules and outputting a similarity score based on the rule. The MCS search above can be recast in this format as a “maximum common substructure rule” (MCSR), which computes the size of the MCS and outputs a score in the range [0,1].

Our rule engine allows straightforward combination of multiple rules, typically by multiplication to maintain the score range. In addition to the MCSR, we also apply a “minimum number of common atoms rule” (MNCAR) which says that the two molecules must share at least n heavy atoms to be regarded as similar. This simple rule outputs a score of 1 if the number of common atoms is larger than n, and 0 otherwise. A composite of the MCSR and MNCAR rules amounts to checking the number of heavy atoms in the MCS, and if it is greater than n, returning a score based on the MCSR, otherwise returning 0. The score of the composite rule is given by the simple formula: S = S_MCSR × S_MNCAR, and thus S remains a number in the range [0, 1] . This approach is useful because it decouples rule definitions from the scoring process, making it simple to add additional rules without modifying existing ones. For example, to add a new “equal charge rule” (ECR), which, given a molecule pair, outputs 1 if they have same the net charge and 0 if not, to we simply calculate S_ECR (the score for the equal charge rule) and add it to the composite rule, which is now using S = S_old × S_ECR. For more details, interested readers are encouraged to read the LOMAP source code and the documentation therein.

Here, we are able to build Goals 1-4 (Section 2.1) into our similarity scores by forming a single composite score out of just four specific rules. These goals are handled as follows:

• – Goal 1 (minimize atomic insertions and deletions): This is built into the definition of the MCS score itself (and the corresponding rule, MCSR), as described above.

• – Goal 2 (preserve rings as much as possible): This, too, is built into the MCSR.

• – Goal 3 (preserve net charge): The equal charge rule (ECR) zeros similarity scores for molecule pairs having different net charges.

• – Goal 4 (avoid breaking rings, and only break them if planar): Here, we examine the MCS to see whether it contains broken or partial ring systems. If it does, we delete atoms in the broken or partial ring systems (and any unconnected moieties due to the deletion). Since this rule is based on the deletion from the MCS, we call it trimmed-MCSR (TMCSR) and calculate resulting score using the formula: S = exp [−2 × N_del], where β is the same constant value as in the MCS rule, and N_del is the number of deleted heavy atoms. Here, we actually assign two different TMCSR scores, one we call “strict ring deletion” and a second we call “loose ring deletion”. In both approaches, ring atoms in one molecule cannot be mapped to non-ring atoms in another molecule. The difference is in handling of joined ring systems, as in Figure 1. In strict ring deletion, if any component of a joined ring system no longer remains a ring after MCS calculation, the entire ring system is deleted. In contrast, in loose ring deletion, ring atoms in the MCS are kept if the portion of the ring system being left behind remains planar. The latter allows transformations like naphthalene to benzene, while the former does not.

Besides applying the above rules and constructing a composite rule by taking the product of their scores, we also define a simple cutoff rule (the minimum similarity score, “MSS”): Compare the similarity score with a threshold value, return 1 if it is greater than the threshold, otherwise return 0. The goal of this rule is to ensure that calculations in the final graph meet at least a certain minimum level of similarity. This rule is not used in construction of the composite similarity scores, and we discuss its application below.

2.2.4 Calculation planning builds up a graph based on similarity scores

We construct our graph of planned RBFE calculations following this procedure:

1. First, we calculate two sets of similarity scores from all pairs of the molecules. The first set, called the loose scores, are obtained by execution of a composite rule composed of the rules from Goals 1-3 and Goal 4 (loose). The second set, called the strict scores, are obtained by execution of a composite rules composed of the rules from Goals 1-3 and Goal 4 (strict). We store these two sets of scores in two separate matrices. The strict scores are used throughout except where otherwise noted.

2. We use the strict score matrix to assign an edge connecting any pair of nodes with a final similarity score greater than zero, and then we remove all the edges with scores less than the MSS cutoff, thus obtaining an initial graph. The following steps will refine this initial graph and reduce the number of edges.

3. The initial graph often has several connected components – subgraphs that have no connections between one other but within which there is a path between every pair of nodes. The more similar molecules are, the more likely they will be within the same connected component, and vice versa. We call all of the nodes within a connected component a cluster. Within each cluster, there are, at this point, typically far too many edges because most nodes are directly connected. We then try to reduce the number of edges while ensuring the cluster continues to meet our design goals (especially Goals 5-6, which are not encoded into the similarity scores), which we can think of as constraints. Specifically, we want the minimum number of edges such that 1) every node should be in a cycle, and 2) the length of the shortest path from any one node in the cluster to any other node in the cluster should be less than a specified maximum distance (MAXDIST). For 1), we use Paton's algorithm [45] to calculate the cycle basis [2], and use this to determine if all the nodes are in a cycle. For 2), we use a breadth first search to calculate the diameter of the cluster; from the diameter, we determine if the cluster meets the distance constraint. Following this procedure, if the constraints are met, we then sort and list the edges by their similarity score, from lowest to highest. We then remove the least similar edge and check if the cluster still meets the constraints. If it does, we then remove the next least similar edge, and so on, until we have checked every edge and there are no remaining edges that can be removed without violating the constraints. Thus, at the end of this process we obtain a graph with a minimum number of connections, which we call the minimized graph.

4. At this point, different structural clusters still remain disconnected. Therefore, we use the loose score matrix to merge clusters from the minimized graph into a final, connected graph. This step has two passes. In the first pass, we connect as many of the clusters as possible, while in the second pass we build in cycles between clusters. The first pass connects clusters via a weighted maximum spanning tree. For the second pass, we repeat the procedure used in the first pass, but omit any edges created in pass one, thus creating a second weighted maximum spanning tree. Thus, each cluster will now be connected via two routes, ensuring our goal about cycles is met. It is important to note, however, that only connections with nonzero similarity scores are allowed, so clusters of different net charge will remain disconnected, as will any compounds or clusters which share no similarity with other compounds.

The MSS rule described above is applied when planning all intra-cluster calculations, but it is not applied at the stage of planning calculations spanning structural clusters, simply because we wish to ensure a path between all compounds of the same net charge if at all possible. Thus the final graph may have connections with similarity below the minimum similarity score, though this will only happen if it is necessary, since there is still a preference for connections with higher similarity scores.

Because MAXDIST (step 3) applies only within each structural cluster, the total number of calculations across the final graph is actually larger than MAXDIST, in a way that depends on the nature of the set of compounds. If there are m initial structural clusters, then the upper bound on the maximum distance across the graph after step 4 is m × MAXDIST + (m − 1) = m(MAXDIST + 1) − 1. In general we expect that for a typical congeneric series, the maximum distance across the final graph will end up being MAXDIST since all molecules will be in a single structural cluster. However, for more diverse compound libraries there may be several distinct structural clusters (such as for the “trypsin” dataset in our Supporting Information, which contains the Maybridge fragment library as a subset).

In some sets of planned RBFE calculations, it may be desirable to include a set of knowns – compounds having known binding free energies – both to allow calculation of absolute binding free energies of the unknowns by referring to the knowns, and as a consistency check. Our code allows the user to provide a set of known compounds which are a subset of the whole, and in this case, the maximum distance, MAXDIST, is set to apply to the distance between any given unknown and some known compound. So the calculation planning algorithm will ensure every compound is within MAXDIST of a known compound. This actually reduces the number of required calculations (since now unknowns are allowed to be more than MAXDIST apart).

2.3 Our implementation is in Python

We implemented the above algorithm in Python 2.7. The third party libraries used here include Schrödinger's [51] or OpenEye OEChem's APIs [43] for general molecular manipulation, MCS searches, and modification of MCS output (such as removing partial rings, etc.), networkx [20] for graph creation, traversal, and manipulation, OpenEye OEDe-pict's APIs [43] for molecule depiction and graphviz [15] for visualization of the graph.

Our toolkit is available through SimTk as Lead Optimization Mapper, LOMAP, at https://simtk.org/home/leadoptmap.

3 Simulation methods

3.1 Topology construction

While a tool for automatic setup of input files for relative free energy calculations is not currently part of LOMAP, this will be a subject of future work. Here, we built a prototype tool to construct GROMACS topologies for relative calculations in a single-topology, explicit-intermediate manner4, essentially the simplest manner possible given LOMAP's output of the common substructure. If one ligand is A, the second is B, and the MCSS is M, we set up the transformations A → M and B → M. We are operating in a deletion-only mode, where transformations always involve only deletion and/or mutation of atoms, never insertion of new atoms. Free energy calculations for these transformations are conducted both in vacuum and in water, and from the respective free energy differences we can obtain the relative hydration free energy. Since the substructure M is based on either A or B, in general it will differ in atom type from one of the two (for example, a “common” atom in a ring might change type, or even a hydrogen atom might be changed into a carbon atom). Thus A → B or B → M will in general involve atom type changes (with associated changes in bonded atoms) as well as transformations of atoms into dummy atoms, and changes in partial charges. We implemented setup of topologies via this approach in a Python tool which will be further developed as part of a separate work

3.2 Simulation protocols

Here, relative free energy calculations were conducted with essentially the same protocol we have used in the past for absolute hydration free energy calculations[28, 41], updated by using the Parrinello-Rahman barostat for production simulations (switching from the constant NVT ensemble to constant NPT) with a time constant of 10 picoseconds. Simulations were conducted at 298.15 K, and a brief overview of our protocol is as follows. We used Langevin dynamics, and production simulations were 5 ns in length, after 50 ps of constant volume equilibration, 50 ps of constant pressure equilibration with the Berendsen barostat and a time constant of 1 picosecond, and a further 50 ps of constant pressure equilibration with the Parrinello-Rahman barostat and the same 10 picosecond time constant used for production. Except as noted below, a time constant of 2 fs was used and bonds to hydrogen were kept constrained. We used 20 λ values, with Coulomb and van der Waals transformations conducted separately, with Coulomb λ values 0.0, 0.25, 0.5 and 1.0, followed by other alchemical changes (van der Waals and bonded interactions) being made according to the scheme λ = 0.0, 0.5, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0. Soft core potentials were used for the van der Waals portion of the transformation as previously. Simulations were conducted with a beta of GROMACS 4.6.2, and because of a bug involving mass changes in this version of GROMACS, atomic masses were left constant for changing atom types, as these are irrelevant for free energies. Free energies were computed with MBAR[55]. Our starting molecule structures and force field parameters were taken directly from our previous work on this set[35].

Our protocol was modified slightly for those transformations in which a hydrogen atom was mutated into a heavy atom upon transforming to the common substructure. Since bonds to hydrogen were kept constrained in our standard protocol, but these transformations involve a change in bond length, they would have been incorrect. Thus in these cases we turned off constraints on hydrogen bonds, reduced the time step to 1 fs, and ran twice as many steps to obtain the same total simulation length and capture the free energy of changing the bond length.

4 Results

4.1 LOMAP calculation plans

In some sense, our key result here is LOMAP itself, which provides a general tool for automatically planning RBFE calculations. It also outputs the trimmed MCS for each planned calculation, making setup of the actual input files for RBFE calculations straightforward in at least several common simulation packages (DESMOND[50, 7] and GROMACS[21], for example). However, it is worth briefly assessing the output of LOMAP on some test sets.

Here, we applied LOMAP to several different sets of molecules, and full detail test sets and output are provided in the Supporting Information. Our main focus here is on a set of 50 Factor Xa (FXa) inhibitors taken from various literature sources[32, 66, 65, 52, 67], and the LOMAP plan for the full set is shown in Figure 2 (with structures for a smaller subset in Figure 3). We also tested a set of potential trypsin inhibitors (a fragment library which was screened for binding to trypsin[42], as well as a substantial number of known trypsin inhibitors), the SAMPL3 [41] set of small molecules, and our set of 504 fragment-like molecules[37, 35]. Results for these are provided in the Supporting Information, and statistics on the resulting graphs are shown in Table 1.

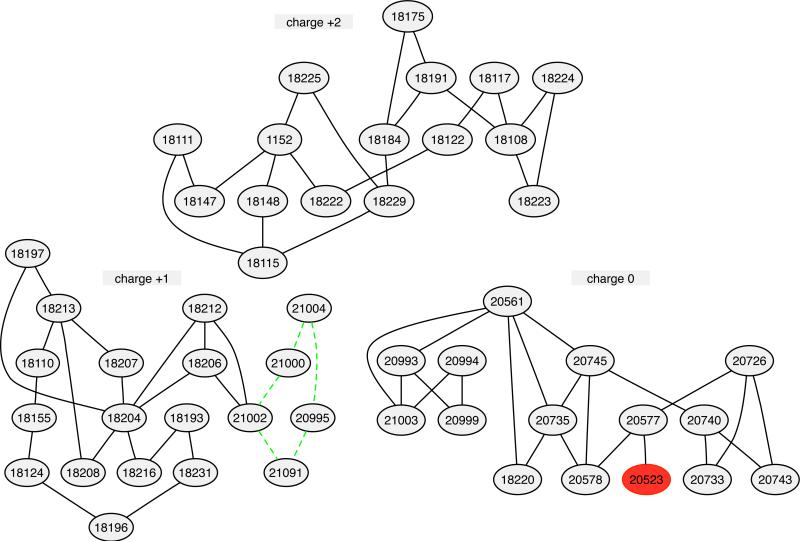
Fig. 2.

Planned RBFE calculations for the FXa set. Ovals represent molecules, the number inside nodes is molecule title, lines represent planned RBFE calculations. Green lines are a cycle example. Every nodes are in cycle except the red one.

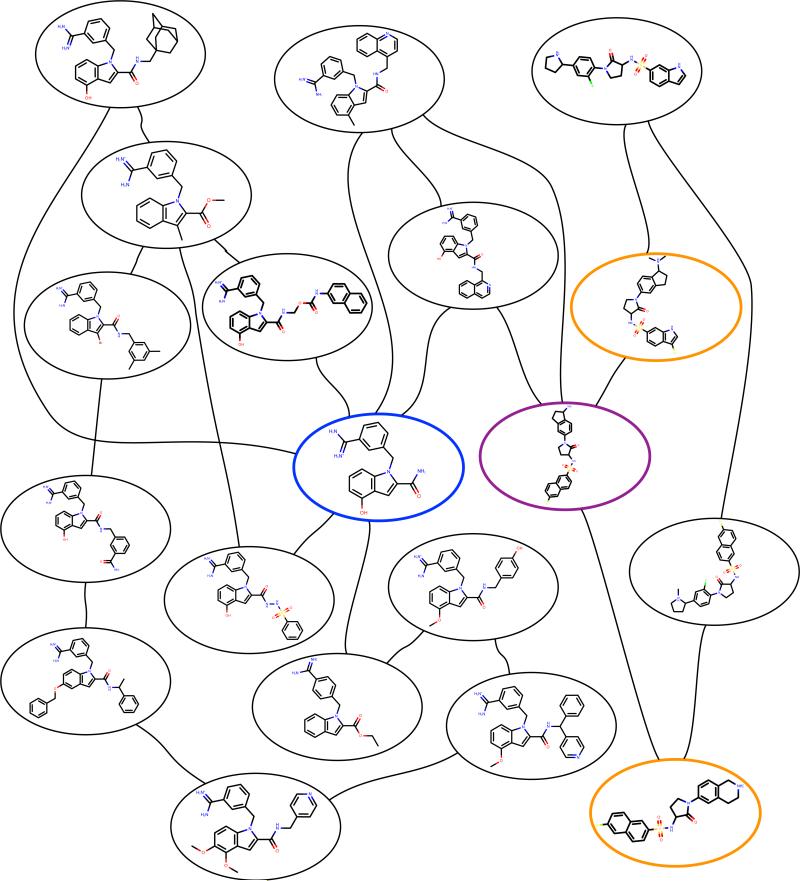
Fig. 3.

Planned calculations for the charge +1 subset of the FXa test set, showing details of molecular structures. Molecules highlighted in colors illustrate features of the output discussed in the main text.

Table 1.

Statistics of LOMAP plans for the sets examined

Dataset	number of nodes (n)	potential edges $\left(\frac{n(n-1)}{2}\right)$	planned edges	final maximum distance
FXa	50	1225	65	9
Trypsin	576	165600	785	23
SAMPL3	36	630	50	6
Fragment	504	126756	763	6

Table 2 Shown are properties of LOMAP plans for relative free energy calculations spanning the different test sets used here. The number of nodes (molecules) is shown, along with the number of possible free energy calculations between these molecules. Planned edges is the number of planned calculations spanning the set, and the maximum final distance is the maximum distance between any pair of molecules across the final graph.

Here, we used LOMAP's default parameters, setting β = 0.1 and the similarity cutoff to 0.05. These parameters correspond to a cutoff of (N_A + N_B − 2N_MCS) = 30.0 in the MCS rule¹. This means that we will not consider any calculations involving 30 or more heavy atom insertions or deletions. This specific choice is somewhat arbitrary and we plan on testing the specific choice using detailed free energy calculations in the future. At this point, our choice was made based on the assumption that for transformations larger than this, the expected error in computed relative binding free energies will be large and/or convergence will be extremely difficult. We also set MAXDIST to 6, again somewhat arbitrarily, knowing that statistical error accumulates with each additional edge (and so larger MAXDIST will introduce additional error) while at the same time smaller MAXDIST requires substantially more computational effort. Again, systematic investigation of the optimal balance here will require a large number of free energy calculations, and is an important topic for future work.

In the FXa set, LOMAP automatically divides the molecules into 3 separate groups with different net charges. The total number of calculations is 65, only marginally larger than the number of molecules in the set (50), and much smaller than the 1225 possible pairwise combinations of molecules. In general, the final product (Figure 2) meets our design goals, including building in closed cycles (Goal 5). (One specific cycle is highlighted via green lines in Figure 2). However, one node, 20523 (red in Figure 2) is not in a cycle. This ends up being because, due to the MSS rule, 20523 and 20577 are the only two members of one structural cluster. While 20577 is similar enough to other molecules that it ultimately gets connected to other nodes, 20523 is not, so it is left not belonging to a cycle. Similar cases are found in the trypsin dataset we examined. The final maximum distance across the graph is 9 (Table 1).

Because the full set of molecules is still relatively large, even for FXa, it is worth examining a more detailed version of the map, along with chemical structures, to see whether the final graph makes intuitive sense. Figure 3 focuses on the portion of the graph with compounds having a net charge of +1. LOMAP automatically generates similar graphs, which contain some additional information (such as the trimmed common substructures), though these are too large to show here and samples are shown in the Supporting Information.

Some features of the FXa subset shown in Figure 3 highlight advantages of LOMAP over planning calculations manually by inspection. For example, the blue node in the center is selected by LOMAP to essentially serve as a hub (particularly highly connected), because it is the structure common to the largest number of molecules in the series. Having this scaffold as a hub dramatically reduces the distance between other compounds sharing the same scaffold. Furthermore, a manual search might propose a calculation between the compounds shown in orange circles. However, these, though sharing substantial similarity, have bicyclic rings of different sizes, which (because we seek to avoid breaking rings) would involve larger mutations – a transformation would involve deleting and reinserting both bicyclic rings. Instead, our algorithm connects these compounds by passing through the purple node, which involves modifying only one bicyclic ring at a time. Observations of this type highlight how automatic planning algorithms are essential for large scale relative free energy calculations, as planning at this level of detail would be impossible on large sets of molecules since there are simply too many possibilities to consider (see the trypsin dataset in the Supporting Information, for example).

Another important result of these calculations is the common substructure for each planned calculation, and the mapping of ligand atoms onto this common substructure, which is also an output. This information makes it simple to set up what we call “single topology, explicit intermediate” binding free energy calculations (Figure 4). In these calculations, each ligand is perturbed to the common substructure, both in the binding site and in solution. From the difference in free energies one can obtain the relative binding free energy. These calculations are conceptually (and algorithmically) typically very straightforward to set up, since they involve simply turning any atoms being “deleted” into dummy atoms and making any changes to atom type (and corresponding bond, angle, and torsion parameters) needed to get to the common substructure. Unlike calculations going directly between ligands, these do not require a mapping of atoms from one ligand onto the other, nor do they require simultaneous transformations to and from dummy atoms, which simplifies setup. We are working on automated tools to set up such calculations in some common simulation packages, and plan to release these separately.

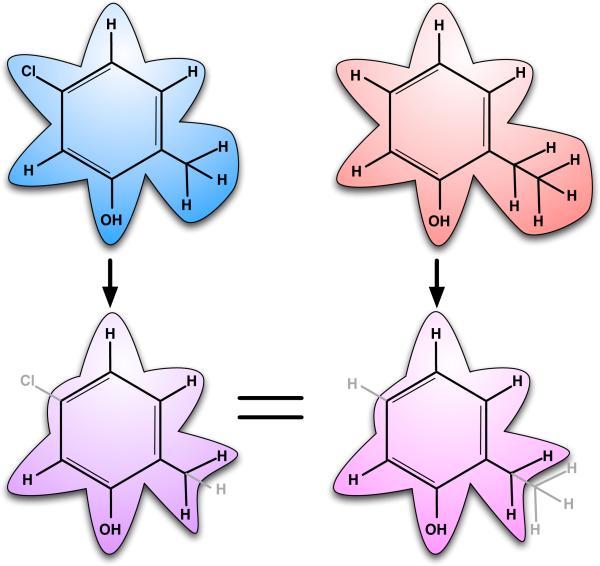
Fig. 4.

Single topology, explicit intermediate free energy calculations. Here, these calculations would be used to compare binding of 5-chloro-2-methylphenol and 2-ethylphenol. Fully interacting atoms are shown in black with underlying shaded contours, while noninteracting atoms (dummy atoms) are shown in gray with no shaded contours. The intermediate (scaffold) is specified explicitly, at the bottom. At left, the chlorine atom and one hydrogen are changed into dummy atoms, while at right, one hydrogen atom and a methyl group are changed into dummy atoms. The two scaffolds at bottom differ in number of dummy atoms, though these contributions cancel when computing free energies. The free energy calculation involves turning the specified atoms into dummy atoms in both molecules.

Automated planning of relative free energy calculations may not be necessary for very small sets, but it becomes increasingly important as the set size grows. Would simpler algorithms for planning calculations work as well as the one proposed here? Perhaps, but the most naive approach of simply randomly connecting compounds appears not to be wise, at least for diverse sets. An exhaustive test of feasibility as a function of chemical similarity and similarity score is beyond the scope of this work, but as a crude test, we picked compound pairs at random from our set and manually inspected them for similarity. We inspected 10 such pairs, shown in Supporting Information Figure 1. From the figure, it is fairly clear that this selection process is far from ideal. Random selection proposes mutating piperazine into n-butyl acetate, for example, a transformation which violates Goal 2 and in fact is probably not possible in many simulation packages (since it involves breaking a ring, which would change the exclusion interactions within the molecule). This ring breaking problem happens in two of the 10 transformations we examined (also tetrahydropyran to n-octane), whereas to the eye, the solution is immediately obvious – mutate piperazine to tetrahydropyran and n-octane to n-butyl acetate or similar. Aside from these two cases which are impractical, a number of others are far from ideal – ptoluidine to 1,1,2-tetrachloroethane, for example, and ethyl phenyl ether to iodomethane. While these transformations could work in principle, there are other molecules which make better partners which are immediately apparent to the eye. In fact, for this set of 10 pairs, there is only one pair which we would not remove based on inspection – the transformation methyl trifluoroacetate to 2-methylpentan-2-ol, since there is no clearly preferable partner for 2-methylpentan-2-ol. Other simple approaches might work better than randomly pairing compounds. We also performed some tests looking at pairing compounds by shape similarity, but these often resulted in molecule pairs without sufficient topological similarity; for example, a flexible molecule which does not contain a ring can have substantial shape similarity to a ring, despite the fact that ring breaking transformations are not practical for us. One might object that a fragment library is an especially stringent test, but the contents of this library are not that dissimilar to functional groups which might be added or modified within a congeneric series, so this simple analysis may provide some useful insight.

4.2 Validation on relative hydration free energies

While an extensive validation of our approach on binding free energy calculations is outside the scope of this work, we here test it on relative hydration free energies of related compounds. These calculations are relatively easy to converge, providing an excellent opportunity for validation, since we already know correct (for the force field) hydration free energies for a large number of small molecules[35]. These also provide a chance to test the approach in the absence of concerns about adequate sampling of the environment.

Thus, we planned 763 hydration free energy calculations spanning our 504 molecule fragment set, and selected 9 of these planned calculations for validation by relative free energy calculation. Future work will look at computational efficiency of relative calculations spanning this library as a function of similarity. However, such a large study is outside the scope of this paper, so our focus here is simply on validation for a small number of compounds. Thus, we ran single-topology relative hydration free energy calculations, and compared computed free energies with those obtained from our previous absolute hydration free energies[35]. Results are shown in Table 4, where uncertainties are reported as the standard error in the mean. Here, our discrepancy from the previous results is always under 0.4 kcal/mol, despite calculated relative free energies spanning a range of −3.7 to 4.6 kcal/mol. The difference between our LOMAP values and those previously calculated is also within twice the standard error in the majority of cases, though not all. This is because the error estimates for our previous calculations were too small by typically around 0.2 − 0.3 kcal/mol, because the transformations were done with constant volume production, with box sizes chosen to match those at the end of the equilibration simulation. In instances (at particular λ values) where the box size at the end of equilibration deviated from the correct average box size, this resulted in a somewhat incorrect density at that particular lambda value, introducing a small amount of noise which we have empirically observed to be up to 0.2 − 0.3 kcal/mol. Our more recent work has instead fixed the box size to yield the correct density[28, 41], or (as here) switched to constant pressure production simulations, both of which eliminate this noise. Thus, our relative hydration free energies from LOMAP are consistent with our previously calculated hydration free energies.

It is worth noting that uncertainties in our computed relative hydration free energies are quite small, and in many cases substantially smaller than those from our previous absolute hydration free energy calculations. This is presumably because transforming one solute into another is an easier (and more precise) calculation than computing the hydration free energy for an entire solute, and hence the resulting uncertainties are smaller. It also may be because LOMAP has selected transformations which are particularly efficient, though tests of this will be the subject of future work.

5 Discussion and conclusions

LOMAP provides an automatic way to plan relative binding free energy calculations, which has been one major hur dle hampering more widespread application of these calculations to problems in drug discovery. As input, it takes a set of potential ligands of interest, and outputs a map of planned free energy calculations spanning the set with relatively few transformations which are designed to be relatively efficient, based on the number of atomic insertions and deletions required. This map also has several other features designed to aid overall accuracy and provide consistency checking. Specifically, it keeps overall distance across structural clusters below a specified threshold, and it builds in closed cycles of mutations to allow consistency checking and provide additional information about when the calculations may be performing poorly. Our approach also folds in several other major considerations for accuracy, such as avoiding calculations between molecules of different net charge, proper handling of partial ring deletions, and so on.

LOMAP provides a first effort at systematically planning efficient free energy calculations. Much follow up work needs to be done to determine whether the choices make here actually lead to the most efficient free energy calculations, or whether other choices are better. While here, we have focused on minimizing the number of atomic deletions and insertions (which is supported by the free energy literature) one might imagine other criteria might also be important measures of the efficiency of potential relative free energy calculations. For example, swapping one bioisostere for another might be preferable even if it results in a larger number of deletions or insertions. Similarly, a transformation which preserves the topological location of hydrogen bond donors and acceptors might be preferable over one that does not, even if it involves a few more deletions and insertions. So far, we are not aware of any efficiency data from free energy calculations which sheds light on these issues, so the current implementation is likely a good starting point.

We believe further work on the issue of efficiency of different possible transformations is needed. Hopefully the approach presented here will provide the foundation a systematic approach to looking at efficiency as a function of transformation type, and we are beginning some new work in this direction. Transformation efficiency can be measured by computing a gold standard estimate of the relative free energy using extremely long simulations, and then looking at how quickly computed relative free energies approach that estimate. Transformations which are more efficient will in general more quickly approach the correct relative free energy (and possibly require fewer alchemical intermediate states) than those which are less efficient. This will be an interesting avenue for future work, and likely can provide new insights to help improve LOMAP.

Since we hope this will be the foundation for much further development in the area, our code is open source, under the BSD license. We have designed the graph planning algorithm itself to be modular, taking a set of arbitrary similarity scores as input, so that the planning component can be easily modified and extended. Also, our rule engine is designed to allow easy incorporation of additional rules, and/or replacement of existing rules with new ones.

Overall, we believe this approach provides a promising way to begin automating the setup of large scale relative binding free energy calculations. As noted above, with the output of these calculations – the plan of calculations and the common substructure for each planned calculation – it is simple to automate setup of input files for many common simulation packages which perturb each ligand in a pair to the common substructure. Thus we hope that Lead Optimization Mapper will pave the way to applying binding free energy calculations on a larger scale in a wide range of applications.

Table 3.

Computed relative hydration free energies

Compound pair	Previous study[35] (kcal/mol)	LOMAP (kcal/mol)	Difference (kcal/mol)
1,1,1,2-tetrachloroethane to 2,2-dimethylbutane	–2.62 ± 0.15	–2.42 ± 0.03	0.20 ± 0.15
1,1,1-trichloroethane to 2,2-dimethylpentane	–2.21 ± 0.17	–2.15 ± 0.03	0.06 ± 0.17
1,1,1-trifluoro-2,2,2-trimethoxyethane to 2-chloro-1,1,1-trimethoxyethane	1.31 ± 0.13	1.04 ± 0.04	–0.27 ± 0.13
1,2,3-trichlorobenzene to 2,3-dimethylphenol	4.60 ± 0.11	4.29 ± 0.04	–0.31 ± 0.12
1,2,3,4-tetrachlorobenzene to 2,6-dimethylaniline	4.49 ± 0.27	4.55 ± 0.04	0.06 ± 0.27
1,2,3,5-tetrachlorobenzene to 1,3,5-trichlorobenzene	–0.21 ± 0.24	–0.47 ± 0.03	–0.26 ± 0.24
1,2,4,5-tetrachlorobenzene to 1,2,4-trichlorobenzene	0.12 ± 0.42	0.43 ± 0.03	0.31 ± 0.42
1-chloro-2,2,2-trifluoroethane to 2,2,2-trifluoroethanol	4.42 ± 0.06	4.11 ± 0.04	–0.31 ± 0.07
1-methyl-imidazole to 1-methyl pyrrole	–3.80 ± 0.04	–3.74 ± 0.04	0.06 ± 0.05

Table 4 Shown are relative hydration free energies for selected compound pairs, computed both from absolute hydration free energies reported in a previous study, and from relative free energy calculations set up via LOMAP here.