Pharmacodynamic Target Attainment for Various Ceftazidime Dosing Schemes in High-Flux Hemodialysis

Angela S Loo; Michael Neely; Evan J Anderson; Cybele Ghossein; Milena M McLaughlin; Marc H Scheetz

doi:10.1128/AAC.00474-13

. 2013 Dec;57(12):5854–5859. doi: 10.1128/AAC.00474-13

Pharmacodynamic Target Attainment for Various Ceftazidime Dosing Schemes in High-Flux Hemodialysis

Angela S Loo ^a, Michael Neely ^b, Evan J Anderson ^c, Cybele Ghossein ^d,^e, Milena M McLaughlin ^d,^f, Marc H Scheetz ^d,^f,^✉

PMCID: PMC3837845 PMID: 24018264

Abstract

Ceftazidime is a broad-spectrum cephalosporin with high-level activity against a variety of Gram-negative pathogens, including Pseudomonas aeruginosa. Improved outcomes are associated with cumulative percentages of a 24-h period that the drug concentration exceeds the MIC under steady-state pharmacokinetic conditions (%T_MIC) of >45 to 70% of the dosing interval. Optimal dosing to achieve a 90% probability of target attainment (PTA) in patients receiving high-flux hemodialysis (HFHD) is unknown. We used existing data from six anephric adults receiving hemodialysis to construct a population model with the Pmetrics package for R. From the final model's joint probability density, we simulated the PTA for various ceftazidime dosing regimens, HFHD schedules, and organism MICs. For HFHD every 48 h and 1 g of ceftazidime given posthemodialysis, the PTA exceeds 90% for all isolates with MICs of ≤8 μg/ml, assuming a goal of 70%T_MIC. For 72-h dialysis intervals, postdialysis dosing of 1 g is adequate for achievement of the 70%T_MIC goal only for organisms with MICs of ≤4 μg/ml, while 2 g is adequate for organisms with MICs of ≤8 μg/ml. A dose of 500 mg once daily, regardless of HFHD schedule, has a 90% PTA for organisms with MICs of ≤16 μg/ml, while 1 g once daily may achieve 100% PTA even for resistant organisms with a MIC of 32 μg/ml. Therefore, to ensure maximal ceftazidime activity, once-daily dosing of 500 mg to 1 g ceftazidime in patients receiving HFHD may be preferable for critically ill patients when MIC data are unavailable and for more resistant organisms with ceftazidime MICs of 16 to 32 μg/ml.

INTRODUCTION

With increasing bacterial resistance, optimal dosing strategies for antibiotics are required to improve outcomes (1, 2). Unfortunately, few dosing schemes have been developed for patients receiving high-flux hemodialysis (HFHD). Furthermore, bloodstream infections are common in hemodialysis patients, with Gram-negative bacilli accounting for 14 to 43% of these events (3–6). With few new drugs for Gram-negative bacilli on the horizon, optimization of potent drugs with activity against Gram-negative organisms, such as ceftazidime, is now more important than ever.

Like all other beta-lactam antibiotics, ceftazidime exhibits time-dependent killing of bacteria (7, 8). The bactericidal effect of these agents correlates with the time during a 24-h period that the drug concentration exceeds the MIC under steady-state pharmacokinetic (PK) conditions (T_MIC). With cephalosporins, the cumulative percentage of a 24-h period that the drug concentration exceeds the MIC under steady-state pharmacokinetic conditions (%T_MIC) has been reported to be at least 35 to 40% for stasis and 60 to 70% for near-maximal kill in neutropenic animal models (9–11). Evaluations of clinical data from humans have demonstrated lower %T_MIC targets for specific cephalosporins (12). More recently, analysis of data from a randomized phase III clinical study found that 45%T_MIC predicted favorable outcomes for ceftazidime in hospital-acquired pneumonia patients (13). Although there are few ceftazidime-specific pharmacodynamic data beyond this study, a goal of 70%T_MIC would represent a more conservative endpoint, particularly for neutropenia, which generally requires a greater %T_MIC.

Ceftazidime MIC₉₀ values from numerous surveillance studies range from 16 to 32 μg/liter (14–19). These elevated MIC values can impede achievement of the goal pharmacodynamic parameter %T_MIC, potentially compromising clinical outcomes. In order to maximize efficacy, changes in antibiotic dosing have been made for patients with normal renal function, including increasing dose, frequency, and infusion time (15, 20–23). However, adjustments in ceftazidime dosing to compensate for increased MICs have not been studied in HFHD patients.

Since 80 to 90% of ceftazidime is eliminated unchanged in the urine (24), the half-life in end-stage renal disease is increased to 28 to 45 h, compared to 1 to 2 h in patients with normal kidney function (25, 26). Given this prolonged half-life, the FDA-approved package labeling recommends a loading dose of 1 g of ceftazidime, followed by 1 g after each hemodialysis session (24). However, different studies have recommended a variety of dosing regimens for hemodialysis patients, ranging from 250 to 500 mg every 24 h to 1 g of ceftazidime after each dialysis session (25–27). Dosing is further complicated by the current widespread use of HFHD, which was only an experimental treatment during the mid-1980s, when the original studies were conducted. Therefore, the aforementioned recommendations may not be relevant to the more rapid clearance observed with HFHD.

It is unknown how HFHD and elevated MICs affect the probability of achieving the target pharmacodynamic parameter. Thus, we modeled the probabilities of target attainment (PTA) of various ceftazidime dosing regimens in anephric adults receiving intermittent HFHD to achieve 45%T_MIC and 70%T_MIC for free drug concentrations.

MATERIALS AND METHODS

To describe the nonrenal elimination of ceftazidime, we searched for published studies in which patient-level, individual concentration-time data were documented for anephric patients during an interdialytic period. The following PubMed keywords were used in a search on 17 February 2013: (“ceftazidime” [MeSH terms] OR “ceftazidime” [all fields]) AND (“renal dialysis” [MeSH terms] OR “renal” [all fields] AND “dialysis” [all fields]), for all years. A single study meeting the inclusion criteria was identified (27). In brief, six anephric adults received 2 g ceftazidime posthemodialysis, with seven blood samples drawn over a period of 24 h.

Population model building.

One- and two-compartment models with simultaneous input and output components were developed with the Nonparametric Adaptive Grid (NPAG) algorithm within the Pmetrics package for R (Los Angeles, CA) (28, 29). Elimination from the central compartment and intercompartmental distribution were modeled as first-order processes. Since no estimates of assay error were provided in the original study, we conservatively estimated a lower limit of sensitivity of 1 mg/liter for the microbiologic assay of ceftazidime in the serum (30). Hence, we utilized an assay error polynomial (i.e., SD = C₀ + C₁Y + C₂Y² + C₃Y³) with inputs of 0.5, 0.15, 0, and 0. The inverse of the estimated assay variance was used as the first estimate for weighting in the PK modeling. Final weighting was accomplished by making the assumption that total observation variance was proportional, with a scalar, gamma, to assay variance. The best-fit model was determined by the rule of parsimony and the lowest Akaike's information criterion (AIC) score. Median Bayesian posterior parameter estimates for each patient were used for calculations of predicted ceftazidime concentrations. Goodness of fit was assessed by regression, with an observed-predicted plot, coefficients of determination, and log-likelihood values. Predictive performance evaluation was based on mean prediction error (bias) and the mean bias-adjusted squared prediction error (imprecision) of the population and individual prediction models.

Simulations and PTA.

For simulations, we used a semiparametric sampling method (29, 31) available in Pmetrics, rather than a normal or log-normal distribution, to best capture any deviances from normality. We simulated free ceftazidime concentrations after pharmacokinetic parameters were derived, using a conservative free fraction of 80% (24). The final model consisted of six support points, and each point was a set of model parameter values and the probability of those values to predict observed ceftazidime concentrations in the population. Each support point then served as the mean for a multivariate normal distribution, weighted by the probability of the point, with covariance equal to the covariance matrix of the full model divided by the number of points, i.e., six. The semiparametric sampling from this weighted, multivariate, multimodal normal distribution generated a novel population of 1,000 parameter sets. From each of the 1,000 sets of parameters, a concentration-time profile was created for each of several interdialysis ceftazidime dosing schemes at steady state: 500 mg every 24 h, 500 mg every 48 h, 500 mg every 72 h, 1 g every 24 h, 1 g every 48 h, 1 g every 72 h, 2 g every 48 h, and 2 g every 72 h. Using the PTA functions in Pmetrics, we assessed the probabilities among the 1,000 profiles for each dosing regimen of achieving the pharmacodynamic goals of 45%T_MIC and 70%T_MIC for free drug at MIC values of up to 32 μg/ml.

To conduct a sensitivity analysis, we simulated the above under differing scenarios based on known nonrenal elimination (27) and hemodialysis clearance of 55 to 88% by conventional hemodialysis (25, 32). First, our primary model conservatively estimated that HFHD would be no more efficient than conventional hemodialysis. This would be the “worst-case scenario” from a safety perspective, as additional drug could accumulate and result in toxicity. Renal replacement was modeled as 4-h hemodialysis sessions, in which the intradialytic drug half-life was 3.3 h (25). The hemodialysis was modeled as a piecewise input in our stochastic model. Second, we created a model that assumed complete removal of residual drug after the HFHD session, so that subsequent concentration-time curves would be isometric to the concentration-time profile from the first dose. This would be the worst-case scenario from an efficacy perspective, as the least amount of drug would accumulate and could result in subtherapeutic concentrations. Finally, to assess/simulate the effects of outliers that would not be captured from our base patient population, we inflated the variances and covariances of the population parameter value distributions 3-fold prior to simulation and allowed sampling to 3 times greater than our original fence limits (i.e., widened parameter ranges for the elimination rate constant [k_el] [0 to 3/h], volume of distribution [V] [0.01 to 60 liters], rate transfer constant from central to peripheral compartment [k_CP] [0 to 15/h], and rate transfer constant from peripheral to central compartment [k_PC] [0 to 15/h]).

RESULTS

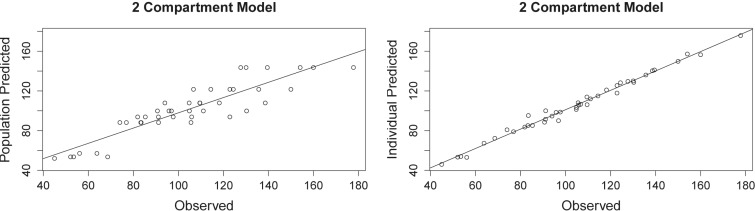
The 2-g concentration-time curves for the six hemodialysis patients (27) are shown in Fig. 1. When we fitted the models, the two-compartment model provided better data fits. Observed versus predicted plots are shown in Fig. 2 for the two-compartment model. The AIC for the two-compartment model was 131.6. Bias and imprecision were −3.09 and 180.2, respectively, for the population and −0.94 and 11.38, respectively, for the individual Bayesian posterior models. The final cycle gamma value was 0.62, indicating that there was low process noise and good-quality data. The six calculated support points and the covariance matrix in the lower triangular form are shown in Tables 1 and 2.

Fig 2 — Two-compartment models of observed versus predicted serum concentrations of ceftazidime (R² = 0.803 and 0.988). Predictions are based on the median population parameter values (left) and median individual Bayesian posterior parameter values (right).

Table 1.

Bayesian posterior density results^a

Support point	k_el (1/h)	V (liters)	k_CP (1/h)	k_PC (1/h)	Weighting fraction
1	0.060	9.23	0.718	0.679	0.167
2	0.097	5.82	2.183	1.855	0.167
3	0.057	11.43	0.830	1.605	0.167
4	0.051	10.29	1.099	1.152	0.167
5	0.049	9.92	0.644	1.072	0.167
6	0.028	12.54	0.296	0.601	0.167

Open in a new tab

k_el, elimination rate constant; V, volume of distribution; k_CP, rate transfer constant from central to peripheral compartment; k_PC, rate transfer constant from peripheral to central compartment.

Table 2.

Covariance matrix in the lower triangular form^a

Parameter	Covariance
Parameter	k_el	V	k_CP	k_PC
k_el	0.00043
V	−0.04094	4.420889
k_CP	0.011582	−1.12161	0.355167
k_PC	0.007308	−0.55211	0.217721	0.205454

Open in a new tab

The full covariances were used in all simulations. See Table 1 and the text for parameter definitions.

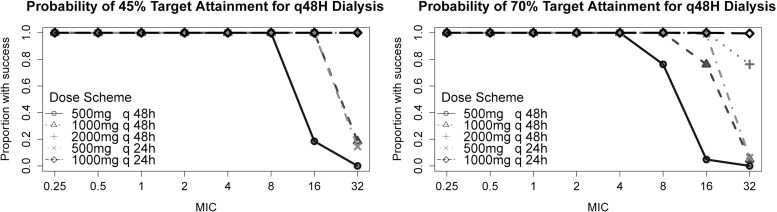
Using Monte Carlo simulation of 1,000 concentration-time profiles for the primary analysis, the PTA for 45%T_MIC and 70%T_MIC were calculated for several ceftazidime dosing regimens, based on dialysis schedules of every 48 and every 72 h. These results are presented in Table 3 and Fig. 3 and 4. For HFHD every 48 h, posthemodialysis dosing of 500 mg was found to achieve 90% PTA for the goal of 45%T_MIC at MIC values of 8 μg/ml or less. In contrast, if the pharmacodynamic goal was 70%T_MIC, only organisms with MICs of 4 μg/ml or less would likely achieve 90% PTA with posthemodialysis doses of 500 mg. For the goal of 45%T_MIC, increasing the dose to 1 g posthemodialysis achieved >90% PTA for MIC values of ≤16 μg/ml, while 2 g achieved >90% PTA even at a MIC of 32 μg/ml. When targeting a goal of 70%T_MIC, however, these regimens achieved >90% PTA for organisms with MICs of ≤8 μg/ml and ≤16 μg/ml, respectively.

Table 3.

PTA values for different dosing regimens^a

Dose and frequency	MIC (mg/liter)	Probability of target attainment (%)
		45%T_MIC, 72-h dialysis period			70%T_MIC, 72-h dialysis period			45%T_MIC, 48-h dialysis period			70%T_MIC, 48-h dialysis period
		Model 1	Model 2	Model 3	Model 1	Model 2	Model 3	Model 1	Model 2	Model 3	Model 1	Model 2	Model 3
500 mg q dialysis	0.25	100	100	100	100	100	100	100	100	100	100	100	100
	0.5	100	100	100	100	100	100	100	100	100	100	100	100
	1	100	100	100	100	100	100	100	100	100	100	100	100
	2	100	100	100	100	100	100	100	100	100	100	100	100
	4	100	100	100	73	73	69	100	100	100	100	100	100
	8	72	70	54	13	13	7	100	100	100	76	76	43
	16	2	3	0	0	1	0	19	20	3	5	5	0
	32	0	0	0	0	0	0	0	0	0	0	0	0
1,000 mg q dialysis	0.25	100	100	100	100	100	100	100	100	100	100	100	100
	0.5	100	100	100	100	100	100	100	100	100	100	100	100
	1	100	100	100	100	100	100	100	100	100	100	100	100
	2	100	100	100	100	100	100	100	100	100	100	100	100
	4	100	100	100	100	100	100	100	100	100	100	100	100
	8	100	100	100	73	73	69	100	100	100	100	100	100
	16	72	70	54	13	13	7	100	100	100	76	76	43
	32	2	3	0	0	1	0	19	20	3	5	5	0
2000 mg q dialysis	0.25	100	100	100	100	100	100	100	100	100	100	100	100
	0.5	100	100	100	100	100	100	100	100	100	100	100	100
	1	100	100	100	100	100	100	100	100	100	100	100	100
	2	100	100	100	100	100	100	100	100	100	100	100	100
	4	100	100	100	100	100	100	100	100	100	100	100	100
	8	100	100	100	100	100	100	100	100	100	100	100	100
	16	100	100	100	73	73	69	100	100	100	100	100	100
	32	72	70	54	13	13	7	100	100	100	76	76	43
500 mg q24h	0.25	100	100	100	100	100	100	100	100	100	100	100	100
	0.5	100	100	100	100	100	100	100	100	100	100	100	100
	1	100	100	100	100	100	100	100	100	100	100	100	100
	2	100	100	100	100	100	100	100	100	100	100	100	100
	4	100	100	100	100	100	100	100	100	100	100	100	100
	8	100	100	100	100	100	100	100	100	100	100	100	100
	16	100	100	100	100	99	88	100	100	100	99	98	44
	32	24	25	4	11	9	0	15	16	1	6	5	0
1,000 mg q24h	0.25	100	100	100	100	100	100	100	100	100	100	100	100
	0.5	100	100	100	100	100	100	100	100	100	100	100	100
	1	100	100	100	100	100	100	100	100	100	100	100	100
	2	100	100	100	100	100	100	100	100	100	100	100	100
	4	100	100	100	100	100	100	100	100	100	100	100	100
	8	100	100	100	100	100	100	100	100	100	100	100	100
	16	100	100	100	100	100	100	100	100	100	100	100	100
	32	100	100	100	100	99	88	100	100	100	100	98	43

Open in a new tab

Model 1, primary model; model 2, primary model with covariance matrix × 3; model 3, full HFHD clearance. q dialysis, every dialysis session; q24h, every 24 h.

Fig 3 — Probability of target attainment for 48-h dialysis.

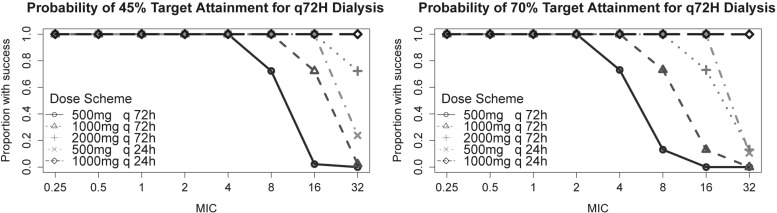
Fig 4 — Probability of target attainment for 72-h dialysis.

For HFHD sessions every 72 h, 500-mg posthemodialysis doses of ceftazidime were unable to achieve goal target parameters for MICs of >4 μg/ml and >2 μg/ml for the goals of 45%T_MIC and 70%T_MIC, respectively. Similarly, posthemodialysis dosing was found to achieve 90% PTA for the goal of 45%T_MIC at MICs of ≤8 μg/ml and ≤16 μg/ml for 1- and 2-g posthemodialysis doses, respectively. In contrast, for a goal of 70%T_MIC, postdialysis dosing of 1 g was adequate only for organisms with MICs of ≤4 μg/ml, while 2 g was adequate for organisms with MICs of ≤8 μg/ml.

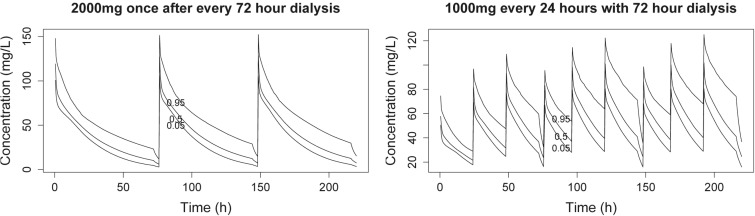
Once-daily dosing of ceftazidime maintained adequate serum concentrations of drug, regardless of the dialysis schedule. For either pharmacodynamic goal, dosing of 500 mg once daily for HFHD sessions every 48 and 72 h allowed over 90% PTA at MICs of up to 16 μg/ml, although the PTA dropped rapidly, to less than 25%, for organisms with a MIC of 32 μg/ml. However, 1 g given once daily achieved 100% target attainment even at a MIC of 32 μg/ml. As shown in Fig. 5, minimal drug accumulation is expected even if HFHD does not entirely remove residual ceftazidime.

Fig 5 — Simulated concentration-time curves for free ceftazidime for hemodialysis every 72 h (5th, 50th, and 95th percentiles are shown).

In our sensitivity analysis, the simulated HFHD method that completely removed all ceftazidime with the first dialysis session had minimal impact on PTA goals for most dosing schemes and clinically relevant MICs (i.e., MICs of ≤8 mg/liter) compared to our primary model. The most significant differences seen between the primary model and the total clearance HFHD model were noted with (i) longer interdialytic periods (i.e., 72 h), (ii) daily dosing of ceftazidime, and (iii) a %T_MIC goal of 70%. In this model, 1 g of ceftazidime daily achieved 100% PTA at MICs of ≤16 mg/liter, and postdialysis dosing of 2 g after each 72-h dialysis session resulted in 100% PTA for MICs of ≤8 mg/liter. Inflating the variance/covariance 3-fold and allowing simulation sampling to 3 times the fence limit did not appreciably change the findings (data not shown).

DISCUSSION

Our findings indicate that 1 g of ceftazidime given once daily, regardless of hemodialysis schedule, is the most likely to achieve goals of 45%T_MIC and 70%T_MIC for organisms with MICs of up to 32 mg/liter. Current Clinical and Laboratory Standards Institute (CLSI) breakpoints define ceftazidime susceptibility as MICs of ≤4 μg/ml for Enterobacteriaceae, based on 1 g every 8 h, and ≤8 μg/ml for Pseudomonas aeruginosa, based on 2 g every 8 h, in patients with normal renal function (33). Based on our analysis, in a patient with a Pseudomonas aeruginosa isolate with a MIC of 8 μg/ml receiving 1 g of ceftazidime posthemodialysis, as recommended in the package insert, ceftazidime concentrations may fall below adequate %T_MIC if hemodialysis and ceftazidime dosing are performed every 72 h. If we were to accept the lower goal of 45%T_MIC as sufficient, our data suggest that the dosing regimen would have a 100% PTA; however, for a higher goal of 70%T_MIC, the PTA would be only 72%, which could be too low for a neutropenic patient. However, increasing the dose to 2 g of ceftazidime posthemodialysis in the latter case achieves an adequate %T_MIC for all “susceptible” organisms (isolates with MICs of up to 8 μg/ml), even for HFHD and dosing every 72 h.

Given that Pseudomonas sp. ceftazidime MIC₉₀ values from surveillance studies range from 16 to 32 μg/liter, we suggest a more aggressive approach of empirical daily dosing of 500 mg to 1 g, depending on local susceptibilities. This dosing would increase the likelihood of achievement of pharmacodynamic goals, even for organisms within the “intermediate” or “resistant” breakpoint categories (e.g., MICs of 16 to 32 μg/ml). Dosing of ceftazidime could perhaps be modified later to a more convenient posthemodialysis regimen after the organism is identified and susceptibility testing is performed. Selection of the posthemodialysis dose would depend on the organism MIC, frequency of hemodialysis, and clinician determination of the most appropriate pharmacodynamic goal for the individual patient. Even with the most aggressive daily dosing scheme and longest dialysis period (i.e., 72 h) tested in our sensitivity analysis, peak concentrations for 95% of our simulations were not grossly different from mean peak concentrations for patients receiving FDA-approved dosages (i.e., 170 mg/liter for a 2-g dose of ceftazidime given over 30 min) (24). Two-gram doses postdialysis (i.e., given every 48 h with 48-h dialysis period) resulted in peak free drug concentrations in serum of <200 mg/liter. While these peak concentrations should be safe for most patients and approximate exposures typically seen in practice (32), clinical studies will be necessary to gain a full understanding of the balance between efficacy and safety. Clinicians should exercise prudence in deciding the level of aggressiveness necessary to safely and effectively treat their patients.

Prior literature has suggested a variety of dosing regimens for ceftazidime in the setting of conventional hemodialysis (i.e., non-HFHD). With this less efficient mode of hemodialysis, authors have recommended that patients should receive 50% of the maintenance dose posthemodialysis (25), 1 g of ceftazidime after every hemodialysis session (26), 250- to 500-mg doses every 24 h (27), and 1 g every 36 to 48 h, with an additional dose of ceftazidime at the end of dialysis (32). The current study is significant, as it is the first, to our knowledge, to (i) consider ceftazidime therapy in light of modern-day HFHD and (ii) assess probabilities of target attainment for elevated MICs by using advanced simulation techniques. Our findings are particularly important for Pseudomonas isolates, which appear more likely to display elevated MIC values than the Enterobacteriaceae, based on surveillance studies (4, 17, 20, 24, 25, 27).

Limitations of this study include the use of a sample size of six patients for model development. While more patients might be preferable, to our knowledge such data are not available. Serum concentrations were drawn posthemodialysis in the original study, allowing the characterization of nonrenal clearance of ceftazidime, which remained unchanged regardless of HFHD clearance. The other ceftazidime studies previously mentioned had incomplete data, fewer concentration-time points, or characterized clearance during nondialysis.

Notably, the data we utilized were published in 1983 and did not provide details regarding assay bias and precision. The original study estimated ceftazidime plasma concentrations through the agar diffusion method, utilizing a standard strain from Glaxo (Proteus morganii 235). Although the authors did not describe this method in detail, the lower limit of sensitivity for the microbiologic assay of ceftazidime in the serum was reported in a separate study to be 1 mg/liter (30). This study similarly utilized a microbiologic assay for ceftazidime and was conducted around the same time as the ceftazidime work by Hoffler et al. (27), allowing us to better estimate assay variance in our model.

We have generated a model describing interdialysis ceftazidime pharmacokinetics in anephric adults receiving HFHD. For 72-h dialysis intervals, our model predicts that organisms with MICs of ≤4 μg/ml could be treated effectively with postdialysis dosing of 1 g and that those with MICs of ≤8 μg/ml could be treated with 2 g postdialysis to achieve the more aggressive endpoint of 70%T_MIC. To ensure maximal ceftazidime activity, daily dosing of 500 mg to 1 g of ceftazidime may be preferable in a critically ill patient when the MIC is unavailable or is 16 to 32 mg/liter. Additional prospective data are needed.

ACKNOWLEDGMENTS

All authors declare that they have nothing to disclose.

This study was supported in part by a Midwestern University Chicago College of Pharmacy Faculty Research Stimulation Grant from Midwestern University, Downers Grove, IL. M. Neely is supported by NIH grants GM068968 and HD070886.

We thank D. Hoeffler for the provision of information not available in his published manuscript (27).

Footnotes

Published ahead of print 9 September 2013

REFERENCES

1. Kolleff M, Golan Y, Micek S, Shorr A, Restrepo M. 2011. Appraising contemporary strategies to combat multidrug resistant gram-negative bacterial infections—proceedings and data from the gram-negative resistance summit. Clin. Infect. Dis. 53:S33–S55 [DOI] [PMC free article] [PubMed] [Google Scholar]
2. Infectious Diseases Society of America 2004. Bad bugs, no drugs. As antibiotic discovery stagnates…a public health crisis brews. Infectious Diseases Society of America, Alexandria, VA: http://www.idsociety.org/uploadedFiles/IDSA/Policy_and_Advocacy/Current_Topics_and_Issues/Antimicrobial_Resistance/10x20/Images/Bad%20Bugs%20no%20Drugs.pdf Accessed 18 November 2012 [Google Scholar]
3. Alexandraki I, Sullivan R, Zaiden R, Bailey C, Mccarter Y, Khan A, Offutt J, Bhatt U, Plott D, Nahman N. 2008. Blood culture isolates in hemodialysis vascular catheter-related bacteremia. Am. J. Med. Sci. 336:297–302 [DOI] [PubMed] [Google Scholar]
4. Al-Solaiman Y, Estrada E, Allon M. 2011. The spectrum of infections in catheter-dependent hemodialysis patients. Clin. J. Am. Soc. Nephrol. 6:2247–2252 [DOI] [PMC free article] [PubMed] [Google Scholar]
5. Dopirak M, Hill C, Oleksiw M, Dumigan D, Arvai J, English E, Carusillo E, Malo-Schlegel S, Richo J, Traficanti K, Welch B, Cooper B. 2002. Surveillance of hemodialysis-associated primary bloodstream infections: the experience of ten hospital-based centers. Infect. Control Hosp. Epidemiol. 23:721–724 [DOI] [PubMed] [Google Scholar]
6. Klevens RM, Edwards JR, Andrus ML, Peterson KD, Dudeck MA, Horan TC, NHSN Participants in Outpatient Dialysis Surveillance 2008. Dialysis surveillance report: National Healthcare Safety Network (NHSN)—data summary for 2006. Semin. Dial. 21:24–28 [DOI] [PubMed] [Google Scholar]
7. Levison M, Levison J. 2009. Pharmacokinetics and pharmacodynamics of antibacterial agents. Infect. Dis. Clin. North Am. 23:791–815 [DOI] [PMC free article] [PubMed] [Google Scholar]
8. Marshall W, Blair J. 1999. The cephalosporins. Mayo Clin. Proc. 74:187–195 [DOI] [PubMed] [Google Scholar]
9. Craig W. 1998. Pharmacokinetic/pharmacodynamic parameters: rationale for antibacterial dosing of mice and men. Clin. Infect. Dis. 26:1–12 [DOI] [PubMed] [Google Scholar]
10. Drusano G. 2003. Prevention of resistance: a goal for dose selection for antimicrobial agents. Clin. Infect. Dis. 36:S42–S50 [DOI] [PubMed] [Google Scholar]
11. Craig W. 1995. Interrelationship between pharmacokinetics and pharmacodynamics in determining dosage regimens for broad-spectrum cephalosporins. Diagn. Microbiol. Infect. Dis. 22:89–96 [DOI] [PubMed] [Google Scholar]
12. Crandon JL, Bulik CC, Kuti JL, Nicolau DP. 2010. Clinical pharmacodynamics of cefepime in patients infected with Pseudomonas aeruginosa. Antimicrob. Agents Chemother. 54:1111–1116 [DOI] [PMC free article] [PubMed] [Google Scholar]
13. Muller AE, Punt N, Mouton JW. 2013. Optimal exposures of ceftazidime predict the probability of microbiological and clinical outcome in the treatment of nosocomial pneumonia. J. Antimicrob. Chemother. 68:900–906 [DOI] [PubMed] [Google Scholar]
14. Bouchillon S, Hoban D, Johnson B, Johnson J, Hsiung A, Dowzicky M. 2005. In vitro activity of tigecycline against 3989 gram-negative and gram-positive clinical isolates from the United States Tigecycline Evaluation and Surveillance Trial (TEST program; 2004). Diagn. Microbiol. Infect. Dis. 52:173–179 [DOI] [PubMed] [Google Scholar]
15. Crandon JL, Kuti JL, Jones RN, Nicolau DP. 2009. Comparison of 2002–2006 OPTAMA programs for US hospitals: focus on gram-negative resistance. Ann. Pharmacother. 43:220–227 [DOI] [PubMed] [Google Scholar]
16. Ramphal R, Hoban D, Pfaller M, Jones R. 2000. Comparison of the activity of two broad-spectrum cephalosporins tested against 2,299 strains of Pseudomonas aeruginosa isolated at 38 North American medical centers participating in the SENTRY Antimicrobial Surveillance Program, 1997–1998. Diagn. Microbiol. Infect. Dis. 36:125–129 [DOI] [PubMed] [Google Scholar]
17. Rhomberg P, Jones R. 2009. Summary trends for the meropenem yearly susceptibility test information collection program: a 10-year experience in the United States. Diagn. Microbiol. Infect. Dis. 65:414–426 [DOI] [PubMed] [Google Scholar]
18. Sader H, Fritsche T, Jones R. 2005. Potency and spectrum trends for cefepime tested against 65746 clinical bacterial isolates collected in North American medical centers: results from SENTRY antimicrobial surveillance program (1998–2003). Diagn. Microbiol. Infect. Dis. 52:265–273 [DOI] [PubMed] [Google Scholar]
19. Zhanel G, Adam H, Low D, Blondeau J, Decorby M, Karlowsky J, Weshnoweski B, Vashisht R, Wierzbowski A, Hoban D. 2011. Antimicrobial susceptibility of 15,644 pathogens from Canadian hospitals: results of the CANWARD 2007–2009 study. Diagn. Microbiol. Infect. Dis. 69:291–306 [DOI] [PubMed] [Google Scholar]
20. Gillespie EL, Kuti JL, Nicolau DP. 2005. Pharmacodynamics of antimicrobials: treatment optimisation. Expert Opin. Drug Metab. Toxicol. 1:351–361 [DOI] [PubMed] [Google Scholar]
21. Koomanachai P, Bulik C, Kuti J, Nicolau D. 2010. Pharmacodynamic modeling of intravenous antibiotics against gram-negative bacteria collected in the United States. Clin. Ther. 32:766–779 [DOI] [PubMed] [Google Scholar]
22. Kuti J, Nightingale C, Nicolau D. 2004. Optimizing pharmacodynamic target attainment using the MYSTIC antibiotigram: data collected in North America in 2002. Antimicrob. Agents Chemother. 48:2464–2470 [DOI] [PMC free article] [PubMed] [Google Scholar]
23. Nicolau D. 2003. Optimizing outcomes with antimicrobial therapy through pharmacodynamic profiling. J. Infect. Chemother. 9:292–296 [DOI] [PubMed] [Google Scholar]
24. GlaxoSmithKline August 2010. Fortaz (ceftazidime for injection) prescribing information. GlaxoSmithKline, Mississauga, Ontario, Canada [Google Scholar]
25. Nikolaidis P, Tourkantonis A. 1985. Effect of hemodialysis on ceftazidime pharmacokinetics. Clin. Nephrol. 24:142–146 [PubMed] [Google Scholar]
26. van Dalen R, Vree T, Baars A, Termond E. 1986. Dosage adjustment for ceftazidime in patients with impaired renal function. Eur. J. Clin. Pharmacol. 30:597–605 [DOI] [PubMed] [Google Scholar]
27. Hoffler D, Koeppe P, Williams K. 1983. Pharmacokinetics of ceftazidime in normal and impaired renal function. J. Antimicrob. Chemother. 12:241–245 [DOI] [PubMed] [Google Scholar]
28. Tatarinova T, Neely M, Bartroff J, van Guilder M, Yamada W, Bayard D, Jelliffe R, Leary R, Chubatiuk A, Schumitzky A. 2013. Two general methods for population pharmacokinetic modeling: non-parametric adaptive grid and non-parametric Bayesian. J. Pharmacokinet. Pharmacodyn. 40:189–199 [DOI] [PMC free article] [PubMed] [Google Scholar]
29. Neely M, van Guilder M, Yamada W, Schumitzky A, Jelliffe R. 2012. Accurate detection of outliers and subpopulations with Pmetrics, a nonparametric and parametric pharmacometric modeling and simulation package for R. Ther. Drug Monit. 34:467–476 [DOI] [PMC free article] [PubMed] [Google Scholar]
30. Thornton JE. 1981. The microbiological assay of ceftazidime. J. Antimicrob. Chemother. 8(Suppl B):225–226 [DOI] [PubMed] [Google Scholar]
31. Goutelle S, Bourguignon L, Maire P, Van Guilder M, Conte JE, Jr, Jelliffe RW. 2009. Population modeling and Monte Carlo simulation study of the pharmacokinetics and antituberculosis pharmacodynamics of rifampin in lungs. Antimicrob. Agents Chemother. 53:2974–2981 [DOI] [PMC free article] [PubMed] [Google Scholar]
32. Leroy A, Leguy F, Borsa F, Spencer G, Fillastre J, Humbert G. 1984. Pharmacokinetics of ceftazidime in normal and uremic subjects. Antimicrob. Agents Chemother. 25:638–642 [DOI] [PMC free article] [PubMed] [Google Scholar]
33. Cockerill F, Wikler M, Bush K, Dudley M, Eliopoulos G, Hardy D, Hecht D, Hindler J, Patel J, Powell M, Thomson R, Turnridge J, Weinstein M, Zimmer B. 2011. Performance standards for antimicrobial susceptibility testing; 21st informational supplement, vol 31 Clinical and Laboratory Standards Institute, Wayne, PA [Google Scholar]

[B1] 1. Kolleff M, Golan Y, Micek S, Shorr A, Restrepo M. 2011. Appraising contemporary strategies to combat multidrug resistant gram-negative bacterial infections—proceedings and data from the gram-negative resistance summit. Clin. Infect. Dis. 53:S33–S55 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B2] 2. Infectious Diseases Society of America 2004. Bad bugs, no drugs. As antibiotic discovery stagnates…a public health crisis brews. Infectious Diseases Society of America, Alexandria, VA: http://www.idsociety.org/uploadedFiles/IDSA/Policy_and_Advocacy/Current_Topics_and_Issues/Antimicrobial_Resistance/10x20/Images/Bad%20Bugs%20no%20Drugs.pdf Accessed 18 November 2012 [Google Scholar]

[B3] 3. Alexandraki I, Sullivan R, Zaiden R, Bailey C, Mccarter Y, Khan A, Offutt J, Bhatt U, Plott D, Nahman N. 2008. Blood culture isolates in hemodialysis vascular catheter-related bacteremia. Am. J. Med. Sci. 336:297–302 [DOI] [PubMed] [Google Scholar]

[B4] 4. Al-Solaiman Y, Estrada E, Allon M. 2011. The spectrum of infections in catheter-dependent hemodialysis patients. Clin. J. Am. Soc. Nephrol. 6:2247–2252 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B5] 5. Dopirak M, Hill C, Oleksiw M, Dumigan D, Arvai J, English E, Carusillo E, Malo-Schlegel S, Richo J, Traficanti K, Welch B, Cooper B. 2002. Surveillance of hemodialysis-associated primary bloodstream infections: the experience of ten hospital-based centers. Infect. Control Hosp. Epidemiol. 23:721–724 [DOI] [PubMed] [Google Scholar]

[B6] 6. Klevens RM, Edwards JR, Andrus ML, Peterson KD, Dudeck MA, Horan TC, NHSN Participants in Outpatient Dialysis Surveillance 2008. Dialysis surveillance report: National Healthcare Safety Network (NHSN)—data summary for 2006. Semin. Dial. 21:24–28 [DOI] [PubMed] [Google Scholar]

[B7] 7. Levison M, Levison J. 2009. Pharmacokinetics and pharmacodynamics of antibacterial agents. Infect. Dis. Clin. North Am. 23:791–815 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B8] 8. Marshall W, Blair J. 1999. The cephalosporins. Mayo Clin. Proc. 74:187–195 [DOI] [PubMed] [Google Scholar]

[B9] 9. Craig W. 1998. Pharmacokinetic/pharmacodynamic parameters: rationale for antibacterial dosing of mice and men. Clin. Infect. Dis. 26:1–12 [DOI] [PubMed] [Google Scholar]

[B10] 10. Drusano G. 2003. Prevention of resistance: a goal for dose selection for antimicrobial agents. Clin. Infect. Dis. 36:S42–S50 [DOI] [PubMed] [Google Scholar]

[B11] 11. Craig W. 1995. Interrelationship between pharmacokinetics and pharmacodynamics in determining dosage regimens for broad-spectrum cephalosporins. Diagn. Microbiol. Infect. Dis. 22:89–96 [DOI] [PubMed] [Google Scholar]

[B12] 12. Crandon JL, Bulik CC, Kuti JL, Nicolau DP. 2010. Clinical pharmacodynamics of cefepime in patients infected with Pseudomonas aeruginosa. Antimicrob. Agents Chemother. 54:1111–1116 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B13] 13. Muller AE, Punt N, Mouton JW. 2013. Optimal exposures of ceftazidime predict the probability of microbiological and clinical outcome in the treatment of nosocomial pneumonia. J. Antimicrob. Chemother. 68:900–906 [DOI] [PubMed] [Google Scholar]

[B14] 14. Bouchillon S, Hoban D, Johnson B, Johnson J, Hsiung A, Dowzicky M. 2005. In vitro activity of tigecycline against 3989 gram-negative and gram-positive clinical isolates from the United States Tigecycline Evaluation and Surveillance Trial (TEST program; 2004). Diagn. Microbiol. Infect. Dis. 52:173–179 [DOI] [PubMed] [Google Scholar]

[B15] 15. Crandon JL, Kuti JL, Jones RN, Nicolau DP. 2009. Comparison of 2002–2006 OPTAMA programs for US hospitals: focus on gram-negative resistance. Ann. Pharmacother. 43:220–227 [DOI] [PubMed] [Google Scholar]

[B16] 16. Ramphal R, Hoban D, Pfaller M, Jones R. 2000. Comparison of the activity of two broad-spectrum cephalosporins tested against 2,299 strains of Pseudomonas aeruginosa isolated at 38 North American medical centers participating in the SENTRY Antimicrobial Surveillance Program, 1997–1998. Diagn. Microbiol. Infect. Dis. 36:125–129 [DOI] [PubMed] [Google Scholar]

[B17] 17. Rhomberg P, Jones R. 2009. Summary trends for the meropenem yearly susceptibility test information collection program: a 10-year experience in the United States. Diagn. Microbiol. Infect. Dis. 65:414–426 [DOI] [PubMed] [Google Scholar]

[B18] 18. Sader H, Fritsche T, Jones R. 2005. Potency and spectrum trends for cefepime tested against 65746 clinical bacterial isolates collected in North American medical centers: results from SENTRY antimicrobial surveillance program (1998–2003). Diagn. Microbiol. Infect. Dis. 52:265–273 [DOI] [PubMed] [Google Scholar]

[B19] 19. Zhanel G, Adam H, Low D, Blondeau J, Decorby M, Karlowsky J, Weshnoweski B, Vashisht R, Wierzbowski A, Hoban D. 2011. Antimicrobial susceptibility of 15,644 pathogens from Canadian hospitals: results of the CANWARD 2007–2009 study. Diagn. Microbiol. Infect. Dis. 69:291–306 [DOI] [PubMed] [Google Scholar]

[B20] 20. Gillespie EL, Kuti JL, Nicolau DP. 2005. Pharmacodynamics of antimicrobials: treatment optimisation. Expert Opin. Drug Metab. Toxicol. 1:351–361 [DOI] [PubMed] [Google Scholar]

[B21] 21. Koomanachai P, Bulik C, Kuti J, Nicolau D. 2010. Pharmacodynamic modeling of intravenous antibiotics against gram-negative bacteria collected in the United States. Clin. Ther. 32:766–779 [DOI] [PubMed] [Google Scholar]

[B22] 22. Kuti J, Nightingale C, Nicolau D. 2004. Optimizing pharmacodynamic target attainment using the MYSTIC antibiotigram: data collected in North America in 2002. Antimicrob. Agents Chemother. 48:2464–2470 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B23] 23. Nicolau D. 2003. Optimizing outcomes with antimicrobial therapy through pharmacodynamic profiling. J. Infect. Chemother. 9:292–296 [DOI] [PubMed] [Google Scholar]

[B24] 24. GlaxoSmithKline August 2010. Fortaz (ceftazidime for injection) prescribing information. GlaxoSmithKline, Mississauga, Ontario, Canada [Google Scholar]

[B25] 25. Nikolaidis P, Tourkantonis A. 1985. Effect of hemodialysis on ceftazidime pharmacokinetics. Clin. Nephrol. 24:142–146 [PubMed] [Google Scholar]

[B26] 26. van Dalen R, Vree T, Baars A, Termond E. 1986. Dosage adjustment for ceftazidime in patients with impaired renal function. Eur. J. Clin. Pharmacol. 30:597–605 [DOI] [PubMed] [Google Scholar]

[B27] 27. Hoffler D, Koeppe P, Williams K. 1983. Pharmacokinetics of ceftazidime in normal and impaired renal function. J. Antimicrob. Chemother. 12:241–245 [DOI] [PubMed] [Google Scholar]

[B28] 28. Tatarinova T, Neely M, Bartroff J, van Guilder M, Yamada W, Bayard D, Jelliffe R, Leary R, Chubatiuk A, Schumitzky A. 2013. Two general methods for population pharmacokinetic modeling: non-parametric adaptive grid and non-parametric Bayesian. J. Pharmacokinet. Pharmacodyn. 40:189–199 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B29] 29. Neely M, van Guilder M, Yamada W, Schumitzky A, Jelliffe R. 2012. Accurate detection of outliers and subpopulations with Pmetrics, a nonparametric and parametric pharmacometric modeling and simulation package for R. Ther. Drug Monit. 34:467–476 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B30] 30. Thornton JE. 1981. The microbiological assay of ceftazidime. J. Antimicrob. Chemother. 8(Suppl B):225–226 [DOI] [PubMed] [Google Scholar]

[B31] 31. Goutelle S, Bourguignon L, Maire P, Van Guilder M, Conte JE, Jr, Jelliffe RW. 2009. Population modeling and Monte Carlo simulation study of the pharmacokinetics and antituberculosis pharmacodynamics of rifampin in lungs. Antimicrob. Agents Chemother. 53:2974–2981 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B32] 32. Leroy A, Leguy F, Borsa F, Spencer G, Fillastre J, Humbert G. 1984. Pharmacokinetics of ceftazidime in normal and uremic subjects. Antimicrob. Agents Chemother. 25:638–642 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B33] 33. Cockerill F, Wikler M, Bush K, Dudley M, Eliopoulos G, Hardy D, Hecht D, Hindler J, Patel J, Powell M, Thomson R, Turnridge J, Weinstein M, Zimmer B. 2011. Performance standards for antimicrobial susceptibility testing; 21st informational supplement, vol 31 Clinical and Laboratory Standards Institute, Wayne, PA [Google Scholar]

PERMALINK

Pharmacodynamic Target Attainment for Various Ceftazidime Dosing Schemes in High-Flux Hemodialysis

Angela S Loo

Michael Neely

Evan J Anderson

Cybele Ghossein

Milena M McLaughlin

Marc H Scheetz

Abstract

INTRODUCTION