Abstract
Streptococcus pneumoniae (pneumococcus) is a significant pathogen that frequently colonizes the human nasopharynx. Environmental factors, including antimicrobial use and host immunity, exert selection on members of the nasopharyngeal population, and the dynamics of selection are influenced by the effective population size of the selected population, about which little is known. We measured here the variance effective population size (Ne) of pneumococcus in a mouse colonization model by monitoring the frequency change of two cocolonizing, competitively neutral pneumococcal strains over time. The point estimate of Ne during nasal carriage in 16 BALB/c mice was 133 (95% confidence interval [CI] = 11 to 203). In contrast, the lower-bound census population exhibited a mean of 5768 (95% CI = 2,515 to 9,021). Therefore, pneumococcal Ne during nasal carriage is substantially smaller than the census population. The Ne during day 1 to day 4 of colonization was comparable to the Ne during day 4 to day 8. Similarly, a low Ne was also evident for the colonization of pneumococcus in BALB/c mice exposed to cholera toxin 4 weeks prior to challenge and in another mouse strain (DO11.10 RAG−/−). We developed a mathematical model of pneumococcal colonization composed of two subpopulations with differential contribution to future generations. By stochastic simulation, this model can reproduce the pattern of observed pneumococcal Ne and predicts that the selection coefficients may be difficult to measure in vivo. We hypothesized that such a small Ne may reduce the effectiveness of within host selection for pneumococcus.
INTRODUCTION
Studies of within-host competition between bacteria typically measure selection by the mean change in the logarithm of the ratio of a favored to a disfavored allele (1–4), sometimes called a “competitive index.” In animal experiments, there is often substantial variation in the competition outcome among animal subjects (1–4), which necessitates the use of a large number of animals to ensure reproducible results (5). Understanding the source of this variation is important for a number of purposes, including sample size calculations in experimental design and results interpretation. For example, modern methods for identifying genes important for fitness in certain environments, such as transposon mutagenesis screens, rely on the ability of many members of a large inoculum to establish infection, so that variations in mutant frequency may be attributed to selection rather than chance. From the opposite perspective, predictions of quantitative models of selection within a host for immune escape or emergence of resistant variants depend not only on the strength of selection but also on the number of pathogen individuals available for selection (3, 6, 7).
The variation in competitive index in experiments is rarely commented on, as if the presence of noise in results was an inevitable consequence of animal experiments. Stochasticity introduced by population bottlenecks and by small effective population size can also contribute to the observed variation. Since the first transposon mutagenesis study that relied on interpretation of allele frequency change to infer fitness effects of gene knockouts (8), this has been an important issue that needs to be accounted for implicitly or explicitly (9). In population genetics, stochasticity in the fate of alleles under selection (as well as that of neutral alleles) is explained by the concept of effective population size, which intuitively is related to the number of individuals in each generation who contribute to the next (10), making allowance for the fact that contributions may be uneven for many reasons. More precisely, the effective size of a population (Ne) is defined by the value that produces an observed distribution of changes in the frequencies of unselected alleles due to stochasticity in the reproduction of a finite population and can be estimated from this distribution, with a larger Ne corresponding to smaller stochastic fluctuations (10). Ne is an important parameter in understanding the dynamics of population diversity since it controls, among other genetic processes, the effectiveness of selection relative to genetic drift. A small Ne increases the relative weight of genetic drift over selection in determining allele frequency, so that the difference between the chance of fixing a favorable mutation and the chance of fixing a neutral mutation in the population is reduced (10). Because bacterial pathogens usually show large census populations (i.e., the number of CFU per host), many experiments have been performed with the assumption that the median or mean change in frequency of one variant compared to another is a good representation of the selective value of those variants in vivo (1, 2, 11–15), although researchers may make allowance for the noise involved when small numbers of each variant are present in a small population, such as in transposon-mutant screens (13). Although little is known about the actual Ne of bacterial populations within individual hosts, it is possible that Ne is smaller than the census population because of the observed subpopulation structure (16), which may lead to heterogeneity in the reproductive potential of members of the population. We therefore hypothesize that limited effective population sizes contribute to the variability of competition outcome when the sizes are small enough to make even a fully neutral marker drift significantly.
Streptococcus pneumoniae (pneumococcus) is an important pathogen that frequently colonizes the human nasopharynx. Although nasopharyngeal colonization is usually asymptomatic, it is a critical step prior to invasive infections (17, 18). The nasopharyngeal carriage population serves as a reservoir of bacteria that may be transmitted to other hosts. In humans, an average carrier harbors at least 103 to 105 pneumococci (19), and the duration of colonization ranges from 1 week to several months (19). More importantly, most transmission of pneumococci occurs from healthy carriers, making the nasopharyngeal colonization a key stage in the evolution and ecology of these organisms. The effect of selection pressures imposed by host immunity, competition with other microflora, and antimicrobial treatment will depend on the effective population size. This is both because a small Ne limits the amount of genetic variation (i.e., mutations and recombination events) available for selection and because, in simple population-genetic models, selection can be effective only if the product of the selection coefficient and Ne is substantially greater than 1; otherwise, selection will typically be overwhelmed by genetic drift. An understanding of within host Ne would be valuable in understanding the population dynamics of pneumococcus in vivo.
We assessed here how much stochastic effects influence the outcome of animal experiments by measuring the Ne of pneumococcus in a mouse colonization model and modeling its effects on within-host selection. We found that Ne was substantially smaller than the carriage population size. It appeared that Ne did not change over time during colonization. Simulation studies suggested that such a small Ne could reduce the efficiency of within-host selection for favored variants.
MATERIALS AND METHODS
Strains and animals.
The OVA and AVO stains were serotype 6B pneumococcal strain 603 derivatives that were described previously (3). Briefly, these were derivatives of clinical strain 603 with either OVA323-339 peptide (ISQAVHAAHAEINEAGR) or the reverse “AVO” peptide (RGAENIEAHAAHVAQSI) fused with two pneumococcal proteins: pneumococcal surface protein A (PspA) and pneumolysin (Ply). Wild-type BALB/c (BALB/c) mice and BALB/c DO11.10 RAG−/− (DO11.10) mice were obtained from the Jackson ImmunoResearch Laboratories, Bar Harbor, ME. All mice were female, 9 to 10 weeks old at the start of experiments, and kept in a BL2 facility. Some mice were intranasally administered 1 μg of cholera toxin (CT; List Biological Laboratories, Compel, CA) 4 or 5 weeks prior to challenge, because these mice were controls in other experiments in which the experimental mice received immunizations using CT as an adjuvant. The data analyzed in the present study are a combination of newly generated data (BALB/c and DO11.10 RAG−/− mice) and the frequencies from controls in experiments previously published for the BALB/c mice with CT (3). The mouse experiment protocols were approved by Institutional Animal Care and Use Committee of Harvard University.
Mouse carriage model and strain quantification.
BALB/c or DO11.10 RAG−/− mice were inoculated intranasally with a mix of the OVA and the AVO strains in 10 μl of phosphate-buffered saline containing approximately 5 × 106 CFU of each strain. Nasal wash samples were collected up to 8 days after challenge according to a method described previously (3). Aliquots of each sample were titered to determine the CFU density in sample. The remaining samples were cultured overnight on blood agar plates supplemented with gentamicin to a final concentration of 2.5 mg/liter, and all bacterial growth was harvested for genomic DNA extraction.
Genomic DNA was purified from cultures of samples collected from animals using a DNeasy blood and tissue kit (Qiagen, Valencia, CA). OVA strain- and AVO strain-specific primer sets were designed based on the nucleotide sequence difference in the pspA locus between the two strains. The quantity of strain-specific genomic DNA in a sample was determined by real-time PCR as described previously (3). The AVO/OVA ratio for each sample was calculated by using the absolute amount of OVA DNA and AVO DNA in the sample. The CFU counts for AVO and OVA bacteria in a sample were estimated from the total CFU and the AVO/OVA ratio (Table 1).
Table 1.
CFU counts used for Ne estimation in the BALB/c mouse experiment
| Mouse | CFU count |
|||||
|---|---|---|---|---|---|---|
| Day 1 |
Day 4 |
Day 8 |
||||
| AVO | OVA | AVO | OVA | AVO | OVA | |
| 1-1 | 1,510 | 2,468 | 877 | 971 | 643 | 233 |
| 1-2 | 8 | 2 | 170 | 76 | 67 | 72 |
| 1-3 | 200 | 249 | 34 | 233 | 386 | 3,163 |
| 1-4 | 378 | 370 | 52 | 364 | 9 | 12 |
| 1-5 | 4,432 | 8,623 | 676 | 8,248 | 2,472 | 7,582 |
| 2-2 | 1,099 | 1,750 | 387 | 1,098 | 292 | 477 |
| 2-3 | 22 | 42 | 77 | 115 | 759 | 1,378 |
| 3-1 | 57 | 28 | 117 | 65 | 288 | 0 |
| 3-2 | 1,948 | 3,858 | 1,328 | 2,651 | 2,316 | 19,628 |
| 3-3 | 3,107 | 2,484 | 1,124 | 1,241 | 4,448 | 6,896 |
| 3-4 | 2,092 | 4,413 | 530 | 891 | 1,980 | 2,429 |
| 3-5 | 283 | 294 | 150 | 95 | 10,254 | 5,579 |
| 4-1 | 31 | 33 | 70 | 58 | 70 | 90 |
| 4-3 | 848 | 765 | 523 | 1,896 | 1,880 | 5,055 |
| 4-4 | 1,775 | 1,988 | 247 | 234 | 765 | 1,171 |
| 4-5 | 95 | 97 | 7 | 15 | 657 | 1,440 |
Bacterial growth curve.
AVO and OVA strains were streaked onto blood agar plates and cultured at 37°C in a 5% CO2 overnight. Four colonies from each strain were subcultured in Todd-Hewitt medium with 0.5% yeast extract (THY; Becton Dickinson, Sparks, MD) until the optical density at 620 nm (OD620) reached ∼0.4 and then diluted into THY medium at a starting culture OD620 of ∼0.005. Growth was monitored in sterile flat-bottom 96-well microtiter plates (Nunc, Denmark) containing 200 μl of culture in each well every 30 min using a VERSAmax microplate reader (Molecular Devices, Sunnyvale, CA) over 6 h. The growth curves were fitted to an exponential growth equation, and the doubling time was estimated using Prism software (GraphPad Software, Inc., La Jolla, CA).
Estimation of variance effective population (Ne).
MLNE software (20, 21) was used to estimate the maximum-likelihood Ne and its 95% confidence interval (CI). Essentially, the software uses the probability of observing the CFU count data (Table 1) in a sample at a given time as a function of the CFU count data in a previous sample, the number of generations during the sampling period, and the (harmonic) mean effective size (Ne) of the population (22). The estimation procedure in MLNE function further accounted for the probability of observing the CFU count data in a sample given a true ratio between the two strains in the underlying population and thus explicitly accounted for sampling error caused by examining the allelic composition of a finite number of bacterial CFU. When the CFU count data in all time points are given, the software will maximize the likelihood of the data by varying the Ne. We assumed that Ne was the same for each mouse, and the frequency of AVO and OVA bacteria in different mice at each time point in a single experiment could be treated as if they were alleles at independently assorting loci. The likelihood maximized by the software in this way corresponds to the assumption that Ne was the same in each mouse, so each mouse contributes independent data to the estimation of that single quantity. To estimate the pneumococcal Ne during colonization in BALB/c mice, the CFU count data on days 1, 4, and 8 were used. To estimate the average pneumococcal Ne during colonization in DO11.10 RAG−/− mice, the CFU count data on days 1, 3, and 7 were used. Allele frequency change from the time of inoculation (day 0) to day 1 was not considered in Ne estimation to minimize the effect of colonization bottleneck. Any mouse with missing data on any of the three sampling time points was also excluded from analysis. The input data for MLNE were prepared according to software instructions with each mouse replicate being treated as an independent locus. The number of pneumococcal generations between two sampling time points was calculated by dividing the length of time between two samplings by the average life span of pneumococcus. We used (cells doubling time)/ln (2) as the average life span according to a simple exponential-growth/exponential-death model at its equilibrium. Due to the haploidy of pneumococcal genome, the Ne and 95% CI estimated by the MLNE software (designed for diploids) were scaled up by a factor of 2 (Jinliang Wang, unpublished data), a scaling that we validated by preliminary simulation (data not shown).
Simulation of pneumococcal colonization population.
A simple model of heterogeneity in bacterial reproduction that could generate a small effective population size is one similar to that described by Balaban et al. (23) for “type 1 persisters.” This model represents the pneumococcal colonization population as composed of two subpopulations, P1 and P2. P1 is a small subpopulation that actively replicates, while P2 represents a large subpopulation where most bacterial death/removal occurs. Each subpopulation is composed of two strains, A and O, that satisfy P1
 A1 + O1 and P2
A1 + O1 and P2
 A2 + O2. The dynamics of A1, O1, A2, and O2 is described by equations 1 to 4:
A2 + O2. The dynamics of A1, O1, A2, and O2 is described by equations 1 to 4:
| (1) |
| (2) |
| (3) |
| (4) |
For competitively neutral strains to achieve stable carriage, we assumed that da = do = d and that μ > d. Essentially, strains in P1 follow exponential growth and clearance, with the probability of the descendant cell's remaining in P1 decreasing with the number of cells in P1; otherwise, it migrates to P2 (equations 5 and 6), with the migration modeled as a separate event. Strains in P2 grow logistically and are also subjected to exponential clearance.
| (5) |
| (6) |
Equation 5 combines equations 1 and 2; equation 6 combines equations 3 and 4. The stable equilibrium subpopulation size of P1 and P2 is given by:
| (7) |
| (8) |
Note that when growth is blocked (μ = 0), the total population (P1 + P2) follows an exponential decay: d(P1 + P2)/dt = −d(P1 + P2). In this situation, the half-life (ln2/d) of pneumococcus during mouse nasal colonization has been estimated to be 161 min (13). Unless otherwise specified, the clearance rate d = 0.0043 min−1 (ln2/161 min−1) and the maximum growth rate μ = 0.0231 min−1 were used. Varied K1 and K2 values were used as indicated.
Our simulation was a stochastic version of the model described by equations 1 to 4. To generate simulation data of allele frequency, we used the “adaptivetau” package in R (24), which implements an adaptive tau leaping to approximate the trajectory of a continuous-time stochastic process. The instantaneous transition rate for each transition and its effects are given in Table 2.
Table 2.
Transition rates for simulation of the colonization population
| Event | Effects (A1, O1, A2, O2) | Transition rate (0)a |
|---|---|---|
| Birth | ||
| A1 | 1, 0, 0, 0 | μA1 |
| O1 | 0, 1, 0, 0 | μO1 |
| Migration | ||
| A1 | –1, 0, 1, 0 | μA1 (A1 + O1)/K1 |
| O1 | 0, –1, 0, 1 | μO1 (A1 + O1)/K1 |
| Clearance | ||
| A1 | –1, 0, 0, 0 | daA1 |
| O1 | 0, 1, 0, 0 | doO1 |
| Birth | ||
| A2 | 0, 0, 1, 0 | Max {0, μA2 [1 – (A2 + O2)/K2]} |
| O2 | 0, 0, 0, 1 | Max {0, μA2 [1 – (A2 + O2)/K2]} |
| Death | ||
| A2 | 0, 0, –1, 0 | –Min {0, μA2 [1 – (A2 + O2)/K2]} |
| O2 | 0, 0, 0, –1 | –Min {0, μO2 [1 – (A2 + O2)/K2]} |
| Clearance | ||
| A2 | 0, 0, –1, 0 | daA2 |
| O2 | 0, 0, 0, –1 | doO2 |
Max, function that returns the largest value of the input values; min, function that returns the smallest value of the input values.
To initialize the simulation, A1 + O1 and A2 + O2 were first set to their equilibrium size (P1* and P2* in equations 7 and 8, respectively). To mimic the allele frequency distribution on day 1 of colonization, a value of log10(a) was randomly drawn from a normal distribution estimated from the BALB/c colonization experiment (equation 9), where a is the ratio between the two strains in each subpopulation (a
 Ai/Oi, i = 1,2). The specific initial state (A1, O1, A2, and O2) was then calculated according to the value of a and equations 10 to 13.
Ai/Oi, i = 1,2). The specific initial state (A1, O1, A2, and O2) was then calculated according to the value of a and equations 10 to 13.
| (9) |
On day 1:
| (10) |
| (11) |
| (12) |
| (13) |
After initiation, the model was first simulated forward for t = 4,320 min (3 days) by using the “ssa.adaptivetau” function in the “adaptivetau” R package (24). The values of A1, O1, A2, and O2 at the end of the t = 4,320 min were recorded as the day 4 output. Continuing from this state, the model was subsequently simulated forward for another 5,760 min (4 days), and the end values of A1, O1, A2, and O2 were recorded as the day 8 output.
The Ne of the simulated population was estimated by the MLNE software using a method similar to what is described in the previous section. Briefly, the values of A2 and O2 on days 1, 4, and 8 of simulation were used as allele count data in the input file of the MLNE software. Twenty replicate simulations were performed for any given set of parameters (μ, d, K1, and K2). The values of A2 or O2 on days 1, 4, and 8 in each replicate simulation were used as allele counts from an independent locus in the input file of the MLNE software. As for the experimental data, the Ne and 95% CI estimated by the MLNE software were scaled up by a factor of 2. To estimate the Ne of the simulated population between days 1 and 4, values of A2 and O2 on days 1 and 4 in each replicate simulation were used. Similarly, the values of A2 and O2 on days 4 and 8 in each replicate simulation were used to estimate the Ne of the simulated population between days 4 and 8.
Simulation of within-host selection in the colonizing population.
To examine the influence of Ne on the efficiency of within host selection, the pneumococcal colonization model was modified to incorporate selection mediated by different clearance rates for a wild-type strain (O) and a mutant strain (A) (i.e., da ≠ do); otherwise, the equations are the same as equations 1 to 4 and Table 2. The parameters used in the simulation were μ = 0.0231 min−1, do = 0.0043 min−1, K1 = 400, and K2 = 40,000, which corresponded to an estimated Ne of 181 according to previous simulations. Varied da values were used as indicated.
To initialize the simulation, A1 + O1 and A2 + O2 were first set to the carrying capacities (400 and 40,000, respectively). The specific values of A1, O1, A2, and O2 were then set to satisfy that A1/O1 = A2/O2 = a, where a is a given initial ratio between mutant and wild-type alleles. After initiation, the model was first simulated forward for t = 5,760 min (4 days). The value of A1, O1, A2, or O2 at the end of the t = 5,760 min was recorded as the day 4 output. Continuing from this state, the model was subsequently simulated forward for another 5,760 min (4 days), and the end value of A1, O1, A2, or O2 was recorded as the day 8 output. The A2 and O2 outputs on days 4 and 8 of simulation were used to calculate the mutant allele frequency [A2/(A2 + O2)]. Twenty replicate simulations were performed. The average census population size (A2 + O2) during the simulation was approximately 33,000.
Simulation of within-host selection by an ideal population model.
The ideal population is a single population with a wild-type strain (O) and a mutant strain (A) undergoing selection mediated by different clearance rates (equations 14 and 15). The parameters used in simulation were μ = 0.0231 min−1, do = 0.0043 min−1, and K = 40,000. Varied da values were used as indicated.
The following equations express the ideal population model:
| (14) |
| (15) |
Simulation data of allele frequency were generated by using the “adaptivetau” package in R (24), and the instantaneous transition rates are listed in Table 3. To initialize the simulation, A + O was first set to the carrying capacity (40,000). The specific values of A and O were then set to satisfy that A/O = a, where a is a given initial ratio between mutant and wild-type alleles. After initiation, the model was first simulated forward for t = 5,760 min (4 days). The value of A or O at the end of the t = 5,760 min was recorded as the day 4 output. Continuing from this state, the model was subsequently simulated forward for another 5760 min (4 days) and the end value of A or O was recorded as the day 8 output. The A and O outputs on days 4 and 8 of simulation were used to calculate the mutant allele frequency [A/(A + O)]. Twenty replicate simulations were performed. The average census population size (A + O) during simulation was approximately 32,000.
Table 3.
Transition rates for simulation of the ideal population
| Event | Effects (A, O) | Transition rate (≥0)a |
|---|---|---|
| Birth | ||
| A | 1, 0 | Max {0, μA2 [1 – (A + O)/K]} |
| O | 0, 1 | Max {0, μA2 [1 – (A + O)/K]} |
| Death | ||
| A | –1, 0 | –Min {0, μA2 [1 – (A + O)/K]} |
| O | 0, –1 | –Min {0, μO2 [1 – (A + O)/K]} |
| Clearance | ||
| A | –1, 0 | daA |
| O | 0, –1 | doO |
Max, function that returns the largest value of the input values; min, function that returns the smallest value of the input values.
Statistical analysis was performed by using the R package (http://CRAN.R-project.org/) and the GraphPad Prism software.
RESULTS
Pneumococcal variants showed genetic drift during nasal colonization.
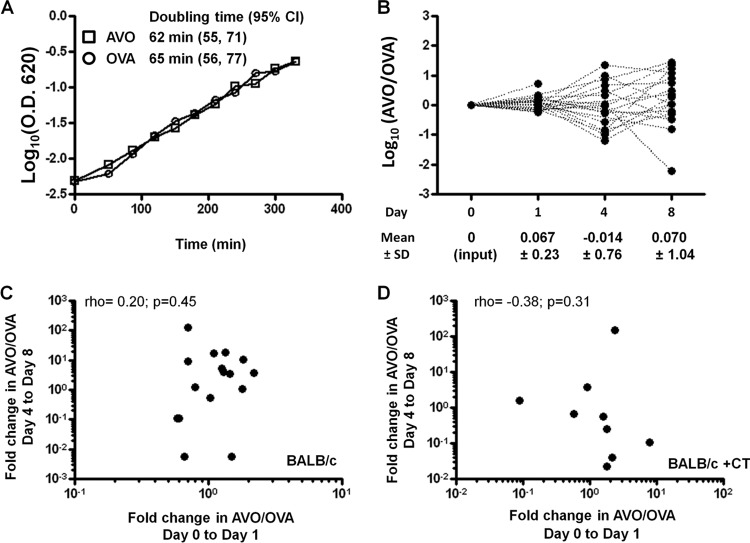
To investigate the effective population size of pneumococcus during nasal carriage, we used two competitively neutral strains, the AVO strain and the OVA strain, which have been described previously (3). The two strains showed similar in vitro growth rates in THY medium (Fig. 1A). The average doubling time of the AVO strain (62 min, 95% CI = 55 to 70) was not significantly different from that of the OVA strain (65 min, 95% CI = 57 to 76) (Fig. 1A, Student t test, P = 0.82).
Fig 1.
AVO and OVA are neutral alleles and show genetic drift during nasal carriage. (A) The AVO and OVA strains were cultured in THY medium at 37°C, and the increase in OD620 was measured every 30 min. The curve was fitted to an exponential growth to estimate the average doubling time. (B) Twenty BALB/c mice were intranasally challenged by a 1:1 mixture of the AVO and OVA strains (day 0). The AVO/OVA ratio in mouse nasal wash was measured on days 1, 4, and 8. Each dashed line connects points for the same mouse over time. (C) Scatter plots to examine correlation between the change in AVO/OVA from day 0 to day 1 and the change in AVO/OVA from day 4 to day 8 in BALB/c mice. (D) Scatter plots to examine correlation between the change in AVO/OVA from day 0 to day 1 and the change in AVO/OVA from day 4 to day 8 in BALB/c mice who had been treated with cholera toxin (CT) 4 weeks prior to challenge.
To quantify genetic drift in vivo, 20 BALB/c mice were intranasally challenged by a 1:1 mixture of the AVO and OVA strains. We measured the total CFU and the AVO/OVA ratio in the nasal washes as described in Materials and Methods. The mean log10(AVO/OVA) values were 0.067 (n = 20, standard deviation [SD] = 0.23), −0.014 (n = 16, SD = 0.76), and 0.070 (n = 19 SD = 1.04) on days 1, 4, and 8, respectively (Fig. 1B). None of the mean log10(AVO/OVA) values were significantly different from the input log10(AVO/OVA) (P > 0.05, one sample t test). In contrast, the variance of log10(AVO/OVA) showed a significant increase over time (Fig. 1B, Levene's test for equal variance, P = 0.034). Furthermore, no significant correlation between change in AVO/OVA from day 0 to day 1 and change from day 4 to day 8 was observed (Fig. 1C, n = 16, rho = 0.20, P = 0.45). In similar colonization experiments carried out in BALB/c mice exposed to immunization adjuvant (cholera toxin) 4 weeks prior to challenge, no correlation between change in AVO/OVA from day 0 to day 1 and change from day 4 to day 8 was observed either (Fig. 1D, n = 9, rho = −0.38, P = 0.31). The lack of consistent AVO/OVA ratio change in an individual mouse argued against selection for heritable fitness differences acquired by a subpopulation of one of the strains during nasal colonization.
Estimation of effective population size.
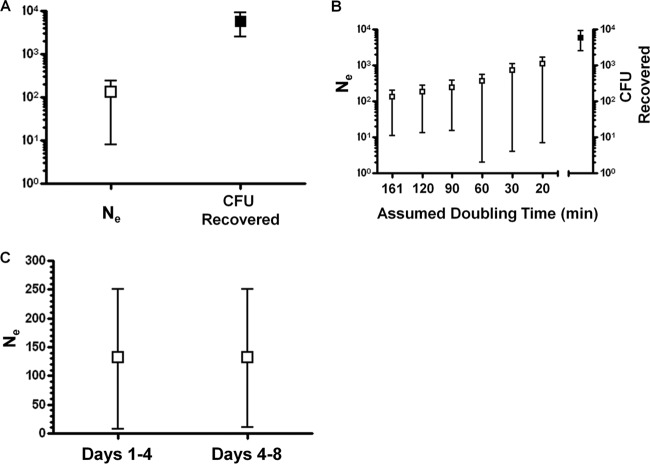
Based on the temporal change of AVO strain frequency in each mouse, we estimated Ne by using the MLNE software (25), which implements a maximum-likelihood method and accounts for sampling error. An in vivo doubling time of 161 min (13) was assumed to estimate the number of generations between two sampling points. In BALB/c mice, the effective population of pneumococcus showed a point estimate of 133 with 95% CI of 11 to 203 (Fig. 2A). In comparison, the CFU recovered on day 8 showed a mean of 5,768 with a 95% confidence interval of 2,515 to 9,021 (Fig. 2A). Since CFU recovered on day 8 represents only a fraction of the carriage population, we concluded that the Ne of pneumococcus is much smaller than the carriage population during nasal colonization.
Fig 2.
Effective population of pneumococcus in BALB/c mice. (A) The estimated Ne in BALB/c mice (□) was lower than the CFU recovered on day 8 (■). (B) A range of in vivo generation time was assumed, and the estimated Ne values (left panel) were compared to the CFU recovered on day 8 (right panel). (C) The Ne for different time intervals was estimated by only using the strain frequency data during the time period specified. Error bars represent the 95% CI.
A number of in vitro studies indicated that the doubling time of pneumococcus could be much shorter than 161 min (13, 26). We therefore tested whether a shorter generation time could explain the discrepancy between carriage population and effective population. A range of generation times was assumed and the corresponding effective population size was calculated (Fig. 2B). As expected, effective population size increased when generation time became shorter (Fig. 2B). However, the effective population size was still substantially smaller than the CFU recovered even an unrealistically short generation time (20 min) was assumed (Fig. 2B). Thus, a short generation time in vivo was unlikely to be the major explanation for the small Ne.
We next examined whether there is temporal change in pneumococcal Ne during colonization. The average Ne from day 1 to day 4 (days 1 to 4) was calculated by using the AVO allele frequency change between day 1 and day 4. The same strategy was used to estimate average Ne during days 4 to 8. As shown in Fig. 2C, the estimation of Ne for days 1 to 4 (point estimate, 132; 95% CI = 7 to 250) was very similar to the estimation of Ne for days 4 to 8 (point estimate, 132; 95% CI = 11 to 250). The Ne estimated for the two time intervals were much lower than the CFU recovered on day 8, a finding consistent with the overall Ne.
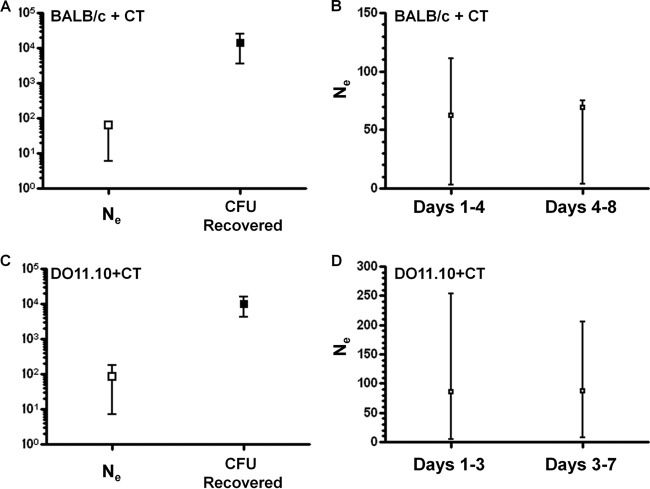
Finally, the effective population size of pneumococcus during nasal carriage in varied experimental conditions, as well as in a different mouse type, was investigated. Cholera toxin (CT) is a commonly used adjuvant in immunization experiments, and here we examined its effect on Ne in BALB/c mice. In BALB/c mice exposed to CT (BALB/c + CT), the effective population of pneumococcus showed point estimate of 64 (95% CI = 6 to 65) (Fig. 3A, n = 8). Similar to what was observed in naive BALB/c mice, the Ne was substantially smaller than the CFU recovered on day 8 (mean, 14,641; 95% CI = 3,620 to 25,655) (Fig. 3A). The estimation of Ne for days 1 to 4 (point estimate, 62; 95% CI = 3 to 111) was similar to the estimation of Ne for days 4 to 8 (point estimate, 69; 95% CI = 4 to 75) (Fig. 3B). It appeared that exposure to CT reduced pneumococcal Ne in BALB/c mice.
Fig 3.
Effective population of pneumococcus in BALB/c and DO11.10 RAG−/− mice. All mice had been exposed to CT 4 to 5 weeks prior to challenge. The point estimate of Ne (□) and mean CFU recovered (■) are shown. The estimated Ne in BALB/c mice (A) or DO11.10 RAG−/− mice (C) was lower than the terminally recovered CFU. The Ne in different time intervals was calculated by only using the strain frequency data during the time period specified in BALB/c mice (B) and DO11.10 RAG−/− mice (D). Error bars represent the 95% CI.
In DO11.10 RAG−/− mice (which lack adaptive B cell and T cell immunity, except for CD4+ T cells specific for a peptide of ovalbumin) exposed to CT (DO11.10 + CT), the effective population of pneumococcus showed point estimate of 87 (95% CI = 7 to 181) (Fig. 3C, n = 7). Again, the Ne was much smaller than the CFU recovered on day 8 (mean, 9,931; 95% CI = 4,155 to 15,708) (Fig. 3C). The estimation of Ne for days 1 to 3 (point estimate, 86; 95% CI = 5 to 245) was similar to the estimation of Ne for days 3 to 7 (point estimate, 87; 95% CI = 7 to 206) (Fig. 3D). Thus, the Ne of pneumococcus in DO11.10 RAG−/− mice showed qualitatively similar patterns as in BALB/c mice.
A mathematical model reproduced the Ne patterns.
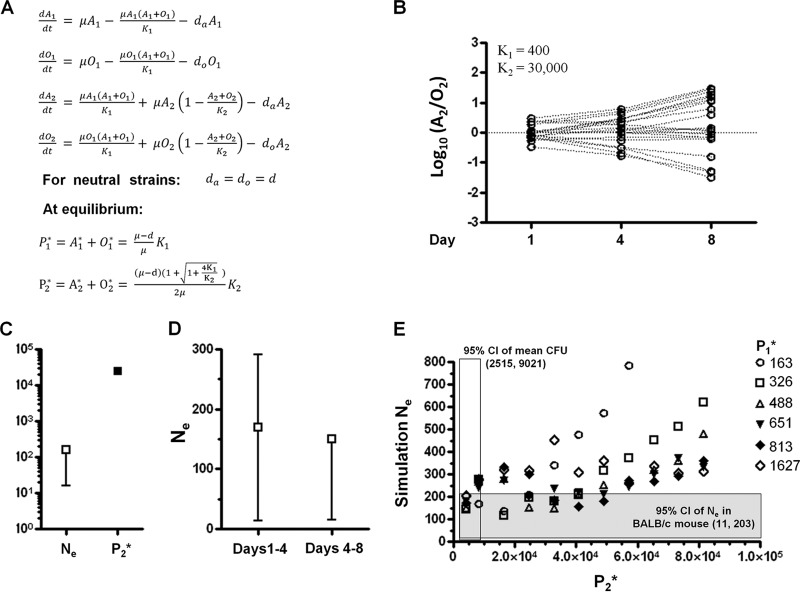
The large discrepancy between Ne and carriage census population size would be most readily explained by heterogeneity in pneumococcal replication during nasopharyngeal colonization. Indeed, the nasal mucosa may support two populations of pneumococci, which can be primarily recovered from the outer surface and the nasal tissue, respectively (16). To examine whether the heterogeneous nasal environment can explain the observed Ne patterns, we modeled pneumococcal colonization by considering two subpopulations, P1 and P2 that are established 1 day after inoculation (Fig. 4A). Loosely based on the idea of the type I persister described by Balaban et al. (23), we hypothesized that a small subpopulation of pneumococci (P1), perhaps tissue associated (16), actively replicates, while a larger population that is in the nasopharyngeal lumen or mucosal surface (P2) may or may not replicate but does not contribute to the future generations which are seeded by the P1 population. Effectively, P2 is the major site of bacterial death and removal. Note that this is a deliberate simplification, in the absence of detailed information concerning the heterogeneity in dynamics of the colonizing population over time.
Fig 4.
Mathematical model of pneumococcal colonization dynamics. (A) Differential equations describing the dynamics of two strains (A and O) in two subpopulations, P1 and P2. A stochastic version of this model was used in simulation. To initialize the simulation, P1 and P2 were set to their equilibrium size (P1* and P2*, respectively), and the ratio between the two strains in each subpopulation was set to follow a log-normal distribution as estimated from the day 1 results of the BALB/c colonization experiment. After initiation, the model was simulated forward for a total of t = 10,080 min (7 days), and the counts of the two strains in each subpopulation on days 1, 4, and 8 were recorded as output. (B) Typical results from 20 simulations with the indicated parameter values. The log10(A2/O2) calculated from the simulation output is shown, and each dashed line connects data points from the same simulation. (C) Simulation of the model produced small Ne despite large census population size. The point estimate of Ne (□) calculated from output of 20 simulations in panel B is shown, which is substantially smaller than the census population size P2* (■) used in the simulation. Error bars indicate the 95% CI. (D) Simulation of the model showed little temporal change in Ne. Ne was calculated from output of 20 simulations shown in panel B and the Ne in different time intervals was estimated by only using the strain frequency data during the time period specified. Error bars indicate the 95% CI. (E) Effects of P1* and P2* size on the estimated Ne. Simulation was performed with varying K1 and K2 values such that the indicated P1* and P2* sizes were achieved. Twenty simulations were performed for each combination of P1* and P2*, and the point estimate of Ne based on that 20 simulation output is shown. The shaded area represents where the simulated Ne values fall within the 95% CI of Ne estimated from the BALB/c colonization experiment, and the census population size used in the simulation (P2*) is no smaller than the census population size observed in the BALB/c colonization experiment (95% CI of mean CFU recovered, open bar).
We simulated this model, tracking OVA and AVO strains separately, in a continuous-time stochastic process. Typical results of 20 simulation outputs for a particular parameter combination (K1 = 400, K2 = 30000) are shown in Fig. 4B. Ne was estimated based on the simulated outputs and compared to the equilibrium size of P2, which was treated as the census population since it represents the vast majority of P1 + P2 in our simulation. As shown in Fig. 4C, the Ne estimated from the simulation outputs (163; 95% CI = 16 to 174) was similar to the Ne estimated for pneumococcus in BALB/c mice and was much smaller than the equilibrium size of P2 (24737) that was used to generate the simulation outputs. For the simulated data, the estimation of Ne for days 1 to 4 (point estimate, 169; 95% CI = 14 to 291) was also similar to the estimation of Ne for days 4 to 8 (point estimate, 150; 95% CI = 15 to 151) (Fig. 4D). In addition, we estimated Ne based on simulation data generated from varied K1 and K2 to examine effects of census population (P2*) on Ne (Fig. 4E). We found that a wide range of simulation census population ([4,226 to 48,993], Fig. 4E) that was consistent with the observed CFU recovered can generate similar Ne to those observed in the BALB/c mice experiment.
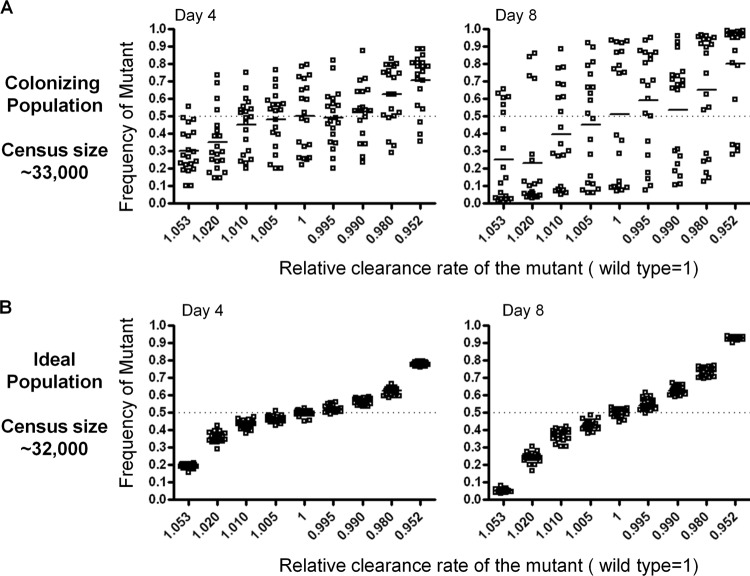
Facilitated by the pneumococcal colonization model, we further investigated the pattern of allele frequency change in the colonizing population when the clearance rate of the A strain bacteria is different from that of the O strain bacteria, as might be the case of under selection for escape from strain-specific immune responses or antimicrobial agents. The results were compared to those from an ideal population in which the census size and effective size are nearly equal (Fig. 5). In both populations, the census size was approximately 30,000 during simulation. Selection would be expected to operate efficiently down to a selection coefficient of order ∼10−4 if the effective population size were equal to the observed census size. The colonizing population was parameterized such that Ne = 183, a finding consistent with Ne estimated in the BALB/c mice. The initial mutant allele frequency was set as 0.5 (1:1 ratio to the wild-type allele), and the mutant allele frequency was monitored for up to 8 days. Clearance rate ratios ranging from 0.952 to 1.053 were used for both the colonizing population and the ideal population. The simulation results indicated that selection was less efficient in the colonizing population than in the ideal population (Fig. 5). For example, when the clearance rate of the mutant allele was 0.990 that of the wild-type allele, mutant allele frequency increased above 0.5 in 13/20 simulations by day 4 in the colonizing population (Fig. 5A), while the mutant allele frequency increased above 0.5 in 20/20 simulations in the ideal population during the same period (Fig. 5C). By day 8, the mutant allele frequency showed a highly significant increase in the ideal population (mean increase = 0.1274, n = 20, P < 0.0001, one sample t test) (Fig. 5D). In the colonizing population, by contrast, the increase in mutant allele frequency was not statistically significant by day 8 (mean increase = 0.038, n = 20, P = 0.57, one sample Student t test) (Fig. 5B). Similar results were observed when the initial mutant allele frequency was set as 0.01 (see Fig. S1 in the supplemental material).
Fig 5.
Effect of small Ne on the effectiveness of within-host selection. Simulations were performed based on a colonizing population model (A) or an ideal population model (B) (see Materials and Methods for details). A range of clearance rates were applied to the mutant allele, while the clearance rate for the wild-type allele was kept constant at 0.0043 min−1. For each mutant clearance rate, 20 simulations were performed. The dotted lines indicate the initial frequency of the mutant allele (0.5 on day 0). Frequencies of the mutant alleles on day 4 (25 generations, left) and day 8 (50 generations, right) are shown. Bars represent means.
DISCUSSION
In this study, we estimated the effective population size of Streptococcus pneumoniae in a mouse colonization model by following the frequency change of two cocolonizing, competitively neutral pneumococcal strains. Since only allele frequency data on or after day 1 were used in Ne estimation, the effect of colonization bottleneck on frequency changes was minimized. In two mouse types, the Ne during nasal carriage was much smaller than the lower bound of census population that is estimated by the number of CFU recovered. The number of CFU recovered in the present study was smaller than the colonization density reported in other studies (9, 27–29), because at no time point did we intend to remove and recover the whole colonizing population. We purposely retrieved only a small fraction of the total population during live sampling in order to keep the colonization minimally disturbed. Even at the terminal sample, we did not exhaustively wash the mouse's upper respiratory tract but rather used a fixed recovery volume of 200 μl. Pneumococcal Ne also showed little temporal variation during colonization. We hypothesized that such a small Ne may reduce the effectiveness of within host selection for pneumococcus.
We constructed a mathematical model of colonization by considering two subpopulations of different growth dynamics that are established after a colonization bottleneck. In this model, a small, fast-replicating subpopulation generates most of the stochastic deviation in allele frequency that is then passed to a large subpopulation that is readily sampled but is not contributing much toward future generations. The model represents one, though not the only, biologically plausible mechanism that could generate such small effective population size. By simulation, we showed that this model could reproduce Ne patterns that were consistent with what was observed in mice experiments over a wide range of parameter values. A small Ne could be consistent with either a large or a small census population size (Fig. 4D), depending on the relative size of the two subpopulations. Thus, subpopulation structure, rather than the total population size, could be a critical determinant of Ne during pneumococcal colonization.
Using stochastic simulation of the model, we also examined the effectiveness of within-host selection for a mutant allele. Compared to an ideal population, the colonizing population showed two features: (i) the increase in frequency of a favorable allele was more variable and (ii) a favorable allele was less likely to become fixed. These observations were consistent with strong genetic drift effects that interfered with the effectiveness of selection. In future investigations, it would be interesting to simultaneously estimate Ne and in vivo selection coefficient by using strains with medium and large fitness effects in competition experiments.
Our model certainly is not the only model that could produce the degree of stochastic variation observed. It is possible, for example, that there are more than two subpopulations with different contributions to successive generations. Alternatively, it is possible that the neutrally marked strains introduced in the experiment go on to mutate, and that some of these mutations (which occur at random with respect to the neutral marker) are advantageous in certain microanatomic sites within the nasopharynx. The consistency of results across experiments and the lack of positive correlation between frequency changes of neutral markers within a mouse over time make this selective explanation less likely. In any case, many models, including heterogeneous contributions to future generations or the presence of different selective microenvironments, which would produce random variation in neutral marker frequency as observed in our experiments, would also interfere with the action of selection to increase the frequency of, for example, a drug resistance mutation. It is for this reason that the concept of effective population size has been useful despite uncertainty about the precise mechanisms determining its value (10).
Studies of within-host competition between bacteria rarely comment on the aspects of stochasticity introduced by population bottlenecks and by a small effective population size. There are exceptions: transposon mutagenesis studies usually account for stochasticity, inexplicitly or explicitly, by focusing on strong and reproducible effects (8, 9), and there has been at least one deliberate experiment with neutrally marked, isogenic strains of enteric bacteria by Maskell and coworkers (30). Since Ne of pneumococcus during nasal colonization is likely to be 50- to 100-fold less than the carriage population, our model suggested that genetic drift may have a notable impact on the selection of pneumococcal variants, even those with substantial selection coefficients. The effects of genetic drift may help to explain the variation in estimated selection coefficients or competitive indexes often seen within an experiment; this is not a problem of noise introduced by the experimental technique but one of noise inherent in studying competition within a mouse. Nasopharyngeal swabs of humans (19) recover numbers of pneumococci similar to the numbers recovered by nasal wash in the present study (admittedly a comparison of limited interpretability, since neither technique quantifies the entire population present). If pneumococcal effective population sizes in humans are of comparable order to those in mice, then genetic drift may in some instances mask or overcome the effect of selection for resistant variants during treatment (31), selection against antimicrobial-resistant strains in the absence of treatment (1, 32), and selection for antigenic variation (3). This would be an interesting hypothesis for future investigation. It should be noted that the mouse is not a natural host for pneumococcal colonization, and more studies are needed to evaluate whether the small effective population size documented here applies to colonization in humans as native hosts.
The effect of small Ne is not limited to pneumococcal colonization. In a chicken model of colonization by Campylobacter, it was reported that the proportion of wild-type isogenic tagged strains present in chicken ceca after oral infection with a mixed population is not predictable from the inoculum (30). The unpredictability could be a result of both colonization bottleneck and a small Ne that increased the variability of the observed proportion. In addition, Grant et al. probed microbial population dynamics in vivo by simultaneously administering wild-type isogenic tagged strains of Salmonella enterica (33). By tracing the disappearance of strains through time, it was shown that independent bacterial subpopulations are established in different organs and that different bacterial populations mix between organs via the blood. Such population heterogeneity in vivo may also cause the effective population size of Salmonella enterica to be much smaller than the census population size and thus may influence the effectiveness of selection. Since the isogenic tagged strains allow tracking frequency change of multiple alleles simultaneously, data generated by this approach would be very informative to estimate the Ne of Salmonella enterica in vivo.
A small Ne could also affect the generation of new alleles. The probability that a neutral mutation occurs at a given position in an individual bacterium that is destined to contribute to future generations is approximated by the calculation 1 − e−Neμt, where μ is the per nucleotide mutation rate and t is the number of generations. When Ne is much smaller than census population, it is possible that the rate of de novo mutagenesis in pneumococcus may be much slower than one would expect from the large census population.
Supplementary Material
ACKNOWLEDGMENTS
We thank Bernice Sim for technical assistance and Chris B. Ford at Harvard School of Public Health for technical assistance.
This study was supported in part by National Institutes of Health grant R01 AI048935 to M.L.
Footnotes
Published ahead of print 30 September 2013
Supplemental material for this article may be found at http://dx.doi.org/10.1128/IAI.00527-13.
REFERENCES
- 1.Trzcinski K, Thompson CM, Gilbey AM, Dowson CG, Lipsitch M. 2006. Incremental increase in fitness cost with increased beta-lactam resistance in pneumococci evaluated by competition in an infant rat nasal colonization model. J. Infect. Dis. 193:1296–1303 [DOI] [PubMed] [Google Scholar]
- 2.Lysenko ES, Lijek RS, Brown SP, Weiser JN. 2010. Within-host competition drives selection for the capsule virulence determinant of Streptococcus pneumoniae. Curr. Biol. 20:1222–1226 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Li Y, Gierahn T, Thompson CM, Trzcinski K, Ford CB, Croucher N, Gouveia P, Flechtner JB, Malley R, Lipsitch M. 2012. Distinct effects on diversifying selection by two mechanisms of immunity against Streptococcus pneumoniae. PLoS Pathog. 8:e1002989. 10.1371/journal.ppat.1002989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Giraud A, Matic I, Tenaillon O, Clara A, Radman M, Fons M, Taddei F. 2001. Costs and benefits of high mutation rates: adaptive evolution of bacteria in the mouse gut. Science 291:2606–2608 [DOI] [PubMed] [Google Scholar]
- 5.Andisi VF, Hinojosa CA, de Jong A, Kuipers OP, Orihuela CJ, Bijlsma JJ. 2012. Pneumococcal gene complex involved in resistance to extracellular oxidative stress. Infect. Immun. 80:1037–1049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cohen T, van Helden PD, Wilson D, Colijn C, McLaughlin MM, Abubakar I, Warren RM. 2012. Mixed-strain Mycobacterium tuberculosis infections and the implications for tuberculosis treatment and control. Clin. Microbiol. Rev. 25:708–719 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Colijn C, Cohen T, Ganesh A, Murray M. 2011. Spontaneous emergence of multiple drug resistance in tuberculosis before and during therapy. PLoS One 6:e18327. 10.1371/journal.pone.0018327 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hensel M, Shea JE, Gleeson C, Jones MD, Dalton E, Holden DW. 1995. Simultaneous identification of bacterial virulence genes by negative selection. Science 269:400–403 [DOI] [PubMed] [Google Scholar]
- 9.van Opijnen T, Camilli A. 2012. A fine scale phenotype-genotype virulence map of a bacterial pathogen. Genome Res. 22:2541–2551 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Charlesworth B. 2009. Fundamental concepts in genetics: effective population size and patterns of molecular evolution and variation. Nat. Rev. Genet. 10:195–205 [DOI] [PubMed] [Google Scholar]
- 11.Son MR, Shchepetov M, Adrian PV, Madhi SA, de Gouveia L, von Gottberg A, Klugman KP, Weiser JN, Dawid S. 2011. Conserved mutations in the pneumococcal bacteriocin transporter gene, blpA, result in a complex population consisting of producers and cheaters. mBio 2:00179–11. 10.1128/mBio.00179-11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Davis KM, Akinbi HT, Standish AJ, Weiser JN. 2008. Resistance to mucosal lysozyme compensates for the fitness deficit of peptidoglycan modifications by Streptococcus pneumoniae. PLoS Pathog. 4:e1000241. 10.1371/journal.ppat.1000241 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.van Opijnen T, Camilli A. 2012. A fine scale phenotype-genotype virulence map of a bacterial pathogen. Genome Res. 10.1101/gr.137430.112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mastroeni P, Grant A, Restif O, Maskell D. 2009. A dynamic view of the spread and intracellular distribution of Salmonella enterica. Nat. Rev. Microbiol. 7:73–80 [DOI] [PubMed] [Google Scholar]
- 15.Giraud A, Fons M, Taddei F. 2003. Impact of mutation rate on the adaptation of gut bacteria. J. Soc. Biol. 197:389–396 (In French.) [PubMed] [Google Scholar]
- 16.Briles DE, Novak L, Hotomi M, van Ginkel FW, King J. 2005. Nasal colonization with Streptococcus pneumoniae includes subpopulations of surface and invasive pneumococci. Infect. Immun. 73:6945–6951 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bogaert D, De Groot R, Hermans PW. 2004. Streptococcus pneumoniae colonisation: the key to pneumococcal disease. Lancet Infect. Dis. 4:144–154 [DOI] [PubMed] [Google Scholar]
- 18.Simell B, Auranen K, Kayhty H, Goldblatt D, Dagan R, O'Brien KL, Pneumococcal Carriage Group 2012. The fundamental link between pneumococcal carriage and disease. Expert Rev. Vaccines 11:841–855 [DOI] [PubMed] [Google Scholar]
- 19.Albrich WC, Madhi SA, Adrian PV, van Niekerk N, Mareletsi T, Cutland C, Wong M, Khoosal M, Karstaedt A, Zhao P, Deatly A, Sidhu M, Jansen KU, Klugman KP. 2012. Use of a rapid test of pneumococcal colonization density to diagnose pneumococcal pneumonia. Clin. Infect. Dis. 54:601–609 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wang J. 2003. Maximum-likelihood estimation of admixture proportions from genetic data. Genetics 164:747–765 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang J. 2001. A pseudo-likelihood method for estimating effective population size from temporally spaced samples. Genet. Res. 78:243–257 [DOI] [PubMed] [Google Scholar]
- 22.Williamson EG, Slatkin M. 1999. Using maximum likelihood to estimate population size from temporal changes in allele frequencies. Genetics 152:755–761 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Balaban NQ, Merrin J, Chait R, Kowalik L, Leibler S. 2004. Bacterial persistence as a phenotypic switch. Science 305:1622–1625 [DOI] [PubMed] [Google Scholar]
- 24.Cao Y, Gillespie DT, Petzold LR. 2007. Adaptive explicit-implicit tau-leaping method with automatic tau selection. J. Chem. Physics 126:224101. [DOI] [PubMed] [Google Scholar]
- 25.Wang J, Whitlock MC. 2003. Estimating effective population size and migration rates from genetic samples over space and time. Genetics 163:429–446 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hathaway LJ, Brugger SD, Morand B, Bangert M, Rotzetter JU, Hauser C, Graber WA, Gore S, Kadioglu A, Muhlemann K. 2012. Capsule type of Streptococcus pneumoniae determines growth phenotype. PLoS Pathog. 8:e1002574. 10.1371/journal.ppat.1002574 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rosch JW, Mann B, Thornton J, Sublett J, Tuomanen E. 2008. Convergence of regulatory networks on the pilus locus of Streptococcus pneumoniae. Infect. Immun. 76:3187–3196 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cron LE, Bootsma HJ, Noske N, Burghout P, Hammerschmidt S, Hermans PW. 2009. Surface-associated lipoprotein PpmA of Streptococcus pneumoniae is involved in colonization in a strain-specific manner. Microbiology 155:2401–2410 [DOI] [PubMed] [Google Scholar]
- 29.Cron LE, Stol K, Burghout P, van Selm S, Simonetti ER, Bootsma HJ, Hermans PW. 2011. Two DHH subfamily 1 proteins contribute to pneumococcal virulence and confer protection against pneumococcal disease. Infect. Immun. 79:3697–3710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Coward C, van Diemen PM, Conlan AJ, Gog JR, Stevens MP, Jones MA, Maskell DJ. 2008. Competing isogenic Campylobacter strains exhibit variable population structures in vivo. Appl. Environ. Microbiol. 74:3857–3867 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Anderson KB, Tan JS, File TM, Jr, DiPersio JR, Willey BM, Low DE. 2003. Emergence of levofloxacin-resistant pneumococci in immunocompromised adults after therapy for community-acquired pneumonia. Clin. Infect. Dis. 37:376–381 [DOI] [PubMed] [Google Scholar]
- 32.Andersson DI, Hughes D. 2010. Antibiotic resistance and its cost: is it possible to reverse resistance? Nat. Rev. Microbiol. 8:260–271 [DOI] [PubMed] [Google Scholar]
- 33.Grant AJ, Restif O, McKinley TJ, Sheppard M, Maskell DJ, Mastroeni P. 2008. Modeling within-host spatiotemporal dynamics of invasive bacterial disease. PLoS Biol. 6:e74. 10.1371/journal.pbio.0060074 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.