Analyzing milestoning networks for molecular kinetics: Definitions, algorithms, and examples

Abstract

Network representations are becoming increasingly popular for analyzing kinetic data from techniques like Milestoning, Markov State Models, and Transition Path Theory. Mapping continuous phase space trajectories into a relatively small number of discrete states helps in visualization of the data and in dissecting complex dynamics to concrete mechanisms. However, not only are molecular networks derived from molecular dynamics simulations growing in number, they are also getting increasingly complex, owing partly to the growth in computer power that allows us to generate longer and better converged trajectories. The increased complexity of the networks makes simple interpretation and qualitative insight of the molecular systems more difficult to achieve. In this paper, we focus on various network representations of kinetic data and algorithms to identify important edges and pathways in these networks. The kinetic data can be local and partial (such as the value of rate coefficients between states) or an exact solution to kinetic equations for the entire system (such as the stationary flux between vertices). In particular, we focus on the Milestoning method that provides fluxes as the main output. We proposed Global Maximum Weight Pathways as a useful tool for analyzing molecular mechanism in Milestoning networks. A closely related definition was made in the context of Transition Path Theory. We consider three algorithms to find Global Maximum Weight Pathways: Recursive Dijkstra's, Edge-Elimination, and Edge-List Bisection. The asymptotic efficiency of the algorithms is analyzed and numerical tests on finite networks show that Edge-List Bisection and Recursive Dijkstra's algorithms are most efficient for sparse and dense networks, respectively. Pathways are illustrated for two examples: helix unfolding and membrane permeation. Finally, we illustrate that networks based on local kinetic information can lead to incorrect interpretation of molecular mechanisms.

INTRODUCTION

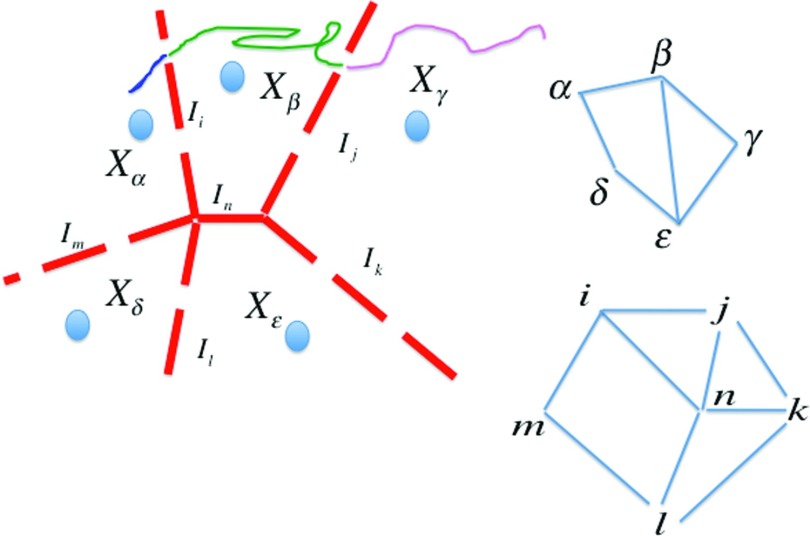
The use of networks to describe and analyze the kinetics and thermodynamics of molecular systems has grown rapidly in recent years. The growing interest is partly a result of the increase in computer power that produces longer Molecular Dynamics (MD) simulations and better sampling for stability and kinetic analysis. Analyzing the vast data produced by these simulations is a significant challenge. One approach to analyze the data is to use networks (Figure 1). For example, metastable states are identified and are mapped to vertices (nodes). Transitions between the states are modeled by edges between the vertices. Mapping continuous phase space trajectories into a relatively small number of discrete states helps in visualization of the data and in dissecting complex dynamics to concrete mechanisms. In particular, mappings that are based on the Transition Path Theory,¹ Master equation,² or Directional Milestoning³ are well-defined mathematical procedures and have been previously used in a number of cases (e.g., in Markov State Model (MSM)^{2, 4, 5} or Milestoning^{6, 7, 8, 9, 10}).

Figure 1.

A schematic representation of mapping continuous space and trajectories to a network. We have five cells in phase space denoted by X_α, X_β, X_γ, X_δ, X_ɛ. Each cell can be mapped to a network vertex and the edges would be between vertices, e.g., (α, β) and (β, γ). Sometimes the cells are represented by specific conformations (anchors) that are illustrated in the figure by the blue ellipses. In an alternate network representation, the vertices can be interfaces or milestones denoted on the figure by dashed red lines, which indicate the boundary between domains. There are six milestones in the above figure, I_i − I_n. Continuous trajectories are mapped to the network either by their location in phase space or by the last milestone that they have passed (color coded curves in the figure). On the right side of the figure we show network representations. The top figure is an anchor-based network and the lower figure is based on the milestones.

While the above analysis is conducted postmortem (data generation is followed by analysis), a less sequential process is also possible, in which the network is generated in parallel to the computations of the MD trajectories. It has been used previously with methods like Hyper-Dynamics,¹¹ MSM,⁴ and Milestoning.⁹ The advantage of frequent exchanges of information between networks and continuous space is the ability to identify “on-the-fly,” regions that are poorly or over-sampled. For example, the network analysis may identify an important transition (or an edge) for which only a few successful events were recorded. As a response we sample more trajectories for that edge, while cutting resources from edges that are converged statistically.

A third scenario in which the network representation has gained popularity is in the field of reaction paths. The reaction path approach is a compact and efficient way to obtain information on the kinetics and thermodynamics of molecular systems under a set of assumptions (e.g., the use of local expansion in coordinates in the neighborhood of a transition or a metastable state). Since no explicit time evolution is considered, the calculations are much cheaper than MD simulation. Reaction pathways can be computed as one-dimensional curves in complex space, dramatically reducing the dimensionality of the original system.^{12, 13, 14, 15, 16, 17, 18, 19, 20, 21} However, with increases in the complexity of systems, the concept of the reaction path was extended to include multiple crossing pathways or networks. Early studies of this type go back to conformational transitions in peptides²² and continue to isomerization of flexible molecules, fluidity of Lennard Jones clusters, and protein folding (see the book²³).

Compared to the single reaction coordinate, the network of pathways is considerably richer. One of the obvious mechanistic questions from a network is, “Are there particularly important pathways in the networks?” and if there are, “how do we find them?” Another question is “Are there bottlenecks in the networks?” These bottlenecks are edges of low flux in the network, that require significant efforts to pass through, but that must be crossed on the way from the reactant to the product state. The information about pathways and bottlenecks is useful for qualitative analysis of the process and to gain more insight into the behavior of the system. The problem of finding these important pathways and bottlenecks is addressed in the present paper.

Various representations of networks for molecular systems are discussed, and efficient and scalable algorithms are presented for finding important pathways and bottlenecks in these networks. We also consider different kinetic measures to represent the mechanism of the process and argue that the flux, being an exact solution of the kinetic equations, is a rigorous yardstick that can be used in qualitative analysis of reaction pathways. This is to be contrasted with the use (for example) of rate coefficients. The discussions are supported by case studies of unfolding of a helix under load and membrane permeation.

DEFINITION OF THE NETWORK

There are multiple plausible definitions for a molecular network, and we discuss some of them below. The most straightforward choices for vertices and edges are local energy minima and first order saddle points, respectively. The weights of the nodes and the edges can be estimated using harmonic partition functions near the stationary points and the (harmonic) transition state theory.²⁴ Solvent effects may be included with effective solvation energies such as GBSA.²⁵ This approach for network construction goes back to 1989.²⁶ Wales and colleagues used these networks extensively²³ to build connectivity trees. These trees are networks of specific topology (no cycles) and are primarily used for qualitative analysis. To extract thermodynamic and kinetic properties, the full network is used.

The definition of vertices and edges is less obvious when we consider time series obtained from molecular dynamic simulations instead of static energy minima and saddle points. Rather than mapping a point to a point (e.g., energy minimum to a vertex) we map a volume in phase space and trajectory fragments to vertices and edges. This mapping can be made in several ways. The two different approaches that we consider are (i) state-based and (ii) flux-based. In the state-based method, we consider the nodes to be volumes in phase space or in conformation space, which is in the spirit of MSMs. In the flux-based method, we consider the nodes to be interfaces (or milestones) and the edges represent transitions between the interfaces. Since there are multiple interfaces for a single phase-space volume element, the network between interfaces is likely to be richer. Furthermore, the definition of arrival and departure of a trajectory fragment to a coarse state can be made more precisely based on passing of an interface instead of arrival to a volume which may require additional relaxation time. The two formulations, in the general case, are not equivalent as shown in Figure 1.

The molecular process is represented as a weighted, directed graph G = (V, E), where V is the set of vertices and E is the set of edges in G. An edge from vertex u to vertex v is represented as (u, v) and has a weight, w(u, v). Note that the edges are directed, i.e., edge (u, v) is not the same as (v, u). The edge weights may have different physical realizations. For example, edge weights and states may be defined by the physical distance between two vertices (as is done by geometric clustering), the phase space flux between nodes, or the rate constant of transitions between the nodes. It is probably best to build the network from the exact solution of the kinetics; namely, based on the flux between the states. Below, we will consider the weights abstractly (to the extent possible) and only after derivation of the algorithms, concrete examples of weights that are typical of kinetic networks will be discussed.

We comment that the use of a directed graph does not violate equi-partition. A vertex v_i will have a directed edge pointing to v_j and at the same time v_j will have a directed edge to v_i which allows balancing of the two fluxes and equipartitioning. Additionally, we note that the words network and graph are equivalent, as are the words node and vertex, and we will use them both. The reader may refer to the Appendix for a list of definitions and alternate terms occurring in this paper.

NETWORK REPRESENTATIONS OF KINETIC DATA

We focus below on network representations used in the method of Milestoning.^{3, 6, 7} However, they are equally applicable to networks generated by other methods such as MSM⁴ or motion planning.²⁷ The representation of directional milestoning data has been previously described in Refs. ³ and ⁶. In brief, we consider a set of anchors, or phase space points ${\left\{X_{\alpha }\right\}}_{\alpha =1}^N$, and milestones (or interfaces) ${\left\{I_j\right\}}_{j=1}^J$ (Figure 1). The milestones are interfaces separating phase space volumes that are associated with the anchors. Henceforth, we use the indices {α, β, γ…} to denote the anchors and indices {i, j, k…} to denote milestones.

The dual representation, by anchors and milestones, makes it possible to visualize more than one network for the same process. Depending on the choice of nodes, as (i) anchors or (ii) milestones, we have two types of networks: (i) state-space network where the nodes are anchors or phase space volumes, and (ii) a flux-space network, where the nodes are milestones.

With the identification of the nodes, we are left with the question of what weights to choose, for the edges of these two types of graphs. We have chosen to concentrate on the flux, as flux between two nodes is the most informative quantity that we can attach to an edge. This choice is in the spirit of Transition Path Theory,²⁸ and in the spirit of the max flux formulations of optimal pathways.^{6, 29, 30, 31} In Milestoning, the flux at milestone i (the number of molecules that pass per unit time the ith milestone) is denoted by q_i. The basic Milestoning equation³² is of conservation of flux,

$$q_i\left(t\right)=2·{\eta }_i\delta \left(t\right)+\sum _j\underset{0}{\overset{t}{\int }}{K}_{ij}\left(t-t^{\prime }\right)q_j\left(t^{\prime }\right)d{t}^{\prime }\forall i,$$ (1)

where q_i(t) is the flux through milestone i at time t, η_i is the initial condition (the probability that the last milestone that passed before or at time zero is i), and K_ij(t) is the transition probability that a trajectory that starts at milestone i will pass through milestone j exactly after time t. Hence, Eq. 1 keeps track of the number of trajectories and ensures that the flux is conserved.

For network calculations it is convenient to consider a stationary flux or steady state condition in which the flux, q_i, is time independent. The stationary matrix is K. It is the time integrated transition matrix $\left(K_{ij}\equiv \underset{0}{\overset{\infty }{\int }}{K}_{ij}\left(t\right)dt\right)$ which is the probability that a trajectory initiated at milestone i will hit (and terminate at) another milestone j before any other milestone. We obtain a stationary flux by setting cyclic boundary conditions. The final milestone f is set to return all the flux that arrives to it, to the first milestone. Hence, the matrix element K_fi is set to one if milestone i is the first milestone and is set to zero otherwise. The above adjustment of K and the requirement of stationary flux/steady state results in a remarkably simple equation for the stationary flux:⁶

$$q\left(Id-K\right)=0K_{fi}=\left\{\begin{array}{cc}1& i=1\\ 0& i\ne 1\end{array}\right\},$$ (2)

where q is the vector of all stationary fluxes. As discussed extensively in earlier papers about Milestoning^{32, 33}K is computed from atomically detailed trajectories as K ≈ n_ij/n_i, where n_i is the number of trajectories initiated at milestone i and n_ij is the number of trajectories that started at i and the first milestone they reach (which is different from i) is milestone j. The length of the vector q is J and the dimensionality of K is J × J, where J is the number of milestones. Id is the identity matrix.

The flux information stored in q is used in graphs as edge weights. As mentioned previously, we have two types of graphs, state-space graphs and flux-space graphs. There are more milestones than anchors and hence the picture obtained by the flux-space graph is more detailed and potentially includes more information than the state-space graph. But the state-space graph is simpler, and for interpretation purposes it can be beneficial to look at the system at the anchor level. We, therefore, convert the flux-space paths to state-space for visualization purposes. Below, we discuss how edge weights are obtained from fluxes for both state-space and flux-space graphs. We also discuss another graph representation based on rate coefficients instead of fluxes. For the flux-space graphs, we additionally explain how to convert the paths to state-space.

State-space (anchor-based) graphs with flux-based edge weights

We create a graph with one vertex per anchor. Consider two anchors α and β, which are associated in directional milestoning, with two fluxes, q_αβ and q_βα, corresponding to the interfaces (milestones) α → β and β → α. The weight of the edge is the net flux w(α, β) = |q_αβ − q_βα|. The direction of the edge is decided according to the larger flux. Hence, if q_αβ > q_βα then the direction of the edge is from α to β and vice versa. The main advantage of using graphs in anchor space, apart from the ease of interpretation, is that the size of graphs tends to be much smaller and hence calculating pathways is less expensive in the flux-space graphs. In directional milestoning, for instance, the number of milestones, i.e. nodes of a flux-space graph, J, is much larger than the number of anchors N, and J can be as large as N(N − 1). However, anchor space graphs are more likely to be dense graphs which means that the number of edges in the graph, E, is much greater than the number of vertices, V (E ≫ V).

Flux-space (milestone-based) graphs with flux-based edge weights

We have one vertex per milestone in this graph. The probability matrix K_ij determines the presence or absence of edges between milestones. That is, an edge from milestone i to milestone j exists if the corresponding matrix entry is positive (K_ij > 0). But determining edge weights is not obvious from first sight since the flux information is for individual milestones, while the edge weights represent information between two connecting milestones. The following simple transformation converts vertex-based (milestone-based) weights to edge weights between pairs of milestones. Consider milestone pair i and j. The edge weight for edge (i, j) is w(i, j) = |q_j|, i.e., weight is equal to the flux associated with the second milestone.

On the path (series of connected edges) from start state s to end state t, the only milestone on the path whose flux we do not encounter as an edge weight on the path is the starting milestone, since we consider only the flux of the latter milestone, j, for every edge (i, j). This is fixed by adding an extra (dummy) milestone, s^′ before the first vertex, with an edge from s^′ to s whose weight is w(s′, s) = q_s, i.e., weight of the edge is equal to the flux of the starting milestone. The pathway calculations are then performed from s^′ to t instead of s to t.

Note that, for a fixed milestone j, all the edges leading to milestone j in such a graph will have the same weight. In other words, w(i, j) = |q_j|  ∀i, s.t.K_ij > 0. Hence, many edges have the same weight (same flux in this case) and this can result in degenerate paths.

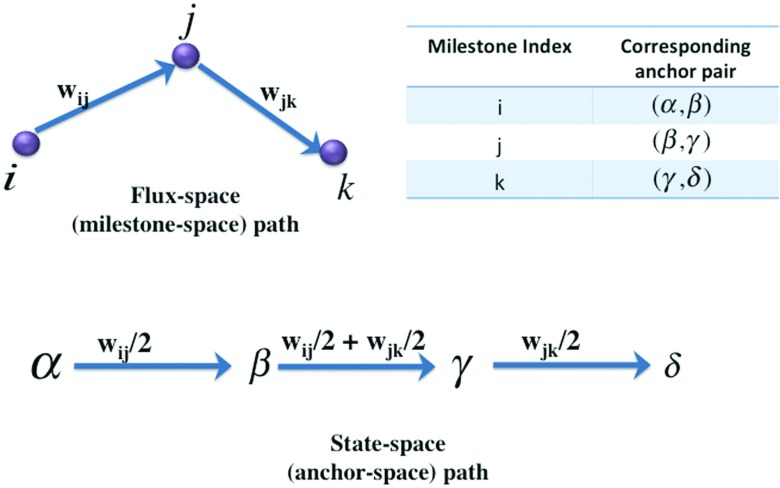
For visualization, we convert the resulting paths from milestone space to anchor space. For every milestone i in the milestone-based path, associated with anchors α and β, we add to the anchor-based path, an edge (α, β) between anchors α and β, with edge weight w(α, β) = q_i, i.e., edge weight is the flux associated with the corresponding milestone. Note that adjacent milestones always share an anchor. For example, path ⟨i, j, k⟩ in milestoning space corresponds to path ⟨α, β, γ, δ⟩ in anchor space, assuming milestone i corresponds to anchor pair (α, β), milestone j corresponds to anchor pair (β, γ), and milestone k corresponds to (γ, δ).

Flux-space (milestone-based) graph based on rate coefficients

Instead of solving Eq. 2 to get the flux, q, for a milestone, a simpler approach is to weigh the edges of the graph with rate coefficients or energy barriers.^{22, 26} This weighting is local and does not take into account global topology and explicit calculations of fluxes and rates. Local information can be misleading and point to less relevant portions of the graph. For example, using rate coefficients, it is possible to weigh some edges highly if they have a fast local transition. But at the same time, these edges may be off the main pathway receiving little reactive flux. Local information is easier to obtain than the global solution of rates, and use of rate coefficients or barrier height is common.

To compute the rate information from milestoning data, we note that in the Markovian limit, the rate coefficients of a Master equation between milestones can be computed directly using the transition matrix K and the vector τ, the average lifetimes of the milestones.³⁴ The rate coefficient for a transition between a milestone pair (i, j) (and the edge weight) is given by

$$w(i,j)=\frac{K_{ij}}{{\tau }_i}.$$ (3)

Converting paths based on rate coefficients in flux-space (milestone-space) to state-space (anchor-space) is more complex. The conversion is performed as follows. For every milestone i (a milestone between anchors α and β) on the path in flux-space, we add an edge in state-space between the anchors α and β. Note that each pair of milestones (i, j) is associated with three anchors, (α, β, γ) with milestone i associated with anchor pair (α, β) and milestone j associated with anchor pair (β, γ). Hence, edge weight between a pair of milestones (i, j) in the path in milestone space is shared equally between anchor-based edges (α, β) and (β, γ). Edge weights from flux-space to anchor-space are converted as shown in Figure 2. Note that each milestone edge contributes to weights on two anchor edges and each anchor edge can get a contribution to its weight from two milestone edges (except the edges at the ends of the path).

Figure 2.

Conversion of a flux-space path with milestones as vertices to a state-space path with the corresponding anchors as vertices. The table in the figure shows the mapping from milestone index to anchor index. The weight on each milestone edge contributes to weights on two anchor edges. Each anchor edge in the middle gets a contribution from two milestone edges.

DEFINITION OF PATHWAYS

Maximum weight path (MWP)

Given a start vertex, s, and end vertex, t, we seek a path between s and t in G (a series of connected edges leading from s to t), which has the maximum possible weight (of all paths between s and t) for the minimum weight edge on the path. In other words, consider all paths from s to t. Each of these paths has a bottleneck, that in the present discussion, is the edge with the minimum weight (EMW) along the path. The s-t path with an EMW, which is larger than the EMW of all other s-t paths, is the maximum weight path between s and t. This has also been referred to as a dominant reaction pathway in Transition Path Theory.¹

The edge weights in the graph can also be referred to as capacities, and the maximum weight path is known as the maximum capacity path in computer science.^{35, 36, 37, 38} When edges in the graph are thought of as allowing material flow through them, within certain capacities, it is easy to see that the overall capacity of a path is limited by the narrowest edge (bottleneck) in the path. Hence, the path with the widest bottleneck is the maximum capacity path or maximum weight path, in our terms. We provide in the Appendix, a concise list of relevant path definitions and alternate terms.

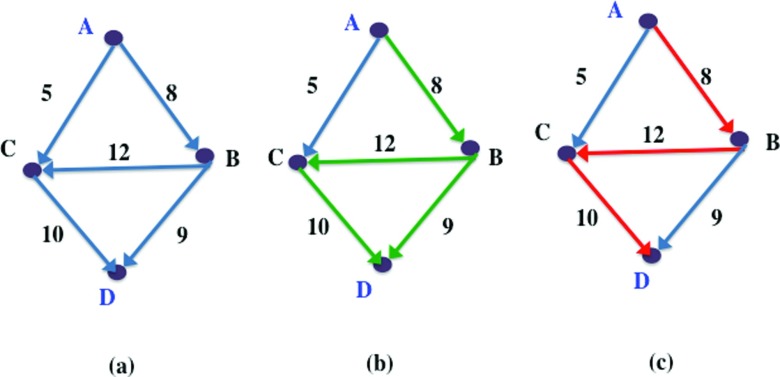
An example graph is illustrated in Figure 3a, which displays start and end vertices A and D, respectively, and capacities (edge weights) marked along the edges. A path from vertex A to vertex D, passing through vertices B and C is written as ⟨A, B, C, D⟩. There are multiple paths between A and D, ⟨A, B, D⟩, ⟨A, C, D⟩, and ⟨A, B, C, D⟩. Of these three paths, the maximum weight paths are ⟨A, B, D⟩ and ⟨A, B, C, D⟩, shown in green in Figure 3b, since the EMW on both these paths is the highest possible for an A to D path, and equal to 8, which is greater than 5, the minimum weight edge on path ⟨A, C, D⟩.

Figure 3.

(a) An example graph with multiple paths between vertices of interest, A and D. (b) Maximum weight paths (MWP) between A and D shown in green. (c) Global maximum weight path (GMWP) between A and D shown in red.

Global maximum weight path (GMWP)

The definition of maximum weight path stated above relies on just one edge in the path, i.e., the EMW. It is possible that more than one path will share the same EMW as shown in the above example. It is useful to have a unique solution to the path determination problem for ease of analysis and communication of the results. We, therefore, define the GMWP, which is an optimal maximum weight path that is as close as possible to being unique. The global maximum weight path is referred to as the representative dominant reaction pathway in Transition Path Theory.¹ Note, however, that the theories and the presentation of the graphs in Transition Path Theory are different from what we discuss here.

Let a path, m, be a maximum weight path between s and t. If for every pair of vertices on m, the subpath on m between those vertices is a maximum weight path, then m is a GMWP. The GMWP for a given pair of vertices is unique up to the degeneracy of paths branching from the same vertex in the graph. GMWP is analogous to a minimum energy path in continuous space, and the EMW is analogous to a transition state. In fact, the analogy between paths can be made stronger in the context of the maximum flux path for diffusive processes, that was introduced by Berkowitz and McCammon²⁹ in continuous space (with the assumption of a small normal cross section at every point along the path) and made into a useful algorithm for optimization of reaction coordinates in continuous space in Ref. 30 and more recently in Ref. 31. In previous studies, we defined a discrete version of the max flux path for a network as a GMWP.^{6, 8, 10}

In the example shown in Figure 3, both ⟨A, B, C, D⟩ and ⟨A, B, D⟩ are maximum weight paths, with the same EMW, (A, B). But the maximum weight path between B and D is ⟨B, C, D⟩ with minimum edge weight 10, and not ⟨B, D⟩, which has a minimum edge weight 9. Hence, the global maximum weight path between A and D, shown in red in Figure 3c, is ⟨A, B, C, D⟩ since all its subpaths are also maximum weight paths.

More formally, we define W(s, t, p), weight of a path, p, from vertex s to t, as

$$W(s,t,p)=\underset{(u,v)\in p}{min}w(u,v).$$ (4)

In Eq. 4, (u, v) represents an edge from vertex u to vertex v, and w(u, v) is the weight or capacity of the edge (u, v). Equation 4 states that the weight of a path p is equal to the weight of the EMW on the path. We define a path μ to be a maximum weight path between vertices s and t if μ satisfies Eq. 5:

$$W\left(s,t,\mu \right)\ge W\left(s,t,p\right)\forall p.$$ (5)

That is, the weight of path μ, from vertex s to t, is greater than the weight of all other paths p from s to t. Or, the EMW on path μ has a higher weight than the EMW of all other paths p. We also represent the EMW of the maximum weight path, μ, between s and t as M(s, t) ≡ W(s, t, μ).

We then define m as a GMWP from s to t, m = ⟨s, v₁,v₂….v_i…v_j…t⟩, if it satisfies

$$W\left({\nu }_i,{\nu }_j,m\right)\ge W\left({\nu }_i,{\nu }_j,p\right)\forall p\forall {\nu }_i,{\nu }_j\in m,i<j.$$ (6)

Equation 6 states that, for any two vertices, v_i and v_j on the path m, with v_i appearing before v_j on the path, the path between v_i and v_j that has the maximum weight, among all paths p from v_i to v_j, is exactly the path through m. We now develop the algorithms for obtaining the MWP and GMWP.

DETERMINATION OF MAXIMUM WEIGHT AND GLOBAL MAXIMUM WEIGHT PATHWAYS

Recursive Dijkstra's algorithm

Dijkstra's single source shortest path algorithm

Explanation and example.

We first describe Dijkstra's algorithm³⁹ which provides the base for efficient calculation of the GMWP using the Recursive Dijkstra's algorithm. Dijkstra's single-source shortest path algorithm finds the shortest paths and shortest path lengths from a single vertex of interest, s, to all other vertices, in a graph G, where a non-negative weight of an edge representing distance, d(u, v), is associated with each edge (u, v). The length of the path, L, is determined by the sum of the edge distances. The difference from our previous discussion is that here, we minimize the sum of edge distances on the path instead of maximizing the weight of the EMW. The algorithm finds at each step, the vertex, u, with the minimum path length from s and updates the shortest path lengths of the vertices neighboring u. In other words, suppose we know the shortest path length from s to u, and say u is connected to v through edge (u, v). We can then update the shortest path length from s to v, if the length obtained from the path passing through u is smaller than the current estimate of the shortest length to v.

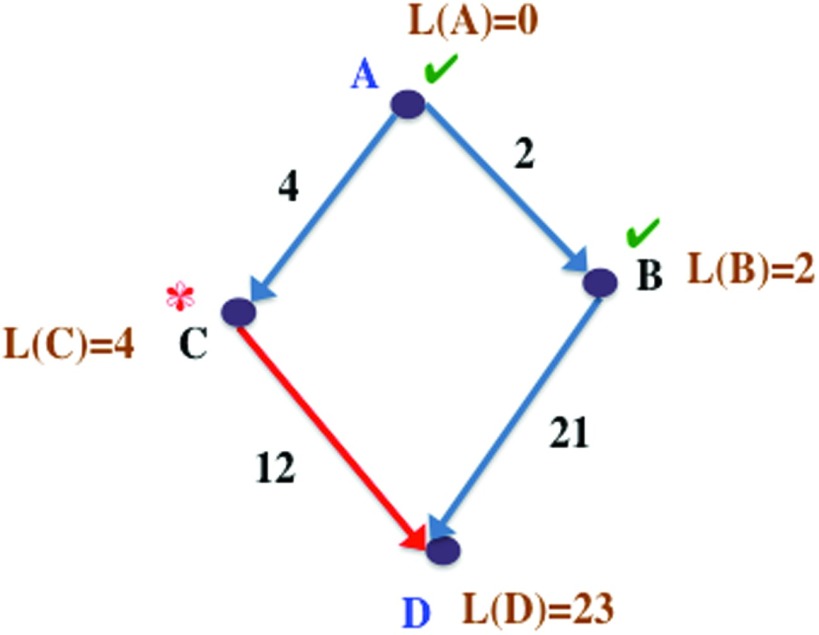
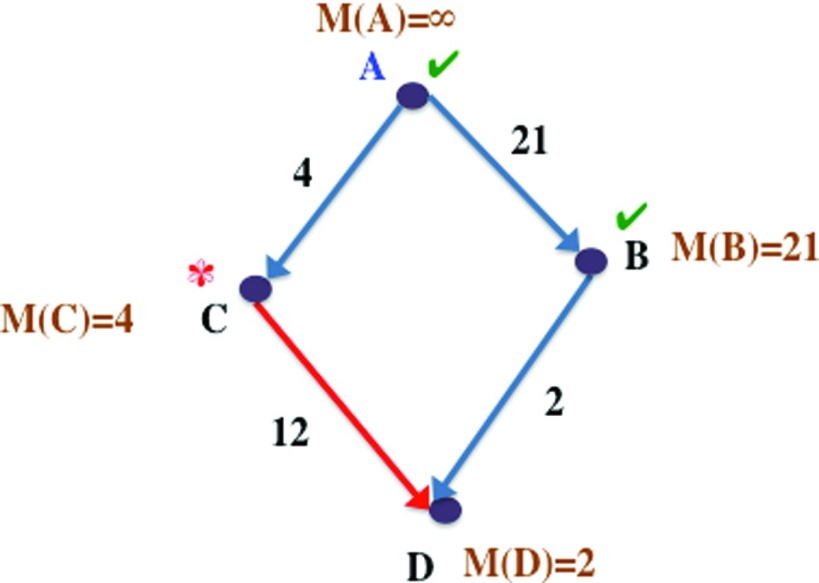
To illustrate this, consider the graph in Figure 4. We are interested in the shortest paths and lengths from vertex A to all other vertices. We first start at vertex A, and update the shortest (and only) path lengths of its neighbors, B and C, as their edge weights, 2 and 4, respectively. In the next step, we proceed to the (currently unexamined) vertex with the minimum path length to A, which is B, and update the shortest path lengths of the neighbors of B. D is a neighbor of B whose initial path length from A is unknown, and is now updated as L(B) + d(B, D) = 2 + 21 = 23, where L(B) is the shortest path length from A to B and d(B, D) is the distance of (B, D). The path lengths L, shown in the figure are the current estimates of the shortest path lengths from A to each vertex at this point in the algorithm. Vertices A and B have already been examined and the next vertex to be processed is vertex C, since it has the minimum length from A among the remaining vertices (D is the only other remaining vertex). D is a neighbor of C whose current best path length from A is 23, through the path ⟨A, B, D⟩. But the shortest path length to D through C is L(C) + d(C, D) = 4 + 12 = 16 (through the edge shown in red). Hence, we update the shortest path length from A to D, and its shortest path as ⟨A, C, D⟩.

Figure 4.

Example graph demonstrating Dijkstra's single-source shortest path algorithm. This is a snapshot during the optimization process and not the final result. We are calculating the shortest path lengths from A to all other vertices. Path lengths marked by L are current estimates of the shortest path length from vertex A to a given vertex. Vertices that have already been explored by the algorithm are marked with ✓ and current vertex being examined is marked with *.

Formally, if the current vertex being processed is u, and vertex v is a neighbor of u, Eq. 7 holds, where L(u) and L(v) represent the current known shortest path length from the source vertex s to vertices u and v, respectively, and d(u, v) is the edge weight distance on the edge (u, v). Note that since the lengths are always computed from the same source vertex s, we omit the explicit “s” in L (i.e., L(v) ≡ L(s, v) ∀v):

$$L\left(v\right)=\min \left(L\left(v\right),L\left(u\right)+d(u,v)\right).$$ (7)

Algorithm description.

Dijkstra's single-source shortest path algorithm is given in Table 1. Note that the algorithm finds the shortest path lengths from a given vertex s to all other vertices, even though we might be interested in the length to only one particular vertex. We maintain an array, L, which is indexed by vertex number and stores the current estimate of the shortest path length from vertex s to a given vertex. The list Adj (stands for adjacent) is our representation of the graph and stores the list of neighbor vertices for each vertex. This is similar to the neighbor list data structure used in molecular dynamics, and is an input to the algorithm. For example, for the graph in Figure 4, Adj(A) = [B, C] and Adj(B) = D.

Table 1.

Algorithm 1 - Dijkstra's algorithm to find the shortest path lengths from vertex s to all other vertices in graph G.

Procedure shortestPath(G,s)
For each v in G	1
L(v) = ∞	2
	3
L(s) = 0	4
Q = V  // Add all the vertices to Q	5
	6
while Q ≠ NULL	7
u = EXTRACT_MIN(Q)	8
for each v in Adj(u)	9
if L(v) > L(u) + d(u,v)   // L(v) = min(L(v),L(u)+d(u,v))	10
L(v) = L(u)+d(u,v)	11
return L	12

Further, the current set of vertices to be processed is maintained in the data structure Q, known as priority queue in literature on algorithms.⁴⁰ A priority queue maintains an ordering of the vertices such that the vertex with the minimum path length from s can be extracted efficiently. A simple implementation of the priority queue is an array with one element per vertex, storing path lengths from s for each vertex. In order to extract the vertex with the minimum length, one would have to do a linear search on this array. The most efficient implementation of the priority queue uses a data structure known as Fibonacci heap.^{40, 41} The procedure EXTRACT_MIN extracts from Q, at each call, the vertex with the minimum path length from s. Vertices that are extracted once are no longer considered again in the algorithm.

Initially, all path lengths are initialized to infinity (lines 1-2), the path length L(s) from the source vertex s to itself is set to 0 (line 4), and all vertices in the graph are added to the queue Q (line 5). The while loop (lines 7-11) executes until all vertices in Q have been examined. At each execution of the loop, a new vertex, u, is extracted from Q, which is the vertex with the minimum path length from s. The first vertex to be extracted is s, since only the path length to s has been set to 0 initially, while all other lengths are infinity. At each iteration of the loop, the path lengths for all the immediate neighbors of current vertex u are then “relaxed” using Eq. 7 (lines 9-11). When the algorithm terminates, all vertices have their shortest path lengths from s in array L (line 12). The proof of this algorithm is found in Ref. 40. The actual shortest path lengths can be obtained by maintaining a pointer to the previous vertex on the path, for each vertex.⁴⁰

Efficiency.

Consider an input graph with V vertices and E edges. The time complexity of Dijkstra's algorithm depends on the implementation of the EXTRACT_MIN operation. Consider the simple case where the graph is represented by a V × V matrix of edge weights, and priority queue Q is represented by an array. EXTRACT_MIN here takes O(V) time since a linear search is necessary to find the vertex with the minimum distance. Also, lines 9-11 inside the while loop take O(V) time per vertex since we are using a matrix representation of the graph, and the time to find the neighbors of a vertex is linear in the number of vertices. Since the algorithm makes V iterations through the while loop, one per vertex, and there are 2 O(V) operations inside the loop, per iteration, the time complexity of Dijkstra's algorithm is O(V · 2V) = O(V²) in the simple case.

The best-known theoretical time complexity of this algorithm is O(Vlog V + E) using Fibonacci heaps for efficiently implementing EXTRACT_MIN in O(log V) time and adjacency lists for efficiently finding the neighbors of a vertex in O(E) time across all vertices. The while loop again iterates V times, with one EXTRACT_MIN operation per iteration, giving a complexity of O(Vlog V). Each edge is examined and relaxed only once throughout the algorithm, hence the addition of E to the time complexity, which denotes the total complexity of lines 9-11 over the course of the algorithm. For sparse graphs (i.e., V ≈ E) the time complexity is O(Vlog V + V) = O(Vlog V) (ignoring the linear term). For dense graphs, (where E ≈ V²), the time complexity is O(Vlog V + V²) = O(V²) (considering only the term that dominates at large V).

Modification to Dijkstra's shortest path algorithm for maximum weight path calculation

Explanation and example.

We are given a graph G with vertex set V and edge set E, with edge weight w(u, v) associated with each edge (u, v). Dijkstra's shortest path algorithm, Algorithm 1, can be easily modified to obtain an algorithm to find a maximum weight path from a given vertex s to all other vertices. The two key points in the modification are that first, the minimization problem (shortest path length) in the previous case is converted to a maximization problem (maximum EMW or maximum capacity). Second, instead of using the length metric as the sum of distances in a path, we use the metric of the weight of the EMW along the path.

Similar to Algorithm 1, the algorithm for maximum weight path calculation finds at each step the vertex u with the maximum weight (or maximum EMW) from s and updates the maximum weights of the vertices neighboring u. In other words, suppose we know the maximum weight of u, and say u is connected to v through edge (u, v). We can then update the maximum weight from s to v, if the weight of the path to v passing through u is higher than the current estimate of the maximum weight from s to v.

An example is shown in Figure 5, where we are interested in the maximum weight paths to all vertices from vertex A. The weights of the MWPs, or the maximum weights from A to each vertex are stored in the vector M. Initially, all vertices have unknown maximum weights. We start at the source vertex A, and update the maximum weights of its neighbors B and C to their respective edge weights, 21 and 4, respectively. In the next step, we proceed to B, the (currently unexamined) vertex with the maximum weight from A. We update the weight of B's neighbor, D, to the minimum of M(B) and w(B, D), which represents the minimum edge weight on the path from A to D through B. D’s maximum weight path is thus updated to ⟨A, B, D⟩ with maximum weight 2. The weights, M, shown in the figure are the current estimates of the maximum weight for each vertex, at this point in the algorithm. Vertices A and B have already been examined and the next vertex to be processed is vertex C. C has one neighbor, D, whose current maximum weight from A is 2, through the path ⟨A, B, D⟩. However, the path from A to D through C has a higher weight of 4 (minimum of M(C) and w(C, D), which is 4), through the edge shown in red. Hence, we revise the maximum weight at D to 4 and change its maximum weight path to ⟨A, C, D⟩.

Figure 5.

Example graph demonstrating single-source maximum weight algorithm. This is a snapshot during the optimization process and not the final result. See text for more details. We are calculating the maximum weights from A to all other vertices. Weights marked by M are current estimates of the maximum weight from vertex A to a given vertex. Vertices that have already been explored by the algorithm are marked with ✓ and current vertex being examined is marked with *.

Instead of Eq. 7, we arrive at the equality in Eq. 8 for each vertex v adjacent to vertex u as before, where M(u) and M(v) represent the current known maximum weight from the source vertex to u and v, respectively, and w(u, v) is the weight of the u-v edge. Note that the sum in the inner bracket is changed to a minimum of two edges and the min condition in the outer bracket is changed to max condition:

$$M\left(v\right)=\max \left(M\left(v\right),\min \left(M\left(u\right),w\left(u,v\right)\right)\right).$$ (8)

Algorithm description.

The algorithm to calculate maximum weights in a directed graph is outlined in Table 2. The algorithm calculates maximum weight paths from a given source vertex s to all other vertices. Note that the variable M keeps track of the weight of the bottleneck edge or EMW, on the maximum weight path from s to a particular vertex. The arrays Q and Adj have the same meaning as in algorithm 1. The only difference here is that the EXTRACT_MAX operation is used instead of EXTRACT_MIN, in order to extract the current (unprocessed) vertex with the maximum weight from s. Hence, the queue Q needs to store the vertices ordered by their weight.

Table 2.

Algorithm 2 - Modified Dijkstra's algorithm for finding maximum weights and bottleneck (EMW) edges from s to all other vertices in a graph G. Refer to the algorithm description for the meaning of all variables.

Procedure maxWeightPath(G,s)
For each v in G	1
M(v) = −1	2
	3
M(s) = ∞	4
Q = V  // Add all the vertices in G	5
	6
while Q ≠ NULL	7
u = EXTRACT_MAX(Q)	8
for each v in Adj(u)	9
if M(v) < min(M(u),w(u,v))  // M(v) = max(M(v),min(M(u),w(u,v)))	10
M(v) = min(M(u),w(u,v))	11
	12
if M(u) < w(u,v)	13
bottleneck(v) = bottleneck(u)	14
Else	15
bottleneck(v) = (u,v)	16
return bottleneck, M	17

An extra array called bottleneck is used here to store the actual vertices corresponding to the EMW (bottleneck edge) in the maximum weight path for a given vertex. This data structure is not required for calculating maximum weight paths, but is required later on, when we use this maximum weight path algorithm to calculate the global maximum weight path.

Initially, all the vertex weights are initialized to −1 (lines 1-2). The algorithm starts by initializing the weight of s from itself to infinity (line 4) and adding all vertices to Q (line 5). At each execution of the while loop (lines 7-16), the vertex with the maximum weight to s is extracted from Q, and the weights of its neighbors are updated, similar to the shortest path case. An extra computation is the updating of the vertices in the EMW (bottleneck edge) along the path, for each vertex (lines 13-16). When the algorithm terminates, the maximum weight among all paths from s to a particular vertex, i, is retained in array element M[i] and the EMW for a particular vertex is in array bottleneck[i] (line 17). The proof of this algorithm is exactly analogous to Dijkstra's shortest path algorithm. To obtain the actual maximum weight paths (and not just the maximum weights), one can maintain a pointer to the previous vertex on the path, for each vertex. This pointer will be used to reconstruct the actual path.

Efficiency.

The time complexity of the modified Dijkstra algorithm exactly follows the time complexity of the Dijkstra algorithm outlined previously. With V vertices in a graph, its complexity is O(Vlog V) for sparse graphs (with priority queue implemented using Fibonacci heaps and graphs implemented as adjacency lists) and O(V²) for dense graphs and for simple implementations of sparse graphs (with priority queue implemented using arrays and graphs implemented as adjacency matrices).

Applicability.

We notice that the maximum weight path can be computed efficiently in O(Vlog V). This is a path from the start to end state containing the transition edge. The transition edge, EMW, is similar to the transition state of chemical reactions. It is a good descriptor for processes dominated by a single and large free energy barrier. In such a case, the location of the transition edge is much more critical than the rest of the GMWP and the algorithm outlined above can be used to compute this path efficiently. However, when the EMW is not dramatically lower in weight compared to other weights along the path, the location of the entire pathway matters, which brings us next to the calculation of GMWP.

Recursive Dijkstra's algorithm for GMWP calculation

Explanation and example.

The algorithm outlined in Table 2 (Algorithm 2) returns a single maximum weight path between s and t. For example, running Algorithm 2 on the graph in Figure 3 returns the path ⟨A, B, D⟩, and not ⟨A, B, C, D⟩ which is the GMWP for that graph. In general, Algorithm 2 is not guaranteed to return the GMWP, and is guaranteed to return only a single maximum weight path. We note that the GMWP is a special maximum weight path between s and t. It is a path where all subpaths between pairs of vertices on the same path are maximum weight paths. There can be multiple maximum weight paths, all of them having the same EMW, but the GMWP is unique up to the possible accidental degeneracy of edge weights of alternate paths.

We now introduce a new algorithm, the Recursive Dijkstra's algorithm, which uses the maximum weight path algorithm (Algorithm 2) repeatedly, to calculate the global maximum weight path. Given a pair of vertices s and t, we first use Algorithm 2, the maximum weight path algorithm, to get the EMW (u, v) between s and t. Note that Algorithm 2 returns the EMW from s to all other vertices, but we only need that piece of information for vertex t. Since w(u, v) is the maximum weight that can pass between s and t, (u, v) is an edge common to all maximum weight paths between s and t and hence it exists also in the GMWP between s and t. We then have two subpaths to be determined in the GMWP, ⟨s…u⟩ and ⟨v…t⟩. We use the above technique recursively, i.e., use Algorithm 2 again to find the EMW (bottleneck edge) edge between s and u, and once more to find the EMW between v and t. Thus, each call to Algorithm 2 provides us with one edge on the GMWP. Once all subpaths are uniquely determined, we have the complete GMWP between s and t.

To illustrate this algorithm, let us refer to the example graph in Figure 6. Suppose we are interested in the GMWP between vertices A and G. Algorithm 2 called on A returns (C, D) as the bottleneck edge between A and G. Hence, the current estimate of the maximum flux path is ⟨A…C, D…G⟩. Next we need to find the bottleneck edges between A and C, which Algorithm 2 returns as edge (A, C) itself, and between D and G, which Algorithm 2 returns as (E, G). Now the global maximum weight path is ⟨A, C, D…E, G⟩. Now we find the bottleneck edge between D and E which is edge (D, E). Thus, the global maximum weight path between A and G is ⟨A, C, D, E, G⟩, the path marked in red in Figure 6.

Figure 6.

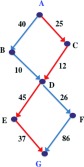
An example graph showing the GMWP between vertices A and G in red.

Algorithm description.

Algorithm 3, detailed in Table 3, relies on recursion. Given vertices s and t, it finds the global maximum weight path between them in a directed graph G. For the base case of a single vertex, i.e., s = t, the path returned by the algorithm is a trivial empty path (lines 2-3). Otherwise, Algorithm 2 is used to find the EMW (u, v) on a maximum weight path between s and t (lines 6-7). Note that Algorithm 2 computes the list of bottleneck edges for each vertex, from a given input vertex, in array bottleneck, and also the maximum weights for each vertex from the input vertex, in array M. Then Algorithm 3 is recursively called to find the global maximum weight paths between subpaths p₁ = ⟨s…u⟩ and p₂ = ⟨v…t⟩ (lines 10-11). Finally, the subpaths are concatenated to get the GMWP between s and t (line 14). We note that once an EMW (u, v) is known, between s and t, the remaining subpaths p₁ and p₂ of the GMWP can be computed independently, since the edges on the subpaths will always be of higher weight than the EMW.

Table 3.

Algorithm 3 – Recursive Dijkstra's algorithm to find the global maximum weight path between vertices s and t, in a directed graph, based on the modified Dijkstra algorithm for maximum weight paths. Refer to the Dijkstra's algorithm description for the meaning of variables.

Procedure GlobalMaxWeightPath(G,s,t)
// base case, return empty path	1
if s = t	2
return <>	3
	4
// call algorithm 2 to find bottleneck edge	5
(bottleneck,M) = MaxWeightPath(G,s)	6
(u,v) = bottleneck(t)	7
	8
// find subpaths by recursion	9
p1 = GlobalMaxWeightPath(G,s,u)	10
p2 = GlobalMaxWeightPath(G,v,t)	11
	12
// concatenate the subpaths	13
return ⟨p1, (u, v), p2⟩	14

If there are degenerate edges in the graph, there can be more than one GMWP, and hence it is recommended to compute the first path, remove the bottleneck edge, and recompute the path, repeating this procedure till no more unique paths are found. This process guarantees that we get a complete picture of the reaction pathways.

Efficiency.

Each call to Algorithm 2 fixes one edge on the GMWP. With V vertices and E edges in the graph, the maximum length of a GMWP is of the order of V, so Algorithm 2 is called a maximum of V times from Algorithm 3. Note that Algorithm 2 itself takes O(Vlog V) for sparse graphs (with priority queue implemented using Fibonacci heaps and graphs implemented as adjacency lists) and O(V²) for dense graphs and for simple implementations of sparse graphs. Hence, Algorithm 3 takes O(V²log V) time for sparse graphs and O(V³) for dense graphs and for simple implementations of sparse graphs.

Optimization.

We note that we are doing some extra computations in Algorithm 3 that can be avoided. For example, we first call Algorithm 2 on the source vertex, s, to get the EMW (bottleneck) of the destination vertex t from s. Then while computing the subpath from s to u, in the recursive step, we again call Algorithm 2 on s to get the EMW of u from s. But, Algorithm 2 calculates the EMWs for all vertices from s, and not just for one particular destination vertex, t. Hence, we can just run Algorithm 2 once on each vertex, and store the EMWs of all other vertices from this vertex. This can be done by making bottleneck a 2D array. For instance, bottleneck(i,j) will give the EMW for the maximum weight path from vertex i to vertex j. Each time we need the EMW from Algorithm 2 between two vertices i and j, we can check whether Algorithm 2 has been already computed on vertex i. We only run Algorithm 2 when it has not been run on i, otherwise we get the information from the lookup table bottleneck.

We note that the optimized procedure does not improve our bounds on the asymptotic time complexities outlined in Sec. 5A3c. The asymptotic complexities are worst-case complexities. In the worst case, the EMW between two vertices is always the first edge on the path between the two, in which case Algorithm 2 needs to be run on every vertex in the GMWP and optimization cannot be performed. Nevertheless, the optimization improves the runtime in the average case, and is useful in practice.

Comparison to edge-elimination based MaxFlux algorithm

Explanation and example

Previously, an approximate algorithm has been described for finding the maximum flux path in continuous space.^{29, 30, 31} The assumption made in those studies is of a narrow tube of trajectories leading from reactants to products. Here, we consider an exact solution for the maximum flux path on a discrete network. This pathway has been used in the context of directional milestoning^{3, 6, 8, 10} and an alternative algorithm for finding these pathways was proposed in Ref. 6. Here, we call it the “Edge-Elimination” Maxflux algorithm. The steps in the algorithm are

• 1.Sort all the edges in the graph G based on their weight, into a list, L_w.
• 2.Initialize path p, between vertices s and t to an empty path. p on exit will be the GMWP.
• 3.
  While the vertices s and t are not connected in p, repeat the following steps.

  • a.
    Proceed to the next edge, (u, v) in L_w with the smallest weight.
  • b.
    Check if removal of (u, v) from G disconnects s from t.

    • i.
      If it does, then this is an edge that is critical to the GMWP, and hence it is added to p.
    • ii.
      If not, then simply remove this edge from G, and proceed to the next edge in L_w.

For the example in Figure 6, the sorted edge list is [(B, D), (C, D), (A, C), (D, F), (E, G), (A, B), (D, E), (F, G)] and we require the GMWP between A and G. We first consider removing (B, D) and see that A is still connected to G through ⟨A, C, D, E, G⟩ so (B, D) is removed. Next, we consider removing (C, D) and see that it disconnects A from G, and hence we add it to p. Same is the case for (A, C) which is added to p. We then proceed to (D, F) and notice that its removal retains connectivity through ⟨A, C, D, E, G⟩, so (D, F) is removed from the graph. The next edge is (E, G) whose removal disconnects A from G, and is hence added to p. Removal of the next edge (A, B) retains connectivity between A and G, hence the edge is removed from the graph. The next edge is (D, E) whose removal disconnects A from G, hence the edge is added to p. At this point, the path p is complete as A is connected to G in the path, and the algorithm terminates here, with GMWP ⟨A, C, D, E, G⟩.

Efficiency

Given a graph with E edges and V vertices, the time for sorting the edges is O(Elog E). Checking if two vertices are connected in a graph can be done efficiently using graph traversal algorithms like breadth first search or depth first search (Cormen et al.⁴⁰), which take O(V + E), i.e., linear time if we use a data structure called adjacency list (similar to the neighbor list) to store the edges of each vertex. If the graph is represented using a V × V matrix, then breadth first search or depth first search takes O(V²) time. The maximum number of iterations we need is E (one per edge), so the time complexity becomes O(Elog E + EV²) when using a matrix representation of the graph and O(Elog E + E(V + E)) when using the adjacency list representation. Note that the Elog E factor comes from the complexity of edge sorting and V² or V + E factors come from the breadth first/depth first traversals to check for connectedness of vertices at each iteration.

For dense graphs, where E ≈ V², both the matrix and list representations yield a complexity of O(V⁴), whereas for sparse graphs where E ≈ V, the matrix representation takes O(V³) while the list representation is faster and takes O(V²).

Comparison to the edge-list bisection algorithm

The approach for determining MWP and GMWP paths that we discussed is closely related to that of Metzner et al.¹ In Ref. 1 the network was based on Transition Path Theory (TPT) while our approaches use the formulation of Milestoning. The TPT algorithm was used to investigate complex folding transitions⁴² and it is as able as the Directional Milestoning approach to pinpoint complex molecular mechanisms and to provide quantitative kinetic and thermodynamic data. Here, we call the path algorithm given in Ref. 1 as the Edge-List Bisection algorithm and describe it below.

Explanation and example

The overall approach used to identify Global Maximum Weight Paths in this algorithm, is identical to the Recursive Dijkstra's algorithm for GMWP calculation (Algorithm 3 in this paper). That means, a bottleneck edge (u, v) is computed between vertices s and t first, and then the path between ⟨s…u⟩ and ⟨v…t⟩ is recursively identified. But the underlying algorithm to calculate a bottleneck each time (which in the Recursive Dijkstra's algorithm is a modification of the Dijkstra's algorithm) is a variant of the Edge-Elimination algorithm. The following steps describe how the bottleneck edge between two vertices s and t is selected each time.

• 1.Sort all the edges in the graph G based on their weight, into a list, L_w = [e₁, e₂….e_|E|]. The edges are stored in ascending order as in the Edge-Elimination algorithm.
• 2.If the last edge in L_w, e_|E| is an edge between s and t, return the last edge as the bottleneck edge.
• 3.Go to the edge in the middle of the current sorted list, e_m. Let the weight of this edge be w_m.
• 4.
  • (i)
    If s and t are still connected by removing all edges with weight less than w_m, then the bottleneck edge has a weight higher than w_m. Hence, it is located in the second half of the edge list between e_{m + 1}….e_|E|, which is the part of the edge list we need to explore next.
  • (ii)
    Else if removing edges with weight less than w_m results in s being disconnected from t, then the bottleneck has a weight lower than w_m and is located in the first half of the edge list between e₁….e_m.
• 5.Note that we obtain a sublist to be explored from step 4 and that this sublist is half the size of the original sorted list. We then repeat steps 3 and 4, exploring the middle edge of the new sublist and using it to halve the edge list each time. These steps are repeated till the final edge list consists of just one edge. This edge is the bottleneck edge returned by the algorithm.

Unlike the Edge-Elimination algorithm, where we go through each edge in the edge list one by one, here we traverse the edge-list in a bisected search manner, bisecting the edge list till we are left with a single edge. The overall algorithm runs in an identical manner to the Recursive Dijkstra's algorithm in terms of identifying the bottlenecks and reconstructing the path. So here we will just describe the trace of the algorithm for finding the first bottleneck in Figure 6.

The sorted edge list for the graph is [(B, D), (C, D), (A, C), (D, F), (E, G), (A, B), (D, E), (F, G)], out of which we need the bottleneck edge between A and G. Since the last edge in the list is not between A and G, we traverse to the middle of the edge list, which has edge (D, F) of weight 26. Removing all edges with weight less than 26, we note that A and G get disconnected. Hence, the bottleneck is in the first part of the list, i.e., in [(B, D), (C, D), (A, C), (D, F)]. The middle edge in this list is (C, D) of weight 12. Removing all edges with weight less than (not less than equal to) 12, we note that the graph is still connected between A and G. Hence, the list is further reduced to [(C, D), (A, C), (D, F)]. In the next step, we note that the middle edge (A, C) has a weight of 25. Removing all edges with weight lower than 25 disconnects A from G, hence we are left with a single edge in our list (C, D), which is the bottleneck.

In contrast to the previous two algorithms the Edge-List bisection algorithm makes the following assumptions: (i) the graph has no edge degeneracy, (ii) the set of all the MWPs includes all the edges of the graphs, and (iii) there are no cycles in the graph. Assumption (ii) requires, for example, that the graph does not include dead-end branches. Hence, some pre-processing of the graphs may be required.

Efficiency

As in the Edge-Elimination algorithm, sorting the edges takes O(Elog E) time for a graph with E edges and V vertices. To find a single bottleneck edge, the bisected edge list search examines O(log E) edges. And for each edge, one connectivity test is performed using Breadth-first Search or Depth-First Search, which takes O(V + E) or O(V²) depending on whether the graph representation is in terms of the adjacency list or adjacency matrix. Hence, the search for a single bottleneck edge takes O(V²log E) for the matrix representation, and O(Elog E) for the list representation. Since there are atmost O(V) edges on the GMWP, the overall algorithm takes O(V³log E) for the matrix representation and O(VElog E) for the list representation. Substituting E ≈ V² for dense networks and E ≈ V for sparse networks, the complexity is O(V³log V) for all networks in the matrix representation and for dense matrices in the list representation, and becomes O(V²log V) for sparse networks in the list representation.

Note that the paths returned by all three algorithms above are identical.

RESULTS AND DISCUSSION

We considered two systems to demonstrate the paths: unfolding of a helix under stress and membrane permeation of DOPC. Below is a description of the systems and the paths we obtained in both.

Helix unfolding under stress

Alpha helices are prime secondary structure elements that are found in proteins. Their stability and folding/unfolding pathways are, therefore, of considerable interest. A recent study^{8, 10} simulated a single molecule experiment of a ∼100 amino acid helix, in which both terminals were pulled by an external force and unfolding events were recorded. For each of 10 load levels from 0 pN to 100 pN, transition kernels, K, and milestone lifetimes, τ, were sampled. A probabilistic model for the transition kernel was developed, which allows the sampling of the kernel from a model distribution. Over 500 kernel matrices were sampled, providing 500 alternative networks for each load level. We calculated paths (GMWP) on the average kernel matrices, lifetimes, and fluxes, averaged over the 500 samples for each load level.

In this system the number of anchors was 14. The maximum possible number of milestones is 14 × (14-1) = 182. For the different load levels, the number of milestones visited were 129, 125, and 109 for 0, 30, and 70 pN, respectively. For path calculations, the starting anchor corresponded to the state alpha3, the fully folded α-helix state, with three hydrogen bonds wrapping an amino acid. The ending anchor corresponded to the unfolded state of the helix, in which no hydrogen bonds are formed and the dihedral angle is in the extended chain configuration, with psi > 90.

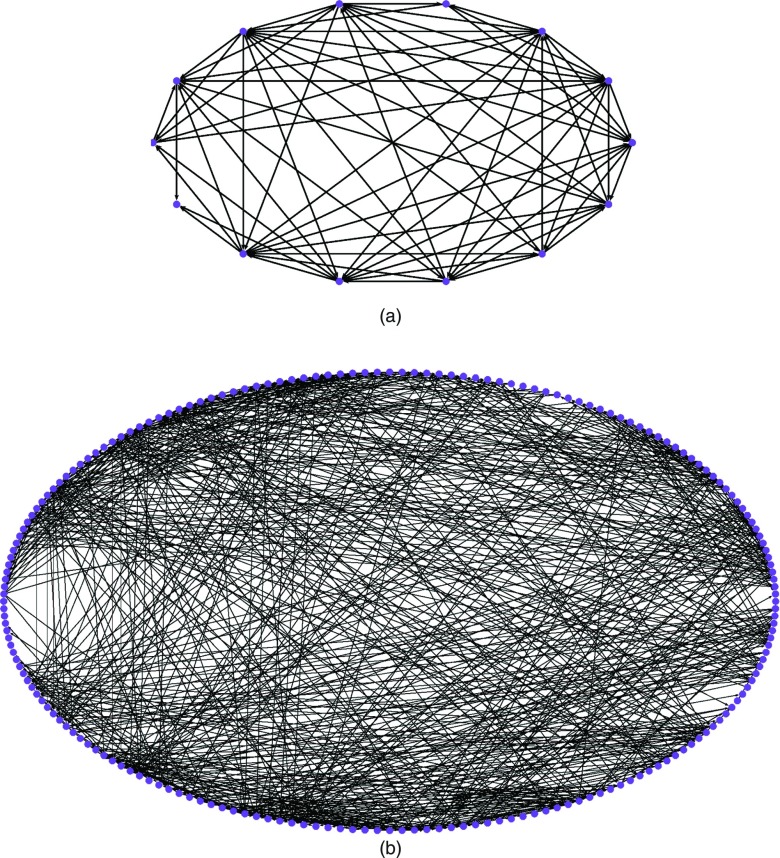
In milestone space, these start and end anchors corresponded to one start milestone and four end milestones, since there were multiple ways to reach the last anchor (unfolded state). All paths were converted to state-space or anchor space for visualization. Figure 7 demonstrates the complexity of the state-space and flux-space networks for the intermediate load level of 30 pN.

Figure 7.

Visualization of average networks for helix unfolding under a load level 30 pN in (a) state-space, with 14 anchors (vertices). (b) flux-space with 125 milestones (vertices). The graphs are to illustrate the complexity of analysis and were prepared with the Pajek program.⁴³

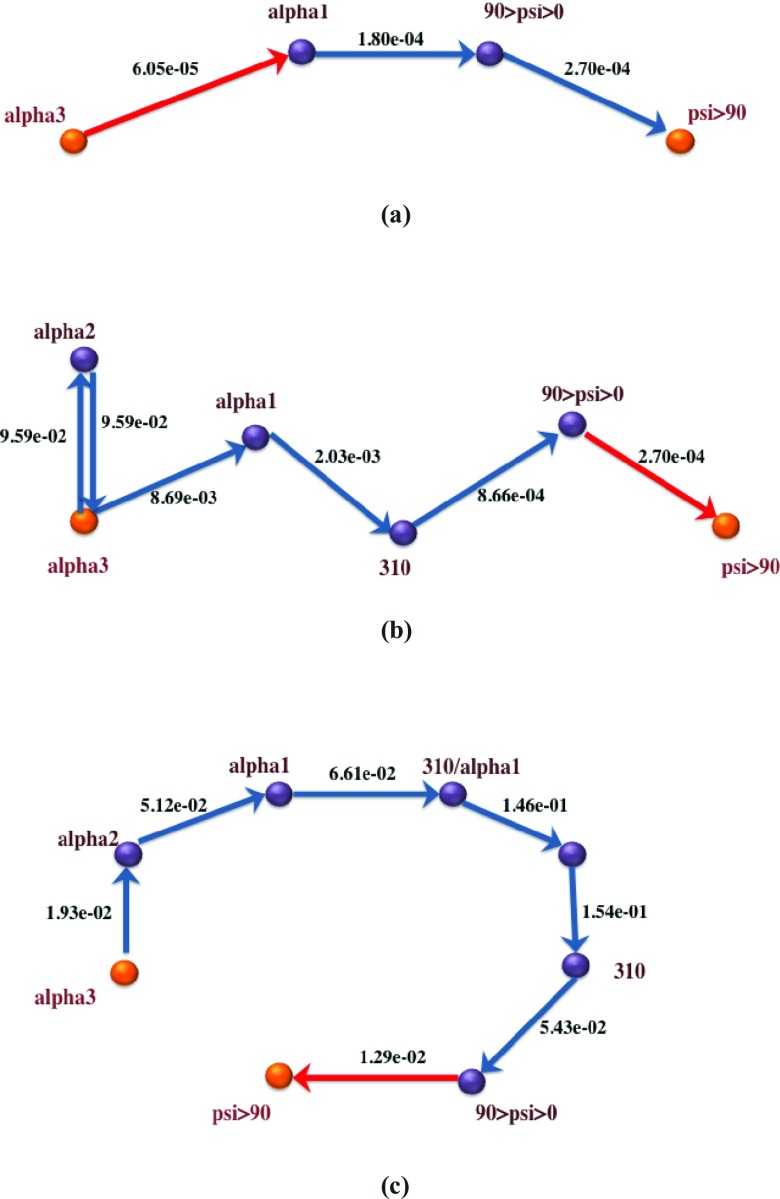
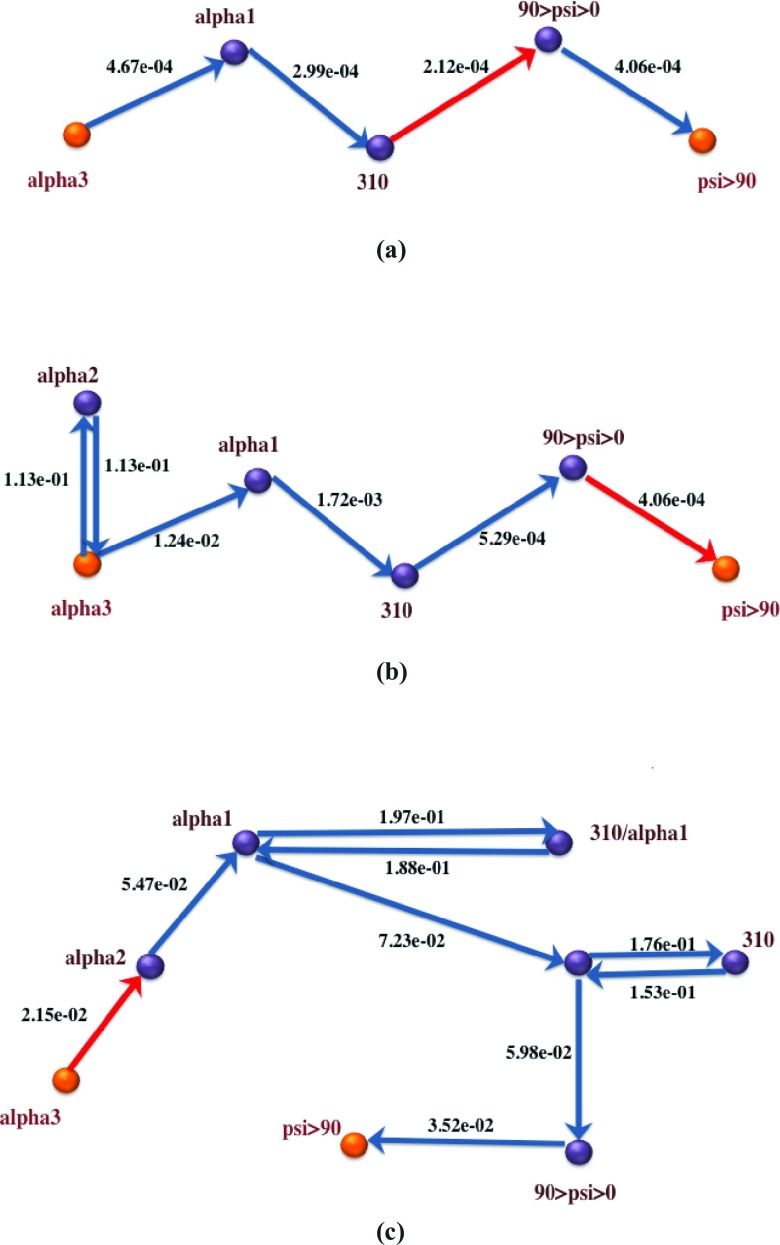
Figures 8910 depict the global maximum weight pathways obtained from the three different graph representations: state-space graph, flux-space graph with flux-based weights, and flux-space graph with rate coefficients, for three different load levels: 0 pN, 30 pN, and 70 pN. Intermediate vertices on the paths represent partially folded states like alpha2 and alpha1 with 2 and 1 hydrogen bonds remaining, respectively, misfolded states like 310, representing the 3₁₀ helix, or nearly unfolded states, like 90 < psi < 0.

Figure 8.

Global maximum weight paths using three different graph representations for helix unfolding under 0pN stress. Bottleneck edges (EMW) are in red. Note that the second path, represented in anchor space, has a loop to from alpha3 to alpha2. Directional Milestoning representation allows for such choices since entry milestones (interfaces) can be different for the same state. The source of the difference between the state-based and flux-based graph is the finer (more detailed) description of the system in the flux-based graph. (a) OpN, Path from state-space graph based on flux-based edge weights; (b) OpN, Path from flux-space graph based on flux-based edge wights; (c) OpN, Path from flux-space graph based on rate coefficients.

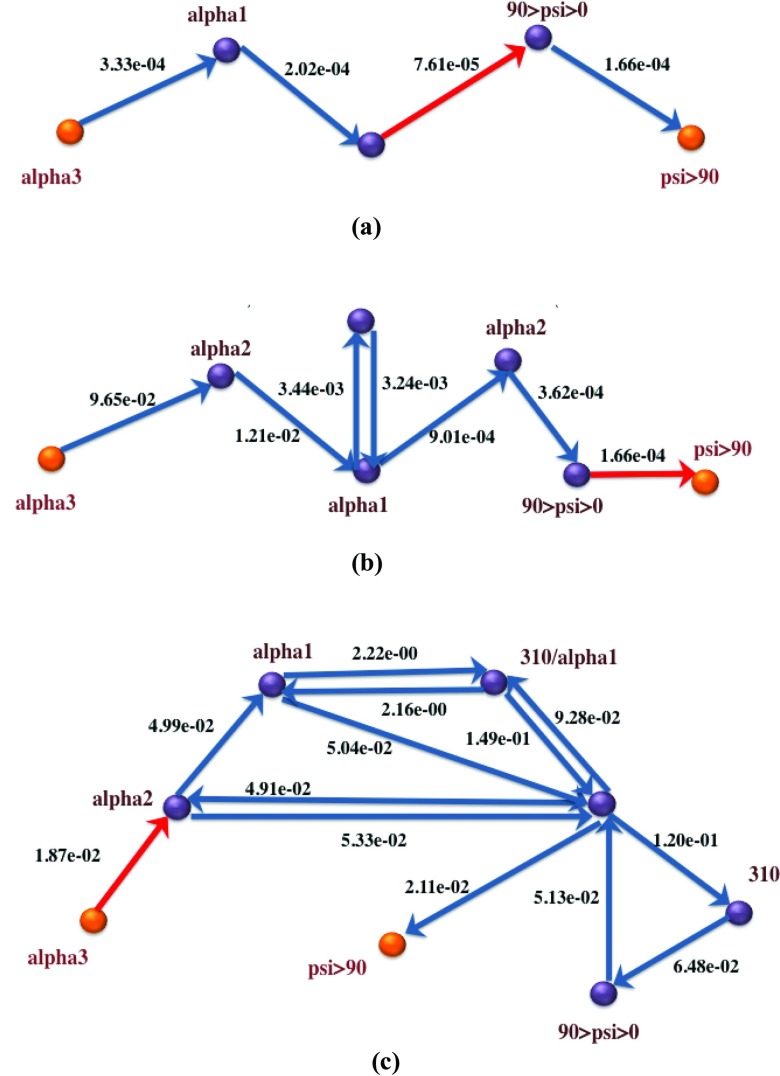
Figure 9.

Global maximum weight paths using three different graph representations for helix unfolding under 30 pN stress. Bottleneck edges (EMW) are in red. (a) 30pN, Path from state-space graph based on flux-based edge weights; (b) 30pN, Path from flux-space graph based on flux-based edge weights; (c) 30pN, Path from flux-space graph based on rate coefficients.

Figure 10.

Global maximum weight paths using three different graph representations for helix unfolding under 70 pN stress. Bottleneck edges (EMW) are in red. (a) 70pN, Path from state-space graph based on flux-based edge weights; (b) 70pN, Path from flux-space graph based on flux-based edge weights; (c) 70pN, Path from flux-space graph based on rate coefficients.

When examining the state-based pathways, we notice that the position of the EMW or the transition state is different for different loads. For example, the state-based path for 0 pN path is direct and moves from the three-hydrogen-bond state to a state with one hydrogen bond and then to a state with positive backbone dihedral, psi. Finally, the system transitions to the unfolded state, where no hydrogen bonds are present. The bottleneck is at the break of the first two hydrogen bonds. A similar path is followed at 30 pN load, with the addition of one more (unlabeled) intermediate state with no hydrogen bonds. The dihedral angles of the unlabeled state are still in the folded region. Interestingly, the bottleneck at 30 pN is different from the 0 pN case, is shifted to a backbone conformational transition, and is not at the dissociation of a hydrogen bond. The 70 pN path illustrates another twist in which a new intermediate hydrogen bond (3₁₀) is formed before the system unfolds. The bottleneck is shifted to the last state in which the psi dihedral completes the rotation to domains greater than 90°. This is consistent with the application of additional load, since the 3₁₀ helix is more extended than the α helix and it is preferred at the high load limit, compared to the random chain less-extended conformation (the unlabeled state) of the 30 pN load.

The most complex paths are obtained at intermediate load level (30 pN). One can understand this by considering the two limits of low and high loads. At low (zero) loads the system does not have sufficient energy to explore the energy landscape and is restricted to a few dominant and low energy reaction coordinates. At high load level, the large external force dominates the energy landscape. The external force washes out many of the molecular details and induces the system to unfold in more direct and straightforward pathways. At the intermediate load level, the external force is sufficient to reduce the free energy barrier to the extent that new states can be found and explored but it is not too strong to overwhelm the features of the energy landscape. This is also consistent with the earlier observation^{8, 10} that the mean first passage time through the system is longer for intermediate load levels.

It is also of interest to explore different graph resolutions. The state-space graph is of the lowest resolution and the paths from this graph have the lowest level of details. A higher level of resolution is provided by the milestone-space graph. Milestones are the interfaces between states and obviously there are more interfaces than states. The milestone representation is the most natural for the authors to use since it provides an exact solution for the kinetics, in the framework of the Milestoning theory. The last representation, which is based on rate coefficients between milestones, is not only more complex but also approximate. The significant differences from the kinetically exact MaxFlux path suggest that it is mechanistically incorrect.

Membrane permeation of DOPC

Phospholipid membranes such as DOPC efficiently separate two aqueous solutions and support concentration gradients of different solutes that are necessary for life processes. However, the membrane barrier is not absolute and passive permeation is possible. It is an intriguing question whether basic ingredients of biological macromolecules (such as amino acids and sugar molecules) can permeate through membranes without the active assistance of transporters. Recently, an investigation was initiated to accurately simulate the permeation of complex molecules through membranes.^{44, 45} In particular, the translocation of a blocked tryptophan was simulated with Milestoning. A network was built that takes into account not only the center of mass of the permeant but also the orientation of the molecule with respect to the membrane axis. The number of anchors here was 217 and the number of milestones was 1204. The start anchor (and milestone) corresponded to the permeant at the left of the membrane and the end anchor (and milestone) corresponded to the permeant in solution at the right side of the membrane.

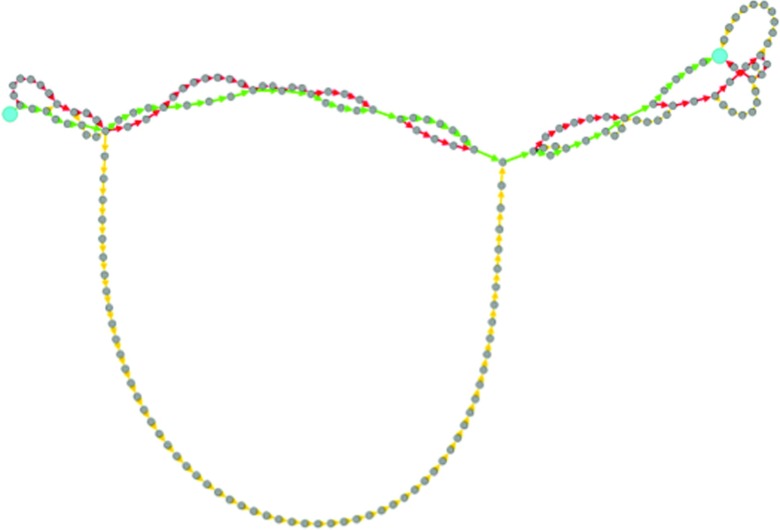
The global maximum weight paths obtained using various graph representations for this system are shown in Figure 11. We note that the paths based on fluxes, in both the flux-space and state-space graphs, are quite similar. But the path based on local rate coefficients is quite different and samples a different part of the conformation space. This difference is emphasized in Figure 12, which is a force-directed graph (Gephi⁴⁶) that shows that the paths based on fluxes share several milestones, while the path based on rate coefficient is dissimilar. Similar to the helix unfolding case, the results suggest that mechanisms extracted from networks based on local kinetic information can be different from mechanisms based on the exact kinetics. Nevertheless, the alternative path based on local kinetics is found at somewhat lower scoring GMWPs of flux-based graphs. Hence, it is still a sensible choice with acceptable weight. We found this path as follows: We remove the EMW (bottleneck) of the first GMWP and re-compute the GMWP of the modified graph to yield the next best scoring path. This process is iterated to find a sequence of high scoring pathways. For dense and degenerate graphs, multiple pathways of similar scores can be obtained, and this may be the case also here. All the pathways pass over free energy barriers of similar absolute heights. The path based on rate coefficients is less “committed” to the low free energy minima shown in gray on the upper part of the left side of the plot and the lower part of the right side of the plot in Figure 11.

Figure 11.

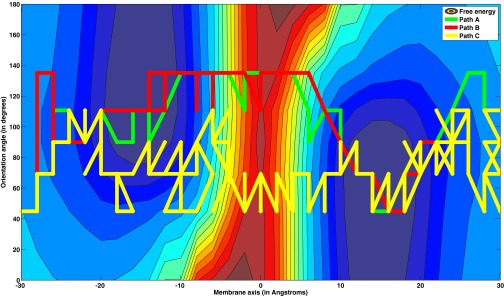
Global maximum weight paths using three different graph representations for membrane permeation of DOPC. The path descriptions are as follows: Path A: Path obtained from the state-space graph with flux-based weights. Path B: obtained from the flux-space graph with flux-based weights. Path C: obtained from the flux-space graph weighted by local rate coefficients.

Figure 12.

Visualization of proximity of paths shown in Figure 11. All the nodes visited by the three paths are collected into a single network. The position of the nodes in the network are optimized using force model proposed in Gephi.⁴⁶ Connected nodes attract each other, while nodes that are far repel each other. The larger cyan nodes are the initial and final milestones. The path descriptions are as follows: Path A (green): Path obtained from the state-space graph with flux-based weights. Path B (red): obtained from the flux-space graph with flux-based weights. Path C (yellow): obtained from the flux-space graph weighted by local rate coefficients. This representation emphasizes similarities between paths A and B (because they both share several milestones), and their difference with respect to path C.

Analysis of runtimes and benchmarks

Table 4 summarizes the worst-case time complexities for dense and sparse graphs for various implementations of the path algorithms. These factors have been derived in detail, under the Efficiency section of each algorithm. Note that the Edge-Elimination algorithm shows a marked difference in complexity between dense and sparse graphs. It is particularly inefficient for dense graphs and works best for sparse graphs when the number of edges is small. For dense graphs, the Recursive Dijkstra's algorithm shows the most favorable asymptotic time complexity. The Edge-List Bisection algorithm possesses complexities comparable to that of the Recursive Dijkstra's algorithm. Generally, state-space graphs are dense while flux-space graphs are usually sparse.

Table 4.

Summary of asymptotic time complexities using various algorithms for dense (E ≈ V²) and sparse (E ≈ V) graphs. G: List means the graph is implemented using adjacency lists, G: Matrix means the graph is implemented using adjacency matrices, Q: Array means the priority queue in Dijkstra's algorithm is implemented using arrays and Q: Heap means the priority queue is implemented using Fibonacci heaps. These scaling factors have been derived in the Efficiency section of each algorithm.

Dense graphs
Recursive Dijkstra		Edge-List Bisection		Edge Elimination
G: List Q: Heap	G: Matrix Q: Array	G: List	G: Matrix	G: List	G: Matrix
O(V3)	O(V3)	O(V3log V)	O(V3log V)	O(V4)	O(V4)
Sparse graphs
Recursive Dijkstra		Edge-List Bisection		Edge Elimination
G: List Q: Heap	G: Matrix Q: Array	G: List	G:Matrix	G: List	G:Matrix
O(V2log V)	O(V3)	O(V2log V)	O(V3log V)	O(V2)	O(V3)

To obtain a consistent and unbiased measure of the algorithm efficiency in practice, we recorded the runtimes of the algorithms on random graphs. We generated several sparse and dense random graphs and runtimes were estimated by averaging the results over different random graphs and different start and end nodes. Simple implementations were used for both algorithms, i.e., graphs were implemented using matrices and queues were implemented using arrays, since the asymptotic complexity is about the same for the simple versus the more sophisticated implementations, for the algorithms considered. Table 5 shows the performance of the algorithms on random graphs. The Edge-Elimination algorithm is much slower than the other algorithms for all graph sizes, and its performance degrades significantly when transitioning from sparse to dense networks. The Recursive Dijkstra's algorithm, on the other hand, requires approximately the same order of magnitude of runtimes in both dense and sparse cases. The runtimes of the Edge-list Bisection algorithm are comparable to that of the Recursive Dijkstra's algorithm. We note that the Edge-List Bisection algorithm is most efficient for sparse graphs while the Recursive Dijkstra algorithm is most efficient for dense graphs.

Table 5.

Average runtimes in milliseconds for random graphs with 100, 1000, and 10 000 vertices, for the Recursive Dijkstra's, Edge-List Bisection, and Edge-Elimination algorithm. Runtimes were calculated on a single core of an 8 core Linux Intel Xeon X5460 processor with clock speed of 3.16 GHz and 16 GB memory shared among 8 cores. Runtimes were not calculated for the Edge-Elimination algorithm for 10 000 vertices since the estimated runtime was too long. Also shown is the number of edges for each size of random graphs.

Dense graphs
Graph size (nodes)	Number of edges	Recursive Dijkstra's	Edge-List Bisection	Edge Elimination
100	9500	0.31	2.93	258.61
1000	600 000	98.70	404.06	1.56 × 106
10 000	60 000 000	49 045.3	117 248.62	…
Sparse graphs
Graph size (nodes)	Number of edges	Recursive Dijkstra's	Edge-List Bisection	Edge Elimination
100	1000	0.23	0.54	13.83
1000	10 000	47.81	36.18	7554.45
10 000	100 000	11 188.2	7228.17	…

We see that though the worst-case complexities of the algorithms are not very different, there is a wide difference in runtimes on the benchmark. Let us consider, for example, the asymptotic complexities of the algorithms in Table 4 for sparse graphs using matrix representations of graph. For the Edge-Elimination algorithm, one needs to traverse through the list of sorted edges, checking for each edge, if its removal disconnects the two end vertices (an operation that takes O(V²) in this case), terminating only when the set of edges on the path is complete. In practice, this leads to a large number of edges being explored before we recover the complete path. So the average time complexity is closer to the worst-case time complexity for the Edge-Elimination algorithm.

In contrast, for the Recursive Dijkstra's algorithm and the Edge-list Bisection algorithm, we run the underlying bottleneck identification algorithms (which are the modified Dijkstra's algorithm which takes O(V²), or the bisection-based algorithm which takes O(V²log V), respectively, in this case) only once per edge in the global maximum weight path. This means we only need to run these underlying bottleneck identification algorithms, E_p times, where E_p is the number of edges on the global maximum weight path. In practice, E_p can be far less than the number of vertices, which in turn is much less than the number of edges. Hence, the average runtime for these algorithms can be much smaller than the time predicted by the asymptotic analysis and is smaller than the time taken by Edge-Elimination.

CONCLUSIONS

In the present paper we discussed different network representations for molecular kinetics and the qualitative analysis of these networks. Network representations are emerging from a number of enhanced sampling techniques for molecular kinetics using methods like Milestoning, TPT, MSM, and more. The push to longer time scales is obtained by calculation of local kinetic information by MD (e.g., local rate coefficients) and using the data in coarser equations such as Master Equation or Milestoning. Networks offer a natural way for coarse-graining without losing too much in spatial resolution, while being able to push temporal scales to significantly longer domains (from nanoseconds to hours⁴⁵). We expect the use of networks as well as the complexity of the networks (number of edges and vertices) to increase significantly in the future. This increase in network complexity is necessary to capture more details of chemical processes, allowing for the interactions of multiple coarse variables and going beyond one-dimensional reaction coordinates. However, the complexity of networks makes them harder to interpret and obtain qualitative insight, compared to lower dimensionality modeling. To obtain such qualitative interpretation, we identify in the network, dominant edges and paths that carry significant fluxes or trajectories and hence are more important than others. Maximum flux or global maximum weight pathways are discussed at length in the present paper as a natural choice for these analyses. Recursive Dijkstra's and Edge-List Bisection algorithms are proposed as efficient and scalable approaches to identify them. We also discussed the interpretation of molecular mechanisms using networks for analysis. We argue that using local kinetic information (such as rate coefficients) instead of exact solution of the kinetic equations may lead to incorrect dominant pathways.

Code for calculating optimal pathways in networks is available as part of the analysis module of the molecular dynamics program MOIL.⁴⁷ It can be downloaded from http://clsb.ices.utexas.edu/web/moil.html

APPENDIX: DEFINITIONS OF TERMS

The following is a list of definitions occurring in this paper. Alternate terms for the same concept are given in brackets.

• 1.Graph (Network) G: Coarse-grained representation of the system defined by a set of nodes and directed edges connecting the nodes.
• 2.Node (Vertex) V: Discrete regions in the network connected by edges. These may represent volumes of phase space or milestones.
• 3.Edge E: A directed connection between two nodes in a graph. Directionality implies that an edge from vertex p to vertex q is not the same as an edge from vertex q to vertex p.
• 4.Edge weight (capacity) w: A real number associated with every edge. It may represent different physical quantities, e.g., flux, distance between vertices, or rates of transition between vertices.
• 5.Distance d: The distance between two vertices, used to optimize path length. Serves in the same capacity as edge weight.
• 6.State-space graph (anchor-space graph): Graph with nodes as anchors or regions in phase space, and edges as transitions between anchors.
• 7.Flux-space graph (milestone-space graph): Graph with nodes as milestones or interfaces, and edges as transitions between milestones.
• 8.Start and end vertex (Emitting and absorbing states) s and t: In a chemical context those are the reactant and product state of the system, respectively.
• 9.Path: Series of connected edges in a graph leading from the start vertex to the end vertex.
• 10.Path Length L: Sum of all distances along a path. A scalar function used in the optimization of path length between vertices.
• 11.Maximum weight path (Maximum capacity path, Dominant Reaction Pathway) M: Among all possible paths between a pair of vertices, it is the path with the maximum possible weight on the edge with the smallest weight on the path. It is not unique for a pair of vertices.
• 12.EMW (Bottleneck, maximum capacity): The edge with the lowest weight on a path. It is the bottleneck on the path and is also the maximum capacity that the path allows.
• 13.Global maximum weight path (Maxflux path, Representative Dominant Reaction Pathway): It is a special maximum weight path between a pair of vertices. It is a maximum weight path where any subpath between any pair of vertices on the path is also a maximum weight path for that vertex pair. For a given pair of vertices, it is unique up to the degeneracy of edge weights in the graph. When fluxes are edge weights, this path is the same as the Maxflux path.