Dynamic rotating-shield brachytherapy

Abstract

Purpose: To present dynamic rotating shield brachytherapy (D-RSBT), a novel form of high-dose-rate brachytherapy (HDR-BT) with electronic brachytherapy source, where the radiation shield is capable of changing emission angles during the radiation delivery process.

Methods: A D-RSBT system uses two layers of independently rotating tungsten alloy shields, each with a 180° azimuthal emission angle. The D-RSBT planning is separated into two stages: anchor plan optimization and optimal sequencing. In the anchor plan optimization, anchor plans are generated by maximizing the D₉₀ for the high-risk clinical-tumor-volume (HR-CTV) assuming a fixed azimuthal emission angle of 11.25°. In the optimal sequencing, treatment plans that most closely approximate the anchor plans under the delivery-time constraint will be efficiently computed. Treatment plans for five cervical cancer patients were generated for D-RSBT, single-shield RSBT (S-RSBT), and ¹⁹²Ir-based intracavitary brachytherapy with supplementary interstitial brachytherapy (IS + ICBT) assuming five treatment fractions. External beam radiotherapy doses of 45 Gy in 25 fractions of 1.8 Gy each were accounted for. The high-risk clinical target volume (HR-CTV) doses were escalated such that the D_2cc of the rectum, sigmoid colon, or bladder reached its tolerance equivalent dose in 2 Gy fractions (EQD2 with α/β = 3 Gy) of 75 Gy, 75 Gy, or 90 Gy, respectively.

Results: For the patients considered, IS + ICBT had an average total dwell time of 5.7 minutes/fraction (min/fx) assuming a 10 Ci¹⁹²Ir source, and the average HR-CTV D₉₀ was 78.9 Gy. In order to match the HR-CTV D₉₀ of IS + ICBT, D-RSBT required an average of 10.1 min/fx more delivery time, and S-RSBT required 6.7 min/fx more. If an additional 20 min/fx of delivery time is allowed beyond that of the IS + ICBT case, D-RSBT and S-RSBT increased the HR-CTV D₉₀ above IS + ICBT by an average of 16.3 Gy and 9.1 Gy, respectively.

Conclusions: For cervical cancer patients, D-RSBT can boost HR-CTV D₉₀ over IS + ICBT and S-RSBT without violating the tolerance doses to the bladder, rectum, or sigmoid. The D₉₀ improvements from D-RSBT depend on the patient, the delivery time budget, and the applicator structure.

INTRODUCTION

The radiation dose deliverable with conventional brachytherapy (BT) is limited by the presence of organs at risk (OARs) adjacent to the tumor. For example, in the case of cervical cancer treated with intracavitary BT, the OARs that need to be taken into consideration are the rectum, bladder, and sigmoid colon. This limitation is clinically important especially in cases where nonradially symmetric tumors need to be treated with radiation sources that produce radially symmetric dose distributions around the applicator. For laterally extended tumors, achieving the desired tumor dose coverage with the single channel intracavitary BT approach may be impossible.

Several approaches have been adopted in overcoming the difficulty of producing nonradially symmetric dose distributions. Interstitial BT is the present treatment of choice, and the American Brachytherapy Society (ABS) recommends the use of Syed/Neblett^{1, 2, 3} or MUPIT applicators⁴ for large tumors. To reduce the invasiveness of interstitial BT, a tandem and ring applicator with supplementary interstitial brachytherapy is one option.⁵ Some recently proposed noninterstitial BT methods may further reduce the invasiveness of this approach. Another approach, called compensator-based intensity modulated brachytherapy (C-IMBT), introduces compensators with nonuniform thickness to adjust the radiation transmission in different directions.⁶ By introducing rotatable shields and partially shielding the source, rotating shield brachytherapy (RSBT) allows the radiation to be better directed.^{2, 3, 7, 8, 9}

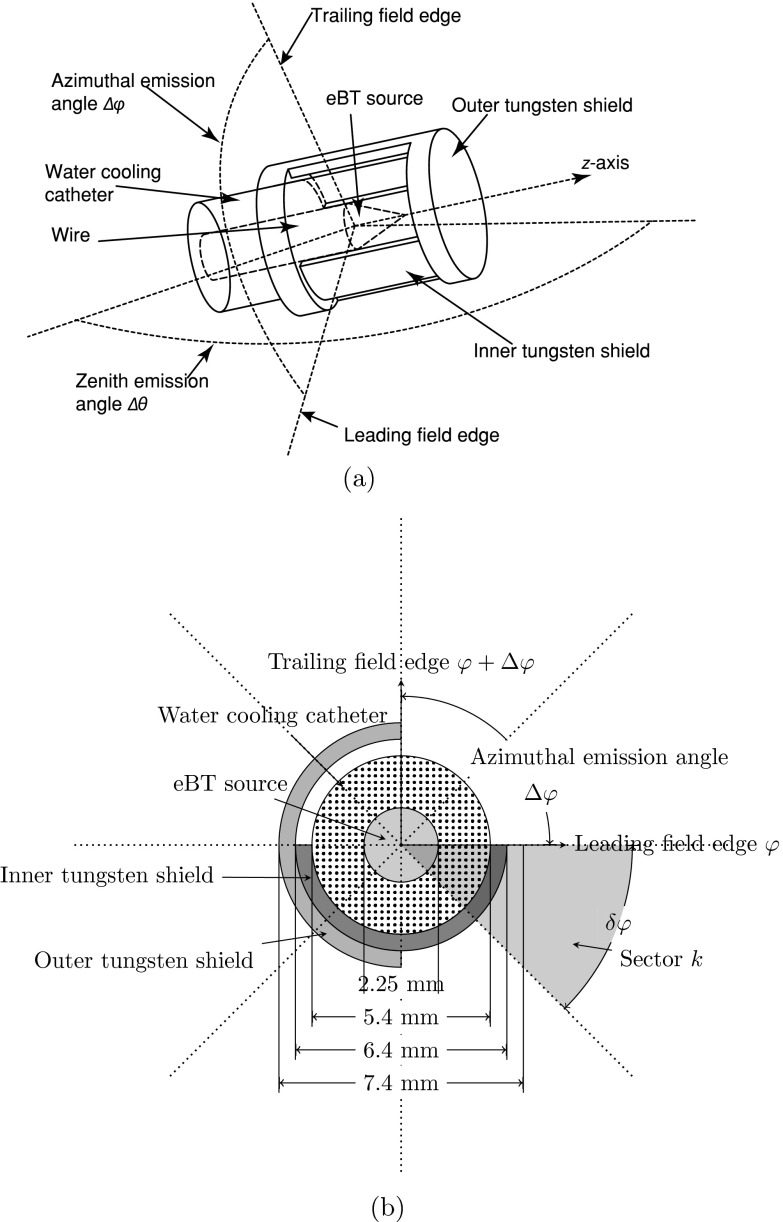
Ebert first introduced RSBT as an option to improve the tumor conformity of BT for single-catheter³ and multicatheter¹⁰ treatments. In these studies, the RSBT dose distributions were modeled with a radiation source with the dosimetric characteristics of ¹⁹²Ir which was partially shielded by an unknown material. The study showed that a shield transmission of 50% is unacceptable.³ To reduce the transmission from an ¹⁹²Ir source to less than 50% with a lead shield, the thickness of the shield would need to be greater than 2.5 mm.¹¹The thickness of the device used with ¹⁹²Ir RSBT makes the effective treatment of some cancer types like cervical cancer difficult, due to the limited space available for the device inside of the intrauterine applicators. In order to control the transmission rate with a thinner shield, one feasible option is the use of a high-dose-rate electronic BT (eBT) source. By using tungsten alloy as the shielding material, the overall diameter of the RSBT system can be less than 10 mm and the transmission rate through the tungsten shield is less than 0.1%.^{8, 9} As the azimuthal emission angles in these previous works^{3, 8, 9, 10} were assumed to be static during the delivery process, it is possible that RSBT can be delivered using shields that are capable of varying the azimuthal emission angle during treatment delivery. We define dynamic-RSBT (D-RSBT) as a technique capable of using a variable azimuthal emission angle which is distinct from single-shield RSBT (S-RSBT),⁹ which uses a constant azimuthal emission angle. The D-RSBT source is assumed to be an eBT source, shielded by two layers of rotatable tungsten alloy shields. On each of the shields, there is a 180° azimuthal shield angle opening. By rotating the shields, any azimuthal emission angle that is less than 180° can be formed during the treatment delivery (Fig. 1). To enable D-RSBT to be used in clinical practice, a systematic approach that can fully exploit its capability is necessary. In this work, we propose a solution to help the D-RSBT users to find the best treatment plan in an efficient way.

Figure 1.

A conceptual design of a partially shielded eBT source for D-RSBT: (a) 3D view and (b) cross section view.

MATERIALS AND METHODS

While D-RSBT may theoretically be able to form any azimuthal emission angle less than 180° by rotating the shields (Fig. 1), an assumption is made to simplify the study. The field edges, which are the boundaries of the nonshielded regions in the cross sectional view, are aligned with N discrete and evenly spaced azimuthal angles in the polar coordinate system centered at the eBT source. As a result, instead of having an infinite number of different shield arrangements at a single dwell position, the number of different arrangements is N²/2 at a single dwell position. Increasing the value of N may lead to better dose distributions;³ however, it will also increase the optimization time due to the increase in the number of degrees of freedom. In this study, N is set to 32 to balance the dose distribution quality and the optimization time based on a previous study.⁹ Thus, δφ = 360°/N = 11.25° is the smallest nonzero azimuthal emission angle that can be formed by a shield arrangement, which we will refer to as the baseline azimuthal emission angle.

Radiation source model and dose calculation

The D-RSBT source is assumed to be a Xoft Axxent^TM (iCAD Inc., Nashua, NH) eBT source operated at 50 kVp, with two layers of 0.5 mm tungsten alloy shields, each providing less than 0.1% energy transmission through the shield. Each shield has an azimuthal shield angle of 180° (Fig. 1). The shape of the nonshielded region is conical, and can be represented by the zenith emission angle Δθ and the azimuthal emission angle Δφ. In this work, it is assumed that Δθ is a constant 120°, but Δφ can be changed by rotating the shields.

A beamlet, ${\dot{D}}_{i,j}\left(\phi ,\Delta \phi \right)$, is defined as the dose rate at the spatial point ${\vec{r}}_i$ due to a shielded radiation source at the dwell position ${\vec{s}}_j$ (j = 0, …, J−1) with the leading and trailing field edges aligned with azimuth φ and φ +Δφ, respectively. The shield arrangement forms a beamlet with an azimuthal emission angle Δφ. The total dose delivered to the point ${\vec{r}}_i$ from all beamlets is calculated as a time-weighted sum of the appropriate beamlets over all dwell positions, emission directions, and angles:

$$d_i=\sum _{j=0}^{J-1}\sum _{\phi }\sum _{\Delta \phi }{\dot{D}}_{i,j}\left(\phi ,\Delta \phi \right){\tau }_{j,\phi ,\Delta \phi },$$ (1)

where τ_{j, φ, Δφ} is the dwell time for beamlet ${\dot{D}}_{i,j}\left(\phi ,\Delta \phi \right)$. The source step length along the source trajectory, Δλ, is set to 3 mm.⁹ Beamlets with baseline azimuthal emission angle, ${\dot{D}}_{i,j}\left(\phi ,\delta \phi \right)$, are called baseline beamlets. It is also assumed that φ = kδφ, k ∈ [0, N − 1] for baseline beamlets.

The beamlets are calculated based on the TG-43 dose calculation model of Rivard et al.¹² The dose rates at the points blocked by the shields are set to zero. Thus, the point source approximation is used and the effects of shield emission angle size on the x-ray scatter component of the Xoft Axxent^TM dose distribution are negated. The approximations are justified since the emission angle selection method can be applied regardless of the accuracy of the beamlet calculation technique. The exact result of the method will likely have a slight, although unknown, dependence on the beamlet calculation technique. It is assumed that the x-ray intensity of the unshielded source has no azimuthal dependence.

A Vienna tandem-and-ring style applicator¹³ (Varian Medical Solution, Inc. Palo Alto, CA), with a ring radius of 21.25 mm and six holes for interstitial needles is used with a VariSource^TM192Ir source for the IS + ICBT treatment planning. Interstitial needles will be used in all six holes except those one that will pass through the bladder. The spacing between adjacent source dwell positions is set to 3 mm. The eBT sources for S-RSBT are the same as those used for D-RSBT, but the shields are 0.5 mm single-layer tungsten alloy detachable shields. The azimuthal emission angles of S-RSBT remain fixed during delivery. Unlike the ICBT method, it is assumed that both S-RSBT and D-RSBT are delivered through a single-channel tandem applicator with no ring.

Optimization methods

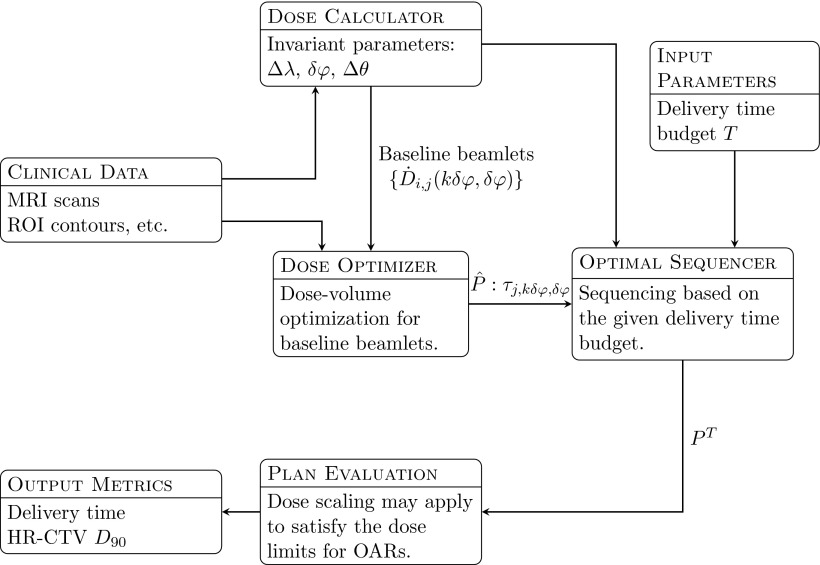
The optimization process for D-RSBT is separated into an anchor plan optimization stage and an optimal sequencing stage (Fig. 2). In the anchor plan optimization stage, anchor plans are obtained by generating delivery plans with baseline beamlets. In the optimal sequencing stage, the anchor plans are converted into deliverable plans that best approximate the dose distributions of the anchor plans within given delivery time budgets, by assembling the baseline beamlets into deliverable beamlets of larger azimuthal emission angles.

Figure 2.

TPS processes for D-RSBT method. The dose calculator generates a set of baseline beamlets ${\dot{D}}_{i,j}\left(k\delta \phi ,\delta \phi \right)$ based on the source tandem path and the user-specified parameters: the source step length Δλ, the baseline azimuthal emission angle δφ, and the zenith emission angle Δθ. Then the dose optimizer will generate an anchor plan $\widehat{P}$ which assigns a dwell time τ_{j, kδφ, δφ} for each baseline beamlet. The dwell time sequence is the input for the optimal sequencer, and the optimal sequencer calculates the best way to approximately deliver the dose map specified by the anchor plan under the delivery time budget T. All the plans will be subject to plan evaluation.

The separation is made based on the fact that any beamlets with azimuthal emission angle Wδφ can be equivalently substituted by a superposition of neighboring baseline beamlets:

$${\dot{D}}_{i,j}\left(\phi ,W\delta \phi \right)=\sum _{p=0}^{W-1}{\dot{D}}_{i,j}\left(\phi +p\delta \phi ,\delta \phi \right).$$ (2)

Equation 2 is an exact case for zero shield transmission, which is a safe assumption for the case under consideration.

The separation makes the optimization of D-RSBT more efficient in three ways. First, compared to the optimization problem with all possible beamlets, the degree of freedom in the anchor plan optimization stage is decreased by a factor of N. Second, as the shadows cast by the shields of neighboring baseline beamlets do not overlap, taking this property into consideration also simplifies the dose optimization. Third, the optimal sequencing problems can be modeled as convex programming problems and efficiently solved.

Anchor plan optimization

The optimization for the anchor plan is done using a simulated annealing algorithm. It attempts to maximize the HR-CTV D₉₀ while keeping the D_2cc of all OARs below the GEC-ESTRO recommended limits.^{14, 15, 16} In order to make the simulated annealing algorithm efficient, a prior optimizer based on the linear least squares method that optimizes the dose homogeneity on the HR-CTV surface¹⁷ is applied to obtain initial solutions. Both these methods were applied in previous studies.^{3, 7, 18, 19, 20, 21} The anchor plans are represented by listing the dwell times of the baseline beamlets, τ_{j, kδφ, δφ}, j ∈ [0, J − 1], k ∈ [0, N − 1].

Optimal sequencing

Anchor plans are generally of a higher dose distribution quality as the baseline azimuthal emission angle is small.³ However, delivery with baseline beamlets is impractical due to its lengthy delivery time. The essence of optimal sequencing is combining neighboring baseline beamlets into larger beams to reduce the delivery time without sacrificing dose distribution quality. For each dwell position, the sequencing can be determined by tracking the motion of the leading and trailing field edge.

The optimal sequencing makes the following assumptions: (i) the rotation of the leading and trailing field edge is limited to a single full rotation (360°), (ii) the leading field edge starts from 0°, and (iii) the rotation is counterclockwise. It has been shown theoretically that these assumptions do not affect the delivery time or the dose distribution.²² Therefore, for any given dwell position ${\vec{s}}_j$, denote x_j,k, y_j,k as the time points when the leading field edge and trailing field edge align with the azimuth (k + 1)δφ, respectively. The dose received by sector k (the region covered by baseline beamlet ${\dot{D}}_{i,j}\left(k\delta \phi ,\delta \phi \right)$) is equivalent to the dose contribution from ${\dot{D}}_{i,j}\left(\phi ,\delta \phi \right)$ with dwell time t_j,k:

$$t_{j,k}=\left\{\begin{array}{cc}\hfill x_{j,k}-y_{j,k},& \hfill \mathrm{if}\mathrm{sector}k\mathrm{is}\mathrm{not}\mathrm{included}\mathrm{in}\mathrm{the}\mathrm{initial}\mathrm{opening}\\ \hfill x_{j,k}-y_{j,k}+T_j,& \hfill \mathrm{otherwise}\end{array}\right.,$$

where the initial opening refers to the region between the leading field edge and the trailing field edge at time point 0 for each dwell position, and T_j is the total dwell time at position ${\stackrel{\rightharpoonup }{s}}_j$. By allowing y_{j, k} < 0 and interpreted as T_j − y_{j, k}, the two cases are unified to: t_{j, k} = x_{j, k} − y_{j, k}.²²

It is clear that if t_{j, k} = τ_{j, kδφ, δφ} for all j and k, then the dose distribution of the anchor plan will be perfectly reproduced. Thus, an expedient treatment plan P^T with a delivery time budget of T was rapidly generated from the anchor plan $\widehat{\mathrm{P}}$ by solving the following optimization problem:

$$\begin{array}{ccc}& & \min \sum _{j=0}^{J-1}\sum _{k=0}^{N-1}({\lambda }_{j,k}^{-}H\left({\tau }_{j,k\delta \phi ,\delta \phi }-x_{j,k}+y_{j,k}\right)+{\lambda }_{j,k}^{+}H(x_{j,k}\hfill \\ & & -y_{j,k}-{\tau }_{j,k\delta \phi ,\delta \phi }\left)\right){\left(x_{j,k}-y_{j,k}-{\tau }_{j,k\delta \phi ,\delta \phi }\right)}^2,\hfill \end{array}$$

$$\mathrm{s}.\mathrm{t}.x_{j,k}\le x_{j,k+1},\forall j\in \left[0,J-1\right],k\in \left[0,N-2\right],$$ (3a)

$$y_{j,k}\le y_{j,k+1},\forall j\in \left[0,J-1\right],k\in [0,N-2],$$ (3b)

$$x_{j,k}\le y_{j,k+w},\forall j\in \left[0,J-1\right],k\in [0,N-w-1],$$ (3c)

$$\begin{array}{c}\hfill x_{j,k}\le y_{j,k+w-K}+T_j,\forall j\in \left[0,J-1\right],k\in \left[N-w,N-1\right],\end{array}$$ (3d)

$$y_{j,k}\le x_{j,k-1},\forall j\in \left[0,J-1\right],k\in \left[1,N-1\right],$$ (3e)

$$y_{j,0}\le 0,x_{j,0}\ge 0,x_{j,K-1}\le T_j,\forall j\in \left[0,J-1\right],$$ (3f)

$$\sum _{j=0}^{J-1}{T}_j\le T,$$ (3g)

where H(x) is a Heaviside function and ${\lambda }_{j,k}^{+}$, ${\lambda }_{j,k}^{-}$ are coefficients for overdosing and underdosing penalties of baseline beamlet ${\dot{D}}_{i,j}\left(k\delta \phi ,\delta \phi \right)$. In this study, ${\lambda }_{j,k}^{+}$ is the largest dose rate contribution measured with Gy/h to the OAR (i.e., ${\max }_{\mathrm{i}\in \mathrm{OAR}}{\dot{D}}_{i,j}\left(k\delta \phi ,\delta \phi \right)$), and ${\lambda }_{j,k}^{-}$ is the largest dose rate contribution to the HR-CTV surface measured with Gy/h (i.e., ${\max }_{\mathrm{i}\in \mathrm{HR}-\mathrm{CTV}\_\mathrm{Surface}}{\dot{D}}_{i,j}\left(k\delta \phi ,\delta \phi \right)$).

In Eq. 3, constraints 3a, 3b refer to the nondecreasing nature of the time sequence; constraints 3c, 3d ensure that the resulting solution keeps the azimuthal emission angle less than the maximal azimuthal emission angle; constraint 3e is used to exclude the case with azimuthal emission angle 0°; constraints 3f, 3g limit the delivery time below the given budget.

With a sufficient delivery time budget T, solving the optimal sequencing problem as described in Eq. 3 can generate a perfect reproduction of $\widehat{P}$. For example, if T is set to the delivery time of the corresponding anchor plan, the anchor plan itself is a trivial solution to Eq. 3. However, as the delivery time budget T decreases, the solution to the optimal sequencing problem tends to use more beamlets with larger azimuthal emission angles and a perfect reproduction of $\widehat{P}$ may not be achieved in such cases. As a result, the expedient plan P^T may be regarded as an approximation of the dose-volume optimized plan $\widehat{P}$. The delivery plan P^T generated by solving Eq. 3 is then scaled to make sure that no delivery time constraint and OAR tolerances are violated.

Optimization methods for IS + ICBT and S-RSBT

The gradient-based linear least squares method¹⁷ is used for IS + ICBT optimization in order to remain consistent with our previous study.⁸ The constraint that the sum of the dwell times along all supplemental needles is less than 20% of the total dwell time is considered.^{5, 23} The S-RSBT delivery plans are generated using the rapid emission angle selection (REAS) method that requires three anchor plans (90°, 180°, and 270°).⁹

Validation and comparison of D-RSBT using cervical cancer patient data

The plans of five cervical cancer patients, treated with MRI-guided high-dose-rate (HDR) BT using an¹⁹²Ir radiation source, were retrospectively analyzed in this study after receiving Institutional Review Board approval. The HR-CTV and the OARs of the rectum, sigmoid colon, and bladder were delineated by a radiation oncologist using the GEC-ESTRO recommendations.¹⁴ The volumes of the HR-CTV were 41.28 cm³, 45.02 cm³, 76.65 cm³, 97.89 cm³, and 73.58 cm³ for patient #1– #5. For the purpose of this study, it was assumed that the HR-CTV and OARs received a dose of 45 Gy of external beam radiation therapy (EBRT) in 25 fractions of 1.8 Gy/fraction. To each patient, it was also assumed that the same BT plan was delivered for all five treatment fractions.

No explicit prescription doses were given for these cases, as the purpose of this study is to test the achievable tumor coverage. Therefore, instead of having fixed prescription doses, the goal of the optimization is set to achieving the highest D₉₀ HR-CTV under the normal structure tolerance.

The HR-CTV doses [Gy₁₀] and OARs doses [Gy₃] are expressed as equivalent doses in 2 Gy fractions of EBRT (EQD2), using α/β values of 10 Gy and 3 Gy, respectively.² The equation for calculating EQD2 is shown as Eq. 4,²⁴

$$EQD2=Nd\frac{1+g\frac{d}{\alpha /\beta }}{1+\frac{2}{\alpha /\beta }},$$ (4)

where parameter N indicates the number of fractions and the parameter d refers to the dose per fraction. To account for the repair during the prolonged delivery process, the parameter g is calculated with Eq. 5:

$$g=\frac{2}{\mu t}\left(1-\frac{1-e^{-\mu t}}{\mu t}\right),\mu =\frac{\ln 2}{T_{1/2}},$$ (5)

where t refers to the delivery time per fraction, T_1/2 is the half time for sublethal damage repair. The value of T_1/2, was assumed to be 1.5 h according to the estimates by GEC-ESTRO working group II.²⁵ The g parameter for EBRT is set to 1 for all cases.

Both the planning time and the plan quality were considered. The plan quality was established by maintaining a balance between the HR-CTV D₉₀ and the corresponding delivery time. The D_2cc of the rectum, sigmoid colon, and bladder were kept under the maximum allowed doses of 75, 75, and 90 Gy,^{2, 15} respectively. The plan quality is determined by the HR-CTV D₉₀ and the delivery time. The HR-CTV D₉₀ was selected as an important metric due to its connection to clinical outcomes. Cervical cancer patients treated with a combination of EBRT and brachytherapy are associated with significantly improved local tumor control probability if the received HR-CTV D₉₀ is 87 Gy or greater, compared with those cases where the HR-CTV D₉₀ is less than 87 Gy.^{26, 27} The V₁₀₀ metric, which is the percentage of the HR-CTV volume receiving 100 Gy in EQD2 units, is also used as a measure of the extent of the HR-CTV hot spots.

For D-RSBT and S-RSBT, the delivery efficiency curves⁹ were used instead of single delivery plans as they better reflect the trade-off between delivery time (x-axis) and HR-CTV D₉₀s (y-axis) of the planning method used. Similarly, a delivery efficiency curve is considered superior to another if it is located to the top-left of the other delivery curves. The delivery efficiency curves of D-RSBT are obtained by solving Eq. 3 with 100 T-values between 5 min/fx and 60 min/fx. The delivery efficiency curves of S-RSBT are obtained using REAS which enumerates all possible azimuthal emission angles for S-RSBT.

Besides the visual comparison between delivery efficiency curves, the BT plans were also quantitatively compared by the delivery times required for D-RSBT and S-RSBT matched the HR-CTV D₉₀ of IS + ICBT. Note that the HR-CTV D₉₀ values of the RSBT technique can be improved by increasing delivery time. Thus, we also compared the HR-CTV D₉₀ values for D-RSBT and S-RSBT under three different delivery time budgets. The three delivery time budgets were determined by increasing delivery time by an additional 10, 20, and 30 min/fx based on the delivery times required for the IS + ICBT method.

RESULTS

The D-RSBT optimization took about 7 min to finish, the IS + ICBT and S-RSBT optimization took about 4 min and 20 min for each case, respectively.

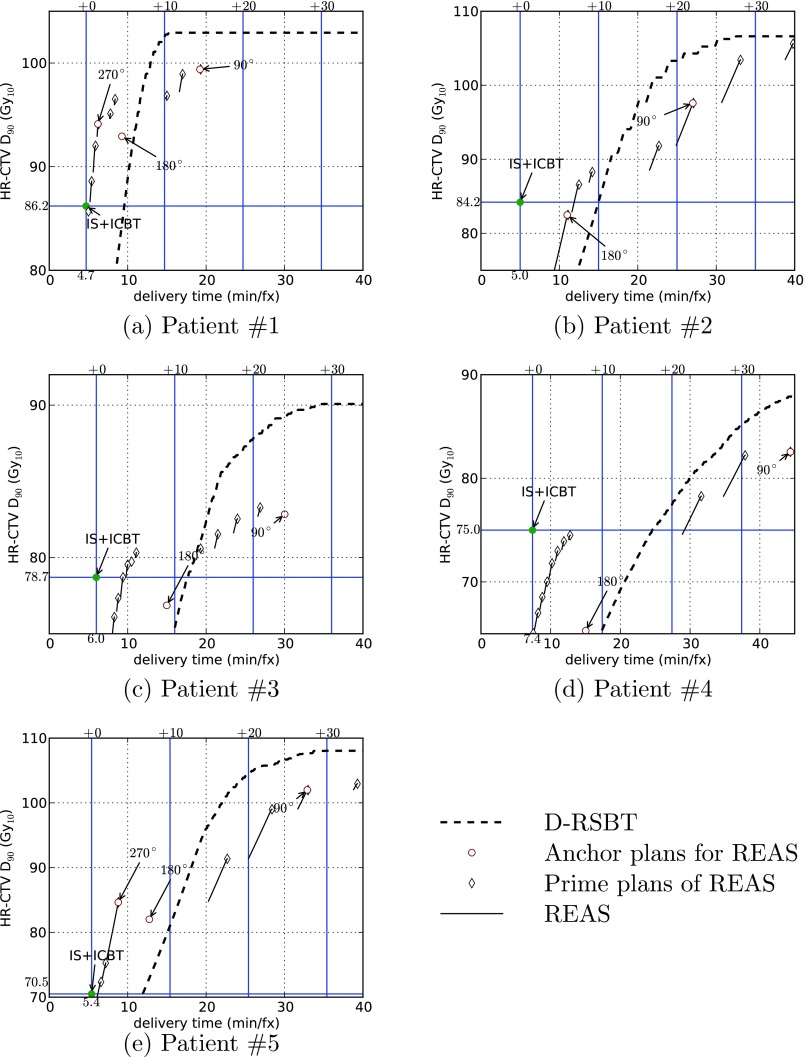
The delivery efficiency curves for each patient plan using the D-RSBT and S-RSBT methods are shown in Fig. 3, and the plans of IS + ICBT are explicitly labeled as such. For any specified delivery efficiency curve in Fig. 3, a point on that curve represents the highest D₉₀ (y-axis) the corresponding planning method can achieve in the corresponding clinical case within the delivery time budget (x-axis). It also represents the fastest delivery time (x-axis) the corresponding planning method can achieve in the corresponding clinical case within the D₉₀ goal. Therefore, a delivery efficiency curve is considered superior to another if it is located to the top-left of another delivery curve.

Figure 3.

Delivery efficiency curves for five clinical cases by using D-RSBT and S-RSBT with REAS. The anchor plans used by REAS are explicitly labeled with the corresponding azimuthal emission angles even if they are not on the delivery efficiency curves. IS + ICBT plans are also marked on the plot with help lines to indicate the corresponding HR-CTV D₉₀'s and delivery times.

As shown in Fig. 3, both D-RSBT and S-RSBT can achieve a higher D₉₀ than IS + ICBT with a longer delivery time. The amount of additional delivery time required is 6.7 min/fx for S-RSBT and 10.1 min/fx for D-RSBT on average. If 10 min/fx of additional delivery time compared to IS + ICBT is allowed, S-RSBT and D-RSBT can boost the HR-CTV D₉₀ from IS + ICBT by an average of 6.2 and 2.8 Gy, respectively. If 20 min/fx of additional delivery time is provided, S-RSBT and D-RSBT can improve the HR-CTV D₉₀ by 9.1 and 16.3 Gy, respectively. In the case of additional 30 min/fx, the D₉₀ improvements are 15.0 and 19.7 Gy.

The more detailed quantitative results are shown in Table 1. And it can be observed that, the HR-CTV V₁₀₀ values for both RSBT techniques are substantially higher than those for IS + ICBT.

Table 1.

Dosimetric comparison for five patients between IS + ICBT, S-RSBT, and D-RSBT methods. The S-RSBT and D-RSBT were evaluated with (i) the D₉₀ from IS + ICBT matched (denoted by Match D₉₀); and (ii) or with delivery time budget set to 10, 20, and 30 min/fx more from what is need in IS + ICBT. The EQD2 values were computed with repair considered using Eq. 5.

Patient #	Method		HR-CTV D90 (Gy)	Bladder D2cc (Gy)	Sigmoid D2cc (Gy)	Rectum D2cc (Gy)	Delivery time (min/fx)	V100(%)	Azimuthal emission angle (deg)
#1	IS + ICBT		86.2	89.6	56.0	70.0	4.7	68.6
	S-RSBT	Match D90	86.2	86.7	53.2	68.2	5.2	78.9	292.5
		+10 min/fx	96.7	88.7	55.3	74.8	8.4	88.0	202.5
		+20 min/fx	99.4	88.5	55.8	74.1	19.2	89.6	90
		+30 min/fx	99.4	88.5	55.8	74.1	19.2	89.6	90
	D-RSBT	Match D90	86.2	87.2	55.5	69.0	9.6	80.9
		+10 min/fx	102.8	88.6	56.4	74.3	14.8	91.3
		+20 min/fx	102.9	88.9	56.3	74.1	15.2	91.4
		+30 min/fx	102.9	88.9	56.3	74.1	15.2	91.4
#2	IS + ICBT		84.2	89.6	65.5	52.0	5.0	70.4
	S-RSBT	Match D90	84.2	82.6	72.4	58.1	11.9	81.4	168.75
		+10 min/fx	88.3	88.9	74.2	57.0	14.1	84.4	157.5
		+20 min/fx	92.2	82.7	70.3	52.1	25.0	86.1	90
		+30 min/fx	103.4	87.4	73.5	53.0	33.1	91.3	78.75
	D-RSBT	Match D90	84.2	81.2	69.2	52.1	15.0	80.5
		+10 min/fx	84.2	81.2	69.2	52.1	15.0	80.5
		+20 min/fx	103.3	88.2	73.4	53.2	24.0	91.3
		+30 min/fx	106.6	87.6	69.4	52.3	32.5	92.0
#3	IS + ICBT		78.7	82.4	57.3	74.7	6.0	49.0
	S-RSBT	Match D90	78.7	89.3	60.5	71.4	9.4	70.8	270
		+10 min/fx	80.3	89.2	63.5	73.2	11.1	73.2	236.25
		+20 min/fx	82.5	88.2	69.9	73.7	23.9	74.5	112. 5
		+30 min/fx	83.3	87.9	71.1	73.8	26.9	75.3	101.25
	D-RSBT	Match D90	78.7	88.1	63.7	71.2	17.7	70.2
		+10 min/fx	75.4	88.7	63.8	70.9	16.0	66.1
		+20 min/fx	87.8	86.6	64.0	73.8	26.0	80.1
		+30 min/fx	90.1	87.1	64.9	73.4	34.8	82.9
#4	IS + ICBT		75.0	86.3	74.6	58.1	7.4	65.3
	S-RSBT	Match D90	75.0	80.5	70.0	70.2	29.2	73.6	112.5
		+10 min/fx	74.7	89.0	73.6	72.8	12.7	75.2	247.5
		+20 min/fx	74.7	89.0	73.6	72.8	12.7	75.2	247.5
		+30 min/fx	81.6	85.3	71.6	72.8	37.4	79.5	101.25
	D-RSBT	Match D90	75.0	88.0	62.7	66.0	24.6	70.4
		+10 min/fx	65.4	86.9	59.4	62.7	17.4	56.8
		+20 min/fx	77.5	87.3	62.6	66.1	27.4	72.6
		+30 min/fx	85.1	87.2	62.6	66.9	37.4	79.4
#5	IS + ICBT		70.5	89.6	58.5	56.3	5.4	43.8
	S-RSBT	Match D90	70.5	87.9	63.3	51.8	6.2	71.9	315
		+10 min/fx	85.6	88.0	74.6	54.0	9.4	82.6	258.75
		+20 min/fx	91.4	77.1	69.0	55.5	25.4	84.8	101.25
		+30 min/fx	102.0	87.6	73.5	58.7	32.9	91.0	90
	D-RSBT	Match D90	70.5	66.3	55.2	48.6	11.9	59.2
		+10 min/fx	81.0	77.4	60.6	50.8	15.4	75.0
		+20 min/fx	104.6	88.1	69.7	52.1	25.4	92.3
		+30 min/fx	108.0	87.4	71.6	51.5	35.1	94.0

DISCUSSION

Both the visual and quantitative comparison confirms that D-RSBT is a superior delivery method relative to the S-RSBT and IS + ICBT technique, provided that there is sufficient delivery time. Trading a longer delivery time for a higher dose-quality may be desirable, depending on the clinical goal. For example, a previous study by Dimopoulos et al.²⁶ showed that treatment plans with a HR-CTV D₉₀ less than 87 Gy may result in poor treatment outcomes, especially when treating large tumors. Based on the five cases studied in this work, the average D₉₀ achieved by IS + ICBT is 78.9 Gy and the average delivery time required is 5.7 min/fx. Note that we cannot increase the D₉₀ to 87 Gy by increasing the delivery time in IS + ICBT as at least one of the OARs has already reached the dose limit. If no additional delivery time is allowed, then IS + ICBT is the best choice among the three methods studied in this work. However, if an additional 10 min/fx is allowed, then S-RSBT may be the best method as it can boost the average D₉₀ to 85.1 Gy. D-RSBT can achieve 81.7 Gy on average within the same delivery time frame. If an additional 20 min/fx is allowed, then D-RSBT can achieve the highest average D₉₀ of 95.2 Gy. For S-RSBT, the average D₉₀ is 88.0 Gy.

The reason that S-RSBT and D-RSBT tend to achieve better D₉₀ with longer delivery time is due to the use of the optimal sequencing algorithms. The optimal sequencing algorithms compute the “best” way to approximate the dose distribution of anchor plans with the constraint of delivery time. The anchor plans are obtained using very fine emission angles, yielding high theoretical D₉₀ values. However, the delivery of an anchor plan in clinical practice is not realistic due to the prohibited long delivery time. We thus introduce the sequencing algorithm to compute the “best” approximated plan to the anchor plan for a given clinically reasonable delivery time. The compromise between plan quality and delivery time mainly depends on the emission angles that the RSBT technique can use. As the delivery time increases, the quality of the approximated plan tends to be increasing, since RSBT can use more small emission angles for delivery.

There are several possible ways to improve the D-RSBT technique. (i) Use a more sophisticated D-RSBT applicator design. For example, with the same set of five patient cases in this study and the same anchor plans, if three layers of shielding could be used, the azimuthal emission angle range can be extended from 0° to 240°, the average HR-CTV D₉₀ achieved by 3-layer D-RSBT are 90.1, 97.9, and 99.6 Gy for delivery time set to IS + ICBT delivery time plus additional 10, 20, and 30 min/fx, respectively. Compared to the 2-layer D-RSBT, the 3-layer D-RSBT boosts the D₉₀ by 8.4, 2.7, and 1.0 Gy in these three settings. This design can help to improve the performance of D-RSBT with limited delivery time. But, on the other hand, it complicates the structure of the applicator and increases the applicator size. (ii) Generate anchor plans with a higher quality. Higher quality refers to a higher D₉₀ with a smoother dwell time sequence in this application. While achieving higher D₉₀ is an obvious aim for the dose optimizer, our preliminary study showed that maintaining the smoothness of the dwell time sequence should also be concerned in generating anchor plans. It is possible that, with limited delivery time, those anchor plans with lower D₉₀ but higher smoothness yield delivery plans with higher D₉₀’s. This phenomenon has already been observed in S-RSBT, and that is the rational of using multiple anchor plans in the REAS method.⁹ (iii) Design properly weighted objective function for the optimal sequencing algorithm. In this study, we include in the optimization objective a weighted error function to incorporate the dose-volume information for the sequencing problem. The experiments showed that it outperformed the unweighted version with respect to the quality of the computed plans. Our experiments also showed that by using the weighted objective function the quality of the anchor plan was able to be well preserved for reduced delivery time even with less demanding smoothness of the dwell time sequences. However, we noticed that only incorporating the dose-volume information was not adequate. A more sophisticated design of the weighting function may be necessary.

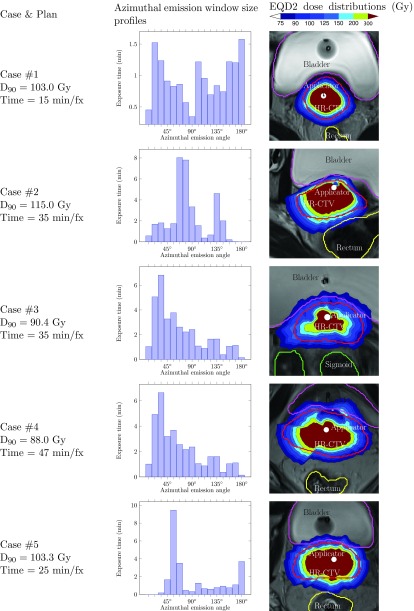
The histogram of the delivery time on all the azimuthal emission angles used in a delivery plan is an informative tool to study the characteristics of the clinical cases. Figure 4 shows an example of the emission window size profile for a delivery plan from each of the five cases studied in this paper. The x-axis stands for the azimuthal emission angles (in this case, we have 16 different sizes), and the y-axis is the total delivery time while using a specific emission angle in the delivery plan. Based on this histogram, we can roughly estimate the delivery hardness of this case and read the dominant emission angles used if necessary. For example, the percentages of the delivery time using maximal azimuthal emission angle are 10.4%, 0%, 0.4%, 0.4%, and 14.6% for five cases in this study. Thus, it can be expected that case #1 and #5 are relatively easier than the other cases. The delivery time in case #1 is relatively uniformly distributed, while in the rest of the cases, Δφ = 67.5°, 33.75°, 67.5°, 56.25° seem to be the dominant emission angles for cases #2– #5, respectively.

Figure 4.

Azimuthal emission window size profiles for D-RSBT plans with corresponding EQD2 dose distributions for five cases. The delivery time selected for each case is the breakpoint on the delivery efficiency curves where the D₉₀'s are about to drop down abruptly.

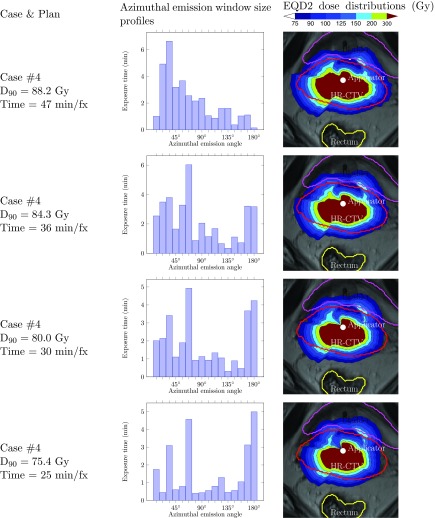
We can also intuitively predict that, if the delivery time is reduced, the histogram tends to shift right and large emission angles tend to be used. For instance, for case #4 shown in Fig. 5, the proportion of large emission angles used increases quickly as the delivery time decreases. This is the essence of D-RSBT: using large emission angles to reduce the delivery time. This is also the case for S-RSBT in which the emission angle size is the dominant factor for reducing the delivery time. However, unlike the noticeable changes on the emission window size profiles, the DVHs only show a slight change while the dose distribution maps on a single slice do not have visible changes.

Figure 5.

Azimuthal emission window size profiles of D-RSBT plans with corresponding EQD2 dose distributions for case #4 with different delivery times.

For the time spent on the optimization, the cost of D-RSBT is about half of the cost of S-RSBT. This is mainly because of the D-RSBT optimization uses fewer anchor plans than S-RSBT, and the computation of anchor plan dominates the time cost of the optimization.

CONCLUSIONS

Patients who need to be treated with HDR-BT may benefit from the D-RSBT technique. Compared to the existing interstitial BT methods such as IS + ICBT, D-RSBT can generate less invasive plans with a better dose distribution at the expense of longer delivery times. D-RSBT is also likely to yield better plans in some cases where S-RSBT may have difficulty in striking a balance between dose quality and delivery time.