Abstract
The calculation of a protein-ligand binding free energy based on molecular dynamics (MD) simulations generally relies on a thermodynamic cycle in which the ligand is alchemically inserted into the system, both in the solvated protein and free in solution. The corresponding ligand-insertion free energies are typically calculated in nanoscale computational boxes simulated under periodic boundary conditions and considering electrostatic interactions defined by a periodic lattice-sum. This is distinct from the ideal bulk situation of a system of macroscopic size simulated under non-periodic boundary conditions with Coulombic electrostatic interactions. This discrepancy results in finite-size effects, which affect primarily the charging component of the insertion free energy, are dependent on the box size, and can be large when the ligand bears a net charge, especially if the protein is charged as well. This article investigates finite-size effects on calculated charging free energies using as a test case the binding of the ligand 2-amino-5-methylthiazole (net charge +1 e) to a mutant form of yeast cytochrome c peroxidase in water. Considering different charge isoforms of the protein (net charges −5, 0, +3, or +9 e), either in the absence or the presence of neutralizing counter-ions, and sizes of the cubic computational box (edges ranging from 7.42 to 11.02 nm), the potentially large magnitude of finite-size effects on the raw charging free energies (up to 17.1 kJ mol−1) is demonstrated. Two correction schemes are then proposed to eliminate these effects, a numerical and an analytical one. Both schemes are based on a continuum-electrostatics analysis and require performing Poisson-Boltzmann (PB) calculations on the protein-ligand system. While the numerical scheme requires PB calculations under both non-periodic and periodic boundary conditions, the latter at the box size considered in the MD simulations, the analytical scheme only requires three non-periodic PB calculations for a given system, its dependence on the box size being analytical. The latter scheme also provides insight into the physical origin of the finite-size effects. These two schemes also encompass a correction for discrete solvent effects that persists even in the limit of infinite box sizes. Application of either scheme essentially eliminates the size dependence of the corrected charging free energies (maximal deviation of 1.5 kJ mol−1). Because it is simple to apply, the analytical correction scheme offers a general solution to the problem of finite-size effects in free-energy calculations involving charged solutes, as encountered in calculations concerning, e.g., protein-ligand binding, biomolecular association, residue mutation, pKa and redox potential estimation, substrate transformation, solvation, and solvent-solvent partitioning.
INTRODUCTION
The accurate calculation of binding affinities is a major challenge in computational (bio)chemistry. Focusing on classical explicit-solvent calculations based on, e.g., molecular dynamics (MD) simulations, the most common approach for evaluating the binding free energy of a ligand to a receptor, e.g., a protein, relies on the application of a thermodynamic cycle. In this approach, the ligand is alchemically transformed from a species exempt of interactions with its environment into the fully interacting species, i.e., inserted into the system, both in the solvated protein and free in solution.1, 2, 3, 4, 5 The binding free energy is then equal to the difference between these two insertion free energies, up to a standard-state correction1, 2, 4 taking into account the possible application of binding restraints.1, 2, 4, 5, 6, 7, 8 The ligand insertion free energies typically encompass two components: a non-polar component, equal to the reversible work of installing the ligand-environment van der Waals interactions in the absence of ligand charges, and a charging component, equal to the reversible work of subsequently installing the intra-ligand and ligand-environment electrostatic interactions. The accuracy of these free-energy calculations is limited by errors in force-fields,9, 10, 11 sampling,12, 13, 14 and methodology (e.g., Jacobian and metric-tensor effects,15 contribution of constraints,16 Hamiltonian lag,17, 18 or singularities19). Beyond these, finite-size effects20, 21, 22, 23, 24 represent another major source of errors in these types of calculations. They arise from a discrepancy between the actual simulation and the ideal bulk situations in terms of system size, spatial boundary conditions, and treatment of the non-bonded interactions. Due to the long range and large magnitude of electrostatic interactions, these errors are nearly exclusively electrostatic in nature, affect primarily the charging component of the ligand insertion process, and are most significant for systems where the ligand bears a net charge, especially when the protein is also charged.
Considering a classical pairwise-additive force field, the ideal bulk (infinite-dilution) situation would be achieved by considering a system of macroscopic size simulated under non-periodic boundary conditions, e.g., a spherical droplet, and in which the electrostatic interactions are defined by the exact application of Coulomb's law. Due to computational limitations, however, simulations typically involve a nanoscale system simulated under periodic boundary conditions, e.g., a periodically replicated cubic computational box, and in which the electrostatic interactions are defined by a periodic lattice-sum,25 e.g., Ewald summation26 or related mesh methods.27, 28, 29, 30 As a result, charging free energies calculated based on MD simulations deviate from their target values by an amount that depends on the size of the computational box, on the protein and ligand charge distributions, on the possible presence of counter-ions, and on the nature of the solvent.21, 22, 23, 24
At present, finite-size effects on charging free energies are best understood in the context of the solvation of monoatomic ions.20, 22, 23, 31, 32, 33, 34 In this case, a numerical correction scheme23 and a corresponding approximate analytical version31 are available. The numerical version of this scheme has also been recently extended to the case of small polyatomic ions35 and to the insertion of such ions into a simple model receptor, namely, a functionalized C60 buckyball in water.36 However, considering the most general case of a complex polyatomic charged ligand inserted into a charged protein in solution, none of the schemes available at present36, 37, 38, 39, 40, 41, 42, 43 are sufficiently general, accurate, and practical (see discussion in Sec. 5C).
For general protein-ligand systems, the finite-size error on the ligand charging free energy arises from four physical effects:
-
1.
Periodicity-induced net-charge interactions. When using lattice-sum electrostatics under periodic boundary conditions, spurious interactions are introduced between the protein-ligand complex in the reference computational box, its periodic replicas, and the homogeneous neutralizing background charge density filling the infinite periodic system.20, 21, 23, 24, 25, 31 Such interactions would be absent in the ideal situation of Coulombic electrostatics under non-periodic boundary conditions and, therefore, represent an artifact. Considering the leading net-charge component of these interactions, the corresponding error in the charging free energy is solvent-independent, inversely proportional to the box-edge length (which determines the distance between periodic replicas as well as the magnitude of the background charge), and proportional to the difference in squared net-charge between the ligand-uncharged and the ligand-charged states of the system.20
-
2.
Periodicity-induced net-charge undersolvation. When using lattice-sum electrostatics under periodic boundary conditions, the solvent in the periodic replicas of the computational box is perturbed by the periodic copies of the protein-ligand complex and thus essentially unavailable for the solvation of the complex in the reference computational box, leading to undersolvation.20, 21, 23, 24, 31 Such a perturbation would be absent in the ideal situation of a macroscopic system with Coulombic electrostatics under non-periodic boundary conditions and, therefore, represents an artifact. Considering the leading net-charge component of this undersolvation effect, the corresponding error in the charging free energy is proportional to one minus the inverse of the solvent dielectric permittivity (which determines the magnitude of the solvent polarization response), inversely proportional to the box-edge length (which determines the distance between the reference complex and its periodic replicas), and proportional to the difference in squared net-charge between the ligand-uncharged and the ligand-charged states of the system.20
-
3.
Discrete solvent effects. When using lattice-sum electrostatics under periodic boundary conditions, the average of the electric potential over the computational box is set to zero. In the ideal situation of a macroscopic system with Coulombic electrostatics under non-periodic boundary conditions, the electric potential is set to zero at infinity. As a result, for a pure-solvent system in the orientational-disorder limit (an idealized situation corresponding to the absence of intermolecular orientational correlations between the solvent molecules), the two representations differ by an offset potential. The sign and magnitude of this offset depends on the quadrupole-moment trace of the solvent model, which determines the integral of the Coulomb potential generated by the atomic partial charges of an isotropically tumbling solvent molecule.22, 31 This offset potential represents an artifact induced by the periodic representation. The corresponding error in the charging free energy is proportional to the solvent equilibrium density, to the quadrupole-moment trace of the solvent model, to the fraction of the computational box occupied by the solvent, and to the net charge of the ligand.
-
4.
Residual integrated potential effects. The three above effects would be sufficient to account for the error in the charging free energy if the protein and ligand were both point charges without solvent-excluded volume and located at the same position in space. However, when these species involve polyatomic charge distributions encompassed within distinct solvent-excluding envelopes, it is necessary to consider an additional contribution to the offset potential between the periodic and non-periodic representations. This additional source of finite-size error can actually be defined by the difference between the above reference situation of naked point charges at the same position and the real situation of polyatomic charge distributions within distinct cavities. The induced offset potential will be determined by the difference in the corresponding potential integrals over the entire space under non-periodic boundary conditions, a difference that is called here a residual integrated potential (RIP). The resulting error in the charging free energy is inversely proportional to the box volume (which converts a RIP into a corresponding average potential) and to the difference of net-charge-RIP product between the ligand-uncharged and the ligand-charged states of the system.
When neutralizing counter-ions are included during the MD simulations, possibly along with an excess of neutral salt, their main influence is to effectively neutralize the protein and to provide additional dielectric screening. However, the corresponding finite-size errors remain qualitatively the same and, if the ligand is charged, can still be of large magnitude.
These effects have been highlighted in previous work,20, 22, 23, 31 and analytical expressions are available to correct for errors due to periodicity-induced net-charge interactions, periodicity-induced net-charge undersolvation, and discrete solvent effects. An analytical correction is also available for residual integrated potential effects when the protein and ligand can be represented by point charges at the center of a single spherical cavity.20 However, this is far too severe an approximation for most protein-ligand binding applications. Thus, at present, there is no general scheme to correct ligand charging free energies for finite-size errors in realistic situations (see discussion of previously proposed schemes in Sec. 5C).
Whereas the importance of finite-size effects is widely recognized in the context of ionic solvation,20, 22, 23, 31, 32, 33, 34, 35, 44, 45, 46 it is often overlooked in the context of binding free energy calculations. A commonly formulated assumption is that these effects largely cancel out between the two alchemical legs of the thermodynamic cycle, involving the charging of the ligand within the solvated protein-ligand complex and free in solution, respectively. However, this assumption is seldom justified and can lead to very large and protocol-dependent errors in the calculated binding free energies when the ligand bears a net charge, especially when the protein is charged as well. Because finite-size errors in the calculated free energies depend on the box size, error cancellation will be poor when the simulations of the protein-ligand complex and of the free ligand are conducted in computational boxes of different sizes, as is typically the case. However, even if identical box sizes are selected, error cancellation is only expected to occur for terms that depend solely on the ligand charge and not on its environment, i.e., on the presence or absence of the protein as well as on the nature of the solvent and the fraction of the box it occupies. In practice, none of the four error components listed above satisfy this condition and the cancellation is likely to remain poor even for relatively large box sizes. The same applies to MD simulations including neutralizing counter-ions. There, although the periodicity-induced net-charge interaction and net-charge undersolvation components will become environment independent, the discrete solvent and residual integrated potential components will still fail to cancel out.
Although the present article focuses on the impact and correction of finite-size errors in protein-ligand binding free energy calculations involving charged species (e.g., for drug design), these errors affect all main types of free-energy calculations relevant to (bio)chemical problems, also including biomolecular association in general (e.g., protein-protein or protein-nucleic acid binding), residue mutation (e.g., for protein engineering), pKa and redox potential estimation, substrate transformation (enzymatic mechanism studies), solvation (e.g., for solubility studies and force-field parameterization), and solvent partitioning (e.g., for bioavailability studies) calculations.
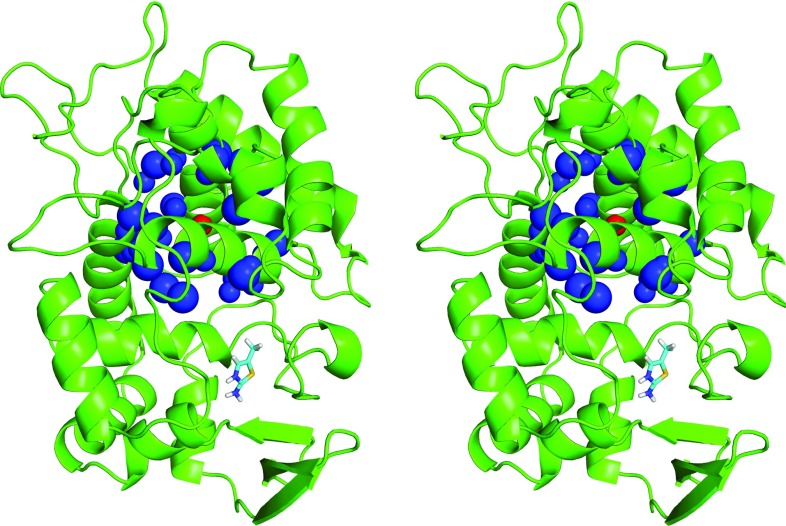
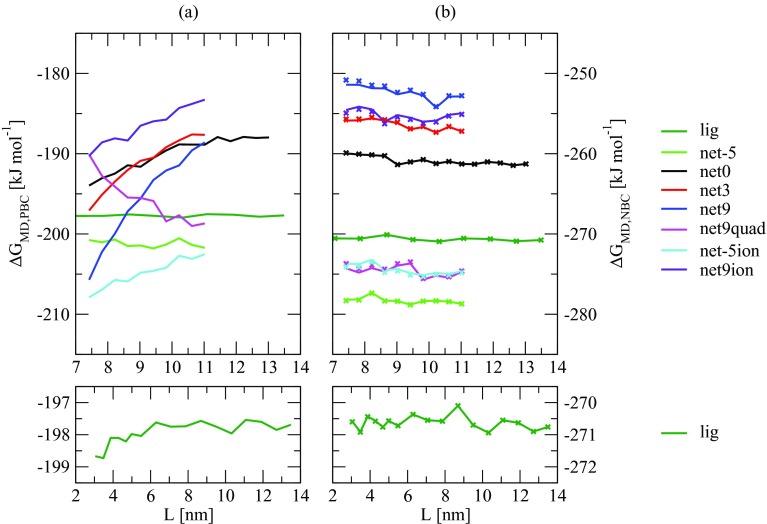
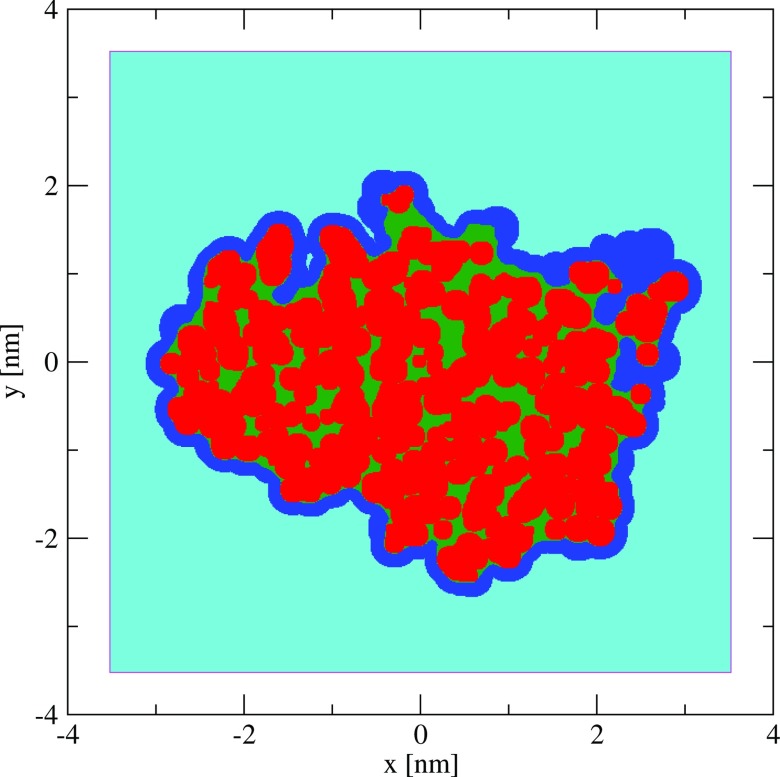
The aim of the present study is to investigate the nature and magnitude of electrostatic finite-size effects on the binding free energies of charged species calculated based on explicit-solvent MD simulations employing lattice-sum methods, and to devise an appropriate correction scheme for eliminating these effects. The binding of the ligand 2-amino-5-methylthiazole (net charge +1 e) to an engineered protein cavity binding site of yeast cytochrome c peroxidase (CCP W191G “Gateless”47, 48) in water is taken here as a test case (Figure 1). Considering differently protonated isoforms of the protein (net charges −5, 0, +3, or +9 e), MD simulations are carried out in the absence of counter-ions considering cubic boxes of edge lengths covering at least the range 7.42–11.02 nm. For the protein net charges of −5 and +9 e, additional simulations are also performed in the presence of a neutralizing atmosphere of sodium and chloride ions corresponding to a molal salt concentration of about 0.1 mol kg−1. For the protein net charge of +9 e, an artificial protein charge distribution is also considered that includes an additional quasi-isotropic quadrupole moment, which is expected to have nearly no impact on the protein-ligand and protein-solvent interactions, but a strong influence on the magnitude of finite-size effects via the residual integrated potential term.22
Figure 1.
Protein-ligand test system. Stereo view of the charged ligand 2-amino-5-methylthiazole (stick representation) bound to the engineered binding site of yeast cytochrome c peroxidase (CCP W191G “Gateless”47). The atomic sites used in the system with protein net charge +9 e for introducing an additional quasi-isotropic quadrupole moment (system net9quad) are also shown, namely, a central point charge of magnitude −80 e (red sphere) and 36 peripheral sites of total charge +80 e within a distance range of 0.81–0.85 nm (blue spheres). Note that the ligand binding mode is the one used in the present simulations, originally chosen based on the experimental binding mode of the same ligand to a related mutant protein,89 and does not exactly correspond to the experimentally inferred binding mode for the CCP W191G “Gateless” mutant.48
Because this study focuses on finite-size effects, possible additional complications related to insufficient conformational sampling are avoided by performing the MD simulations with fixed solute atom positions. Furthermore, the charging free energy of the ligand is evaluated using only the two end-state MD simulations, involving the fully uncharged and the fully charged ligand, respectively, by invoking a linear-response approximation.49, 50 Using fixed solute atom positions justifies the linear response approximation, because the response of the environment to the ligand charging is solely due to the solvent (and, possibly, counter-ion) relaxation. Finally, the investigation of finite-size effects is restricted to the ligand charging process in the different environments. No attempt is made to evaluate actual binding free energies, which would require the calculation of corresponding non-polar contributions and the application of a standard-state correction, but lead to rather unrealistic numbers given the above rigid-solute approach.
The large impact of finite-size errors on the calculated ligand charging free energies is clearly demonstrated, and two alternative correction schemes for eliminating these errors are proposed and compared. The first approach, which is referred to as the numerical correction scheme, relies on comparing the results of continuum-electrostatics Poisson-Boltzmann (PB) calculations performed under either non-periodic or periodic boundary conditions, the latter using the same box size as in the simulation, and considering both the ligand-uncharged and the ligand-charged states of the system. After inclusion of an additional discrete solvent correction term, this leads to the desired correction for finite-size effects. The second approach, which is referred to as the analytical correction scheme, attempts to disentangle the four components of finite-size errors. In this scheme, analytical expressions are formulated for the periodicity-induced net-charge interaction, periodicity-induced net-charge undersolvation, and discrete solvent correction terms. The residual integrated potential term is approximate and quasi-analytical in the sense that it is an analytical function of the box-edge length, although it involves three parameters that must be obtained numerically. The latter three parameters are residual integrated potentials, and their evaluation relies on PB calculations performed under non-periodic boundary conditions, which can easily be performed using free or commercial PB solvers such as UHBD,51, 52 DelPhi,53 or APBS.54
THEORY
Binding free energies based on MD simulations using lattice-sum electrostatics
Calculations of protein-ligand binding free energies based on classical explicit-solvent MD simulations typically rely on a thermodynamic cycle where the ligand is alchemically inserted into the system, both in the solvated protein and free in solution.1, 2, 3, 4, 5 The binding free energy is then equal to the difference between the free-energy changes associated with two insertion processes. If the insertion free energies of the free and bound ligand are noted ΔGfree and ΔGbound, respectively, the binding free energy ΔGbinding is defined by
| (1) |
a similar equation holding for the corresponding standard quantities ΔGobinding, ΔGobound, and ΔGofree after application of a standard-state correction1, 2, 4 taking into account the possible application of binding restraints.1, 2, 4, 5, 6, 7, 8 Note that the two terms in the right-hand side of Eq. 1 are defined within a common constant, which depends on the nature of the intramolecular interactions in the decoupled state of the ligand, i.e., prior to insertion. In the present work, the decoupled state of the ligand is defined by normal intramolecular covalent and van der Waals interactions along with the absence of any intramolecular electrostatic interactions (atomic partial charges set to zero). In this case, the insertion process in each of the two environments can be decomposed into two consecutive subprocesses, involving: (i) the formation of the ligand-environment van der Waals interactions, including repulsion and dispersion components (non-polar insertion process); (ii) the establishment of the intramolecular and ligand-environment electrostatic interactions (charging process). Based on this decomposition, Eq. 1 can be rewritten
| (2) |
The four quantities are calculated independently (see, however, Ref. 55 for a combined procedure), most commonly using alchemical free-energy schemes such as thermodynamic integration56 (TI), free-energy perturbation57 (FEP), the Bennett acceptance ratio58 (BAR), or the multistate Bennett acceptance ratio59 (MBAR). As discussed in Sec. 1, these calculations are affected by finite-size errors, predominantly via the charging terms of Eq. 2. While finite-size effects may in principle also affect the nonpolar insertion terms, the corresponding error is essentially negligible given reasonably large but still computationally affordable system sizes.32, 34 The nature and magnitude of the finite-size errors in the charging free energies depend on the type of electrostatic interaction scheme applied in the MD simulations, and the present discussion is restricted to one of the most commonly employed schemes, namely, lattice-sum electrostatics.
To compensate for finite-size effects, a correction ΔΔGchg,COR must be applied to the charging free energy ΔGchg of the ligand in a given environment (free or bound). For the ease of notation, the subscript “chg” will be omitted in the following, i.e., ΔG will automatically refer to the charging free energy of the ligand and ΔΔG to a finite-size correction contribution to this charging free energy, both quantities being specific to a given environment and a given box size. For simplicity, it will also be assumed here that the computational box is a cube of edge length L. One thus looks for a correction term ΔΔGCOR such that
| (3) |
where ΔGMD,PBC is the raw charging free energy calculated from the MD simulations under periodic boundary conditions (PBC) and ΔGMD,NBC is the corresponding charging free energy corrected for finite-size effects, i.e., corresponding to the same explicit-solvent force-field model, but in the ideal situation of a macroscopic system with Coulombic electrostatics under non-periodic boundary conditions (NBC).
In the present study, the raw charging free energy ΔGMD,PBC is calculated via a simple linear-response approach,49, 50 which approximates the exact TI expression
| (4) |
where λ is a common scaling factor applied to all atomic partial charges of the ligand, taking the total ligand charge Q(λ) from Q(0) = 0 to the full ligand charge Q(1) = QL, U(λ′) is the potential energy of the system in a given instantaneous configuration as evaluated for a charge-state λ′ of the ligand, and ⟨…⟩λ denotes ensemble (trajectory) averaging over configurations generated based on the potential energy U(λ). In the linear-response approximation, the integrand of Eq. 4 is assumed to depend linearly on λ, resulting in
| (5) |
The linear-response approximation is justified in the present context by the fact that the MD simulations involve fixed solute atom positions. Since the ligand atoms in particular are fixed in space, the right-hand side of Eq. 5 may be further simplified into
| (6) |
where ΔU = U(1) − U(0). This follows from the observation that for a given system configuration, U encompasses a linear (ligand-environment) and a quadratic (intramolecular ligand and through-periodicity ligand-ligand) dependence on λ. Writing U(λ) = Aλ2 + Bλ + C, Eq. 6 follows directly from Eq. 5 provided that A is configuration independent, which is the case when the ligand is rigid.
Finally, it is important to be precise on how the lattice-sum energy is defined in the MD simulations, because the form of ΔΔGMD,COR in Eq. 3 will depend on this definition. Here, it is assumed that the lattice-sum (LS) energy of a system of N charges {qi} at locations {ri} within a cubic computational box of edge L is given by the expression25, 44, 60, 61, 62, 63, 64
| (7) |
where ɛo is the permittivity of vacuum, rij = rj − ri, ΨLS is the LS influence function (electric potential generated by a unit point charge at the origin multiplied by 4πɛo) and ΨoLS the corresponding Wigner self-term constant (difference between ΨLS and r−1 in the limit of infinitesimal distances). The influence function and associated self-term are defined by the equations
| (8) |
where δ is the three-dimensional Dirac delta function and ξLS ≈ −2.837297 is the cubic LS (Wigner) integration constant,25, 44, 65, 66 accounting for minus the integral over a unit periodic cube of the LS influence function shifted to the Coulombic limit at infinitesimal distances. Note that Eq. 7 includes a pairwise term and a self-term, but no net-charge term of the form
| (9) |
The inclusion of such a term has been suggested as physically meaningful,67, 68 but is not implemented in standard MD simulation programs at present, or in the calculations performed here. Tinfoil boundary conditions25 were applied as well (no surface term in Eq. 7) and the calculated free energies are all intrinsic33 (no contribution associated to the crossing of an air-liquid interface). In practice, LS calculations are typically performed using Ewald summation,26 particle-particle-particle-mesh27 (P3M), (smooth) particle-mesh-Ewald28, 29 (PME, SPME), or fast-multipole-Ewald30 (FME) methods. The choice of a specific algorithm influences the numerical evaluation but not the physics of the interaction.
Correction schemes for the raw charging free energies
The goal of a correction scheme for finite-size effects is to provide an estimate for the term ΔΔGCOR in Eq. 3. For a given ligand environment, i.e., protein-bound or free in solution, this term will correct the raw charging free energy ΔGMD,PBC calculated from the MD simulations into a corrected charging free energy ΔGMD,NBC corresponding to the situation of a macroscopic system with Coulombic electrostatics under non-periodic boundary conditions. Two alternative correction schemes are proposed here, referred to as the numerical and analytical schemes, their basic principle being illustrated schematically in Figure 2. As explained at the end of Sec. 1, the terms numerical and analytical refer to the evaluation of three of the four components of ΔΔGCOR, the discrete solvent correction term being the same in the two schemes. In the numerical scheme, these three terms are not disentangled and calculated via separate PB calculations at all relevant box-edge lengths. In the analytical scheme, these terms are disentangled and depend analytically on the box-edge length, requiring a single set of PB calculations at a chosen reference box size.
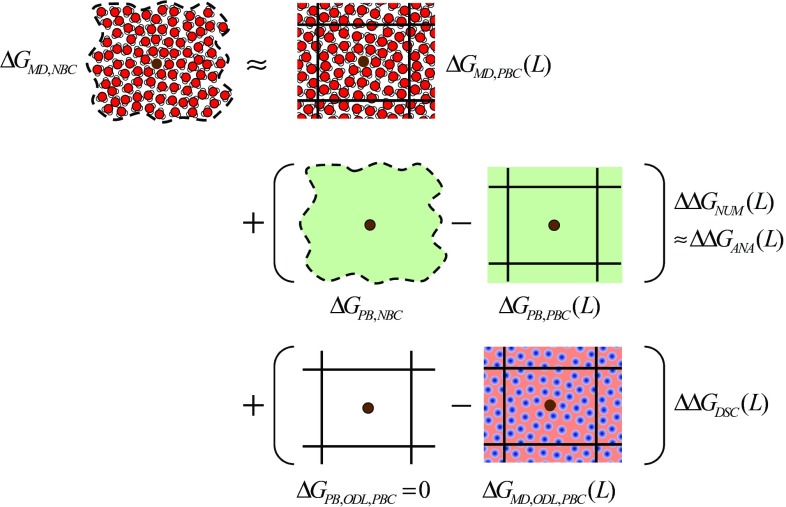
Figure 2.
The working principle of the correction schemes to correct a binding free energy calculated using molecular dynamics (MD) to a value exempt of finite-size artifacts is illustrated conceptually. Top row: a raw charging free energy ΔGMD,PBC calculated based on explicit-solvent MD simulations under periodic boundary conditions (PBC) considering a cubic computational box of edge length L and using lattice-sum electrostatics (actual simulation situation) is to be corrected into a corresponding size-independent value ΔGMD,NBC corresponding to explicit solvation under non-periodic boundary conditions (NBC) in the macroscopic regime and using Coulombic electrostatics (ideal bulk situation). The brown sphere represents the solute and the water molecules the explicit solvent. The wavy dashed line symbolizes the boundary of a macroscopic system under NBC and the straight solid lines symbolize the boundaries between periodic replicas of the computational box under PBC. The correction involves two terms. Middle row: the first term accounts for the corresponding change of boundary conditions (PBC → NBC) based on a continuum-electrostatics Poisson-Boltzmann (PB) model. It can be evaluated using a numerical (Sec. 2C) or an analytical (Sec. 2D) scheme, resulting in corresponding estimates ΔΔGNUM or ΔΔGANA given by Eqs. 12, 14. The green shade represents the dielectric continuum accounting for the solvent in PB. Bottom row: the second term ΔΔGDSC is a discrete solvent correction that accounts for the change of solvent description upon changing the model resolution (PB → MD) in the orientational disorder limit (ODL) for the solvent (i.e., in the absence of intermolecular orientational correlation between the solvent molecules). It can be evaluated analytically for a solvent model with a single van der Waals interaction site (Sec. 2E), according to Eq. 30. In the implicit-solvent PB model, a solvent in the ODL is non-solvating. In the explicit-solvent MD model, the average electric potential within the solvent molecules (e.g., negative for a water model with a negative central charge and positive peripheral charges; shown in blue) is offset by a constant potential (e.g., positive for water; shown in pink) so as to satisfy the constraint of vanishing average potential over the box. This offset potential is responsible for an artifactual contribution −ΔΔGDSC to ΔGMD,PBC (e.g., for water in the ODL, apparent solvation of negatively charged solutes and anti-solvation of positively charged solutes). The correction schemes (Sec. 2B) are defined by Eqs. 10, 11 for the numerical and analytical variants.
The principle of the numerical correction scheme follows from an idea previously developed in Refs. 20, 21, 22, 23, 24, 31, 32, 34, 35, 69, 70, 71, 72, 73, 74, 75, and probably originating from Ref. 46 (see Figure 1 therein). Due to computational limitations, only the quantity ΔGMD,PBC can be calculated in the context of explicit-solvent MD simulations, the quantity ΔGMD,NBC being inaccessible. However, in the context of continuum-electrostatics PB calculations, both of the corresponding quantities ΔGPB,NBC and ΔGPB,PBC can be evaluated numerically, the latter considering a box of the given edge length L, by selecting appropriate boundary conditions. The difference ΔΔGNUM = ΔGPB,NBC − ΔGPB,PBC thus provides a continuum-electrostatics estimate for the correction term required to eliminate three of the four types of finite-size errors listed in Sec. 1 (points 1–4), namely, periodicity-induced net-charge interactions, periodicity-induced net-charge undersolvation, and residual integrated potential effects. The remaining contribution is specific to the explicit-solvent MD approach, and must still be included in the form of an additional discrete solvent correction (DSC) term ΔΔGDSC. As a result, the form of Eq. 3 defining the numerical (NUM) correction scheme reads
| (10) |
The procedures for evaluating ΔΔGNUM and ΔΔGDSC are described in Secs. 2C, 2E, respectively. The numerical correction scheme is formally exact within the limits of the continuum-electrostatics approximation and the numerical precision of the PB calculations.
The principle of the analytical correction scheme is to provide an approximate estimate ΔΔGANA for the term ΔΔGNUM, based on explicit expressions for the three types of finite-size errors encompassed in this correction term. Here also, a DSC term must be added explicitly. As a result, the form of Eq. 3 defining the analytical (ANA) correction scheme reads
| (11) |
The procedures for evaluating ΔΔGANA and ΔΔGDSC are described in Secs. 2D, 2E, respectively, where ΔΔGANA (unlike ΔΔGNUM) is written explicitly as a sum of contributions corresponding to distinct physical effects (see Eq. 14 below). Although this scheme is analytical, it still relies on three parameters that must be evaluated numerically on the basis of PB calculations, so that the term quasi-analytical might be more appropriate. This scheme is technically an approximation, but its accuracy is excellent in practice (see Sec. 4E) and its application is simpler, so that it is the scheme recommended by the authors. The relative merits of the two schemes are further discussed in Sec. 5.
Owning to their typically negligible magnitudes, the two proposed schemes omit two correction terms considered in previous work. These are the terms labeled C2 and D in Refs. 31, 32, 34, 35 concerning monoatomic ion solvation and accounting, respectively, for the existence of an interfacial potential at the solute-solvent boundary and for a possibly inaccurate permittivity of the solvent model employed. On the other hand, the term B therein corresponds to ΔΔGANA (in the special case of a monoatomic spherical solute) and the term C1 to ΔΔGDSC, while the term A is irrelevant for lattice-sum methods. Relative to the work of Ref. 36 on the binding of simple ions to model receptors, the contribution ΔApol + ΔAdir therein corresponds to ΔΔGNUM, ΔApsum corresponds to ΔΔGDSC, and ΔAexc, although relevant,67, 68 is omitted here as not pertaining directly to finite-size effects.
Numerical correction scheme for finite-size effects
The numerical (NUM) correction scheme relies on the application of Eq. 10, where ΔΔGNUM is given by
| (12) |
The first term, ΔGPB,NBC, is obtained by numerical evaluation of the charging free energy of the ligand in a given environment, i.e., protein-bound or free in solution, based on a PB calculation performed under NBC. The result of such a calculation is in principle independent of the size of the computational domain considered, provided that this domain is sufficiently large for the long-distance surface boundary condition employed in the calculation to represent an adequate approximation. A distance of about 1 nm between the solute surface and the box wall is typically sufficient. The second term, ΔGPB,PBC, is obtained by a corresponding evaluation of the charging free energy of the ligand in the same environment based on a PB calculation performed under PBC, considering a box of the same edge length L as used in the MD simulation.
The physical parameters of these PB calculations are the box-edge length L (PBC only), the relative dielectric permittivity ɛI of the solute interior, the relative dielectric permittivity ɛS of the solvent, the inverse Debye screening length κ and Stern layer thickness Rκ of the counter-ion atmosphere (if counter-ions are present), and the solute-solvent interface definition (e.g., van der Waals, solvent-accessible contact surface, or solvent-accessible probe-centered surface). For a given ligand environment and given a specific choice for these parameters, the PB charging free energy of the ligand under either NBC or PBC is evaluated as
| (13) |
Here, ΔGHOM[A] and ΔGHET[A] represent electrostatic free energies calculated using the PB solver considering charges of set A (L: ligand charges; P + L: protein and ligand charges), either in a homogeneous (HOM; interior and exterior permittivities set to ɛI, inverse Debye screening length set to zero) or a heterogeneous (HET; interior permittivity set to ɛI, exterior permittivity set to ɛS, and inverse Debye screening length set to κ) dielectric environment, while ΔUDIR[A] represents a direct (vacuum) electrostatic energy calculated by summation (Coulomb sum for NBC, lattice sum for PBC) considering the charges of set A and a homogeneous permittivity ɛI. For the ligand free in solution, the protein set (P) is omitted. Additional details on these PB calculations are provided in Sec. 3B.
Correctly connecting the MD and PB calculations requires two important considerations. First, although the appropriate physical value for the effective dielectric permittivity of a protein interior is matter of debate,76, 77, 78, 79, 80 the value to be used for the correction of MD simulation results relying on a non-polarizable force field is simply ɛI = 1. All the PB calculations reported in this article were carried out using this value. Second, although the PB model is able to account for the presence of an overall neutral counter-ion atmosphere by means of the parameter κ of the linearized PB equation, it will lead to incorrect results for ΔΔGNUM when counter-ions are included during the MD simulations to neutralize the protein charge, possibly along with an excess of neutral salt. In this case, the best approximate solution for the application of the numerical correction scheme is to explicitly introduce a neutralizing charge density at the surface of the protein prior to performing the PB calculations, possibly along with the use of a non-zero κ value. All the PB calculations reported in this article concerning the numerical correction scheme for systems with counter-ions were carried out using this approach, albeit with a zero κ value. However, tests with non-zero κ values (reported in Tables S2 and S4 of the supplementary material154) showed a negligible influence of this parameter on the results. The details concerning the generation of the neutralizing surface charge density are provided in Sec. 3B. It is important to stress that the neutralizing charge density at the protein surface is only included in the PB calculations to model the neutralizing counter-ion atmosphere present in the MD simulations including explicit counter-ions, and is located at the protein surface because the counter-ion density will be highest in this region. When no explicit counter-ions are included in the MD simulation, the system is implicitly neutralized by a homogeneous neutralizing background charge density, in the MD as well as in the PB calculations. Note that even when explicit counter-ions (MD) and neutralizing surface charge density (PB) are included, they only neutralize the net protein charge, the ligand charge still being neutralized by a homogenous background charge.
Analytical correction scheme for finite-size effects
The analytical (ANA) correction scheme relies on the application of Eq. 11, where ΔΔGANA is an approximation to ΔΔGNUM given by
| (14) |
The first three terms in the right-hand side of this equation are required to eliminate three of the four types of finite-size errors listed in Sec. 1 (points 1–4), namely, periodicity-induced net-charge interactions (NET), periodicity-induced net-charge undersolvation (USV), and residual integrated potential effects (RIP). The fourth term is empirical (EMP). It is introduced to ensure that Eq. 14 reproduces the exact analytical result in the special case of a single point charge at the center of a spherical cavity,20 and can be viewed as a small adjustment to the undersolvation term ΔΔGUSV. The procedures for evaluating ΔΔGNET, ΔΔGUSV, ΔΔGRIP, and ΔΔGEMP are described in turn in Secs. 2D1, 2D2, 2D3, 2D4.
In the equations provided below, note that: the Avogardo constant (NA = 6.02214179 × 1023 mol−1) is never included explicitly, being considered as a mere unit conversion factor; in the units most convenient for the present article, the commonly occurring prefactor (4πɛo)−1 evaluates to 138.93545585 kJ nm e−2 mol−1, where ɛo is the permittivity of vacuum and e the elementary charge (e = +1.602176487 × 10−19 C); the static relative dielectric permittivity ɛI of solute interiors is never written explicitly but automatically set to 1, as discussed in Sec. 2C. A number of quantities are also conveniently already defined here: the net charge of the protein is noted QP; the net charge of the ligand is noted QL; the edge length of the cubic computational box is noted L; the static relative dielectric permittivity of the solvent is noted ɛS; the cubic Coulomb integration constant44, 66, 81, 82, 83 is ; the cubic lattice-sum (Wigner) integration constant25, 44, 65, 66 is ξLS ≈ −2.837297. For the ligand free in solution, the protein charge QP should to be set to zero.
The remarks made at the end of Sec. 2C concerning the application of the numerical correction scheme to MD simulations involving neutralizing counter-ions also apply to the analytical scheme. In this case, one may as well introduce a neutralizing charge density at the surface of the protein prior to performing the PB calculations. However, an even simpler approximate solution is to apply the analytical scheme with a protein charge QP artificially set to zero, accounting for an effective surface neutralization of the protein by the counter-ions. All the PB calculations reported in this article concerning the analytical correction scheme for systems with counter-ions were carried out using the latter approach. Note that unlike the numerical scheme, the analytical scheme is at present unable to account for the presence of an overall neutral counter-ion atmosphere by means of the parameter κ of the linearized PB equation. As a result, all the PB calculations reported in this article concerning the analytical correction scheme for systems with counter-ions were carried out using a zero κ value. However, tests with non-zero κ values in the context of the numerical scheme (reported in Tables S2 and S4 of the supplementary material154) showed a negligible influence of this parameter on the results.
Correction for periodicity-induced net-charge interactions
The first term in the right-hand side of Eq. 14, ΔΔGNET, corrects for periodicity-induced net charge interactions (NET). These spurious interactions involve the protein-ligand complex in the reference computational box, its periodic replicas, and the homogeneous neutralizing background charge density filling the infinite periodic system,20, 21, 23, 24, 25, 31 and are a consequence of the use of periodic boundary conditions in the MD simulations. For lattice-sum electrostatics and considering the leading net-charge component of these interactions, the corresponding correction term reads20
| (15) |
This term is solvent-independent, positive when QP and QL are of the same sign, i.e., when the charging of the ligand increases the magnitude of the net system charge, and vanishes slowly in the limit L → ∞. For the ligand free in solution, or when the MD simulation of the protein-ligand complex is carried out in the presence of neutralizing counter-ions, QP should to be set to zero in Eq. 15. In the case of polyatomic charge distributions, the term ΔΔGNET only accounts for the leading net-charge component of the through-periodicity and charge-background interactions, higher order contributions being accounted for by the residual integrated potential term ΔΔGRIP (Sec. 2D3).
Note that ΔΔGNET is exactly equal to the contribution that would be introduced into the charging free energy by the net-charge term ULS,NET of Eq. 9. This net-charge term is not implemented in standard MD simulation programs at present, but there may be good reasons for doing so.67, 68 If this term is included in the lattice-sum energy during the MD simulations, ΔΔGNET must be omitted from the correction scheme.
Correction for periodicity-induced undersolvation
The second term in the right-hand side of Eq. 14, ΔΔGUSV, corrects for periodicity-induced net-charge undersolvation (USV). This undersolvation arises because the solvent in the periodic replicas of the reference computational box is perturbed by the periodic copies of the protein-ligand complex, and thus essentially unavailable for the solvation of the complex in the reference computational box.20, 21, 23, 24, 31 This effect is a consequence of the use of periodic boundary conditions in the MD simulations, and can be viewed as resulting from the finite effective concentration of the charged solute in the periodic system. For lattice-sum electrostatics and considering the leading net-charge component of this effect, the corresponding correction term reads20
| (16) |
This term, which is equal to ΔΔGNET in Eq. 15 multiplied by −(1 − ɛS−1), is solvent-dependent, negative when QP and QL are of the same sign, i.e., when the charging of the ligand increases the magnitude of the net system charge, and vanishes slowly in the limit L → ∞. It decreases in magnitude with decreasing polarity of the solvent, being maximal for a conducting solvent with ɛS → ∞ and zero for a non-polar solvent with ɛS = 1. For the ligand free in solution, or when the MD simulation of the protein-ligand complex is carried out in the presence of neutralizing counter-ions, QP should to be set to zero in Eq. 16. In the case of polyatomic charge distributions within finite-sized cavities, the term ΔΔGUSV only accounts for the leading net-charge component of the undersolvation effect, higher order contributions being accounted for by the residual integrated potential term ΔΔGRIP (Sec. 2D3) and the empirical correction term ΔΔGEMP (Sec. 2D4).
The sum of the terms ΔΔGNET and ΔΔGUSV is equal to ΔΔGNET multiplied by ɛS−1. For polar solvents such as water and for the computational boxes typically employed in protein MD simulations employing lattice-sum methods, this sum is relatively small compared to, e.g., the contribution of missing solvation shells around a finite droplet of the same volume under non-periodic boundary conditions. This gives the misleading impression that lattice-sum simulations of charged systems present more limited finite-size effects compared to corresponding droplet simulations. In fact, a proper comparison should involve a lattice-sum energy including the net-charge term67, 68ULS,NET of Eq. 9. In this case, the correction term ΔΔGNET would be omitted, leading to the sole correction term ΔΔGUSV. The latter term is large, comparable in magnitude to, e.g., the contribution of missing solvation shells around a non-periodic droplet of the same volume, and presents a dependence on ɛS that appropriately reflects the contribution of missing solvation shells.
Correction for residual integrated potential effects
The third term in the right-hand side of Eq. 14, ΔΔGRIP, corrects for the effect of the residual integrated potential (RIP). The net-charge self-interaction and undersolvation terms ΔΔGNET and ΔΔGUSV would be sufficient to correct for the error in the charging free energy if the protein and ligand were both point charges without solvent-excluded volume and located at the same position in space (omitting the infinite direct Coulomb interaction, which is identical under non-periodic and periodic boundary conditions and thus does not affect the associated periodicity-induced perturbation). However, when the two species involve polyatomic charge distributions encompassed within distinct solvent-excluding envelopes, an additional finite-size effect must be considered. This effect originates from the different boundary conditions applied for the electric potential in calculations (PB or MD) performed under non-periodic and periodic boundary conditions. When using periodic boundary conditions, the average electric potential over the computational box is set to zero, a consequence of omitting the zero-vector term from the reciprocal-lattice summation. Under non-periodic boundary conditions, the corresponding constraint is that of a vanishing value at infinity, imposed in practice in the PB calculation by enforcing an appropriate long-distance potential value at the surface of the computational domain. In the reference situation (naked point-charges at the same position), this effect of this discrepancy is encompassed within ΔΔGNET and ΔΔGUSV. In the real situation (charge distributions within distinct cavities), this discrepancy induces an additional offset potential between the two representations that must be compensated for in the charging free energy by a correction term ΔΔGRIP.
The evaluation of ΔΔGRIP requires the calculation of the difference between the spatial integrals of the electric potential under non-periodic boundary conditions corresponding to the situation of a charge distribution in a cavity within the solvent (real situation) versus a naked point charge of the same total magnitude in the solvent (reference situation). The resulting difference in integrated potential is termed here a RIP. Given the residual integrated potentials IP and IL corresponding to the protein and ligand charge distributions, respectively, within the protein-ligand cavity in solution, the correction term ΔΔGRIP to the charging free energy of the ligand reads
| (17) |
This equation is justified as follows. In the uncharged state of the ligand, the change from non-periodic to periodic boundary conditions induces a residual (real minus reference situations) offset potential −L−3IP to enforce the constraint of vanishing average potential over the computational box, which is probed by a total system charge QP. In the charged state of the ligand, this change induces a residual potential offset −L−3(IP + IL), which is probed by a total system charge (QL + QP). These considerations concerning the nature of the perturbation immediately lead to the correction term of Eq. 17. For the ligand free in solution, IP and QP should to be set to zero in this equation, and IL should be evaluated considering the free ligand cavity (no protein). When the MD simulation of the protein-ligand complex is carried out in the presence of neutralizing counter-ions, QP should to be set to zero in Eq. 17, IP and IL being calculated in the same way as in the absence of counter-ions.
The evaluation of the quantities IP and IL relies on the observation that in both the reference and the real situations, the electric potential has the same limiting dependence at long distances from the solute cavity, i.e., in QPɛS−1r−1 for IP and in QLɛS−1r−1 for IL. In other words, the potential differences contributing to these integrals are short-ranged, only being significant inside and in the close neighborhood of the protein-ligand cavity. It is thus possible, as illustrated in Figure 3, to evaluate them numerically from PB calculations performed under non-periodic boundary conditions considering a heterogeneous (interior permittivity set to ɛI, exterior permittivity set to ɛS, and inverse Debye screening length set to κ) dielectric environment based on the protein-ligand cavity and a sufficiently large box-edge length Lref, as
| (18) |
where
| (19) |
and
| (20) |
Here, X = P or L denotes the protein or the ligand charge distribution, QX a naked (i.e., no solvent-excluded volume) point charge of the same magnitude, and ϕ the electric potential. The BHET integrals are taken over the entire cubic computational domain (box) of edge Lref used in the PB calculation. Due to the short-range nature of the contributions to a RIP, IX in Eq. 18 becomes essentially independent of Lref for sufficiently large boxes. However, an important requirement for the correct application of Eqs. 18, 19, 20 based on finite-system calculations is that in all PB calculations involved, the ligand has to be centered within the computational domain. In this case, and restricting the application of the analytical correction scheme to situations where the inverse Debye screening length κ is zero, the two calculations concerning naked point charges (Eq. 20 with X = P or L) can be omitted and substituted by the analytical expression
| (21) |
where ξCB ≈ −2.380077 is the cubic Coulomb integration constant,44, 66, 81, 82, 83 representing minus the integral of the Coulomb influence function (r−1) over a unit cube. All results reported in this article concerning the analytical correction scheme relied on Eqs. 18, 19, 21 based on two PB calculations (Eq. 19 with X = P or L) centered on the ligand and using ɛI = 1. For systems with neutralizing counter-ions, these PB calculations were performed with a zero κ value, as required for the use of Eq. 21, and with QP = 0 in Eq. 17, as discussed above. Additional details on these PB calculations are provided in Sec. 3B. Note that unlike charging free energies, the charge-RIP products involved in Eq. 17 are exempt of any spurious contribution related to the self-energy of the gridded charges in a PB calculation (mutual interaction of the gridded fractional charges representing a point charge).
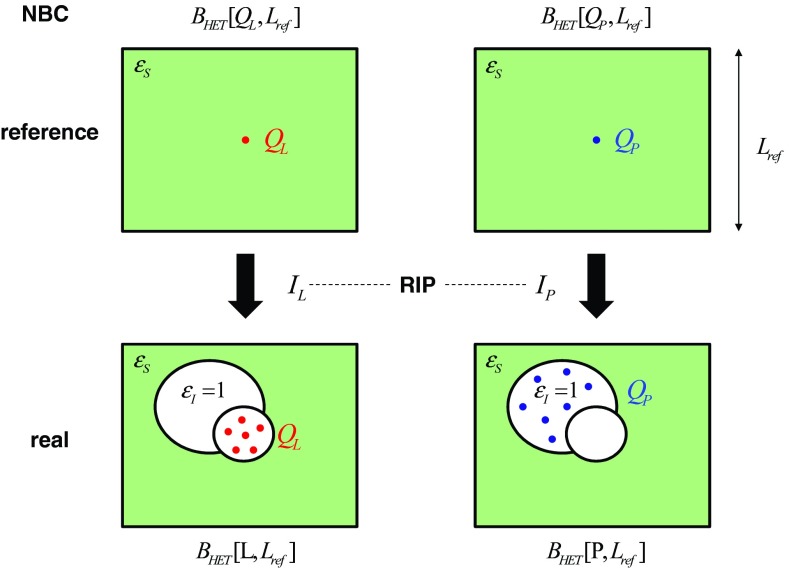
Figure 3.
The calculation of the residual integrated potentials (RIPs) required for application of the analytical correction scheme is illustrated conceptually. Bottom row: real situation of charge distributions inside a cavity within the solvent. Top row: reference situation of a naked point charge of the same total magnitude in the solvent. Left column: calculation of the RIP IL corresponding to the ligand charge distribution (total charge QL). Right column: calculation of the RIP IP corresponding to the protein charge distribution (total charge QP). The RIPs are calculated as a difference between the electric potential corresponding to the reference and real situations, integrated over a cubic computational domain of edge Lref, according to Eq. 18. The potentials themselves are calculated from Poisson-Boltzmann (PB) calculations under non-periodic boundary conditions (NBC) considering a heterogeneous (HET) dielectric environment (interior permittivity set to 1, exterior permittivity set to ɛS) as defined by the protein-ligand cavity. For all calculations, the naked point charge (reference situation) or the ligand (real situation) must be centered within the computational domain. In the case of the free ligand in solution, the protein calculation is omitted (IP = 0 and QP = 0) and the ligand calculation involves the ligand cavity only. The evaluation of IL,SLV in Eq. 27 requires a calculation analogous to that represented in the left column, the only difference being the use of a homogeneous (HOM) permittivity of 1 (for both the interior and the exterior) in the calculation.
Additional empirical correction term
The fourth term in the right-hand side of Eq. 14, ΔΔGEMP, is an empirical (EMP) addition, introduced to ensure that this equation produces the appropriate correction term in the special case of a spherical cavity of radius R with a point charge at its center. In this special case, an analytical solution is available for ΔΔGANA from Ref. 20 (see Eq. (41) therein, adapted here to the ligand charging situation and reformulated as a correction term), namely,
| (22) |
In this special case, analytical expressions can also be formulated for the residual integrated potentials IP and IL of Eq. 18. For a spherical cavity of radius R encompassing a point charge QX at its center (with X = P or L), the potential ϕHET, X of Eq. 19 only differs from the potential of Eq. 20 inside the sphere, the difference being
| (23) |
The three terms between square brackets account for the electric potential caused by the central charge, the reaction-field potential of the solvent, and the negative of the electric potential in the reference naked point charge situation, respectively. Integrating over the sphere gives
| (24) |
Inserting this analytical result into Eq. 17 and considering also Eqs. 15, 16, one sees that the sum ΔΔGNET + ΔΔGUSV + ΔΔGRIP is equivalent to ΔΔGANA,SPH in Eq. 22, except for the last term in L−6R5. For this reason, ΔΔGANA in Eq. 14 has been adjusted to include a fourth correction term ΔΔGEMP defined by
| (25) |
This term represents an adjustment of the net-charge undersolvation term ΔΔGUSV for the presence of the solute cavity. It arises in the spherical cavity case as a higher order term in a Rayleigh expansion of the reaction-field potential of the solvent under periodic boundary conditions (see Appendix B in Ref. 20).
In the protein-ligand case, RL represents an effective radius for the ligand within the protein-ligand complex. Since the corresponding term in Eq. 22 involves the prefactor (1 − ɛS−1), RL should be considered as a solvation radius. Thus, this effective radius is defined here as
| (26) |
where IL,SLV represents the solvation contribution to the residual integrated potential IL of the ligand, namely,
| (27) |
The quantities BHOM are the analogs of the quantities BHET in Eq. 18 with X = L (i.e., only involving the ligand charges), but corresponding to the situation of a homogeneous dielectric medium of permittivity ɛI (vacuum situation). They are evaluated in a similar way, by performing a PB calculation for BHOM[L, Lref] and by application of Eq. 21 with ɛS substituted by ɛI for BHOM[QL, Lref]. The application of the analytical scheme therefore requires three PB calculations in total (to evaluate IP, IL, and IL,SLV). Additional details on these PB calculations are provided in Sec. 3B.
Considering again the special case where the protein and ligand are (excluded) point charges at the center of a spherical cavity of radius R, one has IL,SLV = IL in Eq. 27. Inserting Eq. 24 into Eq. 26 with X = L leads to RL = R, i.e., the effective solvation radius is as expected equal to the cavity radius. Given the full expression for ΔΔGANA in Eq. 14, the analytical result of Eq. 22 is then exactly recovered. In the general case, however, the empirical nature of Eq. 25 leads to a term ΔΔGEMP that only represents an approximate adjustment to ΔΔGUSV, taking into account the effective size of the protein-ligand complex but not its detailed shape. As a result, the analytical scheme is an approximation of the (formally exact) numerical scheme, with an error of order O[L−6] in the absence of counter-ions. In the presence of neutralizing counter-ions, possibly along with a neutral salt excess, additional approximations are involved in the analytical scheme when setting the inverse Debye screening length κ to 0 and taking effective account of charge neutralization by using QP = 0, which may further restrict the accuracy of the correction term.
Correction for discrete solvent effects
Both the numerical and the analytical correction schemes, see Eqs. 10, 11, involve a term ΔΔGDSC representing a discrete solvent correction (DSC). The physical origin of this term is similar to that of the residual integrated potential term ΔΔGRIP. However, unlike the latter term, it cannot be accounted for by comparing the results of PB calculations under periodic and non-periodic boundary conditions, because these calculations do not account for the discrete nature of the solvent molecules. As illustrated in Figure 2, this discrete solvent effect can be quantified in the context of a pure liquid sample in the orientational-disorder limit (ODL), i.e., in an idealized situation corresponding to the absence of intermolecular orientational correlations between the solvent molecules.22 In the implicit-solvent PB representation, due to the total absence of solvent polarization, a solvent in the ODL is non-solvating under any type of boundary conditions, i.e., inert with respect to the insertion of a test charge. However, in the explicit-solvent MD representation under periodic boundary conditions, the average electric potential generated by the isotropically tumbling solvent molecules is offset by a constant potential, so that the average potential over the box is zero. For example, considering a typical three-site water model with a negative central charge (oxygen atom) and positive peripheral charges (hydrogen atoms), the average potential generated by the solvent charges is negative within the molecules and zero outside, so that the homogeneous offset potential is positive everywhere. This offset potential contributes to the solvation free energy of a test charge in the MD representation of the ODL solvent. For example, for a three-site water model, it causes an apparent solvation of a negative test charge and an apparent anti-solvation of a positive test charge. The term ΔΔGDSC is introduced into the correction scheme to remove this artifact.
As discussed in detail in Ref. 22 (see also Ref. 33), for a solvent model with a single van der Waals interaction site, the offset potential induced by the discrete solvent effect within a periodic computational box filled with pure solvent in the ODL is given by
| (28) |
where MS and ρS are the molecular mass and density of the solvent, respectively, and γS is the quadrupole-moment trace of the solvent model relative to its single Waals interaction site. For a solvent model with n interaction sites {qi} at distances {ri} from the van der Waals interaction site, the latter quantity is defined as
| (29) |
Considering the excluded volume VC of the solute, the correction term ΔΔGDSC can thus be written
| (30) |
where ρS now represents the effective density of the solvent in the solvent-occupied region of the computational box. For the charging free energy of the ligand within the protein, the cavity volume VC is defined by the excluded volume of the protein-ligand complex, while for the free ligand, it is defined by the excluded volume of the ligand alone. For simulations with counterions, the ion excluded volume should also be included within VC (constant number of ions) or ρS (constant concentration of ions). It should be stressed that ΔΔGDSC only encompasses a part of the correction for the spurious potential offset induced by the solvent, namely, the component corresponding to the ODL situation, which cannot be captured in a PB calculation. In reality, the solvent surrounding the protein-ligand complex is polarized and not in an ODL situation, but this polarization-related component is already included in the residual integrated potential term ΔΔGRIP.
Whereas the correction terms ΔΔGNUM and ΔΔGANA can really be called corrections for finite-size effects, i.e., they vanish in the limit of infinitely large box sizes, this is not the case for the term ΔΔGDSC. To make the distinction explicit, this term can be rewritten as the sum of an infinite-system discrete solvent correction term (DSI) and an associated finite-size adjustment (DSF), i.e.,
| (31) |
where
| (32) |
is a constant independent of L whereas
| (33) |
is size-dependent and vanishes in the limit L → ∞. The contribution of ΔΔGDSI will often cancel out when considering a thermodynamic cycle in which the two charging legs, which involve the same QL, are carried out in the same solvent. This is in particular the case for binding free energy calculations (Sec. 2A). A notable exception is the calculation of partition coefficients, where the contribution of ΔΔGDSI to the calculated transfer free energy must be considered.
Finally, note that Eq. 30 implicitly assumes the existence of a relationship of the form
| (34) |
between the number of solvent molecules NS in the computational box, its edge length L, and the solute cavity volume VC. This assumption allows ΔΔGDSC to be written as an explicit function of L, which is convenient for discussing the nature of this term, but not really necessary in practice. Considering that NS is an input parameter of the MD simulations, ΔΔGDSC can also be calculated directly as
| (35) |
In this case, the formulation of an estimate for VC becomes unnecessary. Equation 35 is actually the exact equation for ΔΔGDSC, whereas Eq. 30 is a convenient approximation.
COMPUTATIONAL DETAILS
Explicit-solvent simulations
All explicit-solvent MD simulations were carried out using the GROMACS 4.0.7 program61 and employed a slightly modified AMBER99SB force field84 along with the TIP3P water model.85 The slight modification of AMBER99SB involved the replacement of the van der Waals interaction parameters of the hydrogen atom type HO by those of the hydrogen atom type H. The simulations were performed under periodic boundary conditions in cubic computational boxes of edge L encompassing one solute molecule, either the free ligand or the protein-ligand complex including NB bound water molecules, surrounded by NS free water molecules. The solute molecule or molecule group was kept entirely frozen during the simulations, with all atoms fixed in space, including the bound water molecules in the case of the protein-ligand complex. The simulations were carried out in the canonical (NVT) ensemble at a reference temperature T = 300 K and within fixed box volumes V = L3. Thermostatting was ensured by mild Langevin coupling (friction coefficient γ = 1.0 ps−1; see Ref. 86 for details). The equations of motion were integrated using the leap-frog stochastic dynamics integrator87 with a timestep of 2 fs. Position constraints on the solute atoms were enforced by coordinate resetting at every timestep. The solvent molecules were constrained using LINCS.88 The Lennard-Jones interactions were smoothly switched off after 0.8 nm and truncated at 0.9 nm, using a pairlist with 1 nm cutoff which was updated every 10 steps. Electrostatic interactions were calculated using the particle-mesh Ewald (PME) lattice-sum method29 with tinfoil boundary conditions, a real space cutoff of 1 nm, a spline order of 6, a grid spacing of 0.1 nm, and a relative tolerance between long- and short-range energies of 10−6.
The topology and coordinates of engineered cytochrome c peroxidase (CCP W191G “Gateless,”47, 48 289 residues, see Figure 1) bound to 2-amino-5-methylthiazole (protonated form, 14 atoms, net charge QL of +1 e) were prepared as in Ref. 48 with a net protein charge of −5 e, and solvated in the smallest cubic box (7.42 nm edge) using the GROMACS tool genbox.61 Note that the 2-amino-5-methylthiazole pose employed is not the experimentally observed binding pose, but rather the pose of the same ligand bound to the related protein CCP W191G.89 Water molecules in the binding cavity within 0.9 nm of any atom of the ligand were identified and included into the set of bound (frozen) water molecules. The system was then equilibrated at constant volume for 2 ns. During this simulation, several other water molecules became trapped in different solvent-accessible cavities of the protein, causing a noticeable step in the average instantaneous charging energy ⟨ΔU⟩ (see Eq. 6). These water molecules were added to the set of bound water molecules. This process of 2 ns equilibration and addition of new trapped water molecules to the set of bound water molecules was repeated three more times, after which ⟨ΔU⟩ remained stable throughout the trajectories.
Starting from this equilibrated box of 7.42 nm edge, larger boxes with edges up to 11.02 nm were generated by increasing the box size in steps of about 0.4 nm, each time applying genbox to introduce additional water molecules on all sides of the existing ones and removing the genbox-inserted water molecules which were more than 0.4 nm inside the walls of the expanded box. Systems involving net protein charges of 0, +3, or +9 e were then generated in the following way: identifying the five glutamate residues with highest estimated pKa values and converting them to glutamic acids (net protein charge of 0), converting three additional glutamate residues to glutamic acids (net protein charge of +3 e), and converting five additional glutamate residues to glutamic acids and one aspartate residue to aspartic acid (net protein charge of +9 e). The pKa estimations were performed using the program MCCE.90, 91 The four protein charge isoforms can be thought of as corresponding to different pH conditions, although the correspondence between protein charge state and pH conditions remains only approximate. For one system (net protein charge of 0), larger boxes with edges up to 13.02 nm were also created starting from the box of 11.02 nm edge length. For the free ligand simulations, the same ligand topology and coordinates were used as in the complex,48 and boxes with edge lengths ranging from 3.05 to 13.49 nm were generated in an analogous fashion.
For one system (net protein charge of +9 e), a variant of the protein charge distribution was also considered, including an additional quasi-isotropic quadrupole moment, as illustrated in Figure 1. The additional charges were introduced at atomic sites, and involve a central point charge of magnitude −80 e at atom HA1 of residue Gly112 along with 36 peripheral sites of charges summing up to +80 e located at atoms in the distance range 8.1–8.5 nm from the central charge. The charges added on the peripheral atoms were optimized based on 3 × 36 test points located along the vectors connecting the center of the quadrupole to each of the peripheral atoms, at 1.50, 2.25, and 3.00 times their distance to the center. The optimization was performed so as to minimize the sum of the total unsigned electric potential caused by the complete added charge distribution at all the test points. Nevertheless, due to its discretization onto atomic sites, this added charge distribution only approximates an isotropic quadrupole and still exerts a small electrostatic field beyond its peripheral shell.
For two systems (net protein charges of −5 and +9 e), additional simulations were also performed in the presence of a neutralizing atmosphere of sodium and chloride ions corresponding to a molal salt concentration of about 0.1 mol kg−1. The ions were added using the GROMACS tool genion,61 used independently for either system and at each box size. Ions were added by replacement of bulk water molecules, first with just a neutralizing amount of ions (matching the charge QP of the protein alone), and then equal amounts of sodium and chloride ions to reach the desired salt concentration for a given box size.
The systems involving protein-ligand complexes were not pre-equilibrated at constant pressure. As a result, the effective solvent density in the boxes, determined by the application of the genbox tool based on pre-equilibrated pure-solvent configurations, may slightly deviate from the equilibrium density of the pure solvent model. For the free ligand system, the box sizes were slightly readjusted to enforce an effective solvent density close to that of the pure solvent. In practice, an approximate relationship of the form of Eq. 34 holds for the present systems with VC = 0.5 nm3 (free ligand) or 57.0 nm3 (protein-ligand complexes) along with ρS = 997 kg m−3 (experimental value for water at 300 K and 1 bar92), with deviations in NS of at most 3%.
All simulations of the protein-ligand complexes were carried out for 1 ns after 1 ns equilibration. The free ligand simulations were carried out for 9 ns after 1 ns equilibration. A simulation length of 1 ns provides sufficient convergence in the present case considering that the solute coordinates are fixed. It was also verified that no significant changes in ⟨ΔU⟩ occurred between the equilibration and production periods. Statistical uncertainties on the raw charging free energies ΔGMD,PBC were estimated in two different ways, depending on the system. For most systems, the standard error on the mean of ⟨ΔU⟩0 and ⟨ΔU⟩1 was monitored (1 ps sampling interval and accounting for the statistical inefficiency in the time series93), and propagated into an error on ΔGMD,PBC via Eq. 6. For three systems (net protein charge of 0 and the two systems with ions), three independent calculations of ΔGMD,PBC were performed using different initial velocities, and the corresponding standard deviation is reported as the estimated error in ΔGMD,PBC.
Continuum-electrostatics calculations
The continuum-electrostatics calculations were carried out using a custom finite-difference PB solver written in C and implementing a preconditioned Cholesky conjugate-gradient algorithm, commonly used in programs such as UHBD.51, 52 In addition to solving the linearized PB equation under NBC, this program also permits the use of PBC as described in Appendix A of Ref. 20. Routines for the calculation of the direct interaction energy under NBC as a Coulomb sum or under PBC as a lattice sum are also included, the latter implementing Ewald summation.26
These calculations were used to evaluate the terms of Eq. 13 in the numerical correction scheme, or the first terms in the right-hand side of Eqs. 18, 27 in the analytical correction scheme. In the former case, the solute position within the PB computational domain is not critical, i.e., it only affects the numerical accuracy of the results, and the calculations were centered on the center of the protein-ligand complex (or ligand in the free ligand case). In the latter case, the solute position is critical and directly impacts the results. In this case, the calculations must be centered on the ligand, irrespective of its surroundings. In both cases, the center was defined in terms of minimal and maximal atom coordinates along the three Cartesian axes. In the protein-ligand complex, the NB bound water molecules (at fixed coordinates in the MD simulations) were treated as integral part of the solute. The same atomic coordinates were used as in the MD simulations. The atomic charges were also taken from the AMBER99SB force field84 and the TIP3P water model85 (bound water molecules) used in the MD simulations.
The results of the PB calculations depend on the definition of the solute-solvent interface. In the present work, three choices were considered:94 van der Waals (VDW) surface, probe-contact solvent-accessible surface (CTC(RS)), and probe-center solvent-accessible surface (CEN(RS)), where RS is the radius of a spherical probe (solvent molecule) rolled over the VDW surface. Note that VDW = CTC(0) = CEN(0). All the calculations reported in the main article were performed with a CTC(RS) definition, most of them using RS = 0.14 nm as usually selected for the water molecule. The atomic radii defining the VDW surface were taken to be one-half of the Lennard-Jones sigma parameters (zero-energy point of the Lennard-Jones curve) of the AMBER99SB force field84 used in the MD simulations, including the altered HO atom type.
The remaining physical parameters of the PB calculations are: the subset of solute charges considered in the calculation; the system boundary conditions, NBC or PBC; the box-edge length L (PBC only); the relative dielectric permittivity ɛI of the solute interior, set to one for all calculations (see Sec. 2C); the relative dielectric permittivity ɛS of the solvent, set to 97 for all calculations as appropriate for the TIP3P water model;95 and the inverse Debye screening length κ and Stern layer thickness Rκ of the counter-ion atmosphere (if counter-ions are present). Given these choices, the PB solver can be used to produce grid-based finite-difference approximations for the electric potential over the computational domain in two situations. The electric potential ϕHOM in the homogeneous (HOM) situation corresponds to the electric potential generated by the charges considered in a system with homogeneous permittivity ɛI and no counter-ion screening. The electric potential ϕHET in the heterogeneous (HET) situation corresponds to the electric potential generated by these charges in a system with heterogeneous permittivity and in the possible presence of counter-ion screening, i.e., permittivity ɛI and no screening inside the solute cavity vs. permittivity ɛS and inverse Debye screening length κ outside the solute cavity, the latter beyond a distance Rκ from the solute surface.
The first terms BHET[P, Lref], BHET[L, Lref], and BHOM[L, Lref] in the right-hand-sides of Eqs. 18, 27 are calculated under NBC and represent integrals of ϕHOM or ϕHET based on specified sets of charges A (A = P or L), see Eq. 19 and its analog in the homogeneous case. The first four terms of the form ΔGHOM[A] and ΔGHET[A] in the right-hand side of Eq. 13 represent electrostatic free energies of the system of charges defined by set A (A = P or P + L). These free energies are given by
| (36) |
The quantity ΔGHOM[A] can in principle be calculated analytically under NBC,96 but was nevertheless evaluated numerically in the absence of a corresponding expression for PBC. The terms of the first two braces in the right-hand side of Eq. 13 account for the solvation contribution to the electrostatic free energy of the ligand-charged and the ligand-uncharged states of the protein-ligand complex, respectively. Note that the latter equation could also be rewritten as
| (37) |
where ΔGHOM[A,B] and ΔGHET[A,B] represent electrostatic free energies calculated considering set A as source charges and set B as probe charges (L: ligand charges; P: protein charges). The terms of the first two braces in the right-hand side of Eq. 37 now account for the solvation contribution to the ligand charging free energy in the ligand-uncharged and the ligand-charged states of the system, respectively, in tight analogy with the corresponding MD expression of Eq. 6. The terms of the third brace in the right-hand sides of Eq. 13 or 37 account for the remaining direct (vacuum) contribution to the ligand charging free energy, as a difference between the energy of the protein-ligand complex minus that of the protein alone. In the NBC calculation, the energy UDIR[A] corresponds to a Coulomb sum over all charge pairs in the set A (A = P or P + L). In the PBC calculation, the energy UDIR[A] corresponds to a lattice sum over all charge pairs in the set A, calculated as in Eq. 7. For the PB calculations, the numerical parameters were selected as follows.
All calculations relied on a common grid spacing l set to 0.05 nm. The corresponding numbers NG of grid points along each Cartesian direction are20L/l − 1 under NBC (surface boundary points handled implicitly) or L/l under PBC (periodic-connection point included explicitly). To minimize grid-discretization errors, the positioning of the solute relative to the grid points was the same for NBC and PBC calculations. Note that the use of a relatively fine grid spacing for these calculations is recommended. For comparison, the use of coarser grids with l set to 0.1 nm or 0.2 nm, respectively, results in changes in the calculated ΔΔGNUM values for the highest-charge protein (net charge +9 e) by 1.2 and 4.9 kJ mol−1, respectively (0.3 and 1.3 kJ mol−1, respectively, considering the systems with L > 10 nm).
Under NBC, the electric potential at the surface of the computational domain was defined by a Debye-Hückel approximation summed over all solute atoms (Eq. A3 in Ref. 20). Under PBC, the boundary condition on the electric potential is defined by the constraint of periodicity along with the requirement of vanishing average over the computational domain (see last paragraph of Appendix A in Ref. 20). Note that in this case, the neutralizing background charge must be explicitly added to the charge-density grid prior to the calculation. If this is not done, the periodicity constraint will induce a surface charge instead, which is not the target situation.
The implementation of the various solute-solvent interface definitions relied on a threefold finer grid. For CEN(RS), all fine-grid points within a distance RS beyond the atomic VDW radius of any atom were allocated to the interior region and all others to the exterior region. For CTC(RS), all fine-grid points within a distance RS of any fine-grid point of the exterior region of CEN(RS) were allocated to the exterior region and all others to the interior region. The fine grid was subsequently used to generate the three regular permittivity grids, shifted by l/2 relative to the charge-density and potential grids,20 using harmonic averaging97, 98 of the permittivity values (ɛI or ɛS) corresponding to the closest fine-grid points. The finite-difference solver was iterated until convergence within a relative tolerance of 10−5 for the residual.
The lattice-sum calculations under PBC relied on a truncated-parabola charge-shaping function of width a = L/2, no real-space cutoff, and reciprocal-space vectors with integer components up to ±200 along each Cartesian direction together with a cutoff of 200 on the norm. These settings ensure that the accuracy of the calculation is the same for all box sizes.
For the application of the numerical correction scheme to systems where the MD simulations involve neutralizing counter-ions, a neutralizing charge density must be introduced at the surface of the protein prior to performing the PB calculations (see Sec. 2C), possibly along with the use of a non-zero κ value. For these systems, involving net protein charges of −5 and +9 e, respectively, this was done here by introducing small counter charges at 3193 or 10 677 grid points (0.05 nm spacing), respectively, within 0.10–0.15 or 0.18–0.23 nm of the VDW surface of the protein-ligand complex. These distances reflect the ionic radii of sodium and chloride,33 respectively. The charges were determined so as to produce a Boltzmann distribution of electrostatic energy at 300 K assuming monovalent ions and based on a preliminary calculation of ϕHET under non-periodic boundary conditions in the absence of counter-ions. They sum up a total charge of −QP, i.e., neutralize the protein alone. In the subsequent calculations including these surface sites, they were assigned a zero radius and thus do not influence the definition of the protein-ligand cavity. In the main article, these calculations are only reported for the numerical scheme and with an inverse Debye screening length κ = 0. However, tests using these explicitly neutralized systems and the analytical scheme with κ = 0 or the numerical scheme with κ ≠ 0 led to very similar results (reported in Tables S2 and S4 of the supplementary material154). As noted at the end of Sec. 2C, this neutralizing surface charge density is only used in the PB calculations corresponding to MD simulations explicitly including counter-ions.
For all systems, calculations were performed for VDW, CEN(RS), and CTC(RS) solute-solvent interface definitions with RS ranging from 0.01 to 0.18 nm in steps of 0.01 nm, considering in each case box-edge lengths L ranging from 3 (free ligand) or 7 (protein-ligand complexes) to 15 nm in steps of 1 nm. Unless otherwise noted, the results reported in the main article correspond to CTC(0.14). For the numerical scheme, both the NBC and PBC calculations were performed using the same box-edge length, the results of the NBC calculation being essentially independent of this parameter, with a maximal deviation (smallest box size relative to largest one) of at most 0.2 kJ mol−1 over all the systems considered. Values of the numerical correction term ΔΔGNUM corresponding to the box edges L used in the MD simulations (spacing of about 0.4 nm) were interpolated from these data by fitting to a function of the form
| (38) |
where A1, A2, and A3 are fitting coefficients. The fit is typically excellent, with an error of at most 0.3 kJ mol−1 (at the smallest box size) over all the systems considered. Although the functional form of Eq. 38 is empirical, the error did not change significantly upon including 4th and 5th order terms. For the analytical scheme, the reference box-edge length Lref was set to 15 nm for all calculations.
RESULTS
Systems considered
Before discussing the results, it is useful to provide a brief summary of the systems considered and their nomenclature, as well as of the calculations performed and correction schemes applied. The situation of the ligand free in aqueous solution, with a net charge QL of +1 e, is identified by the code lig. The situation of the protein-ligand complex in aqueous solution is identified by the codes net-5, net0, net3, and net9, respectively, corresponding to protein net charges QP of −5, 0, +3, or +9 e, respectively. The system based on net9 and including a large artificial quasi-isotropic quadrupole is referred to as net9quad. Finally, the two systems based on net-5 and net9 which involve a neutralizing counter-ion atmosphere are labeled net-5ion and net9ion.
The explicit-solvent MD simulations of these different systems involve fixed solute coordinates (ligand or protein-ligand complex, in the latter case also including a number of bound water molecules). They are carried out under periodic boundary conditions with lattice-sum (PME) electrostatics considering cubic computational boxes with edge lengths L ranging from 3.05 to 13.02 nm (lig), 7.42 to 13.02 nm (net0), or 7.42 nm to 11.02 nm (all other systems) in steps of about 0.4 nm. They deliver raw estimates ΔGMD,PBC for the ligand charging free energy via Eq. 6. These estimates are affected by finite-size errors and are corrected into estimates ΔGMD,NBC corresponding to the same explicit-solvent MD model, but under non-periodic boundary conditions with Coulombic electrostatics and in the limit of a macroscopic system (and therefore, ideally, without any dependence on L). The numerical correction scheme relies on the application of Eq. 10 and requires, for each system, PB calculations under both non-periodic and periodic boundary conditions, the latter at the specific box edge length L. In practice, these calculations are performed for boxes of edges L ranging from 3 (lig) or 7 (all other systems) to 15 nm in steps of 1 nm, and interpolated by means of Eq. 38. The analytical correction scheme relies on the application of Eq. 11 and requires, for each system, three PB calculations under non-periodic boundary conditions, the dependence on the specific box edge length L being analytical. These relied on a reference box-edge length Lref of 15 nm.
A summary of the simulated systems and simulation conditions is provided in Table 1. Further details on these MD simulations are provided in Sec. 3A and in Table S1 of the supplementary material.154 Further details on the PB calculations are provided in Sec. 3B.
Table 1.
Overview of the simulated systems and simulation conditions. For the different systems (Sec. 4A), explicit-solvent MD simulations were carried out at 300 K and constant volume (effective solvent density appropriate for water at 1 bar) using cubic periodic computational boxes and lattice-sum electrostatics. For each system, the following quantities are reported: the net charge QP of the protein; the net charge QI of the counter-ion atmosphere; the minimal and maximal edge lengths Lmin and Lmax of the box (incremented in steps of about 0.4 nm; see Table 2 for the individual values); the corresponding minimal and maximal numbers NS,min and NS,max of freely moving water molecules (see Table 2 for the individual values); the number NB of bound (fixed coordinates) water molecules (see Sec. 3A); the numbers NNa,max and NCl,max of sodium and chloride counter-ions included in the largest box of edge Lmax; the ionic strength Istr of the system; the inverse Debye screening length κ of the system. For the systems with counter-ions, the number of ions was adjusted to enforce QI = −QP and to keep Istr and κ approximately constant across the different box-edge lengths. The ligand charge is QL = +1 e in all cases. More detailed information on the simulated systems as well as the raw simulation results can be found in Table S1 of the supplementary material.154
| System | QP (e) | QI (e) | Lmin (nm) | Lmax (nm) | NS,min | NS,max | NB | NNa,max | NCl,max | Istr (mol kg−1) | κ (nm−1) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| lig | 0 | 0 | 3.05 | 13.50 | 928 | 80 897 | 0 | 0 | 0 | 0 | 0 |
| net-5 | −5 | 0 | 7.42 | 11.02 | 12 077 | 43 591 | 69 | 0 | 0 | 0 | 0 |
| net0 | 0 | 0 | 7.42 | 13.02 | 12 077 | 72 810 | 69 | 0 | 0 | 0 | 0 |
| net3 | 3 | 0 | 7.42 | 11.02 | 12 077 | 43 591 | 69 | 0 | 0 | 0 | 0 |
| net9 | 9 | 0 | 7.42 | 11.02 | 12 077 | 43 591 | 69 | 0 | 0 | 0 | 0 |
| net9quad | 9 | 0 | 7.42 | 11.02 | 12 077 | 43 591 | 69 | 0 | 0 | 0 | 0 |
| net-5ion | −5 | 5 | 7.42 | 11.02 | 12 022 | 43 424 | 69 | 86 | 81 | ∼0.1 | ∼1.0 |
| net9ion | 9 | −9 | 7.42 | 11.02 | 12 017 | 43 419 | 69 | 81 | 90 | ∼0.1 | ∼1.0 |
Finite-size effects on the raw charging free energies
The raw charging free energies ΔGMD,PBC are displayed as a function of the box edge L in Figure 4a. The corresponding numerical results are reported in Table 2 (see also Table S1 of the supplementary material154 for the raw data used in Eq. 6). Except for the free ligand, ΔGMD,PBC evidences a substantial dependence on L, the differences between the values at 7.42 and 11.02 nm ranging from −8.6 to +17.1 kJ mol−1 for the different systems. For the systems net-5, net3, and net9, the sign of this difference is correlated with the net protein charge, but the corresponding magnitude is not. For example, a small negative change is observed for net-5, whereas a positive change of much larger in magnitude is observed for net3. For system net0, the change is positive and large, although it involves a protein without net charge. It is qualitatively comparable to that observed for systems net-5ion and net9ion, because, to a first approximation, the addition of neutralizing counter-ions leads to an effective surface neutralization of the protein. Remarkably, systems net9 and net9quad evidence the largest positive and negative changes, respectively, in spite of the fact that the quasi-isotropic quadrupole introduced in net9quad has nearly no electrostatic influence on the ligand. This difference is an artifact related to the residual integrated potential IP of the protein (Eq. 18 with X = P), which is dramatically altered by the introduction of the quasi-isotropic quadrupole (see further discussion in Secs. 4C, 4E).
Figure 4.
Raw and corrected charging free energies are shown as a function of the box size for the different systems considered. (a) Raw ligand charging free energies ΔGMD,PBC based on the MD simulations corresponding to the eight different systems (Table 1), displayed as a function of the box edge L. (b) Corresponding corrected charging free energies ΔGMD,NBC. Top row: all systems. Bottom row: lig system only, also considering smaller box sizes and represented on a smaller free-energy scale. The corrected values are obtained by application of either the numerical (Eq. 10; solid lines) or the analytical (Eq. 11; crosses) correction scheme. In both cases, the correction relies on PB calculations with a probe-contact solvent-accessible surface based on a probe radius RS = 0.14 nm (CTC(0.14)). The data are reported numerically in Table 2. A corresponding figure for RS = 0.10 nm (CTC(0.10)) can be found in Figure S1 of the supplementary material.154
Table 2.
Raw and corrected charging free energies. For each system (Table 1) and box edge length L, the following quantities are reported: the number NS of freely moving water molecules in the computational box; the discrete solvent correction terms ΔΔGDSI (infinite system limit) and ΔΔGDSF (finite-system adjustment), see Eq. 31; the finite-size correction terms ΔΔGNUM (numerical estimate) or ΔΔGANA (analytical estimate), see Eqs. 12, 14; the difference ΔΔGANA-NUM between these two quantities; the raw ligand charging free energy ΔΔGMD,PBC based on the MD simulations; the corresponding corrected ligand charging free energies ΔΔGMD,NBC,NUM or ΔΔGMD,NBC,ANA, see Eqs. 10, 11; the estimated statistical uncertainty σ[ΔGMD] on the raw MD results, calculated as described in Sec. 3A. The quantity ΔΔGMD,PBC is calculated from Eq. 6. The corresponding raw data can be found in Table S1 of the supplementary material.154 The terms ΔΔGDSI and ΔΔGDSF are calculated from Eqs. 31, 32, 35 using the indicated NS along with MS = 18.015 g mol−1, γS = 0.0764 e nm2 and ρS = 997 kg m−3. The term ΔΔGNUM is interpolated to the indicated L based on the results of Table 4 using a polynomial fit of the form of Eq. 38. The corresponding coefficients can be found in Table S3 of the supplementary material.154 The term ΔΔGANA is calculated using the parameters reported in Table 3. For both ΔΔGNUM and ΔΔGANA, the correction relies on PB calculations with a probe-contact solvent-accessible surface based on a probe radius RS = 0.14 nm (CTC(0.14)). The data are displayed graphically in Figure 4 (see also Figure S1 of the supplementary material154 for a corresponding graph with CTC(0.10)). Additional results concerning the systems with counter-ions can be found in Table S2 of the supplementary material.154
| ΔΔGDSI | ΔΔGDSF | ΔΔGNUM | ΔΔGANA | ΔΔGANA-NUM | ΔGMD,PBC | ΔGMD,NBC,NUM | ΔGMD,NBC,ANA | σ[ΔGMD] | ||
|---|---|---|---|---|---|---|---|---|---|---|
| L (nm) | NS | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) |
| lig | ||||||||||
| 3.05 | 928 | −74.10 | 1.39 | 0.80 | 0.78 | −0.02 | −198.67 | −270.59 | −270.60 | 0.25 |
| 3.48 | 1380 | −74.10 | 1.26 | 0.67 | 0.66 | −0.01 | −198.73 | −270.91 | −270.92 | 0.25 |
| 3.87 | 1904 | −74.10 | 1.18 | 0.59 | 0.58 | −0.01 | −198.10 | −270.43 | −270.44 | 0.26 |
| 4.28 | 2572 | −74.10 | 1.11 | 0.52 | 0.52 | 0.00 | −198.10 | −270.57 | −270.58 | 0.26 |
| 4.68 | 3362 | −74.10 | 1.08 | 0.47 | 0.47 | 0.00 | −198.21 | −270.76 | −270.76 | 0.26 |
| 4.99 | 4088 | −74.10 | 1.08 | 0.44 | 0.43 | −0.01 | −197.98 | −270.57 | −270.57 | 0.26 |
| 5.49 | 5423 | −74.10 | 1.04 | 0.39 | 0.39 | 0.00 | −198.04 | −270.72 | −270.72 | 0.28 |
| 6.29 | 8174 | −74.10 | 1.02 | 0.34 | 0.34 | 0.00 | −197.62 | −270.37 | −270.37 | 0.27 |
| 7.07 | 11 638 | −74.10 | 1.00 | 0.30 | 0.30 | 0.00 | −197.75 | −270.55 | −270.55 | 0.27 |
| 7.86 | 15 948 | −74.10 | 1.00 | 0.27 | 0.27 | 0.00 | −197.74 | −270.58 | −270.58 | 0.27 |
| 8.69 | 21 472 | −74.10 | 1.33 | 0.24 | 0.24 | 0.00 | −197.57 | −270.10 | −270.10 | 0.27 |
| 9.50 | 28 248 | −74.10 | 0.94 | 0.22 | 0.22 | 0.00 | −197.75 | −270.70 | −270.70 | 0.27 |
| 10.32 | 36 184 | −74.10 | 0.93 | 0.20 | 0.20 | 0.00 | −197.96 | −270.94 | −270.94 | 0.27 |
| 11.08 | 44 761 | −74.10 | 0.91 | 0.19 | 0.19 | 0.00 | −197.54 | −270.55 | −270.55 | 0.27 |
| 11.91 | 55 685 | −74.10 | 0.90 | 0.17 | 0.17 | 0.00 | −197.60 | −270.63 | −270.63 | 0.26 |
| 12.72 | 67 804 | −74.10 | 0.89 | 0.16 | 0.16 | 0.00 | −197.85 | −270.90 | −270.90 | 0.27 |
| 13.49 | 80 897 | −74.10 | 0.88 | 0.15 | 0.15 | 0.00 | −197.69 | −270.76 | −270.76 | 0.28 |
| net-5 | ||||||||||
| 7.42 | 12 077 | −74.10 | 8.33 | −11.66 | −11.77 | −0.11 | −200.76 | −278.20 | −278.30 | 0.31 |
| 7.82 | 14 377 | −74.10 | 7.22 | −10.22 | −10.30 | −0.08 | −201.03 | −278.14 | −278.22 | 0.28 |
| 8.22 | 16 875 | −74.10 | 6.51 | −9.03 | −9.09 | −0.06 | −200.69 | −277.32 | −277.38 | 0.33 |
| 8.62 | 19 798 | −74.10 | 5.34 | −8.04 | −8.08 | −0.04 | −201.50 | −278.30 | −278.34 | 0.27 |
| 9.02 | 22 999 | −74.10 | 4.39 | −7.20 | −7.23 | −0.03 | −201.43 | −278.35 | −278.38 | 0.29 |
| 9.42 | 26 492 | −74.10 | 3.60 | −6.49 | −6.52 | −0.03 | −201.80 | −278.80 | −278.82 | 0.30 |
| 9.82 | 30 296 | −74.10 | 2.93 | −5.89 | −5.90 | −0.01 | −201.30 | −278.36 | −278.37 | 0.36 |
| 10.22 | 34 748 | −74.10 | 1.69 | −5.37 | −5.38 | −0.01 | −200.54 | −278.32 | −278.33 | 0.33 |
| 10.62 | 38 852 | −74.10 | 1.95 | −4.91 | −4.92 | −0.01 | −201.36 | −278.43 | −278.44 | 0.30 |
| 11.02 | 43 591 | −74.10 | 1.65 | −4.52 | −4.52 | 0.00 | −201.72 | −278.70 | −278.70 | 0.33 |
| net0 | ||||||||||
| 7.42 | 12 077 | −74.10 | 8.33 | −0.22 | −0.17 | 0.05 | −193.97 | −259.96 | −259.91 | 0.12 |
| 7.82 | 14 377 | −74.10 | 7.22 | −0.16 | −0.12 | 0.04 | −193.05 | −260.10 | −260.05 | 0.17 |
| 8.22 | 16 875 | −74.10 | 6.51 | −0.11 | −0.08 | 0.03 | −192.48 | −260.18 | −260.15 | 0.12 |
| 8.62 | 19 798 | −74.10 | 5.34 | −0.07 | −0.04 | 0.03 | −191.45 | −260.28 | −260.26 | 0.15 |
| 9.02 | 22 999 | −74.10 | 4.39 | −0.04 | −0.02 | 0.02 | −191.62 | −261.38 | −261.36 | 0.57 |
| 9.42 | 26 492 | −74.10 | 3.60 | −0.01 | 0.00 | 0.01 | −190.53 | −261.04 | −261.03 | 0.48 |
| 9.82 | 30 296 | −74.10 | 2.93 | 0.01 | 0.02 | 0.01 | −189.59 | −260.75 | −260.74 | 0.19 |
| 10.22 | 34 748 | −74.10 | 1.69 | 0.03 | 0.03 | 0.00 | −188.85 | −261.24 | −261.23 | 0.18 |
| 10.62 | 38 852 | −74.10 | 1.95 | 0.04 | 0.04 | 0.00 | −188.86 | −260.97 | −260.97 | 0.19 |
| 11.02 | 43 591 | −74.10 | 1.65 | 0.05 | 0.05 | 0.00 | −188.87 | −261.28 | −261.28 | 0.33 |
| 11.42 | 49 170 | −74.10 | 0.67 | 0.06 | 0.06 | 0.00 | −187.93 | −261.31 | −261.31 | 0.20 |
| 11.82 | 53 925 | −74.10 | 1.47 | 0.07 | 0.06 | −0.01 | −188.45 | −261.02 | −261.02 | 0.04 |
| 12.22 | 60 146 | −74.10 | 0.79 | 0.07 | 0.07 | 0.00 | −187.91 | −261.15 | −261.16 | 0.08 |
| 12.62 | 66 411 | −74.10 | 0.61 | 0.08 | 0.07 | −0.01 | −188.04 | −261.46 | −261.46 | 0.25 |
| 13.02 | 72 810 | −74.10 | 0.73 | 0.08 | 0.08 | 0.00 | −187.98 | −261.27 | −261.28 | 0.38 |
| net3 | ||||||||||
| 7.42 | 12 077 | −74.10 | 8.33 | 6.96 | 7.17 | 0.21 | −197.07 | −255.88 | −255.68 | 0.22 |
| 7.82 | 14 377 | −74.10 | 7.22 | 6.15 | 6.32 | 0.17 | −195.11 | −255.85 | −255.68 | 0.23 |
| 8.22 |
16 875 |
−74.10 |
6.51 |
5.48 |
5.61 |
0.13 |
−193.48 |
−255.60 |
−255.47 |
0.21 |
| 8.62 | 19 798 | −74.10 | 5.34 | 4.91 | 5.02 | 0.11 | −192.03 | −255.88 | −255.77 | 0.22 |
| 9.02 | 22 999 | −74.10 | 4.39 | 4.44 | 4.52 | 0.08 | −190.89 | −256.18 | −256.09 | 0.21 |
| 9.42 | 26 492 | −74.10 | 3.60 | 4.03 | 4.10 | 0.07 | −190.50 | −256.97 | −256.90 | 0.27 |
| 9.82 | 30 296 | −74.10 | 2.93 | 3.68 | 3.74 | 0.06 | −189.19 | −256.68 | −256.62 | 0.24 |
| 10.22 | 34 748 | −74.10 | 1.69 | 3.38 | 3.42 | 0.04 | −188.34 | −257.37 | −257.33 | 0.24 |
| 10.62 | 38 852 | −74.10 | 1.95 | 3.11 | 3.15 | 0.04 | −187.61 | −256.65 | −256.62 | 0.24 |
| 11.02 | 43 591 | −74.10 | 1.65 | 2.88 | 2.91 | 0.03 | −187.65 | −257.23 | −257.20 | 0.22 |
| net9 | ||||||||||
| 7.42 | 12 077 | −74.10 | 8.33 | 20.06 | 20.65 | 0.59 | −205.70 | −251.41 | −250.83 | 0.21 |
| 7.82 | 14 377 | −74.10 | 7.22 | 17.69 | 18.16 | 0.47 | −202.22 | −251.42 | −250.95 | 0.19 |
| 8.22 | 16 875 | −74.10 | 6.51 | 15.72 | 16.10 | 0.38 | −199.97 | −251.84 | −251.46 | 0.22 |
| 8.62 | 19 798 | −74.10 | 5.34 | 14.08 | 14.38 | 0.30 | −197.18 | −251.87 | −251.57 | 0.22 |
| 9.02 | 22 999 | −74.10 | 4.39 | 12.69 | 12.93 | 0.24 | −195.58 | −252.60 | −252.36 | 0.22 |
| 9.42 | 26 492 | −74.10 | 3.60 | 11.51 | 11.70 | 0.19 | −193.28 | −252.27 | −252.08 | 0.21 |
| 9.82 | 30 296 | −74.10 | 2.93 | 10.49 | 10.65 | 0.16 | −192.09 | −252.76 | −252.61 | 0.24 |
| 10.22 | 34 748 | −74.10 | 1.69 | 9.62 | 9.74 | 0.12 | −191.46 | −254.25 | −254.13 | 0.35 |
| 10.62 | 38 852 | −74.10 | 1.95 | 8.85 | 8.95 | 0.10 | −189.59 | −252.89 | −252.79 | 0.23 |
| 11.02 | 43 591 | −74.10 | 1.65 | 8.19 | 8.27 | 0.08 | −188.59 | −252.86 | −252.78 | 0.24 |
| net9quad | ||||||||||
| 7.42 | 12 077 | −74.10 | 8.33 | −18.39 | −17.82 | 0.57 | −190.11 | −274.27 | −273.70 | 0.21 |
| 7.82 | 14 377 | −74.10 | 7.22 | −15.16 | −14.70 | 0.46 | −192.76 | −274.81 | −274.35 | 0.21 |
| 8.22 | 16 875 | −74.10 | 6.51 | −12.56 | −12.19 | 0.37 | −194.10 | −274.26 | −273.88 | 0.25 |
| 8.62 | 19 798 | −74.10 | 5.34 | −10.45 | −10.15 | 0.30 | −195.46 | −274.67 | −274.38 | 0.26 |
| 9.02 | 22 999 | −74.10 | 4.39 | −8.72 | −8.48 | 0.24 | −195.51 | −273.94 | −273.70 | 0.24 |
| 9.42 | 26 492 | −74.10 | 3.60 | −7.29 | −7.09 | 0.20 | −195.89 | −273.68 | −273.49 | 0.25 |
| 9.82 | 30 296 | −74.10 | 2.93 | −6.10 | −5.94 | 0.16 | −198.43 | −275.69 | −275.54 | 0.23 |
| 10.22 | 34 748 | −74.10 | 1.69 | −5.10 | −4.98 | 0.12 | −197.67 | −275.18 | −275.06 | 0.28 |
| 10.62 | 38 852 | −74.10 | 1.95 | −4.26 | −4.16 | 0.10 | −199.01 | −275.43 | −275.33 | 0.22 |
| 11.02 | 43 591 | −74.10 | 1.65 | −3.56 | −3.47 | 0.09 | −198.69 | −274.71 | −274.62 | 0.27 |
| net-5ion | ||||||||||
| 7.42 | 12 022 | −74.10 | 8.63 | −0.31 | −0.71 | −0.40 | −207.89 | −273.68 | −274.08 | 0.31 |
| 7.82 | 14 314 | −74.10 | 7.51 | −0.23 | −0.58 | −0.35 | −206.93 | −273.76 | −274.11 | 0.19 |
| 8.22 | 16 804 | −74.10 | 6.79 | −0.17 | −0.48 | −0.31 | −205.73 | −273.21 | −273.52 | 0.40 |
| 8.62 | 19 715 | −74.10 | 5.63 | −0.13 | −0.39 | −0.26 | −205.91 | −274.51 | −274.78 | 0.53 |
| 9.02 | 22 906 | −74.10 | 4.67 | −0.09 | −0.32 | −0.23 | −204.83 | −274.36 | −274.59 | 0.21 |
| 9.42 | 26 387 | −74.10 | 3.88 | −0.06 | −0.26 | −0.20 | −204.60 | −274.88 | −275.09 | 0.45 |
| 9.82 | 30 177 | −74.10 | 3.21 | −0.03 | −0.22 | −0.19 | −204.19 | −275.11 | −275.30 | 0.16 |
| 10.22 | 34 615 | −74.10 | 1.97 | −0.01 | −0.18 | −0.17 | −202.71 | −274.86 | −275.02 | 0.50 |
| 10.62 | 38 703 | −74.10 | 2.23 | 0.01 | −0.14 | −0.15 | −203.10 | −274.97 | −275.12 | 0.22 |
| 11.02 | 43 424 | −74.10 | 1.93 | 0.03 | −0.11 | −0.14 | −202.52 | −274.68 | −274.82 | 0.32 |
| net9ion | ||||||||||
| 7.42 | 12 017 | −74.10 | 8.66 | 1.15 | 0.76 | −0.39 | −190.27 | −254.56 | −254.95 | 0.34 |
| 7.82 | 14 309 | −74.10 | 7.53 | 1.02 | 0.68 | −0.34 | −188.59 | −254.14 | −254.48 | 0.30 |
| 8.22 | 16 799 | −74.10 | 6.81 | 0.91 | 0.61 | −0.30 | −188.09 | −254.48 | −254.77 | 0.28 |
| 8.62 | 19 710 | −74.10 | 5.64 | 0.81 | 0.55 | −0.26 | −188.36 | −256.01 | −256.27 | 0.43 |
| 9.02 | 22 901 | −74.10 | 4.68 | 0.73 | 0.50 | −0.23 | −186.51 | −255.20 | −255.44 | 0.21 |
| 9.42 | 26 382 | −74.10 | 3.89 | 0.66 | 0.46 | −0.20 | −185.97 | −255.52 | −255.73 | 0.28 |
| 9.82 | 30 172 | −74.10 | 3.23 | 0.61 | 0.42 | −0.19 | −185.75 | −256.02 | −256.21 | 0.11 |
| 10.22 | 34 610 | −74.10 | 1.98 | 0.56 | 0.39 | −0.17 | −184.31 | −255.88 | −256.05 | 0.41 |
| 10.62 | 38 698 | −74.10 | 2.23 | 0.51 | 0.36 | −0.15 | −183.80 | −255.16 | −255.31 | 0.26 |
| 11.02 | 43 419 | −74.10 | 1.93 | 0.47 | 0.34 | −0.13 | −183.27 | −254.97 | −255.10 | 0.28 |
Since the different curves of Figure 4a present crossing points, raw charging free energies calculated using a single box-edge length and interpreted naively may suggest opposite conclusions concerning the relative affinity of the ligand for different isoforms of the protein. For example, simulations performed with L = 7.42 nm would appear to suggest preferential binding of the ligand to the protein in the net9 system compared to the net-5 system, while simulations performed with L = 11.02 nm would lead to the opposite conclusion. Note that the estimation of infinite-system values by fitting of the ΔGMD,PBC curves to analytical functions (e.g., polynomial in L−1) and analytical extrapolation to L → ∞ is not a viable alternative to the application of a correction scheme. The reasons are that: this approach is computationally very expensive (requiring multiple free-energy simulations at different L to calculate a single charging free energy); it would require more converged ΔGMD,PBC values or/and more L points than considered here, so as to uniquely define the fitting function (e.g., order of the polynomial in L−1) and its coefficients; it would still overlook a size-independent correction term (discrete solvent correction term in the infinite-system limit, see ΔΔGDSI in Eq. 32).
Numerical correction scheme
The corrected charging free energies ΔGMD,NBC calculated using the numerical correction scheme (Eq. 10, based on a probe-contact solvent-accessible surface dielectric boundary condition with a 0.14 nm solvent probe radius for the PB calculations) are displayed as a function of the box-edge length L using solid lines in Figure 4b. The corresponding numerical results are also reported in Table 2. Compared to the raw data in Figure 4a, it is immediately seen that the correction scheme successfully removes the largest component of the finite-size errors. The residual dependence on L now ranges from −1.5 to +0.4 kJ mol−1 for the different systems, as estimated by the differences between the values at 7.42 and 11.02 nm. The magnitude of ΔGMD,NBC also differs significantly from that of the raw values ΔGMD,PBC due to the inclusion of the discrete solvent correction term in the infinite-system limit, see ΔΔGDSI in Eq. 32, which amounts to about −74.1 kJ mol−1 for the TIP3P water model at the experimental density of water.
After correction, the ranking of the systems in terms of increasing ligand charging free energies is essentially independent of L. For the systems net-5, net0, net3, and net9, the charging free energy becomes less negative upon increasing the protein charge from −5 to +9 e, as expected for the binding of a positively charged ligand. For the system net9quad, one would expect a value identical to that for the system net9 if the added quadrupole was exactly isotropic. In practice, the slight anisotropy of this quadrupole, which involves very large charges, induces a shift in the ligand charging free energy by about −22 kJ mol−1. Comparing the system net-5ion to net-5, the inclusion of neutralizing sodium counter-ions (plus neutral salt excess) in the MD simulations is seen to cause an increase in the charging free energy by about 4 kJ mol−1. Comparing the system net9ion to net9, the inclusion of neutralizing chloride counter-ions (plus neutral salt excess) in the MD simulations is seen to cause a decrease in the charging free energy by about 3 kJ mol−1. Because the ligand is positively charged, these changes are consistent with the presence of an excess of counter-ions, positive for net-5 and negative for net9, in the neighborhood of the ligand binding site. Although the inclusion of an explicit neutralizing counter-ion charge density in the PB calculations (Sec. 3B) is absolutely essential for obtaining meaningful results, the use of a finite inverse Debye screening length κ = 1.0 nm−1 only has a marginal influence on the result of the calculations (Tables S2 and S4 of the supplementary material154), i.e., for the counter-ion concentration considered here, this additional screening contribution can be neglected in the calculation of the correction terms. Note that the differences in the corrected ΔGMD,NBC values between the different systems are likely to be exacerbated by the use of fixed solute coordinates. In MD simulations considering flexible solutes, conformational relaxation of the solute would probably attenuate these differences.
Choice of dielectric boundary conditions
The numerically corrected charging free energies ΔGMD,NBC (Figure 4, Table 2) are based on PB calculations relying on a probe-contact solvent-accessible surface with a probe radius RS = 0.14 nm (CTC(0.14)). However, the choice of specific dielectric boundary conditions to define the solute low dielectric cavity may have a strong influence on the results. Three possible choices are:94 VDW surface, probe-contact solvent-accessible surface (CTC(RS)), or probe-center solvent-accessible surface (CEN(RS)), where RS is the radius of a spherical probe (solvent molecule) rolled over the VDW surface. The difference between the three types of surfaces is illustrated graphically in Figure 5.
Figure 5.
Alternative choices of dielectric boundary conditions. Boundaries of enclosed volumes are shown for a cut in the xy-plane through the center of the protein-ligand complex, with the van der Waals surface (VDW; red), a probe-contact solvent-accessible surface (CTC(RS); green), or a probe-center solvent-accessible surface (CEN(RS); blue), where RS is the radius of a spherical probe (solvent molecule) rolled over the VDW surface, here RS = 0.14 nm. Note that CTC(0) = CEN(0) = VDW. The solvent region is show in cyan.
The sensitivity of the corrected ligand charging free energies ΔGMD,NBC to the choice of dielectric boundary conditions is analyzed in Figure 6 for the CTC(RS) choice, considering probe radii RS ranging from 0 to 0.18 nm. For the eight systems considered, Figure 6a displays the calculated ΔGMD,NBC value corresponding to the largest box size, which represents the most accurate estimate available. Figure 6b displays the slope of a regression line fitting ΔGMD,NBC as a function of L−1, which measures the ability of the correction scheme to remove the box-size dependence, along with an error estimate on this slope evaluated by bootstrapping. A regression slope of zero, within its error bounds, for all systems would be expected for a correction scheme able to entirely remove finite-size effects. This is essentially achieved by the CTC(0.10) choice. For probe radii smaller than 0.10 nm, the regression slopes rapidly diverge upon decreasing RS, and the ΔGMD,NBC values present an important sensitivity to this parameter, especially for the systems with high net protein charges and no counter-ions (net-5, net9, net9quad, and to a lesser extent, net3). This is because small probe radii lead to the inclusion of high-dielectric cavities within the protein-ligand complex. These high-dielectric cavities, visible in Figure 5 as green volumes within the CTC(0.14) surface but outside the VDW surface, represent an artifact considering that they would be too small to accommodate even a single water molecule. For probe radii larger than 0.10 nm, the regression slopes also slightly diverge upon increasing RS, but the ΔGMD,NBC values only evidence a weak sensitivity to this parameter. This is because once the high-dielectric cavities have been removed, further increasing the probe radius only alters the smoothness of the boundary. The scheme CTC(0.10) therefore seems to represent an optimum for these calculations. However, as shown in Figure S1 of the supplementary material,154 the difference relative to the results with the more commonly used CTC(0.14) choice of Figure 4 is only marginal.
Figure 6.
Influence of the dielectric boundary conditions on the corrected charging free energies. This graph illustrates the sensitivity of the corrected results to the solvent probe radius used in the definition of the solute-solvent dielectric boundary, based on the numerical correction scheme and a probe-contact solvent-accessible surface definition. (a) Sensitivity of the corrected charging free energies at the largest box size. Shown are ligand charging free energies ΔGMD,NBC calculated based on explicit-solvent MD simulations corresponding to the eight different systems (Table 1) at the largest box size Lmax, corrected for finite-size effects using the numerical scheme (Eq. 10) and displayed as a function of probe radius RS used in the PB calculations required for the evaluation of the correction term ΔΔGNUM (Eq. 12). (b) Residual box size-dependence in the corrected charging free energies. The remaining box size-dependence of the corrected ligand charging free energies ΔGMD,NBC for a given system is quantified by the slope of a linear regression of the corrected charging free energies at all box sizes as a function of the inverse box edge L−1 (solid lines). The error on the regression slope (dashed lines) is calculated based on 10 000 resamplings of the ΔGMD,NBC data for a given system, where each resampling includes the same number of points (i.e., box sizes) taken at random from the set of box sizes, the error in the regression slope being estimated by the standard deviation of the corresponding resampled slopes. All PB calculations relied on a solute-solvent dielectric boundary defined as a probe-contact solvent-accessible surface with a probe radius RS (CTC(RS), where CTC(0) = VDW corresponds to a van der Waals surface). A corresponding figure for a probe-center solvent-accessible surface (CEN(RS)) boundary definition can be found in Figure S2 of the supplementary material.154
A figure corresponding to Figure 6 for the CEN(RS) choice is provided in Figure S2 of the supplementary material.154 There, an optimum is found for RS = 0.05 nm, but the sensitivity of the results to the choice of RS is large for both smaller and larger values. A larger dependence upon increasing RS above than 0.05 nm is expected here compared to CTC(RS), because once the high-dielectric cavities have been removed, further increasing the probe radius alters not only the smoothness of the boundary but also its position. For this reason, it is recommended to apply the present correction scheme based on PB calculations relying on a probe-contact solvent-accessible surface, with a probe radius in the range 0.10–0.14 nm for water.
Different research groups advocate the use of different surfaces99 in PB calculations, typically van der Waals79, 80, 100, 101, 102 or molecular103, 104, 105 surfaces, along with different solute permittivity values.76, 77, 78, 79, 80 However, this debate mostly concerns calculations aiming at accounting for the dielectric properties of protein-solvent systems as realistically as possible using the approximate PB approach, usually based on a single system configuration. In those cases, the mean dielectric effects of the protein electronic polarizability, protein conformational fluctuations, and transient bulk-interior water exchanges must be considered, as well as the correlation between various methodological choices (e.g., surface type, atomic radii, solute flexibility, and solute permittivity). In the present study, PB is used for the correction of MD simulation results relying on a non-polarizable force field and constrained solute coordinates. In this case, the interior permittivity must be set to one, and the preference for a molecular surface is determined by the sensitivity analysis of Figure 6 (and Figure S2 of the supplementary material154) rather than by theoretical arguments, although the poor performance of the van der Waals surface in the correction scheme can be intuitively understood as being caused by the presence of spurious high-dielectric cavities in the solute.
The results displayed in Figures 46 show that the PB analysis works remarkably well to correct the results of the MD simulations for finite-size effects. This may be surprising at first sight considering that charging free energies calculated directly using PB calculations are generally qualitative at best, accounting only approximately for numerous physical effects such as electrostriction, dielectric saturation, solute-solvent hydrogen bonding, and solvation-shell structure.33 However, this is irrelevant for the PB correction because these physical effects are short-ranged so that the corresponding errors largely cancel out in the difference between periodic and non-periodic PB calculations. On the other hand, the PB model provides an excellent description of long-range polarization effects, which represent the dominant cause of finite-size artifacts in the MD simulations.
Analytical correction scheme
The corrected charging free energies ΔGMD,NBC calculated using the analytical correction scheme (Eq. 11, based on a probe-contact solvent-accessible surface dielectric boundary condition with a 0.14 nm solvent probe radius for the PB calculations) are displayed as a function of the box edge L using crosses in Figure 4b. The parameters of the correction scheme for the different systems are summarized in Table 3 and the numerical results corresponding to the figure can be found in Table 2.
Table 3.
Parameters of the analytical correction scheme. For each system (Table 1), the following quantities are reported: the effective protein net charge QP used in Eqs. 15, 16, 17, 25, which is set to zero for the systems with neutralizing counter-ions; the ligand net charge QL; the residual integrated potential IP of the protein based on Eq. 18 with X = P; the residual integrated potential IL of the ligand based on Eq. 18 with X = L; the solvent contribution IL, SLV to IL based on Eq. 27; the effective solvation radius RL of the ligand within the protein-ligand complex based on Eq. 26. The evaluation of IP, IL and IL, SLV relied on PB calculations under non-periodic boundary conditions within a cubic box of edge Lref = 15 nm centered on the ligand, with a probe-contact solvent-accessible surface based on a probe radius RS = 0.14 nm (CTC(0.14)). Parameters of additional calculations concerning the systems with counter-ions as well as the fitting parameters of Eqs. 34, 38 for the numerical scheme can be found in Table S3 of the supplementary material.154
| System | QP (e) | QL (e) | IP (kJ nm3 mol−1 e−1) | IL (kJ nm3 mol−1 e−1) | IL, SLV (kJ nm3 mol−1 e−1) | RL (nm) |
|---|---|---|---|---|---|---|
| lig | 0 | 1 | 0 | 3 | 37 | 0.36 |
| net-5 | −5 | 1 | −1088 | 690 | 721 | 1.58 |
| net0 | 0 | 1 | −865 | 690 | 721 | 1.58 |
| net3 | 3 | 1 | −579 | 690 | 722 | 1.58 |
| net9 | 9 | 1 | −484 | 690 | 722 | 1.58 |
| net9quad | 9 | 1 | −16 188 | 690 | 722 | 1.58 |
| net-5ion | 0 | 1 | −1088 | 690 | 721 | 1.58 |
| net9ion | 0 | 1 | −484 | 690 | 722 | 1.58 |
The analytical correction scheme is essentially as successful as the numerical one in removing the largest component of the finite-size errors. This can be seen by comparing the analytically corrected results to the raw data (Figure 4a) and to the numerically corrected results (solid lines in Figure 4b). The maximal differences between ΔΔGNUM and ΔΔGANA are at most of 0.6 kJ mol−1 in magnitude over all systems (0.2 kJ mol−1 considering the systems with L > 10 nm). The differences are most significant for systems net9 and net9quad (high protein charge) as well as net-5ion and net9ion (different ways of accounting for the counter-ions).
The residual integrated potential IL of the ligand is essentially the same for all protein-ligand complexes. This is expected considering that this quantity is determined by the ligand charge distribution and the size and shape of the protein-ligand cavity, the latter being nearly the same for all complexes. This parameter is expectedly much smaller for the free ligand, where the cavity is comparatively small. In contrast, the residual integrated potential IP of the protein for the different protein-ligand complexes is extremely sensitive to the charge distribution of the protein. Note in particular the very large difference between the values for systems net9 and net9quad. The latter system includes a quasi-isotropic quadrupole added to the protein charge distribution (Figure 1). Such a quadrupole is expected to have a negligible influence on the field generated by the protein on the ligand (none if the quadrupole was exactly isotropic and entirely encompassed within the protein volume), because the electrostatic influence of the central atom (charge −80 e) is screened by the shell of peripheral atoms (total charge +80 e). In practice, the slight anisotropy of this quadrupole, which involves very large charges distributed on atomic sites, induces a shift in the ligand charging free energy by about −22 kJ mol−1 in terms of corrected values, as mentioned in Sec. 4C. However, the quadrupole has a large influence on the average electric potential within the computational box. Based on an approximate distance of 0.82 nm between central charge and peripheral shell, the quadrupole-moment trace γIQ is about 54 e nm2 (cf Eq. 29) so that the contribution of the quadrupole to IP should be about IP,IQ = −(6ɛo)−1γIQ = −15 690 kJ nm3 mol−1 e−1. This value is negative, because the potential between the central charge and the screening shell is negative, and matches the IP difference between net9quad and net9 in Table 3 (−15 704 kJ nm3 mol−1 e−1). This very large negative integrated potential IP,IQ induces a positive offset potential −L−3IP,IQ in a lattice-sum MD simulation (or lattice-sum PB calculation) at box edge L, and a positive offset −L−3QLIP,IQ in the calculated ligand charging free energy, for example about +16 kJ mol−1 for L = 10 nm (using QL = 1 e). This artifact is corrected in the analytical scheme by the term ΔGRIP of Eq. 17. Thus the residual integrated potential IP of the protein depends in a complex way on the protein charge distribution, i.e., it is not necessarily simply related to the protein net charge QP.
The effective solvation radius RL of the ligand in the protein-ligand complex, as determined from the solvation contribution IL,SLV to the residual integrated potential IL of the ligand, is essentially the same for all systems, evaluating to 1.58 nm. This is expected considering that this quantity is determined by the ligand charge distribution and the size and shape of the protein-ligand cavity, which is nearly the same for all complexes. This value is somewhat smaller than the volume-based effective radius of the complex, 2.2 nm, estimated as the radius of a sphere with the same volume (based on CTC(0.14)) as the protein-ligand complex. As expected, for the free ligand, the effective solvation radius is much smaller, evaluating to 0.36 nm, while the corresponding volume-based effective radius is 0.29 nm.
The analytical correction scheme permits a partitioning of the correction into terms corresponding to different physical effects. The individual contributions in Eqs. 11, 14 are reported in Table 4. These contributions are also illustrated graphically in Figure 7.
Table 4.
Components of the analytical correction scheme. For each system (Table 1) and box edge length L, the following quantities are reported: the net-charge interaction term ΔΔGNET, see Eq. 15; the net-charge undersolvation term ΔΔGUSV, see Eq. 16; the residual integrated potential term ΔΔGRIP, see Eq. 17; the empirical correction term ΔΔGEMP, see Eq. 25; the analytical finite-size correction term ΔΔGANA, see Eq 14; the discrete solvent correction terms ΔΔGDSI (infinite system limit) and ΔΔGDSF (finite-system adjustment), see Eq. 31; the total numerical ΔΔGMD,COR,NUM (= ΔΔGNUM + ΔΔGDSI + ΔΔGDSF) or analytical ΔΔGMD,COR,ANA (= ΔΔGANA + ΔΔGDSI + ΔΔGDSF) correction terms, see Eqs. 10, 11; and the difference ΔΔGMD,COR,ANA-NUM between these two quantities. The terms ΔΔGDSI and ΔΔGDSF are calculated from Eqs. 31, 32, 33 using VC = 0.5 nm3 for lig or 57.0 nm3 for all other systems along with MS = 18.015 g mol−1, γS = 0.0764 e nm2 and ρS = 997 kg m−3. The term ΔΔGANA is calculated using the parameters reported in Table 3. For both ΔΔGNUM and ΔΔGANA, the correction relies on PB calculations with a probe-contact solvent-accessible surface based on a probe radius RS = 0.14 nm (CTC(0.14)). The data are displayed graphically in Figure 7. Additional results concerning the systems with counter-ions can be found in Table S4 of the supplementary material.154
| ΔΔGNET | ΔΔGUSV | ΔΔGRIP | ΔΔGEMP | ΔΔGANA | ΔΔGDSI | ΔΔGDSF | ΔΔGMD,COR, NUM | ΔΔGMD,COR, ANA | ΔΔGMD,COR,ANA-NUM | |
|---|---|---|---|---|---|---|---|---|---|---|
| L | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) | (kJ mol−1) |
| lig | ||||||||||
| 3 | 65.70 | −65.02 | 0.12 | 0.00 | 0.80 | −74.1 | 1.37 | −71.91 | −71.93 | −0.02 |
| 4 | 49.28 | −48.77 | 0.05 | 0.00 | 0.56 | −74.1 | 0.58 | −72.96 | −72.97 | −0.01 |
| 5 | 39.42 | −39.01 | 0.03 | 0.00 | 0.43 | −74.1 | 0.30 | −73.37 | −73.38 | 0.00 |
| 6 | 32.85 | −32.51 | 0.02 | 0.00 | 0.35 | −74.1 | 0.17 | −73.58 | −73.58 | 0.00 |
| 7 | 28.16 | −27.87 | 0.01 | 0.00 | 0.30 | −74.1 | 0.11 | −73.70 | −73.70 | 0.00 |
| 8 | 24.64 | −24.38 | 0.01 | 0.00 | 0.26 | −74.1 | 0.07 | −73.77 | −73.77 | 0.00 |
| 9 | 21.90 | −21.67 | 0.00 | 0.00 | 0.23 | −74.1 | 0.05 | −73.82 | −73.82 | 0.00 |
| 10 | 19.71 | −19.51 | 0.00 | 0.00 | 0.21 | −74.1 | 0.04 | −73.86 | −73.86 | 0.00 |
| 11 | 17.92 | −17.73 | 0.00 | 0.00 | 0.19 | −74.1 | 0.03 | −73.89 | −73.89 | 0.00 |
| 12 | 16.43 | −16.26 | 0.00 | 0.00 | 0.17 | −74.1 | 0.02 | −73.91 | −73.91 | 0.00 |
| 13 | 15.16 | −15.01 | 0.00 | 0.00 | 0.16 | −74.1 | 0.02 | −73.93 | −73.93 | 0.00 |
| 14 | 14.08 | −13.93 | 0.00 | 0.00 | 0.15 | −74.1 | 0.01 | −73.94 | −73.95 | 0.00 |
| 15 | 13.14 | −13.00 | 0.00 | 0.00 | 0.14 | −74.1 | 0.01 | −73.96 | −73.96 | 0.00 |
| net5 | ||||||||||
| 7 | −253.42 | 250.80 | −11.21 | 0.18 | −13.64 | −74.1 | 12.31 | −75.07 | −75.43 | −0.36 |
| 8 | −221.74 | 219.45 | −7.51 | 0.08 | −9.71 | −74.1 | 8.25 | −75.39 | −75.57 | −0.18 |
| 9 | −197.10 | 195.07 | −5.27 | 0.04 | −7.27 | −74.1 | 5.79 | −75.48 | −75.58 | −0.10 |
| 10 | −177.39 | 175.56 | −3.85 | 0.02 | −5.65 | −74.1 | 4.22 | −75.47 | −75.53 | −0.06 |
| 11 | −161.26 | 159.60 | −2.89 | 0.01 | −4.54 | −74.1 | 3.17 | −75.43 | −75.47 | −0.04 |
| 12 | −147.83 | 146.30 | −2.23 | 0.01 | −3.74 | −74.1 | 2.44 | −75.37 | −75.40 | −0.03 |
| 13 | −136.45 | 135.05 | −1.75 | 0.00 | −3.15 | −74.1 | 1.92 | −75.31 | −75.33 | −0.02 |
| 14 | −126.71 | 125.40 | −1.40 | 0.00 | −2.70 | −74.1 | 1.54 | −75.25 | −75.27 | −0.02 |
| 15 | −118.26 | 117.04 | −1.14 | 0.00 | −2.36 | −74.1 | 1.25 | −75.20 | −75.21 | −0.01 |
| net0 | ||||||||||
| 7 | 28.16 | −27.87 | −0.51 | −0.02 | −0.24 | −74.1 | 12.31 | −61.99 | −62.03 | −0.04 |
| 8 | 24.64 | −24.38 | −0.34 | −0.01 | −0.10 | −74.1 | 8.25 | −65.92 | −65.95 | −0.03 |
| 9 | 21.90 | −21.67 | −0.24 | 0.00 | −0.02 | −74.1 | 5.79 | −68.30 | −68.33 | −0.03 |
| 10 | 19.71 | −19.51 | −0.18 | 0.00 | 0.03 | −74.1 | 4.22 | −69.83 | −69.86 | −0.02 |
| 11 | 17.92 | −17.73 | −0.13 | 0.00 | 0.05 | −74.1 | 3.17 | −70.86 | −70.88 | −0.02 |
| 12 | 16.43 | −16.26 | −0.10 | 0.00 | 0.07 | −74.1 | 2.44 | −71.58 | −71.59 | −0.01 |
| 13 | 15.16 | −15.01 | −0.08 | 0.00 | 0.08 | −74.1 | 1.92 | −72.09 | −72.11 | −0.01 |
| 14 | 14.08 | −13.93 | −0.06 | 0.00 | 0.08 | −74.1 | 1.54 | −72.47 | −72.48 | −0.01 |
| 15 | 13.14 | −13.00 | −0.05 | 0.00 | 0.08 | −74.1 | 1.25 | −72.76 | −72.77 | −0.01 |
| net3 | ||||||||||
| 7 | 197.10 | −195.07 | 6.36 | −0.14 | 8.25 | −74.1 | 12.31 | −53.69 | −53.54 | 0.14 |
| 8 | 172.46 | −170.69 | 4.26 | −0.06 | 5.97 | −74.1 | 8.25 | −59.95 | −59.88 | 0.07 |
| 9 | 153.30 | −151.72 | 2.99 | −0.03 | 4.54 | −74.1 | 5.79 | −63.81 | −63.77 | 0.04 |
| 10 | 137.97 | −136.55 | 2.18 | −0.02 | 3.59 | −74.1 | 4.22 | −66.31 | −66.29 | 0.02 |
| 11 | 125.43 | −124.13 | 1.64 | −0.01 | 2.92 | −74.1 | 3.17 | −68.02 | −68.01 | 0.01 |
| 12 | 114.98 | −113.79 | 1.26 | −0.01 | 2.44 | −74.1 | 2.44 | −69.23 | −69.22 | 0.01 |
| 13 | 106.13 | −105.04 | 0.99 | 0.00 | 2.08 | −74.1 | 1.92 | −70.10 | −70.10 | 0.00 |
| 14 | 98.55 | −97.53 | 0.79 | 0.00 | 1.81 | −74.1 | 1.54 | −70.76 | −70.76 | 0.00 |
| 15 | 91.98 | −91.03 | 0.65 | 0.00 | 1.59 | −74.1 | 1.25 | −71.26 | −71.26 | 0.00 |
| net9 | ||||||||||
| 7 | 534.99 | −529.47 | 18.67 | −0.39 | 23.80 | −74.1 | 12.31 | −38.60 | −37.99 | 0.62 |
| 8 | 468.11 | −463.29 | 12.51 | −0.17 | 17.16 | −74.1 | 8.25 | −49.00 | −48.69 | 0.31 |
| 9 | 416.10 | −411.81 | 8.79 | −0.09 | 12.99 | −74.1 | 5.79 | −55.49 | −55.32 | 0.17 |
| 10 | 374.49 | −370.63 | 6.41 | −0.05 | 10.22 | −74.1 | 4.22 | −59.76 | −59.66 | 0.10 |
| 11 |
340.45 |
−336.94 |
4.81 |
−0.03 |
8.30 |
−74.1 |
3.17 |
−62.70 |
−62.64 |
0.07 |
| 12 | 312.08 | −308.86 | 3.71 | −0.02 | 6.91 | −74.1 | 2.44 | −64.80 | −64.75 | 0.05 |
| 13 | 288.07 | −285.10 | 2.92 | −0.01 | 5.88 | −74.1 | 1.92 | −66.34 | −66.31 | 0.03 |
| 14 | 267.49 | −264.74 | 2.33 | −0.01 | 5.09 | −74.1 | 1.54 | −67.50 | −67.48 | 0.02 |
| 15 | 249.66 | −247.09 | 1.90 | 0 | 4.47 | −74.1 | 1.25 | −68.40 | −68.39 | 0.02 |
| net9quad | ||||||||||
| 7 | 534.39 | −528.88 | −27.11 | −0.39 | −21.98 | −74.1 | 12.31 | −84.36 | −83.78 | 0.58 |
| 8 | 467.59 | −462.77 | −18.16 | −0.17 | −13.51 | −74.1 | 8.25 | −79.64 | −79.37 | 0.27 |
| 9 | 415.64 | −411.35 | −12.75 | −0.09 | −8.55 | −74.1 | 5.79 | −77.01 | −76.87 | 0.14 |
| 10 | 374.07 | −370.22 | −9.30 | −0.05 | −5.49 | −74.1 | 4.22 | −75.45 | −75.37 | 0.08 |
| 11 | 340.07 | −336.56 | −6.99 | −0.03 | −3.51 | −74.1 | 3.17 | −74.49 | −74.44 | 0.05 |
| 12 | 311.73 | −308.51 | −5.38 | −0.02 | −2.18 | −74.1 | 2.44 | −73.88 | −73.84 | 0.03 |
| 13 | 287.75 | −284.78 | −4.23 | −0.01 | −1.28 | −74.1 | 1.92 | −73.48 | −73.46 | 0.03 |
| 14 | 267.2 | −264.44 | −3.39 | −0.01 | −0.64 | −74.1 | 1.54 | −73.22 | −73.21 | 0.02 |
| 15 | 249.38 | −246.81 | −2.75 | 0 | −0.19 | −74.1 | 1.25 | −73.06 | −73.04 | 0.02 |
| net5ion | ||||||||||
| 7 | 28.16 | −27.87 | −1.16 | −0.02 | −0.89 | −74.1 | 12.31 | −61.98 | −62.68 | −0.70 |
| 8 | 24.64 | −24.38 | −0.78 | −0.01 | −0.53 | −74.1 | 8.25 | −65.93 | −66.39 | −0.46 |
| 9 | 21.90 | −21.67 | −0.55 | 0.00 | −0.32 | −74.1 | 5.79 | −68.31 | −68.64 | −0.32 |
| 10 | 19.71 | −19.51 | −0.40 | 0.00 | −0.20 | −74.1 | 4.22 | −69.84 | −70.08 | −0.23 |
| 11 | 17.92 | −17.73 | −0.30 | 0.00 | −0.12 | −74.1 | 3.17 | −70.87 | −71.05 | −0.18 |
| 12 | 16.43 | −16.26 | −0.23 | 0.00 | −0.06 | −74.1 | 2.44 | −71.58 | −71.72 | −0.14 |
| 13 | 15.16 | −15.01 | −0.18 | 0.00 | −0.03 | −74.1 | 1.92 | −72.10 | −72.21 | −0.11 |
| 14 | 14.08 | −13.93 | −0.15 | 0.00 | 0 | −74.1 | 1.54 | −72.48 | −72.57 | −0.09 |
| 15 | 13.14 | −13.00 | −0.12 | 0.00 | 0.02 | −74.1 | 1.25 | −72.76 | −72.84 | −0.07 |
| net9ion | ||||||||||
| 7 | 28.16 | −27.87 | 0.58 | −0.02 | 0.85 | −74.1 | 12.31 | −60.42 | −60.95 | −0.53 |
| 8 | 24.64 | −24.38 | 0.39 | −0.01 | 0.63 | −74.1 | 8.25 | −64.86 | −65.22 | −0.37 |
| 9 | 21.90 | −21.67 | 0.27 | 0.00 | 0.49 | −74.1 | 5.79 | −67.55 | −67.82 | −0.27 |
| 10 | 19.71 | −19.51 | 0.20 | 0.00 | 0.40 | −74.1 | 4.22 | −69.28 | −69.48 | −0.20 |
| 11 | 17.92 | −17.73 | 0.15 | 0.00 | 0.33 | −74.1 | 3.17 | −70.45 | −70.60 | −0.15 |
| 12 | 16.43 | −16.26 | 0.11 | 0.00 | 0.28 | −74.1 | 2.44 | −71.26 | −71.38 | −0.12 |
| 13 | 15.16 | −15.01 | 0.09 | 0.00 | 0.25 | −74.1 | 1.92 | −71.84 | −71.94 | −0.09 |
| 14 | 14.08 | −13.93 | 0.07 | 0.00 | 0.22 | −74.1 | 1.54 | −72.27 | −72.35 | −0.08 |
| 15 | 13.14 | −13.00 | 0.06 | 0.00 | 0.19 | −74.1 | 1.25 | −72.60 | −72.66 | −0.06 |
Figure 7.
Components of the analytical correction scheme for the eight different systems (Table 1), displayed as a function of the box edge L. The components are: the combined net-charge interaction and net-charge undersolvation terms ΔΔGNET+USV, see Eqs. 15, 16; the residual integrated potential term ΔΔGRIP, see Eq. 17; the empirical correction term ΔΔGEMP, see Eq. 25; the finite-system adjustment to the discrete solvent correction term ΔΔGDSF, see Eq. 33. The discrete solvent correction in the infinite-system limit, ΔΔGDSI, is a constant (indicated in the legend only). The sum of these six terms represents the total analytical correction term ΔΔGMD,COR,ANA (= ΔΔGNET + ΔΔGUSV + ΔΔGRIP + ΔΔGEMP + ΔΔGDSI + ΔΔGDSF), see Eqs. 11, 14. Note that ΔΔGNET and ΔΔGUSV are individually very large, but largely cancel each other in their sum ΔΔGNET+USV (= ɛS−1 ΔΔGNET). The data are reported numerically in Table 4.
The terms ΔΔGNET and ΔΔGUSV correcting for periodicity-induced net-charge interactions and undersolvation, respectively, are individually very large. However, for a solvent of high dielectric permittivity such as water, these largely cancel out (compare Eqs. 15, 16). As discussed in Secs. 2D1, 2D2, this cancellation is somewhat misleading. If the net-charge term ULS,NET of Eq. 9 were included in the lattice-sum energy expression of the MD simulations, as suggested in Refs. 67 and 68, ΔΔGNET would be omitted from the correction scheme. The remaining term ΔΔGUSV would then give a more appropriate idea of the real impact of using nanoscale box sizes with lattice-sum electrostatics when considering charged systems (see discussion in Sec. 2D2).
Given the lattice-sum energy expression used in the present work and in current MD programs, which omits ULS,NET, the sum of ΔΔGNET + ΔΔGUSV can be considered. It is most significant for the systems net-5, net3, net9, and net9quad with high protein charge magnitude (up to 5.5 kJ mol−1 in magnitude for L = 7 nm), negative for net-5 (where QP and QL are of opposite signs) and positive otherwise. It is small for the systems lig, net0, net-5ion, and net9ion with zero effective protein charge (up to 0.7 kJ mol−1 in magnitude for L = 7 nm), for which the correction scheme is applied with QP = 0, so that ΔΔGNET + ΔΔGUSV is proportional to Q2L (Eqs. 15, 16).
The correction term ΔΔGRIP for residual integrated potential effects is also large for the systems with high protein charge magnitude (up to 27.1 kJ mol−1 in magnitude for L = 7 nm, or up to 18.7 kJ mol−1 excluding net9quad). It is small for the systems with zero effective protein charge (up to 1.1 kJ mol−1 in magnitude for L = 7 nm), where ΔΔGRIP is proportional to (IP + IL)QL (Eq. 17). This term depends in a complex way on the protein charge distribution and cannot be directly related to the relative signs of QP and QL. Note in particular the large magnitudes and opposite signs of ΔΔGRIP for the systems net9 and net9quad. For these two systems, the terms of Eq. 17 proportional to IL are about the same, and are positive. The remaining component in IPQL is small and negative for net9, leading to an overall positive ΔΔGRIP, while it is very large and negative for net9quad, leading to an overall negative ΔΔGRIP. This comparison illustrates clearly how features of the charge distribution within the protein that should not affect the ligand charging can still lead to very large artifacts in the raw charging free energies from MD simulations. It should also be stressed that in a binding free energy calculation, the term ΔΔGRIP will not cancel out between the two legs of the alchemical thermodynamic cycle. For example, in the present case, this term is large and protein-dependent for the ligand charging in the complex, and nearly zero for the charging of the ligand in solution.
The empirical term ΔΔGEMP enforcing agreement between the correction scheme and the analytical solution for point charges centered in a spherical cavity is small in all cases (at most 0.4 kJ mol−1 in magnitude for L = 7 nm). It is of the same sign as ΔΔGUSV and thus enhances undersolvation. To assess the validity of this term, additional calculations were performed for a model system consisting of a spherical cavity of radius R = 2.5 nm encompassing a protein point charge of +3 e and a ligand charge +1 e at its center (excluded from direct Coulomb interaction), see system sph3 in Table S4 of the supplementary material.154 It was verified in this case that RL evaluates to R, ΔΔGRIP agrees with the analytical result of Eq. 22, and ΔΔGANA is rigorously identical to ΔΔGNUM within numerical precision.
Finally, the discrete-solvent term ΔΔGDSC consists of two parts. The box-size independent term ΔΔGDSI is a constant −74.1 kJ mol−1 for all systems, characteristic of the employed water model and its bulk density. This term is negative and, in the orientational disorder limit, corrects for the positive offset potential in the MD simulations induced by the constraint of vanishing average potential in lattice-sum methods. The finite-size adjustment term ΔΔGDSF is box-edge dependent, identical and positive for all protein-ligand complexes, and typically large (up to 12.3 kJ mol−1 for L = 7 nm). It is small for the free ligand (at most 1.4 kJ mol−1 for L = 3 nm), due to its small excluded volume. In the context of a binding free energy calculation, the contribution of ΔΔGDSI will cancel out between the two legs of the alchemical thermodynamic cycle because it only depends on the nature and equilibrium density of the solvent, whereas that of ΔΔGDSF will in general not.
For the systems net-5ion and net9ion involving neutralizing counter-ions, the analytical correction scheme is applied with an effective protein charge QP set to zero, accounting approximately for a surface neutralization of the protein, and an inverse Debye screening length κ = 0. This scheme has not been generalized to the κ ≠ 0 situation, but tests with non-zero κ values in the context of the numerical scheme showed a negligible influence of this parameter on the results (Sec. 4C). An alternative to the use of QP = 0 is to introduce an explicit neutralizing surface charge distribution as done in the numerical scheme (Sec. 3B). The results of corresponding calculations are reported in Tables S2 and S4 of the supplementary material.154 They do not differ significantly from those reported in Tables 2, 4.
Figure 7 suggests that for a number of systems (lig, net0, net-5ion, and net-9ion), the discrete solvent term ΔΔGDSC alone might represent an adequate correction. However, this observation is tightly linked to the fact that the ligand is small and monovalent with a relatively simple charge distribution. When the analytical scheme is applied with QP = 0, the terms ΔΔGNET, ΔΔGUSV, and ΔΔGEMP become proportional to Q2L, and the term ΔΔGRIP to (IP + IL)QL. These terms are small here because QL = 1 e and IL is small (the most significant contribution being the IPQL component of ΔΔGRIP). In different situations, these terms could become important even in cases where the protein bears no effective net charge.
The application of the analytical correction scheme relies on three PB calculations to determine IP, IL, and IL,SLV. These are done under non-periodic boundary conditions for each system. Just as was the case for the numerical scheme, the results of these calculations depend on the choice made for the solute-solvent dielectric boundary conditions. In this respect, the considerations made in Sec. 4D concerning the influence of the type of dielectric boundary and of the probe radius in the numerical correction scheme also apply to the analytical scheme.
DISCUSSION
Charging free energies from MD simulations can be subject to very large finite-size effects. These errors can be corrected by the proposed numerical and analytical correction schemes. The approximate analytical scheme is in practice essentially as accurate as the numerical one, and presents four main advantages: (i) it only requires three PB calculations for a given system, the dependence on the box-edge length being analytical; (ii) it only requires non-periodic boundary conditions for these PB calculations, which can thus be performed using free or commercial PB solvers such as UHBD,51, 52 DelPhi,53 or APBS;54 (iii) it provides insight into the physical origin of the finite-size effects; (iv) its application to MD simulations involving a neutralizing counter-ion atmosphere is straightforward. This scheme is therefore the one recommended by the authors. With the numerical scheme, care must be taken that the PB solver employed handles periodic boundary conditions in a correct way and, in particular, that a neutralizing background charge is explicitly added to the charge-density grid prior to the calculation, as described in Ref. 20. If this is not done, the application of a periodicity constraint on the electric potential will induce a surface charge instead, which is not the target situation. This can easily be verified for a given PB solver claiming to handle periodic boundary conditions, e.g., by testing the results against the analytical equation (Eq. 22 with QP = 0) for a single spherical ion.
Procedure for applying the analytical correction scheme
The procedure to apply the analytical correction scheme is straightforward. The following steps are necessary to correct the charging free energy of a ligand (net charge QL) within a solvated protein (net charge QP) in water as calculated from MD simulations with lattice-sum electrostatics (cubic box of edge L):
-
1.
Using a standard PB solver, calculate the integrated potentials BHET[P, Lref] and BHET[L, Lref] of Eq. 19, corresponding to integrals over the entire non-periodic cubic computational domain of edge Lref. The solute cavity should correspond to that of the protein-ligand complex and be defined by a probe-contact surface (recommended probe radius 0.10–0.14 nm). The interior permittivity should be set to one, the exterior permittivity to a value ɛS appropriate for the water model used in the MD simulations, and the inverse Debye screening length κ to zero. The edge Lref of the computational domain should be sufficiently large to ensure the box-size independence of the results (in terms of IP, IL, and RL). In practice, a distance of a few nanometers between the solute surface and the box wall is typically sufficient. The ligand should be at the center of this domain. In the calculation of BHET[P, Lref], only the protein charges should be included, with the ligand charges set to zero (the ligand atoms should still be included to ensure a proper cavity size). In the calculation of BHET[L, Lref], only the ligand charges should be included, with the protein charges set to zero (the protein atoms should still be included to ensure a proper cavity size). The integrated potential BHOM[L, Lref], which is the analog of BHET[L, Lref], is evaluated analogously, but with the exterior permittivity set to one instead of ɛS.
-
2.
Use Eqs. 18, 21 with X = L or P to evaluate the residual integrated potentials IP and IL of the protein and ligand, respectively. Use Eq. 27 and the analog of Eq. 21 for BHOM[L, Lref], i.e., Eq. 21 with ɛS replaced by one, to calculate the solvent contribution IL,SLV to IL. Use Eq. 26 to calculate the effective solvation radius RL of the ligand within the protein-ligand complex.
-
3.
Use Eq. 28 to calculate the quadrupole-moment trace γS of the water model used in the MD simulations relative to its single van der Waals interaction site.
-
4.
Use the results of points 1–3 to compute the full correction term as defined by Eqs. 11, 14, 15, 16, 17, 25, 35, where L is the box-edge length and NS the number of explicit solvent molecules in the MD simulations. If the simulations involve a neutralizing counter-ion atmosphere, an effective protein net charge QP of zero should be used in these equations, irrespective of the original net charge of the protein.
The charging free energy of the free ligand in solution can be calculated in a similar way (point 1: calculation of BHET[P, Lref] omitted and cavity defined by the ligand atoms only; point 2: calculation of IP omitted; point 4: QP and IP set to zero). Any standard PB solver can in principle be used, provided that it can report data to calculate the integral of the electric potential over the considered non-periodic computational domain. For example, Figure S3 of the supplementary material154 presents a comparison between the results of test calculations performed using the freely available software APBS54 and those of the custom PB solver employed here in the context of 100 evenly spaced snapshots from an independent 5 ns MD simulation of the system net-5 (ligand uncharged, all protein, ligand, and solvent atoms free to move, i.e., no atoms fixed in space). In spite of minor numerical differences (probably related to slightly different boundary smoothing procedures), the APBS results work perfectly within the analytical scheme, the calculated corrections differing by less than 0.1 kJ mol−1. A sample Python script and input files to perform and analyze such APBS calculations are also provided as the supplementary material.154
Special situations and extensions of the analytical correction scheme
A number of situations that are common in practice have not been encountered in the present work and deserve some additional discussions. They are the following:
-
1.
Non-cubic computational box. MD simulations are sometimes performed using non-cubic shapes for the computational box. In principle, simulations carried out in boxes of arbitrary space-filling shapes can be transformed to correspond to a given triclinic box,106 so that it is sufficient to consider the general triclinic case. In this case, the analytical correction scheme can still be applied in the following way. In Eqs. 15, 16, the quantity L−1ξLS must be replaced by a corresponding expression for the triclinic Wigner integration constant, which will depend on the full 3 × 3 matrix of the box-edge vectors. Although there is no analytical expression for this quantity, it is easily evaluated numerically for a given box-edge matrix,25 e.g., by calculating the lattice-energy of a single point charge in the given box using the MD simulation program. Equations 17, 30, on the other hand, account for average potential effects and can be applied based on the box volume, i.e., replacing L3 by the box volume V. Eq. 25 can also be applied in the same way, i.e., empirically replacing L by V1/3 (this term is generally very small in any case). Finally, since the residual integrated potentials IP, IL and IL,SLV account for short-range effects (potential inside and near the solute) and rely on PB calculations under non-periodic boundary conditions, they can still be calculated using cubic boxes.
-
2.
Variable box size. MD simulations are commonly performed using pressure coupling,107, 108, 109 in which case the box-edge length fluctuates along the simulation. Since the analytical correction scheme is defined by an explicit function of the box-edge length, averaging over the box-edge length distribution from the MD simulations offers a simple way to account for the variable box size. In practice, the box-size fluctuations are typically small and the use of an effective average value for L instead of a distribution would incur essentially negligible errors.
-
3.
Flexible solute. The present calculations were performed with fixed solute coordinates. In a real situation, however, the solute coordinates will vary in time, and the PB calculation should in principle be performed for each (or a subset) of the solute configurations sampled during the MD simulations. In practice, it would be far more convenient to use effective average values of IP, IL, and IL,SLV. To investigate the feasibility of this option, the three quantities were calculated based on 100 evenly spaced snapshots from an independent 5 ns MD simulation of the system net-5 (ligand uncharged, all protein, ligand, and solvent atoms free to move). The distributions of the three quantities are shown in Figure S3(a) of the supplementary material.154 The average and standard deviations of IP, IL, and IL,SLV over this set are −675 ± 97, 321 ± 26, and 352 ± 26 kJ nm3 mol−1 e−1, respectively. For QP = −5 e, QL = +1 e and assuming a box-edge length L of 10 nm, the corresponding estimates for ΔΔGRIP (Eq. 17) and ΔΔGEMP (Eq. 25) are −1.96 ± 0.14 and 0.0036 ± 0.0007 kJ mol−1, respectively. This suggests that the use of effective average values of IP, IL, and IL,SLV, or even of single values calculated based on a representative structure, incurs a relatively limited error, at least for the systems considered here.
-
4.
Solvent with multiple van der Waals interaction sites. Most water models have a single van der Waals interaction site, in which case the corresponding quadrupole-moment trace can be evaluated analytically using Eq. 29. In the case of a solvent involving multiple van der Waals interaction sites, it is possible to evaluate numerically an effective quadrupole moment. This can be done by explicitly performing simulations in the orientational-disorder limit, i.e., where the electrostatic interactions are turned off during the sampling, as described in Ref. 31.
-
5.
Other electrostatic interaction schemes. Electrostatic interaction schemes other than lattice-sum methods are also often employed in MD simulations, one of the most common alternative being the reaction-field scheme.110, 111 The analytical correction scheme remains to be generalized to these interaction forms. However, the numerical scheme can still be applied using a PB solver capable of handling alternative interaction functions,70, 71, 75, 74 see, e.g., Refs. 24 and 36.
The analytical correction scheme is immediately applicable to essentially all types of free-energy calculations relevant for (bio)chemical problems, and its application should become a standard in cases involving charge transformations.
Comparison of the analytical correction scheme with previously proposed schemes
Although several schemes have been previously proposed to circumvent or correct for finite-size effects, none are, in the opinion of the authors, entirely satisfactory. These include:
-
1.
Potential of mean force calculation. In this approach,37, 38, 39 the calculation of the binding free energy is performed by calculation of the reversible work for explicitly dissociating the species. Three shortcomings of this approach are that: (i) depending on the system, explicit dissociation pathways can be more difficult to sample than alchemical pathways;39 (ii) the end-state of the process corresponds to dissociated charged species in the same computational box, which will only yield correct free energies if the residual interaction is negligible; (iii) finite-size effects may still be significant in this end state even if formally neutral, due to its high dipole and to the influence of the residual integrated potential term. With respect to the last point, it is important to stress that the residual integrated potentials IP and IL are configuration dependent (via the solute cavity shape) and cannot be assumed to be identical for the protein-ligand complex and the dissociated species.
-
2.
Simultaneous counter-ion mutation. In this approach,40, 41, 42 the charging of the ligand is performed simultaneously with the uncharging of a distant counter-ion in the same computational box, in such a way that the overall process involves no net-charge change. Three shortcomings of this approach are that: (i) the free energy of the counter-ion mutation must be calculated separately and subtracted from the result, which implies that finite-size effects still have to be appropriately corrected in this second calculation; (ii) the accuracy of the result rests on the assumption that the interaction between the protein-ligand complex and the counter-ion is negligible; (iii) finite-size effects may still be significant, even in the absence of system net charge. The two latter problems are identical to those encountered in the potential of mean force approach (point 1 above).
-
3.
Twin simulations with opposite counter-ion mutations. In this approach proposed by Morgan and Massi,43 two separate calculations are performed, involving a distant counter-ion mutation performed in opposite directions. The two coupled processes are selected in such a way that the total square-net-charge change of the system is zero (e.g., for a neutral protein and a monovalent ligand L, one would select the two coupled processes Lo + C− → L+ + Co and Lo + Co → L+ + C−). The ligand charging free energy (process Lo → L+) is obtained by averaging the two results, while the half difference can be compared to the result of a separate calculation for the counter-ion mutation alone (process Co → C−), as a check for the assumption of weak interaction between the protein-ligand complex and the counter-ion. The apparent advantage of the procedure is that finite-size errors which are quadratic in the system net charge will cancel out in the average. Unfortunately, only the net-charge interaction and the net-charge undersolvation components of the error are exactly quadratic, these terms being straightforward to calculate analytically. Errors which are linear in the ligand charge, such as the discrete solvent term, will not be accounted for (and their effect will not be evidenced by the checking comparison). Similarly, the residual integrated potential term, which has a complex dependence on the protein and ligand charge distributions, will be inadequately captured, leading to unpredictable errors (e.g., the difference between the net9 and net9quad systems would be entirely overlooked). These problems are not obvious from the results reported in Ref. 43 because only small ions are considered (nearly quadratic residual integrated potential term, see, e.g., Eq. 22 for a monoatomic ion) and because the checking comparison is insensitive to the neglect of the linear discrete solvent correction term.
-
4.
Numerical correction scheme. This recently proposed approach of Reif and Oostenbrink36 follows the ideas previously developed in Refs. 20, 21, 22, 23, 24, 31, 32, 34, 35, 46, and 69, 70, 71, 72, 73, 74, 75. The resulting scheme is essentially equivalent to the numerical correction scheme proposed in the present article (see also last paragraph of Sec. 2B), and is general and accurate. However, this scheme: (i) requires a PB solver capable of handling correctly periodic boundary conditions; (ii) requires calculations performed at the specific box-edge length used in the simulation (no analytical dependence on the box-edge length); (iii) does not provide insight into the different error contributions; (iv) is difficult to apply to MD simulations involving a neutralizing counter-ion density because this density must be introduced explicitly (Sec. 3B). Note also that the scheme was applied in Ref. 36 based on a van der Waals dielectric boundary definition whereas the present results suggest that a probe-contact surface should be used instead (Sec. 4D).
So far, the majority of studies concerning the binding free energy of charged species do not apply any of the above schemes, and simply disregard the issue altogether.
CONCLUSION
In this article, finite-size effects on calculated charging free energies are investigated considering as a test case the binding of 2-amino-5-methylthiazole to a mutant form of yeast cytochrome c peroxidase in water. Considering different charge isoforms of the protein, either in the absence or the presence of neutralizing counter-ions, and cubic computational boxes of edges ranging from 7.42 to 11.02 nm, the potentially large magnitude of finite-size effects on the raw charging free energies (up to 17.1 kJ mol−1) is clearly demonstrated. Two correction schemes are then proposed to eliminate these effects, a numerical and an analytical one. Both schemes are based on a continuum-electrostatics analysis and require performing PB calculations on the protein-ligand system. While the numerical scheme requires PB calculations under both non-periodic and periodic boundary conditions, the latter at the box size considered in the MD simulations, the analytical scheme only requires three non-periodic PB calculations for a given system, and depends analytically on the box size.
The analytical scheme also provides insight into the physical origin of the finite-size effects, by separating the correction into terms for periodicity induced net-charge interactions, periodicity induced net-charge undersolvation, discrete solvent, and residual integrated potential effects. Although the first two effects are often recognized in the literature, the latter two are generally overlooked in existing approaches to calculate binding free energies. The residual integrated potential correction can be very large for typical protein-ligand systems and does not depend in a simple way on the net charges of the interacting species. It cannot be assumed to cancel out between the bound and free states in pathway-based methods such as potential of mean force calculations and in alchemical methods such as thermodynamic cycle calculations. The discrete solvent correction can also be very large and persists even in the limit of infinite box sizes. It depends on the quadrupole-moment trace of the solvent model, a quantity that is essentially arbitrary because it does not influence the ability of the model to reproduce the experimental thermodynamic properties of the solvent. Although the infinite-system component of this term can be expected to cancel out between the bound and free states of the system or between the two charging legs of a thermodynamic cycle (unless these legs involve different solvents or solvent densities), its dependence on the system-size remains very significant and must be considered. The physical meaning of this discrete solvent effect has been matter of considerable debate in the classical simulation literature over the last two decades, in the context of ionic solvation free energies22, 44, 45, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121 as well as in the context of surface potential calculations.22, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136 The authors believe that this debate and its conclusions are appropriately summarized in Ref. 22 (see also Ref. 33), which underlies the form of the correction term adopted in the present study. Interestingly, a similar debate is arising at present, in the quantum-mechanical community137, 138, 139, 140, 141, 142, 143, 144 (see also Refs. 145 and 146 at the classical level), the same issues being discussed anew, and the same conclusions being progressively reached.
Application of either the numerical or the analytical correction scheme essentially eliminates the size dependence of the corrected charging free energies over the range of box sizes considered (maximal deviation of 1.5 kJ mol−1), provided that the solute-solvent boundary conditions in the PB calculations are defined appropriately (probe-contact surface with a recommended probe radius of 0.10–0.14 nm). While this work focuses on corrections for binding free energy calculations, the same errors affect all main types of free energy calculations involving charged solutes. Because it is relatively simple to apply, the analytical correction scheme offers a general solution to this problem, with potential applications to protein-ligand binding, biomolecular association, residue mutation, pKa and redox potential estimation, substrate transformation, solvation and solvent-solvent partitioning.
With recent progresses made in the development of dedicated computers147, 148, 149 and softwares accelerated by the use of graphic processing units (GPUs),150, 151, 152 system sizes could soon become large enough to eliminate finite-size effects in molecular simulations in the absence of any correction scheme. But this may not be the best approach. Increased computing power is often used to study new challenging problems involving larger solutes or/and longer timescales, rather than to increase the number of solvent molecules. Furthermore, the number of solvent molecules required to calculate a solvation free energy within chemical accuracy (e.g. kBT) scales with the sixth power of the solute net charge (as can be inferred from the Born model153), implying extremely large systems beyond the simplest monovalent cases. Finally, given that the analytical correction scheme proposed here is straightforward to apply and accurately accounts for long-range solvation in a computationally inexpensive implicit-solvent representation, increasing the explicit-solvation range instead represents an inefficient use of computing power.
In summary, the classical simulation community will always be confronted with finite-size effects, and must learn to deal with them in an appropriate way. The authors believe that the analytical correction scheme presented here represents a significant step in this direction.
ACKNOWLEDGMENTS
The authors are thankful to Maria Reif and Chris Oostenbrink for many inspiring discussions and mail exchanges on the problem of finite-size effects. Note that irrespective of the actual publication dates of the two articles, their study of Ref. 36 slightly antedates ours. G.J.R. acknowledges the National Science Foundation and Department of Defense predoctoral fellowships. D.L.M. acknowledges financial support from the National Institutes of Health (1R15GM096257-01A1), the National Science Foundation LA-SiGMA program (EPS-1003897), and the Louisiana Board of Regents Research Competitiveness and Research Enhancement Subprograms. P.H.H. acknowledges financial support from the Swiss National Science Foundation (Grant Nos. 21-132739 and 21-138020).
References
- Gilson M. K., Given J. A., Bush B. L., and McCammon J. A., “The statistical thermodynamic basis for computation of binding-affinities: A critical review,” Biophys. J. 72, 1047–1069 (1997). 10.1016/S0006-3495(97)78756-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boresch S., Tettinger F., and Leitgeb M., “Absolute binding free energies: A quantitative approach for their calculation,” J. Phys. Chem. B 107, 9535–9551 (2003). 10.1021/jp0217839 [DOI] [Google Scholar]
- Swanson J. M. J., Henchman R. H., and McCammon J. A., “Revisiting free energy calculations: A theoretical connection to MM/PBSA and direct calculation of the association free energy,” Biophys. J. 86, 67–74 (2004). 10.1016/S0006-3495(04)74084-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., Deng Y., and Roux B., “Absolute binding free energy calculations using molecular dynamics simulations with restraining potentials,” Biophys. J. 91, 2798–2814 (2006). 10.1529/biophysj.106.084301 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng Y. and Roux B., “Calculation of standard binding free energies: Aromatic molecules in the T4 lysozyme L99A mutant,” J. Chem. Theory Comput. 2, 1255–1273 (2006). 10.1021/ct060037v [DOI] [PubMed] [Google Scholar]
- Hermans J. and Shankar S., “The free energy of xenon binding to myoglobin from molecular dynamics simulation,” Isr. J. Chem. 27, 225–227 (1986). [Google Scholar]
- Roux B., Nina M., Pomès R., and Smith J. C., “Thermodynamic stability of water molecules in the Bacteriorhodopsin proton channel: A molecular dynamics free energy perturbation study,” Biophys. J. 71, 670–681 (1996). 10.1016/S0006-3495(96)79267-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermans J. and Wang L., “Inclusion of loss of translational and rotational freedom in theoretical estimates of free energies of binding. Application to a complex of benzene and mutant T4 Lysozyme,” J. Am. Chem. Soc. 119, 2707–2714 (1997). 10.1021/ja963568+ [DOI] [Google Scholar]
- Beveridge D. L. and DiCapua F. M., “Free energy via molecular simulation: Applications to chemical and biomolecular systems,” Annu. Rev. Biophys. Biophys. Chem. 18, 431–492 (1989). 10.1146/annurev.bb.18.060189.002243 [DOI] [PubMed] [Google Scholar]
- van Gunsteren W. F., and Berendsen H. J. C., “Computer simulation of molecular dynamics: Methodology, applications and perspectives in chemistry,” Angew. Chem. Int. Ed. 29, 992–1023 (1990). 10.1002/anie.199009921 [DOI] [Google Scholar]
- Kollman P., “Free energy calculations: Applications to chemical and biochemical phenomena,” Chem. Rev. 93, 2395–2417 (1993). 10.1021/cr00023a004 [DOI] [Google Scholar]
- Christen M. and van Gunsteren W. F., “On searching in, sampling of, and dynamically moving through conformational space of biomolecular systems: A review,” J. Comput. Chem. 29, 157–166 (2008). 10.1002/jcc.20725 [DOI] [PubMed] [Google Scholar]
- Hansen H. S., Daura X., and Hünenberger P. H., “Enhanced conformational sampling in molecular dynamics simulations of solvated peptides: Fragment-based local elevation umbrella sampling,” J. Chem. Theory Comput. 6, 2598–2621 (2010). 10.1021/ct1003059 [DOI] [PubMed] [Google Scholar]
- Hansen H. S. and Hünenberger P. H., “Ball-and-stick local elevation umbrella sampling: Molecular simulations involving enhanced sampling within conformational or alchemical subspaces of low internal dimensionalities, minimal irrelevant volume and problem-adapted geometries,” J. Chem. Theory Comput. 6, 2622–2646 (2010). 10.1021/ct1003065 [DOI] [PubMed] [Google Scholar]
- Boresch S. and Karplus M., “The Jacobian factor in free energy simulations,” J. Chem. Phys. 105, 5145–5154 (1996). 10.1063/1.472358 [DOI] [Google Scholar]
- den Otter W. K. and Briels W. J., “The calculation of free-energy differences by constrained molecular-dynamics simulations,” J. Chem. Phys. 109, 4139–4146 (1998). 10.1063/1.477019 [DOI] [Google Scholar]
- Hermans J., “Simple analysis of noise and hysteresis in (slow-growth) free energy simulations,” J. Phys. Chem. 95, 9029–9032 (1991). 10.1021/j100176a002 [DOI] [Google Scholar]
- Wood R. H., “Estimation of errors in free energy calculations due to the lag between the Hamiltonian and the system configuration,” J. Phys. Chem. 95, 4838–4842 (1991). 10.1021/j100165a045 [DOI] [Google Scholar]
- Beutler T. C., Mark A. E., van Schaik R., Gerber P. R., and van Gunsteren W. F., “Avoiding singularities and numerical instabilities in free energy calculations based on molecular simulations,” Chem. Phys. Lett. 222, 529–539 (1994). 10.1016/0009-2614(94)00397-1 [DOI] [Google Scholar]
- Hünenberger P. H. and McCammon J. A., “Ewald artifacts in computer simulations of ionic solvation and ion-ion interaction: A continuum electrostatics study,” J. Chem. Phys. 110, 1856–1872 (1999). 10.1063/1.477873 [DOI] [Google Scholar]
- Kastenholz M. A. and Hünenberger P. H., “Influence of artificial periodicity and ionic strength in molecular dynamics simulations of charged biomolecules employing lattice-sum methods,” J. Phys. Chem. B 108, 774–788 (2004). 10.1021/jp0350924 [DOI] [Google Scholar]
- Kastenholz M. A. and Hünenberger P. H., “Computation of methodology independent ionic solvation free energies from molecular simulations: I. The electrostatic potential in molecular liquids,” J. Chem. Phys. 124, 124106-1–124106-27 (2006). 10.1063/1.2172593 [DOI] [PubMed] [Google Scholar]
- Kastenholz M. A. and Hünenberger P. H., “Computation of methodology independent ionic solvation free energies from molecular simulations: II. The hydration free energy of the sodium cation,” J. Chem. Phys. 124, 224501-1–224501-20 (2006). 10.1063/1.2201698 [DOI] [PubMed] [Google Scholar]
- Reif M. M., Kräutler V., Kastenholz M. A., Daura X., and Hünenberger P. H., “Explicit-solvent molecular dynamics simulations of a reversibly-folding β-heptapeptide in methanol: Influence of the treatment of long-range electrostatic interactions,” J. Phys. Chem. B 113, 3112–3128 (2009). 10.1021/jp807421a [DOI] [PubMed] [Google Scholar]
- Hünenberger P. H., “Lattice-sum methods for computing electrostatic interactions in molecular simulations,” in Simulation and Theory of Electrostatic Interactions in Solution: Computational Chemistry, Biophysics, and Aqueous Solution, edited by Hummer G. and Pratt L. R. (American Institute of Physics, New York, 1999), pp. 17–83. [Google Scholar]
- Ewald P. P., “Die Berechnung optischer und elektrostatischer Gitterpotentiale,” Ann. Phys. 369, 253–287 (1921). 10.1002/andp.19213690304 [DOI] [Google Scholar]
- Hockney R. W. and Eastwood J. W., Computer Simulation using Particles (McGraw-Hill, New York,1981). [Google Scholar]
- Darden T., York D., and Pedersen L., “Particle mesh Ewald: An Nlog(N) method for Ewald sums in large systems,” J. Chem. Phys. 98, 10089–10092 (1993). 10.1063/1.464397 [DOI] [Google Scholar]
- Essmann U., Perera L., Berkowitz M. L., Darden T., Lee H., and Pedersen L. G., “A smooth particle mesh Ewald method,” J. Chem. Phys. 103, 8577–8593 (1995). 10.1063/1.470117 [DOI] [Google Scholar]
- Figueirido F., Levy R. M., Zhou R., and Berne B. J., “Large scale simulation of macromolecules in solution: Combining the periodic fast multipole method with multiple time step integrators,” J. Phys. Chem. 106, 9835–9849 (1997). 10.1063/1.474115 [DOI] [Google Scholar]
- Reif M. M. and Hünenberger P. H., “Computation of methodology-independent single-ion solvation properties from molecular simulations. III. Correction terms for the solvation free energies, enthalpies, entropies, heat capacities, volumes, compressibilities and expansivities of solvated ions,” J. Chem. Phys. 134, 144103-1–144103-30 (2011). 10.1063/1.3567020 [DOI] [PubMed] [Google Scholar]
- Reif M. M. and Hünenberger P. H., “Computation of methodology-independent single-ion solvation properties from molecular simulations. IV. Optimized Lennard-Jones parameter sets for the alkali and halide ions in water,” J. Chem. Phys. 134, 144104-1–144104-25 (2011). 10.1063/1.3567022 [DOI] [PubMed] [Google Scholar]
- Hünenberger P. H. and Reif M. M., Single-ion Solvation: Experimental and Theoretical Approaches to Elusive Thermodynamic Quantities, 1st ed., Theoretical and Computational Chemistry Series Vol. 3 (Royal Society of Chemistry, London, 2011). [Google Scholar]
- Dahlgren B., Reif M. M., Hünenberger P. H., and Hansen N., “Calculation of derivative thermodynamic hydration and aqueous partial molar properties of ions based on atomistic simulations,” J. Chem. Theory Comput. 8, 3542–3564 (2012). 10.1021/ct300260q [DOI] [PubMed] [Google Scholar]
- Reif M. M., Hünenberger P. H., and Oostenbrink C., “New interaction parameters for charged amino acid side chains in the GROMOS force field,” J. Chem. Theory Comput. 8, 3705–3723 (2012). 10.1021/ct300156h [DOI] [PubMed] [Google Scholar]
- Reif M. M. and Oostenbrink C., “Net charge changes in the calculation of relative ligand-binding free energies via classical atomistic molecular dynamics simulations,” J. Comput. Chem. (in press). [DOI] [PMC free article] [PubMed]
- Woo H.-J. and Roux B., “Calculation of absolute protein-ligand binding free energy from computer simulations,” Proc. Natl. Acad. Sci. U.S.A. 102, 6825–6830 (2005). 10.1073/pnas.0409005102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau A. Y. and Roux B., “The hidden energetics of ligand binding and activation in a glutamate receptor,” Nat. Struct. Biol. 18, 283–288 (2011) 10.1038/nsmb.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Ruiter A. and Oostenbrink C., “Protein-ligand binding from distancefield distances and Hamiltonian replica exchange simulations,” J. Chem. Theory Comput. 9, 883892 (2013). 10.1021/ct300967a [DOI] [PubMed] [Google Scholar]
- Dixit S. B. and Chipot C., “Can absolute free energies of association be estimated from molecular mechanical simulations? The biotin-streptavidin system revisited,” J. Phys. Chem. A 105, 9795–9799 (2001). 10.1021/jp011878v [DOI] [Google Scholar]
- Donnini S., Mark A. E., Juffer A. H., and Villa A., “Incorporating the effect of ionic strength in free energy calculations using explicit ions,” J. Comput. Chem. 26, 115122 (2005). 10.1002/jcc.20156 [DOI] [PubMed] [Google Scholar]
- Zhou R., Das P., and Royyuru A. K., “Single mutation induced H3N2 hemagglutinin antibody neutralization: A free energy perturbation study,” J. Phys. Chem. B 112, 15813–15820 (2008). 10.1021/jp805529z [DOI] [PubMed] [Google Scholar]
- Morgan B. R. and Massi F., “Accurate estimates of free energy changes in charge mutations,” J. Chem. Theory Comput. 6, 1884–1893 (2010). 10.1021/ct900565e [DOI] [PubMed] [Google Scholar]
- Hummer G., Pratt L. R., and Garcia A. E., “Free energy of ionic hydration,” J. Phys. Chem. 100, 1206–1215 (1996). 10.1021/jp951011v [DOI] [Google Scholar]
- Hummer G., Pratt L. R., Garcia A. E., Berne B. J., and Rick S. W., “Electrostatic potentials and free energies of solvation of polar and charged molecules,” J. Phys. Chem. B 101, 3017–3020 (1997). 10.1021/jp964037a [DOI] [Google Scholar]
- Hummer G., Pratt L. R., and Garcia A. E., “Ion sizes and finite-size corrections for ionic-solvation free energies,” J. Chem. Phys. 107, 9275–9277 (1997). 10.1063/1.475219 [DOI] [Google Scholar]
- Rosenfeld R. J., Hays A.-M. A., Musah R. A., and Goodin D. B., “Excision of a proposed electron transfer pathway in cytochrome c peroxidase and its replacement by a ligand-binding channel,” Protein Sci. 11, 1251–1259 (2002). 10.1110/ps.4870102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rocklin G. J., Boyce S. E., Fischer M., Fish I., Mobley D. L., Shoichet B. K., and Dill K. A., “Blind prediction of charged ligand binding affinities in a model binding site,” J. Mol. Biol. (in press). [DOI] [PMC free article] [PubMed]
- Åqvist J. and Hansson T., “On the validity of electrostatic linear response in polar solvents,” J. Phys. Chem. 100, 9512–9521 (1996). 10.1021/jp953640a [DOI] [Google Scholar]
- Simonson T., “Gaussian fluctuations and linear response in an electron transfer process,” Proc. Natl. Acad. Sci. U.S.A. 99, 6544–6549 (2002). 10.1073/pnas.082657099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis M. E., Madura J. D., Luty B. A., and McCammon J. A., “Electrostatics and diffusion of molecules in solution: Simulations with the University of Houston Brownian dynamics program,” Comput. Phys. Commun. 62, 187–197 (1991). 10.1016/0010-4655(91)90094-2 [DOI] [Google Scholar]
- Madura J. D., Briggs J. M., Wade R. C., Davis M. E., Luty B. A., Ilin A., Antosiewicz J., Gilson M. K., Bagheri B., Scott L. R., and McCammon J. A., “Electrostatics and diffusion of molecules in solution: Simulations with the University of Houston Brownian Dynamics program,” Comput. Phys. Commun. 91, 57–95 (1995). 10.1016/0010-4655(95)00043-F [DOI] [Google Scholar]
- Nicholls A. and Honig B., “A rapid finite-difference algorithm, utilizing successive over-relaxation to solve the Poisson-Boltzmann equation,” J. Comput. Chem. 12, 435–445 (1991). 10.1002/jcc.540120405 [DOI] [Google Scholar]
- Baker N. A., Sept D., Joseph S., Holst M. J., and McCammon J. A., “Electrostatics of nanosystems: Application to microtubules and the ribosome,” Proc. Natl. Acad. Sci. U.S.A. 98, 10037–10041 (2001). 10.1073/pnas.181342398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen N., Hünenberger P. H. and van Gunsteren W. F., “Efficient combination of environment change and alchemical perturbation within the enveloping distribution sampling (EDS) scheme: Twin-system EDS and application to the determination of octanol-water partition coefficients,” J. Chem. Theory Comput. 9, 1334–1346 (2013). 10.1021/ct300933y [DOI] [PubMed] [Google Scholar]
- Kirkwood J. G., “Statistical mechanics of fluid mixtures,” J. Chem. Phys. 3, 300–313 (1935). 10.1063/1.1749657 [DOI] [Google Scholar]
- Zwanzig R. W., “High-temperature equation of state by a perturbation method. I. Nonpolar gases,” J. Chem. Phys. 22, 1420–1426 (1954). 10.1063/1.1740193 [DOI] [Google Scholar]
- Bennet C. H., “Efficient estimation of free energy differences from Monte Carlo data,” J. Comput. Phys. 22, 245–268 (1976). 10.1016/0021-9991(76)90078-4 [DOI] [Google Scholar]
- Shirts M. R. and Chodera J. D., “Statistically optimal analysis of samples from multiple equilibrium states,” J. Chem. Phys. 129, 124105-1–124105-10 (2008). 10.1063/1.2978177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christen M., Hünenberger P. H., Bakowies D., Baron R., Bürgi R., Geerke D. P., Heinz T. N., Kastenholz M. A., Kräutler V., Oostenbrink C., Peter C., Trzesniak D., and van Gunsteren W. F., “The GROMOS software for biomolecular simulation: GROMOS05,” J. Comput. Chem. 26, 1719–1751 (2005). 10.1002/jcc.20303 [DOI] [PubMed] [Google Scholar]
- Hess B., Kutzner C., van der Spoel D., and Lindahl E., “GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation,” J. Chem. Theory Comput. 4, 435–447 (2008). 10.1021/ct700301q [DOI] [PubMed] [Google Scholar]
- Brush S. G., Sahlin H. L., and Teller E., “Monte Carlo study of a one-component plasma. I,” J. Chem. Phys. 45, 2102–2118 (1966). 10.1063/1.1727895 [DOI] [Google Scholar]
- Hummer G. and Soumpasis D. M., “Correlations and free energies in restricted primitive model descriptions of electrolytes,” J. Chem. Phys. 98, 581–591 (1993). 10.1063/1.464600 [DOI] [Google Scholar]
- Hummer G., Pratt L. R., and Garcia A. E., “Hydration free energy of water,” J. Phys. Chem. 99, 14188–14194 (1995). 10.1021/j100038a062 [DOI] [Google Scholar]
- Redlack A. and Grindlay J., “The electrostatic potential in a finite ionic crystal,” Can. J. Phys. 50, 2815–2825 (1972). 10.1139/p72-375 [DOI] [Google Scholar]
- Nijboer B. R. A. and Ruijgrok T. W., “On the energy per particle in three- and two-dimensional Wigner lattices,” J. Stat. Phys. 53, 361–382 (1988). 10.1007/BF01011562 [DOI] [Google Scholar]
- Bogusz S., Cheatham T. E., and Brooks B. R., “Removal of pressure and free energy artifacts in charged periodic systems via net charge corrections to the Ewald potential,” J. Chem. Phys. 108, 7070–7084 (1998). 10.1063/1.476320 [DOI] [Google Scholar]
- Reif M. M., Oostenbrink C., and Hünenberger P. H., “The missing net-charge term in electrostatic interaction schemes under periodic boundary conditions: Pairwise reformulation of the interaction, group partitioning, and implementation into the GROMOS program” (unpublished).
- Hünenberger P. H. and McCammon J. A., “Effect of artificial periodicity in simulations of biomolecules under Ewald boundary conditions: A continuum electrostatics study,” Biophys. Chem. 78, 69–88 (1999). 10.1016/S0301-4622(99)00007-1 [DOI] [PubMed] [Google Scholar]
- Baker N. A., Hünenberger P. H., and McCammon J. A., “Polarization around an ion in a dielectric continuum with truncated electrostatic interactions,” J. Chem. Phys. 110, 10679–10692 (1999). 10.1063/1.479013 [DOI] [Google Scholar]
- Baker N. A., Hünenberger P. H., and McCammon J. A., “Erratum: “Polarization around an ion in a dielectric continuum with truncated electrostatic interactions” [J. Chem. Phys. 110, 10679–10692 (1999)],” J. Chem. Phys. 113, 2510–2511 (2000). 10.1063/1.482073 [DOI] [Google Scholar]
- Weber W., Hünenberger P. H., and McCammon J. A., “Molecular dynamics simulations of a polyalanine octapeptide under Ewald boundary conditions: Influence of artificial periodicity on peptide conformation,” J. Phys. Chem. B 104, 3668–3675 (2000). 10.1021/jp9937757 [DOI] [Google Scholar]
- Peter C., van Gunsteren W. F., and Hünenberger P. H., “Solving the Poisson equation for solute-solvent systems using fast Fourier transforms,” J. Chem. Phys. 116, 7434–7451 (2002). 10.1063/1.1465396 [DOI] [Google Scholar]
- Peter C., van Gunsteren W. F., and Hünenberger P. H., “A fast-Fourier-transform method to solve continuum-electrostatics problems with truncated electrostatic interactions: Algorithm and application to ionic solvation and ion-ion interaction,” J. Chem. Phys. 119, 12205–12223 (2003). 10.1063/1.1624054 [DOI] [Google Scholar]
- Bergdorf M., Peter C., and Hünenberger P. H., “Influence of cutoff truncation and artificial periodicity of electrostatic interactions in molecular simulations of solvated ions: A continuum electrostatics study,” J. Chem. Phys. 119, 9129–9144 (2003). 10.1063/1.1614202 [DOI] [Google Scholar]
- Warshel A., Sharma P. K., Kato M., and Parson W. W., “Modeling electrostatic effects in proteins,” Biochim. Biophys. Acta 1764, 1647–1676 (2006). 10.1016/j.bbapap.2006.08.007 [DOI] [PubMed] [Google Scholar]
- Li L., Li C., Zhang Z., and Alexov E., “On the dielectric “constant” of proteins: Smooth dielectric function for macromolecular modeling and its implementation in DelPhi,” J. Chem. Theory Comput. 9, 2126–2136 (2013). 10.1021/ct400065j [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antosiewicz J., Briggs J. M., and McCammon J. A., “Orientational steering in enzyme-substrate association: Ionic strength dependence of hydrodynamic torque effect,” Eur. Biophys. J. 24, 137–141 (1996). 10.1007/BF00180270 [DOI] [PubMed] [Google Scholar]
- Dong F. and Zhou H.-X., “Electrostatic contribution to the binding stability of protein-protein complexes,” Proteins: Struct., Funct., Bioinf. 65, 87–102 (2006). 10.1002/prot.21070 [DOI] [PubMed] [Google Scholar]
- Qin S. and Zhou H.-X., “Do electrostatic interactions destabilize protein-nucleic acid binding?,” Biopolymers 86, 112–118 (2007). 10.1002/bip.20708 [DOI] [PubMed] [Google Scholar]
- Sloth P. and Sørensen T. S., “Monte Carlo calculations of chemical potentials in ionic fluids by application of Widom's formula: Correction for finite-system effects,” Chem. Phys. Lett. 173, 51–56 (1990). 10.1016/0009-2614(90)85301-R [DOI] [Google Scholar]
- Sørensen T. S., “Error in the Debye-Hückel approximation for dilute primitive model electrolytes with Bjerrum parameters of 2 and ca. 6.8 investigated by Monte Carlo methods,” J. Chem. Soc., Faraday Trans. 87, 479–492 (1991). 10.1039/ft9918700479 [DOI] [Google Scholar]
- Hummer G., “Electrostatic potential of a homogeneously charged square and cube in two and three dimensions,” J. Electrostatics 36, 285–291 (1996). 10.1016/0304-3886(95)00052-6 [DOI] [Google Scholar]
- Hornak V., Abel R., Okur A., Stockbine B., Roitberg A., and Simmerling C., “Comparison of multiple Amber force fields and development of improved protein backbone parameters,” Proteins: Struct., Funct., Bioinf. 65, 712–725 (2006) 10.1002/prot.21123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., “Comparison of simple potential functions for simulating liquid water,” J. Chem. Phys. 79, 926–935 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- Boyce S. E., Mobley D. L., Rocklin G. J., Graves A. P., Dill K. A., and Stoichet B. K., “Predicting ligand binding affinity with alchemical free energy methods in a polar model binding site,” J. Mol. Biol. 394, 747–763 (2009). 10.1016/j.jmb.2009.09.049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Gunsteren W. F. and Berendsen H. J. C., “A leap-frog algorithm for stochastic dynamics,” Mol. Simul. 1, 173–185 (1988). 10.1080/08927028808080941 [DOI] [Google Scholar]
- Hess B., Bekker H., Berendsen H. J. C., and Fraaije J. G. E. M., “LINCS: A linear constraint solver for molecular simulations,” J. Comput. Chem. 18, 1463–1472 (1997). [DOI] [Google Scholar]
- Musah R. A., Jensen G. M., Bunte S. W., Rosenfeld R. J., and Goodin D. B., “Artificial protein cavities as specific ligand-binding templates: Characterization of an engineered heterocyclic cation-binding site that preserves the evolved specificity of the parent protein,” J. Mol. Biol. 315, 845–857 (2002). 10.1006/jmbi.2001.5287 [DOI] [PubMed] [Google Scholar]
- Alexov E. G. and Gunner M. R., “Incorporating protein conformational flexibility into the calculation of pH-dependent protein properties,” Biophys. J. 74, 2075–2093 (1997). 10.1016/S0006-3495(97)78851-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgescu R. E., Alexov E. G., and Gunner M. G., “Combining conformational flexibility and continuum electrostatics for calculating pKas in proteins,” Biophys. J. 83, 1731–1748 (2002). 10.1016/S0006-3495(02)73940-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lide D. R., CRC Handbook of Chemistry and Physics, 83rd ed. (CRC Press, Boca Raton, FL,2002). [Google Scholar]
- Chodera J. D., Swope W. C., Pitera J. W., Seok C., and Dill K. A., “Use of the weighted histogram analysis method for the analysis of simulated and parallel tempering simulations,” J. Chem. Theory Comput. 3, 26–41 (2007). 10.1021/ct0502864 [DOI] [PubMed] [Google Scholar]
- Wang J., Cai Q., Xiang Y., and Luo R., “Reducing grid dependence in finite-difference Poisson-Boltzmann calculations,” J. Chem. Theory Comput. 8, 2741–2751 (2012). 10.1021/ct300341d [DOI] [PMC free article] [PubMed] [Google Scholar]
- Höchtl P., Boresch S., Bitmosky W., and Steinhauser O., “Rationalization of the dielectric properties of common three-site water models in terms of their force-field parameters,” J. Chem. Phys. 109, 4927–4937 (1998). 10.1063/1.477104 [DOI] [Google Scholar]
- Luty B. A., Davis M. E., and McCammon J. A., “Electrostatic energy calculations by a finite-difference method: Rapid calculation of charge-solvent interaction energies,” J. Comput. Chem. 13, 768–771 (1992). 10.1002/jcc.540130610 [DOI] [Google Scholar]
- Bruccoleri R. B., Novotny J., and Davis M. E., “Finite difference Poisson-Boltzmann electrostatic calculations: Increased accuracy achieved by harmonic dielectric smoothing and charge antialiasing,” J. Comput. Chem. 18, 268–276 (1997). [DOI] [Google Scholar]
- Kottmann S. T., “Harmonic averaging of smooth permittivity functions in finite-difference Poisson-Boltzmann electrostatics,” Theor. Chem. Acc. 119, 421–427 (2008). 10.1007/s00214-007-0397-0 [DOI] [Google Scholar]
- Kim D.-S., Won C.-I., and Bhak J., “A proposal for the revision of molecular boundary typology,” J. Biomol. Struct. Dyn. 28, 277–287 (2010). 10.1080/07391102.2010.10507359 [DOI] [PubMed] [Google Scholar]
- Dong F. and Zhou H.-X., “Electrostatic contributions to T4 lysozyme stability: Solvent-exposed charges versus semi-buried salt bridges,” Biophys. J. 83, 1341–1347 (2002). 10.1016/S0006-3495(02)73904-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tjong H. and Zhou H. X., “On the dielectric boundary in Poisson-Boltzmann calculations,” J. Chem. Theory Comput. 4, 507–514 (2008). 10.1021/ct700319x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pang X. and Zhou H.-X., “Poisson-Boltzmann calculations: van der Waals or molecular surface,” Commun. Comput. Phys. 13, 1–12 (2013). 10.4208/cicp.270711.140911s [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee M. S. and Olson M. A., “Evaluation of Poisson solvation models using a hybrid explicit/implicit solvent method,” J. Phys. Chem. B 109, 5223–5236 (2005). 10.1021/jp046377z [DOI] [PubMed] [Google Scholar]
- Swanson J. M. J., Mongan J., and McCammon J. A., “Limitations of atom-centered dielectric functions in implicit solvent models,” J. Phys. Chem. B 109, 14769–14772 (2005). 10.1021/jp052883s [DOI] [PubMed] [Google Scholar]
- Mongan J., Simmerling C., McCammon J. A., Case D. A., and Onufriev A., “Generalized Born model with a simple, robust molecular volume correction,” J. Chem. Theory Comput. 3, 156–169 (2007). 10.1021/ct600085e [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bekker H., “Unification of box shapes in molecular simulations,” J. Comput. Chem. 18, 1930–1942 (1997). [DOI] [Google Scholar]
- Andersen H. C., “Molecular dynamics simulations at constant pressure and/or temperature,” J. Chem. Phys. 72, 2384–2393 (1980). 10.1063/1.439486 [DOI] [Google Scholar]
- Parrinello M. and Rahman A., “Polymorphic transitions in single crystals: A new molecular dynamics method,” J. Appl. Phys. 52, 7182–7190 (1981). 10.1063/1.328693 [DOI] [Google Scholar]
- Hünenberger P. H., “Calculation of the group-based pressure in molecular simulations. I. A general formulation including Ewald and particle-particle–particle-mesh electrostatics,” J. Chem. Phys. 116, 6880–6897 (2002). 10.1063/1.1463057 [DOI] [Google Scholar]
- Barker J. A. and Watts R. O., “Monte Carlo studies of the dielectric properties of water-like models,” Mol. Phys. 26, 789–792 (1973). 10.1080/00268977300102101 [DOI] [Google Scholar]
- Tironi I. G., Sperb R., Smith P. E., and van Gunsteren W. F., “A generalized reaction field method for molecular dynamics simulations,” J. Chem. Phys. 102, 5451–5459 (1995). 10.1063/1.469273 [DOI] [Google Scholar]
- Ashbaugh H. S. and Wood R. H., “Effects of long-range electrostatic potential truncation on the free energy of ionic hydration,” J. Chem. Phys. 106, 8135–8139 (1997). 10.1063/1.473800 [DOI] [Google Scholar]
- Åqvist J. and Hansson T., “Analysis of electrostatic potential truncation schemes in simulations of polar solvents,” J. Phys. Chem. B 102, 3837–3840 (1998). 10.1021/jp973207w [DOI] [Google Scholar]
- Hummer G., Pratt L. R., Garcia A. E., Garde S., Berne B. J., and Rick S. W., “Reply to comments on “Electrostatic potentials and free energies of solvation of polar and charged molecules,” J. Phys. Chem. B 102, 3841–3843 (1998). 10.1021/jp980145g [DOI] [Google Scholar]
- Ashbaugh H. S. and Wood R. H., “Reply to comment on “Electrostatic potentials and free energies of solvation of polar and charged molecules,” J. Phys. Chem. B 102, 3844–3845 (1998). 10.1021/jp9804852 [DOI] [Google Scholar]
- Darden T., Pearlman D., and Pedersen L. G., “Ionic charging free energies: Spherical versus periodic boundary conditions,” J. Chem. Phys. 109, 10921–10935 (1998). 10.1063/1.477788 [DOI] [Google Scholar]
- Sakane S., Ashbaugh H. S., and Wood R. H., “Continuum corrections to the polarization and thermodynamic properties of Ewald sum simulations for ions and ion pairs at infinite dilution,” J. Phys. Chem. B 102, 5673–5682 (1998). 10.1021/jp9808227 [DOI] [Google Scholar]
- Garde S., Hummer G., and Paulaitis M. E., “Free energy of hydration of a molecular ionic solute: Tetramethylammonium ion,” J. Chem. Phys. 108, 1552–1561 (1998). 10.1063/1.475526 [DOI] [Google Scholar]
- Vorobjev Y. N. and Hermans J., “A critical analysis of methods of calculation of a potential in simulated polar liquids: Strong arguments in favor of “Molecule-based” summation and of vacuum boundary conditions in Ewald summations,” J. Phys. Chem. B 103, 10234–10242 (1999). 10.1021/jp984211q [DOI] [Google Scholar]
- Babu C. S., Yang P.-K., and Lim C., “On the charge and molecule based summations of solvent electrostatic potentials and the validity of electrostatic linear response in water,” J. Biol. Phys. 28, 95–113 (2002). 10.1023/A:1019978119707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herce D. H., Darden T., and Sagui C., “Calculation of ionic charging free energies in simulation systems with atomic charges, dipoles, and quadrupoles,” J. Chem. Phys. 119, 7621–7632 (2003). 10.1063/1.1609191 [DOI] [Google Scholar]
- Christou N. I., Whitehouse J. S., Nicholson D., and Parsonage N. G., “Studies of high density water films by computer simulation,” Mol. Phys. 55, 397–410 (1985). 10.1080/00268978500101421 [DOI] [Google Scholar]
- Aloisi G., Guidelli R., Jackson R. A., Clark S. M., and Barnes P., “The structure of water at a neutral interface,” J. Electroanal. Chem 206, 131–137 (1986). 10.1016/0022-0728(86)90262-7 [DOI] [Google Scholar]
- Brodskaya E. N., “The molecular dynamics simulation of water clusters,” Mol. Phys. 62, 251–265 (1987) 10.1080/00268978700102181 [DOI] [Google Scholar]
- Wilson M. A., Pohorille A., and Pratt L. R., “Molecular dynamics of the water liquid-vapor interface,” J. Phys. Chem. 91, 4873–4878 (1987). 10.1021/j100303a002 [DOI] [PubMed] [Google Scholar]
- Matsumoto M. and Kataoka Y., “Study on liquid-vapor interface of water. I. Simulation results of thermodynamic properties and orientational structure,” J. Chem. Phys. 88, 3233–3245 (1988). 10.1063/1.453919 [DOI] [PubMed] [Google Scholar]
- Wilson M. A., Pohorille A., and Pratt L. R., “Surface potential of the water liquid-vapor interface,” J. Chem. Phys. 88, 3281–3285 (1988). 10.1063/1.453923 [DOI] [PubMed] [Google Scholar]
- Matsumoto M. and Kataoka Y., “Molecular orientation near liquid-vapor interface of methanol: Simulational study,” J. Chem. Phys. 90, 2398–2407 (1989). 10.1063/1.455982 [DOI] [Google Scholar]
- Wilson M. A., Pohorille A., and Pratt L. R., “Comment on “Study on the liquid-vapor interface of water. I. Simulation results of thermodynamic properties and orientational structure,” J. Chem. Phys. 90, 5211–5213 (1989). 10.1063/1.456536 [DOI] [PubMed] [Google Scholar]
- Barraclough C. G., McTigue P. T., and Ng Y. L., “Surface potentials of water, methanol and water+methanol mixtures,” J. Electroanal. Chem. 329, 9–24 (1992). 10.1016/0022-0728(92)80205-I [DOI] [Google Scholar]
- Pohorille A. and Wilson M. A., “Viewpoint 9—Molecular structure of aqueous interfaces,” J. Mol. Struct.: THEOCHEM 284, 271–298 (1993). 10.1016/0166-1280(93)87010-B [DOI] [PubMed] [Google Scholar]
- Brodskaya E. N. and Zakharov V. V., “Computer simulation study of the surface polarization of pure polar liquids,” J. Chem. Phys. 102, 4595–4599 (1995). 10.1063/1.469507 [DOI] [Google Scholar]
- Kuzmin V. L., “Calculation of the surface potential for charge models of water,” Colloid J. 57, 776–780 (1995). [Google Scholar]
- Ashbaugh H. S., “Influence of potential truncation on anisotropic systems,” Mol. Phys. 97, 433–437 (1999). 10.1080/00268979909482843 [DOI] [Google Scholar]
- Yang P.-K. and Lim C., “Nonconvergence of the solute potential in an infinite solvent and its implications in continuum models,” J. Phys. Chem. B 106, 12093–12096 (2002). 10.1021/jp025909d [DOI] [Google Scholar]
- Harder E. and Roux B., “On the origin of the electrostatic potential difference at a liquid-vacuum interface,” J. Chem. Phys. 129, 234706-1–234706-9 (2008). 10.1063/1.3027513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kathmann S. M., I-Feng W. K., and Mundy C. J., “Electronic effects on the surface potential at the vapor-liquid interface of water,” J. Am. Chem. Soc. 130, 16556–16561 (2008). 10.1021/ja802851w [DOI] [PubMed] [Google Scholar]
- Leung K., Rempe S. B., and von Lilienfeld O. A., “Ab initio molecular dynamics calculations of ion hydration free energies,” J. Chem. Phys. 130, 204507-1–204507-11 (2009). 10.1063/1.3137054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rempe S. B. and Leung K., “Response to Comment on “Ab initio molecular dynamics calculations of ion hydration free energies” [J. Chem. Phys. 133, 047103 (2010)],” J. Chem. Phys. 133, 047104-1–047104-2 (2010). 10.1063/1.3456167 [DOI] [Google Scholar]
- Leung K., “Surface potential at the air-water interface computed using density functional theory,” J. Phys. Chem. Lett. 1, 496–499 (2010). 10.1021/jz900268s [DOI] [Google Scholar]
- Kathmann S. M., Kuo I.-F. W., Mundy C. J., and Schenter G. K., “Understanding the surface potential of water,” J. Phys. Chem. B 115, 4369–4377 (2011). 10.1021/jp1116036 [DOI] [PubMed] [Google Scholar]
- Bannerman M. N., Sargent R., and Lue L., “DynamO: A free O(N) general event-driven molecular dynamics simulator,” J. Comput. Chem. 32, 3329–3338 (2011). 10.1002/jcc.21915 [DOI] [PubMed] [Google Scholar]
- Shi Y. and Beck T. L., “Length scales and interfacial potentials in ion hydration,” J. Chem. Phys. 139, 044504-1–044504-10 (2013) 10.1063/1.4814070 [DOI] [PubMed] [Google Scholar]
- Beck T. L., “The influence of water interfacial potentials on ion hydration in bulk water and near interfaces,” Chem. Phys. Lett. 561–562, 1–13 (2013) 10.1016/j.cplett.2013.01.008 [DOI] [Google Scholar]
- Wick C. D., Lee A. J., and Rick S. W., “How intermolecular charge transfer influences the air-water interface,” J. Chem. Phys. 137, 154701-1–154701-9 (2012). 10.1063/1.4758457 [DOI] [PubMed] [Google Scholar]
- Horváth L., Beu T., Manghi M., and Palmeri J., “The vapor-liquid interface potential of (multi)polar fluids and its influence on ion solvation,” J. Chem. Phys. 138, 154702-1–154702-10 (2013). 10.1063/1.4799938 [DOI] [PubMed] [Google Scholar]
- Fukushige T., Taiji M., Makino J., Ebisuzaki T., and Sugimoto D., “A highly parallelized special-purpose computer for many-body simulations with an arbitrary central force: MD-GRAPE,” Astrophys. J. 468, 51–61 (1996). 10.1086/177668 [DOI] [Google Scholar]
- Shaw D. E., Deneroff M. M., Dror R. O., Kuskin J. S., Larson R. H., Salmon J. K., Young C., Batson B., Bowers K. J., Chao J. C., Eastwood M. P., Gagliardo J., Grossman J. P., Ho C. R., Ierardi D. J., Kolossváry I., Klepeis J. L., Layman T., McLeavey C., Moraes M. A., Mueller R., Priest E. C., Shan Y., Spengler J., Theobald M., Towles B., and Wang S. C., “Anton, a special-purpose machine for molecular dynamics simulation,” Commun. ACM 51, 91–97 (2008). 10.1145/1364782.1364802 [DOI] [Google Scholar]
- Ajima Y., Sumimoto S., and Shimizu T., “TOFU: A 6D mesh/torus interconnect for exascale computers,” Computer 42, 36–40 (2009). 10.1109/MC.2009.370 [DOI] [Google Scholar]
- Harvey M. J. and De Fabritiis G., “An implementation of the smooth particle mesh Ewald method on GPU hardware,” J. Chem. Theory Comput. 5, 2371–2377 (2009). 10.1021/ct900275y [DOI] [PubMed] [Google Scholar]
- Hardy D. J., Stone J. E., and Schulten K., “Multilevel summation of electrostatic potentials using graphics processing units,” Parallel Comput. 35, 164–177 (2009). 10.1016/j.parco.2008.12.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yokota R., Bardhan J. P., Knepley M. G., Barba L. A., and Hamada T., “Biomolecular electrostatics using a fast multipole BEM on up to 512 GPUS and a billion unknowns,” Comput. Phys. Commun. 182, 1271–1283 (2011). 10.1016/j.cpc.2011.02.013 [DOI] [Google Scholar]
- Born M., “Volumen und Hydrationswärme der Ionen,” Z. Phys. 1, 45–48 (1920). 10.1007/BF01881023 [DOI] [Google Scholar]
- See supplementary material at http://dx.doi.org/10.1063/1.4826261 for additional figures, tables, and scripts.