Direct Observation of Phosphate Inhibiting the Force-Generating Capacity of a Miniensemble of Myosin Molecules

Abstract

Elevated levels of phosphate (P_i) reduce isometric force, providing support for the notion that the release of P_i from myosin is closely associated with the generation of muscular force. P_i is thought to rebind to actomyosin in an ADP-bound state and reverse the force-generating steps, including the rotation of the lever arm (i.e., the powerstroke). Despite extensive study, this mechanism remains controversial, in part because it fails to explain the effects of P_i on isometric ATPase and unloaded shortening velocity. To gain new insight into this process, we determined the effect of P_i on the force-generating capacity of a small ensemble of myosin (∼12 myosin heads) using a three-bead laser trap assay. In the absence of P_i, myosin pulled the actin filament out of the laser trap an average distance of 54 ± 4 nm, translating into an average peak force of 1.2 pN. By contrast, in the presence of 30 mM P_i, myosin generated only enough force to displace the actin filament by 13 ± 1 nm, generating just 0.2 pN of force. The elevated P_i also caused a >65% reduction in binding-event lifetime, suggesting that P_i induces premature detachment from a strongly bound state. Definitive evidence of a P_i-induced powerstroke reversal was not observed, therefore we determined if a branched kinetic model in which P_i induces detachment from a strongly bound, postpowerstroke state could explain these observations. The model was able to accurately reproduce not only the data presented here, but also the effects of P_i on both isometric ATPase in muscle fibers and actin filament velocity in a motility assay. The ability of the model to capture the findings presented here as well as previous findings suggests that P_i-induced inhibition of force may proceed along a kinetic pathway different from that of force generation.

Introduction

Experiments on skinned single muscle fibers showed that high levels of phosphate (P_i) decrease maximal isometric force in a concentration-dependent manner (1–4). This work helped establish that myosin’s release of P_i is closely associated with (5), if not coupled to (6), force generation. At the level of a single myosin cross-bridge, P_i putatively reduces force by 1), rebinding to actin-bound myosin with ADP in its active site (AM.ADP; see Fig. 1 A) and 2) reversing the steps of force generation, including a reversal of myosin’s lever arm rotation (the powerstroke). Once the powerstroke is reversed, the cross-bridge is thought to rapidly dissociate from actin into a state that only weakly interacts with actin (M.ADP.P_i (7), and Fig. 1 A). Computer simulations of this type of cross-bridge behavior can accurately fit the effects of P_i on isometric force, helping to make this the conventional model of the cross-bridge cycle (6).

Figure 1.

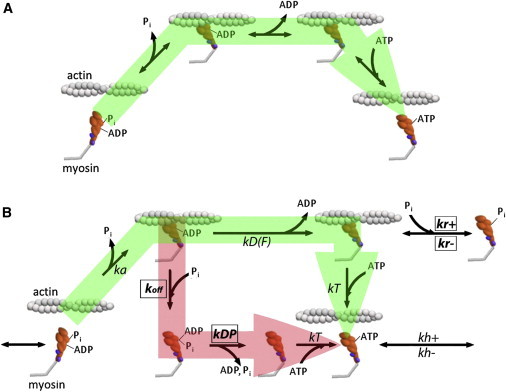
The conventional and branched cross-bridge cycles. (A) A simplified four-state version of the conventional model of the cross-bridge cycle (6). In this model, P_i release is coupled to rotation of myosin’s lever arm and the rebinding of P_i to the AM.ADP state reverses this step. (B) Conventional (green) and branched (red) kinetic pathways where the rebinding of P_i to the AM.ADP state causes myosin to dissociate from actin in a postpowerstroke state and complete the release of P_i and ADP and the rebinding to ATP off actin. In this model, the powerstroke is not reversed with the rebinding of P_i to the AM.ADP state. From Walcott et al. (42), we can specify all parameters of the green pathway. There are then four free kinetic parameters, boxed and shown in bold for the red pathway.

The first key component of this model is that P_i rebinds to the AM.ADP state. In support of this notion, photolysis of caged P_i in isometrically contracting muscle fibers demonstrates that the P_i-induced decrease in force is associated with preferential rebinding to a load-dependent AM.ADP state (2,4,8). More specifically, P_i rebinds to the first of two AM.ADP states (the AM′ADP state (4)) before promoting detachment to the weakly bound M.ADP.P_i state. Similar conclusions were reached based on sinusoidal analysis in single fibers (9) and isometric force measurements in single myofibrils (10). More recently, work at the single-molecule level demonstrated that high P_i increases the population of short-duration binding events, consistent with P_i rebinding to the strongly bound AM.ADP state and inducing dissociation to the M.ADP.P_i state (5,11). This view is also supported by crystal structures of myosin that show a closed actin-binding cleft (corresponding to high actin affinity) when P_i is absent from the active site, but an open cleft configuration (low actin affinity) in an M.ADP.P_i-like state, suggesting that P_i modulates affinity for actin (12). The rebinding of P_i is, however, dependent on strain, since high P_i has little or no effect on unloaded shortening velocity (V_us) in fibers (1,13) or on the analogous measure of actin filament velocity (V_actin) in the motility assay (14–16). Interestingly, P_i can slow V_us (13) and V_actin at micromolar ATP (14–16), leading to the suggestion that P_i may bind to actomyosin with an empty active site (the AM, or rigor state (see Fig. 1 A)) under these conditions (14), but this remains controversial (16,17). Thus, although some ambiguity remains at low ATP, the consensus view is that under loaded conditions, P_i rebinds to an AM.ADP state and induces dissociation to the M.ADP.P_i state (5).

The second key aspect of this conventional model is that the rebinding of P_i to the AM.ADP state is coupled to a reversal of myosin’s powerstroke. Indeed, experiments incorporating P_i with oxygen isotopes were consistent with P_i rebinding to the AM′ADP state and reforming ATP, providing strong, albeit indirect, support for a coupled reversal of the powerstroke (4). Crystal structures reveal that the lever arm occupies a postpowerstroke position in the AM.ADP (18) and rigorlike states (19) but a prepowerstroke position in a state analogous to the ATP-bound state (20), suggesting that the position of the lever arm is determined by the presence or absence of P_i in myosin’s active site. However, when complexed with ADP.BeF₃ (an AM.ADP.P_i surrogate state), myosin’s lever arm can appear in a state consistent with either the pre- (18) or postpowerstroke configuration (21).

The lack of a definitive answer could be due to the fact that the large ensembles in muscle fibers only report myosin’s average behavior, whereas x-ray crystal structures only give a static snapshot of myosin after the rebinding of P_i. Consequently, these studies miss the dynamic behavior of an individual molecule. To address this issue, researchers took advantage of the three-bead single-molecule laser trap assay (22). The effects of P_i were observed by enabling this assay to apply a high dynamic load to a single myosin molecule while the molecule was strongly bound to an actin filament in the absence and presence of P_i (5). Application of load with a time constant of 10 ms produced binding events that were prematurely truncated by P_i, again suggesting that P_i rebinds to an AM.ADP state; but importantly, the load also produced reversals of myosin’s displacement of actin. However, it was unclear whether these reversals represented a reversal of the powerstroke or a forcible detachment of postpowerstroke myosin from actin (5,23). Thus, there is still no definitive evidence that the powerstroke is reversed after the rebinding of P_i to myosin’s active site.

The notion of a P_i-induced reversal of the powerstroke received a more direct challenge based on the observation that P_i has a much more pronounced inhibitory effect on isometric force than on the ATP hydrolysis rate (ATPase) (24,25). In the conventional model, a reversal of the force-generating steps would be expected to decrease the isometric force and ATPase in direct proportion to P_i concentration. Although this discrepancy can be dealt with in the conventional model by having P_i only rebind to highly strained cross-bridges (6), such a mechanism was recently shown to be inconsistent with the observation that the P_i-dependent reduction in force is due to a proportional decrease in the number of strongly attached motors (26). An alternative model with a P_i-dependent branch in the conventional kinetic pathway was proposed to reconcile these results, where the rebinding of P_i to myosin causes dissociation without a reversal of the powerstroke (27). In the model, myosin dissociates from a strained/strongly bound configuration, rapidly completes the release of both P_i and ADP, and rebinds to ATP off actin (Fig. 1 B).

The conventional model is also challenged by our recent observation that P_i can increase velocity at low pH. Specifically, at pH 6.5, the addition of 30 mm P_i can increase V_actin more than twofold (15). Even if the rebinding of P_i to AM.ADP is highly load-dependent, this observation cannot be explained using the conventional model (15). It is also difficult to reconcile with the thermodynamic model described by Hooft et al. (16), since lower pH and increased P_i should decrease free energy, yet V_actin is increased. Therefore, to explain this observation, we constructed a kinetic model similar to that described by Linari et al. (27), with a P_i-dependent branch in the pathway. However in contrast to that model, which focused on isometric force and ATPase, our model focused on explaining the effects of P_i on unloaded velocity. Therefore, in our branched-pathway model, myosin completes its powerstroke on actin before it is dissociated by P_i, enabling the model to accurately capture the P_i-induced increase in V_actin (15).

Our alternative model (Fig. 1 B) suggests that P_i should decrease myosin’s force-generating capacity without causing a reversal of the powerstroke. However, since the actin filament in the motility assay experiences little or no load, it is not clear whether this branched kinetic mechanism also explains the effect of P_i on myosin’s force-generating capacity. To test this aspect of the model, the effect of P_i on myosin’s force-generating capacity must first be directly observed. This is a technical challenge, given that recent evidence from high-time-resolution dark-field experiments using gold-nanoparticle-labeled myosin V indicate that the powerstroke occurs in less than a few hundred microseconds (28), faster than a feedback response can be set in a single-molecule laser trap assay (23), making a single-molecule approach untenable. We can avoid this difficulty by increasing the myosin concentration in a three-bead laser trap assay and assessing the force-generating capacity of a miniensemble of myosin (∼8–12 heads; see Debold et al. (29) for the estimation procedure) (29). The advantage of this approach over the use of muscle fibers and single myofibrils is that the force-generating capacity of myosin can be directly measured with the spatial and temporal resolution of a single-molecule laser trap assay using just a handful of myosin molecules. An additional advantage of this approach is that using multiple molecules more accurately reflects the multiple-motor arrangement of the myosin thick filament in muscle.

In this study, we use a variation of the three-bead laser trap assay approach to directly observe the effect of P_i on the force-generating capacity of a miniensemble of myosin. We use the obtained data to show that a branched kinetic pathway, without a P_i-induced powerstroke reversal, can explain the effect of P_i on force as well as on unloaded filament velocity and isometric ATPase.

Methods

Proteins and solutions

Chicken skeletal actin and myosin were isolated as previously described (15). Myosin was adhered to a nitrocellulose-coated coverslip at a concentration of 25 μg/mL in a high-salt buffer (300 mM KCl, 25 mM imidazole, 1 mM EGTA, 4 mM MgCl₂, and 1 mM dithiothreitol). Given the geometry of the assay and the myosin concentration, we estimate that an average of 12 myosin heads are capable of interacting with the actin filament (29). The surface was then blocked with bovine serum albumin (0.5mg/mL), washed with a low salt buffer (25 mM KCl, 25 mM imidazole, 1 mM EGTA, and 4 mM MgCl₂) that included 100 μM ATP and 30 mM, 10 mM, 5 mM, or 0 mM of added P_i. Solution recipes were determined using available software (30) and the total ionic strength was kept constant at 125 mM by adjusting the amount of KCl in the low-salt buffer. The final buffer was then added to the flow cell, including the constituents of the low-salt buffer, the 1 μm silica beads coated with neutravadin, biotin/TRITC-labeled actin and an oxygen-scavenging system (15). The temperature of the experimental chamber was maintained at 30°C.

Laser trap assay: hardware and software

The optical light path employed to form the laser trap was very similar to those previously described (22,31). For optical trapping, a 5 W, infrared (1090 nm) laser beam (SPI Lasers, Santa Clara, CA) was digitally time-shared between two locations using two orthogonally (x and y) oriented acousto-optic deflectors (AODs) (DTD-274HA6, Intra Action, Bellwood, IL). The AOD was driven by a custom-built digital controller (Elliot Scientific, Hertfordshire, United Kingdom) that interfaced with a personal computer via a field-programmable gate array card (PCI-7830R, National Instruments, Austin, TX) and custom software developed using the real-time module of LabView version 8.6 (National Instruments). The laser beam was expanded to overfill the back aperture of a Nikon (Melville, NY) 1.4 NA, 100× Plan Apo objective mounted on a Nikon Eclipse Ti microscope.

Displacements of one of the trapped beads were determined by imaging the interference pattern of the bead onto a quadrant photodiode (QD) (G6849, Hamamatsu Photonics, Hamamatsu City, Japan) conjugate with the back focal plane of the condenser (32). A separate low-power (∼1 mW) detection laser (784 nm, Microlaser Systems, Garden Grove, CA) was the light source for displacement detection. This displacement signal was digitized via a National Instruments data acquisition module (USB 9162) and collected at 4 kHz. Before each experiment, the trapped bead was moved over the quadrant photodiode to calibrate the linear range of the detector and these data were used to determine trap stiffness, employing equipartition theory (33). For all experiments, trap stiffness was set to 0.02 pN/nm, with the linear springlike nature of the trap enabling force measurements over the range of displacements (34). In our measurements, all displacements remained within (or near) the linear range (see the Supporting Material). Coarse movements of the microscope stage were made using a manual micrometer-driven stage with a capacitive servo-feedback piezoelectric substage (Nano-Bio200, Mad City Labs, Madison, WI) that could generate nanometer movements for fine control. The fluorescent actin filaments were visualized using an intensified CCD camera (Stanford Photonics, Palo Alto, CA) while simultaneously visualizing the silica beads in brightfield using a CCD camera, which interfaced with the PC.

Laser trap assay

The 1-μm-diameter silica beads were incubated at 4°C overnight with neutravidin (0.5 g/mL). Before experimentation, the beads were washed and centrifuged for 5 min (10,000 rpm) in the low-salt buffer five times to remove any unbound or excess neutravidin from the beads, as previously described (29). Flow cells were initially prepped with myosin and washed with a final buffer containing the appropriate amount of P_i but without actin and beads. Once the flow cell was oil-coupled to the objective and condenser, the appropriate solution with beads and labeled actin was added. Two laser traps were created, and a single neutravidin-coated bead was captured in each trap. Fine movements of the piezo-controlled stage enabled attachment of the biotin/TRITC actin filaments to the beads. Once attached, the bead-actin-bead assembly was stretched to apply a pretension of ∼4 pN. This assembly was then lowered to the surface of a 3 μm silica bead (Bangs Laboratories, Fishers, IN) and served as a pedestal for the myosin (Fig. 2 C). The polarity of the filament was determined by the initial interactions with myosin and it was reversed if the myosin pushed rather than pulled the actin filament across the QD. To ensure an identical number of myosin heads at each P_i concentration, the same experimental chamber was used for all conditions. Therefore, at the end of one experiment, the flow cell was washed repeatedly (seven times) with the next final buffer (30 μL) containing the appropriate amount of P_i. Beads and labeled actin were added to the final flow. At each P_i concentration, 15–20 different myosin-coated pedestals (i.e., the 3 μm beads) were sampled, resulting in 101–378 binding events at each concentration of P_i.

Figure 2.

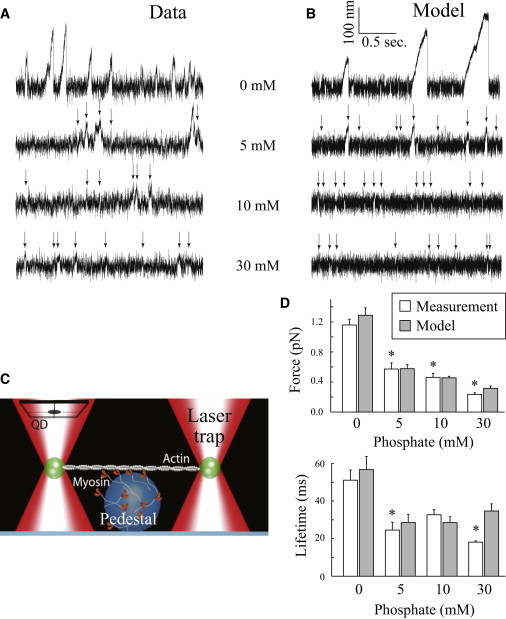
Displacement records from the laser trap assay. (A) Raw displacement records collected from the laser trap assay at increasing P_i concentrations. (B) Output of Monte Carlo simulations based on the branched kinetic model. For the traces at 5, 10, and 30 mM P_i, arrows indicate binding events. (C) Schematic of the laser trap assay. Myosin resting on a nitrocellulose-coated 3 μm bead is brought into contact with the actin filament. Displacements of the bead are tracked using a QD. (D) Average (mean ± SE) force (upper) and event lifetime (lower) at each P_i concentration, calculated for the measured data (unshaded) and the simulated data (shaded). For both graphs, the asterisk indicates a significant difference (p < 0.05) from 0 mM P_i, as determined by nonparametric analysis of variance.

Data analysis

A threshold-crossing routine, based on deviation from baseline in the displacement record, was used within a commercially available software program (Clamp Fit v10.2, Molecular Devices, Silicon Valley, CA) to detect binding events (Fig. S1 in the Supporting Material). The baseline value was determined from a section of data in which the bead-actin-bead assembly was held away from the pedestal and thus was not capable of interacting with myosin. Displacements that exceeded the threshold value for >10 ms were considered binding events. Event duration was measured as the total time spent above or below the defined threshold. The peak force of each event was determined based on the highest force achieved for at least 10 ms, with the duration chosen to coincide with the estimated average lifetime (10 ms) of the strongly bound state at the ATP concentration used in our experiments (11).

The maximum forces and event lifetimes were not normally distributed, as determined using the Shapiro-Wilk normality test; therefore, a nonparametric Kruskal-Wallis analysis of variance was used to identify significant differences among the different P_i concentrations, with any differences identified using the method of Dunn (28). Statistical procedures for the laser trap data were performed in SigmaPlot v11.0 (Systat Software, San Jose, CA) with the alpha level set at p < 0.05.

Modeling

Although single-molecule and solution measurements with myosin can sometimes be modeled with simple exponential fits (11), small-ensemble and large-ensemble experiments are more complex. In particular, when several myosin molecules simultaneously bind to an actin filament, they apply force on each other. These forces affect their ADP release rate (35,36), meaning that an isolated myosin molecule can behave differently from myosin in an ensemble (11). Recently, we performed detailed computer simulations to show that single-molecule, small-ensemble, and large-ensemble experiments with actin and myosin in vitro are consistent with a four-state kinetic scheme. We use this model to describe measurements in the absence of P_i (Fig. 1 B). Briefly, unbound (or weakly bound) myosin with ADP and P_i in its active site transitions to a state where it strongly binds to actin. This transition includes a powerstroke of size d and release of P_i from the active site. All these events are described by a first-order reaction of rate k_a. In the model, myosin can bind actin with nonzero strain. Once strongly bound, myosin releases ADP in a force-dependent process described by the Bell approximation (35–37),

$$k_D=k_d^0\text{exp}\left(-\frac{\delta F}{k_{\text{B}}T}\right),$$

where k_d⁰ is the rate in the absence of force, F, δ is a parameter that determines the force dependence, and k_BT is the product of Boltzmann's constant and the absolute temperature. We consider experiments lacking significant free ADP, so the reverse rate constant is neglected.

When myosin has released both ADP and P_i, its nucleotide binding pocket is empty and the molecule is in the rigor state. Myosin then binds ATP and unbinds from actin, a process that occurs at a rate of k_t[ATP] (38) and is rarely reversed at the pH of the experiments modeled here (39). Now unbound from actin, and with ATP in its active site, myosin hydrolyzes ATP, reverting to a prepowerstroke conformation (40,41). This reaction is reversible (4). Upon hydrolysis, the molecule may strongly bind to actin and restart the mechanochemical cycle. This model is specified by eight parameters: the binding rate, k_a; the ADP release rate in the absence of force, k_d⁰; the ATP binding rate, k_t; the forward and backward hydrolysis rates, k_h⁺ and k_h⁻, respectively; the force-dependent parameter δ; the powerstroke size, d; and the assumed linear stiffness of myosin, k. We have previously estimated all eight of these parameters and use these estimates in this model ((42), see Table S1).

Measurements of in vitro motility at variable pH and P_i support a kinetic scheme for skeletal muscle contraction, where P_i has two effects (15). First, actin-bound myosin in a postpowerstroke state can bind P_i and then rapidly detach, completing its ATPase cycle off actin (Fig. 1 B). Such a branched kinetic scheme has been proposed to explain isometric ATPase in muscle fibers (27). Second, myosin in the rigor state can bind P_i, which then inhibits ATP binding and extends the lifetime of the rigor state (Fig. 1 B). A similar mechanism has been proposed based on single-molecule measurements of the hydrolysis of fluorescent ATP (14); however, such a mechanism remains controversial (16,17). To determine whether this model is consistent with, to our knowledge, novel measurements of force generation in small myosin ensembles, we performed a series of computer simulations. We simultaneously ensured that the model remained consistent with our previous measurements of in vitro motility (15).

To compare the model to our experimental measurements, we performed Monte Carlo simulations of small myosin ensembles. We kept track of the state of every molecule in the small ensemble using the Gillespie algorithm ((43), see the Supporting Material). However, since ADP release depends on force, we also had to keep track of the force on all the bound molecules, as well as the force applied to the actin filament by the laser trap. We calculate these forces by assuming that mechanical equilibrium of the laser trap is reached much faster than the timescale of chemical reactions (44). In addition, although the force on a given myosin molecule fluctuates due to Brownian motion, we assume that reaction rate depends on the average value of the force (36). Thus, the overall simulation algorithm is as follows. 1) Determine the force on every myosin molecule and on actin, assuming mechanical equilibrium. 2), Determine the reaction rates of every possible chemical transition given the force on each myosin molecule. 3), Use the Gillespie algorithm to update the chemical state of the system and the time elapsed. These basic steps were repeated tens to hundreds of thousands of times to generate a single simulated data set. A similar approach was used to model in vitro motility (see the Supporting Material for more details).

These simulations give the average position of the beads attached to either end of the actin filament as a function of time. To compare the simulated bead position to our measurements, we used a linear interpolation to match the time increments to the sampling rate of our laser trap (4000 Hz, or a time step of 0.00025 s). To simulate the Brownian motion of the system, we added random noise from a Gaussian distribution with standard deviation

$$\sigma =\sqrt{\frac{k_{\text{B}}T}{k_T}},$$

where k_T is the overall stiffness of the system (equal to the stiffness of the laser trap plus the stiffness of any attached myosin, k_T = k_trap + N_ak, where N_a is the number of attached myosin molecules). We also added a small amount of random noise to the signal, with a standard deviation of 4 nm, to model electronic, vibrational, or other signal noise. We then analyzed these simulated data using the same algorithm used to analyze our measurements (see Data Analysis, above). To simulate a small ensemble at a given ATP and P_i concentration, we must specify four unknown parameters of the kinetic model, k_off, k_r⁺, k_r⁻, and k_DP. We must also specify the ensemble size, which, for simplicity, is assumed constant for each experimental condition. Finally, the attachment rate is known for a large ensemble of myosin (k_a ≈ 40 s⁻¹ (45)). For a single molecule in the laser trap, the attachment rate is strongly reduced (k_a¹ ≈ 1 s⁻¹ (45),). Presumably, this decrease in attachment rate is due to fluctuations in height of the actin filament in the laser trap above the myosin, but it is unclear how attachment rate depends on the number of myosin molecules attached to actin. We expect that if a sufficient number of myosin molecules bind to actin, the actin filament will be held more tightly, and therefore attachment rate will approach the large-ensemble limit (k_a ≈ 40 s⁻¹). To account for this effect in the model, we assign the binding rate for the first myosin as k_a¹ (1 s⁻¹), the second molecule binds at rate k_a², to be specified by fits to the data, and subsequent molecules bind at rate k_a (40 s⁻¹). All other model parameters are either known (e.g., trap stiffness) or previously estimated by us (e.g., myosin stiffness (42)).

We determined the six unknown parameters (ensemble size, N; binding rate of the second molecule, k_a²; and the four unknown parameters of the kinetic model, k_off, k_r⁺, k_r⁻, and k_DP) by minimizing the difference between the model simulations and our experimental measurements. For small-ensemble force generation, goodness of fit was determined by the sum of the squared difference between cumulative probability distributions of event lifetime and maximum force. For the motility measurements, goodness of fit was determined by the chi-square value (sum of the squared difference between simulation and measurement divided by variance of the measurement). We used a brute force algorithm to minimize this error, scanning through parameter space at regular intervals and evaluating the goodness of fit. To make this approach tractable, we first estimated N and k_a² from fits to measurements in the absence of P_i. We then determined the remaining parameters (k_off, k_r⁺, k_r⁻, and k_DP) from fits to our measurements in the presence of P_i (see the Supporting Material for details).

Results

In our modified three-bead single laser trap, miniensembles of myosin were able to generate long runs of motility against the spring-like load of the trap in the absence of P_i (Fig. 2 A). The addition of P_i had a striking effect on this behavior, causing both the amplitude and the duration of binding events to markedly decrease in a concentration-dependent manner. This directly demonstrates, for the first time that we know of, the ability of P_i to depress myosin’s force-generating capacity. The length of the displacements was significantly reduced at 5 mM P_i, with further reductions elicited by adding 10 and 30 mM P_i. The average displacement of a run in the absence of P_i (54 ± 4 nm) is consistent with five to six myosin heads binding to and translocating the actin filament, assuming that each molecule generates a 10 nm displacement (22,46,47). In contrast, the 13 ± 1 nm displacement in the presence of 30 mM P_i is consistent with one, or occasionally two, myosin heads binding to the actin filament (22,46,47).

Using the stiffness of the laser trap (k_trap = 0.02 pN/nm), the maximal displacement of a binding event can be converted to a maximal force. In the absence of P_i, the average maximum force of a binding event was 1.2 ± 0.08 pN, but this value was decreased by 50%, to 0.6 ± 0.02 pN, at 5 mM P_i and by >80% (0.2 ± 0.02 pN) at 30 mM P_i (Fig. 2 D). The statistical analysis revealed that all pairwise comparisons were significant, indicating that each successive increase in P_i caused a significant decrease in the peak force. This pattern of force decrease as a function of [P_i] is strikingly similar to that observed in fibers (13) and myofibrils (10). A similar pattern was observed for the effect on event lifetime, with a large decrease caused by 5 mM P_i and similar reductions at 10 mM and 30 mM P_i (Fig. 2 D). The nonparametric statistical analysis revealed that although the 0 vs. 10 mM P_i was not significant, the event lifetimes at 0 mM P_i were significantly different from those at both 5 and 30 mM P_i. It is also worth noting that the detection threshold of 10 ms (see Materials and Methods) means that we cannot detect short (<10 ms) events, likely resulting in an overestimate of event lifetime. This effect would be especially strong when event lifetimes are short, e.g., at the higher P_i concentrations, suggesting that the already significant P_i-dependent decrease in event lifetime might be even larger (see the Supporting Material).

Histograms of the events were used to characterize the distributions of event force and lifetimes (Fig. 3). In the absence of P_i, the distribution of forces is broad, with a large portion of events generating force of <1 pN, and >40% of binding events exceeding 1 pN, some ranging to >5 pN. However, in the presence of 30 mM P_i, these long runs were completely absent, with none of the binding events generating >1 pN. Also evident in the histograms are binding events that generated negative forces, meaning that these binding events occurred in the direction opposite to most other events. These are likely caused by Brownian capture, which occasionally occurs when myosin binds to the end bead-actin-bead assembly at the extreme of its Brownian motion (48) (in support of this interpretation, simulated experiments show a similar frequency and amplitude of negative force events; see the Supporting Material and Fig. 3). There is also an absence of events at zero force, which is a consequence of the thresholding method used to classify events (see Materials and Methods). We confirmed this by performing a mean variance analysis on the data. However, the estimate of step size using the mean variance (14 ± 1 nm) was quite similar to the estimate from the threshold analysis, suggesting that the exclusion of the zero-displacement events did not affect the estimated displacement (Fig. S2).

Figure 3.

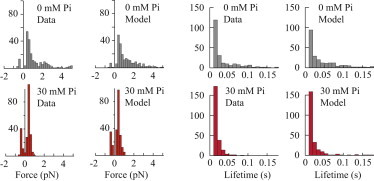
Histograms of event forces and lifetimes. (Left) Distributions of the maximum event forces for the measured data and model simulations for 0 (upper) and 30 mM P_i (lower). (Right) Distributions of individual event lifetimes for the measured and simulated data at 0 (upper) and 30 mM P_i (lower). The numbers of events for 0, 5, 10, and 30 mM P_i were 235, 101, 378, and 232, respectively. For a more detailed comparison between the model and the data, see the Supporting Material.

Measurements of event lifetime show that the average lifetime of a binding event in the absence of P_i was 51 ± 5 ms, with most events having a lifetime of <50 ms, but with a significant portion lasting longer than 50 ms (Fig. 3). In contrast, at 30 mM P_i the population is dominated by very short events, with the average event lifetime reduced to 18 ± 1 ms and few events exceeding 50 ms. We did not observe direct evidence of a reversal of the powerstroke within the displacement records. A reversal could have been evident at 30 mM P_i as a switching of a single binding event (e.g., 10 nm) from positive to negative displacement during attachment, or as an abrupt change in the direction of the displacement within a short run at 5 or 10 mM P_i, when one of the multiple bound molecules experienced a reversal, but neither event was observed. It is possible that such a reversal occurred faster than the time resolution of our instrumentation (∼2 ms), which does not rule out its occurrence but would put limits on the lifetime of a strongly bound prepowerstroke state, as previously suggested (11). Given the lack of direct evidence, we considered the alternative possibility that the rebinding of P_i to myosin may not reverse the powerstroke but rather induces dissociation from actin in a postpowerstroke state, represented as a branched kinetic pathway (Fig. 1 B). Simulations were run with this model to determine whether it could reproduce the data presented here.

Estimating ensemble size, binding rate

To simulate interactions of a small ensemble of myosin with an actin filament, we must determine the ensemble size, N, and the dependence of attachment rate on ensemble size, k_a². Both of these parameters can be estimated from fits of the data in the absence of P_i. We therefore fit these data with a four-state kinetic scheme (Fig. 1 A, (42)). Based on our fits, we estimate that N = 21 ± 3 independent myosin heads are present and that the second myosin head binds almost as slowly as the first, k_a² = 1 + 2 s⁻¹ (see the Supporting Material for a full sensitivity analysis). This estimate of ensemble size is comparable to our independent estimate of 12 heads, calculated from the geometry of the trap and the surface density based on ATPase (29).

Estimating model parameters

To simulate the effect of P_i on myosin’s interaction with actin, we must determine four parameters: k_off, k_r⁺, k_r⁻, and k_DP. To best estimate these parameters, we fit our measurements of event lifetime and maximum force at 5, 10, and 30 mM P_i. We also simultaneously fit our previously published measurements of in vitro motility in the presence of 30 mM P_i (15). Our best parameter estimates are k_off = 30 s⁻¹ mM⁻¹, k_r⁺ = 0.7 s⁻¹ mM⁻¹, k_r⁻ = 10 s⁻¹, and k_DP = 40 s⁻¹ (see the Supporting Material for a full sensitivity analysis).

Simulations/validation

The model is consistent with our measurements. Simulations of the raw data appear qualitatively similar to our measurements (compare Fig. 2, A and B) and the model reasonably reproduces our measured average event peak force and lifetime (Fig. 2 D). The distributions of simulated-event maximum force and lifetimes correspond well to our measurements, reproducing both the broad distribution in the absence of P_i and the elimination of higher forces at 30 mM P_i (Fig. 3). The simulations also reproduced details of the measurements, including negative displacement events and their dependence on P_i concentration (see the Supporting Material for a more extensive comparison between simulated and measured data).

The model can also replicate the effect of a 50% increase in myosin surface density. We performed experimental measurements with increased myosin density (generated by an increase in myosin concentration from 25 μg/mL to 40 μg/mL) at each P_i concentration (0, 5, 10, and 30 mM). Allowing ensemble size to vary, we fit these data with the model. With the exception of 0 mM, at each P_i concentration, the model predicted a larger ensemble size consistent with the 50% increase in myosin concentration. Measured and simulated force distributions at 10 mM P_i are shown in Fig. 4 (for a full analysis, see the Supporting Material). At this P_i concentration, an increase in myosin density leads to an increase in force (a rightward shift of the distribution). This result implies that P_i lowers myosin’s duty cycle and that this effect can be overcome by increasing the number of myosin molecules capable of binding to the actin filament. The model’s inability to predict an increased ensemble size in the absence of P_i might be due to the fact that under these conditions, large ensembles can generate enough force to pull the bead-actin-bead assembly out of the laser trap, thereby destroying the assembly. Re-forming the assembly necessitates creating a new assembly and finding a new pedestal that likely has a different number of available myosin heads. Thus, at the higher myosin density, where assembly destruction occurs more frequently, successful measurements primarily come from pedestals with smaller myosin ensembles, causing the model to underestimate the average number of available myosin heads per pedestal.

Figure 4.

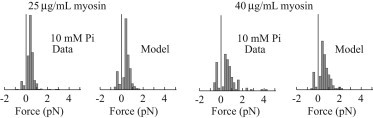
Histograms of event forces and lifetimes at 25 and 40 μg/mL myosin concentration. Distributions of maximum event forces are plotted in the presence of 10 mM P_i at low and high myosin concentrations. Simulations were performed at an ensemble size of 21 for the 25 μg/mL measurements and 32 for the 40 μg/mL measurements.

In addition to being consistent with our measurements of small-ensemble force generation, the model is also consistent with in vitro motility measurements. We have previously shown that in the absence of P_i, the model accurately predicts the ATP-dependent increase in motility speed (as well as small-ensemble force-velocity measurements, single-molecule displacement and event lifetime, and actin filament length dependent motility (42)). Here, we show that the model is also consistent with motility measurements in the presence of 30 mM P_i, showing little effect on V_actin at saturating ATP concentrations and a decrease in V_actin at low (μM) levels of ATP (Fig. 5).

Figure 5.

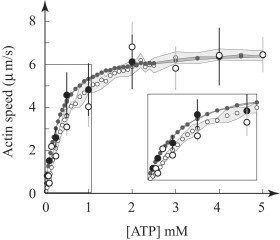
Model fit to motility data. Model and measurements of motility in the absence (solid symbols) and presence (open symbols) of 30 mM phosphate (data from Debold et al. (15)). Simulation results are represented by smaller symbols, with the standard deviation shaded. (Inset) The depressive effect of P_i on V_actin is apparent at low ATP.

Interestingly, at high ATP and P_i, the model predicts that P_i still rebinds to and dissociates the AM.ADP state from actin. This effect alone would lead to an increase in V_actin, but it is offset by two others: first, P_i also competes with ATP for rebinding to myosin, forming the AM.P_i state and prolonging t_on; and second, P_i decreases myosin’s duty ratio (see the Supporting Material for more details). Thus, this unchanged V_actin represents a balance between opposing effects. At micromolar ATP levels, the balance changes, and now, at a concentration of 30 mM P_i, more readily forms the AM.P_i state, prolonging t_on and thus slowing V_actin. This is a distinctly different prediction from those of previous models, where load dependence governs the differential effect of P_i on force and velocity (6).

The model predicts that if we disturb the balance between these opposing effects by changing the ADP release rate, then P_i should have a much larger effect on motility speed. For example, slowing the ADP release increases the AM.ADP lifetime, causing V_actin to slow in the absence of P_i. However, the prolongation of the AM.ADP state also prolongs the time available for P_i to rebind to this state, shortening t_on, and because the powerstroke is not reversed, V_actin increases in the presence of P_i, enabling it to fit the P_i-induced increase in V_actin at low pH (15). This effect, to our knowledge, cannot be described using a model with a force-dependent powerstroke reversal (6,16).

In a final test, we scaled the model up to determine whether it could reproduce the effects of P_i in myofibrils and single muscle fibers (Fig. 6). Without adjusting any parameters, the model was able to qualitatively capture the P_i dependence of isometric force, including the saturation of inhibition near 30 mM P_i, observed in myofibrils (10). In addition, the model was able to accurately reproduce the much less pronounced effect of P_i on isometric ATPase. The larger effect of P_i on force is the result of P_i increasing the flux through the branched kinetic pathway. Progression through this pathway detaches myosin from actin, decreasing force, but myosin still progresses through the ATPase cycle off actin, albeit slightly more slowly than it would on actin, accounting for the mild decrease in ATPase, as it does in the branched kinetic model of Linari et al. (27).

Figure 6.

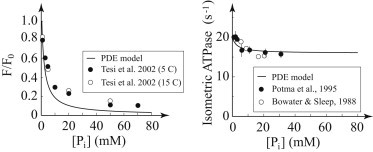
Model fits to data from isolated muscle preparations. Predictions of the model for the effect of P_i on myofibrils and muscle fibers. (Left) Effect of phosphate on isometric force at 4 mM ATP. The model and data are both normalized to the Hill fit of force-velocity at 0 mM P_i. Data are for rabbit psoas myofibrils (10) and are qualitatively similar to the model. (Right) Effect of phosphate on isometric ATPase (24,25). Again, the data are qualitatively similar to the model. Note that these are not fits to the data but rather predictions of the model. (Note that the data are rescaled to have an ATPase in the absence of P_i of 20 s⁻¹.)

Discussion

We have used a modified three-bead laser trap assay to directly observe the effect of P_i on the force-generating capacity of a miniensemble of myosin molecules. Addition of P_i had a striking effect on myosin’s force-generating capacity, with high concentrations (30 mM) abolishing 2–5 pN runs and reducing average force from 1.2 to just 0.2 pN (Fig. 2). P_i had an equally depressive effect on the duration of strong binding, suggesting that P_i decreases the force-generating capacity of myosin by reducing the duration of myosin’s strong binding to actin.

To understand the cross-bridge behavior underlying the present observations, we performed Monte Carlo simulations using our recently published model (42). This simple four-state model, with a force-dependent ADP-release rate, was formulated to help reconcile the discrepancies between myosin’s single-molecule and ensemble behavior. After adjusting only two parameters (N and k_a²), neither of which affect the model’s previous fits to in vitro measurements, this model is able to reproduce our measurements with a high degree of accuracy, reproducing not only the average behavior of the ensembles but also the distribution of event displacements/forces and lifetimes. In the absence of P_i, the model suggests that on average, roughly five myosin molecules bind to and translocate the actin filament before detaching. During these runs, virtually every bound myosin progresses through the conventional pathway, releasing ADP on actin and being dissociated from the strongly bound state by ATP (Fig. 1 B, green; see the Supporting Material for a more detailed analysis). This serves as additional validation of the model and provides strong justification for its ability to interpret the findings in the presence of P_i.

We did not observe any direct evidence of a reversal of the powerstroke in the presence of P_i despite its having a profound depressive effect on myosin’s force-generating capacity. It is certainly possible that such a reversal occurred beyond the time resolution of our instrumentation, which like similar instruments is primarily limited by the roll-off frequency of the power spectrum of the bead in solution, typically 2–3 ms for a 1-μm-diameter bead (44). In this study, we further limited our time resolution to reduce the risk of incorporating false-positive events by excluding from analysis events of <10 ms (see Materials and Methods); thus, we cannot rule out a P_i-induced reversal based on the data presented here. In addition, models developed based on observations in single muscle fibers (6) that include a rapid reversal and dissociation from actin could likely be adapted to fit our data on force.

However, these models cannot explain the effects of P_i on isometric ATPase (24,25) and V_actin at low pH (15,49). Therefore, we considered whether a model without a powerstroke reversal could explain the present observations in addition to these effects. To fit the effects of P_i observed in the present study, we adjusted only the P_i-dependent rates in our existing model (42) and were able to accurately reproduce the effects of P_i on the distribution of event forces and lifetime despite lacking a P_i-induced reversal of the powerstroke (Fig. 3). In the absence of P_i, the model predicts that flux is primarily (∼100%) through the conventional branch in the kinetic scheme (Fig. 1 B, green). However, at high levels of P_i, flux becomes primarily (∼77% at 30 mM P_i) through the P_i-dependent branch (Fig. 1 B, red). In this pathway, P_i rebinds to the AM.ADP state, causing myosin to dissociate from actin in a postpowerstroke state. Myosin then completes the rest of the ATPase cycle off actin. This P_i-induced detachment shortens strong-binding lifetime and strongly decreases the probability of multiple myosin molecules attaching to actin simultaneously (see the Supporting Material for more details). Thus, the long, high-force (2–5 pN) runs seen in the absence of P_i, resulting from successive myosin molecules binding to the actin filament, are abolished in the presence of high P_i. As a consequence of dissociating in a postpowerstroke position, myosin’s active site is presumably capable of releasing P_i and ADP at a faster rate off actin than in the conventional model (27).

From a structural perspective, this postpowerstroke dissociation requires that myosin lose its high actin affinity in the AM.ADP state, thus requiring an uncoupling between closure of the actin binding cleft and the position of the lever arm (20). Although this structure has not been observed, the notion of uncoupling these events was recently proposed (50), and mutations in a novel actin binding loop where the ATPase rate was uncoupled from V_actin provide indirect evidence that such structures may exist (51).

Previous authors have proposed a P_i-dependent branch in myosin’s kinetic pathway to provide a molecular basis for the more pronounced effect of P_i on force versus isometric ATPase in single muscle fibers (27), and a branched kinetic pathway can also explain the effect of P_i on the force-generating capacity of a single myosin V (52). By employing a similar branch, we can fit the data presented here and simultaneously fit the effects of P_i on isometric ATPase. There is, however, a subtle but important distinction between our model and that of Linari et al. (27) with regard to where and when the powerstroke takes place in the branched pathway. The model of Linari et al. (27) is based on the behavior of a cross-bridge at maximal isometric force, and consequently P_i rebinds to a highly strained cross-bridge. In this model, the strain prevents myosin from completing its powerstroke on actin, instead generating a displacement just large enough to account for the isometric force. Once dissociated from the strongly bound state by P_i, myosin completes the remainder of the 10 nm powerstroke off actin. In contrast, in our model the powerstroke is completed on actin before P_i rebinds to the AM.ADP state and induces dissociation. Having the powerstroke occur on actin allows our model to also reproduce the P_i-induced enhancement of V_actin observed at low pH (Fig. 5 (15),).

The difference in the location of the powerstroke is not the only distinction between the two models, as we also sought to explain the depressive effect of P_i on V_us (13) and V_actin (14–16) at subsaturating ATP concentrations. Allowing P_i to bind to the rigor state, forming an AM.P_i state that does not bind ATP and dissociate, captured this aspect of the data (see the Supporting Material for more details of the AM.P_i state’s effects). This mechanism has previously been suggested to underlie the depression in V_us (6) and V_actin in skeletal muscle myosin (14,15). Although it remains controversial and is not the only model capable of fitting such data (16,17), there is compelling evidence from single-molecule fluorescence experiments to suggest that an AM.P_i state forms under these conditions (14). It remains to be seen whether the alternative models that capture this P_i-dependent decrease in speed at low ATP can also explain other observations that our model successfully explains, such as P_I’s effects on isometric ATPase (25) and V_actin at low pH (15).

Thus, we have arrived at a model that includes components of three previous models, the conventional kinetic model (6), a branched kinetic model (27), and a model with P_i binding to the rigor state (14) to fit as many previous findings as possible. Our model includes the basic framework of the conventional model (Fig. 1 A (6)), which alone can fit P_i-dependent decreases in force. However, the introduction of a P_i-dependent branch enables the model to capture the effects of P_i on isometric ATPase. Having this detachment occur from a postpowerstroke state enables the model also to capture the effects on V_actin, and the inclusion of an AM.P_i state captures P_i's effect at low ATP. By incorporating and modifying components of previous models, our model can describe the effects of P_i at the level of large ensembles, in motility and muscle fibers, down to the level of single molecules. A particular strength of the model is its ability to reproduce not just the averages of our measurements, but also the distributions of individual binding events we observed in the laser trap assay. Thus, it provides a much more detailed level of quantitation than most previous models of the molecular mechanisms underlying the effects of P_i.

Despite its simplicity and power to capture diverse findings, our model likely does not represent a unique explanation for the effects of P_i on myosin and muscle function. There are clearly some findings that offer challenges to the model. For example, in the absence of a reversal of the powerstroke it is difficult to explain the observations from medium oxygen-exchange experiments indicating that ATP can be resynthesized in myosin’s active site (4). The fact that we are able to fit the data presented here excluding this mechanism, suggests that, although this pathway is available, the flux through is minimal under the conditions of our experiments (4). The model also does not include multiple AM.ADP states, for which there is strong evidence based on solution (53) and muscle fiber experiments (2). Thus, an additional AM.ADP state would make the model more consistent with these previous data. However, it would have little impact on the aspects we focused on fitting. There are also likely to be other experimental observations not fully captured by the model owing to its simplicity. Our model (42) was developed based on simplified in vitro systems (i.e., in vitro motility and single-molecule laser trap assay) and therefore cannot be expected to fully reflect the complexity of intact muscle with regulation of actomyosin binding and much more complex architecture of the filament arrays. However this model can serve as an excellent starting point from which to incrementally build up the complexity of the system to provide a detailed understanding of how P_i affects muscle function and thus build a more complete understanding of contraction.

We have demonstrated, through direct observation, that P_i profoundly reduces the ability of a miniensemble of myosin to generate force against a laser trap. Fitting these data does not require P_i to reverse the powerstroke; rather, introducing a P_i-dependent branch together with an AM.P_i state enables a model to fit the data presented here in addition to biochemical and mechanical data from isolated proteins to muscle fibers. These measurements and the model therefore suggest that the kinetic steps leading to myosin’s force generation are distinct from the steps underlying force inhibition.