Cells Actively Stiffen Fibrin Networks by Generating Contractile Stress

Abstract

During wound healing and angiogenesis, fibrin serves as a provisional extracellular matrix. We use a model system of fibroblasts embedded in fibrin gels to study how cell-mediated contraction may influence the macroscopic mechanical properties of their extracellular matrix during such processes. We demonstrate by macroscopic shear rheology that the cells increase the elastic modulus of the fibrin gels. Microscopy observations show that this stiffening sets in when the cells spread and apply traction forces on the fibrin fibers. We further show that the stiffening response mimics the effect of an external stress applied by mechanical shear. We propose that stiffening is a consequence of active myosin-driven cell contraction, which provokes a nonlinear elastic response of the fibrin matrix. Cell-induced stiffening is limited to a factor 3 even though fibrin gels can in principle stiffen much more before breaking. We discuss this observation in light of recent models of fibrin gel elasticity, and conclude that the fibroblasts pull out floppy modes, such as thermal bending undulations, from the fibrin network, but do not axially stretch the fibers. Our findings are relevant for understanding the role of matrix contraction by cells during wound healing and cancer development, and may provide design parameters for materials to guide morphogenesis in tissue engineering.

Introduction

The mechanical behavior of animal cells is controlled by a network of stiff protein filaments known as the cytoskeleton. The cytoskeleton is a remarkable material that is maintained out of equilibrium by a variety of molecular processes using chemical energy (1). An important contribution comes from molecular motors, which use energy resulting from ATP hydrolysis to move along actin filaments and microtubules (2). There is strong evidence that myosin II motors, which interact with actin filaments, actively increase cell stiffness by generating contractile prestress (3–7). Measurements on purified actin networks have shown that these networks strongly stiffen when either an external or an internal stress is applied (8,9). Cells can exploit this nonlinear stress response to modify their stiffness rapidly in response to changes in the stiffness of the extracellular environment (10,11). Conversely, the stiffness of the extracellular environment can change in response to activity of the cells, because the contractile actin-myosin cytoskeleton is physically connected to the extracellular matrix (ECM) via integrin transmembrane receptors organized in adhesion complexes (12–14). Cells thus partly transmit their internally generated forces to the ECM. These so-called traction forces are typically in the nanoNewton range (15–19). By pulling on the matrix, cells can actively sense changes in ECM rigidity, on which they base decisions regarding spreading, migration, proliferation, gene expression, and even differentiation (20–24). This mechanoresponsiveness plays a crucial role in normal tissue development and function (25,26). Misregulation of the balance between cell traction and ECM stiffness contributes to cancer progression, fibrotic disease, and artherosclerosis (27–29).

In connective tissues, cells reside within an ECM that is mainly composed of collagen fibers (30). Active cell contraction results in patterning and contraction of the collagen network during tissue morphogenesis and wound healing (31–34). During wound healing, cells are initially recruited to a provisional ECM composed of the blood clotting protein fibrin (35), which is likewise contracted and patterned by active cell contraction (36,37). Similar to actin networks, fibrin and collagen networks stiffen in response to an applied stress (38–41). Therefore, we anticipate—in analogy to the actin cytoskeleton, which is stiffened by myosin contractility—that extracellular networks can be driven into a nonlinear, stress-stiffened regime by cellular contraction. There are indeed several reports of cell-induced stiffening of ECM gels that suggest an active, myosin-dependent origin. A classic example of cell-mediated ECM stiffening is provided by the phenomenon of clot retraction in the initial stage of blood clotting. Here, platelets actively contract and stiffen the fibrin blood clot (42–44). More recently, fibroblasts and mesenchymal stem cells were also shown to cause fibrin gel stiffening, and it was hypothesized that active cell contraction drives the gel into a nonlinear, stress-stiffened regime (45). Similarly, active stiffening by cellular contraction has been reported for collagen networks (46–48). However, the precise physical mechanisms of cellular control over the mechanical properties of the ECM remain unclear, because quantitative measurements comparing the linear and nonlinear rheology of ECM networks in the presence and absence of cells are lacking.

Here, we use a model system of fibroblasts embedded in fibrin gels to study how the contractile activity of cells affects the macroscopic mechanical properties of their environment. We measure the linear and nonlinear rheological properties of the cell-populated fibrin networks and correlate these with the dynamics of cell spreading and fibrin gel contraction. We demonstrate that the cells stiffen the fibrin gels while they spread, by applying myosin-II-driven traction forces that drive the gels into a stiff nonlinear elastic regime. Because fibrin serves as a provisional matrix in wound healing and angiogenesis, and is also involved in pathological states such as tumor invasion, our results are relevant for interpreting the mechanical role of cells in fibrin remodeling during wound repair, angiogenesis, and tumor growth (37,49,50). Moreover, the system studied here is relevant in the contexts of tissue regeneration (37,51,52), and surgery and tissue repair (53).

Materials and Methods

Cell culture

Human CCL-224 fibroblasts (a gift from Prof. J. Boonstra, Biology Department, Utrecht Universiteit, NL) were cultured to near confluency in 75-cm² tissue culture flasks (Nunc, Roskilde, Denmark) in α-Modified Eagle’s Medium (α-MEM, Gibco, Paisely, UK) supplemented with 10% fetal bovine serum (FBS, Gibco), antibiotics (10 μg/ml penicillin/streptomycin, Sigma-Aldrich, Zwijndrecht, Netherlands), and 20 mM HEPES (Sigma-Aldrich). Cultures were incubated at 37°C and 5% CO₂ in a humidified incubator and subcultured at confluency.

Fibrin gel preparation and cell seeding

Cell pellets were resuspended in a CO₂-independent medium composed of αMEM medium supplemented with 20 mM Hepes, 2% FBS, and 0.1% pen/strep. This stock suspension was used within 1 h. The cell density was determined using a microscope counting chamber (Hemacytometer, Optik Labor, Lancing, UK). To prepare fibrin gels, fibrinogen was first polymerized in fibrin assembly (FA) buffer (20 mM Hepes, 150 mM NaCl, 5 mM CaCl₂, pH 7.4) and then overlaid with CO₂-independent medium. For cell-seeded gels, cells were centrifuged for a few minutes, resuspended in FA buffer, and directly mixed with human fibrinogen (Enzyme Research Laboratories, Swansea, UK) to attain a final density of 500 cells/μl unless stated otherwise. Polymerization and cross-linking of fibrinogen was initiated by adding 0.5 units/mL human α-thrombin (Enzyme Research Laboratories) final concentration. Fibrin’s γ- and α-chains were fully cross-linked by FXIIIa present in the stock, according to SDS-PAGE analysis (39). Fibrin gels were prepared at concentrations ranging from 0.1 to 6 mg/ml, where 1 mg/ml is equivalent to a molar concentration of 2.94 μM. Fibrin fibers form in a two-stage process, where fibrin monomers first form double-stranded protofibrils (with a mass/length ratio of 1.5·10¹¹ Da/cm), which then laterally associate into fibers. The fibers prepared under our conditions have a constant diameter close to 100 nm and a mass/length ratio of ∼1 × 10¹³ Da/cm (corresponding to 86 protofibrils per fiber), as determined by wavelength-dependent turbidity measurements (39).

Rheology

Rheology tests were performed with a stress-controlled rheometer (Physica MCR 501; Anton Paar, Graz, Austria). Fibrinogen solutions with or without cells were polymerized at 37°C between the steel cone and plate (40-mm diameter, 1°). After 10 min, the fibrin gel was overlaid with 8 mL of αMEM supplemented with 2% FBS, 20 mM Hepes, and 0.1% antibiotics, (Fig. 1 A). We verified that the rheology measurements are minimally affected by the oxygen/metabolite gradient between the edge and center of the cone-plate geometry, by quantifying cell viability by microscopy (materials and methods section and Fig. S1 in the Supporting Material). The time evolution of the linear shear modulus, G^∗, during fibrin polymerization and cell spreading was monitored by applying a small-amplitude oscillatory strain with amplitude γ = 0.5% and frequency ω = 3.14 rad/s and measuring the stress response, σ(ω) = G^∗γ(ω). The shear modulus is a complex quantity, G^∗ = G′ + iG″, having an in-phase elastic component, G′, and an out-of-phase viscous component, G″. The gels were axially constrained by strong adherence to the rheometer plates throughout the experiment. Networks reached a constant shear modulus after 3 h in the absence of cells and 4 h in the presence of cells. The frequency-dependent rheology of fully polymerized networks was probed across a frequency range of 0.06–38 rad/s using an oscillatory strain of 0.5% amplitude. The high-strain regime was probed by applying a steady prestress, σ₀, and superposing a small stress oscillation of amplitude δσ = 0.1σ₀. The tangent modulus follows from the oscillatory strain response, K^∗(σ₀) = δσ/δγ. K′ was independent of frequency and of waiting time in the prestressed state, indicating negligible viscous flow (54). Unless noted otherwise, rheology data are expressed as mean ± standard deviation from at least three independent experiments. Statistical analysis was performed using the Student’s t-test; p < 0.1 was considered significant.

Figure 1.

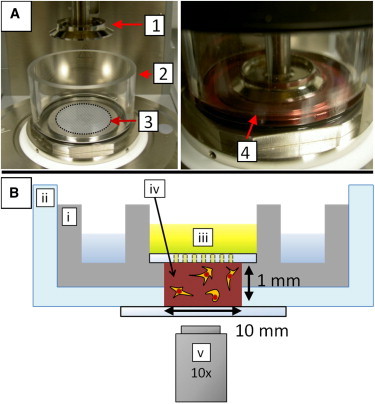
Experimental assays. (A) The viscoelastic properties of cell-populated fibrin gels were measured with a stress-controlled rheometer (left). The top plate is a cone (1) of 40 mm in diameter and 1° angle. The fibrin solution was pipetted on the bottom plate (3), the top plate was quickly lowered (right), and the fibrin was allowed to polymerize in situ at 37°C. The gel was immersed in cell culture medium supplemented with serum (4), using a Perspex ring (2). (B) Schematic representation of the custom-designed microscope holder used for observing cells spreading in fibrin gels (not drawn to scale). The sample (iv) was confined in a stainless steel well (i) topped with a glass plate with holes to enable medium (iii) exchange. The entire geometry was contained in a glass bottom dish (ii). Cell spreading was observed by bright field microscopy using a 10× air microscope objective (v). To see this figure in color, go online.

Microscopy

To visualize cell spreading inside fibrin gels, we observed cell-populated fibrin gels on a Nikon inverted microscope, using an incubation chamber and objective heater to maintain a temperature of 37°C (TokaiHit, Shizuoka-ken, Japan). The cell-seeded gels were prepared in a custom-made holder, consisting of a stainless steel well for maintaining a humid atmosphere and a glass disc with 500 μm-diameter holes to permit medium exchange, as sketched in Fig. 1 B. Bright field images of spreading cells were taken with a 10× air objective using an EM-CCD camera (Roper Coolsnap, Photometrics, Tucson, AZ) at a rate of 1 frame/min and exposure time of 200 ms. Cell viability was maintained by blocking infrared and ultraviolet (UV) light with a bandpass filter and by controlling light exposure with a light shutter synchronized with image frame grabbing.

Traction strains applied by spreading cells were visualized by time-lapse imaging of 1 μm diameter polystyrene beads adhered to the fibrin network in bright field at a rate of 1 frame/min. The particle displacements were tracked at 15 nm resolution using a tracking program written in Labview 7.1 (National Instruments Corporation, Utrecht, NL) that identifies particles by a pattern matching routine (55).

Fluorescent fibrin gels for confocal microscopy were prepared by mixing unlabeled fibrinogen with 24 mol % of Alexa488-labeled fibrinogen (Invitrogen, Breda, NL). The networks were imaged using a scanning confocal microscopy on an inverted Eclipse Ti microscope (Nikon, Nikon Instruments Europe, Amstelveen, Netherlands). Fluorescence images were obtained by illumination with a 488 Ar laser (Melles Griot, Albuquerque, NM) and differential interference contrast images were recorded at the same time. Images were taken at least 50 μm from the surface. Z-stacks were taken with a piezo-driven immersion objective (either 100× oil or 40× oil objective, Nikon). During a time-sequence, an image was taken every 10 min at 5 to 10 regions in the sample. Image stacks were projected along the z axis (for z-stacks) or time axis (for time-lapse movies) in ImageJ (http://rsbweb.nih.gov/ij/).

Results

Cell spreading and traction force generation

We constructed a biomimetic tissue model by dispersing fibroblasts inside a cross-linked fibrin network. The cells were suspended in a solution of initially monomeric fibrinogen and were entrapped in the network during thrombin-triggered fibrin polymerization. To ensure that we look only at effects of cell traction forces, we focus on a time window of 7 h after cell seeding. This time is sufficiently long for cells to spread and apply traction forces to the gels, but not long enough for matrix remodeling by chemical effects such as proteolytic degradation, matrix synthesis, or matrix cross-linking, which require timescales of over 24 h (51,56–59).

To monitor the time dependence of matrix formation, we observed the networks with confocal fluorescence microscopy. Matrix formation started immediately upon thrombin addition and warming to 37°C, resulting in a space-filling network of fibrin fibers within several minutes (see Fig. S2). To monitor the dynamics of cell spreading, we observed the cells with bright field microscopy (Fig. 2). The entrapped cells initially remained round, indicative of negligible attachment to the matrix (first column, 0 h). However, within 2 h, the cell shapes started to change as the cells attached to the matrix and spread.

Figure 2.

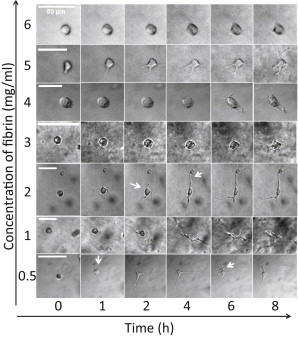
Morphological changes of cells during spreading in fibrin gels of different densities. Representative bright field images of fibroblasts at several stages during cell spreading (time axis on bottom) in fibrin gels of concentrations ranging from 0.5 to 6 mg/ml (concentration axis on the left). Scale bars, 50 μm. Arrows point to examples of pseudopodia.

Though there was some variation in the time needed for different cells within the same gel to spread, all cells in a given gel were fully spread within 4–6 h. The shape change of the cells was most pronounced in dilute (0.5–2 mg/ml) fibrin gels. The cell body became elongated and extended several thin pseudopodial processes into the surrounding matrix with lengths up to 50 μm; in the focal plane we typically observed between 2 and 6 such protrusions. This multipolar morphology is characteristic of cells residing inside fibrin or collagen gels and resembles cell morphologies inside tissues, although being strikingly different from the flat, fan-like morphology of the same cells plated on flat substrates (60–63). Time lapse imaging revealed that the pseudopodial processes underwent cycles of extension and retraction (see Movie S1). The lifetime of pseudopodia was usually 1–3 h. Nearly all protrusions had multiple side branches; some of these were highly dynamic and grew and retracted on timescales of minutes, whereas others were stable for hours (for examples see white arrows in Fig. 2). Fibroblasts in denser (3–6 mg/ml) fibrin gels had a markedly different morphology, exhibiting only short and thin protrusions (Fig. 2 and Movie S2). The overall cell diameter remained close to the original diameter, which was typically <25 μm. This was more noticeable when zooming in with a 40× objective (see Fig. S3).

To test whether cell spreading resulted in matrix remodeling, we performed three-dimensional (3D) imaging of fluorescently labeled fibrin networks using confocal microscopy. In the absence of cells, fibrin networks were homogeneous and isotropic over the entire range of fibrin concentrations. As an example, Fig. 3 A shows the maximum intensity projection of a confocal z-stack for a 1 mg/ml fibrin network. When cells are present during fibrin polymerization, the networks are locally restructured around the cells. Fig. 3 B shows an example maximum intensity projection taken after overnight incubation of a cell (near the center of the image) inside a 1 mg/ml fibrin network (Movie S3 shows the entire z-stack with the fibrin image merged with the bright field image of the cell). There are several signatures of cellular contraction: the fibrin network is highly condensed adjacent to the cell body and fibrin fibers within a distance of ∼30–40 μm from the cell surface are radially oriented toward the cell. Local condensation and alignment of matrix fibers around cells, especially near pseudopodial protrusions, is indeed commonly reported in 3D matrices (63–66). The network becomes noticeably more heterogeneous when the cell density is increased from 125 to 500 and 850 cells/μl (Fig. S4). However, the estimated volume fraction of cells was always below 1%, so the network structure on larger length scales (tens to hundreds of microns) remained homogeneous. Image analysis of the fiber orientations shows that the networks also remained mostly isotropic (Fig. S4).

Figure 3.

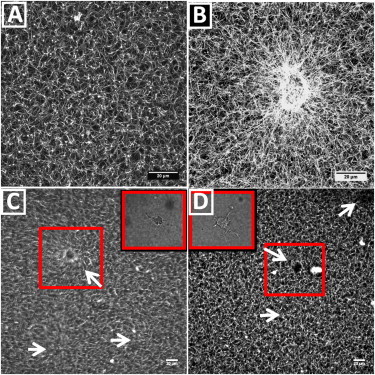
Spreading cells locally remodel the surrounding fibrin network by recruiting and aligning fibrin fibers. (A) Maximum intensity projection of a confocal z-stack of 40 μm of a fluorescently labeled 1 mg/ml fibrin network without cells. (B) Maximum intensity projection of a 40 μm confocal z-stack of a cell-populated 1 mg/ml fibrin network, showing alignment and recruitment of fibrin fibers around the cell located near the center of the image. Movie S3 shows the corresponding z-stack, combining fluorescence images of the fibrin networks with bright field images of the cell. (C and D) Time projections of time-lapse movies (taken at a fixed confocal xy-plane) of cell-populated fibrin gels with fibrin concentrations of 2 mg/ml (C) and 3 mg/ml (D) obtained during fibrin polymerization and subsequent cell spreading. White arrows point to the location of a cell (which can be seen by differential interference contrast microscopy, see insets). Boxes indicate cells that are in focus during the time sequence. The corresponding time-lapse movies are shown in Movie S6 and Movie S7, combined with particle image velocimetry analysis. Maximum intensity projections were obtained from z-stacks of 40 images over a total depth of 40 μm (A and B), whereas the time projections are obtained from 47 images (C, total time 7.5 h) or 54 images (D, total time 9 h). To see this figure in color, go online.

Time-lapse movies of polymerizing networks show that cells exert contractile forces on the network that reach up to distances of at least 100 μm away from the cell surface (see Movie S6 and the time-projection in Fig. 3 C, where the cells are indicated by white arrows). Strikingly, these large network deformations are only seen in dilute networks (2 mg/ml fibrin or less). In denser gels, network deformation is negligible over a time span of at least 7.5 h (Movie S7 and the time-projection in Fig. 3 D, for a 3 mg/ml gel).

To quantify network deformation during cell adhesion and spreading, we tracked the positions of fiducial markers (1 μm spheres) attached to the network in the vicinity of spreading cells. As shown by Movie S4 of a cell spreading in a 1 mg/ml fibrin gel, cells are initially round but start to spread and deform after ∼1 h. As the cell spreads, it pulls the surrounding probe particles inwards. The bead displacements were quantified by tracking their centroid positions over time (Fig. 4, black lines, each corresponding to a different particle). After ∼1 h of culture, the majority of the particles started to be pulled toward the spreading cell. After ∼3 h, the motion of the probe particles ceased, indicating the onset of mechanical equilibrium between the cell traction forces and the elastic resistance of the fibrin gel (67). This timescale is consistent with the time-lapse movies of spreading cells (Fig. 2), which showed that cell spreading was complete within 4 to 6 h. After 6 h, only local rearrangements of the fibrin network occurred, as shown by particle image velocimetry analysis of the time-lapse movies of polymerizing cell-seeded fibrin gels (< 3 mg/ml, see supporting information and Movie S6). To test whether cells are still metabolically active once bead movement ceases, we added the peptide GRGDS to the cell culture medium (see supporting information). This peptide disrupts cell attachment to the fibrin network by competing for the integrin receptor αVβ3 (Fig. S5) (64,68). Around 1 h after addition of GRGDS to the medium, we observe a sudden recoil of the particles surrounding the cells (Movie S5), showing that tension is suddenly released and implying that cells indeed actively maintain tension. Strikingly, cells in denser (≥3mg/ml) gels spread without noticeably deforming the surrounding fibrin network in a timescale of 7.5 h (Movie S7).

Figure 4.

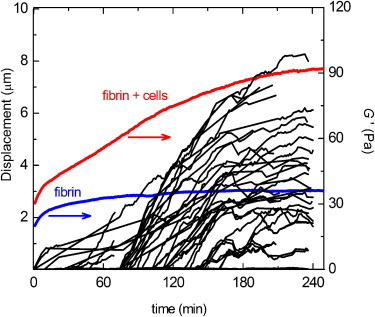
Examples of the increase in traction strain and macroscopic elastic modulus of a cell-populated fibrin gel over time, during fibrin polymerization and subsequent cell spreading. The traction strain was quantified by measuring the displacements of fiducial markers (1 μm diameter beads) embedded in the fibrin networks toward a spreading cell (black lines). The elastic modulus, G′, was measured by macroscopic rheology (red line). The fibrin concentration was 1 mg/ml and the cell density was 500/μL. For reference, the blue curve shows G′ for a fibrin gel without cells. To see this figure in color, go online.

Rheology of cell-populated fibrin gels

Because fibrin gels are known to stiffen strongly when subject to an external load, we hypothesized that active cell contraction may increase the elastic modulus of fibrin gels (38–40). To test this hypothesis, we measured the linear elastic modulus, G′, of fibrinogen solutions with and without cells during polymerization by macroscopic shear rheology. In the absence of cells, G′ immediately started to increase and reached a plateau after ∼3 h (blue line in Fig. 4). This increase reflects fast polymerization of fibrin into a space-filling elastic network, followed by a slower process of covalent cross-linking by FXIIIa (69,70). In the presence of cells, we also observed an immediate increase of G′, but it took 4 h to reach a constant value of G′ and the increase of G′ was biphasic, with an inflection around 2 h (red line in Fig. 4). The first phase of network stiffening likely corresponds to the same network formation process that occurs in the absence of cells. The second phase of network stiffening approximately coincides with the onset of cell spreading (black lines in Fig. 4). We note, though, that the onset of cell spreading varied from 30 to 70 min, probably due to variations in the delay between cell harvesting and the start of the experiments and to the fact that cells need ∼1 h to reexpress integrins after trypsinization (71). A similar biphasic stiffening response was observed in fibrin gels and plasma clots containing contractile platelets (72). Over the entire range of fibrin concentrations (0.2–6 mg/ml) studied, mechanical equilibrium (i.e., a constant G′) was reached within 4–6 h. This timescale is consistent with the bead tracking data and the time-lapse images of spreading cells shown earlier. However, the morphology of cells inside the rheometer might differ from that seen in the cell spreading assays due to strain shielding at small strains, as was seen in collagen gels (73).

In steady state, the fibrin networks behaved as near-perfect elastic solids, with a frequency-independent elastic modulus (Fig. S6) and a very small loss tangent, G″/G′, which decreased about 10-fold, from ∼0.05 to 0.006, when the fibrin concentration was increased from 0.2 to 6 mg/ml (see Fig. 5 B). This solid-like behavior is caused by the presence of covalent bonds between fibrin monomers within and between fibers created by the enzymatic activity of FXIIIa (39). In the absence of cells, the elastic plateau modulus, G₀, increased nearly quadratically with fibrinogen concentration over the range of 0.5–6 mg/ml (blue circles in Fig. 5 A). In the presence of cells, G′ was threefold higher than for the cell-free gels when the fibrin concentration was 2 mg/ml or less (red squares in Fig. 5 A; differences are statistically significant for fibrin concentrations with p < 0.1 below 2 mg/ml and p < 0.01 at 2 mg/ml). However, at fibrin concentrations above 2 mg/ml, the cells did not significantly influence the elastic modulus. The viscous modulus, G″, increased by about the same factor as G′ (Fig. S7). As a result, the loss tangent of gels with cells (solid squares) was indistinguishable from that of gels without cells (open circles).

Figure 5.

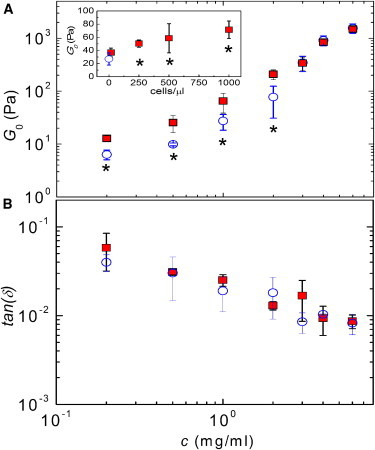
Linear viscoelastic shear moduli of fibrin gels with and without cells (at ω = 1 rad/s). (A) The elastic modulus, G′, is shown as a function of fibrin concentration for fibrin gels without cells (open circles) and with 500 cells /μl (closed squares). Inset: G″ of 1 mg/ml fibrin gels as a function of cell density; the open circle corresponds to the cell-free case. (B) Loss tangent, G″/G′, corresponding to the data shown in A. Asterisks denote statistically significant differences (p ≤ 0.1) compared to the unseeded (cell-free) case. To see this figure in color, go online.

To test whether the stiffening effect depends on cell density, we measured G₀ for fibrin gels of 1 mg/ml and 4 mg/ml. At 1 mg/ml (inset of Fig. 5 A), the cells indeed increased G₀ in a dose-dependent manner (solid squares), giving an increase relative to the cell-free gel (open circle) ranging from a factor 1.4 at 16 cells/μL (not significant, p = 0.18) to a factor 2.7 at 1000 cells/μL (significant with p < 0.1). At 4 mg/ml (Fig. S8), cells also increase G₀, but only at densities of 5000 cells/μl, corresponding to a volume fraction of ∼4%.

To test whether the stiffening of the fibrin gels in the presence of cells is caused by cell-mediated contractile prestress rather than by cells acting as cross-linkers, we compared the nonlinear rheology of fibrin networks with and without cells using a prestress method. We subjected gels to a macroscopic shear stress, σ₀, and measured the differential shear modulus, K′(σ₀), with a small superposed oscillatory stress. If cells stiffen gels by exerting contractile prestress, we expect convergence of the elastic moduli of cell-seeded and unseeded gels as soon as σ₀ exceeds the contractile prestress (9). If, in contrast, cells act merely as cross-linkers, we expect that the cell-seeded gels will be stiffer than unseeded gels independent of σ₀. In the absence of cells, K′(σ₀) increased with stress until the gels broke at a maximum stress level, σ_max, as illustrated for gels of 1 mg/ml (open squares), 2 mg/ml (open circles), and 6 mg/ml (open triangles) fibrin in Fig. 6 A. The maximum extent of strain stiffening before breakage, as quantified by the ratio K_max/G₀, was close to a value of 100 for gels of 0.2–3 mg/ml and decreased to 10 for gels of 6 mg/ml fibrin (open circles in Fig. S9 D). The nonlinear elastic response in the presence of cells (solid symbols in Fig. 6 A) was qualitatively similar to the behavior of unseeded gels. The gels again had a linear regime for stress levels below a critical stress, σ_crit, and stiffened at larger stress levels until the breakage stress, σ_max, was reached. For dense gels (≥3 mg/ml fibrin), the entire stress dependence of K′ of cell-seeded and acellular gels was indistinguishable (triangles). However, for dilute gels (≤2 mg/ml fibrin) the cells caused a clear increase of the linear elastic modulus, while leaving the high-stress response unchanged. The maximum shear stress, σ_max, supported by the gels was unchanged by the presence of cells (Fig. S9 C), and the maximum elastic modulus, K_max, was likewise unchanged. Consequently, the relative degree of stress stiffening before breakage, K_max/G₀, was ∼threefold lower for cell-seeded gels than for acellular gels (Fig. S9 D). When we increased the cell density, we observed an even more pronounced increase of the linear modulus, but the high-stress response still remained unchanged (Fig. 6 B).

Figure 6.

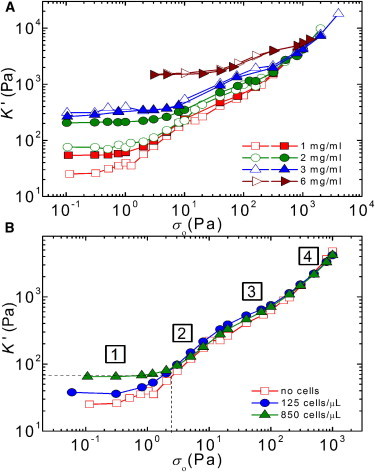
Stress-stiffening response of fibrin gels with and without cells. (A) Tangent elastic modulus, K′, as a function of external (macroscopic) shear stress, σ₀, for fibrin gels with different concentrations (see legend) without cells (open symbols) and with cells (solid symbols, 500 cells/μl). (B) K′ as a function of σ₀ for a fibrin gel (1 mg/ml) containing cells at different densities (see legend). By comparing the stiffening curves of cell-seeded and cell-free gels, we estimate the cell-induced prestress (vertical dotted line) as the σ-value where the apparent linear modulus of the cell-populated gel matches the K′-value on the stiffening curve of the acellular gel (horizontal dotted line). The curves show a linear elastic regime (labeled 1) followed by a nonlinear response with three regimes with a distinct σ₀-dependence (labeled 2 to 4), see main text for details. To see this figure in color, go online.

These observations strongly support our hypothesis that cells stiffen the gels by an active mechanism, involving contractile prestress. Indeed, tests with blebbistatin, which specifically inhibits myosin II contractile activity (74), show that myosin activity is a requirement for cell-induced stiffening (Fig. S10).

The increased stiffness of the cell-seeded gels coincided with a postponement of the onset of stress stiffening (Fig. S9 A). In the absence of cells, the critical stress, σ_crit, increased more than 10-fold when the fibrin concentration was raised from 0.6 to 6 mg/ml (open circles in Fig. S9 A). The corresponding critical strain, γ_crit, was 30% for the most dilute gels (0.2 and 0.5 mg/ml) and only 1–3% for the more concentrated gels (open circles in Fig. S9 B). The cells increased σ_crit and decreased γ_crit for gels with fibrin concentrations below 2 mg/ml (p < 0.06). Similar to the cell-free gels, there appeared to be two distinct concentration regimes for γ_crit, with γ_crit ≈ 10% for 0.2 and 0.5 mg/ml fibrin and γ_crit ≈ 1% at higher fibrin concentrations.

Discussion

Cells stiffen fibrin gels by generating contractile prestress

We showed that fibroblasts seeded inside extracellular matrices prepared from purified human fibrinogen cause macroscopic matrix stiffening. The extent of stiffening increases with increasing cell density, reaching a maximum of threefold stiffening over cell-free gels at 1000 cells/μL. At higher cell densities, cells caused macroscopic contraction and detachment from the rheometer plates. Stiffening was apparent only in dilute fibrin scaffolds of 2 mg/ml or less. These findings are consistent with several prior studies, showing comparable degrees of stiffening in case of fibroblasts and mesenchymal stem cells (factor 2–4 stiffening, at a similar cell density as ours (45)) and platelets (factor 10 stiffening, but at a 100-fold larger cell density compared to our study (44,72)). A similar extent of cell-induced stiffening was also reported for frog embryonic tissue (75). In these earlier studies, it was already hypothesized that the stiffening effect may be caused by active contractility of the cells, which may drive the gel into a nonlinear, stress-stiffened state. In our work, we systematically tested this hypothesis. Here, we showed by rheology measurements in the presence of the myosin inhibitor blebbistatin that cell-induced gel stiffening indeed requires myosin-driven contractility.

We observed a clear correlation between the onset of gel stiffening and the onset of cell spreading. Time-dependent rheometry showed that the cells started to stiffen the fibrin gels ∼1–3 h after cell seeding, which coincided with the moment where microscopy showed that cells started to attach to the gels and spread. Fibrin network formation was largely complete within the first hour (Fig. S2), well before the cells began to spread. In the process of spreading, the cells applied inward (traction) forces to the fibrin fibers and caused fibrin gel compaction, but only near the cell edges. This compaction was only seen in dilute (≤2 mg/ml) fibrin gels. Once the cells were fully spread (∼6 h after seeding), they maintained active tension in the surrounding fibrin network. This was apparent from the abrupt release of tension when GRGDS was added to block the RGD-binding integrins (64,68,76). The elastic modulus of the cell-seeded gels reached a constant value once the cells were well spread.

Cell-induced gel stiffening could in principle arise either from active traction forces, which prestress the network (77–79) or from a passive cross-linking effect of the cells (80,81). We consider the latter explanation unlikely, because the cells take up <1% of the total sample volume, based on an average cell diameter of 25 μm. Moreover, the close correspondence of the time dependence of cell spreading and gel stiffening strongly suggests that cell traction forces are related to gel stiffening. This interpretation is further supported by tests with blebbistatin, showing that myosin inhibition prevents gel stiffening (Fig S10). A direct comparison of the nonlinear elastic behavior of cell-seeded and cell-free gels also supports an active mechanism. The cell-seeded gels have a higher elastic modulus than acellular gels at low shear stress, but an identical elastic modulus at high shear stress. Furthermore, the cell-seeded gels have a smaller critical strain than cell-free gels. These observations indicate that the cells generate an internal prestress that brings the fibrin gels in a nonlinear stress-stiffened state. The stiffness of the cell-seeded gels is controlled by a sum of the active prestress and the externally applied shear stress. Fig. 6 B illustrates the concept by comparing stress-stiffening curves of a cell-seeded fibrin gel (green triangles) with that of a cell-free gel (red squares). The cell-seeded gel has an initial modulus (horizontal dotted line) that corresponds to the modulus of the cell-free gel under an external shear stress of ∼2 Pa (vertical dotted line). At shear stresses larger than 2 Pa, the cell-seeded gel starts to stiffen and its nonlinear modulus coincides with that of the cell-free gel. The maximal modulus reached before breakage is the same for the cellular and acellular gels. Because the cellular gel starts out in a prestressed, stiffened state, the total degree of gel stiffening caused by the external stress (given by the ratio K_max/G₀) is less than for the acellular gel. We note that these observations are qualitatively consistent with prior large amplitude oscillatory shear measurements of fibrin gels and plasma clots containing platelets (72). The platelets, similar to the fibroblasts studied here, increased G₀ (by a factor of 5), although having no effect on gel stiffness at large levels of shear stress. Moreover, similar to the fibroblasts studied here, the platelets postponed the onset of strain stiffening to larger values of σ_crit and reduced the maximum extent of strain stiffening before gel breakage.

The external shear stress where the nonlinear modulus of the acellular gel matches the linear modulus of the cellular gel can provide an estimate of the global prestress in the cell-seeded gels generated by the cells (9). The prestress thus estimated increases roughly linearly with increasing cell density, going from 1 Pa for 16 cells/μL to 3 Pa at 1000 cells/μL in gels of a constant (1 mg/ml) fibrin concentration (open circles in Fig. 7 A). At fixed cell density (500 cells/μL), the prestress increases from 0.5 to 9 Pa as the fibrin concentration is increased from 0.2 to 2 mg/ml (Fig.7 B). However, at fibrin concentrations of 3 mg/ml and higher, there is no measurable prestress, because the elastic moduli of cellular and acellular gels are indistinguishable. This does not necessarily imply that the prestress is zero, because the prestress may be less than the critical stress needed to induce strain stiffening (σ_crit = 7 Pa at 3 mg/ml). However, bright field imaging did show that the cells are less well spread in dense (3–6 mg/ml) fibrin gels than in dilute (0.2–2 mg/ml) gels. Cells in denser gels are less elongated and generate much shorter protrusions than in more dilute gels (Fig. 2 and Fig S3). On two-dimensional (2D) gels, less-spread cells tend to exert smaller traction forces than well-spread cells (16,23,82), which raises the possibility that cells in dense fibrin gels exert smaller traction forces than in dilute gels. Recent work suggests that matrix-embedded cells mainly generate traction along their pseudopodial protrusions (83,84). The reduced tendency of the cells to form pseudopods in dense gels may therefore also contribute to a smaller overall prestress. However, a direct measurement of traction forces on a microscopic scale in the fibrin network immediately adjacent to the cells will be needed to verify this hypothesis (19).

Figure 7.

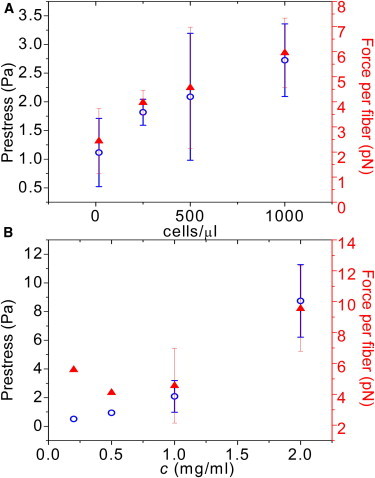
Cell-mediated prestress (left axis, open circles) determined by comparing the stress-stiffening response of cellular and acellular gels according to the procedure shown in Fig. 6B, and corresponding calculated average force per fibrin fiber (right axis, solid triangles). (A) Prestress as a function of cell density in gels of fixed fibrin concentration (1 mg/ml). (B) Prestress as a function of fibrin concentration at a fixed cell density (500 cells/μL). To see this figure in color, go online.

From the prestress values, we can estimate an average traction force experienced by each fibrin fiber by dividing the prestress by the total filament length density, ρ. We find an average force per fiber between 2 and 10 pN, depending on cell density and fibrin concentration (solid triangles in Fig. 7, A and B). These values are considerably lower than traction forces reported by other techniques and in a variety of ECM materials (17–19,85). This is expected, because the numbers reported here are ensemble averages over the entire cell population. In the local vicinity of cells, we expect higher force levels than in the regions between cells.

Interestingly, the reduced cell spreading in denser fibrin gels is in apparent contradiction with studies of cell spreading on planar (2D) elastic substrates, where increased substrate stiffness tends to promote cell spreading (10,20,22,82). However, in 3D matrices several other factors can influence cell spreading behavior, such as differences in local stiffness, ligand density, porosity, and three-dimensionality of cell surface receptor engagement. Changing the fibrin concentration changes not only the stiffness, but also the matrix porosity. The average mesh size determined by confocal microscopy decreases as a square root in fibrin concentration, going from 10 μm at 0.1 mg/ml fibrin to 2 μm at 6 mg/ml fibrin (39). The small mesh size of the denser gels may constrain the cell body and also impede the extension of pseudopods. In the future, it will be interesting to find alternative ways to modify the matrix rigidity without changing the network architecture.

Mechanistic origin of fibrin gel stiffening

The nonlinear elastic modulus of the fibrin gels has a remarkably complex dependence on stress, with four distinct phases, as indicated in Fig. 6 B. We recently showed that these four phases reflect the hierarchical structure of fibrin networks (39). At small stress, excess length between cross-link points stemming from thermal bending fluctuations are pulled out, giving rise to an initial linear regime (regime 1) followed by an entropic stiffening response (regime 2). Despite their large thickness (∼100 nm), the fibers do exhibit significant thermal fluctuations because they are composed of semiflexible protofibrils that are loosely bundled by flexible linker chains. Due to this bundle-like architecture, the fibers have a persistence length of 20–30 μm, ∼100-fold more flexible than anticipated from continuum arguments. However, it is likely that for fibrin gels prepared under conditions where the fibers are thicker or the mesh size is larger, entropy no longer plays an important role. In these cases, we instead expect nonaffinity to govern the low-stress response (86).

As the stress is raised further, the fibers themselves are axially stretched, causing a small regime of constant elastic modulus (regime 3) followed by another strain-stiffening regime (regime 4). The stiffening at large stress suggests that the fibers themselves have an inherently nonlinear force-extension response. Direct force-extension measurements using atomic force microscopy have indeed demonstrated strain stiffening on the level of individual fibrin fibers, though the exact molecular origin is still under debate. Possible explanations are stretching of flexible alpha-C linker regions that connect the protofibrils within a fiber (39,87) or forced-unfolding of the fibrin monomers (40,88–90).

Remarkably, the cells only influence regimes 1 and 2 of the nonlinear response of the fibrin gels. In regimes 3 and 4, where the fibrin fibers themselves are axially stretched, the stiffening curves for cell-populated gels are identical to those of cell-free gels (Fig. 6, A and B). This observation indicates that the stress/strain applied by the cells is sufficient to stretch out thermal undulations of the fibrin fibers between cross-link points, thereby increasing the elastic modulus in regime 1 and shifting the onset of regime 2 to a larger critical stress. However, the cells are apparently unable to stretch out the backbone of the fibrin fibers. Indeed, the forces reported in Fig. 7 are insufficient for causing forced unfolding of fibrin monomers, which requires forces on the order of 100 pN (88). Strain stiffening of individual fibrin fibers requires large strains on the order of 100% (87). We cannot exclude that backbone stretching occurs locally in a few highly strained fibrin fibers, but we can exclude that it occurs on a macroscopic scale.

The cell-induced stiffening of the fibrin gels is an analog of rheological measurements of reconstituted actin-myosin gels (8,9). Contractile prestress generated by myosin II motors was shown to produce identical stiffening as an external stress applied by shearing actin networks (9). The active prestress reached values equivalent to an external stress of 14 Pa. The average force per actin filament (which may be calculated from the known mass concentration and mass per length ratio of actin fibers (91) was 0.3 pN. Consistent with the fact that cells contain many myosin II motor molecules, the average force in the actin-myosin networks is an order of magnitude lower than the forces we find for cell-mediated matrix stiffening.

Implications of cell-induced stiffening

In recent years, various quantitative techniques (collectively known as traction force microscopy) have been developed to measure traction forces exerted by cells on 2D substrates (15,16,92) and inside 3D hydrogels (19,83,85). The basic idea is to measure the strain field in the substrate by tracking the displacements of fiducial markers and to convert strains into traction forces by using an appropriate elastic model for the substrate. This conversion requires certain assumptions, such as continuum elasticity and linearity. These assumptions are reasonable for typical synthetic hydrogels such as polyacrylamide, but are invalid in physiologically relevant fibrous materials such as collagen or fibrin networks (93,94). Our results show that cells are able to induce active stiffening of fibrin matrices, which should be taken into account in future attempts to perform traction force microscopy in 3D matrices.

Cell-induced stiffening also has implications for understanding tissue behavior during tissue development and homeostasis. By locally pulling on the matrix, cells can sense and respond to mechanical changes of the ECM. However, at the same time they also actively change the stiffness and tension in the ECM, thus creating a mechanical feedback loop (95). This effect may explain recent findings showing that fibroblasts and human mesenchymal stem cells plated on soft fibrin gels behaved the same as on stiff 2D substrates, suggesting that the cells respond to the gel’s high-strain modulus (45). Cell-induced matrix stiffening may also result in a feedback loop enhancing cellular contractility, development of stress fibers, and growth of adhesions (27). Furthermore, the nonlinear elastic response of the ECM on cell contractility will likely influence the mechanical interactions among cells during tissue morphogenesis, a phenomenon which has been seen experimentally (31,32,96) as well as theoretically (97–100). Studies of cells cultured in/on linearly elastic materials have shown that stem cell fate can be controlled by changing matrix stiffness (23,101), which implies that scaffold stiffness is a key design parameter for biomaterial scaffolds for tissue repair. Because of its natural function in angiogenesis and wound repair, fibrin is particularly popular for applications in tissue engineering of cartilage, cardiac muscle, skin, nerve, and vascular tissue (53,102). Given that matrix stiffness is an important design parameter, cell-induced stiffening is thus an important factor.

Conclusion

Here, we have shown that fibroblasts stiffen tissue-like fibrin matrices by applying contractile forces against the extracellular matrix that bring it into a stress-stiffened regime. By correlating observations of cell spreading with rheological measurements, we discovered that stiffening starts as the cells start to spread and apply contractile tension. Once the cells are well spread, they maintain an isometric contractile force on the fibrin matrix. Control tests with an actin-myosin inhibitor correlated contractile force with stiffening of fibrin gels. We found that both cell spreading and fibrin gel stiffening were sensitive to the matrix density. Cells assumed well-spread, elongated shapes with long protrusions in gels of low fibrin concentrations and spread progressively less in denser fibrin gel, remaining round with small protrusions in the densest gel tested (6 mg/ml). By directly comparing nonlinear rheology measurements on cell-seeded and cell-free gels, we conclude that cells generate traction forces that are sufficient to pull out large wavelength thermal undulations of the fibrin fibers, but insufficient to axially stretch the fibrin fibers. The mechanical properties of fibrin blood clots during wound healing, fibrosis, and cancer development are probably controlled at least in part by the nonlinear elastic response of the clots to the active internal forces generated by embedded cells.