Catalysis-Enhancement via Rotary Fluctuation of F₁-ATPase

Abstract

Protein conformational fluctuations modulate the catalytic powers of enzymes. The frequency of conformational fluctuations may modulate the catalytic rate at individual reaction steps. In this study, we modulated the rotary fluctuation frequency of F₁-ATPase (F₁) by attaching probes with different viscous drag coefficients at the rotary shaft of F₁. Individual rotation pauses of F₁ between rotary steps correspond to the waiting state of a certain elementary reaction step of ATP hydrolysis. This allows us to investigate the impact of the frequency modulation of the rotary fluctuation on the rate of the individual reaction steps by measuring the duration of rotation pauses. Although phosphate release was significantly decelerated, the ATP-binding and hydrolysis steps were less sensitive or insensitive to the viscous drag coefficient of the probe. Brownian dynamics simulation based on a model similar to the Sumi-Marcus theory reproduced the experimental results, providing a theoretical framework for the role of rotational fluctuation in F₁ rate enhancement.

Introduction

Protein conformational fluctuations, especially the collective motion of residues that usually occurs on a domain scale, are believed to play a key role in the enhancement of catalytic powers (1). Several experimental and theoretical models have shown that dynamic fluctuation of protein conformation contributes to the acceleration of enzyme catalysis (2–5). It is unclear how the timescale of conformational fluctuation correlates with the rate enhancement of enzyme catalysis at the resolution of elementary reaction steps. In this study, we investigated the role of conformational fluctuation of F₁-ATPase, an ATP-driven rotary motor protein, in its catalysis, resolving the catalysis reaction into elementary reaction steps (Fig. 1 a).

Figure 1.

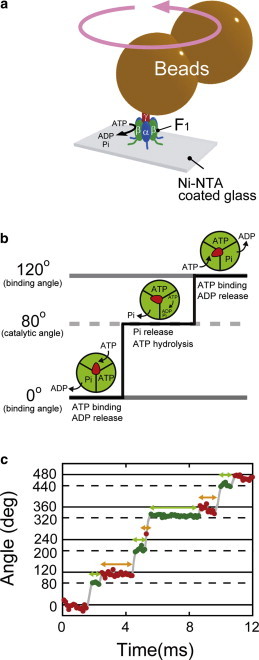
Rotation of F₁ and viscous drag. (a) Schematic diagram of single-molecule observations of F₁. (b) Chemomechanical coupling scheme of F₁. Red arrowheads represent the angular positions of the γ subunit. Green areas represent the catalytic actions of the individual catalytic sites. F₁ rotates 120° upon hydrolysis of one ATP, comprising 80° and 40° substeps. The 80° substep is driven by ATP binding and ADP release, and the 40° substep is driven by ATP hydrolysis and P_i release. (c) Time course of the rotation of wild-type F₁ in the presence of 20 μM ATP. Red and green represent the pauses at the binding angle and catalytic angle, respectively. To see this figure in color, go online.

F₁-ATPase (F₁), the catalytic domain of F_oF₁-ATP synthase, is a rotary motor protein fueled by ATP hydrolysis when isolated from F_o, the membrane-embedded portion of F_oF₁-ATP synthase (6–8). The bacterial type F₁ is composed of α₃β₃γδε; the α₃β₃γ subcomplex functions as the minimum complex as a rotary motor. The α₃β₃ subunits form the cylindrical stator ring and the γ subunit is the rotary shaft that penetrates the center of the cylinder (9). The catalytic sites for ATP hydrolysis reside on each α-β interface, mainly on the β subunit; F₁ possesses three catalytic sites (9). The catalytic reaction centers hydrolyze ATP in a highly cooperative manner, generating a sequential power stroke to drive the unidirectional rotation of the γ subunit (10). F₁ derived from thermophilic Bacillus PS3 (TF₁) exerts a rotary torque of 40 pN·nm (11), whereas F₁ from Escherichia coli (EF₁) generates 60–80 pN·nm torque (12,13).

The process of catalysis and rotation of F₁ is well established (14), although there are some uncertainties (8). Rotation occurs in discrete 120° steps, each coupled to hydrolysis of a single ATP molecule (11) (Fig. 1, b and c). The 120° step is further divided into 80° and 40° substeps (15,16). The 80° substep is triggered by ATP binding and ADP release (15–18), each of which occurs on different β subunits. The 40° substep is triggered by ATP hydrolysis and release of inorganic phosphate (P_i) (16,17,19,20), which also occur on different β subunits (21). The angular positions of the dwell times before the 80° and 40° substeps are referred to as the ATP-binding and catalytic angles. The unique feature of F₁ is that when the rotary shaft is forcibly rotated in the reverse direction, F₁ catalyzes the reverse reaction of ATP hydrolysis, ATP synthesis (22,23). Thus, each reaction step is so tightly coupled with rotary steps that we can measure the waiting time (time constant) of a reaction step as the dwell time before the rotation triggered by the reaction.

A recent study of single-molecule manipulation with magnetic tweezers revealed that the rate and equilibrium constant of ATP binding and hydrolysis are modulated upon γ rotation (24). The ATP-binding reaction was highly dependent on γ rotation; the reaction is accelerated upon forward rotation. ATP hydrolysis is less affected by γ rotation, suggesting that the hydrolysis step at the catalytic site of F₁ does not contribute to the torque as much as does the ATP-binding step. When the angular position of the γ subunit was fixed with magnetic tweezers at the center angle of the ATP waiting state, the rate constant of ATP binding was slightly, but evidently, lower than the ATP-binding rate when the γ subunit was free from the magnetic tweezers. This phenomenon was attributed to the thermally agitated rotary fluctuation that occasionally pushes γ forward, accelerating ATP binding. It is unclear, however, how the timescale of the rotary fluctuation modulates the reaction rate of individual reaction steps of ATP hydrolysis on F₁. Spetzler et al. reported that the viscous drag on the EF₁ γ subunit increases the catalytic dwell time between 120° step rotations under ATP-saturating conditions (12). This finding indicates that the slower rotary fluctuation of the γ subunit suppresses the rate constant of the catalytic dwell time; however, they did not identify which of the elementary reaction steps of ATP hydrolysis is viscosity-sensitive.

In this study, we systematically analyzed the viscosity sensitivity of the catalytic reaction of TF₁, which exhibits clear stepping rotation, allowing us to resolve the catalytic reaction into individual elementary reaction steps, i.e., ATP binding, hydrolysis of bound ATP, and P_i release. The viscous drag on γ rotation varied more widely than in the previous study (12); drag varied >5000-fold with different sizes of rotation probe. We discuss our results in the context of the Brownian dynamics simulation in the framework of a simple physicochemical model conceptually similar to the Sumi-Marcus model.

Materials and Methods

Rotation assay

Wild-type F₁ and mutant F₁(α₃β(E190D)₃γ) were prepared as described (25). To visualize the rotation of F₁, the stator region (α₃β₃) was fixed to a glass surface and a colloidal gold bead (ϕ = 40–80 nm) or polystyrene bead (ϕ = 0.2–0.5 μm) was attached to the rotor (γ) as a rotation probe (19). The rotating beads were observed under a phase-contrast microscope (IX-70 or IX-71, Olympus, Tokyo, Japan) or a custom-built laser dark-field microscope (26). The rotation assay was performed at 28°C. Images of the rotary motion of the gold colloidal and polystyrene beads were recorded at 18,000–109,500 and 1000–3000 frames/s, respectively (FASTCAM 1024PCI-SE, Photron, Tokyo, Japan). Images were stored as an AVI file and analyzed with custom-made software.

Brownian dynamics simulation

Schematic illustrations of the simulation model are depicted below (see Fig. 4, a and b). All parameters needed to build the simulation model were determined from the results of our single-molecule experiments (19,24,25) (see the Results section of the Supporting Material). The time evolution of the Brownian dynamics is described by the Langevin equation, as shown in the Methods section of the Supporting Material. The details of the simulation are described in the Supporting Material.

Figure 4.

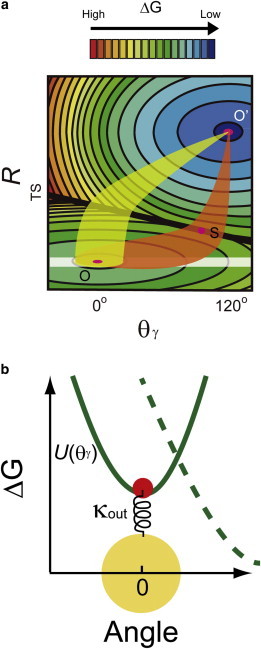
Simulation model of the catalytic reaction rate and viscous drag. (a) Schematic illustration of free-energy surface for pre- or postcatalysis by F₁-ATPase drawn for two reaction coordinates, viz. the rotary angle of the γ subunit (θ_γ) and other degrees of freedom representing the reaction (R). Contours are drawn for evenly spaced energies. The two surfaces intersect on line TS. There are two minima for the surface, located at O and O′ on the pre- and postcatalysis sides, respectively. The saddle point on line TS is denoted as S. When the relaxation time along θ_γ is shorter than the reaction time of catalysis, the reaction occurs passing through the saddle point on line TS (orange). In contrast, when the relaxation time along θ_γ is longer, the reaction occurs before θ_γ has reached the saddle point (light green). (b) Schematic illustration of the Brownian dynamics simulation model. This represents a cross-section view of the 2-D reaction-energy profile cut along the mechanical coordinate. The spring component, κ_out, intermediates between the γ subunit (red) and the rotary probe (yellow) and was set at 150 pN·nm. U(θ_γ) represents the inner rotary potential in the reactant side exerted by the stator ring on γ (solid line). The dashed line represents the rotary potential on the product side. The drag friction of γ inside the α₃β₃ ring, Γ_γ,, is set at 3 × 10⁻⁴ pN·nm s. To see this figure in color, go online.

Results

Catalytic rate at various drag frictions

To visualize the rotary motion of F₁ at the single-molecule level, we attached different-sized rotary probes (ϕ = 40–500 nm) to the protruding part of the γ subunit (27) (Fig. 1 a); these probes could also be used to modulate the frequency of the rotary fluctuation by changing the size of the probe, which determines the viscous drag friction (Γ_B). For example, drag friction increases 8000-fold by changing the diameter from 40 nm to 500 nm. Actually, the corner frequency (f_c) of the rotary fluctuation of the probe, which characterizes the fluctuation frequency of a Brownian particle, decreased exponentially with the size of the probe (Fig. S1, a and c). Although the experimental system had an elastic connection between the γ subunit and the rotation probe (25), the probe size also governed the timescale of rotary fluctuation of the γ subunit, as seen in the significant impact of the probe size on the reaction rate (see below). The Brownian dynamics simulation also showed that the frequency of the γ subunit is largely modulated upon changes in probe size (Fig. S1, b and c).

F₁ rotates in steps, making distinct pauses at particular angles until a waiting reaction occurs. This feature allows us to determine the time constant from the analysis of the waiting time before step rotation (hereafter referred to as dwell time). Taking this feature, we examined the impact of viscous drag of the probes on a particular catalytic reaction step (ATP binding, hydrolysis, and P_i release) by analyzing the dwell time. To measure the ATP binding rate (k_on^ATP), the rotation of wild-type F₁ was observed in the presence of 430 nM ATP, where wild-type F₁ showed a rotational dwell time at the binding angles with a time constant of ∼0.13 s. The ATP-binding dwell time exhibited an exponential distribution, giving the rate constant of ATP binding (Fig. 2 a, upper row). With increasing bead size, the ATP-binding rate slightly decelerated; the rotation speed with a 40-nm bead was slightly faster than that with a 1-μm actin rotation, as previously reported (15) (Fig. 2 b, blue).

Figure 2.

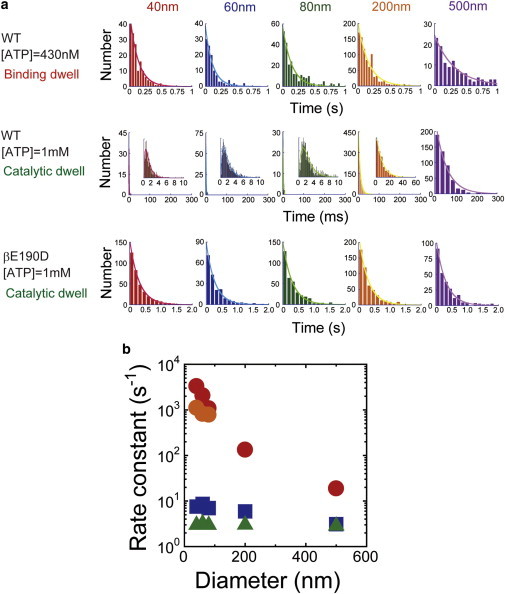
Rate constants of elementary reaction steps and viscous drag. (a) Histogram of the dwell times triggered by ATP binding to wild-type F₁ (upper row), ATP hydrolysis and P_i release by wild-type F₁ (middle row), and ATP hydrolysis by mutant F₁ (α₃β(E190D)₃γ) (lower row). Red, blue, green, orange, and purple represent the histograms of dwell times using rotary probes with ϕ = 40 nm, 60 nm, 80 nm, 200 nm, and 500 nm, respectively. Insets in middle row show close-ups. The numbers of pauses and molecules are 112–1309 and 3–17, respectively. The histograms corresponding to ϕ = 40 nm, 60 nm, and 80 nm in the middle row are fitted with double-exponential curves, y = C(exp(−k₁t) − exp(−k₂t)), whereas the other histograms are fitted with a single-exponential curve, y = Cexp(−kt). (b) Rate constants of the catalytic reaction and the diameter of the rotary probes. The rate constants, determined from the upper, middle, and lower rows in a, are depicted as squares, circles, and triangles, respectively. One of the rate constants determined from ϕ = 40 nm, 60 nm, and 80 nm in the middle column in (a), which strongly depends on ϕ, and the other are red and orange, respectively. To see this figure in color, go online.

Next, to measure ATP hydrolysis (k_hyd^ATP) and P_i release rates (k_off^Pi), we observed the rotation of wild-type F₁ in the presence of 1 mM ATP, where wild-type F₁ showed a dwell time at the catalytic angle. Although we had not detected obvious catalytic dwell times in the rotation assay with large probes (ϕ = 200 nm) in previous experiments, after careful and thorough observations, we found molecules that exhibited distinct catalytic dwell times (Fig. S2), which were the rate-limiting steps of the rotary motions. We then analyzed the catalytic dwell time, which is composed of two waiting times for hydrolysis of bound ATP and P_i release. The dwell-time distribution is a typical convex curve that fits well with the model of a consecutive two-step reaction, except for the distribution obtained with 200- or 500-nm beads, which exhibited an exponential decay (Fig. 2 a, middle row). The rise and decay in the convex distribution represent the kinetic components of faster and slower steps, respectively. The simple exponential decay therefore indicated a large temporal gap between the fast and slow steps. In contrast to ATP binding, either ATP hydrolysis or P_i release, which appeared as the slower component, showed significant deceleration under higher viscous drag conditions, whereas the other did not (Fig. 2 b, red and orange). To identify which reaction step (ATP hydrolysis or P_i release) was suppressed under high viscous drag, we analyzed the catalytic dwell time in the presence of 200 mM P_i. Under this condition, a solution P_i molecule can bind to the catalytic site before the conformational change (i.e., torque generation), which apparently results in elongation of the rotational pause for P_i-release (17). This experiment could yield one of two possible scenarios. First, if P_i release is sensitive to viscous drag (i.e., P_i release is the slower and thus rate-limiting step at the catalytic angle), the decay component of catalytic dwell time would show further elongation at high [P_i]. If ATP hydrolysis is the rate-limiting step, elongation of the P_i release dwell time would appear in the rise component. As shown in Fig. S3, our study revealed that the distribution at high [P_i] exhibits a clear elongation of the exponential decay, supporting the first scenario.

We also analyzed the rotation of the mutant F₁ (α₃β(E190D)₃γ) at 1 mM ATP; ATP hydrolysis was prolonged 300-fold (τ_hyd^ATP ≈ 300 ms) (16) and dominated the catalytic dwell time; i.e., the distribution of the catalytic dwell time exhibited a simple exponential decay (Fig. 2 a, lower row), from which we determined the rate constant of ATP hydrolysis. As seen by the green data points in Fig. 2 b, ATP hydrolysis of the mutant was also not sensitive to viscous drag, consistent with the above contention.

Drag friction exerted on the rotary shaft

We attempted to measure the drag friction of the γ subunit inside of the α₃β₃-ring (Γ_γ) that was required for the Brownian dynamic simulation to reproduce the observed effect on catalytic rates of viscous drag against the γ rotation (see below). For this purpose, rotation with probes of 40- to 80-nm gold colloid were measured in the presence of 1 mM ATP with a laser dark-field microscope equipped with a perforated mirror that allows monitoring of the motion of micron- to nanometer-sized objects with nanometer spatial precision and microsecond temporal resolution (9.1 μs) (26). After trimming the trajectories of rotation pauses, fragmented trajectories of successive 120° steps were overwritten to determine the averaged angular velocity (ω) (Fig. 3 a). From the angular velocity, the net drag friction on the rotary shaft, Γ, which is derived from the drag friction against the gold colloidal or plastic bead rotation probe (Γ_B) and that of the γ subunit (Γ_γ), was estimated assuming a constant torque of 40 pN·nm rad⁻¹; Γ = N/ω (Fig. 3 b) (11,28). For all sizes of the rotary probe (ϕ = 40–500 nm), Γ accorded with the Γ_B estimated from the bead size. This means that Γ_γ is smaller than that of the 40-nm bead that sets the upper limit of Γ_γ, 3 × 10⁻⁴ pN·nm s (Fig. 3 b).

Figure 3.

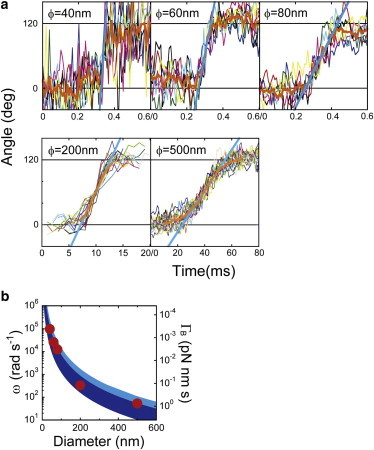
Angular velocity of F₁ with various sizes of rotary probes. (a) Time course of the stepping rotation of wild-type F₁ in the presence of 1 mM ATP. We attached various sizes of rotary probes (ϕ = 40, 60, 80, 200, and 500 nm) to the γ portion of F₁. Thin lines show 17 successive steps, with their average (heavy orange line). The heavy cyan line shows the linear fitting of the average step between 40° and 80°. The trajectories are aligned at 60°. (b) Average angular rate estimated from the slope of the fitted straight line (red circles). Each data point was determined from three to five molecules. Blue and light blue solid areas represent the viscous coefficients of doublet and singlet beads, respectively, calculated using fluid dynamics, as previously reported (15). To see this figure in color, go online.

Modeling the effect of rotary fluctuation on catalytic rate

We built a mechanokinetic model to explain our observations in a simple theoretical framework. To explain the observed viscous drag dependence of the reaction rate, the rotary fluctuation of the γ subunit and the reaction rate at individual angles of the γ subunit must be considered. Therefore, we conceptually assumed a two-dimensional (2-D) reaction-energy profile where the free energy of reaction states is represented as a function of two coordinates; the chemical reaction coordinate (R) and the mechanical coordinate (θ_γ: the rotary angle of the γ subunit) (Fig. 4 a). A cut surface along the chemical coordinate represents a reaction free energy diagram at a particular rotary angle (19,24) whereas a cut surface along the mechanical coordinate gives a potential surface for the γ subunit at a particular reaction state. This model is similar to the Sumi-Marcus model for electron transfer kinetics, which takes into account the role of molecular dynamics on rate enhancement (29) and has been recently applied to theoretical studies on molecular motor proteins (30–32).

In the actual simulation, rotary fluctuation of the γ subunit in a rotary potential was simulated, fixing the reaction state at the reactant state (Fig. 4 a, heavy white line). Then, the stochastically-occurring reaction, the state transition over the ridge of TS along R, was simulated at individual rotary angles (θ_γ) based on the experimentally determined angle dependences of ATP binding, ATP hydrolysis, and P_i release (24). To reproduce the actual experimental situation, the γ subunit was connected with a viscous probe via an external spring representing the external elastic component of the experimental systems (Fig. 4 b). The Brownian dynamics of γ and the bead were simulated according to the Langevin equations (for details, see the Methods section in the Supporting Material)

$${\Gamma }_{\gamma }\frac{\text{d}{\theta }_{\gamma }}{\text{dt}}=-\frac{\text{d}U\left({\theta }_{\gamma }\right)}{\text{d}{\theta }_{\gamma }}-{\kappa }_{\text{out}}\left({\theta }_{\gamma }-{\theta }_{\text{B}}\right)+\sqrt{2{\Gamma }_{\gamma }{k}_{\text{B}}\text{T}}{\text{ξ}}_{\gamma }\left(t\right)$$

and

$${\Gamma }_{\text{B}}\frac{\text{d}{\theta }_{\text{B}}}{\text{d}t}={\kappa }_{\text{out}}\left({\theta }_{\gamma }-{\theta }_{\text{B}}\right)+\sqrt{2{\Gamma }_{\text{B}}{k}_{\text{B}}\text{T}}{\text{ξ}}_B\left(t\right),$$

where Γ_γ and Γ_B are the drag frictions of the γ subunit and the rotary probe, respectively, ξ_γ and ξ_B are Gaussian noise whose intensities are 1, and k_B is the Boltzmann constant. The rotary potential of the γ subunit (U) was estimated from the experimentally determined one (Results and Methods sections in the Supporting Material). The spring constant of the external elastic component (κ_out) was estimated from the apparent rotary potential of the beads (Fig. S4) and our previous work on the rotational elasticity analysis of F₁ (25) (Results section in the Supporting Material).

Fig. 5 shows the simulated time trajectories of the beads when P_i release triggers the 120° steps. The dwell time between rotational steps (Fig. 5 a, gray arrow) was analyzed in each simulation to determine the rate constant of the reaction. The results are summarized in Fig. 5 b, where the simulated rate constants, calculated as 1/τ, are plotted as a function of Γ_B. It is evident that P_i release is highly sensitive to the viscous drag of the rotary probes; the rate decelerates by a factor of 45 with each increase in viscous drag, whereas the ATP binding and hydrolysis steps were not affected. This is consistent with the trend observed in the experimental results. Thus, this computational simulation reproduced the experimental results of viscous drag sensitivities shown in Fig. 2, supporting the validity of this simple mechanokinetic model.

Figure 5.

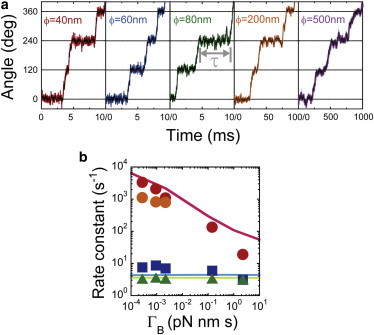
Langevin dynamics simulation of rotary catalysis by F₁. (a) Simulated time course of θ_B and θ_γ based on the simulation model for P_i release. Red, blue, green, orange, and purple represent the results of θ_B for ϕ = 40, 60, 80, 200, and 500 nm, respectively. Black time courses represent the results of θ_γ. (b) Simulation results of catalytic rate and viscous drag of rotary probes. Red, orange, and blue data points represent the experimental results for P_i release, ATP hydrolysis, and ATP binding of wild-type F₁, respectively, whereas green points represent ATP hydrolysis by the mutant F₁ (α₃β(E190D)₃γ). The pink and light blue lines represent the simulation results for P_i release and ATP binding, respectively, by wild-type F₁; the light green line represents ATP hydrolysis by the mutant F₁. To see this figure in color, go online.

Discussion

In this study, we systematically and quantitatively evaluated the effect of conformational fluctuation on almost all of the elementary steps of catalysis by F₁. Individual elementary steps of catalysis exhibited different sensitivities to viscous drag; P_i release was significantly accelerated by conformational fluctuations, which is consistent with previous predictions (12,33). The ATP-binding rate was also dependent on viscous drag, its rate changing by a factor of 1.7 with each increment of viscous drag, although the effect is much smaller than in the case of P_i release. ATP hydrolysis was essentially insensitive to the drag viscosity. The Brownian dynamics simulation based on the simple mechanokinetic model, similar to the Sumi-Marcus model, reproduced the experimental results (Fig. 5 b). The rotary potential before and after reactions was shared; therefore, the observed viscous drag dependence is a reflection of angle dependence of reaction rates.

Sumi and Marcus proposed that the viscous drag sensitivity of a reaction becomes evident only when the position of the transition state is far from the reactant minimum along the coordinate for conformational dynamics and when the timescale of conformational dynamics is slower than that of reaction. In this study, we determined the angle at which the reaction of interest occurs for individual runs of the simulation. The average angles for reactions, θ_TS, were +5.0°, +2.4°, and +34° for ATP binding, hydrolysis, and P_i release, respectively. This trend strongly correlates with the sensitivity to viscous drag, consistent with Sumi and Marcus’s proposal. We also investigated the viscous drag sensitivity of a temperature-sensitive reaction (20,34), which also showed high sensitivity to the viscous drag and high value of θ_TS (Watanabe et al., unpublished data).

The large θ_TS for P_i release means that P_i release occurs only when the γ subunit is rotated counterclockwise far from the catalytic angle. This finding is consistent with a recent biochemical study and structural analysis of the crystal state of F₁. Scanlon et al. showed that once the rotor and stator of F₁ were cross-linked, P_i release was blocked, although ATP hydrolysis was not inhibited (33). A recent comprehensive analysis on the crystal structures of F₁ suggests that the positional shift of the γ subunit in the rotary direction (counterclockwise) accompanies the opening of the catalytic α-β interface as well as the release of P_i (35). Taking this finding into account, our results suggest that large fluctuation of the catalytic α-β interface coupled with the rotary fluctuation of the γ subunit triggers P_i release.

As mentioned above, the simple mechanokinetic model provides a theoretical framework for understanding the enhancement of catalysis by rotary fluctuation of F₁. Mukherjee and Warshel recently proposed a similar model based on the in silico analysis of crystal structures (30), where they also showed a 2-D reaction-energy profile associated with both mechanical and chemical reaction coordinates, providing theoretical insights about the mechanochemical coupling of F₁, such as the directionality of the rotary system. To determine the actual 2-D reaction-energy profile, the activation energy has to be experimentally determined. Single-molecule analysis at different temperatures is awaited.

This study showed that the drag friction of the γ subunit inside the α₃β₃-ring lies between 1 × 10⁻⁷ and 3 × 10⁻⁴ pN·nm s. This is not consistent with the previous estimate of Γ_γ at 8 × 10⁻³ pN·nm s (12). One possible reason for the discrepancy is the species of F₁; thermophilic Bacillus PS3 vs. E. coli. This seems reasonable, considering Γ_γ is determined by the strength of the rotor-stator interaction. In fact, the rotary potential of the γ subunit differs between species; the potential slope of TF₁ is smaller than that of EF₁ (25,36), suggesting a stronger interaction in EF₁.

Conclusion

Using experimental and theoretical approaches, we evaluated the effect of conformational fluctuation on enzyme catalysis at the resolution of elementary reaction steps. In terms of time resolution, the experimental approach of single-molecule measurement is suitable for evaluating large-scale conformational fluctuations at the subunit level (microseconds to milliseconds). On the other hand, Brownian dynamics simulation based on the Sumi-Marcus model validates the experimental results and provides a simple framework for understanding the effect of conformational fluctuation on catalysis. Accordingly, the combination of single-molecule study and Brownian dynamics simulation is a powerful tool for understanding the relationship between conformational fluctuation and catalysis, and holds promise for understanding the function of other enzymes.