Dynamic DNA Underpins Chromosome Dynamics

Abstract

A recent article by Meyer and co-workers provides a detailed description of the dynamics of base-step conformational transitions and of the first steps to the basepair opening. These results underpin the essential role that DNA dynamics place in the DNA structural transitions that accompany the active processes of transcription, replication, and recombination in bacterial and eukaryotic chromatin.

DNA is the predominant genetic material in the living world. The nature of the molecule—an immensely long, very thin polymer—implies that within the cell the molecule be compacted into a small volume while maintaining accessibility for the regulation of genetic expression. These functions require that DNA be both flexible and able to change conformation in response to enzymatic manipulation. Importantly the DNA sequence itself encodes this information. Regions associated with DNA melting—for example, the initiation points for transcription and replication—often contain highly localized, less stable DNA sequences. Other regions, notably those at the convergence points of DNA translocases, are characterized by more delocalized, but still less thermally stable, topologically sensitive sequences, which can potentially act as topological sinks by writhing in response to either positive or negative superhelicity (1). Similarly, such sequences are also characteristic of regions that are repressed by proteins stabilizing writhe. In these contexts, the sequence-dependence of DNA thermodynamics constitutes an essential element of the genetic organization of chromosomes both in bacteria and in eukaryotes.

An understanding of the dynamic nature of DNA sequences is therefore an essential aspect of the elucidation of the mechanisms of chromosome dynamics. For example, the elasticity of a double-helical DNA of particular sequence is strongly dependent on the range of conformations available to component base steps (2–4). Similarly, the probability of basepair melting depends on sequence context (5). In the tradition of earlier studies (6), work by Meyer et al. (7) has applied a powerful molecular dynamics methodology to investigate the temperature-dependent behavior of basepairs and base-steps in DNA 18-mers from 0°C to +77°C, encompassing a substantial part of the range occupied within the biological world. The technique deconvolutes the thermal motions of the molecule into components describing basepair and base-step geometry and so can separate the contributions of the initial stages of basepair melting and base-step-dependent bending. Although the range of sequences studied is not fully comprehensive, the results provide profound insights into the behavior of DNA and especially into the thermodynamics of bending and melting. The studies reveal that, for individual basepair stiffness, the parameters of stretch (involving changing the distance between component bases) and opening (changing the planar angle between bases) have the greatest entropies relative to enthalpic contribution. These motions precede the actual separation of bases in a pair on the pathway to the melting transition. For base-step stiffness, the effects are smaller but nonetheless significant. In this case, the geometrical parameters that have the greatest entropic contribution are roll, tilt, and rise. Of these, roll and tilt are important in conferring the directionality of DNA bending.

By quantitating the thermodynamic parameters of DNA, the relative contributions of bending fluctuations and melting transitions as a function of temperature can be related to the biological properties of the molecule. One such property discussed by Meyer et al. (7) is the large-scale DNA bending flexibility, which is defined by the bending persistence length. In the context of a worm-like chain, where bending flexibility is, by definition, isotropic, bending stiffness dependent on the range of accessible base-step conformations decreases, i.e., on an intact double helix, linearly with temperature. However, because transient local melted bubbles or flipped-out bases greatly increase the flexibility of the polymer (8), the temperature-dependent increase in melting probability provides a more dominant decrease in bending stiffness. The authors show that the experimentally determined decrease in persistence length with temperature (9) is best described by a model that takes into account both the probability of local melting transitions and the changes in base-step stiffness.

The relevant data supporting these conclusions were derived from experiments measuring the rate of circularization of a DNA sequence designed to bend, on average, isotropically (9). However, at the resolution of protein-binding sites, certain stiffer DNA sequences may confer a highly preferred DNA bending direction (10–12). The adopted resulting trajectory (configuration) of the DNA double helix is, then, relative to isotropic bending, restricted and the DNA can no longer be considered to behave like a worm-like chain. This anisotropy, by definition, implies the restriction of some degrees of bending freedom and so results in the occupation of a smaller volume of configurational space (the three-dimensional probability function of the ensemble of bending microstates—a measure of the chain wriggle potential) relative to a chain that bends isotropically.

Importantly, anisotropy is associated with a lower bending entropy (13). But as the temperature increases (Fig. 1), the DNA becomes more flexible and the bending more isotropic. In part, this may be a consequence of the increased probability of bubble formation, which increases flexibility at the cost of minimizing the bending effect of preferred base-step conformations. Such changes can directly affect protein-DNA interactions. An excellent example is nucleosome formation, where high-affinity sites for the histone octamer possess conspicuous bending anisotropy (12,14). The closer the trajectory conferred by a DNA sequence corresponds to the path of the DNA on the octamer, the smaller will be the entropic penalty on binding. Anisotropy will be favored if the net enthalpic cost of distorting the DNA structure on binding to the octamer is relatively small. However, as the temperature increases, so do the degrees of bending freedom increase, and anisotropy may no longer dominate the binding—in principle, changing the sequence-dependent binding preferences of the octamer. In vivo, in both yeast and flies, the sequences with the highest nucleosome occupancy are G/C-rich (15–17) and thus, on average, stiffer than the thermodynamically less stable, more A/T-rich sequences found in the regions flanking genes. This implies that, in vivo, the kinetics of nucleosome formation favor DNA sequences possessing bending anisotropy rather than those of the greatest axial flexibility. Similar principles might also apply to transcription factors interacting with extensive binding sites.

Figure 1.

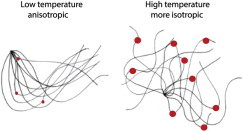
Changes in bendability with temperature. (Left panel) Cartoon of a two-dimensional representation of the potential range of chain configurations occupied by a DNA molecule whose trajectory is dependent on sequence-dependent bending anisotropy. When the temperature is raised, the occurrence of transient bubbles (red dots) locally increases both bending flexibility and isotropy leading to an increase in the potential range of configurations. Adapted from Satchwell et al. (12). To see this figure in color, go online.

Meyer et al. (7) also examine how their results relate to the effects of superhelical stress on DNA structure. They argue that DNA topoisomerases can counteract the melting effects of higher temperatures by preventing adventitious melting using the device of overtwisting a constrained DNA molecule. Indeed, in extremophile bacteria and Archaea, a reverse DNA gyrase increases the DNA linking number (18). By applying a theoretical torque to a constrained DNA chain (19,20), Meyer et al. (7) calculate that such a strategy for stabilizing the double helix would enable the DNA of the extremophile Thermus thermophilus to retain sufficient stability for biological function up to a temperature of 10 or 15°C higher than the maximum value observed in the absence of topological constraints. Indeed, this temperature is much more comparable to the thermal limits of viability of organisms of this type.

The environmental conditions in which extremophiles thrive are ideal for studies of the effects of topological constraint on opening probabilities because of the dominance of the opening motion at high temperatures. However, at lower temperatures the situation is likely more complex. An organism such as the bacterium Escherichia coli can exert fine control of DNA topology over a temperature range of 17–37°C by changing the DNA linking number to maintain a constant superhelical stress (21). This effect, presumably mediated by topoisomerases, compensates for temperature-dependent alteration of double-helical pitch over this temperature range.

The molecular expression of superhelical stress is not limited to twisting and strand separation. Not only can superhelical stress change the rotational angle between successive basepairs—the intrinsic twist—of double-helical DNA but so also can it induce a coiled trajectory, aka writhe, in the double-helical axis. Although both the torsional and axial flexibilities of DNA are sequence-dependent, strand separation may be limited to a few basepairs whereas typically writhe is expressed over a more extensive region (1). In vivo, the superhelical stress applied to a DNA molecule is a dynamic parameter and may vary both with time and within a single chromosomal molecule (22,23). Spatial variations can depend on the local frequency of binding sites for topoisomerases, for example DNA gyrase, and also on the action of processive DNA translocases such as RNA polymerase or replisomes (24). These translocases transiently unwind and wind the DNA, respectively, behind and in front of their movement relative to the DNA. (More strictly, the DNA linking number is decreased behind and increased in front.)

One consequence of these dynamic variations in superhelical density is that a simple prediction of melting probability based on average superhelical density does not capture the subtleties of the probability of DNA sequences melting in vivo. An informative example of an apparent mismatch between melting probabilities and function is the terminus of DNA replication in bacteria. On average, these are the most thermally unstable regions of DNA in bacterial chromosomes, yet they are found where the replicated DNA reanneals (22). One resolution of this apparent paradox is that these sequences will experience positive torque applied by the converging replisomes. This torque would reduce melting probability, but without complete relaxation could concomitantly promote DNA writhing in these same sequences, which, in addition to being relatively thermally unstable, are also more axially flexible than average sequences. The writhed or concatenated DNA would then be a substrate for relaxation by the appropriate topoisomerases.

Even though some complexities remain to be unraveled, the work of Meyer et al. (7) represents an important step toward understanding how DNA dynamics underpins chromatin structure both in vivo and in vitro. Overall in DNA genomes the expectation is that the physicochemical properties of DNA—and hence the DNA sequence itself—be locally finely tuned to optimize the regulatory capacity of the DNA itself. The information so encoded—an analog rather than the digital property that typifies protein-coding sequences (13)—is thus an integral component of the genetic and the structural organization of chromosomes.