The Limitations of an Exclusively Colloidal View of Protein Solution Hydrodynamics and Rheology

Abstract

Proteins are complex macromolecules with dynamic conformations. They are charged like colloids, but unlike colloids, charge is heterogeneously distributed on their surfaces. Here we overturn entrenched doctrine that uncritically treats bovine serum albumin (BSA) as a colloidal hard sphere by elucidating the complex pH and surface hydration-dependence of solution viscosity. We measure the infinite shear viscosity of buffered BSA solutions in a parameter space chosen to tune competing long-range repulsions and short-range attractions (2 mg/mL ≤ [BSA] ≤ 500 mg/mL and 3.0 ≤ pH ≤ 7.4). We account for surface hydration through partial specific volume to define volume fraction and determine that the pH-dependent BSA intrinsic viscosity never equals the classical hard sphere result (2.5). We attempt to fit our data to the colloidal rheology models of Russel, Saville, and Schowalter (RSS) and Krieger-Dougherty (KD), which are each routinely and successfully applied to uniformly charged suspensions and to hard-sphere suspensions, respectively. We discover that the RSS model accurately describes our data at pH 3.0, 4.0, and 5.0, but fails at pH 6.0 and 7.4, due to steeply rising solution viscosity at high concentration. When we implement the KD model with the maximum packing volume fraction as the sole floating parameter while holding the intrinsic viscosity constant, we conclude that the model only succeeds at pH 6.0 and 7.4. These findings lead us to define a minimal framework for models of crowded protein solution viscosity wherein critical protein-specific attributes (namely, conformation, surface hydration, and surface charge distribution) are addressed.

Introduction

Molecularly crowded protein solutions ubiquitously span nature and biotechnology, ranging from macromolecular crowding in cells to therapeutic protein (e.g., monoclonal antibody) solutions (1–6). They represent a frontier of soft condensed matter physics. They are complex systems with diverse intermolecular forces and many-body interactions that cannot be simplified to a single body problem because interactions at high concentrations are coupled to orientational degrees of freedom. Although intracellular proteins typically exist at concentrations up to 400 mg/mL (1,2), therapeutic antibodies are often formulated at high concentrations exceeding 100 mg/mL for parenteral subcutaneous administration. High formulation concentration is driven by the limited volume that can be administered subcutaneously as well as the high-dosing regimens (≈2 mg protein/Kg patient body mass) that are required, given typical potency (5–10). Because proteins have dual macromolecular and colloidal characteristics (1–4), the interplay between viscosity and stability of highly concentrated protein solutions is a concern due to changes in molecular conformation that may drive nonnative aggregation under quiescent conditions and in common unit operations, e.g., purification and filling (5–8). Concentrated protein solutions show an enhanced tendency to aggregate, which results in increased system viscosity (6–10). Understanding the physical underpinnings of the concentration-dependence of protein solution viscosity is of fundamental importance to the bio-pharmaceutical industry, especially for therapeutic protein purification and concentration, and for facile delivery of concentrated protein therapeutic formulations.

We started this exercise with bovine serum albumin (BSA), a single-domain protein. Multidomain proteins such as immunoglobulins (IgGs) have nonnegligible interdomain interactions (11) requiring careful analysis; data on IgGs will be reported in a subsequent publication currently in preparation. Serum albumins are abundant at a concentration of 40 mg/mL in blood plasma and are responsible for a host of biological functions (12) including transporting drugs and hormones and maintaining blood pH at 7.4, where the protein possesses net charge (Z). Although Z = 0 at the BSA iso-electric point, pI (pH = 4.95), BSA still retains surface patches of positive (blue) and negative (red) charge (Fig. 1). While colloidal models are thought to assume uniform point charges, BSA clearly violates this assumption due to surface charge heterogeneity. The result in Fig. 1, which fundamentally motivates this work, was generated in PYMOL molecular visualization software (DeLano Scientific, http://www.delanoscientific.com/) using the BSA PDB crystal structure (PDB:3V03). Although BSA solution viscosity has been widely investigated and reported as a model system, it nevertheless exhibits complex shape and charge distribution. Similar surface charge heterogeneity and more complex molecular conformations are seen in IgGs (13).

Figure 1.

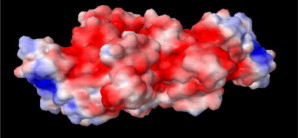
Surface charge distribution on the BSA molecule at its pI (pH 4.95), generated by the software PYMOL using the three-dimensional crystal structure of BSA from the Protein Data Bank (PDB:3V03; www.wwpdb.org). (Red, white, and blue) Negatively charged, positively charged, and neutral regions, respectively.

Published work on protein solution rheology spanned the range from dilute solutions to highly crowded solutions (concentrations >100 mg/mL (8–10,13–15). They invoked either theoretical or empirical models from colloidal dispersion rheology to explain the concentration-dependence of solution viscosity in the dilute or concentrated limit. The invocation of colloidal models to describe protein solution rheology is intuitively appealing, because proteins squarely fall within the colloidal domain on account of their charge and size (16). The seminal work of Tanford and Buzzell (15) focused on the viscosity of BSA solutions up to a concentration of ≈40 mg/mL between pH 4.3 and 10.5. A minimum in the relative viscosity as a function of pH was reported and explained by invoking arguments related to the primary electroviscous effect (3,15). Ross and Minton (17) developed a semiempirical model based on the Mooney equation, which was originally developed for filled elastomers. They demonstrated that corrections to the Mooney equation successfully describe the concentration-dependence of viscosity of Hemoglobin solutions up to concentrations of 400 mg/mL, if one accounts for particle shape and specific volume through the Simha factor (18) and the specific volume of the protein (17,18). However, applying models that describe the concentration dependence of viscosity of hard-sphere dispersions to protein solutions is questionable even if compressibility and shape are accounted for, because the macromolecular surface is heterogeneous and the interaction potential for proteins typically involves both Derjaguin-Landau-Verwey-Overbeek (DLVO) (19) and non-DLVO forces (i.e. hydrophobic interactions and hydration forces) (5,19–21).

Another reason to critically interrogate the applicability of colloidal dispersion rheology models to concentrated protein solutions is that these models typically assume monodispersity. However, in solution, protein monomers can exist in dynamic equilibrium with reversible clusters, and can also form nonequilibrium/irreversible clusters (5,6,22). Essential protein-specific biophysics, such as pH- and concentration-dependent conformation (1,2) and the spatial heterogeneity of charge, are left unaddressed in these models.

An incisive experiment to examine the validity of colloidal models in protein solution rheology would probe the concentration-dependent viscosity over a broad protein concentration range while varying pH to tune the competition between short-range attraction and long-range repulsion. Some published literature studies were limited to either a single pH or a much narrower pH range than the range studied here (15,24–30) (also see Table S2 in the Supporting Material). This limited experimental range, and the use of an inappropriate definition for protein volume fraction that ignores surface hydration, has led to the apparent conclusion that colloidal rheology models apply to protein solutions. We found that the model of Russel et al. (20) fitted the concentration-dependence of viscosity of BSA solutions at pH 3.0, 4.0, and 5.0 but failed at higher pH (6.0 and 7.4). The empirical hard-sphere model of Krieger and Dougherty (21) did not describe the concentration-dependence of BSA viscosity when we held the measured intrinsic viscosity constant in fits while only letting the maximum packing volume fraction float freely. We demonstrate the hitherto unappreciated critical need to account for molecular hydration in the calculation of fundamental protein hydrodynamic quantities such as intrinsic viscosity, which has been selectively accounted for in Iino and Okuda (31), leading to the apparent result that BSA is a hard sphere. We found that the hydration-corrected intrinsic viscosity of BSA did not attain its hard-sphere value (2.5) between pH 3.0 and 7.4.

Materials and Methods

Lyophilized BSA powder ((Cat. No. A7906; Sigma-Aldrich, St. Louis, MO) >99.7% protein, essentially fatty-acid free) of molar mass = 67 KDa, was dissolved at 20 mM ionic strength (I) in buffers comprising sodium citrate/citric acid (pH 3.0), sodium acetate/acetic acid (pH 4.0 and pH 5.0 respectively), histidine hydrochloride (pH 6.0), and phosphate-buffered saline (pH 7.4) (see Acknowledgements). Under these low (20 mM) ionic strength conditions, published literature demonstrated no significant aggregation in BSA solutions. However, under moderate salt conditions, aggregation was pronounced (33). Stock solutions were prepared at 500 mg/mL by dissolving the appropriate mass of lyophilized BSA in 125 mL of 0.02 μm prefiltered buffer (Anotop 10 syringe filter, Lot No. D140746; Whatman, GE Healthcare, Piscataway, NJ) and allowing for complete quiescent dissolution between 2 and 8°C for up to 72 h, and were filtered through 0.22 μm filters of poly(ethersulfone) membranes (Thermo Scientific, Billerica, MA). They were gravimetrically diluted to the final concentration (c_BSA), which was measured using absorbance at λ (wavelength) = 280 nm (A₂₈₀) on a model No. 8453 UV-visible spectrophotometer (Agilent Technologies, Santa Clara, CA). An absorbance coefficient of ε₂₈₀ = 0.667 mL/mg-cm (12) was used for BSA. All solutions were stored between 2 and 8°C until use.

Size exclusion chromatography (SEC) was performed on 10 mg/mL samples: 250 μg mass was injected into a UV-detector-equipped model No. 1100 series HP-SEC (Agilent Technologies) loaded with a model No. G3000WXL column (Tosoh Bioscience, South San Francisco, CA) of 25 nm average pore size. The HP-SEC mobile phase contains 100 mM anhydrous dibasic sodium phosphate (J.T. Baker Cat. No. 5062-05; Mallinckrodt Baker, Phillipsburg, NJ), 100 mM sodium sulfate (J.T. Baker Cat. No. 3898-05; Mallinckrodt Baker), and 50 μM sodium azide at pH 6.8 (titrated with hydrochloric acid). Sodium azide acts as an antimicrobial agent. SEC-multiangle light-scattering was also performed (see Fig. S1 and Table S1 in the Supporting Material) to determine the molar masses of monomer and clusters.

Dynamic light scattering was used to measure the mutual diffusion coefficient D_m of BSA solutions between c_BSA = 2 mg/mL and 12 mg/mL on a DynaPro plate reader (Wyatt Technology, Santa Barbara, CA) with a detector sensitive to λ = 833 nm and at fixed scattering angle (θ) = 130°. A linear fit of D_m versus c_BSA, D_m = D_o(1+k_Dc_BSA) (34,35), was used to obtain the diffusion interaction parameter, k_D (19), which measures intermolecular thermodynamic and hydrodynamic contributions. The aforementioned equation is a generalization of the result derived by Batchelor (35), who determined k_D = 1.45 for hard spheres with no-slip boundary conditions for a purely hydrodynamic problem. Positive and negative k_D values signify net repulsive and attractive intermolecular interactions, respectively. Of course, D_m and η contain contributions from both thermodynamic (DLVO and non-DLVO contributions) and hydrodynamic interactions in crowded protein solutions. Static light-scattering measurements were performed on a Zetasizer Nano (Malvern Instruments, Malvern, Worcestershire, UK) with θ = 90° and λ = 533 nm to construct a Debye-Zimm plot from the average scattering intensities using the analysis (36–38)

$$Kc/R_{\theta }=1/M_w+2B_{22}{c}_{\text{BSA}},$$

where Kc/R_θ and B₂₂ denote the excess Rayleigh ratio and second virial coefficient, respectively.

Infinite shear rate viscosity was measured over a shear rate $\left(\dot{\gamma }\right)$ range of 3 × 10⁴ s⁻¹ ≤ $\dot{\gamma }$ ≤ 1.2 × 10⁵ s⁻¹ using a microfluidic viscometer/rheometer on a chip (m-VROC; Rheosense, San Ramon, CA) equipped with a Type-D chip (see details in Pathak et al. (9)).

Results and Discussion

We first examined dilute solution behavior to characterize the species in solution. SEC chromatograms of BSA solutions buffered between pH 3.0 and 7.4 (Fig. 2) quantify relative populations of monomer and higher-order clusters in solution. Published work (23–28) failed to report this essential biophysical characterization and applied viscosity models while a priori assuming monodispersity and a fixed conformation, which are invariant to molecular shape and concentration. SEC measures the fraction of soluble species (monomers and larger clusters), which is indispensable for understanding and modeling the concentration-dependent solution viscosity because the measured viscosity reflects the sum-total contributions of all these species. Clearly, the BSA solutions studied here were polydisperse, which governed interpretation of the concentration-dependence of viscosity and fitting of colloidal models to protein solution rheology data. The polydispersity reported here is in qualitative accord with published data on BSA (39). Peak integrations provide direct access to the percentage of monomer (≈70%) and higher-order clusters (≈30%). SEC multiangle light-scattering measurements confirm that the elution peak at ∼9.5 min corresponds to BSA monomer (see Table S1). At all other pHs, the percentage of monomer is ≈76% and higher-order clusters are ≈24%. It is worth noting that each injection was infinitely diluted in the pH 6.8 buffered HP-SEC mobile phase inside the column; therefore, the populations of monomer and higher-order species may change with pH and concentration. Our conclusions, however, were unaffected by the limitations of the SEC data, because the models we interrogate assume monodispersity that is invariant with concentration and pH.

Figure 2.

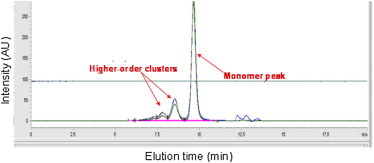
SEC chromatograms for BSA at 10 mg/mL and pH = 3.0 (navy blue), 4.0 (green), 5.0 (blue), and 7.4 (orange). (Inset) Same data, but magnified to emphasize elution times for higher-order clusters.

We next examine how the pH-dependent intermolecular interactions affect the concentration-dependence of viscosity of BSA solutions. To quantify the role of attractive and repulsive interactions, we determined the concentration-dependence of D_m, obtained from the dynamic light-scattering measurements for c_BSA between 2 and 12 mg/mL (Fig. 3 A). The pH-dependence of D_m is reminiscent of the classical behavior of mutual diffusion coefficients in repulsive and attractive colloidal dispersions (20,34). Electrostatic repulsions accelerate concentration fluctuations and dynamics in repulsive systems (27). However, due to stronger protein-protein attractions at the pI, concentration fluctuations slowed down and D_m decreased as concentration increased (20,33,37). Electrostatic repulsion clearly dominates at pH ≠ pI. D_m vs. c_BSA is notably smallest in magnitude at pH 3.0, due to conformational changes of the BSA monomer at low pH because the BSA monomer exists in a partially-unfolded state for concentrations ≤ 10 mg/mL (23). Partially unfolded proteins experience greater hydrodynamic drag relative to the completely folded monomer, due to the increase in effective hydrodynamic diameter (3,18,23,35). These results are qualitatively consistent with published data reported for BSA between pH 4.0 and 7.4 at a fixed ionic strength of 15 mM (27). Slight numerical differences from reported values therein are likely due to differences in ionic strength between our two studies as well as differing BSA lot numbers. The measured k_D and B₂₂ values clearly showed strong electrostatic repulsion at pH distinct from the pI. Surface charge increases the effective diameter of a protein or a colloidal particle, and affects the viscosity of the protein solution or colloidal dispersion through Stokes law considerations.

Figure 3.

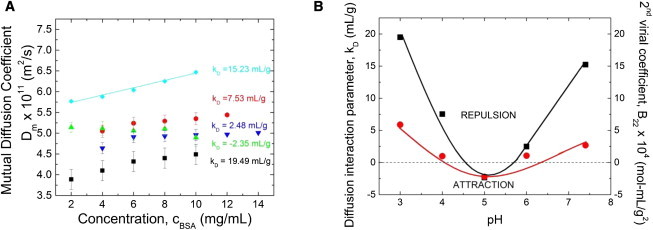
(A) BSA mutual diffusion coefficient (D_m) for BSA concentration, c_BSA, of 2 mg/mL ≤ c_BSA≤ 12 mg/mL at pH = 3.0 (squares), 4.0 (circles), 5.0 (triangles), 6.0 (inverted triangles), and 7.4 (diamonds). (B) BSA second virial coefficient, B₂₂, from static light scattering (circles) and the diffusion interaction parameter, k_D (squares) from dynamic light scattering versus pH. The uncertainties (one standard deviation; determined from the average of five measurements on fresh samples) are smaller than the symbol size.

We now address how colloidal rheology models describe composition-dependence of BSA solution viscosity at varying pH, which controls net charge on protein molecules. Because colloidal rheology models couch the definition of colloid concentration in terms of volume fraction (ϕ), we must first define the protein volume fraction in solution to objectively evaluate these models. The first definition of ϕ that we invoke in Eq. 1 below is the classical polymer solution definition (36). Because it has been applied to protein solutions phenomenologically (insofar as it ignores surface hydration (25)), we refer to it as the “apparent volume fraction”,

$$\phi =\frac{c{N}_A{V}_H}{M_w},$$ (1)

where N_A and V_H denote Avogadro’s constant and BSA monomer hydrodynamic volume, respectively.

Although we considered an alternate definition of ϕ also used by other groups (24,43), we went well beyond their use of this definition to scrutinize the validity of colloidal models in crowded protein solution rheology. This definition rigorously accounts for the protein hydration layer via the pH-dependent protein partial specific volume $\overline{{\nu }_p}$ (2,3), which includes the hydration layer by definition. Specific volume is a critical thermodynamic property (2) that quantifies solute-solvent interactions and protein hydration (40). It depends on intrinsic protein volume (van der Waals volume), changes in volume of surrounding solvent due to protein addition, and protein interactions with all other solution component molecules (2). Whereas appropriate accounting for the hydration-layer effects on protein solution hydrodynamics via $\overline{{\nu }_p}$ (sedimentation, translational and rotational friction/diffusion coefficient, and viscosity) is critical (2,3), it has not been performed in the context of colloidal rheology model fits to protein solution viscosity. Thus, the protein and the solvent are inseparable, because hydration water is critical for protein structure and function (31,40–43). The extent of hydration, of course, depends on the ratio of dry mass to water added. For a fully hydrated protein, $\overline{{\nu }_p}$ saturates to constant value over a certain weight fraction of water added (41,42),

$$\varphi =\frac{m_{BSA}\overline{{\nu }_p}+\delta \overline{{\nu }_w}}{V_w+m_{BSA}\overline{{\nu }_p}+\delta \overline{{\nu }_w}},$$ (2)

where V_w and m_BSA denote solvent (water) volume and BSA mass, respectively, while δ and $\overline{{\nu }_w}$ denote the mass of hydration (bound) water per gram of BSA (0.4 g bound water per g BSA (61,62)) and the partial specific volume of water, respectively. The definition of ϕ in Eq. 2 accounts for the dry (bare) protein and the hydration layer through the $m_{\text{BSA}}\overline{{\nu }_p}$ and $\delta \overline{{\nu }_w}$ terms, respectively. In the context of macromolecular hydrodynamics (viscosity, translational and rotational friction, and the drag aspects of sedimentation), both the bare protein and the hydration layer need to be invoked (61,62). In general, $\overline{{\nu }_p}$ is expected to change with pH for proteins due to protonation or deprotonation below and above the pI. El Kadi et al. (43) have determined $\overline{{\nu }_p}$ for BSA to vary between 0.727 and 0.742 mL g⁻¹ between pH 2.0 and 8.0, respectively. In our calculations, we use pH-dependent $\overline{{\nu }_p}$ reported by El Kadi et al. (43), but hold δ constant (independent of pH).

We now compare these two definitions of ϕ in the context of colloidal rheology models, starting with the model of Russel et al. (20), which accounts for uniform surface charge, inherent to dilute charge-stabilized colloidal dispersions. It provides an electrostatic correction to the quadratic term in the Einstein-Batchelor equation (35), which signifies two-body hydrodynamic interactions:

$$\frac{\eta \left(\phi \right)}{{\eta }_s}=1+2.5\phi +\left(2.5+\frac{3}{40}{\left(\frac{d_{\text{eff}}}{2a}\right)}^5\right){\phi }^2+O\left({\phi }^3\right)=1+2.5\phi +s{\phi }^2+O\left({\phi }^3\right).$$ (3)

In Eq. 3, 2a and d_eff (= 2a for hard spheres) are the actual and effective hard sphere diameters, respectively, η_s is the buffer viscosity. Because d_eff increases due to electrostatic repulsion at pH distinct from pI, the coefficient, s, of the quadratic term in Eq. 3, therefore, relates to hydrodynamic and thermodynamic contributions in colloidal dispersions and protein solutions.

The ϕ dependence of the relative viscosity (η_r =η/η_s) with ϕ defined using Eq. 1, of BSA solutions, is illustrated in Fig. 4 A between pH 3.0 and 7.4 along with nonlinear least-squares regression fits of the model of Russel et al. (20) to the data. By applying the Levenberg-Marquardt algorithm (44,45), with s being the only adjustable parameter, the model of Russel et al. (20) suggests that for proteins bearing zero net charge at the pI, d_eff ≈ 2a. While the model of Russel et al. (20) described the data between pH 3.0 and 5.0, model predictions departed from experimental data at pH > 5.0, likely due to the rather sharp rise in viscosity between 300 mg/mL and 400 mg/mL. BSA undergoes conformational changes at pH 3.0, which invariably contribute to an increase in d_eff and η_r. Therefore, surface charge is not the only contribution to the strong ϕ-dependence of η_r for pH < 5.0. We recovered qualitatively similar results for calculating ϕ rigorously using Eq. 2; see Fig. 4 B. The model of Russel et al. (20) thus lacks sufficient generality to describe the full pH- and concentration-dependence of BSA solution rheology. The subtleties associated with BSA solution biophysical chemistry such as conformational changes that occur at pH 3.0, and the heterogeneous surface charge distribution, are ignored in the model of Russel et al. (20).

Figure 4.

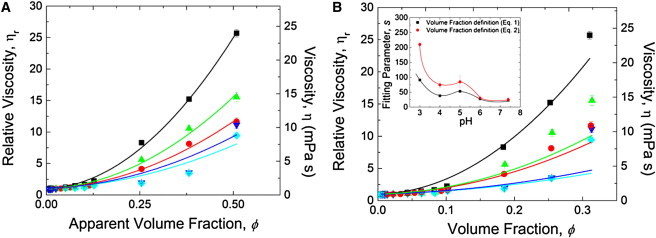
(A) BSA solution relative viscosity η_r versus volume fraction ϕ (defined by Eq. 1) for 2 mg/mL ≤ c_BSA≤ 400 mg/mL at pH = 3.0 (squares), 4.0 (circles), 5.0 (triangles), 6.0 (inverted triangles), and 7.4 (diamonds). Curves denote fits to the model of Russel et al. (20) (Eq. 3). (B) η_r vs. ϕ (defined by Eq. 2). Viscosity data are at shear rate $\dot{\gamma }$ = 10⁴ s⁻¹ (in the infinite shear plateau). The uncertainty in viscosity (standard deviation) was determined from five different measurements with fresh sample loadings. In some cases, the uncertainties are smaller than the symbol sizes. (Inset) Model from Russel et al. (20), (Eq. 3) fitting parameter, s, extracted from panels A and B, with ϕ calculated using Eqs. 1 and 2 (squares and circles, respectively).

Because the O(ϕ²) coefficient, s, in Eq. 3 reflects both hydrodynamic and thermodynamic contributions to η, we examine whether its magnitude extracted from the fits to the data in Fig. 4 A shows similar dependence on pH as those seen for k_D and B₂₂. If these dependences are similar, a correlation between dilute solution physicochemical parameters and s would be implied. Because Connolly et al. (46) recently suggested a similar weak correlation between k_D and η for some monoclonal antibody solutions, we examine BSA data for any similar correlations. Although Russel et al. (20) suggest that the magnitude of s should be minimal when B₂₂/B₂₂,_HS = 1, where B₂₂,_HS denotes the hard sphere B₂₂, its magnitude at the extremes of pH does not correlate well with B₂₂ here (inset, Fig. 4 B). Moreover, between pH 4.0 and 7.4, s attains a maximum at pH = 5.0, contrary to the expected minimum and similar to the observed pH-dependence of η of BSA for concentrations >100 mg/mL (27) between pH 4.0 and 7.4. We therefore infer that the weak correlation between dilute and concentrated solution properties suggested by Connolly et al. (46) is invalid for BSA solutions.

We next evaluated whether the Krieger-Dougherty model (21) can describe the concentration-dependence of viscosity of concentrated BSA solutions. This model has been applied to hard sphere dispersions (20,21) and also to protein solutions with equilibrium clustering (47). It is also applied to systems with arbitrary nonspherical particle shapes and molecular conformations (21),

$${\eta }_r=\frac{\eta }{{\eta }_s}={\left(1-\frac{\phi }{{\phi }_m}\right)}^{-\left[\eta \right]{\phi }_m},$$ (4)

where ϕ_m and [η] denote maximum packing fraction and intrinsic viscosity, respectively. Whereas Eq. 4 has been applied to crowded protein solution rheology (25) by defining ϕ via Eq. 1, its validity must be critically interrogated while accounting for protein hydration (Eq. 2). To minimize the number of freely floating parameters, we determine and fix [η] from dilute solution viscosity data (2 mg/mL ≤ c_BSA ≤ 12 mg/mL) using the method from the literature (48,49). The value of [η] is determined from the slope of a plot of 1-1/η_r vs. ϕ (see Fig. S2 and Fig. S3). Table 1 summarizes pH-dependence of [η]. Clearly [η] is largest at pH 3.0, in agreement with prior studies (29).

Table 1.

Intrinsic viscosity, [η], obtained using polymer definition of volume fraction (Eq. 1) and with hydration correction for volume fraction (Eq. 2)

pH	Experimental intrinsic viscosity, [η] from fit to Eq. 4 using ϕ defined in Eq. 1	Experimental intrinsic viscosity, [η] from fit to Eq. 4, using ϕ defined in Eq. 2
3.0	7.91 ± 0.51	9.06 ± 0.57
4.0	4.19 ± 0.69	4.81 ± 0.79
5.0	5.33 ± 0.61	6.10 ± 0.69
6.0	3.21 ± 0.12	3.72 ± 0.14
7.4	2.86 ± 0.28	3.27 ± 0.33

BSA exists in a partially-unfolded state at pH 3.0 for concentrations nominally ≤10 mg/mL (23). Between pH 4.0 and 8.0, however, we find that [η] varies significantly, in contrast with reports in Tanford and Buzzell (15), where it is implied that dilute BSA solutions exhibit no significant conformational transitions between pH 4.3 and 10.5. This observation suggests that the shape, conformation, and polydispersity of BSA molecules and their aggregates, as embodied in [η], changes between dilute and crowded solutions and with pH. BSA apparently approaches the hard-sphere limit, [η] = 2.5, at pH 6.0 and 7.4, only if one naïvely defines ϕ by Eq. 1. When hydration is invoked (Eq. 2), the hard sphere intrinsic viscosity (2.5) is never established for BSA at the solution conditions studied here. Overemphasis on colloidal properties of proteins at the expense of their macromolecular identity has led to the incorrect conclusion that BSA is a hard sphere. The value of δ (see Eq. 2) chosen here (i.e. 0.4) is at the upper end of the range reported in the literature. We chose this value to demonstrate that [η] never reaches 2.5 (the hard sphere value). When smaller values of δ are chosen instead, the resulting values of [η] become even larger.

We can now interrogate fits of the Krieger-Dougherty model (21) to our data using nonlinear least-squares regression, with ϕ_m kept as the only floating parameter, because [η] is easily experimentally determined. Clearly, as seen in Fig. 5 A, predictions of the Krieger-Dougherty model (21) disagree with data for relatively low ϕ (≈0.1) between pH 3.0 and 6.0. Similar behavior has been reported in the literature for BSA at high concentrations, where clear deviations from hard sphere models were observed (22). The ϕ-values calculated from Eq. 2 are much smaller than those from Eq. 1. The absence of the hydration correction in Eq. 2 and narrow pH-range investigations of BSA solution viscosity have possibly led others to the erroneous conclusion that colloidal viscosity models work well at high BSA concentrations (26–28). The hydration correction, Eq. 2, also strongly affects the curvature of η(ϕ). Finally, when we defined ϕ in Eq. 2 and let ϕ_m and [η] both float freely, as had also been done by Sharma et al. (25), we recover their result that the model of Krieger and Dougherty (21) apparently fits the viscosity of BSA solutions until an upper-concentration limit of 250 mg/mL at pH 7.4 (see Fig. S4). This validation step generated confidence in the robustness of our nonlinear regression algorithm.

Figure 5.

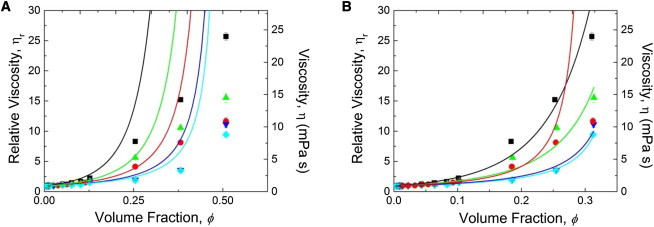
(A) BSA relative viscosity η_R versus volume fraction ϕ (same data and symbol keys as Fig. 4). Curves are fits to the Krieger-Dougherty model (21) (Eq. 4) with ϕ defined by Eq. 1. (B) Same experimental data as in Fig. 5A and Fig. 4; curves are fits to the Krieger-Dougherty model (21) (Eq. 4) with ϕ defined by Eq. 2. Infinite shear plateau viscosity values correspond to a shear rate of $\dot{\gamma }$ = 10⁴ s⁻¹.

The Krieger-Dougherty model (21) can account for particle shape (a determinant of protein solution viscosity/diffusivity/sedimentation coefficient, along with hydration) through [η], which is a dilute solution parameter by definition. However, its major limitation is that it does not appropriately account for the effect of particle compressibility. Variations in compressibility reflect conformational changes (43) that are particularly important in the case of proteins and microgels: particle deformation in microgels and molecular conformation in proteins at high concentrations might significantly affect their rheology (43,50). The ϕ_m of protein solutions and microgels can far exceed the random-close packing limit for hard spheres, which is ≈ ϕ ≈ 0.64 for monodisperse hard spheres and ϕ = 0.71 for prolate ellipsoids (51). Because the Krieger-Dougherty model (21) fits the data too poorly, we cannot assign physical meaning to ϕ_m, even if hydration is accounted for (Fig. 5 B).

Conclusions

In summary, we have demonstrated the breakdown of the colloidal description of buffered BSA solution viscosity across broad pH and concentration ranges. The model of Russel et al. (20), while successful in capturing composition-dependence of viscosity at pH 3.0, 4.0, and 5.0, failed to model the data at pH 6.0 and 7.4. The Krieger-Dougherty model (21) failed at high BSA concentrations exceeding 100 mg/mL for pH 3.0, 4.0, and 5.0, though it succeeded at pH 6.0 and 7.4. Our rigorous analysis and careful conclusions radically differ from all prior studies that proclaimed the success of colloidal dispersion models for understanding protein solution rheology (17,25,28,31). We ascribe their incorrect conclusion to their experimental designs being limited to a single ionic strength or pH, or to narrow ranges of both. The pH-dependent chain conformation and spatially heterogeneous charge distribution (13) influence the concentration dependent solution viscosity, and have been consistently ignored in the literature. We have demonstrated that protein solution hydrodynamics cannot be quantitatively understood without invoking surface hydration. Significantly, we found that BSA never becomes a hydrodynamic hard sphere between pH 3.0 and 7.4 across a concentration range spanning 2 mg/mL to 500 mg/mL.

Because there is extraordinarily complex physics and biophysics underlying protein solution rheology, we now propose a starting point for holistic models of protein solution rheology by unifying concepts rooted in statistical mechanics (60) and protein biophysics (3). The macroscopic viscosity represents the force per unit velocity, embodied in the friction coefficient, ζ, experienced by a protein monomer. A phenomenological expression for the shear rate-dependent viscosity can be written as

$$\eta =\eta \left\{\frac{\zeta }{{\zeta }_e},\frac{{\zeta }_e}{{\zeta }_o},M_w,{\phi }_{\text{monomer}},{\phi }_{\text{cluster}},Z\left(pH\right),I,\left[\eta \right],u\left(r\right),\stackrel{\cdot }{\gamma }\right\}.$$ (5)

The value of η depends on molar weight (M_w) and monomer volume fraction (ϕ_monomer). Friction contains contributions from shape/shape asymmetry (ζ_e/ζ_o) and hydration factor (ζ/ζ_e) (52,53). Here ζ_o denotes the Stokesian friction coefficient of an anhydrous spherical particle with the same mass and partial specific volume as the protein being considered. Clearly, the importance of protein hydration and conformation/shape for understanding solution physical chemistry and transport properties are mainstream ideas in protein biophysics that need to be bridged to solution rheology models. Of course, when clusters coexist with monomers in solution (9,56), cluster volume fraction (ϕ_cluster) is also reflected in viscosity. Clusters can precipitate from solution too (9), significantly complicating any theoretical description of unstable protein solution hydrodynamics, because the system becomes both a solution and a suspension. However, that problem is significantly more complicated than the current case of BSA solutions. Protein conformation (49) is also reflected in solution hydrodynamics and rheology. In dilute protein solutions, [η] contains conformational information (52–55); but in concentrated solutions with nonnegligible intermolecular interactions, the small-angle scattering intensity, I(q), at large wavevectors (q) (23,26,57–59) contains chain conformation information. The intermolecular potential u(r) can be extracted from I(q), the structure factor S(q), and the form factor, P(q). Current models liberally approximate these constitutive inputs to protein solution viscosity.

Appropriate biophysical and statistical mechanical models that account for monomers, clusters, hydration, charge (distribution), and intermolecular forces to solution viscosity are currently being developed by our team for globular proteins and immunoglobulins by leveraging our recent SANS (Small-Angle Neutron Scattering) data over a wide range of pH and concentration. Our future contributions will elucidate the transitions in concentrated BSA solution conformation between pH 3.0 and 7.4.