An Excitable Signal Integrator Couples to an Idling Cytoskeletal Oscillator to Drive Cell Migration

Abstract

It is generally believed that cytoskeletal activities drive random cell migration while signal transduction events initiated by receptors regulate the cytoskeleton to guide cells. However, we find that the cytoskeletal network, involving Scar/Wave, Arp 2/3, and actin binding proteins, is only capable of generating rapid oscillations and undulations of the cell boundary. The signal transduction network, comprising multiple pathways that include Ras GTPases, PI3K, and Rac GTPases, is required to generate the sustained protrusions of migrating cells. The signal transduction network is excitable, displaying wave propagation, refractoriness, and maximal response to suprathreshold stimuli, even in the absence of the cytoskeleton. We suggest that cell motility results from coupling of “pacemaker” signal transduction and “idling motor” cytoskeletal networks, and various guidance cues that modulate the threshold for triggering signal transduction events are integrated to control the mode and direction of migration.

Cells migrate by production of pseudopodia, lamellipodia, or other protrusions ^1–5. It is thought that the morphology and timing of these protrusions derive from regulation of actin polymerization by Rho family GTPases, the SCAR/WAVE complex, and other actin associated proteins ^6–10, whereas signaling events such as activation of Ras GTPases and PI3Ks triggered by external cues only guide cell migration. However, signaling events also occur at the leading edges of spontaneous protrusions in unstimulated cells ^{11, 12} and feedback loops involving Ras, PI3K, Rac, and/or F-actin have been suggested to be involved in cell motility and polarity ^12–14. Recently, flashes, patches, or wave-like propagation of cytoskeletal and signaling activities have been observed at the basal surface of migrating cells or phagocytic cups ^15–25. These events have been modeled as the behavior of reaction-diffusion systems, although direct evidence for excitability is lacking, and are presumed to somehow organize the dynamic behavior of protrusions ^{23, 24, 26–29}. However, it is not clear whether the spontaneous signaling activities are required for motility or how they might coordinate cytoskeletal activities.

Results

To visualize the dynamic behavior of cytoskeletal and signaling events at the basal surface of migrating cells, we used total internal reflection fluorescence (TIRF) microscopy to examine Dictyostelium cells expressing representative biosensors. For cytoskeletal events we used a SCAR/WAVE component HSPC300 (HSPC300) and an actin polymerization sensor, LimEΔcoil (LimE)³⁰. For signaling events we used a Ras activation sensor, Raf1-RBD (RBD)³¹ and a PIP3 sensor, PH-CRAC (PH)³². We previously noted that dynamic HSPC300 activities had a finer structure than those of RBD or PH ²⁴. A more careful analysis revealed closely localized patterns between HSPC300 and LimE and between RBD and PH (correlation coefficients 0.84 ± 0.04 and 0.88 ± 0.04, respectively [mean ± S.D., n=10]) but only partial overlap between RBD and LimE (correlation coefficient 0.68 ± 0.04 [mean ± S.D., n=10]).

To facilitate analysis of the spatiotemporal evolution of these events, we stacked all the frames from a TIRF time-lapse video to create a three-dimensional kymograph, or “t-stack” (Fig. 1a, b and Supplementary Videos S1 and S2; see also Supplementary Fig. S1a for illustration). In this representation, the z-axis is the time axis of the TIRF video. The t-stack can be rotated to view the lateral surface which represents activity near the edge of the basal surface of the cell (Fig. 1b and Supplementary Video S2). T-stacks reveal features of the dynamic activities of biosensors that are not readily apparent by observation of the videos.

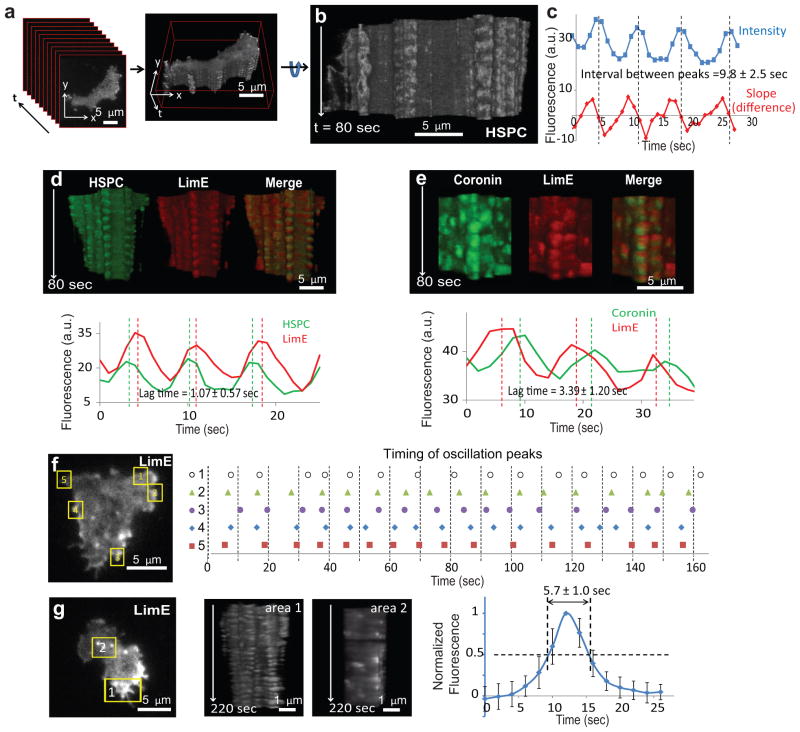
Figure 1. Fast oscillations of the cytoskeletal activities revealed by t-stacking.

(a, b) A t-stack generated by stacking frames of a TIRF video of a cell expressing HSPC300-GFP (Supplementary Video S1). Supplementary Video S2 shows rotation of the t-stack along its t-axis. (c) Intensity plot (blue) and plot of difference between successive points (red) of an oscillatory region. Peaks of the intensity plot were interpolated from the zero points of the difference plot (dotted lines). The mean ± S.D. of intervals between peaks (n=178 cycles from 16 cells) is shown. (d) T-stacks from a cell co-expressing HSPC300-GFP and LimE-RFP (top), and the corresponding intensity plots along an oscillatory region on the periphery (bottom). Dotted lines mark the interpolated peaks. The mean ± S.D. of lags between the peaks of HSPC300 and LimE intensity (n=117 cycles from 16 cells) is shown. Frame rate: 1 spf. (e) T-stacks from a cell co-expressing coronin-GFP and LimE-RFP (top), and the corresponding intensity plots along an oscillatory region on the periphery (bottom). Dotted lines mark the interpolated peaks. The mean ± S.D. of lags between the peaks of coronin and LimE intensity (n=256 cycles from 14 cells) is shown. Frame rate: 2 spf. (f) Timing of peaks of LimE intensity in five oscillatory regions (1–5) within the same cell. (g) T-stacks of a peripheral region (area 1) and an internal region (area 2) from a cell expressing LimE. The temporal profile of the internal flashes and the half-maximum width (mean ± S.D. over n=70 flashes in 14 cells) is shown on the right.

The Fast Oscillatory Cytoskeletal Network

Unexpectedly, t-stacks of cells expressing either HSPC300-GFP or LimE-RFP revealed rapid oscillatory activity at convex, non-expanding points around the perimeter of the basal surface of the cell (Fig. 1b–d). The oscillations had a period of ~10 seconds (Fig. 1c), which was much shorter than the typical interval between pseudopodia. T-stack analyses of published videos of the actin cross-linking protein dynacortin ³³ and Arp3 ³⁰ in wild-type cells as well as WASP in scar- cells ³⁴ also revealed fast oscillations at the basal surface (Supplementary Fig. S1b–d). The oscillations occurred at the front and back of migrating cells, and were often derived from earlier pseudopodia that regressed but remained attached to the substrate (Supplementary Fig. S1b arrowheads). The changes in intensity were not due to displacement of the membrane into the TIRF field since a membrane marker cAR1did not display oscillations (Supplementary Fig. S1e).

A closer examination of a dual-color t-stack showed that the peaks of HSPC300 preceded those of LimE by ~1 second in the oscillatory cycle (Fig. 1d). In contrast, peaks of coronin, a regulator of actin disassembly³⁵, lagged behind those of LimE by ~3 seconds (Fig. 1e).

The cytoskeletal activities display a number of features. First, within the same cell, the oscillations at different spots were not in phase with each other, nor did they have identical frequencies (Fig. 1f). Second, oscillations could also be found in cells lacking the G-protein β-subunit, in cells lacking the PIP3 phosphatase PTEN, in cells treated with the PI3K inhibitor LY294002, and in cells expressing constitutively active RasC (Supplementary Fig. S1f–i). However, inhibition of actin polymerization with latrunculin completely eliminated the oscillatory activity of HSPC300 (Supplementary Fig. S1j). These results suggest that these rapid cytoskeletal oscillations do not require signal transduction events but need actin polymerization, which is preceded by the nucleation promoting activity of the SCAR/WAVE complex. Third, t-stacks from interior regions of cells showed transient non-oscillatory activities of LimE across the cell bottom (Fig. 1g). These bursts of LimE had a width at half maximum of ~5 seconds, reminiscent of the activities at the edges. This may reflect some intrinsic kinetics of actin polymerization ^{36, 37}, although the LimE bursts were not accompanied by HSPC300 recruitment.

The Slow Excitable Signal Transduction Network

In contrast to the cytoskeletal events, the activities of signal transduction markers, which propagated in expanding waves across the basal surface, were broader and lasted longer (Supplementary Fig. 2a and Video S3). The RBD and PH activities were nearly co-localized, and the t-stacks of RBD and PH activities were smooth, indicating the absence of fast oscillations (see below). The progression of a wave is clearly seen by the profiles of temporal changes in intensity at three adjacent points (Supplementary Fig. 2b). The wave velocity in the example shown in Supplementary Figure 2a-c was 12.8 μm/min.

Whereas latrunculin A at 1 μM blocked cytoskeletal oscillations, the propagating waves of RBD and PH persisted at 5 μM (Fig. 2a). In confocal microscopy, the co-localized RBD and PH activities in latrunculin-treated cells appeared as dynamic patches at the rim of the cell (Fig. 2b). We quantitated the patches and found the latrunculin treatment reduced the frequency of new PH patches (Fig. 2c), suggesting that the cytoskeletal activities promote the initiation of signaling events. The signaling activities presented as propagating waves, as irregular zones lasting between 100–150 seconds, or as oscillations with a period of around 200 seconds (Supplementary Fig. S2d–h; Videos S4 to S8).

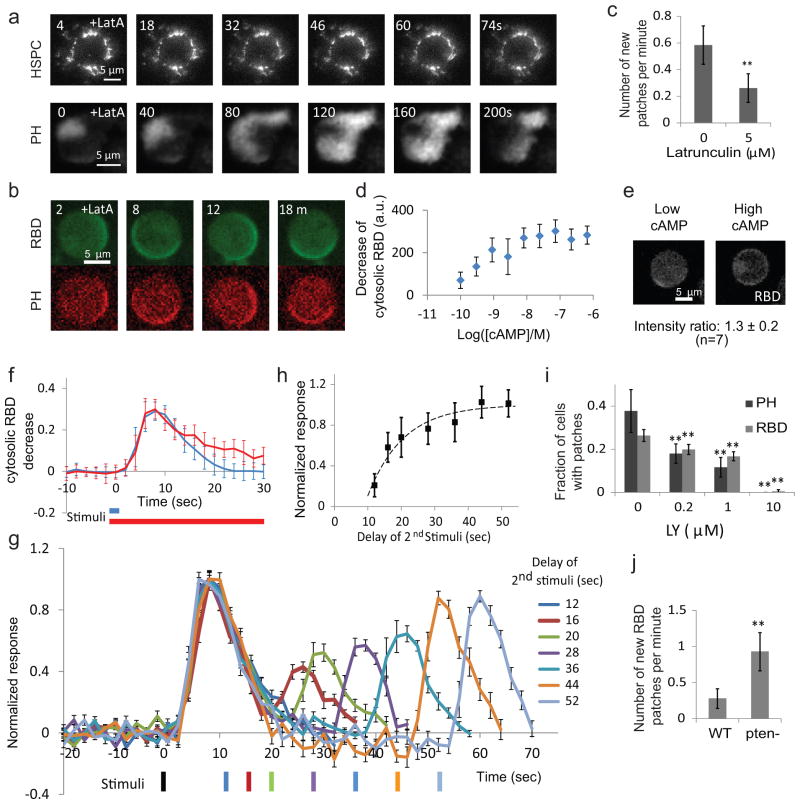
Figure 2. The slow, excitable signaling network.

(a) Frames from time-lapse TIRF videos of HPSC300-GFP in a cell in 1 μM latrunculin (upper), and PH-GFP in a cell in 5 μM latrunculin (lower). (b) Frames from a time-lapse video of a latrunculin-treated cell co-expressing RBD-GFP and PH-RFP observed by confocal microscopy. (c) The effect of latrunculin on the frequency of new PH-GFP patches (mean ± S.D., n=18 and 28, ** p<0.001, t-test). (d) Decrease of cytosolic RBD fluorescence (mean ± S.D. for n=13, 16, 16, 20, 15, 15, 15, 15, 7 cells from lowest to highest cAMP concentrations). (e) Example of partial membrane recruitment of RBD-GFP upon low dose (left) and global recruitment upon high dose cAMP stimuli (right). The intensity ratio of patch to global recruitment is shown (mean ± S.D. for 7 cells). (f) Comparison between responses to 2-second (blue) or 20-second (red) stimuli. Responses (mean ± S.D. for n=27 and 30 cells, respectively) of the cytosolic RBD-GFP decrease were normalized to pre-stimulus level. (g) Responses to two 2-second cAMP stimuli separated by increasing durations. Black bar: first stimulus. The other bars are color-coded to show the delay. All values (mean ± S.E., n=10, 10, 7, 10, 8, 9, 10 for 12, 16, 20, 28, 36, 44, 52 seconds, respectively ) were normalized to the peak of the first response. (h) The peak magnitude (mean ± S.D., n as in (g) for each time point) of the 2^nd response plotted against the interval between stimuli. The absolute refractory period (8.8 ± 1.1 seconds) and recovery half-life (7.38 ± 1.74 seconds) were calculated as described in Methods. (i) Fraction of cells with spontaneous PH and RBD patches in 5 μM latrunculin and increasing concentrations of LY294002 (mean ± S.D., n=10, 10, 12, 15 cells for PH and 40, 40, 50, 80 cells for RBD for 0, 0.2, 1, and 10 μM LY294002, respectively. ** p<0.001, one-way ANOVA). (j) Frequencies of new RBD patches in wild-type and pten- cells in 5 μM latrunculin (n=10 cells each; ** p<0.001, t-test). (b)-(j) were obtained by confocal microscopy.

The propagating waves of RBD and PH suggest the signal transduction network is excitable. To assess this, we stimulated cells expressing RBD-GFP with increasing concentrations of the chemoattractant cAMP and tracked translocation of RBD-GFP to the membrane. The peak decrease of cytosolic RBD-GFP showed a gradual, dose-dependent change saturating at about 10 nM (Fig. 2d). However, with low doses of chemoattractant, recruitment of RBD-GFP to the membrane occurred in discrete patches, while with high doses it occurred around the entire periphery. The intensity of response within a patch was as high as the maximal response (Fig. 2e), indicating that the gradual dose-dependent decrease of the cytosolic signal was due to an increase in the size or number of fully activated patches. As an additional test of excitability, we applied short or long saturating cAMP stimuli to individual cells in the presence of latrunculin. A brief (~2 second) stimulus led to a response that peaked around 8 seconds and returned to baseline by 25 seconds. A longer (20 second) stimulus led to a response with the same rise time, peak and initial decline (Fig. 2f), although there was an additional slowly declining phase corresponding to the start of the secondary responses usually seen during continued stimulation ^{38, 39}. When two brief stimuli were applied to the same cell, the response to the second stimulus depended on the interval (Fig. 2g). A plot of the recovery of sensitivity indicated an absolute refractory period of ~9 seconds and a relative refractory period with an apparent half time of ~7.5 seconds (Fig. 2h). The existence of propagating waves, the elicitation of patches of maximal intensity with low dose stimuli, the ability to induce full responses by short stimuli, and the existence of a refractory period are all hallmarks of excitable systems.

Excitability generally implies that there are positive feedbacks between components. Although PI3K is generally considered to be a direct downstream target of Ras GTPases, inhibition of PI3Ks was shown to reduce the Ras activity in migrating cells, which was attributed to a feedback loop involving, Ras, PI3K, and F-actin ¹². To test whether the feedback between Ras GTPases and PI3Ks can occur independently of the cytoskeleton, we examined the effect of PI3K inhibition on Ras activity in the presence of latrunculin. Treatment with LY294002 reduced the number of RBD patches in a dose-dependent manner, with elimination at 10 μM (Fig. 2i). Moreover, latrunculin-treated pten- cells, which have elevated PIP3, displayed an increased frequency of new RBD patches compared to wild-type cells (Fig. 2j). These observations suggest the existence of a positive feedback loop from PIP3 to Ras activity that is independent of cytoskeletal activities.

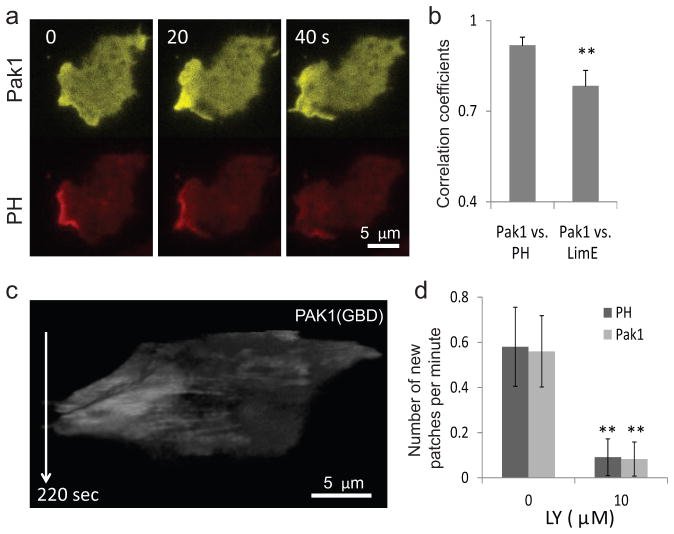
Rac is a key regulator of the cytoskeleton in migrating cells ^{8, 40, 41} and might be expected to behave like the other cytoskeletal markers. To determine the activation pattern of Rac, we expressed PAK1(GBD)-YFP ⁴², which binds specifically to the activated forms of Rac1A and Rac1C. These proteins have been shown to be involved in cell migration⁴³. Surprisingly, the spatiotemporal pattern of PAK1(GBD) recruitment matched that of PH rather than LimE (Fig. 3a, b). Consistently, t-stacks of PAK1(GBD) did not display fast oscillations as did HSPC300 and LimE (Fig. 3c). Treatment with LY294002 decreased the frequency of new PAK1(GBD) patches (Fig. 3d).

Figure 3. Rac activity correlates with the dynamics of the signaling network.

(a) Frames from a time-lapse TIRF video of a cell co-expressing PAK1(GBD)-YFP and PH-RFP. (b) Correlation between pairs of biosensors expressed in the same cells (left: WT cells co-expressing Pak1(GBD)-YFP and PH-RFP; right: WT cells co-expressing PAK1(GBD)-YFP and LimE-RFP; n=10 each, gray bars: mean, error bars: S.D., **p<0.001, t-test). (c) T-stack of a cell expressing the Rac biosensor PAK1(GBD)-YFP showing the absence of fast oscillations. (d) Effect of LY treatment on the frequency of new patches in cells expressing PAK1(GBD)-YFP and PH-RFP observed by confocal microscopy (n=10 cells each; ** p<0.001, t-test).

Coordination of cytoskeletal and signaling networks in protrusions

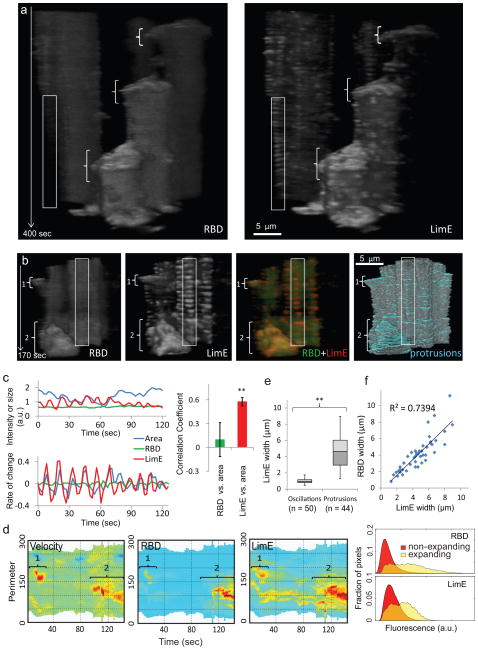
To understand the roles of cytoskeletal and signaling events in cell migration, we examined the cortical recruitment of co-expressed LimE-RFP and RBD-GFP. As shown in Figures 4a, b and Supplementary Figure S3a, RBD and LimE signals were both elevated in large expanding regions (brackets), whereas LimE oscillations unaccompanied by RBD were present in nonexpanding regions (vertical rectangles). Closer examination revealed that the LimE oscillations were correlated with the small amplitude undulations of the cell boundary (Fig. 4c). We quantitated the relationship between RBD and LimE. First, kymographs of RBD and LimE at the cell perimeter confirmed that both were high in expanding regions and low in non-expanding regions (Fig. 4d). Second, the width of LimE activities in protrusions was significantly larger than that in oscillatory regions (Fig. 4e) and was strongly correlated with the width of RBD activities (Fig. 4f). These observations suggest that signal transduction events drive the expansion of cytoskeletal activities in protrusions.

Figure 4. Coupling of signal transduction and cytoskeletal networks in protrusions.

(a) T-stacks from two cells co-expressing RBD-GFP (left) and LimE-RFP (right). In each panel, cell at right extends three large protrusions (brackets) but cell at left does not extend protrusions during the imaging period. Boxed area on non-extending cell at left shows oscillations in LimE-RFP without apparent oscillations in RBD-GFP. (b) T-stacks from another cell co-expressing RBD-GFP and LimE-RFP and used for quantitative analysis. The brackets point to two protrusions (the smaller labeled 1, the larger labeled 2) with high RBD and LimE, which appear yellow in the merged t-stack (third panel). The “protrusion” t-stack shows regions of cell boundary increases in blue (fourth panel). In contrast, fast LimE oscillations accompanying cell boundary undulations appear red (box in third panel). Note that weak oscillations in the RBD t-stacks in (a) and (b) reflect changes in the boundary which delineates cytosolic RBD rather than RBD intensity on the cortex. (c) Intensities of RBD-GFP and LimE-RFP plotted along with the cellular area in a region with LimE oscillation (left upper), as well as the rate of change calculated from difference between values in successive frames (left lower). Rate of change of LimE-RFP shows significantly higher correlation with that of cellular area compared with RBD-GFP (right; n=6 regions from 2 cells, error bars: S.D., ** p<0.001, t-test). (d) Kymographs of velocity, RBD, and LimE around the boundary of the cell in (b) with fast oscillations/undulations filtered out (see Methods). Brackets numbered 1 and 2 correspond to the protrusions in (b). The histogram on right shows the right-shifted intensity distribution of pixels in expanding regions relative to that of non-expanding regions. Similar analyses carried out in 6 cells yielded a mean ± S.D. right shift of 1.44 ± 0.16 (p=0.00075) for RBD and 1.98 ± 0.41 (p=0.0015, t-test) for LimE. (e) Box plot comparison of widths of LimE fluorescence in oscillatory regions and expanding protrusions. The mean ± S.D. for oscillatory and expanding regions were 0.98 ± 0.30 μm (n=50) and 4.69 ± 1.92 μm (n=44) (p<0.001, t-test). For definition of widths see Methods. (f) Correlation between LimE and RBD widths in expanding pseudopods.

Although LimE and RBD activities were both elevated in the expanding regions, their localizations were not identical, with LimE restricted to a thin region near the edge and RBD distributed over a substantial area of the protrusion (Supplementary Fig. S3b, Video S9). Moreover, LimE recruitment occurred in bursts, while RBD displayed a smoother change over the entire event (Supplementary Fig. S3c). Similarly to LimE, HSPC300 recruitment also occurred as a series of bursts within large protrusions (Supplementary Fig. 3d, e, Video S10). A line kymograph across an expanding pseudopodium revealed that the advancement was broken up into steps, each associated with an increase in HSPC300 (Supplementary Fig. 3f). Thus, when accompanied by signaling events, cytoskeletal activities drive expansions of cell boundary.

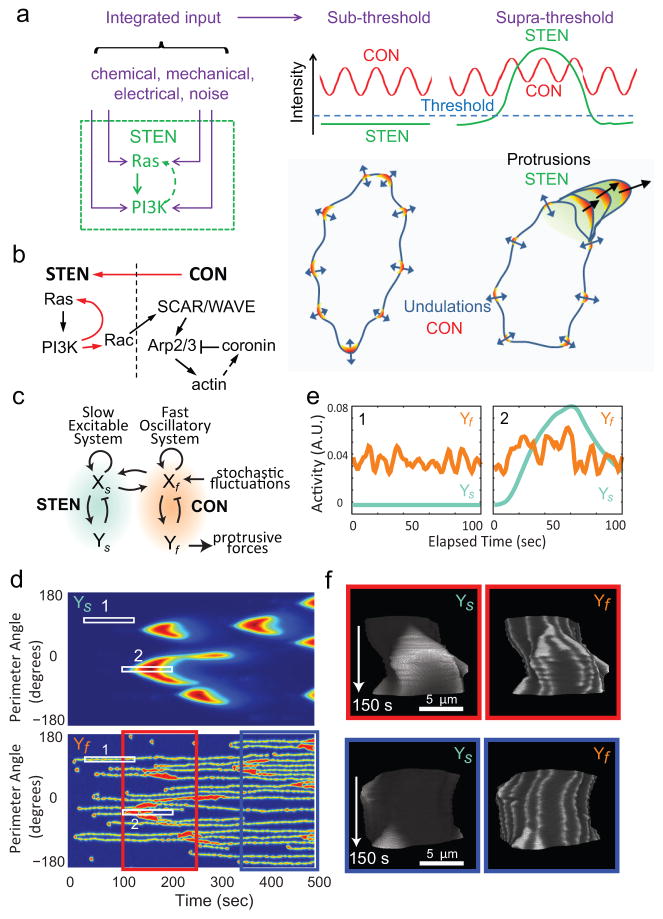
A STEN-CON Coupling Model of Cell Migration

Taken together, our findings suggest that the signaling and cytoskeletal events belong to two different networks with distinct characteristics, which we designated as the Signal Transduction Excitable Network (STEN) and the Cytoskeletal Oscillatory Network (CON), and that cell migration depends on STEN-CON coupling. In this coupling model for cell migration, shown schematically in Figure 5a, the CON provides the “idling” motor force, which by itself only drives small amplitude undulations. In large protrusions, the CON is engaged by the activity of the STEN, which acts as the “pacemaker” for cell migration. As a wave of signal transduction activity propagates, it prevents the retraction of expanded areas during the down phase of the cytoskeletal oscillation or completely shifts existing or newly initiated cytoskeletal activities beyond the oscillatory mode to a continuously active state. In either case, the coupling of STEN and CON leads to a widening protrusion. The STEN will fire when the threshold is crossed, whether due to internal noise or feedback from the CON. The STEN can also be modulated by a variety of external stimuli and perturbations (see Discussion).

Figure 5. The STEN-CON coupling model and computer simulation.

(a) In the STEN-CON coupling model, inputs from various sources enter STEN at different points. When the integrated input reaches a threshold level, STEN becomes fully activated and by coupling to CON causes large protrusions. Without STEN activation, the cytoskeletal oscillations only cause small amplitude undulations of cell boundary. (Note that the stochastic LimE flashes, similar to those reported by Uchida and Yumura ³⁷, were not accompanied by HSPC300 recruitment and were not considered part of CON in our definition despite a similar lifetime of activities as discussed in the main text.). (b) Schematic of the links between components of the STEN and CON. Red arrows highlight the links demonstrated in this study. (c) The behavior of STEN and CON were modeled using reaction-diffusion equations describing coupled slow (X_s, Y_s) and fast (X_f, Y_f) activator-inhibitor systems solved in one dimension around a circle (see Supplementary Methods for details). (d) Kymograph describing the activities of the slow (Y_s) and fast (Y_f) systems around the perimeter of the circle using jet colormap. (e) Intensity plots of the slow and fast systems corresponding to Boxes 1 and 2 in (d). (f) The activities of the slow and fast systems were used to control the boundary of a hypothetical cell (Supplementary Video S11). T-stacks of the activities of Y_s and Y_f on the boundary of the hypothetical cell with gray colormap corresponding to the period from 100s to 250s (red box) and 350s to 500s (blue box) in (d) are shown.

Figure 5b summarizes our current working model of the links between components of the STEN and the CON. The STEN is represented by Ras GTPases and PI3Ks and feedbacks between them. Rac GTPases are considered part of the STEN because the spatiotemporal patterns of activity of our biosensor match those of the STEN rather than the CON. The CON consists of SCAR/WAVE, Arp2/3, F-actin (represented by LimE and dynacortin), and coronin, which all show rapid oscillations. The temporal relationship and the fact that it is involved in actin depolymerization suggest that coronin may be part of a negative feedback loop in the CON. The link from the STEN to the CON is indicated by an arrow connecting Rac to SCAR/WAVE based on literature ^{44, 45} (see Discussion). The link from the CON to the STEN is based on our observation and a recent report ⁴⁶ that latrunculin reduces the probability of the STEN activation.

To test the feasibility of using these coupled networks to describe cell migration, we carried out computer simulations based on the scheme shown in Figure 5c (see Supplementary Methods for details). The scheme consists of slow and fast systems of the activator-inhibitor class ^{28, 47}. The slow system was set as an excitable network while the fast system was set as a stochastic, bi-stable oscillator (Supplementary Fig. S4). Coupling between the two systems is bidirectional such that perturbations in either system influence the activity of the other. The slow and fast systems in the scheme correspond to the STEN and the CON, respectively. In simulations we recapitulated the oscillations of the CON in the absence of activity of the STEN (region 1 in Fig. 5d, e), and the broadening of the CON activities accompanied by the activation of the STEN while preserving the characteristic time constants (region 2 in Fig. 5d, e). We further used the activity of the coupled systems to drive the movement of the boundary of a cell and simulated realistic behavior (Supplementary Video S11). Using the boundary to represent the edge of the basal cellular surface we produced t-stacks resembling those derived from TIRF videos of real cells (Fig. 5f).

Predictions of the STEN-CON Coupling Model

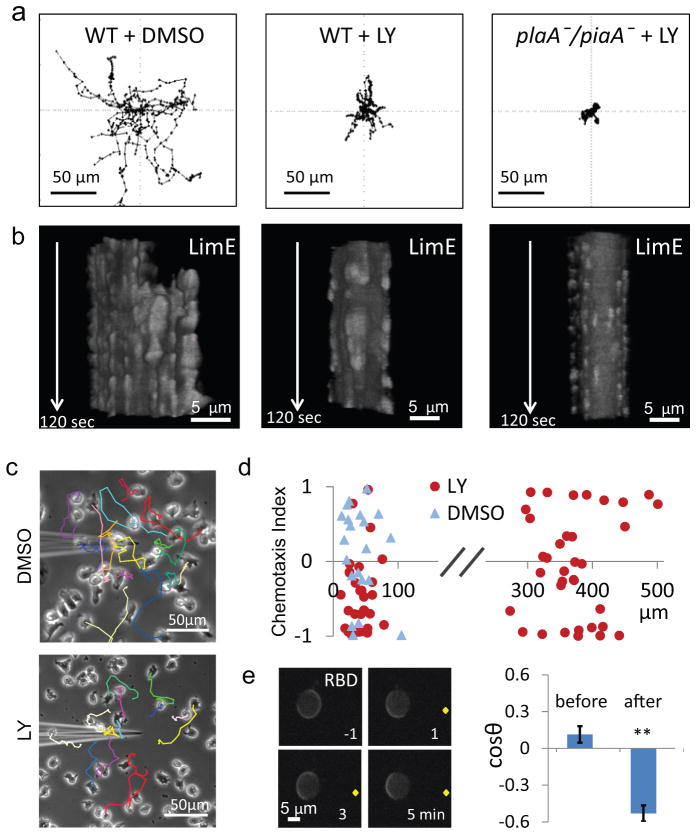
According to the STEN-CON coupling model, blocking activity of the STEN should prevent cells from generating large protrusions and moving substantially but it should not interfere with the CON-driven surface undulations. To test this, we treated wild-type cells with the PI3K inhibitor LY294002. These cells showed diminished spontaneous migration (Fig. 6a). However, the defect faded during prolonged treatment (data not shown), possibly due to compensation in the network ^{38, 48}. For this reason we simultaneously blocked the PLA2, TORC2, and PI3K pathways by treating plaA-/piaA- cells with LY294002. These cells showed minimal migration (Fig. 6a), with net speed, motility speed, and persistence only 5, 24, and 21%, respectively, of those of wild-type cells. Washout of LY294002 restored the motility to that of plaA-/piaA- cells (Supplementary Fig. S5). The frequency of protrusions was 1.35 ± 0.48 (n=17), 0.36 ± 0.23 (n=11), and 0.02 ±0.04 (n=13) per minute for wild-type cells, LY294002-treated wild-type cells, and LY294002-treated plaA-/piaA- cells, respectively. Importantly, while the non-motile cells lacked large patches of LimE activity and protrusions, they still had the fast oscillations and peripheral undulations (Fig. 6b). These results suggest that STEN activity is required to generate pseudopodia for cell motility but is not essential for the CON-induced surface undulations.

Figure 6. Predictions of STEN-CON coupling for cell migration.

(a) Centroid tracks of wild-type cells treated with DMSO (left) or LY294002 (middle), as well as plaA-/piaA- cells treated with LY294002 (right). Duration of tracks: 60 minutes. (b) T-stacks of LimE expressed in cells corresponding to those in (a). (c) The centroid tracks of cells in the vicinity of the micropipette filled with 0.4% DMSO (top) or 0.4% DMSO plus 200 μM LY294002 (bottom) are overlaid on the final image of a 20-min video. (d) The chemotaxis index (C. I.) of cells in a gradient of LY294002 (red circles) or DMSO (blue triangles) versus the distance from the tip of the micropipette. The C. I.s for cells within 100 μm and between 300 to 400 μm from the tip of the LY294002-filled micropipette were −0.48 ± 0.09 (mean ± S.E., n = 32 cells) and −0.07 ± 0.12 (mean ± S.E. n= 30 cells), respectively. The C. I. for cells within 100 μm of the DMSO-filled micropipette was 0.10 ±0.14 (mean ± S.E. n= 21 cells). (e) RBD responses to a gradient generated by a micropipette (tip indicated by yellow dot) filled with 200 μM LY294002 (left). Cosine angles of the direction of patches before and after placement of micropipette is shown on right (mean ± S.E.; n=138 and 99 frames from 5 cells, ** p<0.001, t-test).

A further prediction of the STEN-CON coupling model is that preferential inhibition of STEN activity on one side of the cell should cause the cell to migrate in the opposite direction. To test this idea, we used a micropipette filled with LY294002 to generate a gradient of PI3K inhibition. Upon introduction of the micropipette, cells closest to the tip rounded up and then migrated away from the tip (Fig. 6c). Cells that were initially heading toward the micropipette were deflected away as they approached. The range of repulsion was limited to ~100 μm from the tip of the micropipette; cells farther from the micropipette were unaffected (Fig. 6d). Cells were not repelled by a micropipette filled with a control concentration of DMSO. To demonstrate that the chemorepulsion was due to differential effects on STEN activity we observed spontaneous RBD activity in cells immobilized with latrunculin. Application of the gradient of LY294002 caused initially randomly distributed RBD patches to localize away from the tip of the micropipette (Fig. 6e).

Discussion

The STEN-CON coupling model provides a framework for understanding cell migration. The “idling” activity of the CON provides the force, but it is the “pacemaker” activity of the STEN that determines the timing and size of protrusions in migrating cells. This mechanism has important implications. First, it suggests that activation of the STEN by stochastic noise underlies random cell motility and a cue that affects the threshold for excitation differently on opposite sides of a cell would be expected to guide cell migration. For example, inhibitors of PI3K can act as chemorepellents (Fig. 6c–e). Since a slight increase in threshold could greatly reduce noise-triggered excitation on one side of the cell, the mechanism could account for the ultrasensitivity of chemotaxing cells. Second, there can be multiple entry points into the STEN. For example, perturbations of the level of PIP3 (Fig. 2i, j) and the activity of Ras ^{49, 50} or Rac ^{51, 52} modulate the frequency of STEN activation. Therefore, external cues that might enter the network through different components can have the same effects on overall activity. Third, we speculate that perturbations and inputs from various guidance cues such as chemical gradients, shear flow⁵³, and electric fields⁵⁴ are integrated in the STEN, where the decision to make a protrusion is based on whether a threshold for triggering the network is reached. We have observed that the effects of simultaneously altering PIP3 levels and cytoskeletal activities are additive (Figs 2c, i, j). In the future, additional experiments using multiple cues and perturbations can be designed to further test the role of STEN as an integrator.

The STEN-CON coupling model may explain an array of observations in the literature. First, in mesenchymal cells, small pilot protrusions are reinforced by subsequent PIP3 accumulation⁵⁵, suggesting that the coupled networks we describe may also underlie the migration of fibroblasts and other cells. Second, cells led to migrate by synthetic activation of Rac produce PIP3 at the leading edges, but Rac activation in the absence of PIP3 causes only ruffling^{13, 52}, consistent with our conclusion that the STEN is required for large protrusions and migration. Third, a recent study showing damped oscillations of total actin following a short pulse of chemoattractant ⁵⁶ might be explained by transient synchronization of the CON at different points around periphery of the basal cell surface.

Our work raises several questions to be addressed in future studies. First, what is the negative feedback that causes the refractory period and is required for the excitability of the STEN? Although the molecular basis is not known, cells lacking myosin appear to have extended activation of Ras⁵⁷, and a negative feedback involving RasGEF, TORC2 and PKBs has been described⁵⁸. The role of these components can be tested by measuring the effects of their levels on parameters of excitability such as the threshold and refractory period. Second, how are the two networks coupled to each other? We speculated that Rac GTPases are involved in coupling because activation of Rac 1A/1C displayed the kinetics of the STEN and, as might be expected from observations that Rac GTPases directly link to the SCAR/WAVE complex^{44, 45}, constitutively active Rac 1A causes excessive cytoskeletal activity in these cells⁴³. The mechanism of the reverse coupling, from CON to STEN, remains to be determined. Third, is coordination of CON activity the sole reason that STEN activity is required for motility? In addition to actin polymerization, successful cell migration requires attachment of the protrusions to the substrate and myosin-based contractile events. STEN activity may also control these aspects of migration.

METHODS

Cells

Wild type Dictyostelium discoideum cells are of the AX2 strain obtained from the Robert Kay lab. The gβ- and pten- cells were described previously ^{59, 60}. The parent strains of gβ- and pten- cells were AX3 and AX2, respectively. plaA-/piaA- cells were created by deleting piaA in plaA- cells ⁶¹ using homologous recombination. Cells were used within 3 months of thawing from frozen stocks of the original knockouts. Cells were transformed with plasmids encoding RBD-GFP, PH-RFP, HSPC300-GFP, LimE-RFP, Coronin-GFP, or PAK1(GBD)-YFP by electroporation and maintained in HL-5 medium containing G418 (20 μg/ml) or hygromycin (50 μg/ml) at 22°C. Both growth-stage and developed cells were used for microscopy experiments. For most TIRF microscopy, developed cells were used to reduce photosensitivity, which allowed for prolonged and frequent imaging, although cytoskeletal oscillations and waves of the cytoskeletal and signaling markers were also observed in growth stage cells. Development was also required for cells to respond to cAMP in the excitability experiments (Fig. 2d–h). Cells were developed for 5 hours by pulsing with cAMP every 6 minutes in development buffer (5 mM Na2HPO4, 5 mM KH2PO4, 2 mM MgSO4, and 0.2 mM CaCl2). For all other experiments, growth-stage cells were used.

Microscopy

Total Internal Reflection Fluorescence (TIRF) microscopy was carried out with either an Olympus IX71 inverted microscope illuminated by a Kr/Ar laser source or a Nikon Eclipse TiE microscope illuminated by an Ar laser (GFP) and diode laser (RFP). Images were acquired by a Photometrics Cascade 512B intensified CCD camera controlled by MetaMorph (UCI) or a Photometrics Evolve EMCCD camera controlled by Nikon NIS-Elements. A Dual-View system (Optical Insights, LLC) was used for simultaneous imaging of GFP and RFP fluorescence in doubly labeled cells. For confocal microscopy to visualize signaling patches in latrunculin- or LY294002-treated cells, a Leica DMI6000 inverted microscope equipped with Yokogawa CSU10 spinning Nipkow disk with microlenses and illuminated by a Kr/Ar laser was used. Growth-stage cells were transferred to developmental buffer before imaging. Latrunculin A and LY294002 were diluted to the final concentration from a stock solution in DMSO (concentration: 1 mM for latrunculin A and 50 mM for LY294002). Control cells were always treated with an equivalent concentration of DMSO.

T-stacks

The ImageJ (NIH) software was used for image processing and analysis. For t-stacks, TIRF time-lapse videos were opened and converted to grayscale in ImageJ. The ImageJ 3D Viewer plugin was then used to stack the frames from the video. The resampling factor is set to 1 to avoid blurring of activities between frames. To visualize interior activities in Supplementary Fig. S2d–h, a basal level of cellular fluorescence was subtracted from each video before the t-stacks were generated.

Excitability of Ras activation

RBD-GFP was expressed in aca- cells, which do not produce cAMP on their own. Cells were developed for 5 hours by pulsing with cAMP every 6 minutes in development buffer (5 mM Na2HPO4, 5 mM KH2PO4, 2 mM MgSO4, and 0.2 mM CaCl2) and transferred to one-well chamber.

For Figure 2d, cells in 50 μL buffer were allowed to settle. Stimulations were carried out by mixing an equal volume of buffer containing cAMP to reach the final concentrations ranging from 10⁻¹⁰ M to 10⁻⁶ M. The response was calculated from the decrease in the mean cytoplasmic fluorescence from 13–20 cells for each stimulus. Cells were washed 3–4 times with buffer and allowed to recover for 5 minutes before the next stimulus was applied.

For Figure 2e, cells were stimulated by lowering a micropipette containing 10 μM of cAMP to the viewing field using a FemtoJet Microinjector controlled by a micromanipulator (Eppendorf). Compensation pressure of injection was set at increasingly lower levels in order to elicit partial responses. Patches both facing toward and away from the micropipette were observed. The mean intensity of the patches on the membrane under low pressure was measured and divided by the mean intensity of fluorescence around the same cell under high pressure stimulation to obtain the intensity ratio.

For Figures 2f–h, cells were incubated in 5 μM latrunculin A for 20 min. Stimulation was carried out by lowering a micropipette containing 20 μM of cAMP to the viewing field using a FemtoJet Microinjector controlled by a micromanipulator (Eppendorf). For short stimulation, the micropipette was brought to the viewing field for 1 second before lifting, and the total duration of the stimuli is estimated to be 2 seconds based on the temporal profile of fluorescence from a micropipette filled with Alexa Fluor 594 (not shown). The response was calculated from the decrease in the mean cytoplasmic fluorescence from 7–10 cells for each stimulus. For Figure 2g, the responses were normalized to the peak of the first response. For Figure 2h, the magnitude of second responses was fitted to an exponential curve of the form a-a*0.5^((x-c)/t_1/2) by nonlinear least-square method using the program Gnuplot (http://www.gnuplot.info/), which gave the following values: a = 0.246 ± 0.012, c = 8.8 ± 1.1, t_1/2 = 7.38 ± 1.74 (final parameter ± asymptotic S.E.). In the normalized recovery plot (Figure 2g), second responses (mean ± S.D.) for each time point were divided by a = 0.246 and then plotted along with the curve 1-0.5^((x-8.8)/7.38).

Analysis of signaling and cytoskeletal activities

For measurement of widths of LimE and RBD activities (Fig. 4e, f), the intensity along the cellular boundary was measured. Positions of half maximal intensity were used to define the boundary of the activities. For expanding regions, the maximal widths were reported.

Patches of activity under confocal microscopy (Fig. 2i) were defined as membrane regions whose intensity were 2 standard deviations above the mean cytosolic intensity and were at least 2 μm in width.

Cell boundary and protrusions

To generate the “protrusion” t-stack (fourth panel in Fig. 4b), a cell boundary video was first generated from the RBD-GFP TIRF video using the “Find Edge” plugin in ImageJ. A frame-shifted cell boundary video was then subtracted from the original video to obtain the protrusions, which were colored in blue and superimposed on the cell boundary video (in gray). The “protrusion” video was then used to produce the t-stack.

Undulations

To analyze the fluorescence intensity in undulating regions (Fig. 4c), rectangular areas containing oscillatory LimE recruitment were selected from the RBD-GFP and LimE-RFP TIRF videos. The boundary of the cell was defined by the presence of cytoplasmic RBD-GFP. The average intensities of RBD-GFP and LimE-RFP were calculated by the integrated signal divided by the cellular area within the rectangle. The rates of change for RBD, LimE, and cellular area (used for correlation coefficient calculations) were defined as the difference between successive frames.

Kymographs

Velocity kymographs in Figure 4d were obtained by measuring the distance from each pixel in the boundary (defined by the cytoplasmic RBD fluorescence) of the segmented cell in the present frame to the boundary of the segmented cell in the past frame, using the Matlab command bwdist.m. To filter out fast undulations, the comparison was made between segmented shapes using moving averages of 3 (present) and 12 (past) frames. Because the perimeter of the cell changed in length over time, successive lines on the kymograph were aligned by minimizing the sum of the Euclidean distances between the coordinates in two successive lines. The RBD and LimE kymographs were obtained by averaging the fluorescence in a small area (approximately 4 pixels wide and 8 pixels into the cell) centered at each boundary pixel and using the same moving average scheme. The distributions of fluorescence intensities (histograms) were based on all pixels that are a distance less than 5 pixels from the edges. Expanding regions were those with positive velocity, with minimum size of 25 pixels used to filter noise. The non-expanding regions were those along the edge that were not expanding. The correlation between velocity and fluorescence and the difference in fluorescence intensity distributions were robust to changes in the number of frames averaged as well as the sizes of the areas used to filter the data.

Cell Migration Assay

Wild type AX2 or plaA-/piaA- cells were developed for 5 hours with cAMP pulsing every 6 min. Cells were then transferred to 8 well chambers (Lab Tek #155409) at a density of 100 cells/mm², and treated with 50 μm of LY294002 (Cell Signaling #9901) in 0.1% DMSO or 0.1% DMSO for 1 hour. Migration videos were recorded at 1 min intervals for 1 hour.

Chemorepellent experiments

For LY294002 repellent experiments (Fig. 6c-e), a micropipette filled with 200 μM LY294002 in 0.4% DMSO or 0.4% DMSO alone was introduced into a field of growth-stage Dictyostelium cells at 0 min. Migration videos were recorded at 1 min intervals for 20 min. The chemotaxis index is defined as the cosine of angle between the direction of movement and the direction from the start point to the micropipette.

Statistical analysis and repeatability of experiments

Statistical significance and P values were determined using the two-tailed Student’s t-test. One-way ANOVA was used to compare the four groups in Fig. 2i. Mean values ± either S.D. or S.E.M. were reported as indicated in figure legends except for Fig. 4e, in which a box plot was used to show the minimums, maximums, and quartiles of the distribution.

Two independent experiments were performed for Fig. 1d, 2d, 2e; 2g, 2h, 2i, 2j, 3b, 3d, 4c and 6e; three independent experiments for Fig. 1e, 1g, 2c, 2f, 4e, and 4f; and six independent experiments for Fig. 1c. Statistics were derived by aggregating the n numbers noted in each figure legend across independent experiments.

Representative images associated with Fig. 1d, e, g, 2e, 6e are shown along with statistics. Representative images Fig. 1a, b are associated with Fig. 1c; Fig 3a, c associated with Fig. 3b; and Fig. 4a, b are associated with Fig. 4c.

Representative images are also used for Fig. 1f, 2a, b, 6b, which have been routinely observed in the lab (in more than 3 independent experiments). Fig. 6a and c shows representative results of 3 independent experiments.

Computer simulation of coupled systems

Here we describe the mathematical model of the coupled networks. The model consists of two coupled reaction-diffusion systems: 1) a slow excitable system, reflecting the behavior of the signal transduction excitable network (STEN), similar to the system introduced previously ^{24, 47}; and 2) a fast oscillatory system, reflecting the behavior of the cytoskeletal oscillatory network (CON).

Slow excitable system

Previously we suggested that the signaling network can be described by an excitable system whose activity is biased by the external receptor signal ²⁴. This was illustrated by an activator-inhibitor system that is qualitatively similar to the FitzHugh-Nagumo model for action potentials, which is itself a simplification of the Hodgkin-Huxley model of action potentials ⁶².

The system is described by two species (Supplementary Fig. S4a). Component X_S acts as the activator: it is autocatalytic (it has strong positive feedback), and also activates the downstream component – we refer to this as the feedforward loop. The Y_S component provides negative feedback to X_S. The evolution of the activities of these two species is described by a reaction-diffusion system, consisting of the following partial differential equations:

$$\frac{\partial X_S}{\partial t}={\alpha }_S\frac{X_S^2}{k_S^2+X_S^2}-{\beta }_S{X}_S-{\gamma }_S{Y}_S+U_S+D_{X_S}{\nabla }^2{X}_S$$ (1)

$$\frac{\partial Y_S}{\partial t}={\delta }_S{X}_S-{\epsilon }_S{Y}_S+D_{Y_S}{\nabla }^2{Y}_S$$ (2)

Both components in this system can diffuse spatially, with diffusion coefficients D_XS and D_YS, respectively. The coefficients α_S, β_S, γ_S, δ_S, ε_S, and K_S are constants. The signal U_S is the input to the slow system, which consists of two components: a basal level of activation (B_S) and the contribution from fast system (f (X_f), described below):

$$U_S=B_S+f(X_f).$$

Note that in contrast to the biased-excitable network described previously ²⁴, here we do not incorporate the contribution of receptor signaling. Were this to be included, it would be as an additional term in U_S. We also do not incorporate a stochastic component directly into the slow system, but instead achieve this through the faster system. However, such a stochastic component could explain the signaling patches observed in latrunculin-treated cells (Fig. 2a, b).

In the absence of a triggering from the fast system, the slow system has a single steady state which is stable (Supplementary Fig. S4a, b). Small, sub-threshold disturbances to this steady-state do not trigger the excitable behavior of the system. However, if the perturbation is above a threshold, a large excursion in the phase-plane takes place before the system settles back to the equilibrium.

Fast oscillatory system

To describe the behavior of the CON, we use a stochastic, bi-stable oscillator involving an activator (X_f) and inhibitor (Y_f). The form of the equations is identical:

$$\frac{\partial X_f}{\partial t}={\alpha }_f\frac{X_f^2}{k_f^2+X_f^2}-{\beta }_f{X}_f-{\gamma }_f{Y}_f+U_f+D_{X_f}{\nabla }^2{X}_f$$ (3)

$$\frac{\partial Y_f}{\partial t}={\delta }_f{X}_f-{\epsilon }_f{Y}_f+D_{Y_f}{\nabla }^2{Y}_f$$ (4)

The input to this system (U_f) consists of three parts:

$$U_f=B_f+N_f+g(X_S).$$

As above, B_f represents the basal level of activation and g (X_S) the contribution of the slow system to the fast system (described in detail below). This system also includes a component that incorporates stochastic fluctuations (N_f). These fluctuations are modeled as a zero mean, unit variance white noise process.

Systems involving cubic nullclines such as those described by Equations 3 and 4 can be oscillatory, as in the popular relay oscillator. In our system, however, we chose the coefficients α_f, β_f, γ_f, δ_f, ε_f, and K_f so that, in the absence of noise or a contribution from the slow network (N_f = 0, g (X_S) = 0), the system has three steady states, two of which are stable and the other unstable (Supplementary Fig. S4c, d). These two stable steady states are such that small, but super-threshold perturbations, make the system switch from one equilibrium to the other, resulting in oscillatory-like behavior. In this case, noise endows the system with oscillatory behavior. Similar behavior has been documented previously ^63–65.

Coupling of the slow and fast systems

The two systems are coupled in a bidirectional manner. However, because the only external input to the coupled systems is through the external stochastic component of the fast system, perturbations from the respective equilibria have to be initiated through the fast system.

The function f (X_f)is used as a trigger to the slow system based on the activity of the fast system. First, at each angle θ₀ ∈ (−π, π)along the perimeter of the cell, the activity of the fast system in the neighborhood of θ₀ is summed:

$$\stackrel{\sim }{X_f}({\theta }_0)={\int }_{{\theta }_0-\mathrm{\Delta }\theta }^{{\theta }_0+\mathrm{\Delta }\theta }{X}_f(\theta )\mathrm{d}\theta .$$

We used a width of Δθ = 15°. This is used to generate a switch-like function:

$$h(X_f(\theta ))=\{\begin{array}{ll}0,\hfill & \text{if}\stackrel{\sim }{X_f}(\theta )<{\stackrel{\sim }{X}}_{f-\text{th}},\hfill \\ 1,\hfill & \text{otherwise}.\hfill \end{array}$$

The coupling term, f (X_f) is obtained by multiplying this function by a white noise component:

$$f(X_f(\theta ))=h(X_f(\theta )){\stackrel{\sim }{N}}_f,$$

which represents a probabilistic component of the activation. Here Ñ_f is a white-noise process with unit variance and mean of 0.05.

After the slow system is triggered, the high activity of X_S starts to regulate and synchronize the fast system. During the span that slow system fires up, high input from g (X_S)will drive the fast system into a higher stable steady state. After g (X_S)vanishes, the fast system resumes an oscillatory mode. The function g (X_S) of is simply described with an “on-off” switch function:

$$g\left(X_S(\theta )\right)=\{\begin{array}{ll}{g}_B,\hfill & \text{if}{X}_S(\theta )<X_{S-\text{th}},\hfill \\ g_S,\hfill & \text{otherwise}.\hfill \end{array}$$

Parameters

The model includes a number of parameters. Our starting point for choosing these was the previous model of the biased excitable network ²⁴. However, we adjusted these parameters so that the activity of the slow system spreads out to about 50 degrees around the perimeter and that the activities last about 100 seconds, to match the observed experimental behavior of the STEN. These changes were made by reducing the parameters that dictate the speed of the system and by altering the relative contribution of the two diffusion coefficients. For the fast system we chose the parameters so that the system had two stable equilibria (by changing the slope of the Y_f nullcline). We also adjusted the speed of the system so that the oscillations lasted about ten seconds. This is accomplished by adjusting the level of the noise. The final parameter values are given in Table S1.

Model implementation

The model and all simulations are implemented using Matlab (MathWorks, Natick, MA). The computer code is available on request. The cell was represented as a one-dimensional system using periodic boundaries. The cell boundary was discretized using 360 points.

Spatial diffusion terms, which contain the second derivatives, are approximated by central differences in space (in one dimension); and by doing that, the partial differential equations are converted to ordinary differential equations. The solution of the stochastic differential equations was obtained using the free SDE toolbox for Matlab: (http://www.maths.dur.ac.uk/users/umberto.picchini/). The time step for the simulation is set to 0.025 seconds.

Model of cellular deformations

To determine the effect of the model activities on the shape of a cell we used a level set framework to simulate cell shape changes as previously described ^{66, 67}.

In short, in the level set method (LSM) the cell is described as the zero-level set of a potential function ϕ(x, t), x ∈ R². The evolution of the cell is described by the Hamilton-Jacobi equation

$$\frac{\partial \varphi (x,t)}{\partial t}=v(x,t)·\nabla \varphi (x,t)=0$$ (5)

where the ν (x, t)describes the local velocity of the potential function. To obtain this velocity we apply different stresses on the cell and use a viscoelastic mechanical model of the cell to determine the local velocity. In our case we use:

$$\begin{array}{l}{\stackrel{.}{x}}_m=-(K/D)x_{\mathit{cor}}+(1/D+1/B){\sigma }_{\mathit{tot}}\\ {\stackrel{.}{x}}_{\mathit{cor}}=-(K/D)x_{\mathit{cor}}+(1/D){\sigma }_{\mathit{tot}},\end{array}$$

where σ_tot is the total stress applied on the cell, x_m and x_corr are the local displacements of the membrane and cortex, respectively, and K, D and B are viscoelastic components of the cell describing the elasticity (K) and viscosity (D) of the membrane, and the viscosity of the (B) of the cytoplasm. The velocity in Equation 5 is given by ν = ẋ_m.

The total net stress (σ_tot) includes the vector sum of the stresses acting on the cell. This stress includes contributions from passive components, such as surface tension (σ_ten) and well as protrusive forces (σ_pro) driven by the fast oscillatory network. Unlike previous simulations ^{66, 67}, we do not impose area constraints on the cell, as these simulations are of cells being observed using TIRF microscopy. The component due to surface tension is given by

$${\sigma }_{\mathit{ten}}=\gamma \kappa (x)\mathbf{n},$$

where γ is the local cortical tension, κ is the local curvature, and n is a normal unit vector.

The protrusive stresses are proportional to the fast oscillatory signal Y_f:

$${\sigma }_{\mathit{pro}}={\sigma }_0{Y}_f(\theta )\mathbf{n}.$$

Parameters used in these simulations are provided in Supplementary Table S1. This model was implemented using the Level Set Toolbox for Matlab⁶⁸.