A whole brain fMRI atlas generated via spatially constrained spectral clustering

Abstract

Connectivity analyses and computational modeling of human brain function from fMRI data frequently require the specification of regions of interests (ROIs). Several analyses have relied on atlases derived from anatomical or cyto‐architectonic boundaries to specify these ROIs, yet the suitability of atlases for resting state functional connectivity (FC) studies has yet to be established. This article introduces a data‐driven method for generating an ROI atlas by parcellating whole brain resting‐state fMRI data into spatially coherent regions of homogeneous FC. Several clustering statistics are used to compare methodological trade‐offs as well as determine an adequate number of clusters. Additionally, we evaluate the suitability of the parcellation atlas against four ROI atlases (Talairach and Tournoux, Harvard‐Oxford, Eickoff‐Zilles, and Automatic Anatomical Labeling) and a random parcellation approach. The evaluated anatomical atlases exhibit poor ROI homogeneity and do not accurately reproduce FC patterns present at the voxel scale. In general, the proposed functional and random parcellations perform equivalently for most of the metrics evaluated. ROI size and hence the number of ROIs in a parcellation had the greatest impact on their suitability for FC analysis. With 200 or fewer ROIs, the resulting parcellations consist of ROIs with anatomic homology, and thus offer increased interpretability. Parcellation results containing higher numbers of ROIs (600 or 1,000) most accurately represent FC patterns present at the voxel scale and are preferable when interpretability can be sacrificed for accuracy. The resulting atlases and clustering software have been made publicly available at: http://www.nitrc.org/projects/cluster_roi/. Hum Brain Mapp, 2012. © 2011 Wiley Periodicals, Inc

INTRODUCTION

Whether constructing computational models of brain function, exploring the human connectome, or investigating the role of functional connectivity (FC) in disease, a prerequisite step is defining functionally distinct brain regions for analysis and modeling. An alternative approach is to conduct a whole‐brain voxel‐wise analysis, but such an approach is computationally expensive, sensitive to noise, and difficult to interpret. Furthermore, there is redundant information present at the voxel scale and such redundancy makes it possible to significantly reduce the dimensionality of the fMRI data. The optimal means of combining voxels into functionally distinct regions of interest (ROIs) remains to be determined.

Several criteria exist for evaluating the suitability of a set of ROIs for whole brain resting state FC analyses. First, the ROIs should be functionally homogeneous [Thirion et al., 2006], which for FC analysis requires that a ROI's voxels have similar time courses [Zang et al., 2004] or produce similar FC patterns [Cohen et al., 2008]. Second, the ROIs should be spatially contiguous to preserve the distinction between network nodes and large‐scale networks of nodes [Bellec et al., 2006; Smith et al., 2009]. Additionally spatial contiguity ensures that the resulting ROIs represent anatomically homogeneous regions, and hence preserve the interpretability of the connectivity results [Thirion et al., 2006]. Third, ROIs generated by a group level parcellation should match the functional segregation present at the individual level. The fourth and arguably most crucial criterion is that FC patterns derived using the ROIs should accurately represent the FC present at the voxel scale.

Several methods have been used to develop a set of ROIs for FC analysis. One method is to manually define ROIs using anatomical images or templates. This requires hypothesizing the shape, size, and location of functional areas based upon neuroanatomic literature or a meta‐analysis of functional neuroimaging results [Craddock et al., 2009; Dosenbach et al., 2010]. This is a laborious process prone to experimenter bias and error. These issues can be overcome using standardized ROI atlases developed from anatomical [Talairach and Tournoux, 1988] or cyto‐architectonic [Zilles and Amunts, 2009] boundaries. While using these atlases has become a popular approach (c.f. [Shehzad et al., 2009; Wang et al., 2008]), their suitability for resting state FC analysis has yet to be determined. Since anatomical atlases are derived from a higher resolution source than most fMRI data is acquired, it is unknown how well the boundaries and shapes of these anatomical regions apply at the fMRI scale given partial volume effects, EPI distortions and co‐registration errors [Thirion et al., 2006]. Additionally, while the regions defined by these atlases are anatomically or cyto‐architectonically homogeneous, they do not necessarily have homogeneous connectivity. Indeed, it has been shown that adjacent regions of the anterior cingulate cortex (ACC) have drastically different structural [Beckmann et al., 2009] and FC patterns [Margulies et al., 2007], even though the ACC is typically represented as a single ROI in brain atlases [Talairach and Tournoux, 1988]. Also, small world network statistics can vary significantly based on the atlas used [Wang et al., 2008] and a simulation study has shown that mixing BOLD timecoures as is likely to happen with atlas‐based ROIs has a substantial impact on the ability to accurately estimate network structure [Smith et al., 2010]. Shortcomings of these atlases related to the size of their ROIs can be mediated by subdividing the ROIs either randomly [Hagmann et al., 2008; Zalesky et al., 2010], which does not guarantee functional homogeneity, or by using a data‐driven clustering approach [Patel et al., 2008], which does not guarantee spatial contiguity.

Another approach is to employ spatially constrained clustering algorithms to define ROIs based on the correlation structure of the data without incorporating anatomical priors. Several approaches have been proposed for clustering task based and resting state fMRI data (e.g., fuzzy C‐means [Baumgartner et al., 1997], independent components analysis [McKeown et al., 1998], self‐organizing maps [Ngan and Hu, 1999; Peltier et al., 2003], normalized‐cut spectral clustering [van den Heuvel et al., 2008], K‐means [Mezer et al., 2009], and hierarchical clustering [Goutte et al., 1999]]). However, these methods require additional constraints or post‐processing steps to guarantee spatial coherence. This can be accomplished by increasing the number of clusters estimated by these approaches until their results are spatially contiguous [Smith et al., 2009] or by splitting clusters that are not spatially contiguous.

A few methods have been proposed for clustering that directly incorporate a spatial constraint into the clustering algorithm [Bellec et al., 2006; Flandin et al., 2002b; Heller et al., 2006; Lu et al., 2003; Thirion et al., 2006; Tomassini et al., 2007]. Region growing methods have been proposed that iteratively merge voxels with their most similar neighbor until the resulting set of clusters is disjoint [Heller et al., 2006; Lu et al., 2003] or a size threshold is met [Bellec et al., 2006]. Thirion et al. [2006] proposed a spatially constrained spectral clustering approach for deriving ROIs from task‐based fMRI data.

We extend this research by developing a spatially constrained spectral clustering approach for group clustering whole brain resting state fMRI data into functionally and spatially coherent regions. This method incorporates a spatial constraint similar to those previously proposed for other ROI generating clustering methods [Flandin et al., 2002b; Thirion et al., 2006; Tomassini et al., 2007] into the normalized cut (NCUT) method previously proposed for unconstrained clustering of resting state data [van den Heuvel et al., 2008]. In this method, data is represented as a graph where voxels are nodes that are connected to other voxels in their 3D (26 voxel, face and edge touching) neighborhood by weighted edges; edge weights correspond to the similarity between neighboring voxels. These edges are iteratively removed until a pre‐specified number of clusters are obtained such that the similarity between voxels within the same cluster is maximized compared to the similarity between voxels in different clusters.

The proposed method differentiates itself from previously proposed methods in several ways. Unlike region growing techniques [Bellec et al., 2006; Heller et al., 2006; Lu et al., 2003], which solely maximizes within cluster similarity, NCUT simultaneously optimizes within cluster similarity and between cluster dissimilarity [Shi and Malik, 2000]. A result of this difference is that in regions of the brain where a clear clustering is not obvious, NCUT will produce clusters of uniform size, whereas region growing will result in clusters that only contain a single voxel. Other methods have been proposed that incorporate both spatial and functional information using different clustering algorithms [Flandin et al., 2002b; Tomassini et al., 2007], but spectral clustering has been shown to outperform other clustering algorithms [Shen et al., 2010; Shi and Malik, 2000; von Luxburg, 2007] and the implementation used here is less sensitive to initial conditions than other methods (e.g., k‐means) [Yu and Shi, 2003].

Developing this method requires choosing between several parameters with inherent trade‐offs. One parameter is whether to measure similarity based on the temporal similarity between voxels or the spatial similarity in their FC maps. Another is selecting the method for clustering information across subjects. A third parameter is selecting the number of clusters (ROIs) to generate for the resulting parcellation. We assess the impact of varying these parameters upon the parcellation method. Additionally, we will compare generated parcellations against randomly generated parcellations and against four commonly used ROI atlases derived from anatomical or cyto‐architectonic parcellations.

METHODS

Subjects and Scanning

Forty‐one healthy control subjects (age: 18–55; mean 31.2; std. dev. 7.8; 19 females) were recruited in accordance with Emory University Institutional Review Board policy. To qualify for inclusion, subjects were required to be between the ages of 18–65, have no contraindications for MRI, to be medication free, and have no current or past neurological or psychiatric conditions.

Subjects were scanned on a 3.0 T Siemens Magnetom TIM Trio scanner (Siemens Medical Solutions; Malvern PA) using a 12‐channel head matrix coil. Anatomic images were acquired at 1 × 1 × 1 mm³ resolution with an MPRAGE sequence using: field of view (FOV) 224 × 256 × 176 mm³, repetition time (TR) 2,600 ms, echo time (TE) 3.02 ms, inversion time (TI) 900 ms, flip angle (FA) 8°, and GRAPPA factor 2. Resting state fMRI data were acquired with the Z‐SAGA sequence to minimize susceptibility artifacts [Heberlein and Hu 2004]. One hundred and fifty functional volumes were acquired in 30 4‐mm axial slices using the parameters: TR 2920 ms, TE¹/TE² 30/66 ms, FA 90°, 64 × 64 matrix, in‐plane resolution 3.44 × 3.44 mm².

For resting state functional scans, subjects were instructed to passively view a fixation cross while “clearing their minds of any specific thoughts.” The fixation cross was used to discourage eye movement and help prevent subjects from falling asleep. Compliance was assessed during an exit interview; all subjects confirmed they had performed the task as requested without falling asleep.

Preprocessing

All preprocessing of MRI data was performed using SPM5 [Friston et al., 1994] running in MATLAB 2008a (The Mathworks; Natick, MA). Anatomic and fMRI data were evaluated for imaging artifacts such as excessive ghosting, banding, and other imaging errors; no images were removed. Anatomic scans were simultaneously segmented into white matter (WM), gray matter (GM), and cerebral‐spinal fluid (CSF) and normalized to the MNI152 normalized brain atlas using SPM5′s unified segmentation procedure [Ashburner and Friston, 2005]. fMRI volumes were slice timing corrected, motion corrected, written into MNI152 space at 4 × 4 × 4 mm³ resolution using the transformation calculated on the corresponding anatomic images, and spatially smoothed using a 6‐mm FWHM Gaussian kernel. No images were removed due to excessive head motion (motion 0.2–1.82 mm; mean 0.84 mm; std. dev. 0.41 mm). fMRI data were restricted to GM and denoised by regressing out motion parameters, WM timecourse, as well as CSF timecourse [Fox et al., 2005; Lund et al., 2006]. Each voxel timecourse was band‐pass filtered (0.009 Hz < f < 0.08 Hz) to remove frequencies not implicated in resting state FC [Cordes et al., 2001; Fox et al., 2005].

Whole Brain Clustering of Resting State Data

Normalized cut (NCUT) spectral clustering

The normalized cut spectral clustering (NCUT) algorithm was chosen for clustering due to its robustness to outliers [Shi and Malik, 2000; von Luxburg, 2007], favorable performance when compared to other algorithms [Shen et al., 2010], and the simplicity with which it can be adapted to incorporate constraints [Kamvar et al., 2003; Xu et al., 2005]. NCUT begins by representing fMRI data as an undirected weighted similarity graph, G = (V,E), with N vertices, V, corresponding to voxels and edges, E, connecting neighboring voxels [von Luxburg, 2007]. Edges between two voxels, v _i and v _j are weighted by the non‐negative similarity, w _ij, of the voxels' FC (described in detail in the next subsection). The algorithm proceeds by cutting the graph into a pre‐specified number of clusters, K, such that the similarity between voxels within a cluster is greater than the similarity between voxels in separate clusters. Several criteria have been proposed for determining graph cuts, all of which involve minimizing a cut cost. The cut cost associated with partitioning graph G into the disjoint sets A and B is equal to the sum of the weights on edges connecting voxels in A to voxels in B:

(1.1.1)

where i indexes the voxels in cluster A and j indexes the voxels in cluster B. The minimum cut criterion solely minimizes this cut cost, which will likely result in clusters which contain a single voxel. Normalized cut, however, normalizes the cut cost by the sum of weights on all edges connecting voxels in a partition to every voxel in the graph [Shi and Malik, 2000]:

(1.1.2)

where n indexes the N voxels contained in graph G. There are at least two advantages to this normalization. First, whereas the minimum cut criterion solely minimizes the similarity between clusters; NCUT simultaneously minimizes the similarity between clusters as well as maximizes the similarity within clusters [Shi and Malik, 2000; von Luxburg, 2007]. Second, NCUT results in clusters that are “balanced” as determined by the sum of edge weights within each cluster, which reduces the likelihood of obtaining clusters that only contain a single voxel [Shi and Malik, 2000]. A potential drawback of this normalization is that it might bias the results toward equal‐sized clusters. When a cut cannot be uniquely determined by minimizing the numerator of Eq. (1.1.2), the cut is determined by maximizing the denominators of the two ratios. This will result in partitions containing a similar sum of edge weights, which, when the number of edges is similar across voxels, will result in partitions containing similar numbers of voxels. Although this bias exists, empirical evidence shows that NCUT is able to correctly identify partitions of unequal size [Shen et al., 2010]. Practically, G is represented as a N × N weighted adjacency matrix W (described in detail below) consisting of the edge weights, w _ij, and the NCUT problem is solved by linear algebra. NCUT clustering was performed using a Python implementation of the algorithm presented in [Yu and Shi, 2003]. A caveat to this method is that it may result in empty clusters, that is, the number of clusters in the solution may be less than K.

Subject specific similarity matrices

Each w _ij of a subject specific similarity matrix, W, corresponds to the similarity between the FC of two voxels, v _i and v _j separated by a distance d _ij:

(1.1.3)

The radius ε was chosen to include the 26 nearest neighbors (3D neighborhood; face and edge touching) of a voxel. This constrains the resulting clusters to contain contiguous, rather than spatially distributed, voxels [Kamvar et al., 2003; Xu et al., 2005]. An additional benefit of this spatial constraint is that it results in sparse similarity matrices that reduce computational overhead.

The similarity of FC between voxels, s(v _i,v _j), can be defined in a number of ways. An anatomically constrained [Flandin et al., 2002a] or random parcellation [Hagmann et al., 2008; Zalesky et al., 2010] can be achieved by setting the similarity between neighboring GM voxels to one. Functional information is incorporated by either the similarity between timecourses extracted from the voxels [van den Heuvel et al., 2008] or the similarity between whole brain FC maps generated by the voxel timecourses [Cohen et al., 2008].

A metric for measuring similarity must also be chosen. An obvious choice is Pearson's correlation coefficient, which is only appropriate if a threshold is applied to make it non‐negative:

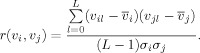(1.1.4)

Here l (0 ≤ l ≤ L) corresponds to a sample of a time series or a voxel of a FC map, v _i (v _j) is the mean of v _i (v _j), and σ_i (σ_j) is the sample standard deviation of v _i (v _j). Correlation between voxel time series will be referred to as r _t and between FC maps will be referred to as r _s. A r ≥ 0.5 threshold was applied to correlation coefficients to exclude negative and weak correlations. The eta ² statistic has been proposed as an alternative for measuring similarity between FC maps [Cohen et al., 2008]. This statistic is identical to Pearson correlation for standardized (mean centered, std. dev. = 1) variables but it is shifted to be non‐negative. This approach was not performed since due to the shifting, a correlation of −1 refers to an eta ² of 0, but we want 0 to indicate no correlation (no connection).

The choice between using r _t and r _s is application specific. r _t is desired when temporal homogeneity within a cluster is desired, whereas r _s is used when homogeneity of FC maps is preferred. At first consideration, these should be quite similar since they are both determined from voxel time‐courses, but Figure 1 illustrates that while the two are highly correlated, their relationship is nonlinear, and there are several pairs of voxels for which one metric is positive and the other is negative (Fig. 1, red points).

Figure 1.

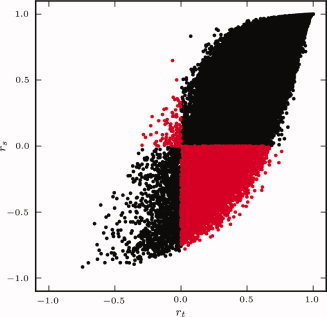
Comparison of r _t and r _s similarity metrics calculated from the resting state data of a single subject. Each point corresponds to a pair of voxels. Voxel pairs for which one metric is positive and the other is negative are shown in red. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Group level clustering

Group level clustering was accomplished either by averaging the individual similarity matrices and then submitting the average to clustering [Patel et al., 2008] or by performing clustering for each individual followed by a second level group clustering [van den Heuvel et al., 2008]. In the second case, an N × N adjacency matrix A was constructed for each subject from the results of the first level clustering (see Fig. 2). The elements a _ij of A equal one if both v _i and v _j were contained in the same cluster and zero otherwise [van den Heuvel et al., 2008]. The adjacency matrices were averaged across subjects to form a group coincidence matrix that is subsequently clustered using the NCUT algorithm. The first method results in faster computation since clustering must only be performed once, but may result in poor quality clustering. When performing random parcellation, each subject's data will result in identical connectivity graphs (assuming that the same GM mask was applied to each subject), and there is no need for group level clustering.

Figure 2.

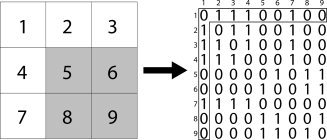
Illustration of the method for creating connectivity matrices from a clustering solution. On the left is a two‐dimensional patch of 9 voxels that are clustered into two regions: white and gray. This is translated into a 9 × 9 connectivity matrix where a voxel from a cluster is connected to every other voxel from the same cluster with connection strength of 1, and unconnected to voxels that are not in the same cluster. The connectivity matrix entry for voxel 1 is highlighted on the right. It is connected to voxels 2, 3, 4, and 7, which are also in the white cluster.

Model selection

The proposed spatially constrained group clustering method requires the specification of similarity metric (random, r _t or r _s), method for combining individual level data to perform group level analysis (clustering then averaging or averaging then clustering), and the desired number of clusters. Parameter selection was assessed by using every combination of similarity metric and group‐level clustering to generate clustering solutions containing between 50 and 1,000 clusters, in increments of 50. The resulting clustering solutions were compared using two commonly applied strategies: leave‐one‐out cross‐validation (LOOCV) and silhouette width (SI) [Goutte et al., 1999; Kelly et al., 2010].

LOOCV is an iterative procedure in which group‐level clustering is performed after excluding a single subject. The adjacency matrix generated from the group clustering with the m ^th subject excluded, A _−m, is compared to the adjacency matrix calculated by clustering the data from the m ^th subject, A _m. Similarity between group and individual level clustering solutions was calculated using Dice's coefficient [Dice, 1945]. This value was averaged across all possible ways to exclude one subject.

Dice's coefficient measures the similarity between two adjacency matrices. It is the ratio of twice the number of connections common to both matrices, divided by the total number of connections present in both matrices:

(1.1.5)

Dice's coefficient results in numbers between zero and one, where one corresponds to perfect correspondence between matrices, and zero corresponds to no similarity [Dice, 1945].

The silhouette width was chosen to quantify the functional homogeneity of ROIs. SI measures cluster compactness compared to cluster separation [Rousseeuw, 1987]. SI has been defined in terms of both similarity and distance metrics; the similarity formulation is used here. The average similarity, a _k, between every pair of voxels assigned to cluster c _k of clustering C ( 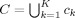), is:

(1.1.6)

where n _k corresponds to the number of voxels assigned to cluster c _k and s(v _i,v _j) is a measure of the similarity between voxels v _i and v _j, which, for our purposes is either r _t or r _s. Standard SI normalizes a _k by the maximum similarity between every voxel assigned to c _k and every out‐of‐cluster voxel. This is likely to be similar (or higher) than the average similarity within a cluster due to the spatial constraint as well as the strong correlations between spatially distant areas present in whole brain fMRI data. For this reason, SI was modified to use the average similarity between in‐cluster and out‐of‐cluster voxels:

(1.1.7)

The silhouette width for the clustering C can then be calculated from:

(1.1.8)

When using correlation as the similarity metric, −∞ ≤ si(C) ≤ ∞. Negative values indicate an incorrect clustering and values near 1 indicate a good solution. SI was calculated for each clustering solution using each subject's data and then averaged across subjects.

Evaluation of ROIs

Once a set of parameters was chosen for spatially constrained group clustering, the results of this method were compared to four commonly used ROI atlases derived from anatomical parcellation as well as random parcellation. This comparison was performed in terms of ROI homogeneity as well as the ability of ROIs to accurately represent FC patterns present at the voxel scale. To avoid the circular logic of testing the parcellation on the same dataset from which it was derived [Kriegeskorte et al., 2010], the analysis was performed on an independent dataset, the New York University test‐retest dataset [Shehzad et al., 2009] freely available through the 1,000 Functional Connectomes Project [Biswal et al., 2010] (http://fcon_1000.projects.nitrc.org). The data set consists of 6.5‐min resting state scans acquired from 25 healthy controls at three different time points on a 3.0T Siemens Allegra scanner (time repetition [TR] = 2,000 ms; time echo [TE] = 25 ms; flip angle = 90°; 39 slices, matrix = 64 × 64, field of view [FOV] = 192 mm; acquisition voxel size = 3 × 3 × 3 mm³). Only the first scanning session was used for each subject. fMRI preprocessing was performed using the previously described methods.

The anatomical atlases used for this comparison were the automated anatomical labeling (AAL) atlas [Tzourio‐Mazoyer et al., 2002] distributed with the AAL toolbox (http://www.cyceron.fr/web/aal__anatomical_automatic_labeling.html), the Eickhoff‐Zilles (EZ) atlas distributed with the SPM Anatomy Toolbox (http://www2.fz-juelich.de/inm/inm-1/spm_anatomy_toolbox) [Eickhoff et al., 2005], the Talairach and Tournoux (TT) atlas [Lancaster et al., 2000] distributed with AFNI (http://afni.nimh.nih.gov/afni/), and the Harvard‐Oxford (HO) atlas distributed with FSL (http://www.fmrib.ox.ac.uk/fsl/). The TT atlas was co‐registered and warped into MNI152 template space using nearest‐neighbor interpolation. The Harvard‐Oxford atlas is split into cortical and subcortical probabilistic atlases. A 25% threshold was applied to these atlases and the cortical atlas was then split into left and right regions by bisecting the mask at x = 0. The subcortical HO atlas contains seven large ROIs corresponding to left/right WM, left/right GM, left/right CSF, and brain stem; these ROIs were excluded from the mask. The remaining subcortical ROIs were then combined with the cortical ROIS.

The EZ atlas was derived from the max‐propagation atlas distributed in the SPM5 Anatomical Toolbox. This atlas was coregistered to the MNI152 template using the Colin 27 template distributed with the atlas as an intermediary. The EZ atlas was subsequently warped into MNI152 space using nearest‐neighbor interpolation. The AAL mask did not require any additional processing. Each of the AAL, EZ, HO, and TT atlases was fractionized, using the 3dfractionize tool of the AFNI toolset [Cox, 1996], to the same voxel size as the fMRI data using nearest neighbor interpolation with a voting algorithm to resolve assignment conflicts. The GM mask used in fMRI preprocessing was applied to each atlas. Parts of the brain stem are included in this GM mask but not in the anatomical atlases. The cerebellum is included in the cluster results, AAL, EZ, and TT but not HO. The number of ROIs and average ROI size for each of these atlases are listed in Table I.

Table I.

Comparison between anatomical atlases and clustering solutions with a similar number of clusters

Atlas	# ROIs	Volume	Mean Within Cluster	Mean Within Cluster r s	vPCC Sim	M1 Sim	V1 Sim
AAL	115	156 (119)	0.14 (0.04)	0.22 (0.05)	0.51 (0.06)	0.48 (0.10)	0.51 (0.10)
EZ	115	156 (116)	0.14 (0.04)	0.21 (0.05)	0.50 (0.06)	0.48 (0.10)	0.50 (0.09)
HO	110	150 (136)	0.14 (0.03)	0.22 (0.05)	0.50 (0.07)	0.47 (0.12)	0.52 (0.10)
TT	93	190 (173)	0.12 (0.03)	0.23 (0.05)	0.45 (0.06)	0.43 (0.10)	0.47 (0.10)
r t 2‐Level	110	167 (34)	0.20 (0.04)	0.34 (0.06)	0.58 (0.07)	0.54 (0.11)	0.55 (0.09)
Random	109	169 (36)	0.20 (0.04)	0.34 (0.06)	0.57 (0.07)	0.54 (0.11)	0.55 (0.09)

Values represent the mean across all subjects in the validation dataset with standard deviations in parenthesis. The best values are highlighted for each metric. Abbreviations of atlas names are consistent with text. # ROIs: number of regions of interests; Sim: Pearson correlation between voxel‐wise FC map and ROI‐wise FC map derived for vPCC (ventral posterior cingulate cortex), M1 (primary motor cortex, left), and V1 (primary visual cortex, left) seed regions.

Clustering solutions from functional parcellation were compared to the four anatomical atlases and random parcellation in terms of cluster homogeneity and their ability to represent FC patterns present at the voxel scale. Consistent with previous definitions of regional homogeneity, cluster homogeneity was measured as the average r _t [Zang et al., 2004] and r _s [Cohen et al., 2008] between every pair of voxels within a cluster. Accuracy of representation was measured by comparing FC maps derived at the voxel level to those derived using the ROI atlases. Six‐millimeter spherical seed ROIs were hand placed in the ventral posterior cingulate cortex (vPCC), left primary motor cortex (lM1), and left primary visual cortex (lV1). These regions were used as seeds for the default mode network, motor network, and visual networks respectively. For each seed ROI, voxel timecourses were extracted and averaged, resulting in a single timecourse per subject, per seed ROI. Voxel‐wise FC maps were generated by correlating the seed ROI timecourses with the timecourse of every gray‐matter voxel of the brain. For the ROI atlases and clustering solutions, each ROI was represented by its mean timecourse, and these values were correlated with the seed timecourses. ROI‐derived correlation coefficients were written to each voxel within an ROI to generate voxel‐level FC maps. The FC maps derived from different ROI atlases and clustering solutions were compared to the voxel‐wise FC maps using Pearson's correlation. The result of this procedure was one similarity metric per subject, per seed ROI, per ROI atlas and clustering solution, these values were averaged across subjects for comparison. This procedure was repeated using the first eigen‐variate from a principle components analysis (PCA) [Friston et al., 2006], instead of averaging, to summarize voxel timecourses.

RESULTS

Whole brain clustering of resting state data was performed using every combination of similarity metric, and group level clustering method (r _t group mean, r _t two‐level, r _s group mean, and r _s two‐level) and random clustering for K between 50 and 1,000, in multiples of 50. Clustering results containing 50, 200, and 1,000 ROIs are illustrated in Figure 3 and are alternatively visualized on an inflated view of the cortical surface in the online Supporting Information Figure 1. Note that ROI numbering and coloring by the parcellation method are arbitrary; the maps have been recolored to emphasize the ROI homology across analysis methods. All clustering methods produced ROIs of similar shape, size, and location with variations around ROI borders.

Figure 3.

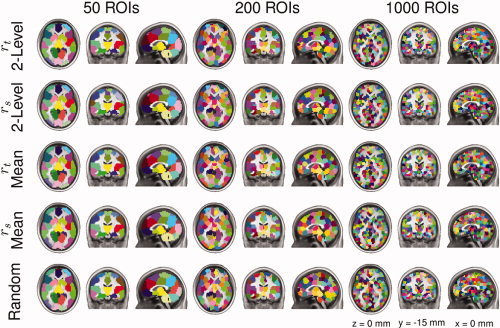
Illustration of clustering results for the four combinations of functional parcellation methods and random parcellation containing 50, 200, or 1000 ROIs. Each parcellation is depicted as three orthogonal views. Color‐coding is arbitrarily used to best emphasize ROI boundaries. ROI coloring was matched across parcellation results to emphasize similarities in ROI locations between methods.

Figure 3 demonstrates that the number of ROIs being estimated strongly influences the interpretation of resulting ROI maps. Choosing too few ROIs (as in the 50 ROI parcellations) produced broad, over‐generalized ROIs. These parcellations have numerous examples of functionally and anatomically distinct regions (i.e., hippocampus and amygdala; basal ganglia and thalamus; superior parietal lobule and supramarginal gyrus) being condensed into a single ROI. Conversely, too many ROIs (as in the 1,000 ROI parcellations) produced scattered ROI maps of questionable interpretative value. For example, these parcellations divide the anterior cingulate into ∼40 ROIs, whereas previous parcellations of the cingulate suggest fewer than 10 anatomically, functionally, and histologically distinct subunits [Beckmann et al., 2009; Margulies et al., 2007; Palomero‐Gallagher et al., 2009].

Qualitatively, the 200‐ROI parcellations are a good compromise between these two extremes. ROIs are suitably large to accommodate individual anatomic variability. For example, the location of the primary motor cortex hand knob averages 31 mm from the midline, with a width of approximately 14 mm [Yousry et al., 1997]. The distal range of the 200 ROI map's primary motor cortex ROI is 24 mm ‐ more than sufficient to house the hand knob. Yet the 200 ROI parcellation maps are suitably small to discriminate primary motor from premotor ‐ which is not possible for the 50 ROI maps.

The resulting cluster maps were quantitatively evaluated using LOOCV and silhouette width; the results are illustrated in Figure 4a–d. Results of random clustering were also included as a comparison. The ability of group‐level clustering solutions to generalize to individual‐level clustering solutions is poor for all clustering methods investigated (Fig. 4a–d). The r _t similarity metric outperforms r _s (P < 5 × 10⁻⁹, FDR corrected, Wilcoxon signed‐rank tests) for all clustering levels and the two‐level approach outperforms the group mean approach (P < 0.005, FDR corrected, Wilcoxon signed‐rank tests) for clustering solutions containing more than 50 regions (Fig. 4a–d). Clustering results generated using r _s mean outperform random clustering for cluster solutions with 50 clusters, whereas results of the r _s two‐level approach outperform random clustering for cluster solutions containing 50–200, 300, and 350 clusters (P < 0.05, FDR corrected, Wilcoxon signed‐rank tests; Fig. 4c). Clusterings generated using r _t mean outperform random clustering for cluster solutions with 50–150 and 350 clusters and results of the r _t two‐level approach outperform random clustering for cluster solutions containing up to 750 clusters (P < 0.05, FDR corrected, Wilcoxon signed‐rank tests; Fig. 4d). There are no practical differences in r _t or r _s silhouette width obtained using the various clustering methods and random clustering; the number of clusters in the clustering solution has the greatest impact on this metric (Fig. 4e,f).

Figure 4.

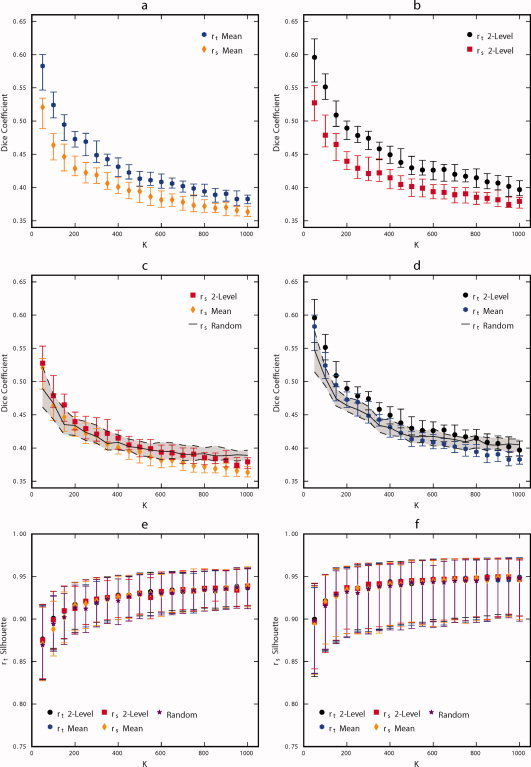
Comparison of parameter selection performance for each combination of parcellation strategy (r _t group mean, r _t two‐level, r _s group mean, and r _s two‐level) for K between 50 and 1,000, in multiples of 50. Panel (a) compares the LOOCV accuracy of r _t group mean to r _s group mean, (b) compares r _t two‐level to r _s two‐level, (c) compares r _s group mean to r _s two‐level, and (d) compares r _t group mean to r _t two‐level. The similarity between random parcellation and individual level functional parcellation results using r _t and r _s are included in panels (c) and (d) for comparison. Panel (e) compares the methods in terms of silhouette width calculated with the r _t metric and (f) in terms of silhouette width calculated with the r _s metric. Symbols are located at the median and error bars indicate 0.25 and 0.75 quartiles. Results from different parcellation strategies are overlapping and obscure one another. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

The random parcellation is similar to the functional parcellation (see Fig. 3) and performs nearly as well (see Fig. 4). A possible reason for this similarity could be that the connectivity graphs calculated using functional information is very similar to the random connectivity graph. To investigate this phenomenon further, cumulative distribution functions (CDF) were calculated for the edge weights of subject‐specific and subject‐mean connectivity matrices for both similarity metrics (Supporting Information Fig. 2). These curves are substantially different from the CDF for the random connectivity matrix (all edge weights = 1), which indicates that the similarity in performance of the random clustering results is due to some phenomena other than the similarity of the connectivity graphs. Interestingly, r _s values result in higher local connectivity than r _t values (p(r _s > .8) ≈ 0.57, o(r _t > .8) ≈ 0.39), this trend reverses and is much less substantial for values calculated from group mean data (Supporting Information Fig. 2).

Based on the results of the LOOCV procedure, the two‐level r _t approach was chosen for further comparisons with the AAL, EZ, HO, and TT anatomical atlases as well as random clustering using an independent dataset. Cluster homogeneity was evaluated by the average within‐cluster temporal and spatial correlation; these values were averaged across ROIs for each subject in the validation dataset and are illustrated in Figure 5. The temporal homogeneity of clustering solutions derived from the two‐level r _t approach is significantly higher than those of random parcellation for all K (P < 5 × 10⁻⁶, FDR corrected, Wilcoxon signed‐rank tests), although the differences are marginal. Both clustering methods outperform the anatomical atlases for K > 50, (P < 1 × 10⁻⁷, FDR corrected, Wilcoxon signed‐rank tests) in terms of temporal homogeneity, which improves monotonically with the number of clusters (Fig. 5a). The anatomical atlases perform better in terms of spatial homogeneity than temporal homogeneity, but both clustering methods outperform the anatomical atlases for K > 150 (P < 0.005, FDR corrected, Wilcoxon signed‐rank tests). Results of two‐level r _t functional parcellation exhibit better spatial homogeneity than random parcellation for all K except K = 150 (P < 0.01, FDR corrected, Wilcoxon signed‐rank tests).

Figure 5.

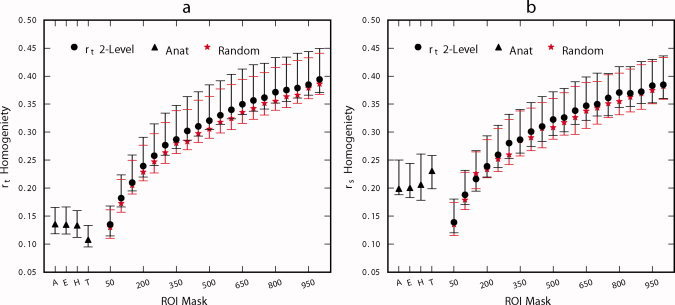
Comparison of ROI homogeneity for r _t 2‐level functional parcellation, anatomical atlas (A: AAL, E: Eickhoff‐Zilles, H: Harvard‐Oxford, T: Talairach and Tournoux), and random parcellation. The vertical axis corresponds to the average correlation between every pair of voxels (temporal in panel a, spatial in panel b) within an ROI, averaged across ROIs. Symbol is located at the subject median and error bars indicate inter‐quartile range. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

The accuracy of representation for the various ROI atlases and clustering results was evaluated for motor, visual, and default mode resting state networks (Fig. 6), the statistical significance for a few of these comparisons are shown in Table II. As expected, as the number of clusters increases, so does the similarity between voxel‐wise and cluster‐wise connectivity maps. Representation accuracy of the vPCC network is significantly higher for the results of the two‐level r _t method compared to random clustering for all K (P < 0.05, FDR corrected, Wilcoxon signed‐rank tests). Functional parcellation outperforms random parcellation for all K except K = 100 (P < 0.005, FDR corrected, Wilcoxon signed‐rank tests) for the V1 network and all K except K = 150,200 (P < 0.005, FDR corrected, Wilcoxon signed‐rank tests) for the M1 network. Again, there is a dramatic difference between ROI atlases and clustering results. Clustering significantly outperforms the anatomic parcellations for K > 50 (P < 0.005, FDR corrected, Wilcoxon signed‐rank test). To better understand this phenomenon, Figure 7 illustrates group mean default mode network maps derived voxel‐wise, using clustering, and using the best performing (HO) and worse performing (TT) anatomic atlases. Major distinctions between functional and anatomical parcellations exist throughout cingulate and prefrontal cortex, important regions of the default mode network.

Figure 6.

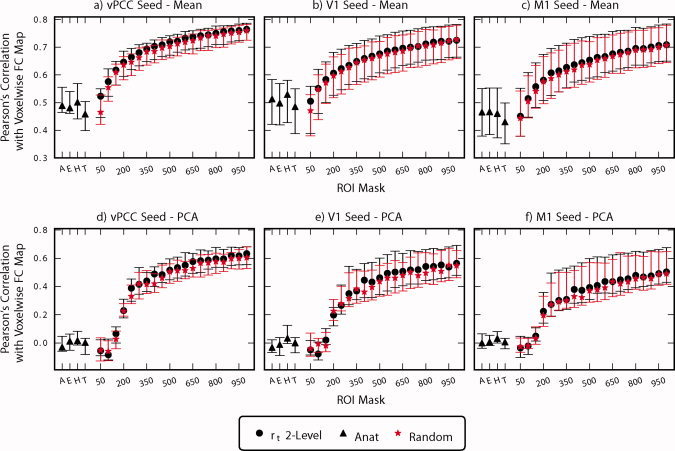
Comparison of accuracy of representation for r _t 2‐level functional parcellation, anatomical atlas (A: AAL, E: Eickhoff‐Zilles, H: Harvard‐Oxford, T: Talairach and Tournoux), and random parcellation. Symbol is located at the mean and error bars indicate standard deviation. Voxel‐wise FC maps for vPCC (ventral posterior cingulate cortex), M1 (left primary motor cortex), and V1 (primary visual cortex) were compared to ROI‐wise FC maps calculated from the same seeds using Pearson's correlation. ROI summary time courses were derived either by averaging (a–c) or using the first eigenvariate of a principle components analysis (PCA) (d–f).

Table II.

Statistical comparison of representation accuracy between 2‐level rt and random parcellation as well as the AAL, EZ, HO, and TT atlases for vPCC, M1, and V1 seeds

	K	rt 2‐level > Random			rt 2‐level > AAL			rt 2‐level > EZ			rt 2‐level > HO			rt 2‐level > TT
		W	P	q	W	P	q	W	P	q	W	P	q	W	P	q
M1	50	305	1.1E‐05	2.5E‐04	18	1.00	1.00	29	1.00	1.00	80	0.99	1.00	257	4.8E‐03	0.06
	200	259	4.0E‐03	0.06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06
	1,000	324	6.0E‐08	2.5E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06
V1	50	311	3.3E‐06	8.5E‐05	0	1.00	1.00	0	1.00	1.00	0	1.00	1.00	34	1.00	1.00
	200	295	6.0E‐05	1.1E‐03	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06
	1,000	308	6.2E‐06	1.5E‐04	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06
vPCC	50	270	1.4E‐03	0.02	0	1.00	1.00	0	1.00	1.00	1	1.00	1.00	115	0.90	1.00
	200	323	8.9E‐08	3.2E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06
	1,000	324	6.0E‐08	2.5E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06	325	3.0E‐08	1.6E‐06

Results are from one‐tailed Wilcoxon signed rank tests and are FDR corrected across all comparisons. Abbreviations of atlas names are consistent with text. W: Wilcoxon signed rank statistic; P: uncorrected P‐value; q: FDR corrected P‐value. vPCC (ventral posterior cingulate cortex), M1 (primary motor cortex, left), V1 (primary visual cortex) seed regions.

Figure 7.

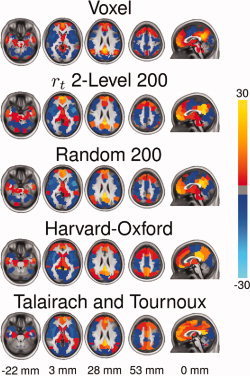
Comparison of voxel‐wise FC map of the default mode network to maps generated from a 200 ROI parcellation using r _t 2‐level, random parcellation, the Harvard‐Oxford atlas and the Talairach and Tournoux atlas. FC maps were Fischer transformed, combined across subjects using a one‐sample t‐test and converted to z‐scores. No threshold was applied to the images.

The method employed to summarize voxel time courses (mean or PCA) within an ROI has a substantial impact on the ability of the clustering solutions and anatomic atlases to represent FC present at the voxel scale (Fig. 6). There is a decrease in the similarity between ROI derived FC maps and voxel derived FC maps across the board when using PCA to summarize time courses (Fig. 6d–f). This decrease is most prominent for the anatomic atlases as well as clustering solutions containing 150 clusters or fewer. The performance of PCA summarization improves for clustering solutions containing more than 200 clusters and shows a similar trend of improvement for greater number of clusters as the mean time course summarization approach (Fig. 6d–f vs. 6a–c).

Since all of the metrics employed vary with choice of K, the data was additionally clustered with K = 110 to provide a more direct comparison between clustering results and the anatomical atlases (average number of clusters = 110). The metrics calculated on these clustering solutions are presented in Table I. The proposed group‐level clustering method outperforms the anatomical atlases even when number of clusters is controlled for. Again, random clustering shows similar performance to the group‐level clustering technique.

DISCUSSION

A major challenge for performing whole brain connectivity analysis of functional neuroimaging data is subdividing the brain into ROIs to be used as network nodes. The resulting ROIs should be few enough to ensure the computational feasibility of the desired analysis, while maintaining voxel scale accuracy. Several methods have been proposed for defining ROIs including the use of anatomical atlases, randomly splitting the brain into ROIs, and clustering functional data. These methods were systematically evaluated to compare their relative merits for FC analyses.

A key requirement for ROIs is that they be spatially coherent (connected) to preserve the distinction between local network nodes and large‐scale networks [Bellec et al., 2006; Smith et al., 2010]. Spatial coherence additionally improves the ability to interpret the neuroscientific relevance of the ROIs [Thirion et al., 2006]. This motivated the development of a spatially constrained group level clustering approach, which incorporates several aspects of previously proposed methods for generating ROIs [Bellec et al., 2006; Flandin et al., 2002b; Heller et al., 2006; Thirion et al., 2006] and clustering fMRI time‐series [van den Heuvel et al., 2008]. The proposed spatially constrained clustering algorithm provides a means to perform functional as well as random parcellation in the same framework. Other constraints can be introduced to force other properties onto the solution, for example, to explicitly ensure inter‐hemispheric symmetry, or to respect anatomical boundaries.

Two‐level clustering combined with the r _t similarity metric outperformed other functional parcellation strategies (Fig. 4). The differences in generalization performance between r _t and r _s may be due to higher intersubject variability of the r _s metric, which can also be visualized by the large standard deviations associated with high spatial correlation values (r _s ≥ .9) as compared to r _t (Supporting Information Fig. 2). The differences between two‐level and group mean clustering may be due to the tendency of the averaging process to degrade functional boundaries between regions. However, the small advantage in generalization of the two‐level approach comes at a great computational expense, justifying the use of the group mean approach for large datasets. Quality of clustering, as evaluated by silhouette width, does not differentiate the different methodological choices (Fig. 4e,f). Silhouette width was close to one for all of the employed methods, indicating that the proposed algorithm is correctly maximizing within cluster homogeneity to background correlation. Clustering using r _t and r _s similarity metrics optimize for temporal homogeneity (Fig. 4e) and spatial homogeneity (Fig. 4f) equally well, which further justifies the use of r _t even when spatial homogeneity is desired.

Parcellations generating 100 or less ROIs show high mean LOOCV accuracy, but also have high variance, indicating that some subjects did not fit these group level clusters well (Fig. 4a–d). These also fall into a “trivial” range, where ROIs are so large that high reproducibility is almost a certainty. Conversely, the silhouette metric is poor for parcellations with few ROIs and improves with increasing K (Fig. 4e,f). Ideally, a positive (Dice or silhouette) peak would identify the best clustering based on the data; but there is no peak and performance generally improves with the number of clusters. Thus, while this method was not able to identify the fundamental functional organization of the brain, it provides a multiresolution set of atlases of data‐derived ROIs, where the experimenter chooses the atlas resolution to use based on the demands of the analysis to be performed.

The anatomy based atlases all performed worse than the results of functional and random parcellation. The anatomical atlases' poor average within cluster temporal and spatial correlation indicates that ROIs from these atlases include functionally heterogeneous regions (see Fig. 5). This non‐specificity is further reflected in their poor accuracy in representing the FC that is present at the voxel level (Figs. 6 and 7). This network‐dependent phenomenon suggests that the FC of some brain regions is better represented than others. Differences in representation accuracy between parcellation results and anatomical atlases is greatest for the default mode network, which is likely due to the atlases poor representation of the ACC and other regions of the frontal cortex (see Fig. 7). Although these differences are largely influenced by cluster size, they persist when controlling for cluster size (Table I). We do not suggest that anatomical and cyto‐architectonic parcellations are irrelevant to resting state FC; rather, we suggest these atlases do not represent the anatomy in sufficient detail to distinguish between regions relevant to resting state FC analyses. Incorporating finer anatomical details as well as structural and FC measures into these atlases, or otherwise subdividing their constituent ROIs [Hagmann et al., 2008; Patel et al., 2008; Zalesky et al., 2010], will likely improve their performance.

The clustering results of random parcellation and functional parcellation are similar (Fig. 3, Supporting Information Fig. 1) although not identical (Figs. 3 and 4). One explanation for this finding—that the correlations between neighboring voxels are so high that they are approximately similar to the trivial connectivity graph (all edges = 1) used for random parcellation—is not supported by Supporting Information Figure 2. The random parcellation performs nearly as well as the functional parcellation in cluster homogeneity (see Fig. 5) as well representation accuracy (see Fig. 6). This leads to the conclusion that ROIs will perform well for FC analysis as long as they are relatively small, regardless of their position. Similar results were shown in an evaluation of random parcellation for calculating small world network statistics from DTI data [Zalesky et al. 2010]. While this suggests that resting state fMRI data could be acquired at a lower voxel resolution without a substantial loss of information (unless studying the FC between finer structures of the brain), this is unadvisable due to partial volume effects as well as susceptibility artifacts, which are exacerbated by thick slices.

The spatial constraint appears to dictate much of the size of the clusters, whereas the functional information refines the boundaries. This is an important point when choosing between functional parcellation and random parcellation. The results of functional parcellation generalize better to individuals than random clustering for solutions involving fewer than 800 clusters (Fig. 4c). Additionally functional parcellation offers marginal (although statistically significant) gains in terms of functional homogeneity (see Fig. 5) and accuracy of representation (see Fig. 6). Thus, functional parcellation is preferred over random parcellation when generalizability, homogeneity, and accuracy of representation are to be maximized. These metrics do not necessarily measure the correctness of ROI placement; this will require a more in‐depth comparison of these methods.

The application of clustering methods for delineating functional boundaries of the brain has become increasingly popular [Cohen et al. 2008; Kelly et al. 2010; Margulies et al. 2009]. It is unlikely that the method proposed here is appropriate for this type of analysis due to the volumetric bias induced by NCUT clustering as well as the spatial constraint. Clearly, functional units within the brain do not have uniform size: for example, functional units in the prefrontal cortex are larger than units in the thalamus, amygdala, or brainstem. However, the primary aim of the proposed clustering method is to reduce the dimensionality of the data while incorporating local FC data to help identify functionally homogeneous and spatially constrained clusters; a task for which it is well suited.

The choice of preprocessing pipeline is likely to have a large impact on clustering results. For example, using a different co‐registration strategy, or incorporating parcellation information into the co‐registration process [Thirion et al. 2006] may well improve the LOOCV results presented in Figure 4. Additionally the amount of spatial smoothing will affect parcellation results. Sources of spatial smoothing in the performed analysis include the MRI point spread function, motion correction, normalization to standardized space, and applying a spatial smoothing filter (6‐mm FWHM Gaussian) to improve the correspondence of brain regions across subjects. This smoothing will induce correlation that will no doubt influence the clustering results, although Supporting Information Figure 2 suggests that the data used for this analysis was not “over‐smoothed.” These comparisons were made using standard preprocessing steps for resting state fMRI data. Investigating the impact of preprocessing on clustering results is beyond the scope of this article.

Two commonly used methods for summarizing ROI time courses are averaging and alternatively using the first eigenvariate from a PCA analysis [Friston et al. 2006]. The PCA method preformed worse than simple averaging for all ROI sets considered, and this difference was most dramatic for the anatomical atlases as well as parcellations containing fewer than 200 clusters (Fig. 6d–f). This illustrates PCA's increased sensitivity to ROI functional heterogeneity. For an ROI that contains voxels from two separate functional units with linearly independent time courses, the PCA approach will extract but one of these time courses and the resulting FC pattern will reflect only the FC of one of the functional units in the ROI. However, the average time course will represent both functional units from the ROI (as long as the time courses do not add destructively) and the resulting FC pattern will incorporate contributions from both functional units.

The proposed methods for generating spatially constrained ROI atlases can be used to either generate a normative set of ROIs that are applied to independent data or to generate study‐specific ROIs. As with most data reduction techniques, this approach can be used to generate ROIs from the same data that is to be analyzed. Indeed, this approach may be preferred when the data to be analyzed is substantially different from the data used to generate ROIs–as may be the case for particularly old or young subjects, patients with neurological or psychiatric disorders, or data collected using substantially different scanning methods.

Future Applications of method

Future work will compare this functionally derived parcellation against those derived from anatomy, cytoarchitecture, and diffusion tensor imaging. The use of task data (as opposed to resting‐state data) may produce more refined and functional subdivisions. Additionally, the parcellation method presents a platform allowing unbiased assessment of parameter selection–for example, the weighting of edges by similarity metric, as we have demonstrated ‐ upon resulting parcellations. This is a crticial contribution to the neuroimaging field, which currently lacks such means for comparing parcellations.

CONCLUSION

In conclusion, the proposed method successfully parcellated group resting state fMRI data into spatially coherent functionally homogeneous clusters. ROIs generated from this parcellation outperform the anatomically derived ROI atlases evaluated in this study in the context of resting state FC analyses. Random parcellation outperformed the anatomical atlases and performed nearly as well as the results of functional parcellations in terms of cluster homogeneity and accuracy of representation. Functional parcellation outperformed random parcellation for all metrics but most substantially in terms of the generalizability of group level results to the individual. While there is no apparent best number of clusters, the method offers a multiresolution approach in which a level of clustering can be chosen based on the needs of the analysis at hand. If region interpretability is paramount, then K ≈ 150–200 can be used while preserving cluster homogeneity and without substantial loss of information. On the other hand, if interpretability can be sacrificed for highly accurate representation (e.g., for reproducibility studies) then K ≈ 1,000 offers a good choice. Either way, functional parcellation and random parcellation offer substantial reduction in dimensionality with minimal impact on the correlation structure of the data. Since this analysis was performed on resting state data, applying the derived atlases for task‐based analysis will require validation. We remain optimistic that parcellation derived on resting state data is applicable to task based on recent results using ICA [Smith et al. 2009].

The software used for this analysis and the resulting ROI maps have been made available at NITRC for public use http://www.nitrc.org/projects/cluster_roi/.

Supporting information

Additional Supporting Information may be found in the online version of this article.

Supporting Information Figure 1

Supporting Information Figure 2