Multivariate Modeling of Age and Retest in Longitudinal Studies of Cognitive Abilities

Abstract

Longitudinal multivariate mixed models were used to examine the correlates of change between memory and processing speed and the contribution of age and retest to such change correlates. Various age- and occasion-mixed models were fitted to 2 longitudinal data sets of adult individuals (N > 1,200). For both data sets, the results indicated that the correlation between the age slopes of memory and processing speed decreased when retest effects were included in the model. If retest effects existed in the data but were not modeled, the correlation between the age slopes was positively biased. The authors suggest that although the changes in memory and processing speed may be correlated over time, age alone does not capture such a covariation.

Practice effects are one source of possible confounding effects in longitudinal studies. Individuals who repeat a test may perform better merely as a result of the influence from the previous assessment. In the context of a longitudinal study with repeated observations, the effects attributed to age might be contaminated with retest effects (Donaldson & Horn, 1992; Hertzog & Nesselroade, 2003). Several articles have illustrated this issue and the need to model separate effects for age and retest (Ferrer, Salthouse, Stewart, & Schwartz, 2004; Lövdén, Ghisletta, & Lindenberger, 2004; McArdle & Anderson, 1990; McArdle, Ferrer-Caja, Hamagami, & Woodcock, 2002; McArdle & Woodcock, 1997; Rabbitt, Diggle, Holland, & McInnes, 2004; Rabbitt, Diggle, Smith, Holland, & McInnes, 2001; Salthouse, Schroeder, & Ferrer, 2004; Wilson et al., 2002). Important findings from these studies indicate that both age and retest should be modeled simultaneously when examining change of cognitive abilities over time. When practice effects exist as a result of repeated assessments, ignoring the retest component underestimates the negative age effects, with larger bias for stronger retest effects. In this study, we extend this work to multivariate analyses. We argue that similar bias existing in univariate studies may occur in multivariate analyses that focus on correlates of change. Such correlates of change have age and retest components, and both need to be modeled separately to identify their own contribution to the change correlation.

One essential question in current research in cognitive aging is the extent to which various cognitive domains change in a parallel way. Researchers are interested in examining whether cognitive abilities covary over age or whether they change independently as a function of different underlying mechanisms (e.g., Deary, 2001). A large number of cross-sectional studies have examined this question by comparing age-related variance in various cognitive abilities and then estimating the shared part of the variance (Baltes & Lindenberger, 1997; Lindenberger & Baltes, 1994; Rabbitt, 1993; Salthouse & Ferrer-Caja, 2003). In general, results from these studies suggest that age-related decline is common to most abilities: When one cognitive function deteriorates, the other functions weaken, too. However, a full account of this age-related covariation among multiple cognitive abilities needs to consider both general and specific factors (Salthouse & Ferrer-Caja, 2003).

One limitation of cross-sectional studies, however, is that the age-related covariation among different domains is examined indirectly. Longitudinal studies, on the other hand, can directly examine such covariation because they can follow the changes in each variable over time. Unfortunately, not many longitudinal studies have addressed this issue, and moreover, their results are not uniform. For example, Hultsch, Hertzog, Dixon, and Small (1998) found only moderate correlations between the rates of change of various cognitive functions over 6 years. Similarly, Anstey, Hofer, and Luszcz (2003) detected a small relationship between sensory and cognitive changes over 8 years, and Christensen et al. (2000) found only moderate correlations between processing speed and memory among older individuals. Finally, weaker—or not detectable—correlations were found between longitudinal changes of perceptual speed and episodic memory (Sliwinski & Buschke, 1997; Sliwinski, Hofer, & Hall, 2003; Taylor, Miller, & Tinklenberg, 1992) and between the rates of change of various forms of memory over up to 25 years (Giambra, Arenberg, Zonderman, Kawas, & Costa, 1995).

Although these longitudinal studies are informative—and more suitable to examine change correlations than cross-sectional analyses—the analyses used in these studies are based on the assumption that age is the only factor contributing to correlations among measures of change. This assumption, however, might not be realistic in cases when age alone does not capture all of the changes in a particular variable. In those cases, a broader conceptualization may be needed to examine the correlates of change. In other words, if both age and retest effects are found to underlie changes in various cognitive abilities, it is reasonable to assume that both effects may also play a role in the correlation between the changes in those variables. Moreover, if ignoring retest effects can underestimate age effects in univariate analysis, it is reasonable to question whether similar biases exist in multivariate models that focus on correlates of change without considering retest effects.

Understanding the different components underlying the correlates of change among cognitive abilities has important implications. For example, correlations of change could be primarily due to retest, in which case they might reflect common learning processes. If, on the other hand, the correlations of change were primarily due to age, they would potentially reflect a common maturation—or aging—process.

Despite the important implications of understanding the components of correlates of change, this question has received very little attention. In an exception, Wilson et al. (2002) examined the covariation in change among different cognitive abilities over 6 years. Using univariate models, the researchers estimated individual longitudinal age slopes and then used these slopes to compute the correlations for each pair of variables. The results from these analyses yielded correlations ranging from .37 (word knowledge and visuospatial ability) to .78 (story retention and word retention), with a median of .54, and all loaded on a single factor in a principal-components analysis. Further, when retest effects were considered, the correlations were not altered, and again, a single factor of change was found to account for about 62% of all the covariation.

Wilson et al.’s (2002) approach is innovative but might not be ideal to decompose the different components of the change correlates. It is a two-stage process of estimation of individual slopes from univariate models to then compute multivariate comparisons. By definition, however, each of these univariate models assumes independence, which is exactly the question at hand. We propose that a potentially more powerful approach is to model directly the correlation between the changes of two—or more—variables in a single model that includes both hypothesized components (i.e., age and retest). This approach seems more appropriate to make inferences about correlations between variables, especially when examining whether the correlations depend on the within- or between-person variation. Moreover, a multivariate approach is more powerful than the univariate analyses to examine the age and retest effects for the various cognitive abilities, particularly when they are correlated and have different patterns of missing data (e.g., see Raudenbush & Bryk, 2002; Snijders & Bosker, 1999).

Examining relations among the growth of two or more variables is possible with multivariate models of change (Goldstein, 1995; MacCalum, Kim, Malarkey, & Kielcolt-Glasser, 1997; McArdle, 1988; Rogosa & Willett, 1985; Tisak & Meredith, 1990; Willett & Sayer, 1994, 1995). In fact, since the appearance of these models, researchers have been interested in understanding correlates of change between the growth of variables. That is, the focus is on the relationships between patterns of change on two or more variables (Hertzog & Nesselroade, 2003). If one is interested in examining the different components underlying the correlates of change between two variables for which retest effects may exist, any of these models can be extended to accommodate such components.

Our goal in this study is to fit such models to longitudinal data to examine the contribution of age and retest effects to the correlates of change between cognitive abilities during adulthood. To achieve our goal, we first give some theoretical background of the models and their specification in the multivariate case with retest components. We then fit these models to two different longitudinal data sets and examine the resulting change correlations when retest components are included and omitted from the model.

Age- and Occasion-Based Mixed-Growth Models

A basic growth model for a dependent variable Y measured over time (t = 1 to T) on a person (n = 1 to N) can be written as

$$Y{[t]}_n=y_{0n}+\mathit{\text{Age}}{[t]}_n·y_{sn}+e{[t]}_n,$$ (1)

where Y[t]_n is the observed score on person n at measurement t; y_0n is the latent initial level score of person n; Age[t]_n is the observed age of person n at measurement t; y_sn is a latent score of person n, representing the slope, or the individual change over time; and e[t]_n is the latent error score of person n at measurement t. This model includes sources of individual differences in the level and slope, whose terms can be decomposed at a second level as

$$y_{0n}={\mu }_0+e_{0n}\text{and}{y}_{sn}={\mu }_s+e_{sn},$$ (2)

where the level and slope scores have fixed group means (μ₀ and μ_s) and residuals (e_0n and e_sn), and these residuals have variance components (σ₀², σ_s², and σ_0s).

This initial age-based model can be extended to incorporate retest effects as

$$Y{[t]}_n=y_{0n}+\mathit{\text{Age}}{[t]}_n·y_{\mathrm{s}\mathrm{n}}+B{[t]}_n·y_{pn}+e{[t]}_n,$$ (3)

where y_pn represents the slope, or individual change in retest over time, for person n; and B[t] represents the set of coefficients that define the shape of the retest effects. Similar to the model in Equation 1, the terms of this model can be decomposed at a second level as

$$y_{0n}={\mu }_0+e_{0n},y_{sn}={\mu }_s+e_{sn},\text{and}{y}_{pn}={\mu }_p+e_{pn},$$ (4)

where the level, slope, and practice scores have fixed group means (μ₀, μ_s, and μ_p) and residuals (e_0n, e_sn, and e_pn), and these residuals have variance components (σ₀², σ_s², and σ_p²) and could covary among themselves (σ_0s, σ_0p, and σ_sp) According to this model, change in Y can be described as a function of two processes that unfold over time: chronological age and retest. Age[t]_n · y_sn can vary over time for each person, so this term represents an age-based growth process. In turn, the practice term, B[t]_n · y_pn, reflects a process based on the measurement occasion (i.e., average change in Y per unit change in retest for a person n).

By varying the specification of age and retest, these models can be used to test different hypotheses of change. For example, questions regarding linear age and retest could be examined by setting the basis coefficients for age as Age[t]_n fixed = 0, 1, 2, …, age[t], and the retest coefficients as B[t]_n = 0, 1, 2, …, occasion[t]. Similarly, this general model can accommodate other hypotheses regarding the age function, the retest function, or both. For instance, a specification of B[t]_n = 0, 1, 1, 1, … 1 would imply that retest effects occur at the second measurement occasion (first retest) and that they remain constant over time. Similarly, a specification of B[t]_n = 0, 1, ?, ?, …, 1 would examine the extent to which retest takes place in a nonlinear way, with unequal effects at different measurement occasions (for more details, see Ferrer et al., 2004).

In the bivariate case, this model can be written for variables Y[t] and X[t] over time as a model of two growth curves as

$$Y{[t]}_n=y_{0n}+{\mathit{\text{Age}}}_y{[t]}_n·y_{sn}+B_y{[t]}_n·y_{pn}+e_y{[t]}_n,\text{and}X{[t]}_n=x_{0n}+{\mathit{\text{Age}}}_x{[t]}_n·x_{sn}+B_x{[t]}_n·x_{pn}+e_x{[t]}_n,$$ (5)

with all covariances allowed among the latent variables (σ_y[i],x[j]). Among these covariances, two are key to examine correlates of change between Y and X: σ_ys,xs and σ_yp,xp; the former represents the covariance between the age slopes of the two variables, whereas the latter represents the covariance between the retest slopes of the two variables. In subsequent sections, we examine how both covariances contribute to the overall correlation of change between the two variables; thus, omitting one from the model may lead to bias in the estimation of such a change correlation.

This bivariate model can also be written by using a random coefficient or multilevel notation as a model with a single outcome variable Y_ntk for individual n at occasion t on variable k, where the variables k do not need to be measured at the same occasions for all individuals, as

$$Y_{ntk}=\sum _{k=1}^m{d}_k({\beta }_{0nk}+{\beta }_{1nk}·{\mathit{\text{Age}}}_{ntk}+{\beta }_{2nk}·p_{ntk}+e_{ntk}),$$ (6)

where k = 1, …, m represents the number of variables (two in this study); d_k is a dummy variable d₁ to d_m (1 or 0) to indicate the dependent variables; β_0nk is the intercept for person n on variable k; β_1nk is the slope associated with age for person n on variable k; β_2nk is the slope associated with retest p for person n on variable k; and e_ntk is the residual for person n at occasion t for variable k. Similar to Equations 2 and 4, the intercepts and slopes for the k variables can be decomposed as

$${\beta }_{0nk}={\beta }_{0k}+u_{0nk},{\beta }_{1nk}={\beta }_{1k}+u_{1nk},\text{and}{\beta }_{2nk}={\beta }_{2k}+u_{2nk},$$ (7)

which indicates that for each variable k, the intercept, slope, and practice have fixed group means (β_0k, β_1k, and β_2k) and random residuals (u_0k, u_1k, and u_2k), and these residuals have variance components (σ_0k², σ_1k², and σ_2k²) and could covary among themselves (σ_01k, σ_02k, and σ_12k). In addition to these within-variable k random effects, covariances between intercepts and slopes are also allowed between variables. Among all these covariances, two are fundamental to examine correlates of change between the outcome variables: σ_1y,1x represents the covariance between the age slopes of variables y and x, and σ_2y,2x represents the covariance between the retest slopes of variables. The former is an indicator of the degree of association between the rates of age-related change on both variables, and the latter is an indicator of the degree of association between the rates of change related to retest. It follows from this decomposition that both covariances contribute to the overall correlation of change between variables y and x.¹ Moreover, to test specific hypotheses—or merely due to data constraints—restrictions can be imposed as needed in the covariance matrix of individual residual variances T = cov(E_nt) and in the between-individual covariance matrix Σ = cov(U_t). This model can now be estimated by using any standard multilevel program.

Method

Participants

In this study, we used data from two different studies. The first data set is from the Age, Lead Exposure, and Neurobehavioral Decline (ALEND) study (Walter F. Stewart, principal investigator). The second data set is from the National Growth and Change Study (NGCS; John J. McArdle, principal investigator). Detailed information about the first project is available in previously published studies (e.g., Schwartz et al., 2000; Stewart et al., 1999). Characteristics of the specific data used here are also available elsewhere (Ferrer et al., 2004). Extensive information about design, participants, and measures of the second project is also available (McArdle et al., 2002).

The participants from the ALEND Study were 834 individuals who took part in a 4-year prospective study to evaluate the effects of lead exposure on changes in cognitive function. All participants were men between 40 and 70 years of age at the first assessment, with data from one to four occasions, and a first retest interval ranging from 0.6 to 2.8 years. The NGCS is an ongoing project focused on the study of cognitive abilities over the life span. Individuals in the NGCS initially participated in the Woodcock-Johnson Psycho-Educational Battery—Revised (WJ–R, Woodcock & Johnson, 1989–1990) norming study and were selected from the norming sample on the basis of a stratified randomized sampling following such criteria as geographic region, demographic density, gender, and ethnicity. From this pool of individuals with two measurement occasions (N = 1,193), a third wave of data was collected by using similar criteria, but with an emphasis toward older individuals (n = 176). To match the ALEND sample on age, we selected a subsample of 382 individuals from the NGCS retest pool whose ages ranged from 30 to 80 at the first measurement occasion, with data from two to three occasions and a first retest interval ranging from 0.8 to 10 years.

Measures

Participants in the ALEND study visited a clinical setting for up to four occasions at which time they completed a comprehensive neurobehavioral battery and were assessed on a number of biological measures. The current analyses involve two composites representing verbal learning and memory and processing speed, which were created on the basis of an exploratory factor analysis on the original variables (for details and results of this procedure, see Ferrer et al., 2004). The verbal learning and memory composite was composed of several measures from the Rey Auditory Verbal Learning Test (total score across five recall trials, delayed recall, and recognition test score). The processing speed composite was composed of a choice reaction time task, the Stroop test (A, B, and C forms), Trail Making Tests A and B, and the Digit Symbol subtest from the Wechsler Adult Intelligence Scale—Revised. The same versions of the tests were administered on each occasion.

To maximize across-sample comparisons, measures that hypothetically represented similar constructs were selected from the NGCS data. Specifically, two tests of the WJ–R battery (McGrew, Werder, & Woodcock, 1991) were used to compute, as unit-weighted composites and according to WJ–R guidelines, scales of short-term memory and processing speed. The selected tests were Memory for Words and Memory for Sentences (Short-Term Memory, Gsm), and Visual Matching and Cross Out (Processing Speed, Gs). All these scales are reported to have very high internal consistency (McArdle et al., 2002; McGrew et al., 1991).

Data Description

A description of the participants’ age and retest intervals at all time points and across samples is presented in Table 1. To facilitate comparisons, information is presented for the overall sample and for different age groups (i.e., younger than 50 years, between 50 and 59 years, and 60 years and older). It can be seen that participants from the NGCS sample have a wider age range than the ALEND participants. Of the initial 827 ALEND participants who reported their age, 86.7%, 72.3%, and 66.0% were present at the second, third, and fourth occasions, respectively. Of the 382 NGCS participants present at the first and second occasions, about 31% were assessed at the third occasion. For both samples, the retention rates are smaller for the younger individuals and similar in the two older age groups.

Table 1.

Description of Ages and Time Retests

	Time 1		Time 2		Time 3		Time 4
Age group	ALEND	NGCS	ALEND	NGCS	ALEND	NGCS	ALEND	NGCS
50 years	45.9	39.1	47.1	42.1	47.9	45.9	49.0	—
Δ age			0.987	2.97	0.885	3.30	0.946	—
n	181	181	153	180	130	47	102	—
50–59 years	55.0	54.9	56.1	57.9	56.9	61.2	57.8	—
Δ age			1.04	3.04	0.856	3.44	0.923	—
n	357	60	319	60	265	21	249	—
>60 years	64.8	69.8	65.9	72.2	66.5	74.7	67.5	—
Δ age			1.05	2.38	0.835	2.49	0.924	—
n	289	141	244	141	203	51	194	—
All	56.5	52.9	57.5	55.7	58.2	60.9	59.6	—
Δ age			1.03	2.79	0.857	5.20	0.927	—
n	827	382	717	381	598	119	545	—

Note. Dashes indicate that data were not obtained. ALEND = Age, Lead Exposure, and Neurobehavioural Decline Study; NGCS = National Growth and Charge Study.

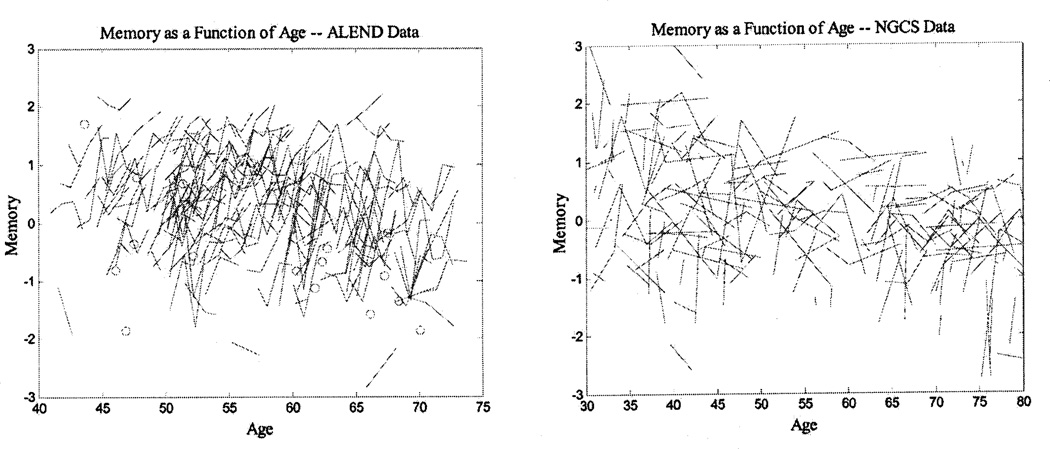
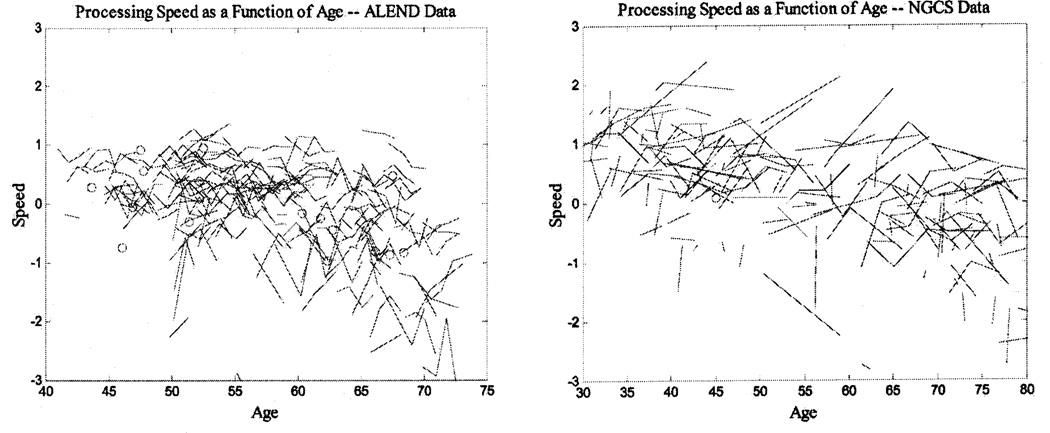
Table 2 presents means and standard deviations for the memory and processing speed composites across the different measurement occasions for both samples. These descriptive statistics indicate an increase in memory scores across occasions for the ALEND participants and a smaller increase for the NGCS participants, but only from the first to the second occasion. For speed scores, the increases appear to be smaller overall. These patterns of change across measurement occasions and over age are displayed in Figures 1 and 2, for memory and speed, respectively.

Table 2.

Descriptive Statistics Across Samples and Measurement Occasions

	Time 1		Time 2		Time 3		Time 4
Variable	M	SD	M	SD	M	SD	M	SD
Memory ALEND	−0.005	0.881	0.275	0.831	0.442	0.802	0.529	0.860
Memory NGCS	0.000	1.00	0.104	0.959	0.054	0.927
Speed ALEND	−0.012	0.754	0.066	0.766	0.068	0.686	−0.013	0.868
Speed NGCS	0.000	1.00	0.077	1.06	0.130	1.06

Note. All values are based on Z scores computed from Time 1. ALEND = Age, Lead Exposure, and Neurobehavioural Decline Study; NGCS = National Growth and Charge Study.

Figure 1.

Individual longitudinal data for each data set. All figures represent a random 30% of all the cases. ALEND = Age, Lead Exposure, and Neurobehavioral Decline Study; NGCS = National Growth and Change Study.

Figure 2.

Individual longitudinal data with the same variables superimposed across data sets. All figures represent a random 30% of all the cases. ALEND = Age, Lead Exposure, and Neurobehavioral Decline Study; NGCS = National Growth and Change Study.

Results

Multivariate Age- and Occasion-Based Mixed-Growth Analyses

All the analyses reported here were conducted by using the MIXED procedure in SAS (Littell, Miliken, Stoup, & Wolfinger, 1996) with a maximum likelihood estimation method. This method generates parameter estimates by using all available data under the assumption that incomplete data are missing at random.

Previous analyses using the ALEND data focused on the age versus age and retest issue at the univariate level. Extensive information about background and results from these analyses was provided by Ferrer et al. (2004). In this article, we focus on multivariate analyses in which memory and processing speed were considered simultaneously. In particular, three progressively more complex models were fitted to the multivariate data: (a) a model with only correlated age components and their associated random effects, (b) a model with age and retest components but not random effects associated with the retest components, and (c) a model including random effects for retest and a correlation between both retest slopes. In all these models, age was coded in years and centered at 40 years. Retest was coded as 0, 1, 2, and 3 for the ALEND data and 0, 1, and 2 for the NGCS data. If participants had only 2 measurements, they were coded as 0 and 1. Results from these analyses are presented in Tables 3 and 4, for the ALEND and NGCS data sets, respectively.

Table 3.

Parameter Estimates From the Multivariate Growth Model for Memory and Speed (ALEND Data)

	Age only				Retest components				Retest variance
Parameter	Memory		Speed		Memory		Speed		Memory	Speed
Fixed effects
μ0 intercept	.247 (.067)		.539 (.047)		.574 (.065)		.661 (.049)		.563 (.064)	.648 (.051)
μa linear age	.001, ns (.004)		−.029 (.003)		−.033 (.004)		−.038 (.033)		−.032 (.033)	−.038 (.003)
μp retest	—	—	—	—	.201 (.008)		.023 (.006)		.202 (.008)	.022 (.008)
Random effects
${\sigma }_0^2$ intercept	.7202 (.1413)		.2622 (.0634)		.6815 (.1285)		.2679 (.0615)		.6496 (.1170)	.3689 (.0863)
${\sigma }_a^2$ age	.0013 (.0005)		.0012 (.0003)		.0010 (.0004)		.0010 (.0003)		.0006, ns (.0004)	.0012 (.0004)
${\sigma }_p^2$ retest	—	—	—	—	—	—	—	—	.0110 (.0030)	.0256 (.0026)
ρ00 level–level	.3012 (.1378)				.3199 (.1342)				.2793 (.1318)
ρaa age–age	.7344 (.1753)				.6753 (.2122)				.6290 (.3033)
ρpp retest–retest	—		—		—		—		.5920 (.1158)
ρ0a level–age	−.5558 (.1236)		−.3314 (.1682)		−.5665 (.1228)		−.3123, ns (.1767)		−.4694 (.1662)	−.5333 (.1442)
ρ0p level–retest	—	—	—	—	—	—	—	—	−.2573, ns (.2100)	.4597 (.1015)
ρap age–retest	—	—	—	—	—	—	—	—	.0590, ns (.3731)	−.4530 (.1056)
${\sigma }_e^2$ residual	.1977 (.0069)		.0821 (.0028)		.1529 (.0051)		.0822 (.0028)		.1363 (.0056)	.0527 (.0022)
σee residual	.0162 (.0032)				.0133 (.0027)				.0016, ns (.0025)
Goodness of fit
−2 log-likelihood	8,259				7,677				7,404
BIC	8,373				7,805				7,599
Parameters NP	17				19				30
Δ RMSEAa	—				.593				.188

Note. Number of subjects = 828. Number of data points = 5,359. Age at Time 1 = 39–74 years. First retest interval = 1.03 years (0.60–2.80). All parameters are maximum likelihood estimates obtained with SAS MIXED. Dashes indicate a parameter that was not estimated. ALEND = Age, Lead Exposure, and Neurobehavioural Decline Study; ns = not significant (p > .05); BIC = Bayesian Information Criterion; NP = number of parameters; RMSEA = root-mean-square error of approximation.

^aRMSEA of the fit difference.

Table 4.

Parameter Estimates From the Multivariate Growth Model for Memory and Speed (NGCS Data)

	Age only				Retest components				Retest variance
Parameter	Memory		Speed		Memory		Speed		Memory	Speed
Fixed effects
μ0 intercept	.391 (.060)		.621 (.037)		.395 (.061)		.605 (.037)		.415 (.061)	.628 (.037)
μa linear age	−.018 (.003)		−.030 (.002)		−.024 (.003)		−.037 (.002)		−.025 (.003)	−.040 (.002)
μp retest	—	—	—	—	.124 (.027)		.145 (.018)		.110 (.028)	.125 (.019)
Random effects
${\sigma }_0^2$ intercept	.6202 (.0811)		.2473 (.0300)		.6221 (.0809)		.2482 (.0294)		.6764 (.0911)	.2731 (.0354)
${\sigma }_a^2$ age	.0007 (.0002)		.0003, ns (.0002)		.0006 (.0002)		.0002, ns (.0001)		.0006 (.0002)	.0001 (.0000)
${\sigma }_p^2$ retest	—	—	—	—	—	—	—	—	.0458, ns (.0257)	.0173, ns (.0154)
ρ00 level–level	.5180 (.0671)				.5087 (.0674)				.5182 (.0737)
ρaa age–age	.8211 (.2945)				.7484 (.3536)				.5773, ns (.5775)
ρpp retest–retest	—		—		—		—		.4490, ns (.3620)
ρ0a level–age	−.6262 (.0991)		.6805, ns (.4523)		−.6258 (.0993)		.7358, ns (.5339)		−.5736 (.1102)	−.5926, ns (.4821)
ρ0p level–retest	—	—	—	—	—	—	—	—	−.3291, ns (.2307)	−.2285, ns (.2553)
ρap age–retest	—	—	—	—	—	—	—	—	−.0627, ns (.3428)	.7714, ns (.8808)
σe2 residual	.2568 (.0169)		.1141 (.0076)		.2487 (.0163)		.1053 (.0069)		.2202 (.0209)	.0907 (.0109)
Goodness of fit
−2 log-likelihood	3,303				3,227				3,211
BIC	3398				3,334				3,377
Parameters NP	16				18				29
Δ RMSEAa	—				.312				.035

Note. Number of subjects = 382. Number of data points = 1,734. Age at Time 1 = 30–80 years. First retest interval = 2.76 years (0.80–10.00). All parameters are maximum likelihood estimates obtained with SAS MIXED and NLMIXED. Dashes indicate that a parameter that was not estimated. NCGS = National Growth and Change Study; ns = not significant (p > .05); BIC = Bayesian Information Criterion; NP = number of parameters; RMSEA = root-mean-square error of approximation.

^aRMSEA of the fit difference.

The first columns (“Age only”) in Table 3 display the parameter estimates from a model with only linear age effects for memory and processing speed. These estimates are comparable to the ones reported using separate univariate models for each variable (Ferrer et al., 2004). These results indicated a flat trajectory over age for memory (µ_a = .001, p > .05) with small variation across persons (σ_a² = .0013) and a linear declining trajectory for processing speed (μ_a = −.029 units of decline per year), also with very small variation across persons (σ_a² = .0012). Note, however, that the low variability could also be due to the scaling of the variables (i.e., z scores from first occasion) and the time metric (i.e., 1-year units). Other random effects in this model indicated a moderate correlation between initial levels of both variables (ρ = .30, at age 40); a strong correlation between the age slopes of both variables (ρ = .73), suggesting that the rate of change in memory is associated with the rate of change in processing speed; and a small correlation between both residuals (ρ = .13; σ_ee = .016), representing the part in common between both variables not accounted for by the model.

The second columns (“Retest components”) in Table 3 present the estimates from a model in which retest components (fixed effects only) were added to the model. In line with findings from univariate models (Ferrer et al., 2004), these estimates indicated a decline in both memory (μ_a = −.033) and processing speed (μ_a = −.038); both were more substantial than in the previous model without the retest component. The estimates from retest indicated nontrivial effects for both memory and processing speed (μ_p = .201 and .023, respectively), representing increases in performance from one measurement occasion to the next. Compared with the previous model, the random effects now indicate a similar correlation between initial levels (ρ = .32), a smaller correlation between the age slopes of both variables (ρ = .67), and a similar correlation between both residuals (ρ = .12). The residual variance (i.e., representing unexplained within-individual variation) was reduced for memory, which showed a larger retest effect, and the overall model misfit was reduced significantly, as compared with the previous model, by including the two retest parameters (χ²/df = 582/2; Δ root-mean-square error of approximation [RMSEA] = .593).

The third columns (“Retest variance”) in Table 3 present parameter estimates from a model in which random effects for retest were included. Adding these new parameters to the model did not alter the estimates of the fixed effects, suggesting linear declines in both memory and processing speed over age and positive effects associated with retests (μ_p = .202 and .022, for memory and speed, respectively), although much larger for memory. The random effects, however, were different, indicating nontrivial between-person variation in retest effects for both variables (σ_p² = .011 and .026), a slight decrease in the correlations between the intercepts (ρ = .28) and between the age slopes (ρ = .63), and a larger decrease in the correlation of the residuals (ρ = .02, p > .05). This model also presents a nontrivial correlation between the retest effects for both variables (ρ = .59). Adding these new parameters resulted in smaller residual variances and a much better fit, as compared with previous models (χ²/df = 273/11; Δ RMSEA = .188).

In addition to the correlations of the change components between both variables, this last model also presents within-variable correlations that are informative about the change for each variable. For example, for both variables, age was negatively correlated with the initial level (ρ = −.47, and −.53), suggesting that age-related declines in memory and processing speed were slower for individuals with higher initial scores. In contrast, the correlation between level and retest is zero for memory (ρ = −.25, p > .05) and positive for processing speed (ρ = .46), the latter indicating that individuals with higher scores benefited more from the repeated assessments. Finally, age was not correlated with retest for memory (ρ = .06, p > .05), but this correlation was negative for processing speed (ρ = −.45), suggesting that individuals with greater age declines had larger retest gains, and vice versa.

Although results in Table 3 refer to models with linear age, other nonlinear functions were examined. For example, a model with a quadratic age component (in addition to the linear function) yielded a better fit to the data but suggested (a) no linear effects for any variable, (b) a very small quadratic effect for memory (−.001) and no quadratic effect for speed, and (c) out-of-bounds correlations between the quadratic slope for each variable and all other components. Because of the large number of parameters in these models and the lack of interpretation of some estimates, we decided to retain models with linear age effects.

Results from similar models fitted to the NGCS data are presented in Table 4. These results indicate the existence of age and practice components in both variables. Adding practice effects to the model (i.e., the second columns: “Retest components”) reduced the age–slopes correlation (from ρ = .82 to .75) and the residual variances in both variables (σ_e² = .257 to .249, and .114 to .105, for memory and processing speed, respectively). These two retest parameters also helped to reduce the misfit of the model considerably (χ²/df = 80/2; Δ RMSEA = .312). The third model considered the variance components associated with the two retest effects, but these were negligible for both variables. In this model, the correlation between both levels remained unchanged (ρ = .52), but the correlation of the age slopes between both variables decreased and was no longer significantly different from zero (ρ = .58, p > .05). The correlation between both retest slopes was also not significant (ρ = .45, p > .05). For memory, age was negatively related to initial level, suggesting smaller declines for those individuals with higher starting scores. This association, however, was not significant for processing speed. Finally, the level–retest and age–retest correlations were all not different from zero for both variables. Although this model reduced the residuals substantially, it did not improve the fit (χ²/df = 16/11; Δ RMSEA = .035). Because of the reduced sample size at the third measurement occasion, the residuals correlation was not estimated for these data.

As compared with the results from the ALEND data, the estimates from the NGCS data indicate slightly lower stalling points for memory and similar starting points for processing speed (age was also centered at 40), smaller age slopes for memory (perhaps due to the participants being 10 years younger at the beginning of the sample) and similar age slopes for processing speed, and smaller practice effects for memory and larger practice effects for processing speed.

Alternative Age and Retest Hypotheses

The numerical results presented in Tables 3 and 4 are from models specifying age and retest as linear functions. In a new set of analyses, we considered alternative hypotheses of age and retest. In the first set of analyses, we examined the possibility that memory and processing speed follow independent trajectories over time. For this, we tested a model in which all the correlations between both variables were fixed to zero, leaving the within-variable correlations free to estimate. For both data sets, these models yielded much worse fit than any model that included across-variable correlations (χ²/df = 158/4, 126/4, and 162/9, as compared with the models included in Table 3; χ²/df = 82/4, 76/4, and 80/9, as compared with the models from Table 4). These results indicate that the hypothesis of independent trajectories is not tenable for these data and, instead, suggest that memory and processing speed follow trajectories that covary over time.

The second set of analyses examined different hypotheses of retest effects. Linear retest may not be a realistic hypothesis, but it was used here both for statistical convenience (i.e., simplicity) and as an adequate reference to evaluate alternative specifications. First, a model was fitted in which retests effects were allowed to vary at each repeated assessment (i.e., using dummy codes that represented each measurement occasion). For the ALEND data, this “stepwise” retest model improved the fit relative to a model with a linear retest function (χ²/df = 77/4) and yielded estimates that indicated noticeable retest effects across all measurement occasions for memory (β_p = .284, .173, and .179, for the first, second, and third retests, respectively) but not for processing speed (β_p = .099, .018, and .001; the latter two were not different from zero). For the NGCS data, in contrast, a similar stepwise model did not substantially improve the fit of a model with a linear retest function (χ²/df = 5/2). The retest estimates from this model suggest that retest effects occurred at the first repeated assessment only for memory (β_p = .164 and .035; the latter value was not different from zero) and at both retests for processing speed (β_p = .172 and .084).

In the last set of analyses, we investigated the extent to which retest effects were associated with age and with the age slope. This question was initially addressed by examining whether retests effects depended on the age at which individuals were assessed for the first time. To test this hypothesis, we included age at the first occasion as a predictor of retest. For the ALEND data, the results of this model indicated a nonsignificant effect for memory (μ_a1*p = −.0004) and a very small effect for processing speed (μ_a1*p = −.0024), in the direction of smaller retest effects for those older individuals who started the study at older ages. Although this model slightly improved the fit (χ²/df = 12/2), adding these parameters did not alter any other estimates in the model. Similarly, for the NGCS data, this model indicated a nonsignificant effect for memory (μ_a1*p = −.002) and a very small effect for processing speed (μ_a1*p = −.004), with also a minor improvement in fit (χ²/df = 11/2).

A second approach to examine the relationship between age and retest effects was via spline models. In these models, the age span is fragmented into segments and linear functions are fitted to each of these segments. In our analyses, the model tested considered two linear age segments with a knot (i.e., inflection point) at age 60. For the ALEND data, the estimates indicated similar age-related declines across the two segments (μ_a1 = −.031 and μ_a2 = −.032, for memory; μ_a1 = −.039 and μ_a2 = −.038, for processing speed). The retest estimates, however, indicated similar effects across the two age segments for memory (μ_p1 = .201 and μ_p2 = .201) but not for processing speed (μ_p1 = .035 and μ_p2 = .011, p > .05); these results were in line with the age–retest correlations from previous models. In addition, the age–slope correlation between both variables was different across the two segments (ρ₁ = .87 and ρ₁ = .79), indicating that such covariation declines for older ages. The fit of this model, however, was worse than that of previous models for the same data (−2 log-likelihood = 7,673; Bayesian Information Criterion = 7,895, with 33 parameters).

A similar spline model was fitted to the NGCS data also with a knot point at age 60. The estimates of this model also indicated comparable age-related declines across the two segments (μ_a1 = −.022 and μ_a2 = −.023, for memory; μ_a1 = −.037 and μ_a2 = −.035, for processing speed). In contrast to the ALEND data, the retest estimates indicated weakening effects across the two age segments for both memory (μ_p1 = .139 and μ_p2 = 096) and processing speed (μ_p1 = .179 and μ_p2 = .087). For these data, the correlation between age slopes of both variables was not different from zero for either segment. As was the case for the ALEND data, the fit of this spline model was not better than that of previous specifications (−2 log-likelihood = 3,212; Bayesian Information Criterion = 3,408, with 33 parameters).

Discussion

Summary of Results

In this study, we examined the correlates of change between two cognitive abilities and the contribution of age and retest to such change correlates. We investigated this issue by fitting various age- and occasion-mixed models to two longitudinal data sets of adult individuals. For both data sets, our findings indicate that the correlation between the age slopes of memory and processing speed decreases—albeit only slightly in some cases—when retest effects are included in the model. If such retest effects exist in the data but are not included in the model, the age–slopes correlation is positively biased because it absorbs all the covariance in the change between both variables. Moreover, not controlling for retest effects would have allowed an inference that there was no age-associated decline in memory scores.

The two data sets used in these analyses present some distinct features. The first data set (i.e., ALEND) included information from men only and had a shorter age range, shorter retest intervals, and up to four data points per person. The second data set (i.e., NGCS) included information from a nationally representative sample and had long interval retests and information from up to three assessments. In spite of these differences, both data sets yielded similar results: The correlation between the age slopes of memory and processing speed is reduced when retest effects are included in the model.

This study extends recent univariate analyses showing that when analyzing longitudinal data in which retest effects may exist as a result of repeated assessments, ignoring such retest effects tends to underestimate the age effects, and thus, both terms should be modeled simultaneously (Ferrer et al., 2004; McArdle et al., 2002; Rabbitt et al., 2001, 2004; Salthouse et al., 2004; Wilson et al., 2002). In the current study, we extended this issue to the multivariate level, and we showed that a similar bias existing in univariate analysis may be present in multivariate correlates of change. Such correlates of change have age and retest components, and both terms need to be modeled to identify their separate contribution to the change correlation.

This study also extends previous longitudinal studies that investigated correlates of change between various abilities. These studies have yielded different patterns of correlations, ranging from moderate–large (Wilson et al., 2002), to moderate–weak (Anstey et al., 2003; Hultsch et al., 1998), to weak or nonexistent (Giambra et al., 1995; Taylor et al., 1992). Of these studies, however, only Wilson et al. examined whether retest effects could affect the correlations of change.

Methodological Considerations

As specified in our models, the retest component comprises the changes in a variable that occur from one occasion to the next. Such changes can include effects due to practice (i.e., items could have been remembered after the first assessment) and effects due to other more general factors, such as increased familiarity with the testing situation and decreased test anxiety. It is quite possible that the correlations of retest between variables (i.e., memory and processing speed here) are different depending on the components of retest. For example, it is likely that the correlation between the retest slopes for memory and processing speed identified here for the NGCS data is more influenced by general factors man, for example, by remembering items from previous occasions, which should not have much of an effect for processing speed. Similarly, retest effects for memory alone could have been influenced by both types of factors. The distinction between specific and general retest factors, however, was not specified in our models, so separating the different components of a retest correlation between variables was unfortunately not possible.

Although memory and processing speed may present some common covariation over time, age alone does not fully capture whether, and how, both variables go together over time (Ferrer & McArdle, 2004; McArdle et al., 2002). If the covariation between both variables over time is not captured by age alone—or by age and retest, as in the NGCS data—what are the components underlying it, or, more substantively, what is the relationship between the trajectories of memory and processing speed? It is quite possible that both variables follow a relationship different than the one examined by our models. For example, it is possible that processing speed precedes and brings about the changes in memory (Birren, 1974; Salthouse, 1996). If this is the case, our models were not suited to identify such lagged sequences. The models used in our analyses can be informative of the association (i.e., strength and valence) between the changes in two variables; changes in one variable are related—or not—to changes in the other variable. But such changes are time independent, and different models that represent the desired theories of change need to be fitted (McArdle, 2001; McArdle & Hamagami, 2001). Some of these dynamic models have been used to examine hypotheses positing developmental lagged sequences (Ferrer & McArdle, 2003, 2004; Guisletta & Lindenberger, 2003; McArdle, Hamagami, Meredith, & Bradway, 2000). It is possible for such time sequences between cognitive abilities to exist in the absence of age–slope correlations (Ferrer & McArdle, 2003).

Estimating age and retest effects simultaneously can be problematic when these components are highly correlated (i.e., increment in age and increment in retest occasion; Ferrer et al., 2004). In our analyses, we were able to estimate both effects because of the data conditions in both samples. In the ALEND data set, the retest intervals were close to 1 year, but the age range was wide, ranging from 40 to 74 years. This feature allowed us to weaken the age–retest correlation and to model age and retest simultaneously, although with age estimates being dominated by cross-sectional differences, more than longitudinal changes. In the NGCS data set, there was an even wider age range combined with a wide (and varying) retest interval range (i.e., from several months to 10 years). This feature of the NGCS was implemented in the design of the study in order to model retest and to minimize confounding effects due to this factor.

Several other methodological issues deserve clarification. For example, all our analyses included models with linear age functions. Other nonlinear functions, however, were examined. For example, the spline models included two age segments with an inflection point. Although the fits of these models were not superior, their estimates were informative and in line with other linear age models discussed in more detail. Similarly, we examined a model with a quadratic age function that indicated a good fit to the data. However, the estimates from this model were hard to interpret and did not alter the results about coupling between variables. On the basis of these analyses, we concluded that the loss in fit of a linear model outweighed the complexity and interpretation of a higher order polynomial age model, and thus we decided to retain the models with linear age effects.

Another assumption of the models presented here is convergence; that is, all the individuals are from the same cohort. This is a convenient assumption for modeling purposes that was never tested, as neither were the assumptions of age and cohort and of cohort and retest interactions (see Schaie, 1986). For example, given the differences in age among the participants in these samples, it is possible that cohort effects exist such that, for example, younger and older individuals may follow distinct age and/or retest processes as a result of differences in historical influences. Equally untested was the assumption of equal residual variances across time and age. Because our models used age as a continuous variable with a large range—especially in relation to the data density—we could not test this assumption. Similarly, the correlation between the residuals of memory and speed could not be estimated for the NGCS data, likely because of the reduced data density at the third measurement occasion. This correlation was very small for the ALEND data—and did not alter the estimates from models that did not include such a parameter—and thus, it does not seem unreasonable to assume a similar pattern for the NGCS data.

Finally, all the models examined here assume that incomplete data were missing at random. This was never formally tested here, and it is a rarely met assumption in longitudinal studies. In previous analyses with the ALEND data, Ferrer et al. (2004) reported results from individuals with complete data on all four measurement occasions (n = 492). As compared with individuals with some kind of missing data, these persons had higher baseline scores, similar age effects, and smaller practice effects for both memory and processing speed. For the NGCS data, there were incomplete data only at the third occasion, but the degree of incompleteness was substantial. It is possible that this could have limited the power to estimate random effects for age and retest. It is important to note, however, that this NGCS subsample was selected at random from the previous pool, although with an emphasis toward older individuals.

In sum, in this study we examined the correlates of change between memory and processing speed among adults. We found that when retest effects are ignored in multivariate models of growth, the correlation between the slopes of both variables is positively biased. When retest effects are included in the model, however, such age–slope correlations weaken, indicating that sources other than age contribute to the overall covariation between memory and processing speed over time.