Quantifying Lead-Time Bias in Risk-Factor Studies of Cancer through Simulation

Abstract

Purpose

Lead-time is inherent in early detection and creates bias in observational studies of screening efficacy, but its potential to bias effect estimates in risk-factor studies is not always recognized. We describe a form of this bias that conventional analyses cannot address and develop a model to quantify it.

Methods

Surveillance Epidemiology and End Results (SEER) data form the basis for estimates of age-specific preclinical incidence and log-normal distributions describe the preclinical duration distribution. Simulations assume a joint null hypothesis of no effect of either the risk factor or screening on the preclinical incidence of cancer, and then quantify the bias as the risk-factor odds ratio (OR) from this null study. This bias can be used as a factor to adjust observed OR in the actual study.

Results

Results showed that for this particular study design, as average preclinical duration increased, the bias in the total-physical-activity OR monotonically increased from 1% to 22% above the null, but the smoking OR monotonically decreased from 1% above the null to 5% below the null.

Conclusion

The finding of nontrivial bias in fixed risk-factor effect estimates demonstrates the importance of quantitatively evaluating it in susceptible studies.

Rarely if ever do studies of risk factors for chronic disease take into account bias from screening, even though many behavioral risk factors may be associated with use of screening. Weiss[1] and Joffe[2] describe some ways in which screening modifies the observed risk-factor-disease associations and complicates interpretation of results. Lead-time, the interval by which disease diagnosis is advanced by screening,[3–9] has rarely been recognized to bias such comparisons of incidence or mortality, [10] and when it has, it has been approached heuristically rather than analytically.[11] Differential ascertainment can occur within a study between subjects who are screened routinely and their counterparts who are not, regardless of screening efficacy. Because the factors that drive the differential ascertainment act prior to the data collection period, conventional methods for confounding adjustment cannot adequately address such selection bias. For these reasons, lead-time-biased case-ascertainment (LTBCA) may be more widespread than generally recognized and also problematic to control, thus motivating new methods.

This bias can affect any observational study type including a cohort study where a disease-risk factor is also associated with screening – for example, a study of physical activity and prostate cancer in which physically active men are screened more often. LTBCA arises because of the discrepancy in the screening pattern (i.e. the proportion screened and the associated screening rate) between risk-factor strata. To assess the potential impact of LTBCA on estimates of risk ratios involving fixed risk factors correlated with screening behavior, we modified a previously published model[10] based on the counterfactual concept[12] to evaluate the bias from screening in a population-based case-control Minnesota and Wisconsin Prostate Cancer Study.

METHODS

Model Development

For simplicity we addressed only studies wherein the outcome is incidence of disease and the risk factor is fixed over the study period. Thus, each stratum defined by a level of the risk factor can be modeled separately. To eliminate the effect of other potential confounding bias and to isolate the LTBCA, we assumed an otherwise unbiased study design; that is, we assumed that each stratum is a perfect counterfactual for the others, except for a different risk factor value and associated screening behavior.

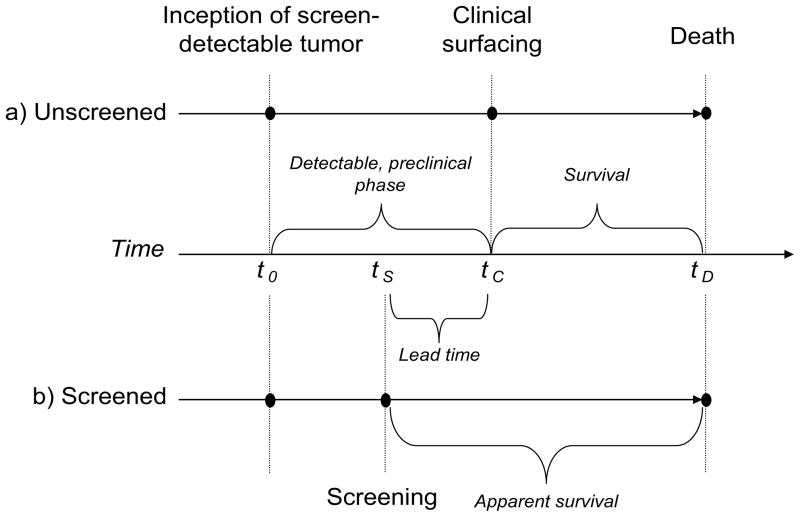
To represent the natural history of cancers we adopted a progressive disease model and overlaid it with a simple screening model, represented in Figure 1. If unscreened (Figure 1a), the subject’s tumor becomes screen-detectable (“preclinical incidence”) at time t_P, followed by clinical surfacing (i.e., symptomatic detection) at time t_C, and death at time t_D. The interval [t_P, t_C], called the “detectable, preclinical phase”, and its length, d = t_C − t_P, is the “preclinical duration.” If a subject undergoes screening, the tumor may be screen-detected (Figure 1b) at an earlier time, t_S and this creates lead-time t_C – t_S.

Figure 1.

Theoretical representation of the progression of disease for a subject in the a) absence and b) presence of screening. This diagram demonstrates for the screen-detected case that the date of diagnosis is advanced (from tC to tS) and survival time is extended (from [tC, tD] to [tS, tD]) both by the length of the lead-time interval. Notice that once a screen-detectable tumor develops (t0), over time the disease passes through a preclinical phase (either [t0, tS] or [t0, tC]), a diagnosis (either at tS to tC), a survival period, and eventually leads to death (tD). (With permission from 2, copyright 1999. Elsevier Science Inc. All rights reserved.)

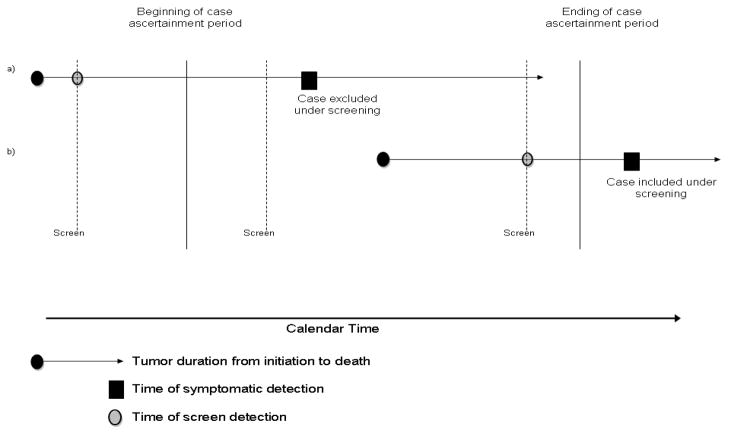
In observational studies wherein some disease is screen-detected either before or during the case-ascertainment period, the timing of screening and detectable preclinical phase of the disease relative to the case-ascertainment period will determine if a case becomes part of the study.[10] If a subject is actually screen-detected before the beginning of the ascertainment period, the counterfactual situation is the subject would have been symptomatically detected within the case-ascertainment period; therefore this case was removed from the study because of screening (subject a in Figure 2). On the other hand, a screen-detected case during the ascertainment period whose symptomatic detection would have occurred after the ascertainment period would be added because of screening (subject b in Figure 2). Unless the frequency and timing of screening is the same between the levels of a risk-factor of interest, the potential for bias arises.

Figure 2.

Representation of the influence of screening on the ascertainment of cases for a study.

Dependent upon when case-ascertainment for a study begins and ends, a subject with preclinical disease can be included (b) or excluded (a) as a case entirely based on his or her screening pattern. In the absence of screening the case in a) would have symptomatic diagnosis at time X and be included in the study. In the other situation, this case is screen-detected and he or she is diagnosed before the ascertainment period; excluded him or her from the study. For the case in b) we see the opposite effect of screening on case-ascertainment where the case is included if screen-detected and excluded if unscreened.

To accommodate such incidence studies, we modified a mathematical model based on an underlying cumulative mortality G_u(t).[10] We dropped the survival function from G_u(t), so that it became the cumulative incidence function, G_un(t), and then applied the model separately to each risk-factor stratum. Within each risk-factor stratum, for each age stratum m, defined by the age of the individual at the start of the ascertainment period (t₀), a specific ascertainment start time t₀ = m and study ascertainment end time t_E = m + Δ are defined, where Δ is the duration of the ascertainment period. Multiplying the result for age stratum m by the proportion of stratum m within the total study population (ω_m) and summing over all m yields the underlying incidence for the unscreened in each risk-factor stratum, G_un(t), where w(·) is the preclinical incidence function and f(·) is the preclinical duration probability density function:

$$G_{un}(t)=\sum _m{\omega }_m\underset{0}{\overset{min(t,t_E)}{\int }}w(x)\underset{max(x,t_0)}{\overset{t_E}{\int }}f(z-x)\mathit{dzdx}.$$

To adjust for differential screening patterns between each risk-factor stratum, we define a corresponding set of age-stratum-specific screening proportions, k_3,(m) (the fraction who begin screening at some time before age m), and rates, k₁(_,m) (the number of screens per year which the screening fraction averages). We assume a constant sensitivity (ξ) for the screening test. The expected incidence for each age stratum within each risk-factor stratum is calculated and the weighted sum over age categories is taken to get the expected incidence for each risk-factor stratum. The details of the mathematical model and how it was derived are presented in the appendix.

Under the joint null hypothesis of no effect of the risk factor or of screening on the preclinical incidence of cancer and assuming no bias, the risk ratio (RR) between risk-factor strata should equal 1. Deviations from this ideal value are used to quantify the amount of bias in the study. In the following, G_uni represents the incidence expected during the study in risk-factor stratum i in the absence of screening (as above) and G_Si represents an adjustment to this incidence based on risk-factor-specific screening patterns. For a two-level risk factor:

$${RR}_{\mathit{stratum}1vs2}=\frac{R_{\mathit{stratum}1}}{R_{\mathit{stratum}2}}=\frac{G_{un1}+G_{S1}}{G_{un2}+G_{S2}}=\mathit{Bias}$$

From the equation it is obvious that if the stratum-specific values G_S1 = G_S2, then RR_{stratum 1 vs. 2} will be equal to 1 and the study unbiased, given the above assumptions. The simulations are essentially a sensitivity analyses as each set of parameterization values (as demonstrated in the next section) provides a unique, reproducible simulated relative risk.

EXAMPLE

Study design

A primary goal of the Minnesota and Wisconsin Prostate Cancer Study (National Cancer Institute grant 1R01CA074103-01A2) was to examine the associations between prostate cancer and farming and pesticide exposure, while adjusting for potential confounding risk factors. Cases were obtained from the state cancer registries; frequency matched (1-year age intervals) controls were selected from the year 2000 driver’s license and identification card databases. There were 1583 cases and 1665 controls selected. We used only the data from the controls to estimate the age-and-risk-factor-specific proportions screened and frequency of screening in order to avoid the potential confounding of prostate cancer detection with screening frequency. We used SEER age-specific incidence rates of prostate cancer to derive preclinical incidence. We present results using a case-ascertainment period of 2 years.

Model parameterization for the Minnesota and Wisconsin Prostate Cancer Study

The first set of simulations examined the smoking variable stratified as “ever smoked” vs. “never smoked” (prior to 1998); the second set examined the average total physical activity variable stratified as “3 or more hours per week” vs. “less than 3 hours per week” (prior to 1998). This simulation was developed and run using the program Mathcad^® 12 (Cambridge, MA)[13] and analyses of SEER data used R version 2.1.1[14].

The study participants were asked if prior to 1998 they ever had received a digital rectal examination (DRE) or a prostate-specific antigen (PSA), and the number of times between 1990 and 1998 they had received a PSA screening test; for these simulations only PSA screening information was used. There were at most seven percent of participants in any stratified risk-factor group who answered “unknown”. Based on this PSA information, we determined the age-specific proportion screened (Figure 3a and 3c) and the rate of screening (Figure 3b and 3d) among both strata of the risk-factors (smoking and total physical activity). We assumed a constant sensitivity of 0.89 for the PSA screening test.[15]

Figure 3.

Representation for our study population of the proportion screened (number of participants who ever received a PSA test out of total number of participants) in each smoking stratum (a) and in each total physical activity stratum (c). Also represented is the screening rate per year (log(# of screening tests from 1990–1998 divided by 9 years)) of the proportion screened in each smoking stratum (b) and in each total physical activity stratum (d). The smoking variable separates those 40–79 that ever smoked from those that never smoked. Total physical activity variable separates the total physical activity in those 50–79 into categories of an average of 3 or more hours per week or less than 3 hours per week.

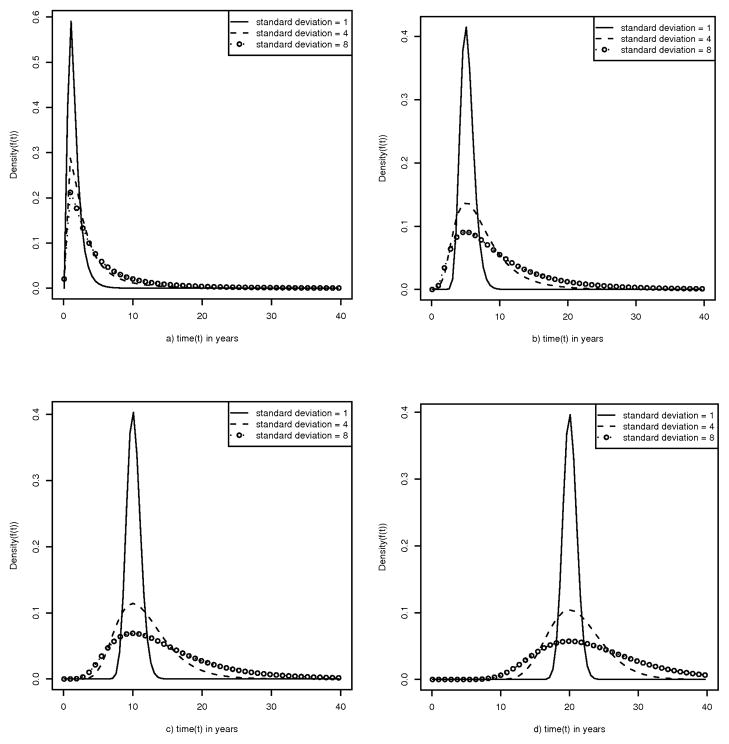
Prostate cancer has different incidence rates based on different population characteristics;[16–18] and it is conceivable that the preclinical duration may vary based on those specific population characteristics. Additionally, the true preclinical duration pattern for prostate cancer is unknown, so we perform a sensitivity analysis by simulating several plausible values for the mode (1, 5, 10, 20 years) and standard deviation (1, 4, 8 years) for a lognormal distribution (Figure 4).

Figure 4.

Presentation of several plausible preclinical duration distributions for prostate cancer based on a log normal distribution with standard deviations of 1, 4, and 8 years for each of the following modes: 1(a), 5(b), 10(c), and 20(d). Because the preclinical duration distribution is unknown for prostate cancer, all of these reasonable distributions are used in the simulations.

The SEER 9 registry[19] provides estimates for the incidence rate of prostate cancer in the entire U.S. population based on nine long standing cancer registries. For our simulation, we specifically focused on the years 1973–1986 to identify only the non-PSA-screen-detected cases (before wide-spread use of the PSA screening test). The distributions of the age-specific incidence rates for years 1973 to 1986 were similar and, therefore, averaged to form one overall distribution for this simulation (Figure 5) and shifted by the mean of the preclinical duration to produce an age-specific preclinical incidence distribution.

Figure 5.

Relationship of age (5-year age groups; age range 0–85+) to incidence rate (per 10,000) of prostate cancer based on average SEER 9 registry data from 1973 to 1986. The incidence intensity function, w(x) was fit to the SEER data using non-linear minimization to create an estimate of the continuous age-specific incidence (solid line where Mean = 0). The incidence function is also plotted using a preclinical duration mean of 5 (dashed line) which approximates the preclinical incidence of a man aged 50 by the SEER 9 incidence at age 55.

The OR is used to approximate a RR with the equation OR_observed = (a/b)/(c/d) ≈ (a/(a + b))/(c/(c + d)) = RR_estimated. If the simulated RR is the ratio between the observed incidence rates in two risk-factor strata under the joint null hypothesis, then the unbiased RR between the strata equals 1; any deviation represents bias. To correct a biased observed RR, multiply the incident cases in the denominator stratum (i.e., c) by the simulated RR (i.e., amount of bias).

RESULTS

Twelve combinations of preclinical duration distributions (modes=1, 5, 10, 20; standard deviations=1, 4, 8) for two risk factors (smoking and total physical activity) categorized into age groups (40–59 and 60–79; 50–59 and 60–79), produced 48 different simulated risk ratios (figure 6a and b). Although the direction of the bias differs between the two risk factors, negatively for smoking and positively for physical activity, in both graphs, as mode increases, so does the magnitude of the bias. Looking at the bias variation with different standard deviations at each mode, the impact of increasing standard deviation is associated with higher bias at modes 1 and 5, but over mode 10 higher standard deviation is associated with less bias.. For the smoking variable (figure 6a), age group 40–59 has greater bias as the mode increases but both age groups follow a similar decreasing trend and are almost entirely below 1 with estimated bias from 1–5%. Similarly, for the total physical activity variable (figure 6b), the younger age group (50–59) again has greater bias and the trend for both age categories is almost linear with the slope decreasing between mode 10 and 20. In contrast, all bias factors in the total physical activity variable are above 1 with estimated bias from 1–22%.

Figure 6.

Observed relative risks for smoking and physical activity simulated under the null hypothesis for men age < 60 and for men age 60+. The observed relative risks were simulated using four preclinical duration distribution parameters for the mode (1, 5, 10, 20) and three standard deviation (sd) (1,4,8). For the smoking variable, the risk is for “ever smoked” compared to “never smoked.” For total physical activity ages 50 and up, the risk is for 3 or more hours per week compared to less than 3 hours per week; men less than 50 years were not included.

The hypothetical example (table 1) used here focuses on men aged 40–59 classified as ever smokers. The general trend is that the percentage of expected cases (with no screening) actually observed (with specific screening behavior) increases as study duration and standard deviation increase and mode decreases. This is logical; a longer study period (relative to the preclinical duration) captures more total cases of disease (screen-detected or symptomatically detected) and thus decreases the relative number of screen-detected cases included or excluded specifically due to screening and thereby reducing the potential for bias.

Table 1.

Simulated incidence in subjects aged 40–59 classified as ever smoked in the Minnesota and Wisconsin Prostate Cancer Study^*

Study Duration (years)	Preclinical Duration (mode, σ)	Expected Incidence w/No Screening	Included Incidence Due to Screening†	Excluded Incidence Due to Screening	Risk Ratio-Ever vs. Never Smoked†
2	5, 4	1.2E-3	1.4E-3	5.3E-4	0.998
2	5, 8	1.6E-3	2.1E-3	6.7E-4	0.973
2	15, 4	1.3E-3	4.2E-3	6.4E-4	0.950
2	15, 8	2.0E-3	5.5E-3	9.6E-4	0.953
12	5, 4	1.6E-2	1.3E-2	1.9E-3	0.998
12	5, 8	1.9E-2	1.9E-2	2.9E-3	0.997
12	15, 4	1.7E-2	4.3E-2	7.5E-3	0.996
12	15, 8	2.3E-2	4.9E-2	9.1E-3	0.998

^*Using the simulation techniques described above with two study durations (2, 12 years) and four combinations of preclinical durations in years(mode, standard deviation: (5, 4), (5, 8), (15, 4), (15, 8)), we estimated among those 40–59 classified as ever smoked the cases seen under each of the specified conditions in the table.

^†Screening proportions and screening rates used in model are same as above (Figure 4a and 4b).

DISCUSSION

When a screening test for a disease is used in a population from which subjects in an observational study are drawn, the screen-detected cases will have an earlier date of diagnosis compared to non-screen-detected cases, resulting in ascertainment probabilities being changed due to lead-time. If differential screening exists between risk-factor strata, case-ascertainment probabilities will be changed differentially and thereby potentially distorts the observed measure of association between the risk factor and disease. Under simple, plausible assumptions about preclinical incidence and duration, our simulations show the possibility for lead-time to bias risk ratio estimates.

Simulating the Minnesota and Wisconsin Prostate Cancer Study as an example, we have demonstrated a broad possible range for such bias in the estimates of smoking and physical activity relative risks for prostate cancer, with a consistent direction for each risk factor. Given the mechanism by which the bias arises, it stands to reason the greater the discrepancies in screening rates or proportions, the greater the bias, and that effect can be observed in our simulation data (Figure 3a, 3c, and 6). The discrepancy in screening proportions between levels of smoking are smaller than those between exercise levels; consequently, the magnitude of the bias gets much larger as the mode of the preclinical duration increases for physical activity compared to smoking. Note also that the different directions of the bias between the two risk factors can be explained by the reversal in association between the risk factor and screening. Smoking is related to lower screening proportions, whereas higher physical activity is related higher screening rates. These observations and the different directional effects of LTBCA simulated between the two risk factors in our study emphasizes the importance of representing the relationships between study design parameters and the associations between screening and the risk factors of interest when evaluating the potential impact of lead-time.

Without a consensus on the benefits of PSA screening, [3, 17, 20, 21] care guidelines for prostate cancer screening have been inconsistently implemented.[22–24] Recent randomized trials have not resolved the controversy about the potential efficacy of prostate cancer screening.[25–28] Additionally, the preclinical stage of prostate cancer is believed to be very long, allowing for extended lead times in screen-detected cases. Thus there is a potential for a large amount of LTBCA in studies of risk factors for prostate cancer.[3, 21]

For the model, we are assuming a null effect between the potential risk factor (i.e., smoking and physical activity) and disease (i.e., prostate cancer). Therefore, if a risk factor effect is added into the model, we are essentially shifting the y-intercept value from 0 (null effect) to whatever the published risk factor effect would be. Interestingly for these two risk factors, the observed relative risks from the simulations (figure 6) demonstrate that the bias is moving in the opposite direction of what we would expect the effect of the risk factor to be meaning the published effects would be attenuated. In our example, smoking would be expected to increase the risk of prostate cancer and would be biased toward the null and physical activity would be expected to decrease the risk of prostate cancer and would be biased toward the null as well.

Broader implications

Although the specific quantitative results presented in this article are specific to the Minnesota and Wisconsin Prostate Cancer Study and cannot be generalized to other studies, the qualitative findings of potential LTBCA and its relationship to differential screening have implications beyond this study. Because many of the common risk factors of chronic disease, especially those related to lifestyle choices, are correlated with the frequency of medical visits and the probability of earlier detection of disease, the potential for LTBCA exists in such studies designs, even though the exact magnitude may not be predictable. With study-specific modifications to our models, special attention paid to underlying assumptions, and differences (from our example) in study type and risk-factor information collected, the simulations demonstrated here can be adapted to other observational studies (including cohort studies) to quantify and adjust for their LTBCA. Additional complications, such as time-dependent covariates, other confounding variables, and selection bias, are unlikely to obviate the potential bias from LTBCA, but would certainly modify it either by increasing or decreasing the overall bias.

Limitations

Since we used a mathematical model for the simulation and all models are wrong, there will be some divergence from the results of actual studies. For example, like most models of screening, we use a constant sensitivity for the test over the entire preclinical phase, whereas in reality screening tests most likely increase in sensitivity from the earliest to the latest times in the preclinical phase. The fixed sensitivity can be regarded as an approximation of the average sensitivity over the duration of the preclinical phase and across all subjects. This may overestimate the sensitivity for smaller, earlier lesions and underestimate it for larger, later lesions. An increasing sensitivity function could affect the size of the estimates. Efforts to characterize the sensitivity function for different cancers and screening methods and incorporate such a function into these models would be useful research endeavors.

As with all statistical analyses and simulations, it is important to assess the assumptions that underlie the procedure. In our study, major assumptions were made involving the preclinical incidence distribution, the preclinical duration, and screening test sensitivity. We assumed the incidence distribution from the SEER 9 registry for the years 1973–1986, after shifting by the mean of the preclinical distribution, is reasonably representative of the preclinical incidence for the Minnesota and Wisconsin Prostate Cancer Study population in the absence of screening. There are a wide range of estimated preclinical durations for prostate cancer in the literature,[29] and as a result we used several combinations of plausible parameters for our preclinical distribution. Because it is an unknown, presenting a range of values is more informative than presenting a single, and likely incorrect, value.

The associations between risk factors and screening are more complex and our model may have considerable uncertainty about the degree of bias, in either direction. We have deliberately not tried to put uncertainty regions around our estimates because of this. A more accurate estimate of the true measure of association would be achieved by developing an approach that not only would allow for more flexible sensitivity functions, but also for simultaneous adjustment for multiple potential confounding factors and addressing other forms of screening bias, such as from self-selection[6, 30] and length-biased sampling[5–7].

Conclusions

Some observational studies of time-invariant risk-factor/disease associations may be biased by variations of the voluntary use of screening or other form of early detection between subgroups in the population of interest. Lead-time bias affects case-ascertainment when the lead-time interval for some cases overlaps the beginning or end of the ascertainment period, thus affecting which cases are enrolled into the study. This bias increases as the differences in proportion screened and the screening rate increase between strata of the risk factor. Simulating the Minnesota and Wisconsin Prostate Cancer Study with the presented model under plausible assumptions, we found that lead-time may bias the risk ratio for the total physical activity variable in the age group 50–59 by up to 22 percent. Thus, when early detection methods can influence case-ascertainment in a risk-factor study, it is important to not only perform the usual due diligence regarding standard potential biases for the study, but also examine risk factors of interest that are correlated with screening for their stratum-specific screening proportions and rates and apply a model such as ours to evaluate the possible effect bias may have on the measures of association.

Abbreviations

SEER

Surveillance Epidemiology and End Results

OR

Odds Ratio

LTBCA

lead-time-biased case-ascertainment

RR

Risk Ratio

DRE

digital rectal examination

PSA

prostate-specific antigen