Kinetic and Isotopic Characterization of L-Proline Dehydrogenase from Mycobacterium tuberculosis

Abstract

The monofunctional proline dehydrogenase (ProDH) from Mycobacterium tuberculosis performs the flavin-dependent oxidation of L-proline to Δ¹-pyrroline-5-carboxylate (P5C) in the proline catabolic pathway. The ProDH gene, prub, was cloned into the pYUB1062 vector, and the C-terminal His-tagged 37 kDa protein was expressed and purified by nickel-affinity chromatography. A steady-state kinetic analysis revealed a ping-pong mechanism with an overall k_cat of 33 ± 2 sec⁻¹ and K_m values of 5.7 ± 0.8 mM and 3.4 ± 0.3 μM for L-proline and 2,6-dichlorophenolindophenol (DCPIP), respectively. The pH dependence of k_cat revealed that one enzyme group exhibiting a pK value of 6.8 must be deprotonated for optimal catalytic activity. Site-directed mutagenesis suggests that this group is Lys110. The primary kinetic isotope effects on V/K_Pro and V of 5.5 and 1.1, respectively, suggest that hydride transfer from L-proline to FAD is rate-limiting for the reductive half-reaction, but that FAD reoxidation is the rate-limiting step in the overall reaction. Solvent and multiple kinetic isotope effects suggest that L-proline oxidation occurs in a stepwise rather than concerted mechanism. Pre-steady state kinetics reveal an overall k_red of 88.5 ± 0.7 sec⁻¹, and this rate is subject to a primary kinetic isotope effect of 5.2. These data confirm that the overall reaction is limited by reduced flavin reoxidation in the second half-reaction.

Mycobacterium tuberculosis (Mtb), the causative agent of tuberculosis (TB), is a global health concern [1]. In 2011, there were an estimated 8.7 million new cases of TB, with 1.4 million deaths from TB. In spite of research into the eradication of TB, the rise of drug-resistant strains of MTb are becoming alarming common, and new drug targets need to be discovered [2].

Recently, the oxidation of L-proline has come under scrutiny for its possible protection of Mycobacterial cells under hypoxic conditions [3, 4]. Berney and Cook observed an increase in the production of proline dehydrogenase (ProDH) at low [O₂], and argued that the product of ProDH, Δ¹-pyrroline-5-carboxylate (P5C), reacts with methylglyoxal, a toxic by-product of several metabolic pathways, to form 2-acetyl-1-pyrroline (2-AP) [5–9].

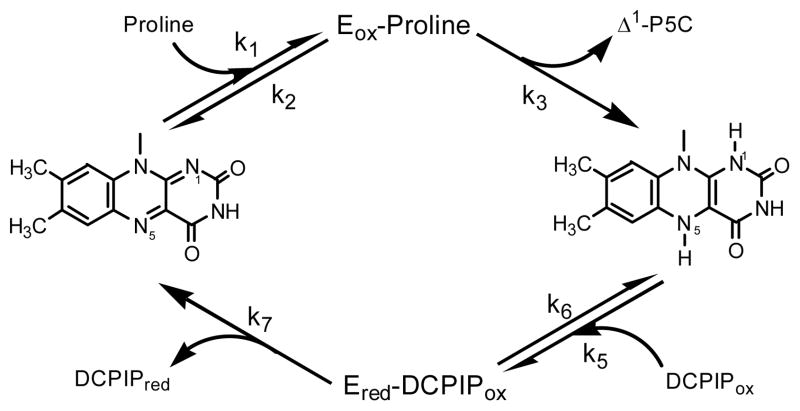
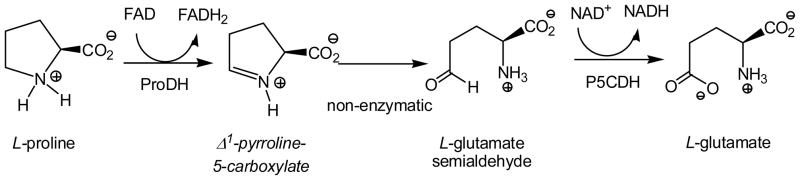
The oxidation of L-proline to L-glutamate follows a two-enzyme pathway with Δ¹-pyrroline-5-carboxylate as an intermediate (Scheme 1). In most prokaryotes, the two enzymes, proline dehydrogenase (ProDH) and Δ¹-pyrroline-5-carboxylate dehydrogenase (P5CDH) are a single fused protein, named proline utilization A (PutA), while in eukaryotes and some prokaryotes they are separate enzymes [10]. The L-proline dehydrogenase activity of both the fused multifunctional and the mono-functional enzymes have been studied [11, 12]. Crystal structures have also been solved for both forms of the enzyme, suggesting two residues equivalent to K110 and Y203 in the Mtb ProDH, as potential active site bases [12, 13]. The flavin-dependent ProDH activity of PutA from E. coli was recently characterized, both in the steady- and pre-steady state [11, 14]. It was found to follow a two-site ping-pong mechanism utilizing various electron acceptors. Pre-steady state experiments allowed the k_red and k_ox rates of PutA of 38 sec⁻¹ and 7.5 sec⁻¹, respectively, to be determined. No studies of Mycobacterium tuberculosis ProDH have been reported to date, and we present here a kinetic and mechanistic analysis of the enzyme.

Scheme 1.

Materials and Methods

Materials

Chemicals, biochemicals, buffers, and solvents were purchased from Sigma-Aldrich Chemical Co. (St. Louis, MO) or Fisher Scientific Inc. (Pittsburgh, PA), unless stated otherwise. LB Broth, agar, Middlebrook 7H9 and BBL Middlebrook ADC Enrichment were obtained from Becton, Dickinson and Company (Franklin Lakes, NJ). Nucleic acid primers were from Invitrogen. The pET-29a(+) vector was from Novagen. The Mycobacterium smegmatis mc²4517 cells and pYUB1062 vector were a gift from William R. Jacobs Jr. (Einstein College of Medicine). Hygromycin B and Ni-NTA were purchased from Gold Biotechnology (St. Louis, Missouri). Enzymes, reagents and deoxynucleotide triphosphates (dNTPs) used for the cloning procedures were purchased from New England Biolabs (Ipswich, MA). 99.9% deuterated water was from Cambridge Isotope Laboratories (Andover, MA). [2,5,5-²H₃]-L-proline was from Medical Isotopes, Inc (Pelham, NH). Prepacked PD-10 Sephadex G-25 columns were purchased from GE Healthcare Lifesciencs (Piscataway, NJ).

Cloning, Overexpression, and Purification of ProDH

The Mtb prub gene (Rv1188) was PCR amplified from Mtb H37Rv DNA using the forward primer 5′-ATCCCGCTCATATGGCCGGCTGGTTCGCGCAC-3′ and reverse primer 5′-ATCCCGCTAAGCTTGCGCTCGGCGCACCCCCG-3′. Amplification mixtures contained the appropriate synthetic primers, deoxynucleotide triphosphates, genomic DNA, and PCR reagents. The resulting PCR product and the pET29a(+) vector were digested with NdeI and HindIII restriction enzymes, purified, and ligated using T4 DNA ligase. An aliquot of the ligation mixture was transformed into competent E. coli DH5α cells. Transformants were selected at 37 °C on LB (10 g Bacto-tryptone, 5 g yeast extract, 10 g NaCl) plates with kanamycin (30 μg/ml) for selection. Plasmid DNA was isolated from several randomly selected colonies and analyzed by restriction analysis for the presence of the insert. The cloned prub gene was sequenced to verify that no other mutations had been introduced during the amplification of the gene. The newly constructed expression vector was named pET29:prub.

Because of a lack of protein expression, the gene fragment was subcloned into the mycobacterial pYUB1062 expression vector using the same NdeI and HindIII restriction sites. After the sequence had been verified, the recombinant plasmid, pYUB1062:prodh, was transformed into Mycobacterium smegmatis mc²4517 cells. A single bacterial colony was selected and grown for 19 hr at 37°C in media containing 27 mL Middlebrook 7H9 broth medium supplemented with 3 mL of BBL Middlebrook ADC Enrichment, 0.05% Tween 80, 0.2% glycerol, kanamycin (20 μg/ml), and hygromycin B (100 μg/ml). Cells were then inoculated into 12 x 1L of the above medium and grown to mid-exponential phase (OD₆₀₀= 0.5–0.6) at 37°C before induction with acetamide (4 mL of a 0.5 g/mL solution made in water) and allowed to grow for 18 h. Cells were harvested by centrifugation, and the pellets were resuspended in cold 50 mM Tris (pH 8.0) containing 300 mM NaCl, 10 mM imidazole and 0.1% Triton X-100 (lysis buffer), lysed using an EmulsiFlex-C3 homogenizer (Avestin, Ottawa, Canada) and centrifuged at 17,000 rpm for 45 min to remove cellular debris. Batch purification was performed with a Ni-NTA agarose column. The column was washed with lysis buffer, and the protein was eluted with 250 mM imidazole in lysis buffer and stored at 4 °C.

K110A and Y203F ProDH Mutants

K110A and Y203F ProDH were prepared using overlap extension PCR [15]. The forward primer (5′-ATCCCGCTCATATGGCCGGCTGGTTCGCGCAC-3′) is designated primer F1 and contains an NdeI restriction site (underlined) followed by 18 bases corresponding to the coding sequence of the prub gene. The reverse primer (5′-ATCCCGCTAAGCTTG-CGCTCGGCGCACCCCCG-3′) is designated primer R1 and contains a HindIII restriction site (underlined) followed by 18 bases corresponding to the complementary sequence of the prub gene. The internal PCR primers for K110A were oligonucleotides 5′-GTGTCGCTCGCGCTGTCGGCGCTC-3′ and 5′-GAGCGCCGACAGCGCGAGCGACAC-3′, where the mutated codons are in bold. The internal PCR primers for Y203F were oligonucleotides 5′-CAAGGGCGCCTTTGACGAACCCGC-3′ and 5′-GCGGGTTCGTCAAAGGCGCCCTT-3′, where the mutated codons are in bold. Expression, purification and storage of the mutant forms of the enzyme followed the same protocol that was used for the wild type.

Protein Concentration

The concentration of WT ProDH and the two mutants was determined spectrophotometrically using an ε₄₅₁ of 11,300 M⁻¹ cm⁻¹.

Measurement of Enzymatic Activity

Unless otherwise stated, all steady-state kinetic assays were performed at 25 °C and pH 7.1 in 20 mM Tris-HCl. ProDH activity was assayed by measuring the reduction of the artificial electron acceptor 2,6-dichlorophenolindophenol (DCPIP). The reaction mixture was composed of 20 mM Tris-HCl, ProDH, DCPIP and L-proline in a total volume of 1 mL. The reaction was initiated by the addition of L-proline. Reactions were monitored spectrophotometrically until 10% substrate conversion to product. Rates were calculated using the molar extinction coefficient of DCPIP (ε₆₀₀ = 18,700 M⁻¹ cm⁻¹) and the total enzyme concentration (E_t).

Initial Velocity of WT, K110A and Y203F ProDH

Initial kinetic parameters were estimated by saturating with one substrate and varying the concentration of the other substrate. The resulting curve was fit to eq 1:

$$\text{v}=({{\text{V}}_{max}}^{\ast }\text{A})/(K_{\text{m}}+\text{A})$$ (1)

where V_max is the maximal velocity and A is the concentration of the varied substrate. Initial velocity studies were conducted at fixed, saturating concentrations of proline and varying concentrations of DCPIP and vice versa. The resulting patterns were fit globally to eq 2 for a ping-pong mechanism:

$$\text{v}=(\text{VAB})/(K_{\text{a}}\text{B}+K_{\text{b}}\text{A}+\text{AB})$$ (2)

where V is the maximal velocity, A and B are the substrate concentrations, and K_a and K_b are the respective Michaelis constants for each substrate.

pH Dependence of ProDH Activity

The pH dependencies of the kinetic parameters were determined in a mixed buffer solution (20 mM each MES, Bis-tris propane and CHES) at the desired pH under saturating conditions of DCPIP and varying concentrations of L-proline. The resulting k_cat and k_cat/K_pro data were fit to eq 3:

$$log{k}_{\text{cat}}\text{or}log{k}_{\text{cat}}/K_{\text{pro}}=log\text{C}/(1+[{\text{H}}^{+}]/K)$$ (3)

where C is the pH-independent plateau value, K is the observed dissociation constant for the ionizing group, and [H⁺] is the hydrogen ion concentration. This equation describes the pH dependence where the protonation of a single group decreases the magnitude of the kinetic parameter.

Primary Kinetic Isotope Effects

Assays were performed under saturating DCPIP conditions and varying concentrations of either L-proline or [2,5,5-²H₃]-L-proline in 20 mM tris-HCl pH 8.0, where the enzymatic rate is independent of pH. The results were globally fit to eq 4:

$$\text{v}=(\text{VA})/(\text{K}(1+{\text{F}}_{\text{i}}({\text{E}}_{\text{V}/\text{K}}-1))+\text{A}(1+{\text{F}}_{\text{i}}{\text{E}}_{\text{v}}-1)$$ (4)

where V is the maximal velocity, A is the concentration of L-proline or [2,5,5-²H₃]-L-proline, F_i is the fraction of isotope (0 or 0.982), E_V/K is the effect on k_cat/K_pro, and E_V is the effect on k_cat.

Solvent Kinetic Isotope Effects

Solvent kinetic isotope effects were measured at saturating concentrations of DCPIP and varying concentrations of L-proline and globally fit to eq 4 where F_i = 0 for H₂O and F_i = 0.92 for D₂O. A viscosity control of 9% glycerol did not show any effect on either V or V/K_pro. A proton inventory was determined under saturating conditions of both DCPIP and L-proline at 10% increments from 0 to 90% of D₂O.

Stopped-Flow Measurements

All measurements were conducted on a SX-20 stopped-flow spectrophotometer operating in the absorbance mode at 451 nm (Applied Photophysics). Assays contained 14 μM ProDH (after mixing) and variable concentrations of L-proline or [2,5,5-²H₃]-L-proline, to ensure that binding is not contributing to the observed rates. Measurements were performed in 50 mM Tris-HCl (pH 8.4) containing 100 mM NaCl, 5 mM DTT and 5% glycerol made in water or D₂O. The reduction of flavin by substrate was monitored over time and fit to eq 5:

$$\text{A}={\text{A}}_{\text{f}}+{\text{A}}_1{\text{e}}^{-\text{k}1\text{t}}+{\text{A}}_2{\text{e}}^{-\text{k}2\text{t}}$$ (5)

where A is the absorbance at time t, A_f is the final absorbance, and A₁ and A₂ are the absorbance changes associated with each of the first-order rate constants, k₁ and k₂, respectively [16]

The k_obs values obtained at various concentrations of substrate were replotted as a function of enzyme concentration and fit to eq 6:

$$k_{\text{obs}}=(k_{\text{H}}\text{S})/(K_{\text{d}}+\text{S})$$ (6)

where k_obs is the observed rate constant after the single-exponential fitting at different concentrations of enzyme, k_H is the rate obtained with L-proline used as the substrate, S is the L-proline concentration, and K_d is the dissociation constant for L-proline. The isotope effect on the hydride transfer step or proton extraction step (^Dk_H) was obtained by dividing k_H/k_D, using the values obtained after fitting with eq 6.

Results and Discussion

Cloning, Expression and Purification

The prub gene was amplified from genomic DNA of M. tuberculosis H37Rv and fused into the start codon of expression vector pET29a(+), resulting in the pET29:prub construct. The construct was sequenced to verify that no mutation was introduced by PCR. The prub gene in pET29:prub is under the control of a T7 promoter, and expression of the enzyme was attempted in E. coli T7 express, with no success. The gene was then sub-cloned into the pYUB1062 vector, to generate pYUB1062:prodh, for protein expression. The K110A and Y203F mutants genes were amplified from the pYUB1062:prodh construct and sequenced to confirm only the designated mutant was introduced by PCR. Over-expression of the C-terminally His₆-tagged WT and mutant forms of the enzyme yielded soluble protein of the expected mass, ~37 kDa.

Initial velocity studies

The parallel initial velocity pattern obtained using L-proline and DCPIP (Figure 1), an artificial electron acceptor, reveals that ProDH exhibits a ping-pong kinetic mechanism, as observed for all other mono- and bi-functional proline dehydrogenases [11, 12, 14]. (Figure 1) A k_cat of 33 ± 2 sec⁻¹ was determined. This value is similar to what was found for the E. coli ProDH measured with various other electron acceptors [11]. The K_m values for L-proline and DCPIP were 5.7 ± 0.8 mM and 3.4 ± 0.3 μM, respectively (Table 1).

Figure 1.

Bisubstrate kinetic analysis of ProDH. The initial velocity of proline oxidation was measured in 50 mM Tris-HCl (pH 7.4) with varying concentrations of L-proline (4-15 mM) and fixed concentrations of DCPIP: 1 (●), 1.5 (■), 2 (◆), 3.5 (▼), and 15 μM (▲). Shown is the double-reciprocal plot of the initial velocity as a function of DCPIP concentrations. Global fitting of the data to eq 2 (solid lines) gave a k_cat of 33 ± 2 sec⁻¹, a K_L-pro of 5.7 ± 0.8 mM, and a K_DCPIP of 3.4 ± 0.3 μM.

Table 1.

Kinetic Parameters for ProDH and the Y203F Mutant^a

enzyme	kcat (sec−1)	KDCPIP (μM)	Kpro (mM)	kcat/Kpro (M−1sec−1)
ProDH	33.5 ± 2.2	3.4 ± 0.3	5.7 ± 0.8	5877
Y203F	100.6 ± 2.1	NDb	860 ± 31	117

^aThe steady-state kinetic parameters were measured in 20 mM tris-HCl buffer (pH 7.1) at 25 °C. Errors are standard deviations. Substrate concentrations are described in the Methods section.

^bNot determined

pH dependence of the kinetic parameters

To probe the potential involvement of general acid or general base catalysis in the mechanism of ProDH, the pH dependencies of k_cat and k_cat/K_m were examined between pH 5.5 and 9.0, the range in which the enzyme was found to be stable. The pH profile was determined at a saturating concentration of DCPIP and varying concentrations of L-proline. The pH dependencies of k_cat and k_cat/K_pro are determined by a single ionizable group exhibiting pK_a values of 6.8 ± 0.1 and 7.1 ± 0.2, respectively (Figure 2) that needs to be deprotonated for catalysis and binding. The k_cat/K_pro data at low pH values deviate somewhat from the fit to a single ionizable group, but clearly is not consistent with two ionizable groups that must be deprotonated (dashed line in Figure 2).

Figure 2.

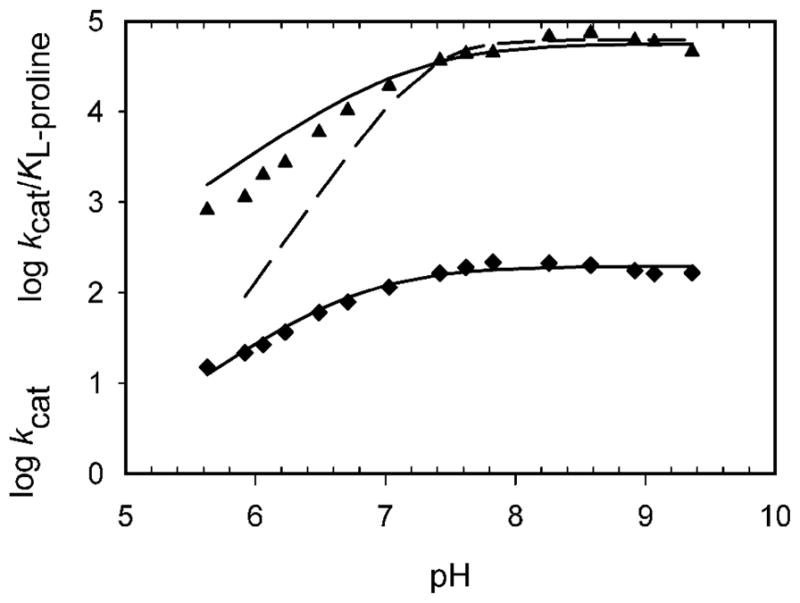
pH dependence of ProDH. k_cat(app) (●) and k_cat/K_L-pro(app) (▲), determined at saturating DCPIP and varying L-proline concentrations. The solid lines are fits to eq 3, yielding a pK_a of 6.8 ± 0.1 for k_cat(app) and 7.1 ± 0.2 for k_cat/K_L-pro(app). The dashed line in the k_cat/K_L-pro pH profile represents a fit where two groups must be deprotonated.

The crystal structure of E. coli PutA in complex with the competitive inhibitor, L-tetrahydro-2-furoic acid, provides clues into which residues could function as an active site base, Lys329 or Tyr437 [13]. In the active site, Tyr437 is hydrogen-bound to a water molecule, which is the closest neighbor to what would be the amine group of proline. The ε-amino group of Lys329 is 3.5 Å from L-tetrahydro-2-furoic acid, suggesting it could also play a role in catalysis. A more recent structure of the monofunctional ProDH from Deinococcus radiodurans similarly shows the ε-amino group of Lys98 (equivalent to K110 in the Mtb ProDH) is 3.5 Å from the ring oxygen atom of the same inhibitor [23]. Sequence alignments of the bifunctional E. coli PutA with the monofunctional ProDH’s from Deinococcus radiodurans, Thermus thermophilus, Mycobacterium smegmatis and Mycobacterium tuberculosis shows both these residues, Lys110 and Tyr203 (Mtb numbering), are conserved in Mycobacterium tuberculosis ProDH (Figure 3). We therefore generated the K110A and Y203F mutant forms of the enzyme. The K110A mutant has no measurable catalytic activity, while the Y203F mutant exhibited an increase in the K_pro but no change in k_cat (Table 1). These data strongly argue that Y203 serves to bind and orient L-proline in the active site, but that the active site base observed in the pH profile of k_cat is K110.

Figure 3.

Sequence alignment of ProDH from various organisms. Highlighted are the two residues believed to play a role as the general base.

Steady-state Kinetic Isotope Effects

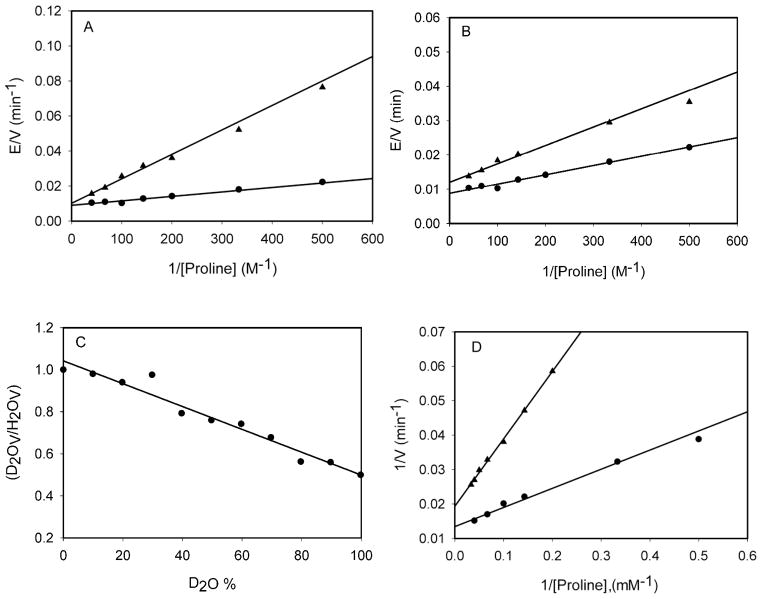
To investigate the rate-limiting nature of the catalytic oxidation of L-proline, primary kinetic isotope effects (KIEs) were measured at pH 8.1, using L-proline and [2,5,5-²H₃]-L-proline as substrates (Figure 4A). Normal KIEs were observed with a very large primary effect on ^DV/K_pro of 5.6 ± 0.1 and a small effect on ^DV of 1.1 ± 0.2. The equations that describe the V and V/K_pro isotope effects can be derived from the model shown in Scheme 2, neglecting any contribution from the reverse commitment factor. The commitment factor that determines the extent and degree to which the intrinsic primary kinetic isotope effect is observed for V/K_pro is k₃/k₂, that is, the ratio of the rate of the chemical step defining the oxidation of L-proline to form Δ¹-pyrroline-5-carboxylate divided by the rate of dissociation of L-proline from the binary Michaelis complex. The large size of ^DV/K_pro argues that chemistry is much slower than dissociation, and thus, L-proline is not a “sticky” substrate. The commitment factor for V for a ping-pong reaction sequence is k₃/k₇, the ratio of the two chemical steps that result in enzyme-bound flavin reduction (k₃) and enzyme-bound reduced flavin oxidation (k₇). The small size of ^DV, relative to either ^DV/K_pro or any reasonable value for ^Dk₃, requires that k₇ be less than k₃, and that the oxidative half-reaction is the overall rate-limiting step of the two chemical steps.

Figure 4.

Kinetic isotope effects. (A) Primary kinetic isotope effects at saturating DCPIP (80 μM) and varying (2 – 25 mM) L-proline (●) or [2,5,5-²H₃]-L-proline (▲) concentrations at pH 8.05. Data was fit to eq 4, which gave a ^DV of 1.1 ± 0.2 and a ^DV/K_L-pro of 5.6 ± 0.1. (B) Solvent kinetic isotope effects at saturating DCPIP (80 μM) and varying (2 – 25 mM) L-proline concentrations in H₂O (●) or D₂O (▲) at pH 8.05. Data was fit to eq 4, which gave a ^DV of 1.3 ± 0.1 and a ^DV/K_L-pro of 2.1 ± 0.4. (C) Proton inventory at saturating DCPIP (80 μM) and saturating L-proline (20 mM) concentrations at pH 8.05 in 10% D₂O increments from 0 to 100% (D) Primary kinetic isotope effects at saturating DCPIP (80 μM) and varying (2 – 25 mM) L-proline (●) or (5 – 25 mM) [2,5,5-²H₃]-L-proline (▲) concentrations performed in D₂O at pH 8.05. Data was fit to eq 4, which gave a ^DV of 1.5 ± 0.1 and a ^DV/K_L-pro of 3.4 ± 0.4.

Scheme 2.

To investigate the involvement of proton transfer steps occurring in the reactions, solvent KIEs were measured at pH 8.1, a region where the kinetic parameters are not changing as a result of the isotopic composition of the solvent. At saturating concentrations of DCPIP and variable concentrations of L-proline, SKIE’s for ^D2OV of 1.3 ± 0.1 and for ^D2OV/K_pro of 2.1 ± 0.4 were determined (Figure 4B). A viscosity control using 9% glycerol to mimic the relative viscosity of D₂O was conducted, and no effect of viscosity on the rate was observed (data not shown). In order to determine the number of protons involved in the solvent isotope-dependent step, a proton inventory experiment was performed (Figure 4C). ^D2OV/^H2OV was determined in 10% increments between 0 and ~100% D₂O. The observed linear proton inventory is indicative of a single solvent-derived proton involved in the step that is solvent sensitive. Similar to the case of primary KIE’s on V/K_pro, only those steps involving proton transfer in the first half-reaction influence the magnitude of ^D20V/K_pro. The oxidation of L-proline requires both a deprotonation of the secondary amine nitrogen of L-proline (by K110), and the transfer of a hydride ion from C5 to the N5 position of FAD. The deprotonation step will be sensitive to solvent isotopic composition, and the magnitude of ^D20V/K_pro is relatively small (2.0), suggesting that it is not rate-limiting, as least compared to the hydride transfer step reported on by the primary KIE (^DV/K_pro = 5.5). The magnitude of ^D20V suggests that cleavage of the N5-D flavin bond of reduced FAD is similarly not rate-limiting in the oxidative half-reaction.

In order to probe the stepwise versus concerted nature of L-proline oxidation, the primary kinetic isotope effect on L-proline and [2,5,5-²H₃]-L-proline oxidation was determined in D₂O. The measured value of ^DV_D2O was 1.5 ± 0.1 while ^DV/K_pro-D2O was 3.4 ± 0.4 (Figure 4D). The decrease in the primary V/K KIE from 5.5 in H₂O to 3.4 in D₂O argues that the proton and hydride transfer steps are uncoupled, and that the reaction precedes via an initial deprotonation of the protonated ring nitrogen of L-proline (pK = 10.6) by K110, followed by hydride transfer from the C5 position of L-proline to FAD resulting in the formation of Δ¹-pyrroline-5-carboxylate [17, 18].

Pre-Steady State Kinetic Isotope Effects

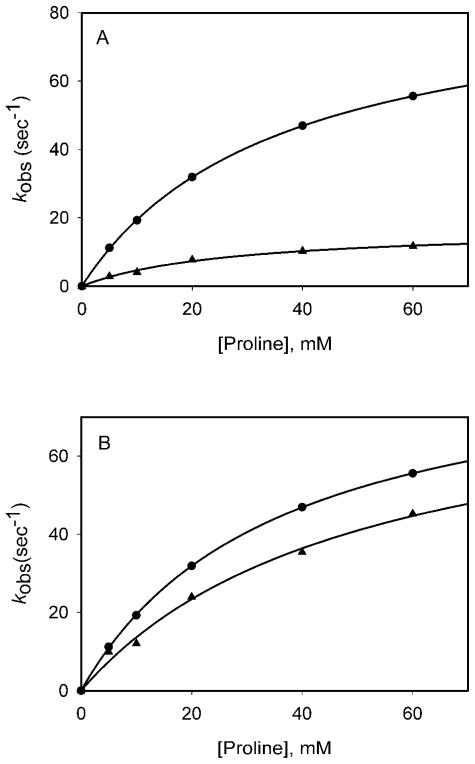
In order to confirm our interpretations of the steady-state isotope effects, we measured the rate of the individual first half-reaction, the reduction of flavin, using single turnover stopped-flow techniques. Using L-proline, a k_red rate of 88.5 ± 0.7 s⁻¹ was measured with an apparent K_d of 33.5 ± 0.5 mM. This k_red is ~3-fold faster than that of the ProDH from E. coli [14]. The k_red was then measured using [2,5,5-²H₃]-L-proline as the substrate, allowing for the calculation of the primary kinetic isotope effect on ^Dk_red of 5.2 (Figure 5A). These data confirm that L-proline is not “sticky’ and that the forward commitment factor is near zero. It also confirms our interpretation, based on the much smaller magnitude of the determined steady-state values of ^DV compared to ^DV/K_pro, that oxidation of the reduced flavin by DCPIP is slower than flavin reduction by L-proline. For a ping-pong mechanism the reciprocal of the k_cat is equal to the sum of the reciprocal rates of the two half-reactions (1/_kcat = 1/k_red + 1/k_ox). Using values of k_cat = 33 sec⁻¹ and k_red = 88 sec⁻¹, the rate of k_ox can be calculated as 52 sec⁻¹. Finally, k_red was then measured in H₂O and D₂O yielding a ^D2Ok_red of 1.1, again confirming the steady-state data (Figure 5B).

Figure 5.

Stopped-flow Kinetic Isotope Effects. (A) Primary KIEs. Each point represents the average of three traces collected with 14 μM ProDH and various concentrations of L-proline (●) or [2,5,5-²H₃]-L-proline (▲) (5–60 mM) (B) Solvent KIEs. Each point represents the average of three traces collected with 14 μM ProDH and various concentrations of L-proline (5–60 mM) in H₂O (●) or D2O (▲).

Chemical Mechanism

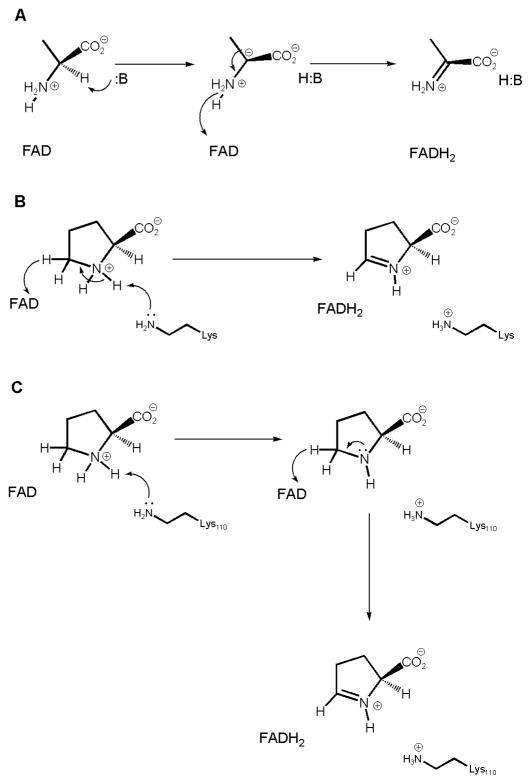
Various mechanisms have been proposed for the oxidation of amines by flavoproteins [19, 20]. However, the mechanism of L-proline oxidation by ProDH is different in two significant ways: oxidation occurs at a secondary amine and oxidation involves the N1-C5 bond rather than the typical N1-Cα bond. For years, the mechanism of D-amino acid oxidase (DAAO) was thought to involve base abstraction of the α-hydrogen, to form a carbanion, with the subsequent formation of the N1-Cα double bond after hydride transfer to FAD [21] (Scheme 3A, shown for alanine). More recent work on various amino acid oxidases have led to an alternative mechanism in which the amino hydrogen is removed first, followed by either a concerted hydride transfer (Scheme 3B) or a step-wise transfer [17, 18, 22] (Scheme 3C). Based on our results reported here, most importantly the multiple kinetic isotope effects, we propose a mechanism for the reductive half-reaction (Scheme 3C). After L-proline enters the active site, it interacts with Y203, positioning it to allow for interaction of the amino ring nitrogen and the uncharged K110. Deprotonation of the ring nitrogen by K100 gives the neutral amino acid, which then collapses with donation of a hydride ion from C5 to the FAD. The proton transfer step is less energetically difficult than the hydride transfer step, as supported by our observation of a modest SKIE but a very large primary KIE on V/K_pro. It is this later step that is rate-limiting in the reductive half-reaction, but it is reduced flavin reoxidation that is rate-limiting for the overall reaction. This same stepwise chemical mechanism has recently been proposed for the D-arginine dehydrogenase reaction using similar isotopic approaches [24].

Scheme 3.

Abbreviations

DTT

dithiothreitol

LB

Luria broth

MES

2-(N-morpholino)ethanesulfonic acid

Ni-NTA

nickel nitriloacetic acid

PCR

polymerase chain reaction

SDS–PAGE

sodium dodecyl sulfate–polyacrylamide gel electrophoresis

Tris

tris(hydroxymethyl)aminomethane

WT

wild type

FAD

flavin adenine dinucleotide

Bis-tris propane

1,3-bis(tris(hydroxymethyl)methylamino)propane

CHES

N-Cyclohexyl-2-aminoethanesulfonic acid