Nonscalar elastic light scattering from continuous media in the Born approximation

Abstract

A three parameter model based on the Whittle-Matérn correlation family is used to describe continuous random refractive index fluctuations. The differential scattering cross section is derived from the index correlation function using nonscalar scattering formulas within the Born approximation. Parameters such as scattering coefficient, anisotropy factor, and spectral dependence are derived from the differential scattering cross section for this general class of functions.

The process of elastic light scattering from weakly scattering turbid media is important in many applications ranging from radar, remote sensing, and atmospheric sciences to light propagation in biological media. Commonly used models of the continuous refractive index distributions include the Booker-Gordon formula (exponential correlation), the Gaussian model, and the Kolmogorov spectrum (von Kármán spectrum) [1]. Evidence exists for other distribution types [2] and recently, several groups have proposed a fractal model for index distributions of biological tissue [3, 4]. In this paper, we make use of a general model that includes the mass fractal, exponential, Gaussian, and other index correlation functions and expand on the work of Sheppard [5] to include the effect of vector waves. We also provide simplified relationships for limiting cases and discuss how the spectral dependence relates to the shape of index correlation function.

A three parameter model with parameters l_c, dn², and m is used to describe the refractive index correlation function. The model is represented by the Whittle-Matérn correlation family

$$B_n(r)=d{n}^2\frac{2^{\frac{5}{2}-m}}{|\mathrm{\Gamma }(m-\frac{3}{2})|}{(\frac{r}{l_c})}^{m-\frac{3}{2}}{K}_{m-\frac{3}{2}}(\frac{r}{l_c})$$ (1)

which reduces to several important specific functions for certain values of m [6]. K_ν(·) denotes the modified Bessel function of the second kind. The parameter l_c describes the index correlation distance or turbulence scale and the parameter dn² is the variance of the refractive index, sometimes written as <n₁²>. The third parameter m determines the shape of the correlation function.

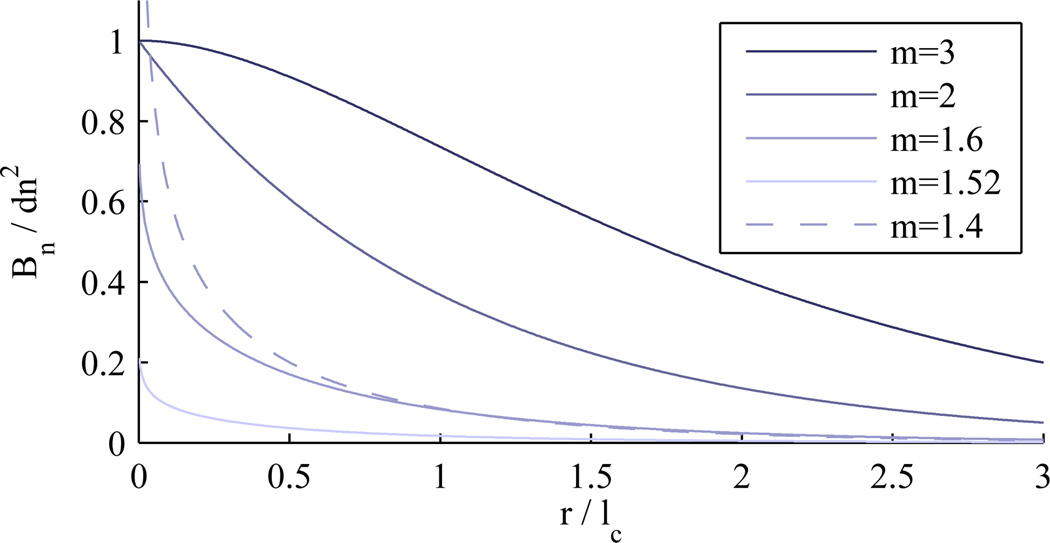
Eq. 1 is normalized such that B_n(0) = dn² for m > 3/2. As m → ∞, the function approaches a Gaussian distribution. When m = 2, the function is a decaying exponential. Values of m between 2 and 3/2 result in a stretched exponential (for small values of r). A singularity exists at m = 3/2 and the function collapses to zero because of the normalization factor of Γ(m − 3/2). However, the unnormalized B_n(r) approaches a delta function for m = 3/2 and the corresponding spectral density is the often used Henyey-Greenstein function. This can be interpreted as describing point like scatterers or a discrete rather than continuous medium. Values of m < 3/2 correspond to a mass fractal index distribution with correlation function described by a power law in which case m is related to the mass fractal dimension by d_mf = d_E − (3 − 2m), where d_E is the Euclidean dimension. Here, d_E = 3, the dimension of the embedding medium and is not related to the shape of the scattering bodies. Fig. 1 shows B_n(r) for several representative values of m.

Fig. 1.

Index correlation functions for some values of m.

When m < 3/2, the function B_n(r) is infinite at r = 0 and as a consequence the function can not be normalized. This is non-physical and in reality the correlation must roll off to a finite value below some minimum length scale r_min. This can be represented by a truncated version of the function such that B̃_n(r) = B_n(r_min) for r < r_min. When r_min ≪ l_c, the error between the model and truncated version is minimal as discussed later. For r > l_c, the function drops quickly to zero. The model can be thought of as a fractal over the range r_min to l_c where r_min is the inner length scale and l_c is the outer scale beyond which, the function drops quickly to zero.

In the Born approximation, the spectral density Φ is the Fourier transform of B_n(r) [1]. For this model, B_n(r) is of the form of the Pearson distribution type VII.

$$\mathrm{\Phi }(k_s)=ℱ\{B_n(r)\}=\frac{d{n}^2{l_c}^3\mathrm{\Gamma }(m){(1+{k_s}^2{l_c}^2)}^{-m}}{{\pi }^{3/2}|\mathrm{\Gamma }(m-\frac{3}{2})|}$$ (2)

The spectral density is related to the differential scattering cross section per unit volume σ by

$$\sigma (\theta ,\varphi )=2\pi k^4(1-{\text{sin}}^2(\theta ){\text{cos}}^2(\varphi ))\mathrm{\Phi }(2k\text{sin}(\theta /2))=\frac{2d{n}^2{k}^4{l_c}^3\mathrm{\Gamma }(m)}{\sqrt{\pi }|\mathrm{\Gamma }(m-3/2)|}\frac{(1-{\text{sin}}^2(\theta ){\text{cos}}^2(\varphi ))}{{(1+{[2k{l}_c\text{sin}(\theta /2)]}^2)}^m}$$ (3)

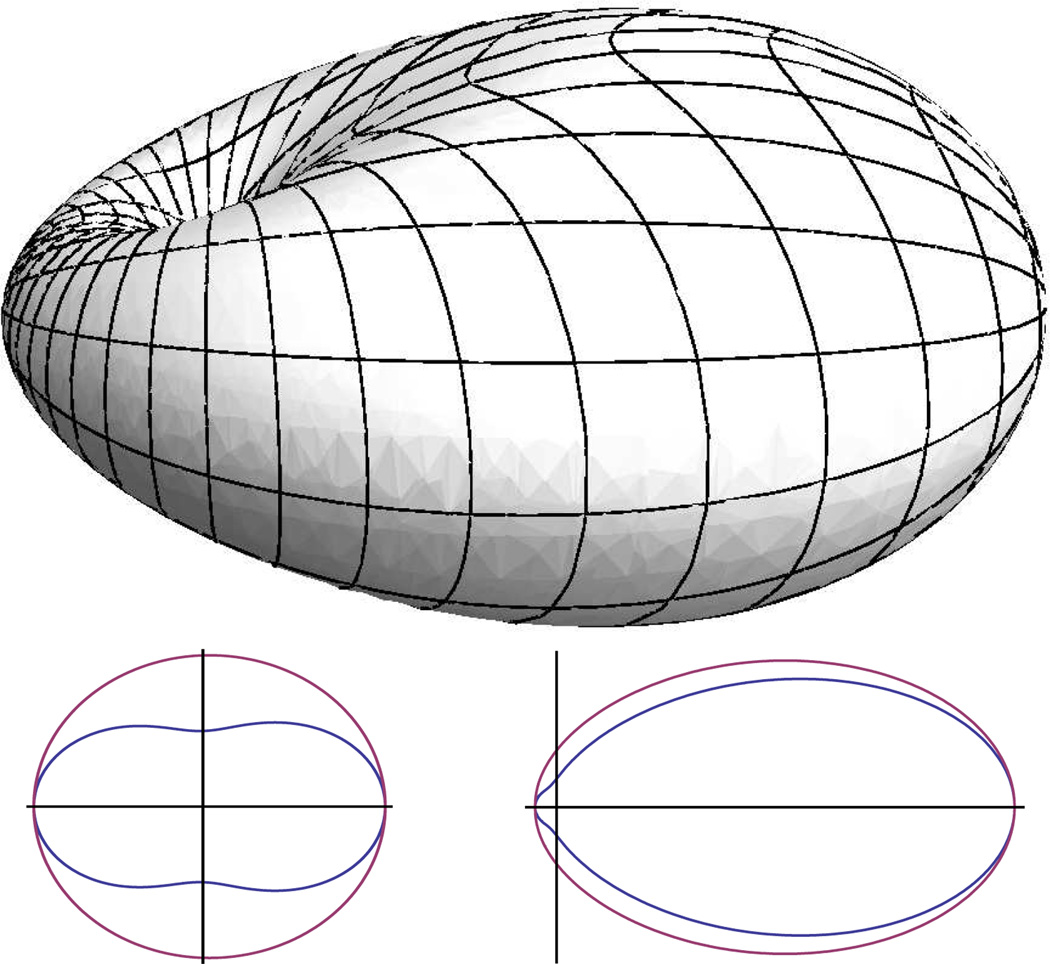
Note that the factor (1 − sin²(θ)cos²(ϕ)) = sin²χ depends on the polarization orientation ϕ of the incident light. For kl_c ≪ 1 (isotropic scattering), this factor results in the dipole radiation pattern. Fig. 2 (top) shows an example σ with slightly forward directed scattering.

Fig. 2.

Above: An example differential scattering cross section plotted in spherical coordinates. The incident wave propagates from left to right and the polarization is such that electric field is in the vertical plane. The dimple is located at the origin. Below: Comparison of the rotationally averaged σ_up (inner) corresponding to unpolarized incidence and the scalar wave approximation σ_sw (outer) for kl_c = 0.1 (isotropic scattering) shown left, and kl_c = 1 (forward scattering) shown right.

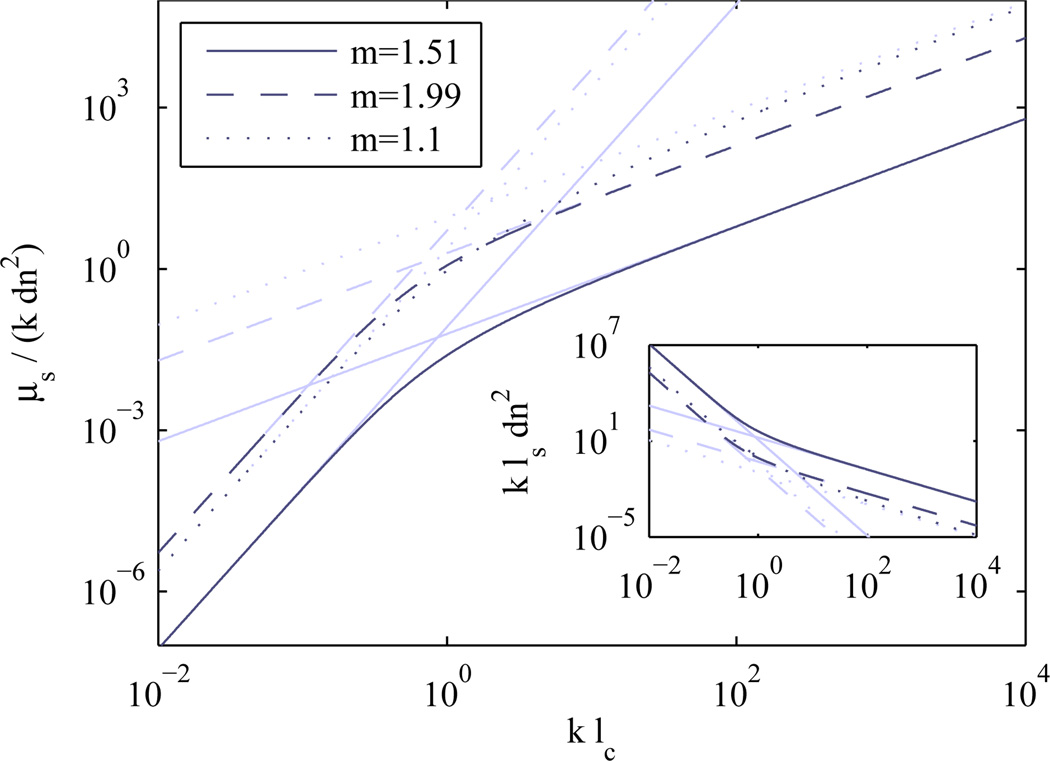
The scattering coefficient μ_s is derived by integrating σ(θ, ϕ) over all angles and is shown in Fig. 3. The mean free path l_s is the inverse of the scattering coefficient μ_s. All length scales are normalized by wavelength so that the relationships depend only on kl_c and kl_s (or μ_s/k).

$$\frac{{\mu }_s}{k}=\frac{d{n}^2\sqrt{\pi }\mathrm{\Gamma }(m-3)}{2k^3{l_c}^3|\mathrm{\Gamma }(m-\frac{3}{2})|}[(1+(2k^2{l_c}^2(m-2)-1)\times 2k^2{l_c}^2(m-3))-(1+2k^2{l_c}^2(1+m)+4k^4{l_c}^4(4+(m-3)m)){(1+4k^2{l_c}^2)}^{1-m}]$$ (4)

Eq. 4 is not easy to interpret, so insight can be gained by considering the equation for either very small or very large kl_c. In the limit of kl_c ≪ 1 or kl_c ≫ 1 and m > 1, the relationship simplifies dramatically.

$$\frac{{\mu }_s}{k}=\{\begin{array}{cc}\frac{16\sqrt{\pi }\mathrm{\Gamma }(m)}{3|\mathrm{\Gamma }(m-3/2)|}d{n}^2{(k{l}_c)}^3\hfill & \text{if}k{l}_c\ll 1\hfill \\ \frac{2\sqrt{\pi }\mathrm{\Gamma }(m-1)}{|\mathrm{\Gamma }(m-3/2)|}d{n}^{2}k{l}_c\hfill & \text{if}k{l}_c\gg 1\&m>1\hfill \end{array}$$ (5)

Fig. 3.

Wavelength normalized scattering coefficient μ_s/k as a function of wavelength normalized index correlation length kl_c. Inset shows the normalized mean free path kl_s = k/μ_s dependence. It should be noted that although no limit is shown for μ_s, the value is inherently limited by the requirement that l_s > l_c. This weak scattering limit requires that the value of dn²(kl_c)² ≪ 1.

The anisotropy factor g is used to describe the degree of forward directed scattering and is defined as the average value of the cosine of the scattering angle, < cos(θ)>. For this model, g is given by

$$g=[{(1+4k^2{l_c}^2)}^m(3+2k^2{l_c}^2(m-4)(-3-4k^2{l_c}^2\times (k^2{l_c}^2(m-2)-1)(m-3)))-(1+4k^2{l_c}^2)\times (3+6k^2{l_c}^2(2+m)+8k^6{l_c}^{6}m(10+(m-5)m)+8k^4{l_c}^4(6+(m-1)m))]/[2k^2{l_c}^2(m-4)({(1+4k^2{l_c}^2)}^m(-1-2k^2{l_c}^2\times (2k^2{l_c}^2(m-2)-1)(m-3))+(1+4k^2{l_c}^2)(1+2k^2{l_c}^2(1+m)+4k^4{l_c}^4(4+(m-3)m)))]$$ (6)

Again, the limiting cases for small and large kl_c can be calculated. For g the equation in the large kl_c limit depends on the value of m:

$$g=\{\begin{array}{cc}\frac{4}{5}m{(k{l}_c)}^2\hfill & \text{if}k{l}_c\ll 1\hfill \\ 1-\frac{1}{2(m-2)}{(k{l}_c)}^{-2}\hfill & \text{if}k{l}_c\gg 1\&m>2\hfill \\ 1-b{2}^{3-2m}{(k{l}_c)}^{2-2m}\hfill & \text{if}k{l}_c\gg 1\&1<m<2\hfill \\ \hfill \text{where}\hfill & b=\frac{(m-1)(8+m(m-5))}{(4-m)(6+m(3-m))}\hfill \end{array}$$ (7)

Combining equations for μ_s and g provides the reduced scattering coefficient μ_s′ = (1 − g)μ_s (or transport mean free path, $l_s^{\prime }=1/{\mu }_s^{\prime }$). Fig. 4 shows the dependence of wavelength normalized ${\mu }_s^{\prime }$ on kl_c.

Fig. 4.

Reduced scattering coefficient as a function of index correlation length (each normalized by wavelength).

A key feature of ${\mu }_s^{\prime }$ is the wavelength dependence. Measurements of ${\mu }_s^{\prime }$ typically exhibit a power law dependence on wavelength [7, 8]. Note that for kl_c ≪ 1, g → 0 and ${\mu }_s^{\prime }={\mu }_s$. In this case, μ_s ∝ λ⁻⁴ which is consistent with Rayleigh scattering.

In most biological tissues, measurements indicate that g is large [9] implying that kl_c ≫ 1 (Eq. 7). When kl_c ≫ 1 and m > 2, ${\mu }_s^{\prime }$ does not depend on wavelength at all. When kl_c ≫ 1 and 1 < m < 2 (the most likely regime for biological media), then ${\mu }_s^{\prime }\propto {\lambda }^{2m-4}$. This link between the spectral dependence of the reduced scattering coefficient and the shape of the index correlation function parameterized by m in this model enables the determination of mass fractal dimension. Many scattering techniques can measure ${\mu }_s^{\prime }(\lambda )$ and thus can be used to determine m simply by determining the power law dependence on wavelength. This spectral dependence combined with the previous relationships provides the connection between measurable optical properties μ_s, g, ${\mu }_s^{\prime }(\lambda )$ and the model parameters l_c, dn², m.

There are two major approximations that can be made to simplify the resulting differential scattering cross section. The first is needed for the mass fractal regime when m < 3/2 and B_n(r) → ∞ as r → 0. Since this situation cannot exist in reality, the actual correlation function must level off. However, this would complicate the model significantly, so provided that the error is small, the simple model can be legitimately used even for values of m that result in infinite correlation. To verify this, the normalized error is calculated numerically by computing the difference in μ_s from the model and a truncated version of B_n where B̃_n(r) = B_n(r_min) for r < r_min. This approximation can be used for values of r_min ≪ l_c. The normalized error (μ_s − μ̃_s)/μ_s is negligible for all values of kr_min when m → 3/2. As m → 1 the error increases for large values of kr_min but remains small when kr_min is small. For example, for normalized error less than 1% when m = 1.01 and kl_c = 1, kr_min must stay below 1/6.

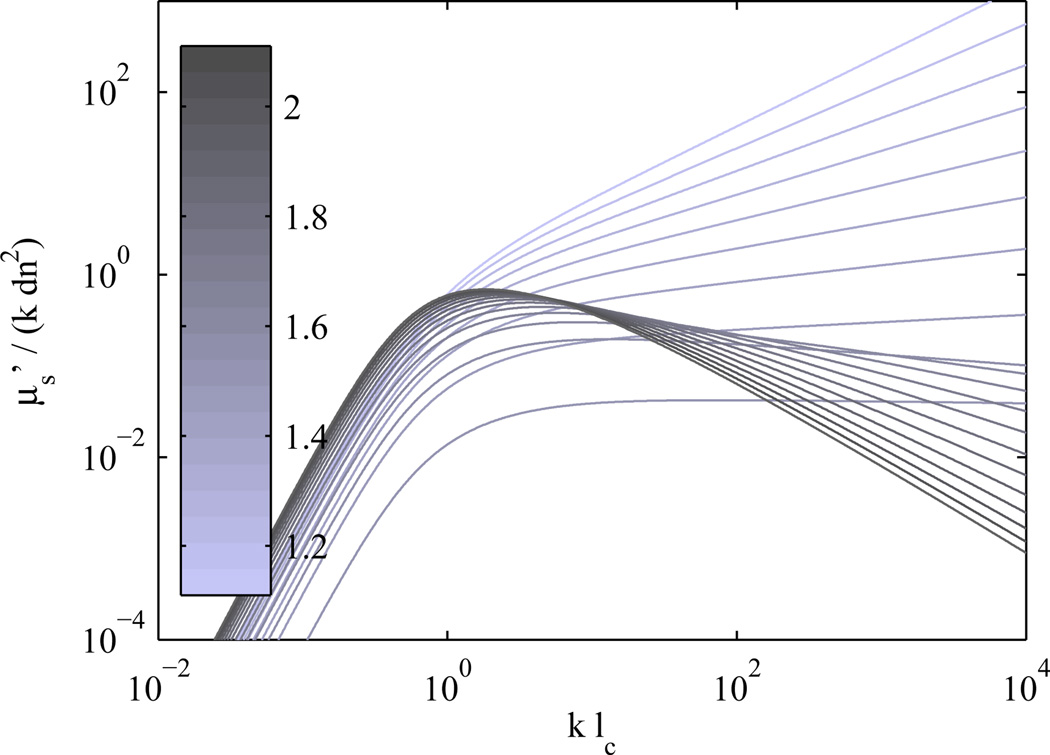
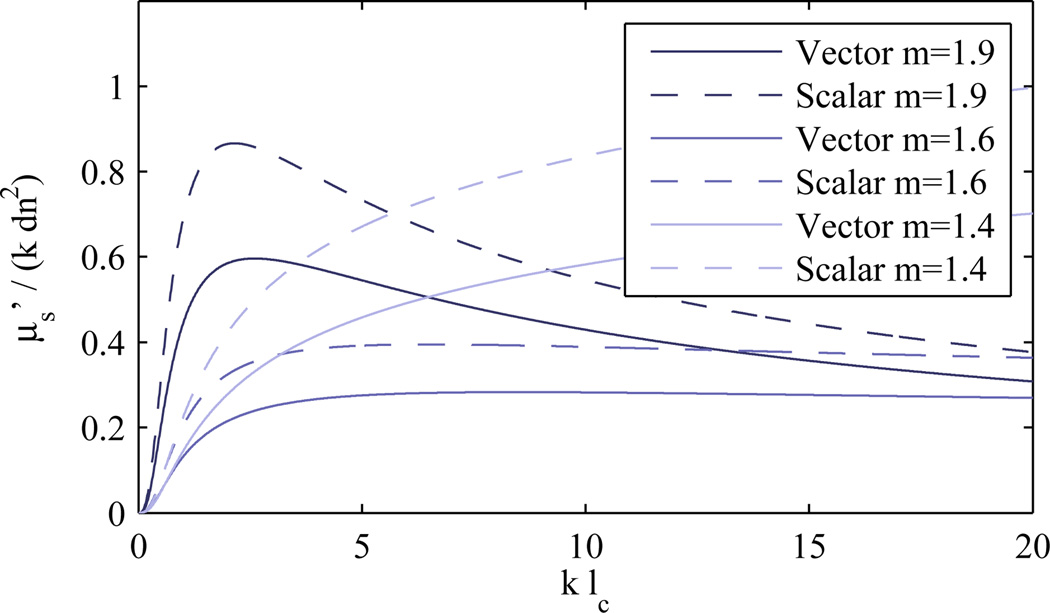
The second approximation that is often used is to assume scalar wave incidence and neglect the dipole factor (dependence on ϕ), which results in an axially symmetric σ_sw (without dimples). In the case of unpolarized illumination, σ is sampled at all orientations of ϕ and the result can be expressed by averaging over ϕ to produce a rotationally symmetric σ_up. The lower part of Fig. 2 shows the difference between the scalar wave approximation and the result of averaging over polarization orientations. To quantify the error in this approximation, the normalized error in the scattering coefficient μ_s is calculated and is maximum for the case of isotropic scattering where $({\mu }_s^{sw}-{\mu }_s)/{\mu }_s\to 1/2$. The error in neglecting the dipole factor also affects the anisotropy factor g and hence ${\mu }_s^{\prime }$ as shown in Fig. 5. Since this second approximation can introduce large error and the complexity of the relationships is not significantly reduced, inclusion of the dipole factor is advisable.

Fig. 5.

Plots of ${\mu }_s^{\prime }$ vs kl_c with and without the dipole factor.