Functional identification and characterization of sodium binding sites in Na symporters

Significance

Symporters or cotransporters are proteins that use sodium electrochemical potential gradients to drive sugars, amino acids, anions, and neurotransmitters into cells. Progress in structural biology has provided important clues about substrate binding sites, but the identification of Na⁺ in binding sites has been a challenge owing to the high resolution required. We use a biophysical method to determine the Na⁺ affinity of electrogenic transporters, and, together with site-directed mutagenesis, we identify the two Na⁺ binding sites in the human intestinal Na⁺/glucose cotransporter SGLT1. The results provide insights into the Na⁺ binding sites of symporters and the mechanism of active transport.

Abstract

Sodium cotransporters from several different gene families belong to the leucine transporter (LeuT) structural family. Although the identification of Na⁺ in binding sites is beyond the resolution of the structures, two Na⁺ binding sites (Na1 and Na2) have been proposed in LeuT. Na2 is conserved in the LeuT family but Na1 is not. A biophysical method has been used to measure sodium dissociation constants (K_d) of wild-type and mutant human sodium glucose cotransport (hSGLT1) proteins to identify the Na⁺ binding sites in hSGLT1. The Na1 site is formed by residues in the sugar binding pocket, and their mutation influences sodium binding to Na1 but not to Na2. For the canonical Na2 site formed by two –OH side chains, S392 and S393, and three backbone carbonyls, mutation of S392 to cysteine increased the sodium K_d by sixfold. This was accompanied by a dramatic reduction in the apparent sugar and phlorizin affinities. We suggest that mutation of S392 in the Na2 site produces a structural rearrangement of the sugar binding pocket to disrupt both the binding of the second Na⁺ and the binding of sugar. In contrast, the S393 mutations produce no significant changes in sodium, sugar, and phlorizin affinities. We conclude that the Na2 site is conserved in hSGLT1, the side chain of S392 and the backbone carbonyl of S393 are important in the first Na⁺ binding, and that Na⁺ binding to Na2 promotes binding to Na1 and also sugar binding.

Ion coupled symporters, or cotransporters, such as hSGLT1 use electrochemical potential gradients to drive solutes into cells. A common finding for these transporters is that external Na⁺ binds before the substrate. Na⁺ binding induces a conformational change of the protein, resulting in the substrate vestibule becoming open to the external membrane surface. After substrate binding, the two ligands are transported across the membrane and are released into the cytoplasm. The atomic structures of several sodium dependent transporters have been solved [leucine transporter (LeuT), vibrio parahaemolyticus sodium glucose (vSGLT), sodium hydantoin (Mhp1), and sodium betaine (BetP)] (1–6). They share a common structural fold with a five-helix inverted repeat, the “LeuT fold”. The substrate binding sites are located in the middle of the protein, isolated from the external and membrane surfaces by hydrophobic gates, and putative Na⁺ sites have been identified. Testing these binding sites is a problem due to the fact that phenomenological kinetic constants for ligand transport (K_0.5, half-saturation values) are interdependent on each other (7). Here we have developed a method to estimate the intrinsic Na⁺ dissociation constants (K_d) for human sodium glucose cotransport (hSGLT1) that may be broadly applicable to other symporters. We then use this to investigate the importance of hSGLT1 residues predicted to be at or near the two Na⁺ binding sites, Na1 and Na2.

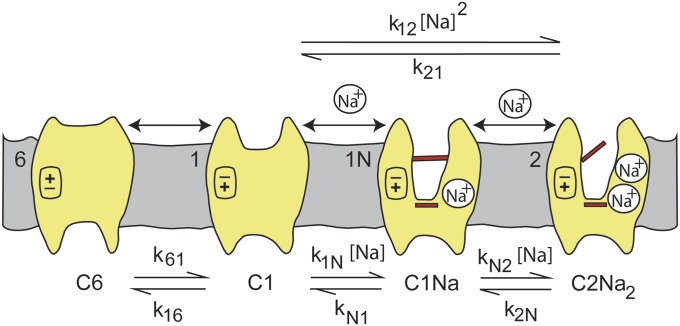
The method is based on the fact that voltage-dependent membrane proteins exhibit transient charge movements (capacitive transients) in response to step changes in membrane potential (8, 9). Voltage-dependent transport proteins, including Na⁺ cotransporters and pumps, exhibit these capacitive currents (7, 10–12). Transient charge movements may be fit with a Boltzmann relation to estimate the voltage at half-maximal charge transfer (V_0.5), where the protein is equally distributed between the two extreme states, the apparent valence of the moveable charge (z) and the number of transporters in the plasma membrane (Q_max) (10, 13). The hSGLT1 Boltzmann parameters are sensitive to the external Na⁺ concentration [Na⁺]_o: As [Na⁺]_o is lowered there is a reduction in Q_max and z and a shift of V_0.5 to more negative voltages. The V_0.5 shift is used to determine the Na⁺ affinity (K_d) for hSGLT1. Basically, it is a thermodynamic method where we determine the voltage where the transporter is equally distributed between two extreme states (outward-facing Na⁺-bound C2Na₂ and inward-facing ligand-free C6), as a function of [Na⁺]_o (Fig. 1). A similar approach has been used to measure the kinetics of Na⁺/Na⁺ exchange by the Na⁺/K⁺ pump (14, 15). Here we use the method with hSGLT1 mutants to locate the two Na⁺ binding sites. The results show that Na1 is part of the sugar binding pocket and Na2 is at the same location as other members of the LeuT structural family.

Fig. 1.

Cartoon representing three- and four-state models for Na⁺ binding to SGLT1. For clarity of presentation, we assume the number (n) of Na⁺ ions binding to the empty transporter is 2. The ligand-free protein carries a net negative charge and transient capacitive SGLT1 currents are associated with reorientation of the empty transporter between external and internal membrane surfaces (C1 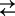C6) and Na⁺ binding/dissociation (C1 + 2Na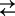⁺ C2Na₂ for the three-state and C1+Na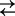⁺ C1Na + Na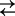⁺ C2Na₂ for the four-state model). K_d is the lumped sodium dissociation constant for the three-state model, and K_dA and K_dB are the sodium dissociation constants for the first and second binding sites for the four-state model (Theory section). Hyperpolarizing voltages drive the transporter to the outward conformation (C6 → C1), as well as promoting the transition C1 → C2Na₂.

Theory

First, consider a three-state model for hSGLT1, where n external Na⁺ ions bind simultaneously to the empty transporter in the absence of external sugar (Fig. 1). The empty transporter is assumed to be negatively charged and opens to the internal (C6) or external (C1) membrane surfaces, depending on membrane voltage (V). Voltage also affects external Na⁺ binding and/or the conformational changes associated with it. The transporter is distributed between C6, C1, and C2Na_n, depending on voltage and [Na⁺]_o.

We assume the rate constants k₁₂, k₂₁, k₁₆, and k₆₁ depend on voltage according to rate theory with symmetric energy barriers (16, 17)

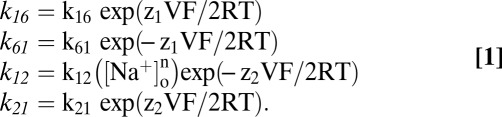k₁₆, k₆₁, k₁₂, and k₂₁ are voltage-independent rate constants. z₁ and z₂ represent the apparent valence of the moveable charge for the empty transporter (z₁) and Na⁺ binding (z₂). F is the Faraday constant, R is the gas constant, and T is absolute temperature.

The occupancy probabilities in C6, C1, and C2Na₂ are

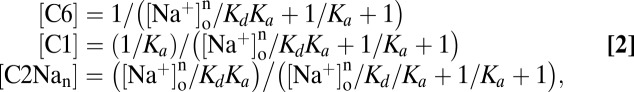where

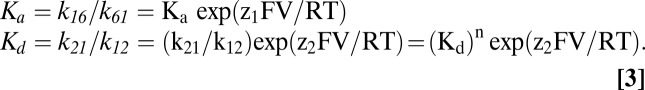K_a (k₁₆/k₆₁) is the equilibrium constant of the distribution of the empty transporter between states C6 and C1 (at 0 mV), and K_d ((k₂₁/k₁₂)^1/n) is the intrinsic Na⁺ affinity at 0 mV. Note that K_d is a lumped parameter for the binding of n Na⁺ ions.

Our focus is on the ability of [Na⁺]_o to alter the distribution of hSGLT1 conformations. The distribution (in steady state) is characterized by the midpoint voltage V_0.5, where the protein is equally distributed between C2Na_n and C6.

To obtain the relation for any given [Na⁺]_o, consider the charge moved (Q) when membrane voltage (V) is stepped from a very negative (where all transporters are in C2Na_n) to a more positive value (17, 18). Q is the sum of the charge transferred from C2Na_n to C1 (each transition contributing a net charge z₂) and from C2Na_n to C6 (contributing a total charge z = z₂ + z₁). For a membrane with a transporter density N_T, the total charge is

and maximal charge Q_max (= N_Te(z₁ + z₂), where e is elementary charge). The Q-V relation is obtained by substituting for [C2Na_n], [C1], and [C6] from Eq. 2:

At V = V_0.5, Q = Q_max/2, and rearranging (with u = F/RT), we obtain the relation between V_0.5 and [Na⁺]_o:

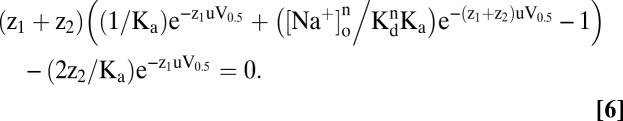Simulation of the V_0.5/[Na⁺]_o Relations.

K_a and K_d can be estimated from Eq. 6 (18). In the absence of external Na⁺, the empty transporter alternates between C6 and C1, depending on voltage. The voltage where C6 and C1 are equally distributed, V_0.5, is given by

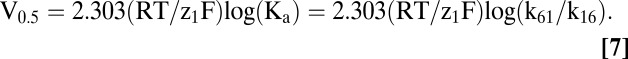At high [Na⁺]_o (>>K_d), the transporter is distributed between C2Na_n and C6 as a function of voltage. It can be shown from Eq. 6 (18) that as [Na⁺]_o approaches saturation, V_0.5 is linearly related to log [Na⁺]_o with slope given by the ratio of the number (n) of Na⁺ ions bound and the net charge (z) of the protein:

Eq. 8 is equivalent to the conservation of energy: The energy required to move charge z (z = z₁ + z₂) through a potential difference (ΔV_0.5) is provided by the chemical potential for n Na⁺ ions.

The theory may be extended to the sequential binding of n Na⁺ ions. For clarity, we restrict our discussion to n = 2 (Fig. 1) (18), but retain “n” to emphasize the dependence on the number of Na⁺ ions. The V_0.5 vs. [Na⁺]_o relation for sequential binding is given by

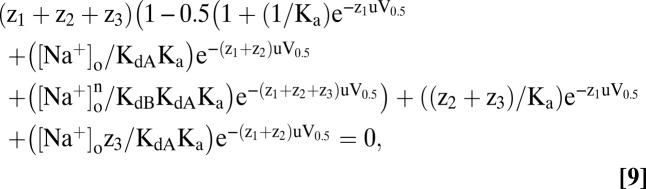where K_a is the equilibrium constant of the empty transporter, and K_dA (= k_N1/k_1N), and K_dB (= k_2N/k_N2) are the Na⁺ affinities of the first and second sites (at 0 mV), respectively. z₁, z₂, and z₃ are the charge associated with the empty transporter and the first and second Na⁺ binding steps (Fig. 1). K_dA and K_dB are related to the lumped K_d by K_d = √ (K_dAK_dB).

The limiting behaviors of the V_0.5 vs. [Na⁺]_o relations are identical to those for the three-state model. In the absence of Na⁺, V_0.5 depends on the apparent valence (z₁) of the empty transporter and the ratio of rate constants k₁₆/k₆₁ (Eq. 7); and in saturating [Na⁺]_o, V_0.5 is linearly related to log [Na⁺]_o with the slope given by the ratio (n/z) of the number of Na⁺ ions and the total charge z (Eq. 8). The difference lies in the approach to the limits. For the four-state model, as [Na⁺]_o approaches zero, the V_0.5 vs. [Na⁺]_o relations are governed by the affinity (K_dA) of the first Na⁺ site. In contrast, as [Na⁺]_o nears saturation the approach to maximal slope (115.6 mV/decade) is determined by the affinity (K_dB) of the second binding site. We anticipate differences in the predictions of the three- and four-state models if there are significant differences between K_dA and K_dB (see below).

Estimating Parameters.

K_a is estimated from V_0.5 in the absence of Na⁺ (Eq. 7) and k₁₆ and k₆₁ from the ratio and the time constant (τ_o) [τ_o = 1/(k₁₆ + k₆₁) and K_a = k₆₁/k₁₆]. Apparent valences z₁ and z (= z₁ + z₂) are obtained from the Q-V curves in the presence and absence of external Na⁺. For hSGLT1 mutant Q457C, we have shown that n = 2 (19). Na⁺ affinities (K_d or K_dA and K_dB) can then be extracted by numerically fitting the V_0.5 vs. [Na⁺]_o data to Eqs. 6 and 9 (see Figs. 5 and 6).

Fig. 5.

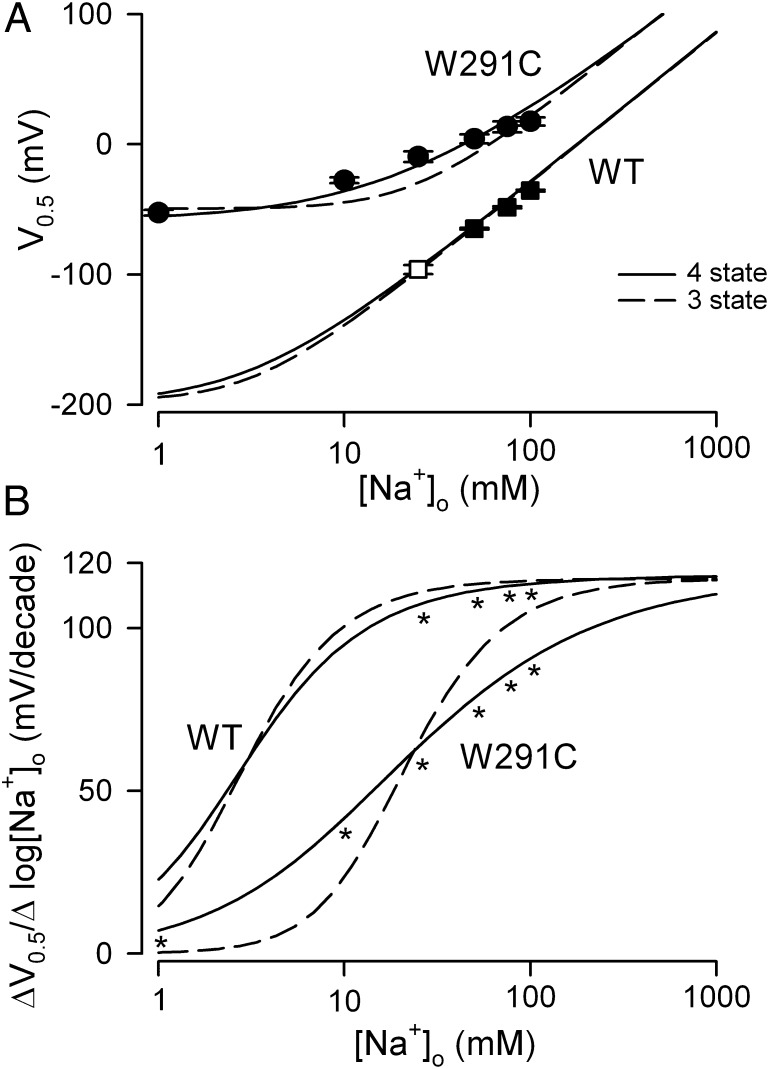
Dependence of V_0.5 on [Na⁺]_o for WT hSGLT1 and mutant W291C. (A) The V_0.5 vs. log [Na⁺]_o data are from Fig. 4. The error bars (SE) for V_0.5, less than the size of the symbols, are the error of the fit to the experimental data in Fig. 4. The curves are simulations of the three- and four-state models (Eqs. 6 and 9) for the individual oocytes shown in Fig. 4. For WT, K_d = 20 mM for the three-state and K_dA = 33 mM, K_dB = 10 mM for the four-state model. For W291C, K_d = 55 mM for the three-state and K_dA = 30 mM, K_dB = 110 mM for the four-state model. k₁₆/k₆₁ = 100 for WT and 1.6 for W291C. For both transporters, z₁ = 0.7, z₂ = 0.15, and z₃ = 0.15. Net charge z (= z₁ + z₂ + z₃) = 1. (B) Replots of the three- and four-state simulations for WT and W291C as the slope of V_0.5 vs. log[Na⁺]_o (ΔV_0.5/Δlog [Na⁺]_o). This shows the transition between the two limiting slopes for each model and the distribution of the experimental data. The asterisks indicate the [Na⁺]_o where V_0.5 could be reliably estimated (A).

Fig. 6.

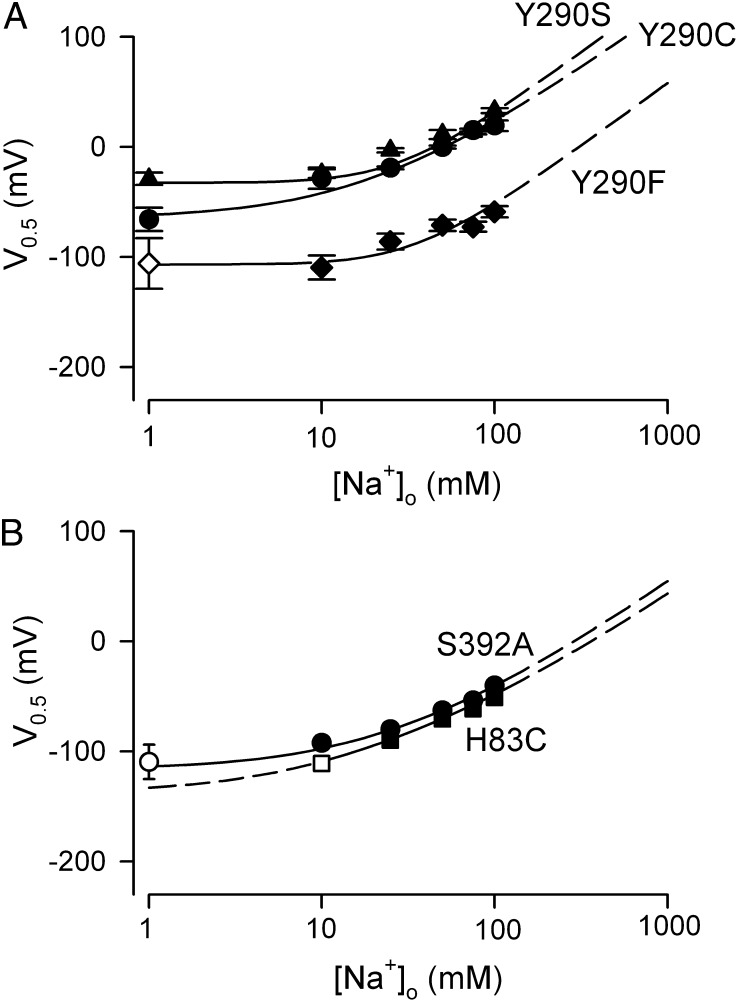
Dependence of V_0.5 on [Na⁺]_o for Y290C, Y290S and Y290F (A) and H83C and S392A (B). Data shown are from individual oocytes, with error of the fit. When V_0.5 was more negative than −100 mV (for Y290F, H83C, and S392A at low [Na⁺]_o), the open symbols were obtained from fitting the Q/V curves under the constraint that z = 0.7. The curves are from simulations of the four-state model (Eq. 9): K_dA = 30 mM, K_dB = 110 mM, and k₁₆/k₆₁ = 1 for Y290S; K_dA = 30 mM, K_dB = 110 mM, and k₁₆/k₆₁ = 2.4 for Y290C; K_dA = 30 mM, K_dB = 112 mM, and k₁₆/k₆₁ = 8 for Y290F; K_dA = 30 mM, K_dB = 480 mM, and k₁₆/k₆₁ = 15 for H83C; and K_dA = 50 mM, K_dB = 300 mM, and k₁₆/k₆₁ = 10 for S392A. z₁ = 0.7, z₂= 0.15, z₃ = 0.15, z = 1 (z = 1 = z₁ + z₂ + z₃), and n = 2 for all five proteins.

Results

The selection of mutants at putative Na1 and Na2 sites was guided by previous findings on the kinetics of hSGLT1 mutants (20, 21) and the location of the Na1 and Na2 sites in LeuT (6). Fig. 2 shows the location of the glucose binding site and the Na2 site in a homology model of hSGLT1 (20). The glucose binding site mutants that express well in the plasma membrane of oocytes are H83C, Y290C/S/F, W291C, and Q457C. All showed an increase in sugar K_0.5 compared with WT, consistent with their role in sugar binding (20), but the K_0.5 for Na⁺ also increased >10-fold for Y290C and W291C (21). The interpretation of reductions in apparent sugar and Na⁺ affinities is ambiguous because the apparent affinities (K_0.5) for sugar and Na⁺ are interdependent (17, 20, 22).

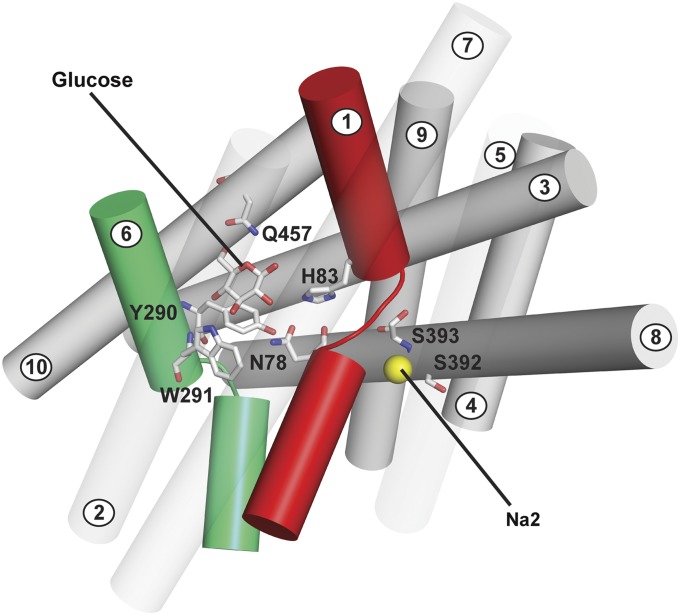
Fig. 2.

Homology model (side view) of hSGLT1 in the inward-occluded conformation (20) based on the inward-occluded vSGLT structure (Protein Data Bank ID code 3DH4) (2). Glucose coordinates with H83 and N78, Y290 and W291 (CH–π interactions), Q457 (O5 and O6), and E102 (not shown for clarity). The hydroxyl (OH⁻) of Y290 forms an H bond with N78; Y290 and W291 are involved in a π T-stacking interaction. Na⁺ (yellow sphere) is shown 10 Å away from the sugar site at the Na2 site with S392 and S393.

The putative Na2 site is 10 Å from the sugar binding site (Fig. 2) and is formed by residues on TM1 and TM8—S393, S392, and the backbone carbonyls of S389, I79 and A76. Mutations of S392 (S392A/C) produced dramatic increases in K_0.5 for both sugar and Na⁺, whereas mutations of S393 (S393A/C) resulted in only modest changes (20). Our aim was to measure the intrinsic Na⁺ affinity (K_d) for H83C, Y290C/S/F, W291C/F, Q457C, and S392A and other mutants not expected to be involved in ligand binding, i.e., T287C, F101C, F453C, and G507C (20, 23).

WT hSGLT1.

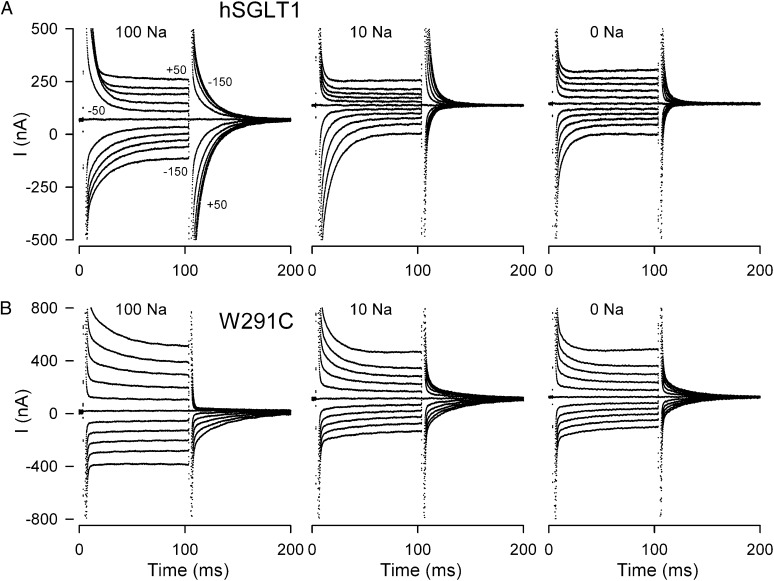
Representative current records for an oocyte expressing wild-type hSGLT1 in 0-, 10-, and 100-mM NaCl buffers are shown in Fig. 3A. The membrane potential was held at −50 mV (V_h) and stepped (ON pulse) to test values (between +50 mV and −150 mV) for 100 ms before returning to V_h (OFF pulse). In response to the voltage jump, total membrane current relaxation consists of an initial capacitive spike (with a time constant τ ∼ 1 ms) due to the membrane lipid bilayer, followed by a slower hSGLT1 transient current that decays to a steady state (τ ∼ 3–30 ms). When membrane voltage was returned to V_h, both the bilayer and the hSGLT1 transient currents were in the opposite direction. hSGLT1 pre–steady-state currents were blocked by phlorizin (a SGLT1-specific inhibitor) and glucose (10, 22, 24). In 10 mM Na⁺, the currents were smaller and the relaxations were faster. In the absence of Na⁺, charge movements were clearly observed when membrane voltage was returned from a large hyperpolarizing voltage (e.g., −150 mV) back to the holding potential, but these were less than 1 nC (Fig. 3A). The small charge movements in the absence of Na⁺ are due, in part, to the fast time constants, <2 ms at −50 mV (see Fig. 7) and the shift of V_0.5 to extreme negative values beyond the range of the experimental measurement: Theory predicts that V_0.5 approaches −200 mV in the absence of [Na⁺]_o (see Fig. 5A).

Fig. 3.

Current records for oocytes expressing wild-type hSGLT1 and mutant W291C. The experiments were performed with membrane potential held at −50 mV (V_h) and stepped to a series of test voltages (from +50 mV to −150 mV) for 100 ms before returning to V_h. Current records for hSGLT1 (A) and for mutant W291C (B) in 0 mM, 10 mM, and 100 mM. Na⁺ concentration was varied by equimolar replacement of NaCl with choline chloride.

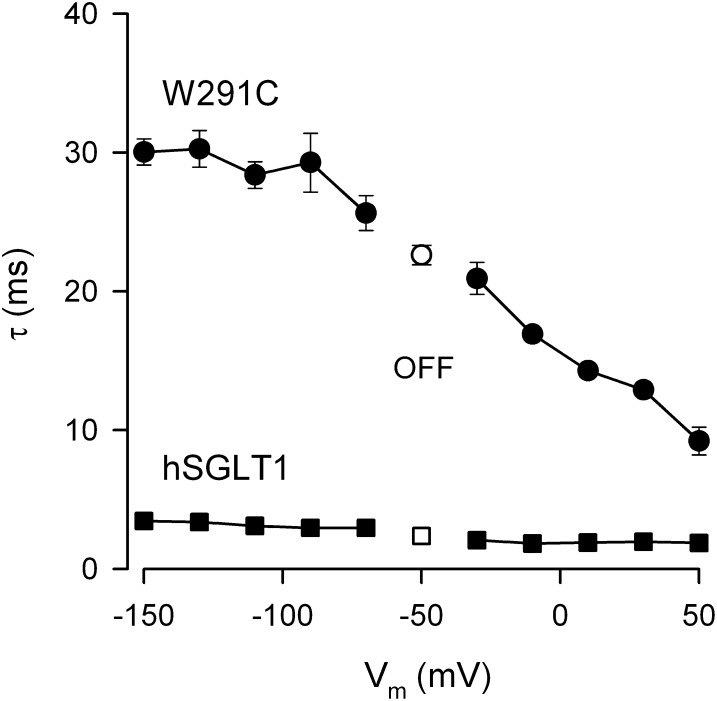
Fig. 7.

Dependence of relaxation time constants (τ) on membrane voltage (V_m) for WT hSGLT1 and mutant W291C in the absence of Na⁺. Data were obtained from the experiments in Fig. 3. The solid symbols represent the ON response when V_m was stepped from holding (V_h = −50 mV) to various test values, and the open symbols are from the subsequent OFF response when V_m was returned from test voltage to V_h. For the OFF, τ was independent of test voltage, and data shown are the mean of the 10 voltage pulses. The error bars are SEs of the fit and when absent were smaller than the size of the symbol.

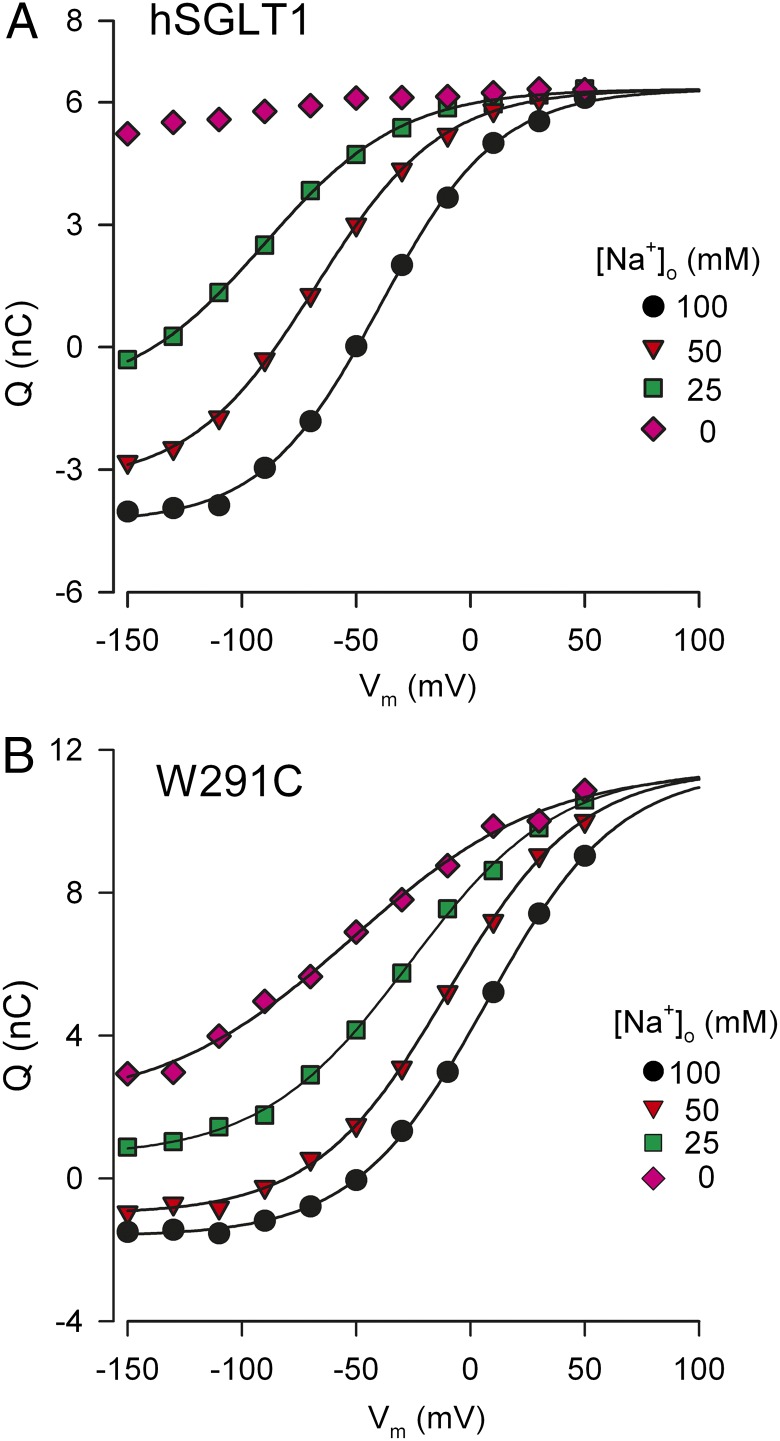
The hSGLT1 transient currents were integrated to obtain the total charge transferred (Q) for each voltage pulse. Q's for the ON and OFF transients were equal and opposite at each voltage. A Boltzmann relation (Eq. 11) was used to fit the charge vs. voltage (Q-V) curves (Fig. 4A) to obtain Q_max, V_0.5, and z. In saturating [Na⁺]_o, Q_max provides an index of the number of hSGLT proteins in the plasma membrane. Q_max was 10.6 nC in 100 mM [Na⁺]_o, corresponding to 1 × 10¹⁰ transporters in the oocyte plasma membrane (10, 13). V_0.5 was −39.5 ± 2 mV; and z was 1.0. Reducing [Na⁺]_o decreased Q_max and z and shifted V_0.5 to more negative voltages. At 25 mM Na⁺ V_0.5 shifted from –39.5 ± 1 mV at 100 mM Na⁺ to −90 ± 2 mV (Fig. 4A). Q_max decreased 30% from 10.6 ± 0.2 nC to 7.6 ± 0.2 nC and z from 1.0 ± 0.1 to 0.8 ± 0.1. Below 25 mM Na⁺, the Q-V curves did not saturate at the largest hyperpolarizing voltage that could be applied (−150 mV).

Fig. 4.

Characteristics of the charge movement for wild-type hSGLT1 and mutant W291C. The data shown are from individual oocytes. The charge vs. voltage (Q-V) relations are shown for hSGLT1 (A) and W291C (B) when [Na⁺]_o varied from 100 mM to 0 mM. The curves were obtained by fitting the Q/V curves to the Boltzmann relation (Eq. 11) and are aligned at the depolarizing limit. Q/V data for hSGLT1 at 0 mM could not be fitted due to the extremely negative V_0.5 (∼ −200 mV, Fig. 5).

W291C.

Representative current records for mutant W291C are shown in Fig. 3B. In 100 mM Na⁺, the pre–steady-state currents were observed only with depolarizing voltage pulses. In the absence of Na⁺, the pre–steady-state currents are similar for both hyperpolarizing and depolarizing voltage pulses—the symmetry of the current is particularly clear in the OFF records.

The Q-V relations for mutant W291C as a function of [Na⁺]_o are shown in Fig. 4B. In 100 mM Na⁺, the Boltzmann parameters Q_max, V_0.5, and z were 13 ± 1 nC, 7 ± 2 mV, and 0.9 ± 0.1. As [Na⁺]_o is reduced to zero, Q_max decreased by 20% from 13 nC to 10 nC, z decreased from 0.9 ± 0.05 to 0.6 ± 0.05, and V_0.5 shifted from 7 ± 2 mV to −52 ± 5 mV. The values obtained for V_0.5 and z in 0 mM and 100 mM Na⁺ for W291C and all mutants are summarized in Table 1. Note that the apparent valence (z) averaged 1.0 in 100 mM Na⁺ and 0.7 in the absence of Na⁺, consistent with the hypothesis that 70% of the charge transfer was associated with the reorientation of the empty transporter (between C1 and C6) and 30% to Na⁺ binding (C1 to C2Na₂), possibly through a Na⁺-well effect and/or a change in conformation (10, 17).

Table 1.

V_0.5 and z at 100 and 0 mM [Na⁺]_o

	V0.5, mV		Z
Mutant	100 Na+	0 Na+	100 Na+	0 Na+
hSGLT1	−39 ± 2	< −120	1.0 ± 0.1	n.m.
Near sugar binding
H83C	−42 ± 3	−120 to −140	0.9 ± 0.1	n.m.
T287C	−47 ± 1	< −120	1.0 ± 0.1	n.m.
Y290C	3 ± 4	−54 ± 4	0.9 ± 0.1	0.6 ± 0.1
Y290S	18 ± 1	−40 ± 6	0.9 ± 0.1	0.7 ± 0.1
Y290F	−49 ± 13	< −120	0.9 ± 0.1	n.m.
W291C	12 ± 2	−53 ± 2	0.9 ± 0.1	0.6 ± 0.1
W291F	−49 ± 9	< −120	1.0 ± 0.1	n.m.
Q457C	−55 ± 4	< −120	1.0 ± 0.1	n.m
Near Na2 site
D204E*	−50 ± 2	−67 ± 3	∼1	∼1
S392A/C	−56 ± 3	−100 to −140	0.9 ± 0.1	n.m.
Other
F101C	−3 ± 3	< −120	1.0 ± 0.1	n.m.
F453C	−28 ± 4	< −120	1.0 ± 0.1	n.m.
G507C	−35 ± 1	< −120	1.0 ± 0.1	n.m.

Kinetics are mean ± SE of three to nine oocytes from at least two donor frogs. For mutants with Q/V curves that did not saturate (within the range −150 mV and +50 mV) at 0 Na⁺, we were unable to obtain reliable estimates of V_0.5 and z. V_0.5 was more negative than −120 mV (< −120 mV) and z was designated by nonmeasurable (n.m.). At 0 Na⁺, z = z₁, and at 100 mM Na⁺, z = z₁ + z₂ + z₃ (Eq. 9).

^*Data are from Quick et al. (25), where the data at 0 Na⁺ were actually obtained in 5 mM Na⁺.

Dependence of V_0.5 on [Na⁺]_o.

The V_0.5 vs. log [Na⁺]_o data for WT hSGLT1 are shown in Fig. 5A. Between 25 mM and 100 mM Na⁺, the regression line through the data yielded a slope of 93 ± 5 mV per 10-fold change in [Na⁺]_o, but above 50 mM the slope approached the theoretical limiting value of 115.6 mV/decade (Eq. 8 at 22 °C) (ref. 10, figure 23E in ref. 22, and figure 3C in ref. 25). The limiting slope data are consistent with two Na⁺ ions binding to hSGLT1 (Eq. 8 with n = 2 and z =1 for hSGLT1). For all mutants studied the V_0.5 vs. log [Na⁺]_o curves also approached the limiting value at high [Na⁺]_o (for example, Figs. 5A and 6). Together with z values of 1 (Table 1), we conclude n = 2 for these mutants.

As the [Na⁺]_o is reduced toward zero, the theory predicts that V_0.5 approaches the limiting value determined by Eq. 7 (V_0.5 = 2.303 (z₁F/RT) log(k₆₁/k₁₆)). For wild-type hSGLT1, V_0.5 is predicted to be between −150 mV and −200 mV (Fig. 5), well beyond the experimental working range. However, for W291C, V_0.5 was essentially independent of [Na⁺]_o, below 10 mM with a limiting value of −57 mV (Fig. 5A); i.e., there is a charge movement associated with the ligand-free protein. Similar observations were made for Y290C, Y290S, Y290F, H83C, and S392A (Fig. 6) with limiting values between −40 mV and −120 mV. The V_0.5 at 0 [Na⁺]_o yields k₁₆/k₆₁ ratios for the reorientation of the empty transporter between the outward and inward facing conformations (Eq. 7), and these range from 100 for WT to 2 for Y290C, Y290S, and W291C (Table 2).

Table 2.

Na⁺ affinity of hSGLT1 mutants

	Kd, mM	KdA, mM	KdB, mM	k16/k61	τo, ms	k16, s−1	k61, s−1
hSGLT1	20	33*	10*	100	<2†	530	5
Near sugar binding site
H83C	120	—	>150	6	6	170	10
T287C	20	—	—	200	—	—	—
Y290C	57	30	110	2.4	9	80	33
Y290S	57	30	110	1.4	17	60	25
Y290F	120	30	>150	24	10	100	4
W291C	55	30	110	2	16	21	43
W291F	20	—	—	100	4	275	3
Q457C	20	—	—	250	2	530	2
Near Na2 site
D204E	>150	—	—	2.6	—	—	—
S392A	122	50	>150	10	19	48	5
Other
F101C	18	—	—	35	—	—	—
F453C	20	33*	10*	125	—	—	—
G507C	20	33*	10*	100	—	—	—

Na⁺ affinities, K_d (= √(k₂₁/k₁₂)) for the three-state and K_dA (= k_N1/k_1N) and K_dB (= k_2N/k_N2) for the four-state model (Fig. 1), were estimated from the V_0.5 vs. log [Na⁺]_o data (Figs. 5 and 6). Parameters are those obtained in individual cells, but representative of three to five experiments conducted on different batches of oocytes. For all proteins, the variation in K_d was 10% and, excluding the WT group, the variation in K_dA was 10%. τ_o was obtained from the time constants for relaxation of the transient charge movements in the absence of sodium (e.g., Fig. 7). The values given for K_dA and K_dB are for those where V_0.5 in the absence of Na⁺ fell within the experimental range (Table 1), reducing the number of unknown parameters in Eq. 9. For all proteins, the number of Na⁺ ions (n) was 2, and net charge (z) was 1. z₁ = 0.7, z₂ = 0.3, for the three-state model and z₁ = 0.7, z₂ = 0.15, z₃ = 0.15 for the four-state model. The absence of data for mutants (—) reflects those where V_0.5 in the absence of Na⁺ fell outside the experimental range (Table 1) and those not determined.

^*The Na⁺ affinities of the two sites for the WT group are similar, because the three-state model fitted the data, and K_d = √K_dAK_dB.

^†Loo et al. (24).

Estimation of K_d.

First we use the three-state model to estimate the lumped Na⁺ binding constant K_d, by simulation of Eq. 6. The unknowns in Eq. 6 are K_a and K_d given that z₁ = 0.7, z = 1 (Table 1), and n =2 (see above): In some cases K_a is known for those mutants where V_0.5 falls within the experimental range at [Na⁺]_o = 0 (Table 1). In general, K_d and, if necessary, K_a were varied until the simulated V_0.5/log [Na⁺]_o curves fit the experimental data. For WT and for F101C, T287C, W291F, F453C, Q457C, and G507C, the estimated parameters were K_d ∼ 20 mM and k₁₆/k₆₁ ∼ 100 (Table 2). In contrast, the K_d for mutants at the glucose and Na⁺ binding sites, H83C, Y290C/S/F, W291C, and S392A, was three- to sixfold higher than for WT, 57–122 mM, and the k₁₆/k₆₁ ratio decreased from 100 to less than 25 (Table 2). Replacing the cysteine side chains at W291C with W291F restored the K_d to the wild-type value, but replacing Y290C with Y290F did not.

Next, we use the four-state model to estimate K_dA and K_dB by numerical simulation of Eq. 9. The limiting conditions, at [Na⁺]_o = 0 and at high saturating [Na⁺]_o, are identical for both the three- and four-state models; therefore, n = 2, z₁ = 0.7, and z₁ + z₂ + z₃ = 1. Assuming that z₂ = z₃ = 0.15, the unknowns in Eq. 9 are reduced to K_dA and K_dB. For WT hSGLT1 (Fig. 5) and F101C, T287C, W291F, F453C, Q457C, and G507C, the data are equally well simulated by both models with a K_d = 20 mM, K_dA = 33 mM, and K_dB = 10 mM. Recall that K_d = √ (K_dAK_dB) = √ (33 × 10) ∼ 20 mM. This indicates that Na⁺ affinities for the two sites in hSGLT1 are similar. To distinguish between these requires that we extend the experiments to lower [Na⁺]_o but this is impractical as V_0.5 moves well outside the experimental range (more negative than −120 mV, Fig. 5).

For some mutants, for example W291C, the V_0.5 at 0 mM [Na⁺]_o falls within the experimental range, 0 mV to −120 mV (Figs. 5 and 6 and Table 1), and K_a is determined experimentally (Eq. 7) (Table 2). For W291C the four-state model gives a better fit to the data with K_dA = 30 mM and K_dB = 110 mM: This was facilitated by the distribution of the experimental data between the two limiting slopes (Fig. 5B). Similar results were obtained for Y290C/S/F with K_dA ∼ 30 mM and K_dB > 100 mM (Fig. 6 and Table 2).

The V_0.5 vs. log [Na⁺]_o plots for H83C and S392A were intermediate between those for WT and W291C, with V_0.5 in the absence of Na⁺ falling just outside the experimental range, −100 mV to −140 mV. For S392A, with the constraint that z = 0.7 (at 0 Na⁺), we estimated the K_dA = 50 ± 5 mM (4) and K_dB > 150 mM. We were unable to obtain reliable estimates of K_dA for H83C.

Time Constants for Charge Transfer.

The time constants (τ_o) for charge transfer in the absence of Na⁺ at 0 mV are needed to resolve K_a into its components, k₆₁ and k₁₆ (Eq. 7). These are shown in Fig. 7 for hSGLT1 and W291C. τ_o was <2 ms for WT, F101C, T287C, W291F, F453C, Q457C, and G507C (Table 2). τ_o was 16 ms for W291C and ranged between 6 ms and 19 ms for H83C, Y290C/S/F, W291C, and S392A (Table 2). Making the simplifying assumption that the transitions between C1 and C6 occur in one step, the k₁₆/k₆₁ values obtained from V_0.5 in the absence of Na⁺ (Eq. 7 and Table 1) and the relationship τ_o = 1/(k₁₆ + k₆₁) give estimates of k₁₆ and k₆₁ (Table 2). The most striking results were for Y290C, Y290S, and W291C, which show a reduction in k₁₆ from ∼500 s⁻¹ to 20–80 s⁻¹ and an increase in k₆₁ from 5 s⁻¹ to 25–45 s⁻¹. These changes caused by removing the aromatic side chains were partially restored with Y290F and W291F, suggesting aromatic interactions between Y290 and W291 play an important role in the transitions between C1 and C6 (Fig. 1).

Discussion

Na⁺ plays a key role in the alternating mechanism of Na⁺ cotransporters. Substituted cysteine accessibility method (SCAM) studies on hSGLT1 show that external Na⁺ binding triggers a conformational change to open the sugar binding pocket to the external membrane surface (20, 26, 27). Identifying the Na⁺ binding sites and the coupling between Na⁺ and glucose transport is crucial to our understanding of the transport mechanism. Locating Na⁺ binding sites in membrane proteins is a nontrivial task even with the recent advances in structural biology. To distinguish between the densities of sodium and water in crystals it is necessary to resolve structures to greater than 1.2 Å (28). So far, the resolution for the LeuT structural family of transporters is between 1.6 Å and 3.5 Å (2, 4–6).

A structural motif was obtained from a survey of Na⁺ binding sites in 132 proteins in the Protein Data Bank (29), showing that approximately half are “neutral” and half contain one charged coordinating residue. In both the coordination number is ∼5 with an average Na⁺ to ligand distance of 2.35 Å. In the highest-resolution structure of cotransporters obtained to date, LeuT at 1.6 Å (6), two Na⁺ sites have been proposed on the basis of an indirect valence test (30). Na1 has six bonds between Na⁺ and the protein, including two carbonyl oxygens (A22 and T254), the hydroxyl oxygen from T254, side–chain amide oxygens from N27 and N286, and the charged carboxylate group from the leucine substrate. The Na2 site is neutral with five bonds between Na⁺ and the protein, including three backbone carbonyl oxygens (G20, V23, and A351) and two side chain –OH groups (T354, S355). The Na2 site is conserved in the three other members of the LeuT structural family, vSGLT, Mhp1, and BetP, and the mammalian SGLTs, but not in the Na⁺-independent transporters (1, 3). Substrate transport by SGLT1 is driven by two Na⁺ ions, unlike vSGLT and Mhp1, which are driven by one (20, 21, 25, 31). Thus, there is a second binding site in hSGLT1 (Na1).

We and others have attempted to identify ligand binding sites by mutating residues and measuring the kinetics of Na⁺ and substrate transport. However, it is not generally appreciated that the K_0.5 for Na⁺ and the K_0.5 for substrate are interdependent, and changes in Na⁺ K_0.5 may actually be due to changes in the substrate K_0.5 and vice versa (7, 23). New methods are needed to determine the K_d of ligand binding to cotransporters in the absence of the cosubstrate, and we have developed a method to determine the Na⁺ K_d in electrogenic cotransporters. The underlying principle is that external Na⁺ binding in the absence of substrate alters the equilibrium distribution of the transporter between two conformational states, C6 and C2Na₂ (Fig. 1). We measure the midpoint voltage (V_0.5) where the protein is equally distributed between C6 and C2Na₂ as a function of [Na⁺]_o. Na⁺ binding shifts the proteins from C6 to C2Na₂, and the Na⁺ affinities are determined from the relationship between V_0.5 and [Na⁺]_o (Figs. 5 and 6).

Overall, the theoretical predictions are borne out experimentally in that there are two limiting cases for both the three- and four-state models in the absence of Na⁺ and at high [Na⁺]_o, and the Na⁺ affinity determines the transition between the two limiting conditions. For wild-type hSGLT1 (and mutants F101C, T287C, W291F, F453C, Q457C, and G507C) the experimental data are equally well described by both three- and four-state models (Fig. 5) with K_d = 20 mM, K_dA = 33 mM, and K_dB = 10 mM (K_d = √ (K_dAK_dB)). This is in part due to the similarity of the K_ds for the two sites and/or the lack of data within the experimental limits (Fig. 5). At low [Na⁺]_o, V_0.5 falls outside the experimental range (Fig. 4). However, for some mutants, a better fit is obtained with the four-state model (e.g., W291C in Fig. 5), permitting a robust measure of K_dA and K_dB (Table 2). How specific are the observed reductions in Na⁺ affinity? We found that K_d was unaffected by mutation of other residues at (i) the sugar coordinating residue Q457C; (ii) residue T287C, near the sugar binding pocket; (iii) two outer gate residues, F101C and F453C; and (iv) a remote residue, G507C, on the external loop linking TM11 and TM12.

hSGLT1 Na2 Site.

This putative site is conserved between vSGLT (A62, I65, A361, S364, and S365) and hSGLT1 (A76, I79, S389, S392, and S393) (Fig. 8A). We have previously reported that mutation of one (S392) of the two conserved serines (S392, S393) produced significant decreases in the apparent affinity for Na⁺, sugar, and phlorizin. The increase in sugar K_0.5 (from 0.5 mM to >100 mM) and phlorizin K_i for this mutant (20) can be explained by the loss of intrinsic Na⁺ affinity. The lack of effect of S393 mutations (S393A/C) suggests that it is not the side chain, but perhaps the backbone carbonyl of this residue that serves as a Na2 site. Mutations of T467 and S468 in the Na2 site in BetP produce similar increases in the K_d (32).

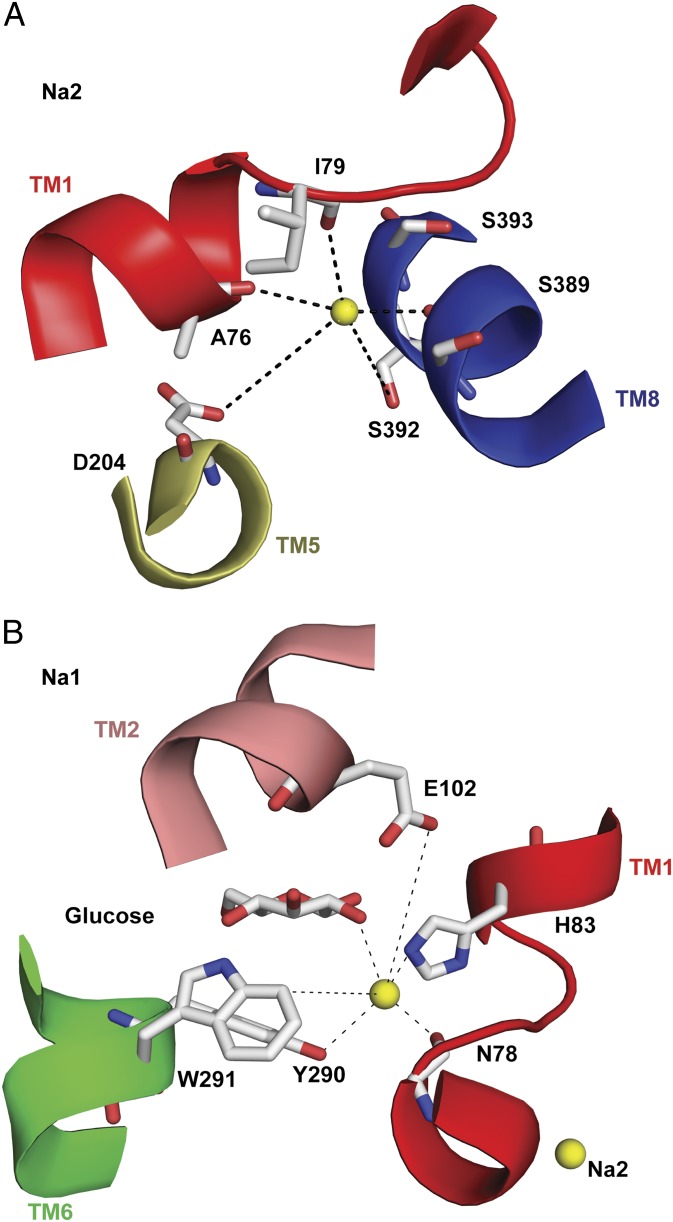
Fig. 8.

Predicted Na1 and Na2 sites shown in a homology model of hSGLT1 (Fig. 2). Na⁺ ions are colored yellow. (A) Na2 site. The Na2 site is 10 Å from the sugar binding site. Na⁺ binding is predicted to involve H bonds with carbonyl oxygens of A76, I79, and S389 (bond length <4 Å) and the side chain hydroxyl (OH⁻) from S392 (bond length 5 Å). The Na⁺ bond with D204 is predicted to occur via a water bridge (35). No Na⁺ bonding is shown to the side chain of S393 in accordance with the experimental data. (B) Na1 site. A Na⁺ ion is placed ∼2.5 Å from the carbonyl oxygen of N78 and H83 [corresponding residues are in the LeuT Na1 site (6)]. Also shown are distances between Na⁺ and Y290 (3.3 Å), W291 (6.3 Å), E102 (7.5 Å), and the O2 of glucose (3.5 Å).

In our study, there was a fivefold increase in K_d for S392A from 20 mM to 122 mM (Table 2), and this was due to an increase in both K_dA from 30 mM to 50 mM and K_dB from 10 mM to >150 mM. Because K_dB is a measure of Na⁺ binding to Na1 (see below), we infer that mutation of S392 produces a direct reduction in Na⁺ binding to Na2 and a long-range effect on Na⁺ binding to Na1 and indirect effects on the sugar and inhibitor binding pocket.

D204 has a low Na⁺ affinity (Table 2), consistent with molecular dynamics (MD) studies on vSGLT showing that Na⁺ leaving the Na2 site interacts with the conserved aspartate (33, 34). Na⁺ may coordinate with D204 through a water bridge as predicted from the bond distance of 6.4 Å between Na⁺ and the equivalent D189 in vSGLT (35) (Fig. 8A).

hSGLT1 Na1 Site.

The starting point in our search was the finding that Na1 is close to the substrate binding site in LeuT (6). Residues predicted to be involved in coordinating glucose in hSGLT1 include H83, N78, E102, Y290, W291, K321, and Q457 (20). There were dramatic increases in the lumped K_d for H83C, Y290C, and W291C, but not for Q457C or another residue, T287C, in the sugar binding pocket. The 3- to 6-fold increases in K_d are due to a >10-fold increase in K_dB with no change in K_dA (Table 2). This suggested that H83, Y290, and W291 are involved in sodium binding to the Na1 site (Fig. 8B) and that K_dB is the affinity for this site. Interestingly, the apparent affinity for glucose decreased by >100-fold for these mutants (20) and indicates that Na⁺ and glucose share binding to H83, Y290, and W291. How is it compatible that sugar and Na⁺ share binding sites? MD simulations on vSGLT have shown that substrate and Na⁺ binding is not static, but dynamic: e.g., galactose at the crystal binding sites rapidly exchanges bonds with water and other adjacent residues (34, 36, 37).

Residues W291, Y290, and W289 form an aromatic triad conserved in glucose and inositol transporters, and W291 and Y290 are involved in a T-stacking π–π interaction (21). We have previously found the loss of aromaticity at residue 291 (with mutant W291C) resulted in sugar (αMDG) K_0.5 > 100 mM and restoring an aromatic side chain (W291F) largely restored sugar affinity (K_0.5 = 4 mM compared with 0.6 mM for WT hSGLT1) (21). The present study shows that Na⁺ binding to Na1 is also recovered when the aromatic side chain is restored (W291C to W291F) (Table 2), indicating the aromatic side chain at W291 is important in Na⁺ binding. We also found the Na⁺ binding affinity to Na1 was lost with the Y290C mutation, but this was not recovered by replacing cysteine with either serine or phenylalanine (Table 2). We conclude that both the aromatic and −OH groups at Y290 are needed for Na⁺ binding. Sugar binding to Y290F was partially restored relative to Y290C (21), and we suggest that an H bond between Y290 and N78, which increases the electrostatic potential of the aromatic system (38), is important for the strength of the interaction between Y290 and glucose (21). We further suggest that this H bond is crucial for Na⁺ binding.

N78 corresponds to A22 of LeuT, proposed to bind Na⁺ (via carbonyl oxygen) to the LeuT Na1 site. We have searched for suitable Na1 coordinating residues within ∼3 Å from the carbonyl oxygen of N78, and a possibility is shown in Fig. 8B. Without modification of our homology model, the distance (in angstroms) between Na⁺ and N78 (carbonyl oxygen) is 2.6, that for Y290 is 3.3, that for W291 (aromatic plane) is 6.3, and that for H83 is 2.0. H83 corresponds to N27 in the Na1 site of LeuT (6). In LeuT the carboxylate (COO⁻) of the substrate (leucine) is predicted to coordinate with Na⁺, but in hSGLT1, E102 in the sugar binding site may substitute for this bond. When sugar is bound, Na⁺ is 3.5 Å away from the O2 group of glucose, suggesting a direct interaction (39, 40). The distance between the Na⁺ and aromatics Y290 and W291, 4–7 Å, indicates that cation–π interactions might be involved in Na⁺ binding.

An intriguing question that has yet to be addressed is cation selectivity; i.e., How can Na⁺ sites in some transporters recognize H⁺ and/or Li⁺ but not Cs⁺ and Rb⁺? For example, H⁺ and Li⁺ can drive sugar transport by hSGLT1 with exquisite sensitivity for H⁺ (K_0.5 of 7 μM for H⁺, 12 mM for Li⁺, and 4 mM for Na⁺) (22).

Transitions Between C1 and C6.

The data on V_0.5, z, and τ₀ for 13 mutants in the absence of [Na⁺]_o provide preliminary information on the transitions of hSGLT1 between C1 and C6 (Table 2). The most compelling results are those with the Y290 and W291 mutants, where the k₁₆/k₆₁ ratio was reduced 25- to 50-fold for the cysteine mutants. Replacing the W291C cysteine chain with phenylalanine restored the ratio to that for wild type, but for Y290C there was only partial recovery for Y290F. These changes in k₁₆/k₆₁ were largely due to a decrease in k₁₆ and a smaller increase in k₆₁. We conclude that π–π interactions between Y290 and W291 play an important role in the transitions between C1 and C6, as well as in the formation of the Na1 and sugar binding sites and coupling between Na⁺ and sugar cotransport (21).

Mechanism of Na⁺ and Sugar Cotransport.

Voltage sensitivity.

The results provide an insight into the voltage dependence of hSGLT1 in that the ligand-free transporter has an apparent valence of 0.7, and the binding of extracellular Na⁺ ions is associated with a total charge of 0.3. Originally, we assumed that the valence of the ligand-free protein was 2, as two Na⁺ bind in the absence of glucose (17, 19, 23). This led to unaccounted discrepancies between models and the observed shift of V_0.5 with varying [Na⁺]_o and we had attributed this to a simplifying assumption about simultaneous binding of two external Na⁺ ions (22, 23). Given the structure of the Na1 and Na2 binding sites and the data presented here, it is no longer necessary to assume that the valence of SGLT1 is 2, especially as a valence of 1 now accounts for the charge movements as a function of [Na⁺]_o. However, because two Na⁺ ions are coupled to each glucose molecule transported by WT hSGLT1 (20, 21, 26, 27, 31), this raises questions about what other step of the overall transport cycle is voltage dependent (41). Clues may come from closer inspection of the kinetics of Y290F, W291F, and hSGLT2, where the coupling ratio is 1/1 (21, 42).

Na⁺ binding order.

For hSGLT1, two Na⁺ ions bind to the empty transporter before glucose. The order of binding to the two Na⁺ sites (Na1, Na2) is not known, but the available evidence tends to favor Na⁺ binding first to the Na2 site: First, the Na2 site is conserved in vSGLT and hSGLT2, and these proteins couple only one Na⁺ to sugar transport (42–44); second, MD studies on LeuT have led to the predictions that Na⁺ binds first to the Na2 site and then to the Na1 site even in the absence of substrate (45); third, Na⁺ has also been proposed to bind first to the Na2 site in BetP (32); and fourth, Na⁺ is proposed to bind first to the Na2 site on the human GABA transporter GAT-1, followed by cooperative binding of the second Na⁺ to the Na1 site (46). In all cases Na⁺ binding stabilizes the transporter in an outward-open conformation to facilitate substrate binding, but it is not yet clear whether substrate binding increases the Na1 affinity for Na⁺.

The coupling ratio between Na⁺ and sugar transport is 1:1 Na⁺:sugar for Y290F and W291F, even though the Hill coefficients for Na⁺ activation are 1.5 and 2.2, respectively (21). Thus, two Na⁺ ions bind to the mutants to allow sugar binding to hSGLT1, but for these mutants only one Na⁺ is released to the cytoplasm along with a sugar molecule. We hypothesize the Na⁺ ion at the Na1 site may be released from these mutants back into the external solution.

Molecular dynamic simulations on vSGLT also predict that water plays an important role in the exit of sugar into the cytoplasm. After Na⁺ release from the Na2 site (Fig. 8A), water enters the sugar binding site and causes large fluctuations in the position of galactose, in part due to hydration of the sugar and formation of new H bonds before exiting to the cytoplasm (34, 36, 37). Presumably water also causes dissociation of Na⁺ from the Na1 site and this second Na⁺ follows sugar exit to account for the coupling of two Na⁺ ions to sugar transport across the protein.

Summary

A biophysical assay has been used to determine multiple sodium equilibrium binding constants (K_d) for electrogenic cotransporters. In hSGLT1 where binding of two sodium ions drive sugar transport, we could resolve the K_d for each site, K_dA and K_dB. Combined with studies on hSGLT1 mutants, the assay has been used to identify the binding sites.

The Na1 site has been constructed from several residues in the sugar binding pocket, as individually changing sugar crystal contacts at H83, Y290, and W291 to cysteine decreased the Na⁺ affinity—K_dB increased more than 10-fold with no change in K_dA. For W291C, but not Y290C, restoring the aromatic side chain with phenylalanine restored sodium affinity to the wild-type value. Mutation of these binding residues also dramatically reduced the apparent sugar and phlorizin affinities.

The canonical Na2 binding site is conserved in hSGLT1, with two –OH side chains, S392 and S393, and three backbone carbonyls. Mutation of S392 to cysteine reduced the lumped sodium affinity by sixfold (due to increases in both K_dA and K_dB), resulting in a dramatic decrease in the apparent sugar and phlorizin affinities. We conclude that mutation of S392 in the Na2 site produces a structural rearrangement of the sugar binding pocket that disrupts both the binding of the second Na⁺ and that of sugar. In contrast, the S393 mutations produce no significant changes in sodium, sugar, and phlorizin affinities. We conclude that the Na2 site is conserved in hSGLT1, the side chain of S392 and the backbone carbonyl of S393 are important for the binding of the first Na⁺, and it subsequently promotes the binding of Na1 in the sugar binding pocket.

Methods

Molecular Biology.

Mutants used (H83C, F101C, D204E,Y290C/S/F, W291C/F, S392A/C, F453C, Q457C, and G507C) were described previously (20, 21, 23, 26). The same procedures were used to generate a new mutant, T287C.

Functional Expression of hSGLT1 in Oocytes.

Protocols were approved by the University of California Chancellor’s Committee on Animal Research. Stage V–VI oocytes were harvested from mature female Xenopus laevis frogs, selected, and maintained at 18 °C in modified Barth’s solution (20, 21). Oocytes were injected with 50 ng of cRNA coding for WT and mutant hSGLT1 and incubated at 18 °C for 4–7 d. Noninjected oocytes served as controls. Experiments were conducted on oocytes bathed in a NaCl buffer containing 100 mM NaCl, 2 mM KCl, 1 mM CaCl₂, 1 mM MgCl₂, and 10 mM Hepes, pH 7.5, and the Na⁺ concentration was varied by isomolar replacement of NaCl with CholineCl. The internal Na⁺ concentration was assumed to be constant (5–10 meq/L) throughout each oocyte experiment and was supported by no observed change in the electrical parameters between the beginning and the end of the experiment. Data were collected on single oocytes, where we randomly varied the external NaCl concentration from 100 mM to 0 mM.

Electrophysiological Experiments.

These were performed using a two-electrode voltage clamp (19, 20, 23, 26). A standard pulse protocol was applied, where membrane potential was held at −50 mV (V_h) and stepped to various test values (V_t from +50 mV to −150 mV in 20-mV decrements) for 100 ms before returning to V_h. The current records were the averages of three sweeps and were filtered at 500 Hz. All experiments were performed at room temperature (20–23 °C).

Total membrane current (I_tot) in response to a voltage pulse is composed of the oocyte membrane bilayer capacitive transient (I_cm), pre–steady-state SGLT1 currents (I_pss), and steady-state currents (I_ss). I_tot was fitted to

where I_ss is the steady-state current, I_cm exp(−t/τ_cm) is the bilayer capacitance current with initial value I_cm and time constant τ_cm, and I_pss exp(−t/τ) is the SGLT1 pre–steady-state current (23). SGLT1 pre–steady-state currents (I_pss exp(−t/τ)) were isolated by subtraction of the bilayer capacitive and steady-state components from total current (I_pss exp(−t/τ) = I_tot(t) − I_cm exp(−t/τ_cm) − I_ss).

At each membrane voltage, SGLT1 charge movement (Q) was obtained from the integral of the pre–steady-state currents. The charge vs. voltage (Q-V) relations were fit to a single Boltzmann function (10, 24, 47),

where Q_max = Q_dep − Q_hyp, Q_dep and Q_hyp are the Q (absolute value) at depolarizing and hyperpolarizing limits, V is membrane potential, F is the Faraday constant, R is gas constant, T is absolute temperature, V_0.5 is midpoint voltage (membrane potential at 50% Q_max), and the apparent valence, z, is the maximum steepness factor for the dependence of Q on voltage.

For some transporters, the determination of Q_max, z, and V_0.5 was problematic, due to (i) practical limits on the range of voltage jumps, generally to −150 mV and +50 mV, because dielectric breakdown and/or activation of ion channels may occur at larger voltages, and (ii) V_0.5 falling outside the experimental range; e.g., lowering the external [Na⁺]_o shifts the V_0.5 to more negative than −100 mV, leading to errors in estimation of the Boltzmann parameters (Figs. 4–6).

Fits of data to Eqs. 10 and 11 were performed using either Sigmaplot 10 (SPSS) or Clampfit 8.1 (Axon Instruments). On data obtained on a single oocyte, the statistics are given by the estimates and SE of the fit. For a population, the statistics are given by the means and SEMs. Although data may be shown for representative experiments, all experiments were performed on at least three oocytes from different batches. The Na⁺ affinities (K_d) and the ratio k₁₆/k₆₁ were estimated by numerically solving the equation relating V_0.5 and [Na⁺]_o (Eqs. 6 and 9), using Berkeley Madonna (www.berkeleymadonna.com), and the procedure was kindly provided by Ian Forster of the University of Zurich.