Mechanism of vibrational energy dissipation of free OH groups at the air–water interface

Significance

Interfaces of liquid water play an important role in a wide variety of biological, environmental, and technological processes. These interfaces have many unusual macroscopic properties, e.g., the high surface tension, the tendency to sequester ions at the air–water interface, and the high proton conductivity, that are difficult to understand given simple descriptions of bulk liquid water. To understand what differentiates interfacial water from the bulk, insights into the molecular level structure and dynamics of water at interfaces are crucial. We quantify the dynamics of vibrational energy dissipation of interfacial water using ultrafast time-resolved surface specific vibrational spectroscopy and show that the relaxation pathways differ markedly from bulk water and reflect surface structural dynamics.

Abstract

Interfaces of liquid water play a critical role in a wide variety of processes that occur in biology, a variety of technologies, and the environment. Many macroscopic observations clarify that the properties of liquid water interfaces significantly differ from those of the bulk liquid. In addition to interfacial molecular structure, knowledge of the rates and mechanisms of the relaxation of excess vibrational energy is indispensable to fully understand physical and chemical processes of water and aqueous solutions, such as chemical reaction rates and pathways, proton transfer, and hydrogen bond dynamics. Here we elucidate the rate and mechanism of vibrational energy dissipation of water molecules at the air–water interface using femtosecond two-color IR-pump/vibrational sum-frequency probe spectroscopy. Vibrational relaxation of nonhydrogen-bonded OH groups occurs at a subpicosecond timescale in a manner fundamentally different from hydrogen-bonded OH groups in bulk, through two competing mechanisms: intramolecular energy transfer and ultrafast reorientational motion that leads to free OH groups becoming hydrogen bonded. Both pathways effectively lead to the transfer of the excited vibrational modes from free to hydrogen-bonded OH groups, from which relaxation readily occurs. Of the overall relaxation rate of interfacial free OH groups at the air–H₂O interface, two-thirds are accounted for by intramolecular energy transfer, whereas the remaining one-third is dominated by the reorientational motion. These findings not only shed light on vibrational energy dynamics of interfacial water, but also contribute to our understanding of the impact of structural and vibrational dynamics on the vibrational sum-frequency line shapes of aqueous interfaces.

Interfaces of liquid water play an important role in a wide variety of biological, environmental, and technological processes (1–3). A variety of studies have shown that these interfaces have many unusual macroscopic properties––e.g., the high surface tension and tendency to sequester ions of the air–water interface (4), and the high proton conductivity of the membrane water interface (5)––that are difficult to understand given simple descriptions of bulk liquid water. Driven by the desire to explain such observations, decades have been spent trying to understand the molecular level structure and dynamics of water at aqueous interfaces. Experimentally probing these systems is a formidable challenge. Performing similar measurements at solid surfaces in ultrahigh vacuum (UHV) is more straightforward: electrons, photons, or atoms can be brought to, and retrieved from, the surface through vacuum (6). Although notable progress has been made in applying UHV surface science tools to the vacuum/liquid water interface by interrogating liquid jets in vacuum (7–10), the resulting observables cannot exclude some bulk contribution and the experimental approach is not generally applicable to aqueous interfaces: e.g., one cannot use it to probe water/organic liquid interfaces.

Because optical vibrational spectroscopy has no intrinsic requirement for vacuum and because the frequency and intensity of the OH stretch change dramatically as a function of local environment, probing the spectral response of the OH stretch of H₂O has proven extremely useful in characterizing the structure and dynamics of bulk liquid water (11–15). However, in conventional vibrational spectroscopies (i.e., IR absorption or spontaneous Raman) it is very difficult to distinguish the response of H₂O molecules at extended interfaces from the much larger number in bulk. This challenge was initially overcome by Shen and coworkers in 1991 by using the laser-based technique vibrational sum-frequency (VSF) spectroscopy to probe the air–water interface (16).

In a VSF experiment, an IR pulse is overlapped at the surface in both time and space with a visible (VIS) pulse and the output at the sum of the frequencies of the two incident fields monitored. This VSF emission is, within the dipole approximation, interface specific in media with bulk inversion symmetry and is a spectroscopy because it increases in intensity by typically several orders of magnitude when the frequency of the incident IR is tuned in resonance with a normal mode of the molecules at an interface (17). As initially shown by Shen and coworkers, and subsequently a variety of others, because the quadrupole response from liquid water is relatively low, VSF spectroscopy furnishes the OH stretch response of just the water molecules within one to two layers of an interface (18–20).

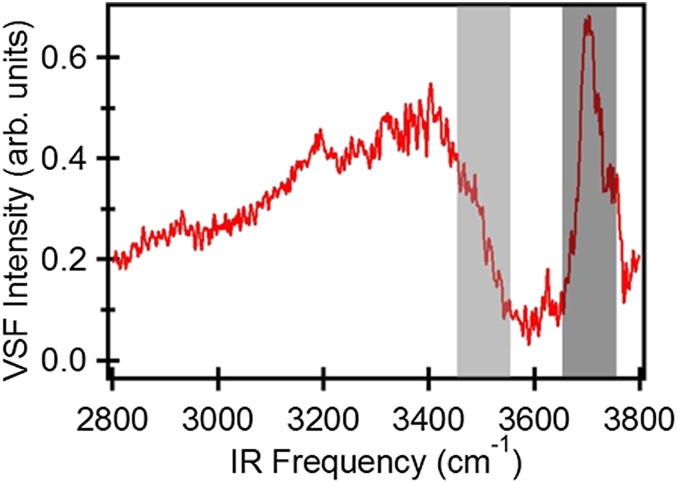
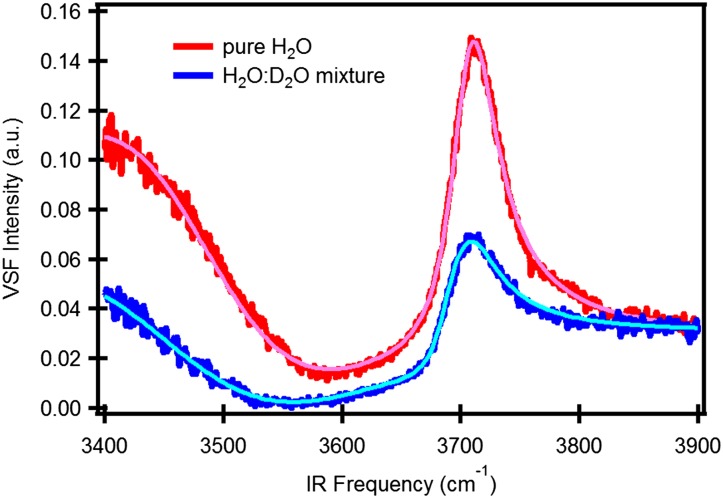
Because of its environmental ubiquity, experimental simplicity, and its relevance to understanding hydrophobic solvation more generally, much work has focused on the spectral response of interfacial water at the air–water interface (21–23). A VSF intensity spectrum (Fig. 1) for the air–water interface shows a broad band at lower frequency (3,100–3,500 cm⁻¹), attributed to hydrogen-bonded (H-bonded) OH groups, and a narrow peak at higher frequency (∼3,700 cm⁻¹), attributed to free OH groups (22, 24–26). While it is clear that these spectral features report on the structure of interfacial water, extracting structural insight from the measured response has proven challenging. In particular, much prior work has shown that the VSF spectral response of H-bonded OH groups is significantly influenced by inter/intramolecular coupling, the spectral response of both free and H-bonded OH groups is partly determined by rapid (subpicosecond) molecular motion, and the extent to which each effect influences the spectral response cannot be straightforwardly inferred from the observed spectrum. The fact that multiple possible effects may explain the observed spectral response of interfacial water has been clearly demonstrated, for the low-frequency portion (∼3,100 cm⁻¹) of the H-bonded OH at the air/H₂O interface, by Morita and coworkers and Skinner and coworkers, who have shown that the experimental spectral response can be equally well reproduced by computational models with quite different underlying physics (19, 27).

Fig. 1.

Static VSF spectrum of the air/H₂O interface. Dark-gray and light-gray rectangles mark the spectral region of free and H-bonded OH, respectively, that is excited and detected in the pump–probe experiments.

Whereas the VSF spectral response of H-bonded OH groups is apparent at all aqueous interfaces, the free OH appears only at nominally hydrophobic surfaces: this resonance is a molecular level indicator of hydrophobic solvation (28, 29). These free OH groups are important: e.g., they are thought to play a critical role in on-water catalysis, are thought to determine qualitative trends in solvation free energies, and their structural dynamics are likely linked to the local water density fluctuations that underlie hydrophobic assembly (30–32). Hence, we would like insight into both vibrational and structural dynamics of interfacial free OH groups: the efficiency of on-water catalysis depends, in part, on the efficiency with which the free OH transfers excess energy to the aqueous phase, whereas understanding the role of free OH in hydrophobic assembly requires elucidating free OH structural dynamics. Prior work has established that free OH vibrational and structural relaxation and homogeneous dephasing all occur on similar timescales (33–36). Indeed, the line width, peak amplitude, and peak frequency have been observed to change, at the air–water interface, with the composition of the aqueous phase (26), indicating that the dynamics change as the interface changes. It is not clear, however, how precisely these spectral changes correlate with changes in either vibrational or structural dynamics. It is therefore apparent that quantifying vibrational structural dynamics at water interfaces is relevant in its own right to understand, e.g., chemistry occurring at those interfaces, but also to understand spectral line shapes observed in VSF spectroscopy.

To address these challenges we require a method of directly following the dissipation of excess vibrational energy and/or interfacial structural dynamics with interfacial specificity. We and others have recently applied a time-resolved ultrafast IR-pump/VSF-probe scheme to elucidate vibrational energy relaxation dynamics of OH groups at a variety of interfaces (33–35, 37, 38). In these experiments, an IR pump pulse excites OH groups at a specific vibrational frequency, and the effect of that excitation is followed in time with the VSF probe–pulse pair. For the excited OH groups, the VSF intensity is temporarily decreased (“bleached”), and the recovery of the signal is a result of vibrational relaxation. For the free OH both at the air–water and hydrophobic self-assembled monolayer/water interface, slow relaxation (0.85–1.2 ps) has been reported (33, 34). As the homogeneous dephasing time (T₂) of the free OH is 221 fs (given a measured FWHM in Fig. 1 and assuming inhomogeneous contributions to the line width are negligible), it is clear that the line width of the free OH spectral response is influenced by the vibrational lifetime and thus that even understanding changes in free OH spectral response with aqueous phase composition requires understanding the free OH vibrational relaxation mechanism.

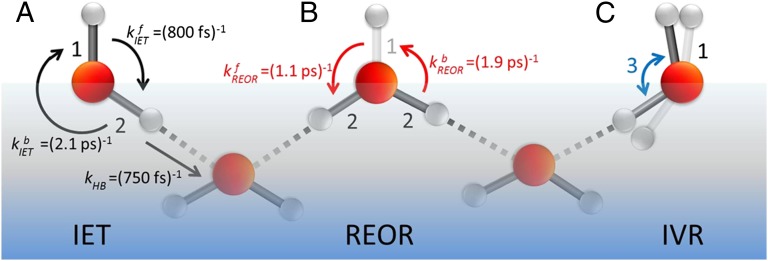
Three possible relaxation pathways can be identified. Previously, we have shown that free OH groups reorient on a timescale (∼1 ps) very similar to vibrational relaxation (33, 36). This observation suggests that one possible relaxation mechanism is the rotation of excited OH groups toward the bulk and formation of a hydrogen bond after which energy dissipation occurs rapidly as a result of the increased anharmonicity of the OH vibrational potential. In what follows we term this mechanism the REOR vibrational relaxation pathway (relaxation through reorientation). A second relaxation mechanism has been proposed from the appearance of the cross-peaks in 2D VSF spectra of D₂O at the air/D₂O interface: the vibrational energy of the excited free OD is transferred to the H-bonded OD in the same D₂O molecule, which is weakly H-bonded, on subpicosecond timescales (35). Hereafter we describe this as the intramolecular energy transfer (IET) relaxation pathway. Finally, in liquid water much prior experimental and computational work has shown that the vibrational relaxation of the OH stretch proceeds through the overtone of the bending mode, to the bend fundamental, to whole molecule librations (39). Absent additional information, it seems plausible that relaxation of the excited free OH might occur in a similar manner; in what follows we term this mechanism the intramolecular vibrational relaxation (IVR) pathway. These mechanisms are schematically illustrated in Fig. 2.

Fig. 2.

Schematically depicting the pathways for vibrational relaxation of free OH groups. (A) IET, which indicates the energy coupling between free OH (label 1) and H-bonded OH (label 2). (B) Reorientational motion of the free OH (label 1) which rotates into the bulk and forms a hydrogen bond (REOR). (C) IVR, which represents the coupling between the free OH stretching (label 1) and the bending modes (label 3) of the water molecules.

In this study we resolve the relative roles of these mechanisms in the vibrational relaxation of interfacial free OH groups at the air–water interface. By analyzing two-color time-resolved infrared-pump/VSF-probe signals we show that the exchange of excited vibrational energy between free OH and H-bonded OH occurs on a subpicosecond timescale. Using isotopically diluted water, we suppress intra- and intermolecular coupling while leaving structural relaxation processes relatively unaffected. Our results show that IET explains two-thirds of the vibrational relaxation of the free OH groups in pure H₂O, whereas the remaining one-third is the result of REOR.

Our quantification of vibrational lifetime and relaxation mechanism of the free OH at the air–water interface thus shows the relationship between aqueous interfacial spectral response and structural dynamics. More generally, because the free OH is a ubiquitous feature of how water meets hydrophobic materials we expect this insight to be of general interest to a wide range of bio- and soft-matter chemists and physicists interested in free OH structural dynamics and inorganic chemists interested in how this interfacial feature acts to transfer energy across aqueous/organic phase boundaries.

Results and Discussion

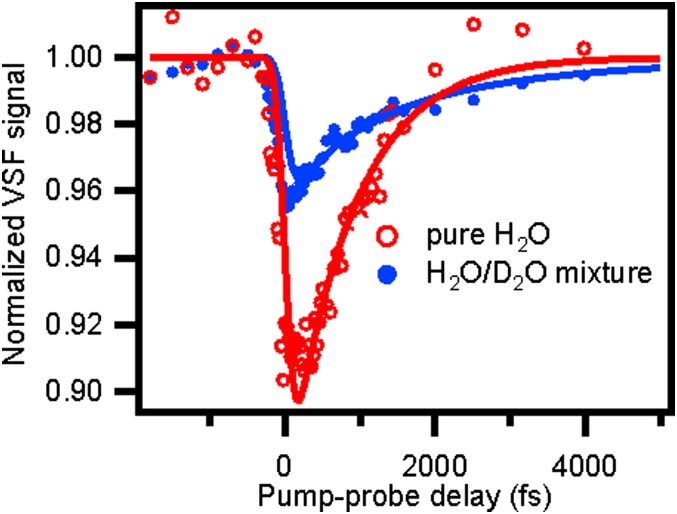
To study the vibrational energy dynamics of the free OH group (dark-gray area in Fig. 1), we excite these OH groups at ∼3,700 cm⁻¹ with an IR pump pulse and probe the response with VSF probe–pulse pair as a function of delay time. The data, after integrating the measured VSF intensity from 3,650 cm⁻¹ to 3,750 cm⁻¹ (with respect to the IR probe frequency; red curve in Fig. 3), show a 10% bleach which recovers on a subpicosecond timescale. A single-exponential fit to the data gives a time constant for the recovery of the VSF signal of 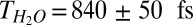for the free OH in pure H₂O. This timescale can of course be a result of a combination of the three prospective relaxation pathways: IET, REOR, and IVR. Put in more formal notation, we expect that 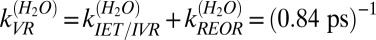, where k is the rate constant associated with the energy relaxation process and we have lumped together the IET and IVR pathways into a single term for reasons that will become clear below.

Fig. 3.

IR-pump/VSF-probe data for excitation and detection of free OH groups at the air–water interface for pure (red, open circles) and isotopically diluted H₂O (H₂O:D₂O = 1:1, blue, filled circles). The red curve is the monoexponential fitting of the pure H₂O sample and the blue curve is the biexponential fitting of the H₂O-D₂O mixture, which shows that the time constant of the vibrational relaxation of free OH for H₂O and HDO is 840 fs and 2.6 ps, respectively. Both fit curves are convoluted with the system response.

To help us quantify the contribution of each of these pathways we require an experiment that allows us to selectively switch off one (or more). To do so we next performed a similar IR-pump/VSF-probe experiment probing the free OH of HDO at the air–water interface. Because of the large energy mismatch between the free OH (∼3,700 cm⁻¹) and H-bonded OD (∼2,600 cm⁻¹) stretch and the HDO, H₂O, and D₂O bend frequencies (40–42), neither near-resonant energy transfer between the OD and OH stretch on the same water molecule nor relaxation from the OH stretch through the overtone of the bend is probable in HDO (11, 43). Put another way, in HDO we expect the IET and IVR pathways to be shut down 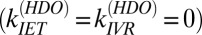and vibrational relaxation to be therefore dominated by REOR.

The blue curve in Fig. 3 displays the IR-pump/VSF-probe result for exciting and probing the free OH stretching mode at the air–water interface for a H₂O–D₂O mixture (1:1 molar ratio). As is clear from inspection, the timescale of the VSF signal recovery is much slower for the mixture than pure H₂O (the red curve). This qualitative observation strongly suggests that the IET and/or IVR pathways are important in describing the vibrational relaxation of the free OH of H₂O. To quantify the importance of IET/IVR relative to REOR we fit the data. For the H₂O–D₂O mixture [given a small interfacial isotope fractionation (44)], half of the free OH groups in our excitation volume are part of an H₂O molecule; the other half are part of HDO (45). Assuming these two types of free OH groups contribute equally to the measured signal from the mixture, and therefore fitting these data using a biexponential with two equal amplitudes and taking 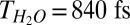for free OH in H₂O, we find that the timescale of signal recovery of the free OH in HDO, 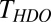, is 2.6 ± 0.3 ps: three times slower than that of the free OH in H₂O. Taking, 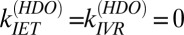, and assuming that the reorientation rate of an OH group in HDO is similar to that of an OH group in H₂O, we thus have 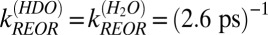. Recalling that, 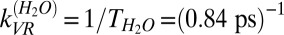, we obtain .

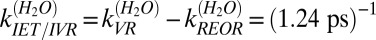Because both IET and IVR are suppressed in HDO, quantifying the relative importance of these two pathways requires different types of experiments. Here we do so by performing an IR-pump/VSF-probe experiment in which we excite the free OH (i.e., the frequency range shown in the dark-gray rectangle) and probe the blue side (weakly H-bonded) of the H-bonded OH spectral response (i.e., the light-gray rectangle in Fig. 1). Prior computational, 2D VSF, and polarization-dependent VSF studies have all shown that this frequency range corresponds to the OH stretch of the H-bonded half of a water molecule that contains a free OH (35, 46, 47).

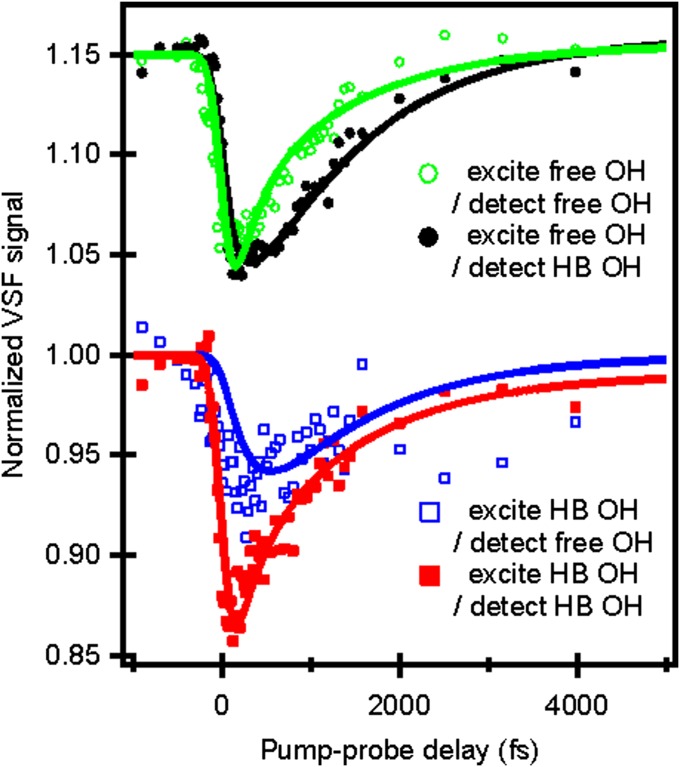
The IR (free OH) pump/VSF (weakly H-bonded OH) trace, with probe intensities integrated from 3,450 cm⁻¹ to 3,550 cm⁻¹, is shown in black in Fig. 4. For comparison the free OH IR pump and free OH VSF probe are shown as a green curve in Fig. 4 (same data as red curve in Fig. 3). Three qualitative features of the comparison are readily apparent: there is an ∼300-fs delay between the directly free OH pumped signal (green trace) and the coupling signal (black trace), the bleach magnitudes (the signal size) are similar for both experiments, and both traces have an initial bleach followed by a monotonic recovery. The relatively small delay between the pumped and coupling traces is consistent with a scenario in which vibrational energy is effectively transferred from the free OH to weakly H-bonded OH populations by energy transfer and/or reorientation of free OH groups to become H-bonded. Similarly, the nearly identical size of the bleach for both signals suggests that no energy is lost from the system in this transfer, and that the great majority of the vibrational excitation deposited in the free OH is transferred to the bond stretch modes of OH groups that are weak hydrogen bond donors. Because vibrational relaxation of the free OH through IVR would require energy to leave the free OH stretch and move rapidly into the bending mode (i.e., well outside of our probe window), both of these observations suggest that IVR is relatively unimportant in describing free OH relaxation. Finally, we note that prior works have shown that the interfacial H-bonded OH stretch shifts to higher frequencies when heated (24). If vibrational relaxation and subsequent thermalization of the free OH excitation were sufficiently rapid we would expect to see a transient increase, rather than decrease and recovery, in the coupling trace. Clearly the data are inconsistent with such rapid thermalization.

Fig. 4.

IR-pump/VSF-probe data for free OH and H-bonded (HB) OH groups at the air–water interface. (Upper) The two traces are data with 3,700 cm⁻¹ IR pump/3,700 cm⁻¹ (green, open circles) and 3,500 cm⁻¹ (black, filled circles) probes. (Lower) The two traces are data with 3,500 cm⁻¹ IR pump/3,700 cm⁻¹ (blue, open squares), and 3,500 cm⁻¹ (red, filled squares) probes. Solid lines are fits with a vibrational relaxation model (for details, see SI Text). The green and black curves have an offset of 0.15.

This comparison between the free OH pump/free OH probe and free OH pump/weakly H-bonded OH probe traces thus suggests a conceptual model in which a free OH group is initially excited and this excitation is either transferred to the H-bonded OH group on the other half of the same molecule or the excited OH group rotates down and forms a hydrogen bond. Clearly, however, this is only the first part of the vibrational relaxation pathway. To investigate what happens next we performed two additional IR-pump/VSF-probe experiments: one in which weakly H-bonded OH groups are pumped and the free OH probed (blue trace in Fig. 4) and one in which weakly H-bonded groups are both pumped and probed (red trace in Fig. 4). Interestingly, these two signals (the two bleach amplitudes) are notably different: The bleach for the free OH is appreciably smaller than for the H-bonded OH probe. This difference suggests that, on excitation of weakly H-bonded OH groups, some energy transfer likely occurs via IET or REOR to the higher-energy free OH groups, while the rest, possibly through rapid intermolecular energy transfer to more strongly H-bonded OH stretches on other water molecules or IVR, dissipates through other channels.

Taken as a whole, the data discussed thus far suggest that free OH vibrational relaxation proceeds by IET and REOR (but not IVR) and that there is an effective time constant of (1.24 ps)⁻¹ associated with the IET pathway and (2.6 ps)⁻¹ with the REOR. As discussed above, these data further suggest that these time constants are a combination of forward and backward rates for both processes: an initially excited free OH group that has either reoriented to form a hydrogen bond or transferred its excitation to the H-bonded OH group on the same molecule can either rotate back to become free or transfer its excitation back to the free OH on ultrafast timescales. We have previously shown in experiment and simulation that the characteristic time for a free OH to rotate toward bulk liquid and form a hydrogen bond is ∼1 ps (33, 36). On the face of it the (2.6 ps)⁻¹ time constant associated with the REOR pathway appears to conflict with this previous observation. To explore whether the (2.6 ps)⁻¹ could be the result of this observable convoluting both forward and backward rates, we developed a model to account explicitly for the possibility of a return of the excitation to the free OH either because the newly hydrogen bond OH is once again free or because of excitation transfer back from a H-bonded OH to the free OH on the same molecule.

To do so we first assume free OH vibrational relaxation occurs in two stages: a first step that is reversible and leads to an initially excited free OH group either becoming (through REOR) or transferring its excitation to (through IET) a weakly H-bonded OH group, and a second step that describes the relaxation of the weakly H-bonded OH group (with rate constant 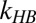) and is nonreversible (for details, see SI Text and ref. 35). Given these assumptions, we wish to ask whether the model can describe all data in Fig. 4 simultaneously. The solid lines in Fig. 4 are the results of the model (including the ∼200-fs temporal resolution) with transfer rates 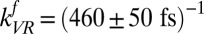, , 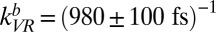and 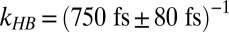. The superscript f denotes the forward process (the excited vibrational stretching mode changes from the free OH to the H-bonded OH) and b denotes the backward process (the excited vibrational stretching mode changes from the H-bonded OH to the free OH).

As shown above, the excitation transfer from free to H-bonded OH groups, the rate constant of which is 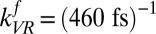, is the sum of relaxation via IET 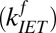and REOR 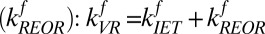. To solve for the backward rate of IET we assume that there is no energy barrier and the system is at equilibrium with respect to IET, i.e., the ratio of forward to backward rates of IET is related to the frequency difference between these modes, as described in an Arrhenius equation, and is 2.6: 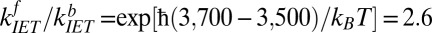at T = 300 K. Similarly, to determine the backward rate of REOR, we assume that the relative number of interfacial H-bonded OH groups does not change as a result of the IR pump, and given that the population of H-bonded OHs is 1.7× larger than the population of free OHs (discussed in detail in SI Text), the reorientation rate for the H-bonded OH to break the hydrogen bond and become a free OH must be 1.7× slower than the converse: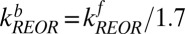. Substituting we find, for the free OH to H-bonded OH transition, 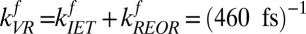, and for the H-bonded OH to free OH 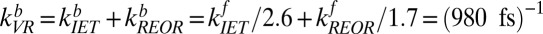. Rearranging terms leads to 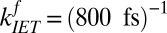and 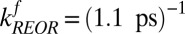. These time constants are summarized in Fig. 2. The 1.1-ps time constant for the reorientational motion of the free OH group and formation of a hydrogen bond is thus consistent with our earlier estimates for the rates of this process (33, 36).

To summarize, we have thus calculated the characteristic rate constant for free OH vibrational relaxation in two independent ways: a simple exponential fit and a rate model that solves the system of coupled differential equations describing population transfer in a three-state model. Summing the forward and backward time constants for each process extracted from the rate model allows direct comparison with the exponential analysis offered above. We find that the time constant of vibrational relaxation of the free OH due to IET calculated using the rate model is 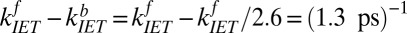and that due to REOR is 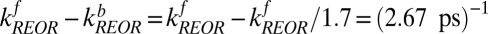_. Clearly both time constants are in good agreement with the exponential description, in which 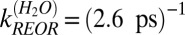and 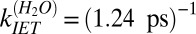, offered above. Both ways of analyzing the data thus appear to reach a similar conclusion: about one-third of the vibrational relaxation of the free OHs in H₂O is due to structural relaxation and the remaining two-thirds to IET.

Prior work suggests that, although inhomogeneous broadening is important in determining the H-bonded OH spectral response at the air–water interface, it is relatively unimportant in understanding the free OH (21, 27, 46). This then implies that we are justified in describing the VSF spectral response of the free OH at both the air/H₂O and air/H₂O:HDO:D₂O interface as a sum of Lorentzians: I_VSF∝ |χ_NR⁽²⁾+Σ_n[A_n/(ω_IR-ω_n+iΓ_n)]|², where A_n, ω_n, and 2Γ_n are the amplitude, frequency, and FWHM, respectively, of mode n. Γ is related to the decay rate (1/T₂) of the polarization (induced by the IR pulse), 2πΓ = 1/T₂, where T₂ is the homogeneous dephasing time. This homogeneous dephasing time can be decomposed into two contributions, 1/T₂ = 1/(2T₁) + 1/T₂*, where T₁ is the population lifetime and T₂* is the pure dephasing time. The spectral fits in Fig. 5 including the convolution with the system spectral response function (limited by the 9-cm⁻¹ VIS spectral width), indicate that the FWHM of the free OH is 48 cm⁻¹ (Γ = 24 cm⁻¹) for H₂O and 40 cm⁻¹ (Γ = 20 cm⁻¹) for HDO, i.e., a difference of 4 cm⁻¹ in Γ. For H₂O the lifetime 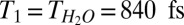results in a contribution of 3.2 cm⁻¹ to Γ, whereas for HDO 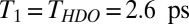, resulting in a contribution of only 1.0 cm⁻¹. As changes in T₁ thus explain only 2.2 cm⁻¹ of the 4-cm⁻¹ difference in Γ between the spectral response of the interfacial free OH of H₂O and that of HDO, the remaining 1.8 cm⁻¹ must be due to differences in the pure dephasing time T₂* of the two systems, presumably due to subtle differences in low-frequency modes of the H-bonded network for the isotopologues. As expected, the pure dephasing time T₂* of free OH groups both for H₂O, ∼250 fs, and HDO, ∼280 fs, are 3× longer than the H-bonded OH of HDO in bulk D₂O (∼90 fs) (48), presumably due to the absence of the frequency modulation of free OH groups by the surrounding water molecules at the air–water interface.

Fig. 5.

VSF spectrum of pure (red) and isotopically diluted H₂O (H₂O:D₂O = 1:1, blue) and their spectral fitting curves (pink and light blue).

Free OH groups at hydrophobic interfaces are important: they are one of few molecular scale observables whose presence correlates with macroscopic indicators of hydrophobicity such as contact angle. The air–water interface is the simplest representative of systems in which water is adjacent to a hydrophobic surface. To understand how this molecular scale observable connects with macroscopic indicators requires quantitative insight into the structure and dynamics of this species. VSF spectroscopy is the most straightforward way to observe this free OH experimentally but understanding the physical chemistry underlying this spectral response is challenging. Armed with only a VSF measurement it is not possible to understand what factors control the free OH line shape and therefore understand the implications of changes in line shape for molecular structure. In this study we show that free OH groups at the air–water interface have a vibrational lifetime of ∼850 fs. Two-color IR-pump/VSF-probe measurements of both the free OH of H₂O at the air/H₂O interface and of HDO at the air/H₂O:D₂O mixture interface allow us to clarify that one-third of this energy relaxation happens via structural relaxation, the free OH rotates toward the bulk liquid, at which point it forms a hydrogen bond, whereas two-thirds are the result of intramolecular energy transfer––excitation transfer from the excited free OH to the H-bonded OH on the other half of the same molecule. Given this knowledge of lifetimes for both species, we further calculate pure dephasing times of 250 fs for free OHs in H₂O and 280 fs for HDO. Taken together this work gives us, in addition to understanding of the structural and vibrational dynamics, comprehensive insight into the VSF free OH spectral response at the air–water interface: we can now completely specify the factors that control the spectral line shape. Such insight, and similar experiments to those described here for other aqueous solutions, is necessary in quantitative description of the free OH stretch spectral response, clarifies the manner in which structural dynamics is recorded in the free OH spectrum, and establishes how excess vibrational energy flows from the free OH into bulk liquid water. We thus expect this work and similar experiments on other aqueous systems to be important steps in understanding hydrophobic solvation and on-water catalysis more generally.

Materials and Methods

The IR-pump/VSF-probe setup is briefly described as follows. A Ti:sapphire regenerative amplifier (Spitfire Ace, Spectra-Physics) was used to generate laser pulses centered at 800 nm with an FWHM of 30 nm and a pulse duration of 40 fs. The amplifier produces ∼5 mJ of energy/pulse with a repetition rate of 1 kHz. Two commercial optical parametric amplifiers (TOPAS-C, Spectra-Physics) are each pumped with 1 mJ of the amplified 800-nm beam. For one TOPAS-C the signal and idler were used in a difference frequency mixing process in a silver gallium disulfide crystal, resulting in 3-μJ IR pulses, tunable around a central wavelength of ∼2,850 nm (∼3,500 cm⁻¹) with an FWHM of 300 cm⁻¹, which was used as IR probe. Another TOPAS-C was used to produce an idler field (2,272 and 2,222 nm). The field was then doubled in a β-barium borate crystal and subsequently the difference frequency was generated in a 6-mm-thick potassium titanyl phosphate crystal with 2 mJ of the 800-nm Ti:sapphire output. This produces ∼100-μJ mid-IR pulses (centered at 3,500 and 3,700 cm⁻¹) with an FWHM of 100 cm⁻¹, used as the pump pulse. The remaining 800-nm pulse of the laser output was narrowed by an etalon (SLS Optics Ltd.) to 9 cm⁻¹ and was used for the VIS probe. The 9-cm⁻¹ width of the visible probe pulse limits the spectral resolution in the experiment. The IR-pump/VSF-probe measurements were made in reflection geometry. The VIS probe, IR probe, and IR pump beams lay in the same plane orthogonal to the air–water interface and had incident angles of 50°, 45°, and 55° with respect to the surface normal, respectively. The energy of the IR pump, IR probe, and VIS probe at the sample was 40, 1, and 4 μJ per pulse, respectively. The time 0 (overlapping of the IR pump and VSF probe) and the experimental time resolution is determined by the third-order cross-correlation between the IR pump and the VSF probe pulses. The width of this third-order cross-correlation determines the temporal resolution in the experiment and amounts to ∼200 fs. The samples were distilled Millipore filtered H₂O (18-MΩ-cm resistivity) mixed with D₂O (Cambridge Isotope Laboratories, Inc., 99.93% purity, used without further purification) and placed in a homemade Teflon trough which was rotated at 8 rpm to reduce cumulative heating. The IR-pump/VSF-probe spectra were recorded with p-polarized IR pump, s-polarized VSF, s-polarized VIS probe, and p-polarized IR probe. The IR pump pulse was variably delayed with respect to the VSF probe signal using a mechanical delay line. The normalized VSF signal was computed as the ratio between the integrated intensities with and without the pump with an integrated bandwidth of 100 cm⁻¹.