Prediction of Cognitive Decline Based on Hemispheric Cortical Surface Maps of FDDNP PET

Abstract

Objectives

A cross-sectional study to establish whether a subject’s cognitive state can be predicted based on regional values obtained from brain cortical maps of FDDNP Distribution Volume Ratio (DVR), which shows the pattern of beta amyloid and neurofibrillary binding, along with those of early summed FDDNP PET images (reflecting the pattern of perfusion) was performed.

Methods

Dynamic FDDNP PET studies were performed in a group of 23 subjects (8 control (NL), 8 Mild Cognitive Impairment (MCI) and 7 Alzheimer’s Disease (AD) subjects). FDDNP DVR images were mapped to the MR derived hemispheric cortical surface map warped into a common space. A set of Regions of Interest (ROI) values of FDDNP DVR and early summed FDDNP PET (0-6 min post tracer injection), were thus calculated for each subject which along with the MMSE score were used to construct a linear mathematical model relating ROI values to MMSE. After the MMSE prediction models were developed, the models’ predictive ability was tested in a non-overlapping set of 8 additional individuals, whose cognitive status was unknown to the investigators who constructed the predictive models.

Results

Among all possible subsets of ROIs, we found that the standard deviation of the predicted MMSE was 1.8 by using only DVR values from medial and lateral temporal and prefrontal regions plus the early summed FDDNP value in the posterior cingulate gyrus. The root mean square prediction error for the eight new subjects was 1.6.

Conclusion

FDDNP scans reflect progressive neuropathology accumulation and can potentially be used to predict the cognitive state of an individual.

I. INTRODUCTION

Hemispheric Cortical Surface Maps (HCSM) of 2-(1-{6-[(2-[F-18]fluoroethyl)(methyl)amino]-2-naphthyl}ethylidene)malononitrile (FDDNP) provide good visualization of beta amyloid plaque (BA) and neurofibillary tangle (NFT) distribution in the human brain (Braskie et al., 2010; Protas et al., 2010). HCSM, a 3D coordinate system of only the cortical surface developed from segmenting T1 MRI images, was originally developed to quantify 3D structural characteristics (Fischl and Dale, 2000; Rasser et al., 2005; Thompson et al., 2003; Thompson et al., 2004; Van Essen and Drury, 1997). It allows for visualization of the structural characteristics over the cortex as a whole. More recently, cortical surface-based methods have been used in analysis of PET imaging probes such as FDDNP PET and FDG PET to examine the pattern of differences in normal aging and Alzheimer’s disease (AD) (Apostolova et al., 2010; Braskie et al., 2010; Protas et al., 2010). In a prior paper (Protas et al., 2010), we showed how to optimize the FDDNP HCSM, how to correct for partial volume effects (PVE), and finally how HCSMs offer insight into BA and NFT patterning with respect to cognitive decline in living subjects.

Several image analysis models have been developed to quantify FDDNP binding (Wong et al., 2010; Wong, 2007b; Yaqub et al., 2009). These models require either a reference tissue (e.g., cerebellum where FDDNP binding is low) or the gold standard arterial input, which is invasive. Distribution Volume Ratio (DVR) derived from Logan graphical analysis (Logan et al., 1996) is generally used for FDDNP analysis due to its ease to use and robustness compared with other simplified reference tissue models. For brain BA probe analysis the reference region used is generally the cerebellum due to the negligible or low amyloid deposition in comparison with other cortical regions in AD patients (Kepe et al., 2006). In this cross-sectional study, we investigated the use of regional data from HCSMs of study participants’ early summed FDDNP PET values and FDDNP DVR values to predict a common measure of cognition, the Mini Mental State Examination (MMSE) (Folstein et al., 1975) score. MMSE, despite being a rough screening test, is widely used in clinical practice to track the course of the disease. Positive answers in this investigation would further confirm that FDDNP PET images contain robust information about the cognitive state of individual subjects.

Before PET scans were performed, subjects underwent extensive neuropsychiatric testing to diagnose and determine the severity of disease. One of the most commonly used examinations is the MMSE, which evaluates an individual’s cognitive functions of orientation, registration, attention and calculation, recall, and language (Folstein et al., 1975). MMSE and other tests are generally used to help in the diagnosis of AD. Although these cognitive measures give a preliminary measure of the severity of the disease, imaging can provide more insights (Petrella et al., 2003; Small et al., 2008) and, more critically, early accurate identification of a disease progression pattern leading to AD. With this objective, we examined in this work the feasibility and reliability of using a statistical method to predict a subject’s MMSE based on the regional cortical FDDNP uptake pattern.

II. METHODS

A. Subjects

Two groups of subjects were studied--the first group to create a statistical prediction model (23 subjects) and a validation group (8 subjects). Table 1 shows the demographic data for both groups of subjects. The first group includes 7 AD patients, 8 control subjects, and 8 MCI subjects while the second group contains 1 AD patient, 3 MCI subjects and 4 NL subjects. All subjects of the first group were part of a previously reported cohort (Braskie et al. 2010;Protas et al. 2010). One extra female control was used for the cortical surface construction but was later excluded from rest of the study because of corrupted FDDNP dynamic imaging files. The patient MRI was still used to generate the average cortical map. The replication group had 8 subjects; their MMSE and diagnosis was blinded to the investigators who constructed the models during the testing period.

Table 1.

Demographic Table

Group 1:
	NL (n=8)	MCI (n=8)	AD (n=7)	P-value
Age	76.6 ± 10.4	66.7± 9.9	76.3 ± 10.3	0.11
Education	15.8 ± 3.2	17.0 ± 3.3	15.9 ± 1.2	0.62
Gender (F/M)	5/3	6/2	4/3	0.75
Family History(N/Y)*	4/4	4/4	4/3	0.95
Apolipoprotein E ε4 (HM/HT/NC)**	0/4/4	1/1/4	1/3/3	0.61
MMSE	29 ± 1	28 ± 1	23 ± 2	9.6e-07
Max MMSE	30	29	25
Min MMSE	27	26	19
WAIS digit symbol	59.5 ± 6.6	61.9 ± 19.0	33.1 ± 9.7	6.1e-04
Buschke Free Recall Test	99.5 ± 20.7	82.4 ± 23.6	53.2 ± 9.3	1.3e-03
Buschke Free Recall Test-Delay	8.5 ± 3.4	3.9 ± 2.5	0.2 ± 0.4	2.7e-05
Rey- Osterrieth Copy test	29.4 ± 3.4	30.8 ± 3.2	19.2 ± 6.6	1.6e-04
Rey Osterrieth Copy Delay	13.1 ± 7.7	8.5 ± 4.7	3.0 ± 3.1	8.8e-03
Total Logical Memory test	44.8 ± 10.6	28.6 ± 8.4	15.3 ± 9.7	3.7e-05
Logical Memory Test –Delay	28.4 ± 9.3	12.3 ± 7.3	3.3 ± 3.9	6.9e-06

Group 2:
	Groups*
Age	51.1 ± 9.0
Education	15.9 ± 2.2
Gender (F/M)	5/3
Family History(N/Y)	6/2
Apolipoprotein E ε4 (HM/HT/NC)	4/4/0
MMSE	29 ± 2
Max MMSE	30
Min MMSE	26
WAIS digit symbol	68.6 ± 32.8
Buschke Free Recall Test	108.1 ± 20.1
Buschke Free Recall Test-Delay	7.4 ± 2.9
Rey- Osterrieth Copy test	27.0 ± 8.9
Rey Osterrieth Copy Delay	12.4 ± 6.8
Total Logical Memory test	39.9 ± 18.3
Logical Memory Test –Delay	23.1 ± 11.1

^*Family history is defined as having a parent, grandparent, or sibling with dementia (Y)

^**For APOE –ε4 HM: homozygous, HT: heterozygous, NC: noncarrier

^*NL/MCI/AD =4/3/1

For each subject, a FDDNP PET scan and a MR imaging were collected (see below for details). Standard neurological and psychological tests, including MMSE, were performed on all studied subjects. Exclusion criteria included a history of stroke, serious head injury, or any disease that would confound their cognition. The AD and MCI subjects met diagnostic standard for AD and amnestic MCI, respectively (American Psychological Association., 2000; Petersen, 2004). Control subjects might have some memory complaints but did not meet the standard of MCI or AD. The AD patients had an average MMSE score of 23±2. The control subjects had an average MMSE score of 29±1 and the MCI had an average score of 28±1. For the test group, the average MMSE score was 29±2. For each subject, a FDDNP PET scan and a MR imaging were performed (see below for details).

B. PET scanning

A bolus of FDDNP (320 to 550 MBq) (Liu et al., 2007) was injected through an indwelling venous catheter and a dynamic PET scan performed for up to 125 minutes (six 30-second frames then four 180-second frames followed by five 600-second frames, finished with three 1200-second frames) using an ECAT EXACT HR+ scanner (Siemens Corp.). There was no head restraint for the patients. Scans were corrected for decay and reconstructed with a filtered back-projection algorithm (Hann filter; 0.3 of the Nyquist frequency with a zoom factor of 3.5) with attenuation correction factors calculated from transmission measurements (acquired for 20 min in 2D acquisition mode with the same PET scanner at ~10 min before the injection of FDDNP)). The resulting images had a resolution of 9 mm full width at half maximum (FWHM) and contained 63 contiguous slices with image plane separation of 2.42 mm and in-plane pixel size of 1.47 mm by 1.47mm.

C. MRI scanning

A whole brain spoiled gradient echo MRI (MPRAGE) volumetric scan was taken for each individual with a 3T Siemens Allegra MRI scanner (sagittal plane; repetition time (TR) 2300 ms; echo time (TE) 2.93 ms; 160 slices; slice thickness 1 mm, skip 0.5mm; in-plane voxel size 1.3 × 1.3 mm; field of view 256 × 256; flip angle 8°) (Thompson et al., 2004).

D. Cortical Surface Mapping for Creation of the Model

An affine transformation (or a linear transformation followed by translation) was performed on the MRI of each subject to put it first into the International Consortium for Brain Mapping (ICBM) common space (Mazziotta et al., 2001). ICBM is a reference system for structural and functional anatomy. A 3D hemispheric cortical surface model for each subject was extracted from his/her MRI in the ICBM space as described by Thompson et al (1997). To improve the MRI alignment among individuals, 36 major fissures and sulci were manually identified. For each hemisphere, some of the 3D sulcal curves drawn were the Sylvian fissure, superior, middle and inferior frontal, central, post-central, precentral, intraparietal, superior and inferior temporal, collateral, olfactory and occipito-temporal sulci, transverse occipital, primary intermediate, and secondary intermediate (Sowell et al., 2000; Thompson et al., 1997). Each of these landmarks was warped to an average on the flattened 2D surface. Inter-rater reliability was discussed in a previous study (Sowell et al., 2002). The reliability was determined by two raters, independently defining the sulci. Differences in the 3D RMS distances between tracings of the same sets of sulci of six subjects between the two raters were measured in mm. Almost all regions had an average difference of less than 2 mm everywhere. The areas of poorest inter-rater reliability were in the posterior temporal and ventral occipital region (Sowell et al., 2002).. This cortical surface map procedure is described in detail previously (Protas et al., 2010). Cortical surface maps were not determined for the test group of eight subjects. [See subsection J below for a description of how the ROI values for these eight subjects were determined].

E. Correction of Movement Artifacts in Dynamic FDDNP scans

Dynamic FDDNP scans were corrected for head movement during the up-to–two-hours-long scan by first determining the proper attenuation of the emission (EM) frames, by co-registering the transmission image to each EM frame. After that each corrected EM frame was aligned to a reference frame. The co-registration was done using SPM2 (Statistical Parametric Mapping, Institute of Neurology, University College of London, UK) software package (Frackowiak, 2004) and with the criterion of maximizing the normalized mutual information. More details of this procedure were described previously (Wardak et al., 2010; Wong, 2007b).

F. Generation of FDDNP DVR images

Parametric FDDNP DVR images were generated following the procedure described previously (Kepe et al., 2006; Small et al., 2006). Briefly, Logan graphical analysis (Logan et al., 1996) were applied to the dynamic FDDNP PET images using the cerebellar ROI as the reference region to determine the DVR values of FDDNP in all brain tissue voxels. The reference ROI was drawn on the cortical cerebellar region of the summed images from 0 to 6 minutes. The ROI was projected to all time frames of the dynamic images, and the time activity curve (TAC) corresponding to the cerebellar region was obtained. This cerebellar TAC was used as the input function in the Logan analysis of the dynamic image. The DVR value for each image voxel location was the linear slope of the Logan plot (Logan et al., 1996) for the corresponding image values between 15 and 125 minutes (Small et al., 2006).

Early summed FDDNP images were obtained by summing (weighted by the scan durations) of the dynamic images from 0 to 6 min, which represent the brain perfusion pattern in the subject.

G. Intensity Normalization of Early Summed FDDNP images

We have previously determined (Wu et al., 2004) that early FDDNP images in a giving patient represent their brain perfusion pattern that closely mimics the 2-FDG glucose metabolism pattern as expected from a match between nutrient supply and utilization in normal cerebral tissues. With FDG, a whole brain reference region is generally used for intensity normalization. Therefore for summed FDDNP we use the same procedure to examine the perfusion-related image pattern.

A thresholding method used by SPM2 (Frackowiak, 2004) and written in Matlab was applied to all of the early summed FDDNP images. We thresholded the image by the average of the entire image divided by eight (Average1). All voxel values above the threshold were averaged (Average2) and the image was divided by this new average (Average2). Of the remaining non-zero voxels of Average 2, the lowest 20 percent were set to zero.

H. Alignment of PET with MR Images

Using SPM2 (Frackowiak, 2004), the early summed FDDNP PET image was aligned to the MR image of the subject by rigid-body co-registration. Maximizing the normalized mutual information was the criterion used. The early summed (0-6 min perfusion) FDDNP image preserved the anatomical information needed for accurate co-registration to MRI. The FDDNP DVR image, which was in the same space as the summed FDDNP image, was then warped to the right orientation following the same transformations to align with the MRI. An affine linear mapping by “minctracc”, a program for elastic image registration (Collins et al., 1994), was performed to have MR images mapped to the ICBM space. This mapping was then applied to the co-registered early summed FDDNP images and the DVR PET image, so they were all in the same ICBM common space, and thus in the same cortical surface derived from the warped MRI as described in subsection D above (also see Protas et al. 2010).

I. Calculating PET values for the cortical surface map

The cortical surface model described in subsection D above was applied to the aligned and masked FDDNP DVR PET image, giving a cortical surface map of PET signal at each cortical surface vertex. The average PET intensity within a sphere (excluding the extra-cerebral space) around each cortical point in the 3D PET image in the ICBM space was calculated to give a PET value for that cortical point on the surface map. The radius of the sphere (referred to as the kernel size or cortical surface smoothing factor) was 9 mm. For the early summed FDDNP images, a kernel size of 11 mm was used. The procedure is the same as the one optimized and reported previously (Protas et. al. 2010).

J. ROI analysis

A cortical surface ROI drawing program (Protas et al, 2010) written in MATLAB (version 6.5, The Mathworks Inc., Natick, MA 2002) was used to draw various surface ROIs directly on the average cortical surface by picking all points on the cortex within a sphere of user defined radius. For each ROI, we pick a set of spheres on the average cortical surface that make up the area of interest. All cortical points within the spheres make up the surface ROI. With this surface ROI tool, values in nine regions on the cortical surface corresponding to the frontal, temporal, parietal, and posterior cingulate areas were defined. Each cortical surface ROI was also made into a 3D mask on the corresponding original PET image by selecting all voxels within a radius of 7 mm around each individual cortical point. For the test group of subjects, the average HCSM ROIs was used, since the subjects in the test group did not have individual HCSMs. To create a set of average HCSM ROIs, we first created an average HCSM by averaging each cortical point of the 23 subjects. A 7-mm radius sphere was made around each of the many cortical surface points within the HCSM ROI and the final mask for each ROI is the union of all voxels within all spheres in the HCSM ROI. Based on this average 3D mask, regional FDDNP DVR values on the PET images from the test group corresponding to these surface ROIs were calculated.

K. Regression analysis for estimation of MMSE score

Two approaches--inverse prediction and linear regression—were used to examine the relationship between FDDNP values and MMSE. Both approaches were based on linear regression (y=mx+b+ε). In inverse prediction, we solve for x from a series of equations for all ROI. More detailed discussion of the inverse prediction can be seen in the appendix. For both approaches, 12-fold cross validation and leave-one-out cross validation (Hastie et al., 2009) were used to evaluate the robustness of the estimates.

For the regression models, we examined two extra measures, adjusted R2 and Cp(Mallow’s), for goodness of fit and comparison between the different subsets of ROIs. Cp(Mallow’s) is often used to choose a model with fewer regressors to reduce collinearity or the similarity between regressors (i.e., to pick the important predictors of the dependent variable). The best models are those that have the number of predictors approaching p, the number of variables in the model plus one (the intercept). Addition of an extra regressor would be accepted to improve the model, if and only if the value of the adjusted R2 (adjusted coefficient of determination) is increased with the addition.

III. Results

A. Model for Predicting MMSE Scores Based on Regional Cortical Surface DVR FDDNP and Early Summed FDDNP values

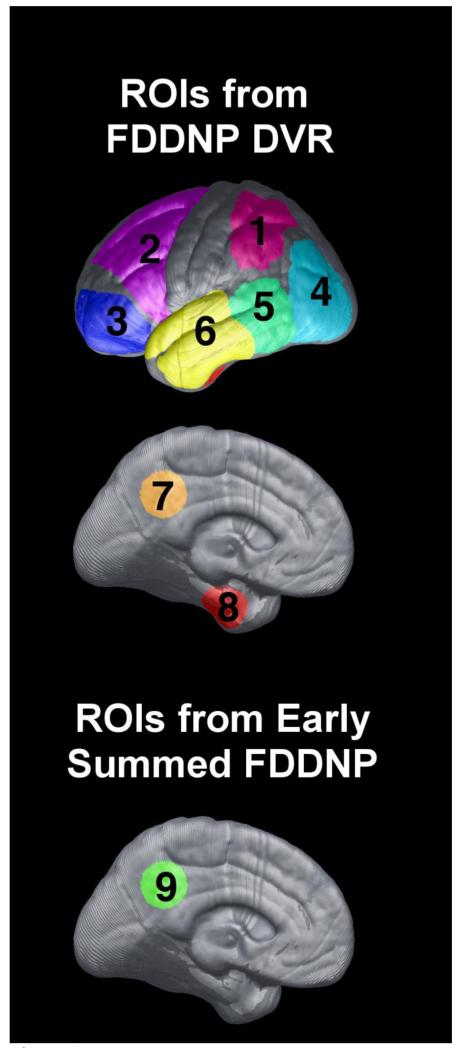
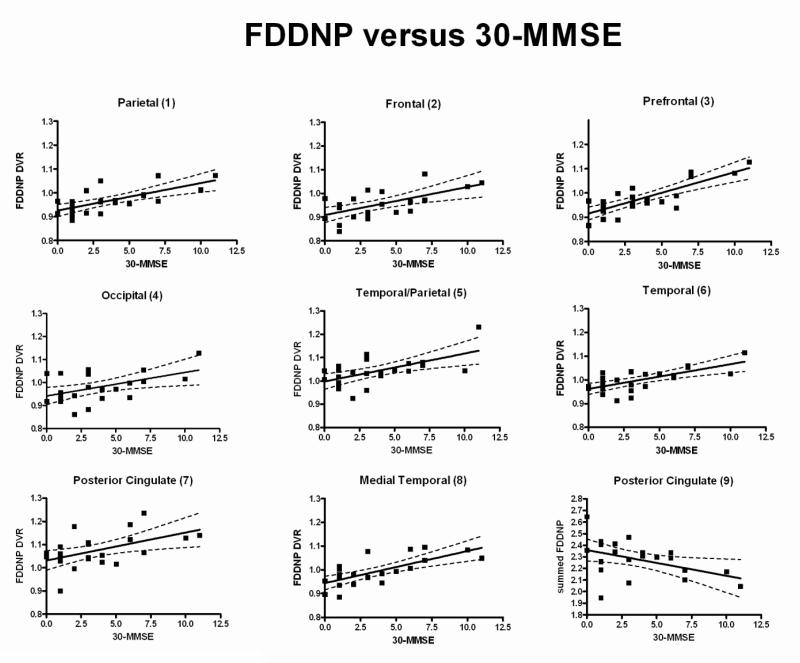
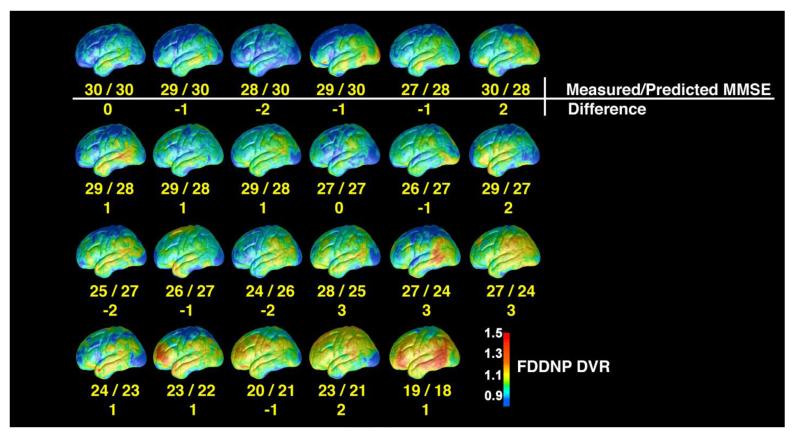
All ROIs used for calculating both FDDNP DVR and early summed (0-6 min perfusion) FDDNP values are shown in Fig. 1. The ROI numbers shown in Fig. 1 are used also to refer to the corresponding ROI values in describing the regression and estimation models later. Figure 2 shows, for each cortical surface region in Figure 1, the scatter plot of the FDDNP DVR value versus (30-MMSE score) and the regression line through it. The dotted lines denote the 95 percent confidence intervals. For all cortical surface regions, the relationship between FDDNP DVR value and (30-MMSE score) has a positive slope. As expected, the posterior cingulate gyrus values for the early summed (0-6 min perfusion) FDDNP images had a negative slope with respect to (30-MMSE score). In Table 2, the correlation of regional FDDNP versus 30-MMSE and other cognitive measures such as Buschke Free Recall Total (Buschke and Fuld, 1974) and Delay Tests, Rey Osterrieth Complex Copy (Osterrieth, 1944) and Delay tests as well as WMS Logical Memory Total and Delay tests are shown. 30-MMSE has the highest correlation with FDDNP in the prefrontal region (3) of the brain (r=0.8, p=3.7e-06) and in the medial temporal region (8) (r=0.71, p=1.6e-04) areas of build up of BA and NFT in AD (Braak and Braak, 1991). Each of the regional FDDNP intensity is significantly correlated with 30-MMSE. Many of the regional FDDNP intensitites are significant at a <0.05 level with the other cognitive measures except, Rey-Osterrieth Delay Copy test and Logical Memory Delay test. Overall, the correlation of regional FDDNP is highest with 30-MMSE among all cognitive measures. In inverse prediction, the weight used for each ROI was the inverse of the sum squared error (SSE) of the regression, so ROI values with smaller data scatter weighted more in the prediction. An inverse prediction model that included the parietal (1), prefrontal (3), temporal (5), medial temporal (8) cortices of the FDDNP DVR image and the posterior cingulate gyrus (9) of the early summed (0-6 min perfusion) FDDNP image was found to give estimated MMSE closely matching the measured score. Figure 6 shows the cortical surfaces of the 23 subjects ordered according to the estimated MMSE score based on this model. The actual MMSE score and the deviation from the estimated score are also shown. The maximal deviation between the estimated MMSE and the actual MMSE score is 3 among this group of subjects.

Fig. 1.

The cortical surface ROIs included in the models of the present investigation. ROIs on FDDNP DVR images are shown on the top panel. The ROIs are : parietal (1), frontal (2), prefrontal (3), occipital(4), temporal/parietal border (5), temporal (6), posterior cingulate (7), and medial temporal (8). The posterior cingulate (9) from the summed (0-6 min perfusion) FDDNP cortical surface used is shown in the lower panel.

Fig. 2.

The scatter plot of the intensity of FDDNP versus 30-MMSE in 9 cortical regions. The regression lines were also shown. In the bottom right panel, the y-axis is the early the summed (0-6 min perfusion) FDDNP value of the posterior cingulate. All other plots show FDDNP DVR versus 30-MMSE.

Table 2.

Correlation of Regional FDDNP Intensities and various cognitive measures.

	ROI1	ROI2	ROI3	ROI4	ROI5	ROI6	ROI7	ROI8	ROI9
30-MMSE	r=0.69 p=2.8e-04	r=0.62 p=1.6e-03	r=0.80 p=3.7e-06	r=0.50 p=0.015	r=0.60 p=2.3e-03	r=0.68 p=3.6e-04	r=0.52 p=0.012	r=0.71 p=1.6e-04	r=−0.44 p=0.034
Buschke Free Recall Test	r=−0.55 p=7.5e-03	r=−0.49 p=0.021	r=−0.57 p=6.1e-03	r=−0.29 p=0.19	r=−0.48 p=0.024	r=−0.59 p=4.2e-03	r=−0.42 p=0.050	r=−0.56 p=6.8e-03	r=0.52 p=0.014
Delay Buschke	r=−0.48 p=0.023	r=−0.40 p=0.065	r=−0.55 p=8.7e-03	r=−0.24 p=0.29	r=−0.32 p=0.14	r=−0.42 p=0.051	r=−0.19 p=0.41	r=−0.53 p=0.011	r=0.64 p=1.3e-03
Rey Osterrieth Copy	r=−0.52 p=0.010	r=−0.47 p=0.023	r=−0.67 p=5.3e-04	r=−0.52 p=0.012	r=−0.51 p=1.3e-03	r=−0.57 p=4.5e-03	r=−0.35 p=0.11	r=−0.49 p=0.018	r=0.29 p=0.18
Delay Rey Osterrieth Copy	r=−0.22 p=0.31	r=−0.14 p=0.54	r=−0.31 p=0.16	r=−0.17 p=0.45	r=−0.18 p=0.42	r=−0.12 p=0.58	r=−0.12 p=0.58	r=−0.37 p=0.079	r=0.18 p=0.42
Logical Memory test	r=−0.44 p=0.036	r=−0.40 p=0.056	r=−0.44 p=0.036	r=−0.10 p=0.663	r=−0.30 p=0.16	r=−0.45 p=0.030	r=−0.30 p=0.17	r=−0.49 p=0.018	r=0.51 p=0.013
Delay Logical Memory test	r=−0.37 p=0.079	r=−0.30 p=0.17	r=−0.42 p=0.049	r=−0.12 p=0.60	r=−0.24 p=0.26	r=−0.32 p=0.13	r=−0.16 p=0.46	r=−0.49 p=0.019	r=0.62 p=1.8e-03

Fig. 6.

Ordering of the FDDNP DVR cortical surface map based on the estimated Mini-Mental State Examination (MMSE) score using inverse prediction and a model based on five ROI values (lateral temporal, medial temporal, parietal, and prefrontal from the Distribution Volume Ratio (DVR) on the FDDNP HCSM and posterior cingulate value of the early summed (0-6 min perfusion) FDDNP HCSM). The left lateral side of each DVR FDDNP cortical surface maps in the group of 23 subjects (10 Control, 7 Alzheimer Disease (AD) , and 6 Mild Cognitive Impairment (MCI) subjects) is shown with measured vs. predicted MMSE scores and the absolute value of the difference between the two below each map. The absolute value difference is 3 or less for each subject. This ordering of the cortical surfaces is not significantly different from the one based on the measured MMSE (Wilcoxon Signed Rank test: p=.903). If the direct regression method with the same ROIs was used, the ordering was not significantly different from the one based on the measured MMSE (Wilcoxon Signed Rank Test: p=.693) or from the ordering shown in this figure that used inverse prediction model (Wilcoxon Signed Rank Test: p=.808). The results show that the model based on the pattern of FDDNP imaging predicts well the cognitive decline. Thus, FDDNP cortical surface maps can provide not only good visualization of beta amyloid plaque (BA) and neurofibillary tangle (NFT) load, but also, through statistical analysis, reliable estimates of MMSE scores.

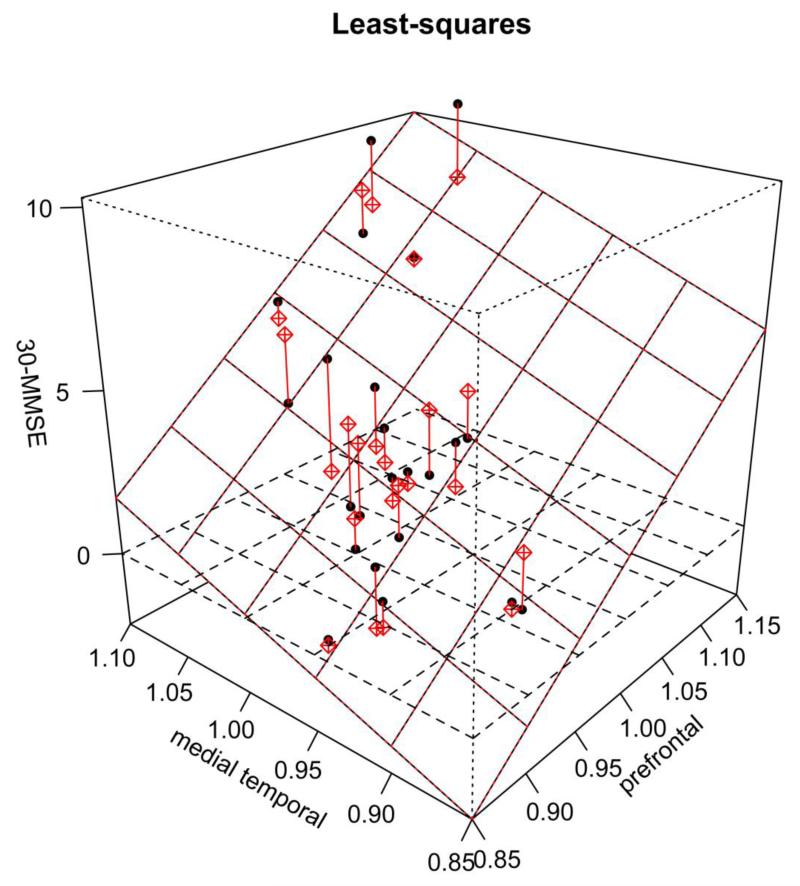
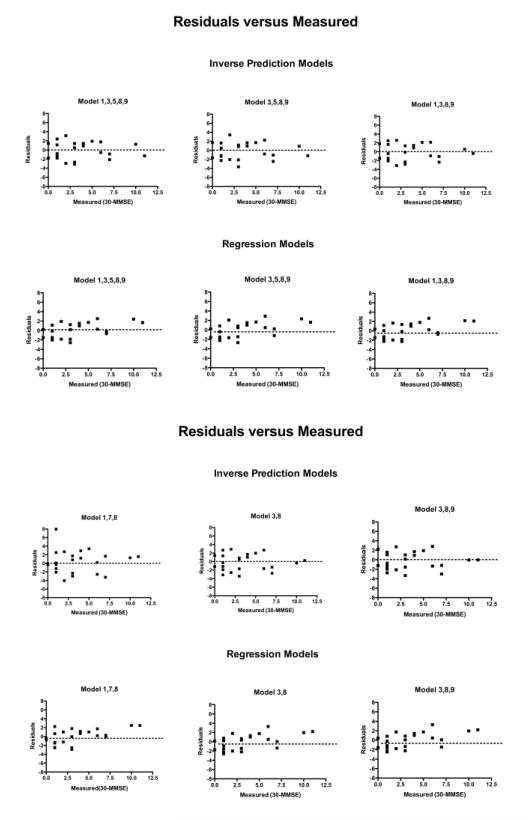
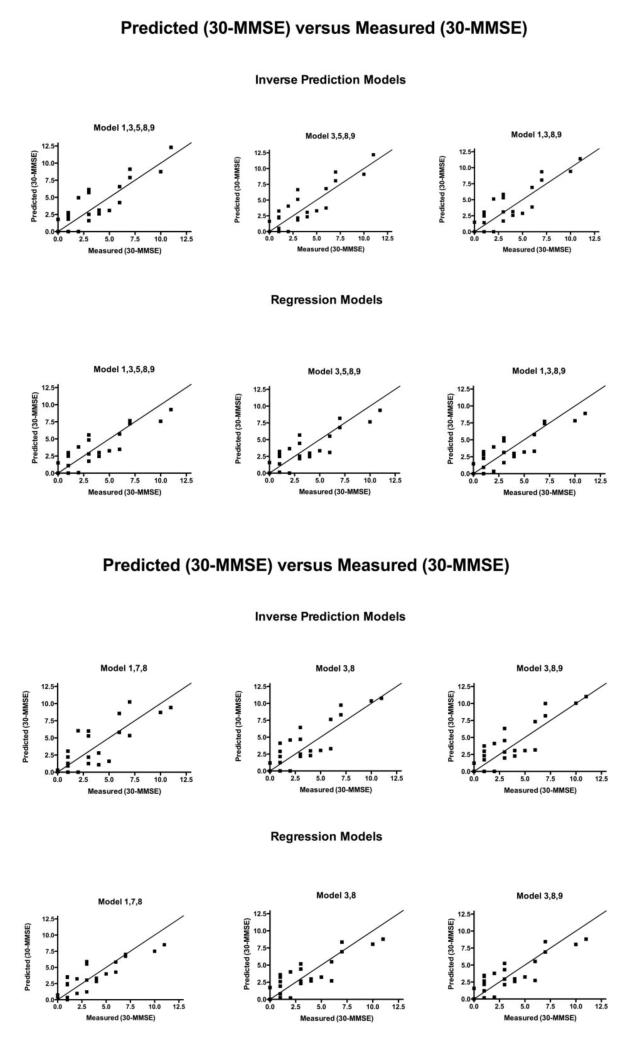
For the direct regression method (the second approach), a 3D plot of 30-MMSE score versus the FDDNP DVR intensities of the prefrontal region and the temporal region is shown in Figure 3. The regression plane is also shown in the figure. The differences between the actual data points and those based on the regression plane are marked as red lines in the figure. A comparison of the residuals for 6 different models versus the 30-measured values is shown in Figure 4. Residuals in this paper are defined as predicted MMSE minus measured MMSE. These models were chosen because they had the lowest leave-one-out cross validation. Figure 5 shows the predicted 30-MMSE scores from each model and the measured 30-MMSE scores. The line indicates where predicted MMSE scores equal measured MMSE scores. The parameters of various regression models of different combinations of regions (i.e., different models) are shown in Table 3 along with the residual sum of squares. The model with frontal (3), medial temporal (8) regions from the FDDNP DVR image and posterior cingulate (9) from the early summed (0-6 min perfusion) FDDNP image had the smallest residual sum of squares of 60.4 between the estimated and the measured MMSE scores. Using the global mean value of all 8 regions of the DVR image and the posterior cingulate gyrus for early summed FDDNP has the largest residual sum of squares, 71.0

Fig. 3.

3D scatter plot of 30-MMSE with FDDNP DVR ROI values from prefrontal and medial temporal. The regression plane is also shown. The red lines show the distance between each value and the plane.

Fig. 4.

Residuals of linear regression for 6 models of inverse prediction and regression methods versus 30-measured MMSE scores.

Fig. 5.

30-predicted MMSE scores for 6 models of inverse prediction and regression methods are shown versus the 30-measured MMSE scores. The black line shows where predicted MMSE scores equal measured MMSE score.

Table 3.

Residual sum of squares (RSS) for each Regression

ROIs included for each model	Coefficients of the ROI for Each Regression Model	RSS#
Inverse Prediction
1,3,5,8,9	M1=17.2, M3=23.7, M5=10.5, M8=16.3, M9=−2.4	85.4
3,5,8,9	M3=29.5, M5=13.1, M8=20.3, M9=−3.0	84.9
1,3,8,9	M1=19.6, M6=27.1, M8=18.6, M9=−2.8	84.0
Regression
1,7,8	M1=38.5*, M7=−15.4, M8=32.7*	61.6
3,8	M3=28.3*, M8=16.5	61.0
3,8,9	M3=26.0*, M8=17.3, M9=−1.3	60.4
Mean(1-8)**, 9	M(1-8)=46.5*, M9=−3.6	71.0

^*significance at a p=0.05

^**The ROIs used for this model are the global mean of the 8 regions of the FDDNP DVR image (Mean(1-8))

^#Residual sum of squared differences between the estimated and the measured MMSE scores.

B. Cross Validation Study of Predicted MMSE Scores Based on Regional Cortical Surface DVR FDDNP and Early Summed FDDNP Values

The performance of different models of using different combinations of the regions and between the two estimation approaches was evaluated by cross-validation studies. For inverse prediction, the use of all ROI values of DVR and the early summed FDDNP posterior cingulate ROI to predict MMSE gave a leave-one-out cross validation error of 2.3. Using a stepwise cross validation, two models have the smallest leave-one-out cross validation error of 1.8, one model included the parietal (1), prefrontal (3), temporal (5), medial temporal (8) cortices of the DVR FDDNP image and the posterior cingulated gyrus (9) of the early summed (0-6 min perfusion) FDDNP and the other model contained all ROIs from the first model except the parietal cortex.

For the second estimation approach, the two best models -- one with the prefrontal cortex (3) and medial temporal (8) and the other with the parietal (1), posterior cingulate (7), and medial temporal regions (8) -- have a cross validation of 1.8 comparable to the lowest cross validation results of the models by the inverse prediction approach. The model with the highest adjusted R² is the model using only the prefrontal (3) and the medial temporal cortices(8). All three regression models shown have Cp much smaller than p. Therefore, Cp cannot be used to distinguish further which models are better.

C. Comparison of the Subject Ordering Determined by Predicted MMSE values

We use the predicted MMSE to order the cortical surfaces from a set of HCSM as previously stated. One such example is shown in Figure 6 using an inverse prediction model with ROI values from the lateral temporal, medial temporal, parietal, and prefrontal cortices of the DVR image and posterior cingulate gyrus of the early summed (0-6 min perfusion) FDDNP image (regions 1, 3, 5, 8, 9). No predicted MMSE deviated by more than 3 from the measured MMSE. This ordering of the cortical surfaces is not significantly different from the ordering based on the measured MMSE (Wilcoxon Signed Rank test: p=.903). The Spearman correlation of the predicted MMSE from this model versus the measured MMSE is 0.811 with a confidence interval from 0.613 to 0.917. If we used regression with the same ROIs, we found that the ordering was also not significantly different from the one based on the measured MMSE (Wilcoxon Signed Rank Test: p=.693) or from the one based on the inverse prediction model (Wilcoxon Signed Rank Test: p=.808). The Spearman correlation of the predicted MMSE from a regression model versus the measured MMSE is 0.797 with a confidence interval from 0.597 to 0.911, while the Spearman correlation of the predicted MMSE from the inverse prediction model versus the predicted MMSE using regression is 0.976 with a confidence interval from 0.880 to 0.985.

D. Predicted MMSE values in a New Set of FDDNP PET Images

In testing the performance of the estimation models on the 8 new cases, the root mean squared prediction error for each of the models listed in Table 4 is shown in Table 5. The lowest prediction error (1.33) was obtained with the linear regression model (the second approach) using only prefrontal (3), medial temporal (8) regions from the DVR FDDNP image, and posterior cingulate (9) from the early summed FDDNP images. The regression model with prefrontal (3) and medial temporal (8) regions had the second lowest prediction error of 1.36. The lowest prediction error for the inverse prediction models was 1.51 that used the parietal (1), prefrontal (3), lateral temporal (5) and medial temporal (8) of the DVR FDDNP image and the posterior cingulate (9) of the early summed FDDNP image. Due to the relatively small number of subjects, the prediction errors of the models shown in Table 5, however, were not statistically significant among the different models (ANOVA p=0.80).

Table 4.

Cross Validation, Adjusted R² and Cp (Mallow’s) determined for prediction/regression models of best performances.

	Slopes (M) for each of the ROI for Each Regression Model #	Cross Validation (Leave One Out/ K=12)	Adjusted R2	Cp (Mallow’s)
Inverse Prediction
1,3,5,8,9	M1=17.2, M3=23.7, M5=10.5, M8=16.3, M9=−2.4	1.8/1.9	N/A	N/A
3,5,8,9	M3=29.5, M5=13.1, M8=20.3, M9=−3.0	1.8/1.8	N/A	N/A
1,3,8,9	M1=19.6, M3=27.1, M8=18.6, M9=−2.8	1.8/1.8	N/A	N/A
Regression**
1,7,8	M1=38.5*, M7=−15.4, M8=32.7*	1.8/1.8	0.65	1.71
3,8	M3=28.3*, M8=16.5	1.8/1.8	0.67	−0.46
3,8,9	M3=26.0*, M8=17.3, M9=−1.3	1.9/1.9	0.66	1.39

^*significance at a p=0.05

^**significance of slopes was only calculated for regression and not for inverse prediction models.

^#intercepts are not included

Table 5.

Root Mean Square Prediction Error for each Model in Table 4.

Models	Prediction Error	Standard Error
Inverse Prediction
1,3,5,8,9	1.51	2.46
3,5,8,9	1.60	2.26
1,3,8,9	1.53	2.17
Regression
1,7,8	2.12	2.68
3,8	1.36	1.57
3,8,9	1.33	1.68
Mean(1-8),9	2.13	2.46

IV. Discussion

We determined in this work that, like FDDNP DVR, early summed FDDNP image (0-6 min after IV administration) has its own pattern of changes as MMSE decreases. In building a model to describe the relationship between FDDNP and MMSE, we found that including the posterior cingulate gyrus ROI value of the summed FDDNP image helped predict the subject’s MMSE score. With a model relating these FDDNP ROI values to MMSE scores, it is possible to estimate MMSE scores based on ROI values of FDDNP PET images as shown in Figure 6. The results of the present study show that an estimation model that included a subset of the regions from the DVR and early summed FDDNP image could predict well the MMSE for each subject with small errors. Furthermore, it reveals the possibility of establishing a cognitive scale/measure based solely on FDDNP PET imaging that can be used to assess objectively a subject’s progression toward AD. This is possible because FDDNP brain cortical accumulation increases with disease progression in a rather predictable pattern (Small et al, 2006; Protas et al, 2010) that is consistent with known progressive pathology deposition (Braak and Braak, 1991), starting in medial temporal lobe and later spreading to other cortical areas. However, it is more likely that FDDNP will remain complementary to cognitive assessments rather than replace them. It should be noted that a longitudinal study still needs to be done first before one should contemplate the replacement of the cognitive scores with FDDNP derived measures in a clinical trial.

There are other tracers such as Pittsburgh Compound B (PIB) that bind neuropathology deposits. Unlike FDDNP, generally in AD subjects, PIB has a high pattern in most brain regions except at medial temporal region (Shin et al., 2008). In part this could be due to the fact that PIB does not bind to NFTs such as FDDNP. The regions for any model using PIB to determine cognition would be very different than that of FDDNP. PIB also has the “on/off” pattern of accumulation not normally found in pathology (Braak and Braak, 1991). This pattern makes it difficult to use a linear model such as the ones employed in this study. Another problem for constructing a model for PIB to predict cognition is that there are control subjects who have a high PIB uptake pattern (Mintun et al., 2006), and AD subjects without PIB binding (Leinonen et al., 2008).

As previously stated, the brain perfusion pattern of early summed FDDNP resembles that of 2-FDG glucose metabolism (Wu et al., 2004). Furthermore, the 2-FDG posterior cingulate gyrus metabolic deficit is the earliest signal observed in AD (Minoshima et al., 1997), which is consistent with the early summed (0-6 min perfusion) FDDNP deficits seen in the posterior cingulate gyrus, providing further support to the results presented in this work.

MMSE along with Buschke total Free Recall, Rey-Osterrieth Complex Figure Copy and Logical Memory total test are significantly correlated with the regional FDDNP. We developed a model with the cognitive measure, 30-MMSE, that had the highest correlation with most regions of FDDNP PET images. A possible explanation for the high correlation of MMSE with FDDNP than with other cognitive test scores is that MMSE evaluates the overall cognitive functions, such as orientation, registration, attention and calculation, recall, and language, while other memory tests, such as Buschke Free Recall total, Rey-Osterrieth Copy and Logical Memory test are very specific for certain types of memory tasks. FDDNP binds both to BA and NFT which accumulates with progression of the disease throughout the brain in a defined pattern (Braak and Braak, 1991). It affects many regions related to memory. Perhaps a composite score of the memory tests along with other measures that evaluate similar cognitive functions as MMSE does might have better correlation with FDDNP. However, more investigations are clearly needed.

There are many ways to build the model using regression. With inverse prediction we can evaluate each region separately with respect to 30-MMSE as shown in Figure 2 and weight the regions according to the inverse of the SSE. One can also use the usual regression (the second estimation approach). Figure 3 shows a typical result of regression by looking at multiple ROIs with respect to 30-MMSE.

We used cross validation as one of the methods to determine the accuracy of the model and help determine the regions that were appropriate to be included in the estimation model. In our cross validation study, we discovered that the error for the model-building group of 23 subjects was 1.8. The ROIs needed for the lowest cross validation were at the medial temporal, lateral temporal, prefrontal from the FDDNP DVR image and the posterior cingulate from the summed (0-6 min perfusion) FDDNP image and one that included all previously mentioned ROI and also included the parietal cortex from the FDDNP DVR image. This is what would be expected based on our previous study (Protas et al, 2010), which showed that all these regions had the largest change in intensity as a function of the subject’s MMSE score. The lowest cross validation error however does not necessarily provide the best model. Cross validation only helps identify a group of good models. We looked at a model using all cortical regions implicated in AD which included the parietal, prefrontal, lateral temporal, and medial temporal cortices (FDDNP DVR images) and the posterior cingulate gyrus (early summed FDDNP images). It makes sense that both medial temporal and prefrontal cortex are in the model of cognitive decline since medial temporal is important in long term memory and prefrontal cortex is important in the working memory (Petrella et al., 2003). In Figure 6, the individual brains were ordered according to their estimated MMSE from this model. No individual has an absolute difference between predicted and measured MMSE of more than 3. The cross validation results indicate that FDDNP is highly related to cognitive status and could be used as a brain biomarker of cognition for future studies.

It is interesting that two regions that were not found in most models are the frontal (2) and temporal (6) ROI. These regions are important in Alzheimer’s disease according to Braak and Braak (1991). The subjects that we have in the Alzheimer’s group are predominantly early Alzheimer’s disease. According to Braak and Braak (1991), accumulation of BA occurs in prefrontal before the rest of the frontal region. Therefore although there are changes in BA deposition in the prefrontal of Alzheimer’s subjects with respect to control subjects, the BA deposition in the rest of the frontal region may not be so different between these particular subject groups with Alzheimer’s disease and control subjects. For the temporal ROI, there might be difference in these Alzheimer’s disease subjects, but it is possible that the changes did not occur throughout the whole ROI. BA accumulates earlier in the inferior part of the lateral temporal lobe than the rest of lateral temporal (Braak and Braak, 1991). If we had an ROI with only the inferior part of the temporal region, it might have appeared in the best models.

Re-sampling methods, like cross validation, are important for evaluating the accuracy of a statistical estimation model. Cross-validation, a common method in data mining, machine learning and model fitting, was performed to evaluate the model. Cross-validation is a standard procedure to estimate models and evaluate the prediction error on independent data that do not overlap with the data used to fit the model. The results from an additional test group further strengthened the results from cross-validation. We found, in the test group, an error even lower in most cases than those by cross validation. Even though this small test group of subjects are much younger, over twenty years younger on average, the results indicate that the models are rather robust for predicting MMSE scores based on FDDNP PET images. This is indeed a very rewarding observation because it shows the possibility of establishing a predictive model at the earliest possible stages of the disease when clinical diagnosis would be more difficult and also when the probability of successful therapeutic interventions increase. However, one would need a larger test group to prove this. We believe the introduction of the prediction model based on cortical surfaces is itself quite significant. Cross-validation and an additional small test group together confirmed the value of these kinds of models and approaches. In addition, the result of the testing of the eight new cases suggested that constructing individual HCSM for each subject was not necessary in applying the MMSE prediction models since individual HCSMs were not available for any of the new cases. To prove that individual HCSMs are not necessary and to truly validate the models, a much larger test group is needed. This indicated that it might be possible to use a template created from a typical HCSM to be used on images that do not have MR images and still get results similar to those that have the extra information from the individual cortical surface. This versatility of not needing to create cortical surface for each individual could allow the use of FDDNP images to estimate a subject’s cognitive state to be more practical in a clinical setting. We are currently testing this concept in subjects with memory complaints with excellent predictive results.

V. Conclusion

HCSM of FDDNP can provide not only good visualization of brain cortical distribution of BA and NFT, but also reliable estimates of subjects’ MMSE, when proper statistical estimation is employed, confirming that FDDNP PET images contain robust information about the cognitive state of individual subjects. This observation permits – using a PET imaging marker of brain neuropathology - the previously unrealized determination of the cognitive status of a given patient. The sensitivity of the FDDNP PET approach described in this work also has potential implications for its use for early diagnosis and identification of subjects for early therapeutic interventions.

Appendix

For the approach of inverse prediction, FDDNP DVR (y) versus MMSE (x) of a group of subjects was first determined by least-square regression for each ROI on the HCSM. So, a set of linear equations of all ROIs was first derived, with each equation having the following form:

$$y_k=m_{k}x+b_k,$$ (1)

where the subscript k=1,…,n denotes the kth region. The residual sum of squares of the linear regression are denoted as SSE = [SSE₁,…,SSE_n]. Solving for x in terms of y_k’s, one obtains a subject’s estimated MMSE in terms of the regional FDDNP image values as

$$x=inv\left(M^{T}WM\right)M^{T}W(Y-B),$$ (2)

where M = [m₁,…,m_n], B = [b₁,…,b_n], Y=[y₁, … y_n], and W is a diagonal weighting matrix with its kth diagonal element equal to $\frac{1}{SS{E}_k}$. The superscript T denotes transpose of the vector/matrix, and inv(.) denotes the inverse of the matrix inside the parentheses. Based on this equation, a subject’s MMSE can be estimated based on the ROI values obtained from the FDDNP image of the subject.

For the second approach, MMSE score (x) is assumed to be a linear function of multiple ROI values and the measured MMSE of the subjects in the group was regressed based on the linear function to yield a set of coefficients. The regression equation is as follows,

$$x=c_1{y}_1+c_2{y}_2{+}_{\cdots }+c_n{y}_n+dI$$ (3)

where I is the identity matrix. The equation above can be used to predict the MMSE of a subject from a set of ROI values obtained from the FDDNP DVR image of that subject. We used the iterative weighted least squares (IWLS) (O’Leary, 1990) used in general linear model estimation to determine the c_i coefficients.