Logistic Regression with Multiple Random Effects: A Simulation Study of Estimation Methods and Statistical Packages

Abstract

Several statistical packages are capable of estimating generalized linear mixed models and these packages provide one or more of three estimation methods: penalized quasi-likelihood, Laplace, and Gauss-Hermite. Many studies have investigated these methods’ performance for the mixed-effects logistic regression model. However, the authors focused on models with one or two random effects and assumed a simple covariance structure between them, which may not be realistic. When there are multiple correlated random effects in a model, the computation becomes intensive, and often an algorithm fails to converge. Moreover, in our analysis of smoking status and exposure to anti-tobacco advertisements, we have observed that when a model included multiple random effects, parameter estimates varied considerably from one statistical package to another even when using the same estimation method. This article presents a comprehensive review of the advantages and disadvantages of each estimation method. In addition, we compare the performances of the three methods across statistical packages via simulation, which involves two- and three-level logistic regression models with at least three correlated random effects. We apply our findings to a real dataset. Our results suggest that two packages—SAS GLIMMIX Laplace and SuperMix Gaussian quadrature—perform well in terms of accuracy, precision, convergence rates, and computing speed. We also discuss the strengths and weaknesses of the two packages in regard to sample sizes.

1. MOTIVATION

Our interest in generalized linear mixed models (GLMMs) stemmed from an investigation into the influence of smoking-related television advertising on adult smoking in the U.S. The primary hypotheses of our study were that smoking status is associated with exposure to antismoking television advertisements and that the effects of the advertisements on an individual’s smoking status vary geographically. The smoking-related advertising is sponsored by state governments, the American Legacy Foundation (Legacy), pharmaceutical companies, and the tobacco industry. Although individual television viewing patterns may vary, the amount of exposure is measured at the media market level in a given time frame. Relevant studies of smoking-related media campaigns and aggregate measures of exposure can be found in Gilpin et al. (2001), Szczypka et al. (2003), Ibrahim and Glantz (2007), Emery et al. (2005), and Emery et al. (2012). A mixed-effects logistic regression with media markets as clusters was determined to be the most suitable approach for our study because (1) individuals living in the same media markets share a similar environment and culture, and people are likely to resemble each other with respect to behavior and anti- or pro-smoking sentiment, and (2) we were interested in quantifying the amount of between-market variability in the effects of advertisements.

Information on individual characteristics and smoking behavior was obtained from the 2000, 2001–2002, 2003, and 2006–2007 waves of the Tobacco Use Supplements to the Current Population Survey (TUS-CPS). Nielsen Media Research provided television ratings data for antismoking advertisement broadcasts across the top 75 media markets in the U.S¹. The proportion of current smokers in 2000–2007 was about 0.20 according to the TUS-CPS data. The individual-level TUS-CPS data were linked to media market-level exposure data based on the media market identifiers and survey dates. Respondents in areas other than the top 75 media markets and proxy respondents were excluded from the analyses. We used a two-level mixed-effects logistic regression model for the analysis. The model can be written as

$$\log \frac{P(y_{\mathit{ij}}=1)}{P(y_{\mathit{ij}}=0)}={{\mathit{x}}^{\prime }}_{\mathit{ij}}\beta +{{\mathit{z}}^{\prime }}_{\mathit{ij}}{\mathit{u}}_i,$$

where y_ij denotes the smoking status (1= current smoker, 0=non-current smoker) of a respondent j living in a media market i, and x_ij is the vector of predictors: exposure measures of state-sponsored ads and Legacy-sponsored ads, age, sex, marital status, race, region (South, East, Midwest, and Northeast), education, employment, time that TUS-CPS was administered, and tobacco control policy variables. The measures of ad exposure GRPs were aggregated, so that one unit of GRPs indicated an average of 10 viewings by all households in a given media market for four months prior to the survey. Tobacco control policy variables are the average real price per pack of cigarettes and a smoke-free air index by state in the year of the survey. z_ij is the vector of predictors of which relevant coefficients vary between media markets: the exposure measures of state ads and Legacy ads. The vectors x_ij and z_ij also include a 1 for the intercept and the media market-specific deviation from the intercept respectively, β is the fixed-effect parameter vector associated with x_ij, and u_i is the random-effect parameter vector associated with z_ij. We call u_i a vector of random effects and assume that it is normally distributed with mean 0 and covariance matrix of Σ(θ) where θ is a vector of all distinct variances and covariances in the matrix. The number of TUS-CPS respondents ranged from a few hundred to several thousand per media market, and the total number of respondents in the data was 391,389. The descriptive statistics of the respondents are presented in the Appendix.

The parameter estimation of a mixed-effects model for a binary response variable is complicated compared to that for a normally distributed response variable. This is because the equations to find maximum likelihood estimates cannot be analytically derived in a closed form for a nonlinear model in contrast to a linear model. The marginal likelihood function is formed by integration over the distribution of random effects and this integration requires numerical evaluation or approximation. Further, the extent to which binary responses vary is difficult to measure because there are only two possible outcomes, which leaves the response with little room to vary. Longford (1994) also pointed out that information about variation contained in clustered binary data is very sparse unless the number of clusters and the cluster sizes are large. As a result, it is more challenging to estimate between-cluster variation with binary responses than with continuous or count responses. Additionally, when there are k(≥ 2) correlated random effects in a model (i.e., the vector u_i is of k-dimension), up to k(k + 1)/2 unique θ parameters in Σ need to be estimated. More parameters implies more complex computation, which is likely to cause nonconcave log-likelihood, numerical overflows, or failure to proceed to the next iteration, given the limited information contained in data.

Parameter estimation for the mixed-effects logistic models of smoking status has presented significant challenges. The intercept and two slopes for the state ad exposure and Legacy ad exposure were allowed to vary across media markets; thus the model contained three random effects that were assumed to have an unstructured covariance matrix. We performed analyses using SAS 9.2 GLIMMIX (SAS Institute Inc. 2008a), R 2.11 package lme4 (Bates, Maechler, and Bolker 2010), and HLM 6 (Raudenbush, Bryk, and Congdon 2004). First, we observed differences in the regression coefficients, their standard errors, and the estimates of Σ between the three statistical packages even when the same estimation method was chosen. We fit the model by using Laplace approximation of SAS GLIMMIX and R lme4; (co)variance estimates $\left(\widehat{\theta }\right)$ were fairly different and so were hypothesis test results for some elements of β between the two packages. For example, the slope of the region (West vs. South) was estimated as −0.039 (SE=0.034, p=0.244) from SAS GLIMMIX, and the corresponding estimate from R lme4 was −0.039 (SE=0.018, p=0.031); the standard error from R lme4 was about half that from SAS GLIMMIX. We also fit the same model by using Laplace of HLM. The estimates of θ from HLM were somewhat similar to SAS GLIMMIX, but results for a few regression coefficients were rather inconsistent. One of them was the fixed-effect slope of Legacy-sponsored ads; HLM Laplace produced −0.007 (SE=0.021, p=0.734), whereas SAS GLIMMIX Laplace produced −0.033 (SE=0.015, p=0.028). The degrees of discrepancy in the parameter estimates increased as more random slopes were included in the model (by adding the measures of exposure to pharmaceutical company ads and tobacco industry ads in x_ij and z_ij. Second, the computation was very intensive. The computing time until convergence was about 15-20 minutes with Laplace approximation in these three packages using a PC equipped with Intel Core i7 CPU 2.93 GHz and RAM 4GB. We fit the same model by using Adaptive Gauss–Hermite quadrature (AGQ) in SAS NLMIXED, but had to manually stop the program because the algorithm did not converge after running for 5 days. An integer overflow occurred with a penalized quasi-likelihood (PQL) estimation in SAS GLIMMIX. With our dataset, this computational burden substantially increased as we included three or more random effects, regardless of which estimation method was chosen. Further, in our data the number of respondents in each media market was hundreds to thousands. Owing to the huge sample size, the computation became even more intensive, and the convergence speed was extremely slow even if it converged.

These challenges motivated us to conduct a literature review of the mathematical and computational complexity of multilevel models for binary responses. Many researchers have evaluated the performance of estimation methods for logistic mixed-effects models. However, most of them focused on models with no more than two random effects (k ≤ 2), and investigators experienced biased estimates in certain circumstances even with those relatively simple models (Breslow and Clayton 1993; Rodriguez and Goldman 1994; Zhou et al. 1999; Lesaffre and Spiessens 2001; Diaz 2006). Although estimation techniques for logistic mixed-effects models have improved over the past two decades (Wolfinger 1993; Breslow and Lin 1995; Goldstein and Rasbash 1996; Raudenbush et al. 2000), there are few studies that have specifically evaluated estimation techniques for fitting a model with multiple random effects.

Statistical packages capable of estimating GLMMs include HLM, R package lme4, Stata xtmelogit, and SAS NLMIXED procedure, and more recently the SAS GLIMMIX procedure (available from version 9.2) and SuperMix. Each package provides at least one of the following estimation methods: (a) PQL approximation, (b) Laplace approximation, and (c) Gauss–Hermite numerical integration. Technically, (b) and (c) are approximation methods of integration and (a) is an estimation method, but in this article the “estimation methods” refers to these techniques for ease of exposition. These (a)-(c) are the most widely used methods that seek maximum likelihood estimates. The Bayesian approach using Markov chain Monte Carlo is available with WinBUGS and R. The Bayesian model allows flexible distribution for random effects and inference does not depend on asymptotic distribution of estimators. However, the computation is no less challenging than the maximum likelihood estimation (e.g., nonconvergence to stationary distribution, low simulation efficiency, etc.), and specifying prior distributions for the random-effects covariance matrix is sometimes not straightforward. For these reasons, we focus on the three methods that seek maximum likelihood estimates in this study.

The purposes of this article are to describe the strengths and weaknesses of estimation methods through a comprehensive literature review and to find a reliable estimation method(s) and/or statistical package(s) via simulation in situations where multiple random effects are involved in a logistic regression for a large dataset. In Section 2, we describe the theoretical background of the logistic mixed-effects regression model. In Section 3, we provide a comprehensive literature review of the most widely used estimation methods and compare their advantages and disadvantages. In Section 4, using a few commonly used statistical packages, we conduct simulations in which we know the true model and compare their performance. We focus our simulation study on the following packages: HLM 6 (Raudenbush, Bryk, and Congdon 2004), R package lme4 (Bates, Maechler, and Bolker 2010), SAS 9.2 GLIMMIX (SAS Institute Inc. 2008a), SuperMix 1.1 (Hedeker, Gibbons, Du Toit, and Patterson 2008), and Stata 12 xtmelogit (StataCorp. 2011). In Sections 5 and 6, we fit the logistic mixed-effects model to our data based on the simulation results and carry out another limited simulation study to examine statistical packages’ performance associated with sample sizes. In Section 7, we summarize our findings and make recommendations.

2. THE LOGISTIC MIXED-EFFECTS MODEL

The GLMM is used for modeling outcomes in the exponential family to account for hierarchical structure of the data, inter-cluster heterogeneity and intra-cluster correlations. Distributional assumptions on random effects allow for estimating the degree of inter-cluster heterogeneity. Denote the j^th dichotomous outcome within the i^th cluster by y_ij (for i = 1, … , N; j = 1, … , n_i). Let x_ij be a vector of explanatory variables associated with a p-dimensional vector of fixed-effects parameters β. Let u_i be a k-dimensional vector of random effects for the i^th cluster and z_ij a vector of the associated variables (typically a subset of x_ij). The conditional probability of y_ij given the cluster-specific effects vector u_i is written as

$$\begin{array}{cc}\hfill p(y_{\mathit{ij}}=1\mid {\mathit{u}}_i)& =\frac{\exp ({{\mathit{x}}^{\prime }}_{\mathit{ij}}\beta +{{\mathit{z}}^{\prime }}_{\mathit{ij}}{\mathit{u}}_i)}{1+\exp ({{\mathit{x}}^{\prime }}_{\mathit{ij}}\beta +{{\mathit{z}}^{\prime }}_{\mathit{ij}}{\mathit{u}}_i)},\hfill \\ \hfill p(y_{\mathit{ij}}=0\mid {\mathit{u}}_i)& =\frac{1}{1+\exp ({{\mathit{x}}^{\prime }}_{\mathit{ij}}\beta +{{\mathit{z}}^{\prime }}_{\mathit{ij}}{\mathit{u}}_i)}.\hfill \end{array}$$ (1)

The observations within a cluster i are assumed to be independent given the random effects u_i. As a result, the conditional probability of the response vector y_i = (y_i1, y_i2, … , y_ini)^T is

$$g({\mathit{y}}_i\mid {\mathit{u}}_i;\beta )=\prod _{j=1}^{n_i}p{(y_{\mathit{ij}}=1\mid {\mathit{u}}_{\mathit{i}})}^{y_{\mathit{ij}}}p{(y_{\mathit{ij}}=0\mid {\mathit{u}}_i)}^{1-y_{\mathit{ij}}}.$$ (2)

The marginal likelihood function of the i^th cluster is obtained by averaging over the distribution of u_i, that is,

$$L_i(\beta ,\theta )=\int g({\mathit{y}}_i\mid {\mathit{u}}_i;\beta )f({\mathit{u}}_i;\theta )d{\mathit{u}}_i,$$ (3)

where f(u_i; θ) is the probability distribution of u_i with a parameter vector θ. The vector u_i is typically assumed to have a multivariate normal with mean 0 and variance-covariance matrix Σ(θ). The full marginal likelihood function from all N clusters is $L={\prod }_{i=1}^N{L}_i(\beta ,\theta )$. To determine maximum likelihood estimates a numerical maximization procedure is applied, which requires partial derivatives of the log L. Starting from an initial value, a parameter estimate is iteratively updated by a function of partial derivatives until convergence. Therefore, equation (3) as well as the partial derivatives need to be evaluated numerically or approximated.

3. THE ESTIMATION METHODS

Several methods for evaluating Equation (3) have been developed. Investigators often use one of the three methods (PQL, Laplace approximation, and Gauss–Hermite numerical integration) because it is the default option of the package. However, the choice of method should be made according to the characteristics of data and the purpose of modeling. In this section we briefly describe those methods and summarize their advantages and disadvantages (Table 1). We assume f(u_i;θ) is a multivariate normal distribution, although other distributions can be used.

Table 1.

Summary of the advantages and disadvantages of estimation methods.

	Advantages	Disadvantages	Statistical packages	References
GQ†	Very accurate approximation to the integral when a large number of quadrature points (≥20) are used.a Results by other methods are often compared to those by GQ method. The deviance can be calculated; the model fit can be assessed.b	Using a small number of quadrature points (<10) might cause convergence to a local maximum.a As the number of quadrature points increases, the computation time increases rapidly and numerical integration becomes very demanding.a,b Accuracy decreases as the magnitude of correlation between random-effects increases and as the magnitude of a fixed-effect parameter increases.c	SuperMix SAS NLMIXED (method=GAUSS)	Lesaffre and Spiessens (2001) Hedeker and Gibbons(2006) Gozalez et al. (2006)
AGQ*	The quadrature points are optimally chosen to cover high density area of the function to be integrated.b Needs fewer quadrature points, so computationally faster than GQ.a The deviance can be calculated; the model fit can be assessed. b	• Still computationally intensive especially for models with >3 random effects that are correlated.	SuperMix SAS NLMIXED (method=GAUSS) SAS GLIMMIX (method=QUAD) R lme4 Stata xtmelogit	Lesaffre and Spiessens (2001) Hedeker and Gibbons(2006)
Laplace	Computationally more efficient than GQ and AGQ. a Produces more accurate estimates than the PQL.a,b The estimates by Laplace6 are at least as accurate as those by GQ with 20 quadrature points and AGQ with 7 quadrature points.a The deviance can be calculated; the model fit can be assessed.	Potentially less accurate approximation than GQ and AGQ because it is based on an expansion of log-likelihood around a single point (the mode).c The Laplace6 estimates have higher mean square errors than PQL estimates.b Tends to produce biased estimates for small sample sizes (small number of clusters or small cluster sizes).a,b,c,d The MSE increases for both of the fixed effects and the variances of random effects when the proportion of an event approaches zero.b	SAS GLIMMIX (method=Laplace) R package lme4(nAGQ=1) HLM6 Stata xtmelogit (Laplace)	Raudenbush et al. (2000) Diaz (2007) Clarkson et al. (2002) Joe (2008)
PQL§	Usually easily converged and computationally feasible. REML estimation for covariance matrix of random effects.c,d	Produces seriously biased estimates (downward bias) for both of the fixed effects and the variances of random effects when the random effect variance(s) is large (high ICC‡) and/or the proportion of an event is close to zero or 1.a,b,c The deviance unavailable; the model fit cannot be assessed.e	SAS GLIMMIX (method=RSPL) HLM6	Diaz (2007) Zhou, Perkins and Hui (1999) Breslow and Clayton (1993) Wolfinger (1993) Hedeker and Gibbons (2006)

^†GQ: Gauss-Hermite quadrature,

^*AGQ: Adaptive Gauss-Hermite quadrautre,

^§PQL: Penalized quasi-likelihood,

^‡ICC: Intra-class correlation.

3.1 Gauss–Hermite Quadrature

Gauss–Hermite quadrature, also called Gaussian quadrature (GQ), approximates the marginal likelihood function. GQ computes the integral by direct numerical evaluation. The area under the curve is calculated by summing over split areas. The accuracy of approximation depends on the number of these areas that are represented by quadrature points and corresponding weights. The equation (3) can be rewritten as

$$L_i(\beta ,\theta )=\int g({\mathit{y}}_i\mid {\mathit{v}}_i;\beta ,\Gamma )\varphi \left({\mathit{v}}_i\right)d{\mathit{v}}_i,$$

where u_i = Γv_i, ΓΓ’ = Σ(θ), and v_i has the standard normal density ϕ(v_i). Let b_q denote a vector of quadrature points having the same dimension as u_i and w(b_g) its related weight. The approximated marginal likelihood is

$$L_i(\beta ,\theta )\approx \sum _{q}g({\mathit{y}}_i\mid {\mathit{b}}_q;\beta ,\Gamma )w\left({\mathit{b}}_q\right).$$

The quadrature points are preset centered around zero. The precision of GQ increases as the number of quadrature points increases (Givens and Hoeting 2006). When the model includes multiple random effects, the number of quadrature points that GQ needs increases exponentially (Lessaffre and Spiessens 2001; Hedeker and Gibbons 2006). For instance, if a model has k random effects and GQ uses Q points per random effect, then a total of Q^k quadrature points are needed. Results estimated by other methods are often compared to GQ method because the computation is very accurate when Q is large. However, the exponential increase in the number of quadrature points with each additional random effect creates a problematic computational burden.

3.2 Adaptive Gauss–Hermite Quadrature

This technique is an adaptive version of GQ. While the GQ method uses preset quadrature points, AGQ adaptively finds the quadrature points centered at the approximate mode of g(y_i∣v_i;βΓ) ϕ(v_i) according to its shape (Lesaffre and Spiessens 2001; Hedeker and Gibbons 2006). This is especially efficient when the mode is far from 0. The associated weight is also adjusted accordingly. As a result, AGQ needs fewer quadrature points to obtain the same degree of precision as GQ reducing the computational burden.

3.3 Laplace Approximation

The Laplace method also approximates the marginal likelihood function. Unlike GQ, it is not a direct numerical integration. Equation (3) can be rewritten as

$$L_i(\beta ,\theta )={\left(2\pi \right)}^{-k∕2}{\mid \Sigma \mid }^{-1∕2}\int \exp \left\{h\right({\mathit{u}}_i\left)\right\}d{\mathit{u}}_i,$$ (4)

where h(u_i) = lon g(y_i∣u_i;β) − (u_i^T Σ⁻¹u_i)/2 First, this method expands h(u_i) around the mode ${\tilde{\mathit{u}}}_i$ by using a Taylor series expansion and then evaluates the integral by Laplace’s method (Khuri 2003, p. 531). The accuracy of Laplace approximation depends on how far the objective function is expanded. Usually a second-order Taylor series expansion is applied:

$$\exp \left\{h\right({\mathit{u}}_i\left)\right\}=\exp \left[h\left({\tilde{\mathit{u}}}_i\right)+\frac{1}{2}{({\mathit{u}}_i-{\tilde{\mathit{u}}}_i)}^T\frac{{\partial }^{2}h}{\partial {\mathit{u}}_i\partial {\mathit{u}}_i^T}({\mathit{u}}_i-{\tilde{\mathit{u}}}_i)+R_i\right]$$

and the remainder R_i is ignored because the magnitude of higher-order terms diminishes as the cluster size increases. Thus, its accuracy depends on the sample size. Raudenbush et al. (2000) improved the precision of the Laplace approximation by further approximating exp(R_i) using up to sixth-order terms, and called it Laplace 6. They showed via a simulation study that the estimates obtained by Laplace 6 were as accurate as those obtained by GQ and AGQ. The advantage of the Laplace method is that it approximately integrates the objective function expanded at the mode, ${\tilde{\mathit{u}}}_i$, leading to asymptotically unbiased estimates, and yet it is computationally less intensive than GQ and AGQ. The disadvantage is that it tends to provide less accurate estimates for data with small cluster sizes.

3.4 Penalized Quasi-Likelihood

This method approximates the marginal quasi-likelihood function rather than the full log-likelihood function. The quasi-likelihood function (McCullagh and Nelder 1989) replaces log g(y_i∣u_i;β) in Equation (4) Denote h(u_i) = Q(μ_i;y_i) − u_i^T Σ⁻¹u_i/2 where μi is a conditional mean of y_i given u_i. However, for logistic regression the quasi-likelihood function has the same expression as the log-likelihood function, i.e., log g(y_i∣u_i;β) = Q(μ_i;y_i). h(u_i) is expanded about the mode ${\tilde{\mathit{u}}}_i$ by a second-order Taylor series and then the integral is evaluated by Laplace’s method. The PQL is different from the Laplace approximation because it proceeds in the following two alternating steps until convergence. The first step is to estimate (u_i,β) by maximizing h(u_i) for fixed Σ. The second step is to estimate Σ by constructing an approximate profile quasi-likelihood based on updated estimates of (u_i,β) by maximizing h(u_i) for fixed Σ. The second step is to estimate Σ by constructing an approximate profile quasi-likelihood based on updated estimates of (ui, β) and applying estimating equations for a normal linear mixed model. Pinheiro and Bates (1995) called the first step a penalized nonlinear least squares step and the second a linear mixed effects step. The REML version of the profile likelihood is available too. More technical details and variations can be found in Breslow and Clayton (1993), Pinheiro and Bates (1995), and Wolfinger (1993). PQL is generally considered computationally more feasible than the aforementioned methods; however, it produces biased estimates in certain circumstances (Table 1).

4. SIMULATION I

We considered two scenarios to simulate the data—two-level and three-level logistic regression models. For each scenario 100 independent datasets were simulated with different seed numbers using R. We estimated model parameters for each replicate using SAS GLIMMIX, R lme4, HLM, SuperMix, and Stata xtmelogit. The estimation methods used within each package are (i) SAS: PQL, Laplace, AGQ with 10 quadrature points (AGQ-10); (ii) R: Laplace and AGQ-10; (iii) HLM: PQL (REML version) and Laplace 6; (iv) SuperMix: AGQ-10; (v) Stata: Laplace and AGQ-10. Laplace 6 is only available with HLM 6.

We used the following maximization algorithms: Newton–Raphson in SAS GLIMMIX, SuperMix (with step-halving), and Stata (with step-halving); EM for two-level models and Fisher-scoring for three-level models in HLM; and Gauss–Newton in R lme4. Only SAS GLIMMIX provides various options for maximization, such as quasi-Newton, Newton–Raphson with ridging, trust-region, and so on (SAS Institute Inc. 2008b). The maximum number of iterations was set to 1,000 when possible. The initial values were determined by fitting the fixed-effects logistic regression in SAS GLIMMIX and R lme4 and by maximizing the posterior density with respect to random effects in SuperMix (Bock and Du Toit, 2004). For HLM Laplace method, PQL estimates were used as the initial values. R lme4 and SuperMix also allow users to explicitly assign starting values.

We calculated the average of the parameter estimates, standardized bias, and root mean square error (RMSE) over 100 replications to assess accuracy and precision of estimates. The quantities to evaluate average performance were defined as the following (Burton et al. 2006):

$$\begin{array}{cc}\hfill \text{Average}& =\Sigma {\widehat{\phi }}_i∕m=\overline{\widehat{\phi }}\hfill \\ \hfill \text{Standardized bias}& =(\overline{\widehat{\phi }}-\phi ){\left\{\frac{\Sigma {\left({\widehat{\phi }}_i-\overline{\widehat{\phi }}\right)}^2}{m-1}\right\}}^{-1∕2}\hfill \\ \hfill \mathrm{RMSE}& ={\left\{{\left(\overline{\widehat{\phi }}-\phi \right)}^2+\frac{\Sigma {\left({\widehat{\phi }}_i-\overline{\widehat{\phi }}\right)}^2}{m-1}\right\}}^{1∕2}\hfill \end{array}$$ (5)

where m is the number of replicated datasets, φ is the true value for the parameter of interest, and ${\widehat{\phi }}_i$ is an estimate obtained by fitting a model to the i^th replicated data. The standardized bias ranges from −1 to 1.

4.1 Two-Level Data Simulation

The assumed model equation for the j^th dichotomous outcome nested in the i^th cluster is

$$\log \frac{P(y_{\mathit{ij}}=1)}{P(y_{\mathit{ij}}=0)}=({\beta }_0+u_{0i})+({\beta }_1+u_{1i})x_{1\mathit{ij}}+({\beta }_2+u_{2i})x_{2\mathit{ij}}+{\beta }_3{x}_{3i},$$

where (β₀, β₁, β₂, β₃)^T = (−1.2, 1.0, 1.0, −0.5)^T and $\left(\begin{array}{c}\hfill u_{0i}\hfill \\ \hfill u_{1i}\hfill \\ \hfill u_{2i}\hfill \end{array}\right)\sim \mathit{MVN}\left(\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right],\left[\begin{array}{ccc}\hfill 3.0\hfill & \hfill -0.69\hfill & \hfill 0.23\hfill \\ \hfill -0.69\hfill & \hfill 1.0\hfill & \hfill 0.00045\hfill \\ \hfill 0.23\hfill & \hfill 0.00045\hfill & \hfill 0.2\hfill \end{array}\right]\right)$ for all i. The vector u_i has a multivariate normal distribution (MVN). This is a typical assumption for random effects, and the statistical packages considered in our study were developed based on this assumption. The variance of the random intercept was set to 3. Such a large variance has been reported to cause problematic computation, and specifically PQL tends to underestimate a large variance (Table 1). Moderate and small variances were assumed for two random slopes. The variance-covariance matrix of the random effects determines the following correlation matrix,

$$\left[\begin{array}{ccc}\hfill 1\hfill & \hfill -0.4\hfill & \hfill 0.3\hfill \\ \hfill -0.4\hfill & \hfill 1\hfill & \hfill 0.001\hfill \\ \hfill 0.3\hfill & \hfill 0.001\hfill & \hfill 1\hfill \end{array}\right].$$

This correlation matrix was intended to include both negative and positive correlations, and small to moderate strength of correlation. x_1ij and x_2ij are individual-level covariates distributed as N(0,4) and N(0,1), respectively. x_3i is a cluster-level covariate with half of clusters in each group. The three covariates were generated independently. The linear predictor value on the right side of the equation was converted to a probability, which was used to simulate a binary outcome using the algorithm developed by Kachitvichyanukul and Schmeiser (1988). β₀ = −1.2 is related to the response probability of 0.23, given x₁ = x₂ = x₃ = 0 and u₀ = u₁ = u₂ = u₃ = 0. The marginal probability y = 1 was about 0.30. Each simulated dataset had 100 observations in each of 50 clusters, so a total of 5,000 observations (i=1, …, 50; j=1, …, 100). This sample size was according to the recommendation of Moineddin et al. (2007).

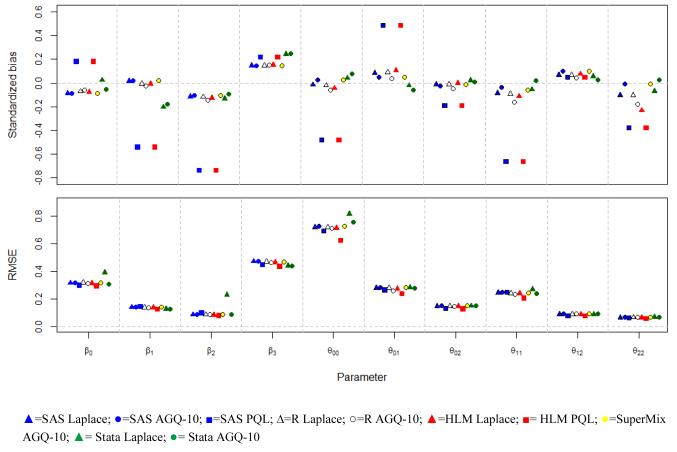
Simulation results are presented in Table 2 and Figure 1. A numerical overflow occurred for 20 models with Stata xtmelogit; the quantities in (5) were computed based on 80 converged models. The PQL estimates of SAS and HLM are biased towards zero for both β and Σ, except for the tiny variance (θ₁₂ =0.00045). Figure 1 displays the standardized biases and RMSEs for each parameter. The software is marked by different colors; triangles exhibit Laplace, circles AGQ, and squares PQL. The PQL estimates from both SAS and HLM tend to have a larger standardized bias than other estimates. This result is consistent with the previous research studies (Table 1). The intercept variance (θ₀₀) has higher RMSE than other parameters for all estimation methods and packages. In summary, the estimates from the Laplace and AGQ are better than the PQL estimates across the five statistical packages on the basis of criteria (5).

Table 2.

Simulation results for the two-level logistic model:the average of parameter estimates (RMSE).

Software	SAS GLIMMIX			R lme4		HLM		SuperMix	Stata xtmelogit
Estimation	PQL	Laplace	AGQ-10	Laplace	AGQ-10	PQL	Laplace6	AGQ-10	Laplace	AGQ-10
True Values	Regression Coefficients
β0= −1.2	−1.146 (0.301)	−1.227 (0.318)	−1.228 (0.318)	−1.223 (0.319)	−1.219 (0.315)	−1.146 (0.296)	−1.223 (0.315)	−1.228 (0.317)	−1.190 (0.394)	−1.217 (0.307)
β1= 1.0	0.930 (0.147)	1.002 (0.141)	1.003 (0.141)	0.999 (0.140)	0.996 (0.139)	0.930 (0.129)	0.999 (0.140)	1.003 (0.141)	0.973 (0.131)	0.977 (0.130)
β2= 1.0	0.940 (0.102)	0.990 (0.088)	0.991 (0.088)	0.999 (0.088)	0.988 (0.088)	0.940 (0.082)	0.989 (0.087)	0.991 (0.087)	0.969 (0.230)	0.992 (0.089)
β3= −0.5	−0.403 (0.449)	−0.431 (0.474)	−0.431 (0.473)	−0.430 (0.473)	−0.429 (0.467)	−0.403 (0.438)	−0.428 (0.465)	−0.431 (0.468)	−0.391 (0.442)	−0.390 (0.440)
Variance-Covariance Matrix of Random Effects
θ00= 3.0	2.698 (0.694)	2.990 (0.721)	3.018 (0.729)	2.986 (0.722)	2.959 (0.713)	2.698 (0.625)	2.969 (0.715)	3.018 (0.728)	3.032 (0.820)	3.061 (0.760)
θ01= −0.69	−0.573 (0.267)	−0.666 (0.280)	−0.677 (0.282)	−0.664 (0.280)	−0.680 (0.259)	−0.573 (0.240)	−0.660 (0.275)	−0.677 (0.282)	−0.696 (0.285)	−0.707 (0.279)
θ02= 0.23	0.205 (0.134)	0.228 (0.150)	0.226 (0.151)	0.228 (0.150)	0.223 (0.149)	0.205 (0.131)	0.230 (0.149)	0.227 (0.151)	0.233 (0.151)	0.232 (0.151)
θ11= 1.00	0.861 (0.250)	0.979 (0.245)	0.991 (0.247)	0.978 (0.243)	0.962 (0.235)	0.861 (0.208)	0.973 (0.243)	0.991 (0.247)	0.986 (0.270)	1.005 (0.240)
θ12= 0.00045	0.00423 (0.07955)	0.00681 (0.09136)	0.00949 (0.09265)	0.00671 (0.09119)	0.00460 (0.09248)	0.00423 (0.07946)	0.00755 (0.09133)	0.00947 (0.09221)	0.00575 (0.09028)	0.00842 (0.09197)
θ22=0.2	0.177 (0.064)	0.193 (0.067)	0.199 (0.068)	0.193 (0.068)	0.188 (0.067)	0.177 (0.060)	0.185 (0.067)	0.199 (0.068)	0.195 (0.070)	0.202 (0.069)

Figure 1.

Simulation results for the two-level logistic model: the standardized biases and RMSEs.

4.2 Three-Level Data Simulation

The assumed level-1 model equation for the k^th observation nested in the j^th subcluster within the i^th cluster is

$$\log \frac{P(y_{\mathit{ijk}}=1)}{P(y_{\mathit{ijk}}=0)}=({\beta }_0+u_{0i}+{\gamma }_{\mathit{ij}})+({\beta }_1+u_{1i})x_{1\mathit{ij}}+({\beta }_2+u_{2i})x_{2\mathit{ij}}+{\beta }_3{x}_{3\mathit{ijk}},$$

where (β₀, β₁, β₂, β₃)^T = (−1.2, 1.0, 1.0, −0.5)^T, $\left(\begin{array}{c}\hfill u_{0i}\hfill \\ \hfill u_{1i}\hfill \\ \hfill u_{2i}\hfill \end{array}\right)\sim \mathit{MVN}\left(\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right],\left[\begin{array}{ccc}0.5\hfill & \hfill 0.28\hfill & \hfill 0\hfill \\ 0.28\hfill & \hfill 1.0\hfill & \hfill 0.31\hfill \\ 0\hfill & \hfill 0.31\hfill & \hfill 0.6\hfill \end{array}\right]\right)$ and y_ij ~N(0, Γ = 0.8) for all i and j. We denote the “level-1” units k, the “level-2” subclusters j, and the “level-3” clusters i. The correlation coefficients are 0.4 between u_0i and u_1i, and 0 between u_0i and u_2i. The covariates x_1ij and x_2ij vary with clusters and subclusters and were simulated from N(0,4) and N(0,1) respectively. The dichotomous variable x_3ijkl forms that half of the level-1 units within a subcluster is in each group. The variance of y_ij represents variability across the subclusters within each cluster, and it is constant across all clusters. The marginal probability of the response is about 0.30. Each simulated dataset has a total of 15,000 level-1 units (i=1, …, 30; j=1, …,10; and k=1, …, 50).

The selected packages have the following limitations in fitting a three-level logistic regression model: (a) R lme4 does not provide AGQ, (b) PQL-REML version of HLM is only available for a two-level logistic model, and (c) HLM executes Fisher-scoring for maximization, although an EM algorithm has been implemented for fitting a two-level logistic model (HLM6, SSI 2004). We experienced substantially more computational burden with the three-level models than the two-level models. SAS GLIMMIX AGQ could not estimate model parameters for all 100 replications due to “insufficient resources to perform AGQ,” and Stata xtmelogit gave a message “numerical overflow” for 95 replications. SuperMix AGQ had one nonconvergence within 1,000 maximum iterations. With HLM Laplace 6, 67 models did not converge or produce parameter estimates; therefore, only 33 converged models were used to evaluate simulation results. HLM PQL had 10 nonconvergences and produced fitted models for 90 datasets. We had 38 “false convergence” messages with R lme4 Laplace, but it produced fitted models for all datasets.

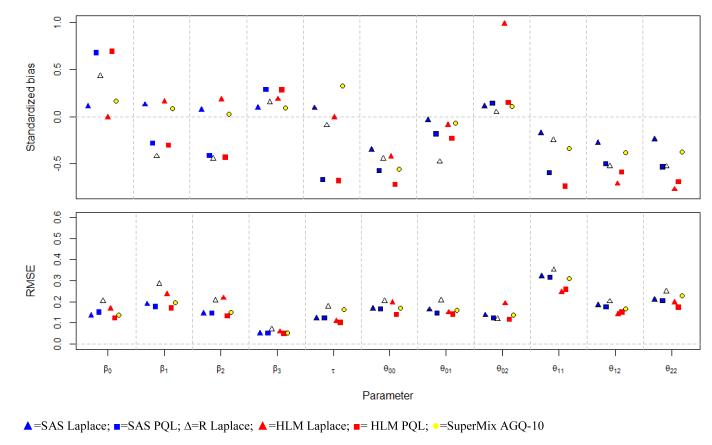
Table 3 and Figure 2 show the simulation results for the three-level logistic models. The summary results were not calculated for SAS GLIMMIX AGQ, R lme4 AGQ, and Stata. Overall, Laplace of SAS GLIMMIX and AGQ-10 of SuperMix produced better estimates than the others on the basis of the criteria (5). PQL, marked by squares in Figure 2, tends to shrink estimates toward zero as in the simulation for the two-level models. The Laplace of R lme4 also tends to result in biased regression coefficients with slightly higher RMSEs. For the zero covariance component (θ₀₂ = 0), HLM Laplace 6 produced seriously biased estimates.

Table 3.

Simulation results for the three-level logistic model:the average of parameter estimates (RMSE).

Software	SAS GLIMMIX			R lme4		HLM 6		SuperMix	Stata xtmelogit
Estimation	PQL	Laplace	AGQ-10†	Laplace‡	AGQ-10╤	PQL§	Laplace6§§	AGQ-10*	Laplace†	AGQ-10†
True Values	Regression Coefficients
β0=−1.2	−1.115 (0.151)	−1.185 (0.134)		−1.118 (0.204)		−1.113 (0.125)	−1.201 (0.167)	−1.177 (0.136)
β1=1.0	0.952 (0.178)	1.025 (0.189)		0.890 (0.284)		0.948 (0.172)	1.039 (0.235)	1.018 (0.196)
β2=1.0	0.944 (0.146)	1.011 (0.146)	N/A	0.917 (0.206)	N/A	0.942 (0.135)	1.041 (0.218)	1.005 (0.150)	N/A	N/A
β3= −0.5	−0.485 (0.053)	−0.495 (0.052)		−0.489 (0.070)		−0.485 (0.050)	−0.489 (0.058)	−0.495 (0.051)
Variance-Covariance Matrix of Random Effects
τ=0.8	0.730 (0.125)	0.811 (0.122)		0.784 (0.177)		0.734 (0.102)	0.799 (0.110)	0.854 (0.163)
θ00=0.5	0.418 (0.166)	0.444 (0.167)		0.417 (0.204)		0.399 (0.140)	0.416 (0.197)	0.406 (0.169)
θ01=0.28	0.254 (0.148)	0.275 (0.163)	N/A	0.191 (0.206)	N/A	0.248 (0.142)	0.267 (0.150)	0.269 (0.160)	N/A	N/A
θ02=0	0.018 (0.124)	0.015 (0.137)		0.006 (0.118)		0.018 (0.119)	0.208 (0.192)	0.015 (0.138)
θ11=1.00	0.838 (0.316)	0.945 (0.321)		0.916 (0.352)		0.809 (0.259)	0.655 (0.246)	0.895 (0.309)
θ12=0.31	0.231 (0.176)	0.261 (0.185)		0.215 (0.202)		0.221 (0.151)	0.208 (0.142)	0.246 (0.168)
θ22=0.6	0.503 (0.206)	0.552 (0.210)		0.483 (0.250)		0.479 (0.174)	0.446 (0.197)	0.515 (0.227)

^†Unable to compute for 95 to 100 datasets;

^╤Not currently available;

^‡Had 38 false convergence warning messages;

^§Had 10 nonconvergences within the preset maximum number of iterations;

^§§Failed to compute or proceed to next iterations for 67 datasets.

^*Had 1 nonconvergence within the preset maximum number of iterations.

Figure 2.

Simulation results for the three-level logistic model: the standardized biases and RMSEs.

5. ILLUSTRATION

We now return to fitting the two-level logistic regression model for the smoking status and antismoking advertising data. Our simulation, presented in Section 4, provided evidence that SAS GLIMMIX Laplace and SuperMix AGQ perform the best among the packages and estimation methods considered. Therefore, we fit our model using SAS GLIMMIX Laplace and SuperMix AGQ-10 (in this and next sections, we call them SAS and SuperMix for short). The datasets were prepared so that the parameter estimates were comparable between the two packages. The intercepts and slopes for the state ad and Legacy ad exposures were allowed to randomly vary by media markets. Treating the effect of exposure to the Legacy ads as random, controlling for the random effect of exposure to the state ads, did not improve the model fit (likelihood ratio test χ²=3.7 from SAS; χ²=0.02 from SuperMix; df=3); therefore, the effect of Legacy ads was included as a constant across media markets. SAS Laplace converged in 5 iterations and SuperMix AGQ-10 converged in 38 iterations. We expected trivial differences in estimates between SAS and SuperMix because of different starting values (the default starting values were used) and other computational and operational settings that cannot be controlled by users.

The two packages, however, produced remarkably different estimates that led to different qualitative conclusions for some parameters. The fixed-effect of state ad exposure on the log odds of smoking was estimated as −0.013 (SE=0.014) from SAS, whereas the corresponding estimate from SuperMix was 0.053 (SE=0.064). The slopes were in opposite directions, although both estimates were not significantly different from zero. The effect of Legacy ad exposure was estimated as −0.034 (SE=0.014, p=0.013) from SAS, whereas the corresponding estimate from SuperMix was −0.176 (SE=0.096, p=0.066). The variance estimates of random intercepts were 0.011 (SE=0.002) from SAS and 0.003 (SE=0.001) from SuperMix, although the variance estimates of the random slopes were close between the two packages. Another interesting result was that the computed −2 times the log-likelihood values (−2LL) were quite different: SAS=361,633 versus SuperMix=100,496. These different values of −2LL were observed even in a simpler model that had only intercepts randomly vary across media markets.

We suspected that this different result between SAS and SuperMix might be related to the huge sample size of the data (N=391,389), ranging from a few hundred to several thousand per media market. When the likelihood function is formed for a given cluster as in Equation (2), the product of individual likelihood values becomes extremely close to zero when n_i is very large and the probability of an event is close to zero or one. Statistical packages are not identically programmed in handling “positive tiny numbers” and “negative huge numbers”. To investigate whether the observed difference between SuperMix and SAS is due to the huge sample size, we conducted a small simulation study, which we discuss in the next section.

6. SIMULATION II

We generated data that resembled our smoking and TV advertising data. The assumed model equation for a respondent j nested in media market i is given by

$$\log \frac{P(y_{\mathit{ij}}=1)}{P(y_{\mathit{ij}}=0)}={\beta }_0+u_{0i}+{\beta }_1{x}_{1\mathit{ij}}+{\beta }_2{x}_{2\mathit{ij}}+{\beta }_3{x}_{3\mathit{ij}},$$

where (β₀, β₁, β₂, β₃)^T = (−2, −0.03, −0.002, 0.278)^T, u_0i, is normally distributed with mean 0 and variance, θ₀ = −0.002, and x₁, x₂ and x₃ correspond to the time of survey dates, the state-sponsored ad exposure, and gender, respectively. The variable x₁ has values of (0, 0.67, 1, 2, 2.5, 2.75, 4, 4.5, 7, 7.25) within each media market. The variable x₂ has a mixture distribution; random variables having exponential distribution with a rate parameter 0.2 were generated, and then among those, 0 was assigned to randomly selected values with the probability 0.25. This distribution was intended to reflect the right-skewed distribution with inflated probability at zero for GRP values. x₃ is an individual-level dichotomous variable with the probability 0.45. Each dataset has 70 clusters with varied sizes from 50 to 7000. The total number of observations is 139,300, which is smaller than the sample size of our smoking and TV advertising data. The simulation involved 20 replications, and we computed averages and RMSEs of the estimates. We also computed the mean of −2LL values, which was obtained from the fitted models, to compare their average model-fit. The mean values of −2LL from fitted fixed-effects models (i.e., u_0i = 0 for all i) were 104,097 and 104,101 for SAS and SuperMix, respectively, and the maximum absolute difference in −2LL values was 0.005.

The simulation results are presented in Table 4. The mean values of −2LL are quite different between two packages; the mean −2LL from SAS is more plausible, considering the mean −2LL values of the fixed-effects models. The parameter estimates of both packages appear to be unbiased, but the RMSEs of SuperMix estimates are larger than those of SAS. The initial value is the main difference between SAS and SuperMix in this simulation, as well as the integration methods. For SAS, the estimates obtained by fitting a fixed-effects model with a limited number of iterations (at most four iterations according to the SAS User’s Guide) are used as the default starting values. The starting values in SuperMix are maximum a posteriori (MAP) estimates, but they can also be completely assigned by users. Accordingly, to eliminate any differences attributable to starting values, we also set the SAS GLIMMIX Laplace estimates and the true values as the initial values for SuperMix. However, SuperMix provided the same parameter estimates and −2LL values for all 20 data sets resulting in the identical numbers in Table 4. This suggests that the starting values were not responsible for the different log-likelihood values. This simulation result indicates that SAS computes the log-likelihood better than SuperMix does in fitting logistic mixed models to the data with very large clusters. We elaborate further about SAS and SuperMix in connection with the sample size in Section 7.

Table 4.

Simulation results for the random-intercept logistic model:The average of parameter estimates (RMSE).

Parameter	SAS GLIMMIX Laplace	SuperMix AGQ-15
β0=−2.00	−1.9950 (0.0262)	−2.0143 (0.0324)
β1=−0.03	−0.0302 (0.0035)	−0.0307 (0.0072)
β2=-0.002	−0.0018 (0.0018)	−0.0024 (0.0041)
β3= 0.278	0.2790 (0.0122)	0.2924 (0.0300)
θ00= 0.027	0.0275 (0.0050)	0.0272 (0.0102)
−2LL	103,805.38 (1278.76)§	71,636.92 (418.28)§

^§Empirical standard deviations

7. DISCUSSION

In this article we conducted simulation studies to compare the maximum likelihood estimation methods available in several statistical packages in order to find a reliable estimation method and statistical package for fitting a logistic regression with multiple correlated random effects. The number of replications was 100, and the proportion of events was close to 0.30. The PQL estimates were noticeably biased in the simulation of both two- and three-level logistic regression models. This is because PQL estimates tend to be biased towards zero when (a) the proportion of events is close to zero or one, or (b) the variances of random effects are large, or both. This was reported in other studies as well (Breslow and Clayton 1993; Zhou et al. 1999; Diaz 2007). In our simulation study for the three-level logistic model, which clearly demonstrated differences between estimation methods and statistical packages, SAS GLIMMIX Laplace and SuperMix AGQ performed better than other packages and estimation methods considering the criteria in (5) and the convergence rate. The estimates obtained by HLM Laplace 6 and R lme4 Laplace had larger RMSEs than others; the same pattern was observed when we restricted computation of RMSE to only the 33 fitted models in which the algorithm of HLM Laplace 6 had converged.

There are limitations in our simulation study. First, we did not consider correlation between covariates. In most situations one covariate is correlated with another to some degree. Although assuming correlation among covariates may be more realistic, we believe that our main findings are still valuable. Second, there are other statistical packages that have the ability to estimate the GLMM—SPSS, SAS NLMIXED, etc. We chose SAS GLIMMIX and SuperMix because they were recently released, and thus up-to-date developments were likely to have been incorporated in those packages. Furthermore, there is no published research article to date that evaluated their performance. SAS NLMIXED was widely used to estimate GLMM until SAS Institute Inc. released the GLIMMIX procedure, but its exceedingly slow convergence has been a major drawback. We did not examine it in our simulation study because one of our purposes was to find a statistical package with endurable convergence speed for fitting a large dataset. We would like to comment that SAS NLMIXED is still an excellent procedure in estimating nonstandard mixed models. In late 2010, SPSS released version 19 with a new tool for GLMM and HLM released version 7 that offers AGQ. Since SPSS and HLM are widely used in the social and educational sciences, it would be worthwhile to explore their performance via simulation. Nonetheless, our study provides the most comprehensive assessment to date of statistical packages and estimation methods in fitting logistic mixed-effects models. Third, we simulated data assuming multivariate normal random effects primarily because the algorithms implemented in the statistical packages considered in this article were developed based on that assumption. Although the normal random effects assumption is reasonable in many situations, it would be interesting to see how well these packages and estimation methods perform when that assumption is moderately to seriously violated, especially in making an inference. When the normality assumption is not reasonable, Bayesian models are particularly useful. We leave this for our future research.

We observed substantial computational burden in estimating the three-level logistic models. The integration over the multivariate random effects distribution is a difficult numerical problem in association with the optimization of a likelihood function. HLM Laplace 6 failed to produce parameter estimates for 67 datasets out of 100. The error message was “Fisher scoring is unable to compute a maximum likelihood estimate within the parameter space.” In HLM, Fisher scoring is employed to estimate a three-level logistic model, but an EM algorithm is used for a two-level logistic model. The EM algorithm converges to an estimate within the parameter space, but its convergence speed can be very slow (Raudenbush and Bryk 2002; West et al. 2006). Fisher scoring, on the other hand, quickly converges in most situations, but it may produce estimates outside the parameter space such as a nonpositive definite variance-covariance matrix of random effects. A Cholesky decomposition of the variance-covariance matrix sometimes helps, but not all software provides this alternative (as SAS GLIMMIX does). Some algorithms are numerically more stable or feasible than others depending on the characteristics of data and complexity of models. For instance, for fitting more complex mixed-effects models to our smoking and advertisement data, Newton–Raphson often failed to compute a positive definite variance-covariance matrix, whereas quasi-Newton was able to compute it. An algorithm that requires the second-order partial derivatives, like Newton–Raphson, tends to be more reliable yet computationally more demanding than an algorithm that requires only the first-order partial derivatives, like quasi-Newton. West et al. (2006) discussed different algorithms for the likelihood function optimization for linear mixed models. Further studies are necessary to find reliable and efficient maximization techniques for GLMM estimation that involve multidimensional integrals.

In the simulation for the three-level models using SAS GLIMMIX, AGQ-10 failed to perform the computation from the first iteration for all 100 datasets because of “insufficient resources”, yet Laplace produced reliable results. This confirms that AGQ is computationally intensive. Estimation with more quadrature points appears to require more memory in SAS because reducing the number of quadrature points for AGQ sometimes solve this problem. In addition, AGQ is time-intensive at every iteration. However, we experienced a 99% convergence rate and fast computing time with SuperMix AGQ; specifically, 40% of the models fit to the simulated data converged in less than 10 iterations and in 15 CPU minutes. The MAP estimation is integrated in SuperMix to find initial parameter estimates. This unique feature helps reduce the required number of iterations by providing good candidates for parameter estimates.

SuperMix should be used carefully when the sample size is huge, particularly the cluster size, as demonstrated in Section 6. How does the large cluster size start affecting the computation of log-likelihood function? We made a few sets of data by randomly sampling varying numbers of respondents from our smoking and TV advertising data and fit the logistic mixed-effects model. When we fit the model to randomly sampled data with 30,000 or more respondents, the evaluated values of log-likelihood functions were quite different between SAS GLIMMIX Laplace and SuperMix AGQ. In another dataset with 25,000 respondents, there were four clusters with 1,000 to 1,500 respondents and one cluster with more than 1,500 respondents; the difference between two −2LL values was about 200. In a dataset with 20,000 respondents, all cluster sizes were below 1,500; −2LL values were virtually identical, and parameter estimates and their standard errors were fairly close between the two packages. This provides evidence that the difference between the two packages observed in Sections 5 and 6 were not due to different programming of the likelihood function. A small difference in the log-likelihood function can result in a significant difference in parameter estimates (Lesaffre and Spiessens 2001). We do not recommend using SuperMix when fitting a logistic mixed-effects model to a large dataset especially when the number of subjects nested in clusters is larger than 2,000.

Finally, the accuracy of Laplace approximation depends on sample sizes, the number of clusters and the number of subjects per cluster, due to its asymptotic properties (Table 1; Clarkson et al. 2002; Diaz 2007). Therefore, we recommend using AGQ when analyzing data with a small sample size. For instance, AGQ is more suitable than Laplace approximation for a longitudinal study with a few time points. Clarkson and Zhan (2002) observed in their simulation study, which considered 100 subjects and 7 time points per subject, that Laplace estimates were biased. The first and second derivatives of the likelihood function involved in maximization are often not a smooth function of random effects (Lesaffre and Spiessens 2001). AGQ calculates the first and second partial derivatives more precisely than Laplace does, provided that a sufficient number of quadrature points are used. This is because Laplace is an approximation that expands the objective function around one point, whereas AGQ uses multiple points (Clarkson and Zhan 2002). The difference between Laplace and AGQ estimates, however, decreases as the sample size increases. In addition, with respect to computing time, Laplace approximation is far superior to AGQ when the sample size is very large.

APPENDIX.

Table A.1.

Descriptive statistics of 2000-2007 TUS-CPS and Nielsen ratings data (N=391,389)

Smoking Status	N (%)
Current smokers	79040 (20.2)
Non-smokers	312349 (79.8)
Antismoking TV advertising1	Mean (Median, Min-Max)
State (/1000)	0.42 (0.08, 0 – 4.65)
Legacy (/1000)	0.37 (0.31, 0 – 1.80)
Other Predictors	Mean (SD)
Cigarette price/pack($)2	1.98 (0.31)
SFA3 score with preemption	11.82 (10.18)
Age (in year)	41.45 (14.50)
Race/ethnicity	N (%)
White	278809 (71.2)
American Indian/Alaskan Native	2240 (0.6)
Asian/Pacific Islander/Hawaiian	17403 (4.4)
Hispanic	46075 (11.8)
Black	44724 (11.4)
Others	2138 (0.5)
Education
Less than 12th grade	62231 (15.9)
High school Grad/GED	110557 (28.3)
Some college/Associate's	106211 (27.1)
Bachelor/Master/Prof/Doctor	112390 (28.7)
Gender
Male	170191 (43.5)
Female	221198 (56.5)
Marital status
Married	213485 (54.5)
Widow/Divorced/Separated	69277 (17.7)
Never Married	108627 (27.8)
Employment/work area
Full-time/indoor	187773 (48.0)
Part-time/indoor	48274 (12.3)
Part & full-time/home	5749 (1.5)
Part & full-time/outdoor	23719 (6.1)
Not in labor force	109508 (28.0)
unemployed	16366 (4.2)
Region
South	122225 (31.2)
Midwest	91029 (23.3)
Northeast	85737 (21.9)
West	92398 (23.6)

¹10 exposures for four months prior to the date of TUS-CPS

²The average real price per pack of cigarettes calculated using information from The Tax Burden on Tobacco and the US Bureau of Labor Statistics Consumer Price Index.

³Smoke-free air index