Towards dynamical network biomarkers in neuromodulation of episodic migraine

Abstract

Computational methods have complemented experimental and clinical neurosciences and led to improvements in our understanding of the nervous systems in health and disease. In parallel, neuromodulation in form of electric and magnetic stimulation is gaining increasing acceptance in chronic and intractable diseases. In this paper, we firstly explore the relevant state of the art in fusion of both developments towards translational computational neuroscience. Then, we propose a strategy to employ the new theoretical concept of dynamical network biomarkers (DNB) in episodic manifestations of chronic disorders. In particular, as a first example, we introduce the use of computational models in migraine and illustrate on the basis of this example the potential of DNB as early-warning signals for neuromodulation in episodic migraine.

1. From bifurcation to bench and bedside

The mathematical theory of bifurcations is part of dynamical systems theory, which can straightforwardly be applied to neurological and psychiatric diseases with episodic manifestations. The term ‘bifurcation’ in this context refers to abrupt changes of brain dynamics when some physiological parameter values are smoothly changed and, at a critical point—the bifurcation point—the qualitative structure of the dynamical behavior changes towards new pathological dynamics. When physiological control is lost in such a scenario, the pathological process is called a dynamical disease [1]. Epilepsy is the best studied neurological dynamical disease where the theoretical concepts of bifurcation theory have been translated to animal models (bench) and clinical studies (bedside) [2].

The theory of such bifurcations, or ‘tipping points’ [3], complements experimental and clinical neurosciences with mathematical analysis and simulations to interpret data and guide a principle understanding of the nervous systems in health and disease. One particular interest is in defining dynamical network biomarkers (DNB) as early-warning signals based on an analytical understanding of the behavior at the imminent tipping point [4–7]. We will focus on this in this paper and firstly extend this concept to obtain a framework for a systematic evaluation of the subtle symptoms that often occur in the prodromal phase before the main episodic manifestations of chronic disorders. In a second step, we suggest using DNB beyond monitoring early-warning signals and explore ways in which DNB can lead to biofeedback signals in a control paradigm for episodic treatment.

One central aim in translational computational neuroscience is to fuse dynamical systems theory with control theory [8] and drive innovation in therapeutic brain stimulation in neurological and psychiatric diseases with theoretical concepts. At this stage, let us only name two further dynamical diseases other than epilepsy [2], first (i), Parkinson’s disease, which we do not further explore but see [9] and, second (ii), primary headaches, which we set the focus on in this paper. In these dynamical diseases, theoretical concepts are used (i) to illuminate the role of the coupling architecture and abnormal activity patterns in the subthalamopallidal network of the basal ganglia and with that knowledge to explain the mechanisms underlying the therapeutic efficacy of deep brain stimulation in Parkinson’s disease [10,11], and (ii) to understand the dynamics of pain as a process of central sensitization in the migraine generator network and define neuromodulation targets and stimulation protocols for episodic migraine treatment [12] that possibly can also be explored for neuromodulation in cluster headache [13], though we will focus mostly on migraines.

A brief note on the history is due. Despite the fact that the fields of translational computational neuroscience and neuromodulation are still in their relative infancy, let alone their fusion, they both actually have a long partly overlapping history. Neuromodulation for example in form of non-drug treatment in headache dates back to the mid-first century CE to Scribonius Largus, a physician who practiced at the court of the Roman Emperor Claudius and who recognized the seemingly beneficial effects of discharges from electrical fish in headache [14]. Not astonishingly, these primitive neuromodulation concepts gained much new interest in the 19th century, when Emil du Bois Reymond—himself a migraine sufferer—devised the first very precise instruments for measuring and monitoring electrical biosignals and his pupil Julius Bernstein developed the first membrane theory of electrical resting and action potentials in neurons. At the same time, driven by the industrial revolution James Clark Maxwell invented closed-loop feedback to control the speed of steam engines, which provides the first theoretical framework that later led to the field of cybernetics as the scientific study of “control and communication in the animal and the machine” [15]. The modern aspects of this field with some further notes on the history have been recently described in the textbook entitled “Neural control engineering: the emerging intersection between control theory and neuroscience” [16].

In the following, we first briefly introduce dynamical network biomarkers (Sec. 2) and then adapt the concept DNB to chronic disorders with episodic manifestations (Sec. 3) and highlight migraine as an example (Sec. 4). To this end, we introduce migraine theories (Sec. 5) and computational models of spreading depression (Sec. 6) on microscopic and macroscopic scale where the concept of DNB must be applied. We end with an overview of neuromodulation and concluding remarks (Sec. 7).

2. Dynamical network biomarkers

Traditional biomarkers are some objectively measured and evaluated indicators of a particular biological state that occurs in association with a pathological process. Usually static measurements of some traceable substances are called biomarkers. Also genetic biomarkers exist, defined as mutations or polymorphisms that predict some clinically relevant measure for example risk of disease, its outcome or response rate to treatment.

In contrast, a DNB is a dynamical feature of a biological network under consideration. Such features were originally suggested to be of particular interest in complex diseases with sudden deterioration phases or critical transition points during their progressions [4,5]. Depending on the progression level of such disorders three stages are distinguished: a normal state, a critical pre-disease state, and a disease state (Figure 1). The normal state is a steady state with functional homeostatic control, representing a (relatively) healthy stage yet maybe in an incubation period. The critical pre-disease state is still clinically silent and is considered as the state just before the first clinical onset. Mathematically, the critical pre-disease state is defined as the limit of the normal state immediately before a well-defined tipping point is reached. Finally, the disease state is with control failure but otherwise, in particular from a mathematical perspective, also simply a stable state.

Figure 1.

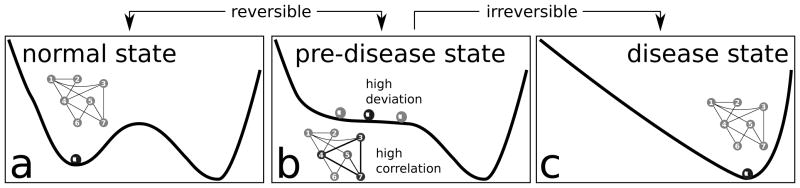
Schematic illustration of the dynamical features of disease progression from a normal state to a disease state through a pre-disease state (modified from [4]). (a) The normal state is a steady state or a minimum of a potential function, representing a relatively healthy stage. (b) The pre-disease state is situated immediately before the ‘tipping point’. At this stage, the system is sensitive to external stimuli and still reversible to the normal state when appropriately interfered with. A small change in the parameters of the system may suffice to drive the system into collapse, which often implies a large phase transition to the disease state. When the system approaches the pre-disease state, the deviations of the set of nodes (3, 4, 7) increase drastically, and the correlations (positively or negatively) among them also increase drastically whereas their correlations with other nodes (1, 2, 5, 6) decrease drastically. We call (3, 4, 7) the DNB. (c) The disease state is the other stable state or a minimum of the potential function, where the disease has seriously deteriorated and thus the system is usually irreversible to the normal state.

A DNB is essentially a group of traceable substances or, in general, signals that while highly fluctuating are strongly correlated only during the pre-disease stage. Therefore a DNB is different from the conventional biomarkers in two ways. First, it is not required for DNBs to keep consistent values for the respective disease and normal samples. Only the presence of highly fluctuating and strongly correlated signals is important. Second, the aim of DNB is to detect the pre-disease state, i.e., early-warning signals associated with the imminent tipping point, but not to distinguish the respective disease and normal states.

If the pre-disease state is detected by a DNB, early treatment can be started, see Figure 1. It was first analytically shown that a DNB serves as an early-warning signal by defining particular but rather abstract critical states as coherent subnetworks that were then recognized as the physiological correlate of the pre-disease state. DNBs were successfully identified in medicine for lung injury disease, liver cancer, and lymphoma cancer [4,5].

3. Chronic disorders with episodic manifestations — dynamical systems theory view

The idea of a transition in form of a sudden deterioration from the health to the disease state via a specific pre-disease state can be transferred to the cycle of recurrent episodic symptoms in chronic disorders. The pre-disease state corresponds there to the prodrome, a stage that is relatively clinically silent but subtle symptoms announcing the ictal phase. It is worthwhile noting that the theoretical concepts are completely independent of the application and can be transferred to various complex systems. Early-warning signals near tipping points exist in systems ranging from medicine to financial market (and their crashes), to power grid systems to which a large amount of renewable energy is introduced, to ecosystem, and to the global climate system [3]. Many common neurological and psychiatric disorders fit into the category of chronic disorders with episodic manifestations including not only migraine and epilepsy but also stroke, multiple sclerosis, sleep-wake disorders, addictive disorders, schizophrenia and depression. But, it remains to be investigated which are likely candidates for dynamical diseases, which, we define here, accompany abrupt changes in natural rhythms in some organ systems due to bifurcations.

The existence of a prodrome with subtle symptoms before the ictal phase is a promising indicator of such a mechanism based on a bifurcation that shows early-warning signals. A prodrome stage is actually what would be expected from DNB being a subnetwork that is both highly fluctuating and strongly correlated but still in the physiological range. So let us consider again the two ways described before in which DNBs are different from conventional biomarkers. If the concept is transferred to chronic disorders with episodic manifestations, DNBs are by definition only present during the prodrome. Therefore, the DNB should be considered as the neural correlate of the prodrome. In other words, the existence of DNB is not a prediction in these cases but rather one possible a posteriori explanation for the prodrome.

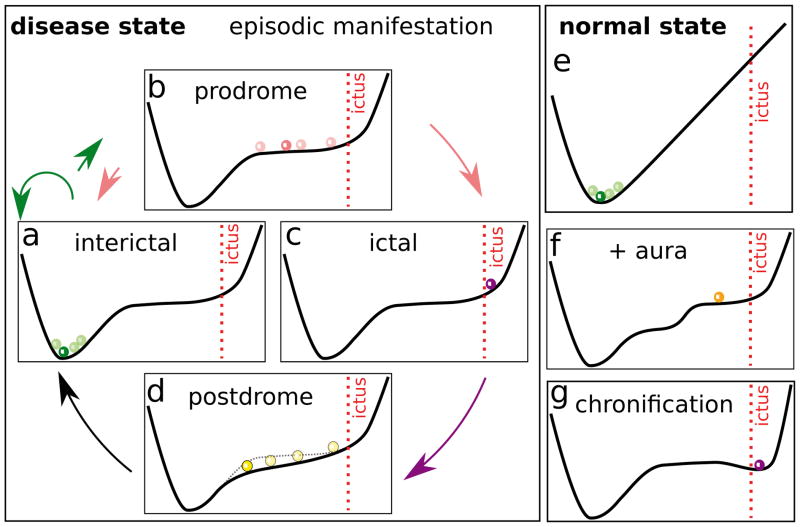
The cycle of recurrent episodic manifestations is illustrated in a simplified way in Figure 2. The states are associated to a potential function with a steady state or a minimum of this potential function corresponding to the attack-free interval and a prodrome phase corresponding to a plateau level, which can be reached by spontaneous fluctuations that are able to escape the potential barrier from the minimum level to the plateau level. At the far end of the plateau level, the ‘ictus’ is marked as the state that initiates the attack. The plateau leads to long transients and DNB dynamics, see also Figure 3. Long transients dynamics were for example also suggested in a neural mass model of epileptogenic tissue [17]. However, another possible landscape is that of a bi-stable regime, for example, the dynamics of epileptic phenomena were determined from statistics of such ictal transitions without occurrence of a prodrome phase and DNBs [18].

Figure 2.

Possibly dynamical scenario of recurrent episodes as a cycle (a)–(d) in chronic disorders (disease state) vs normal state (e) described in pictorial ‘landscapes’. (a) interictal: stable state where the disease under control; (b) prodrome: when the state escapes over the potential barrier to a relative flat plateau, the transient meta stable state is characterised by a strongly fluctuating and correlated subnetwork (cf. Figure 1); (c) ictal: at a certain point, the episodes manifest in form of a transient excursion that is recovered in (d) postdrome (possibly changed landscape); (e) normal state remains stable because the potential barrier toward the ictal state is too high. (f ) Additional premonitory symptoms such as migraine aura or aura in epilepsy indicates the existence of different plateaus (cf. Figure 3). (g) Chronification of diseased state: landscape changes such that the attack state persists.

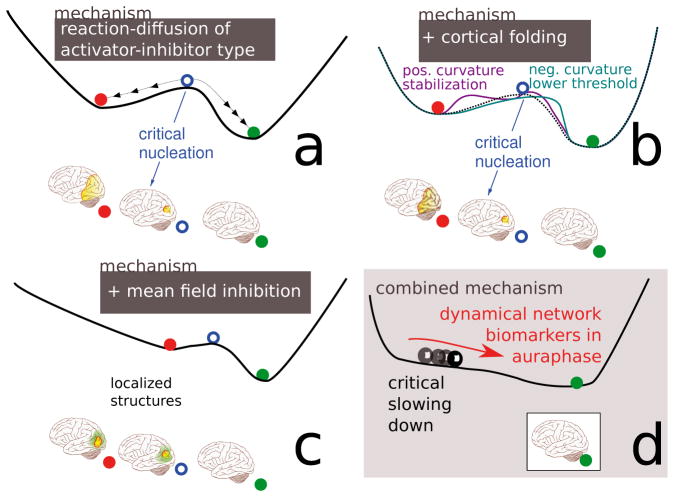
Figure 3.

Schematic illustration of the ‘landscape’ in a macroscopic model of SD (for details see Sec. 6.2). (a) Reaction-diffusion systems describe excitable media that support traveling waves and can engulf a cortical hemisphere. (b) Cortical folding modulates the pattern forming features. (c) Additional mean field control can stabilize localized SD structures. (d) A critical slowing down of localized SD structures is observed in a model with large mean field feedback control and the patterns are modulated (breathing spots) in curved geometries.

For a DNB being possibly an a posteriori explanation for the prodrome sets the aim expressed by the second difference between DNB and classical biomarkers (see Sec. II) into a broader perspective. While in complex diseases with sudden deterioration phases the aim of DNB is to detect the pre-disease state, now in chronic disorders with episodic manifestations the question is: What is the neural correlate, i.e., what is the DNB, of the prodrome? The aim could still be to more reliably detect the prodrome stage. However, migraine patients, for example, already very often can correctly predict upcoming attacks by their premonitory prodromal symptoms [19]. Thus, the broadened aim is to use the understanding of the slow and still gradual physiological changes in the prodrome to prevent the imminent abrupt attack, that is, to quantify the prodrome by DNB to construct a biofeedback signal for therapeutic control techniques.

4. Primary headaches as examples

The theoretical concept of early-warning signals is independent of its application [3] and the concept of DNB is actually a model-free concept [4,5]. Still specific computational models are needed to approach the broadened aim of therapeutic strategies. We cannot outline the potential use of DNB as early-warning signals in general terms and therefore focus on primary headaches and in particular on migraine. Migraine patients can very often correctly predict with premonitory symptoms their attacks [19] and various neuromodulation methods are today available to treat headaches [13]. Furthermore, computational models of migraine exist and describe the complex processes on a wide range of time and space scales, see Figure 4.

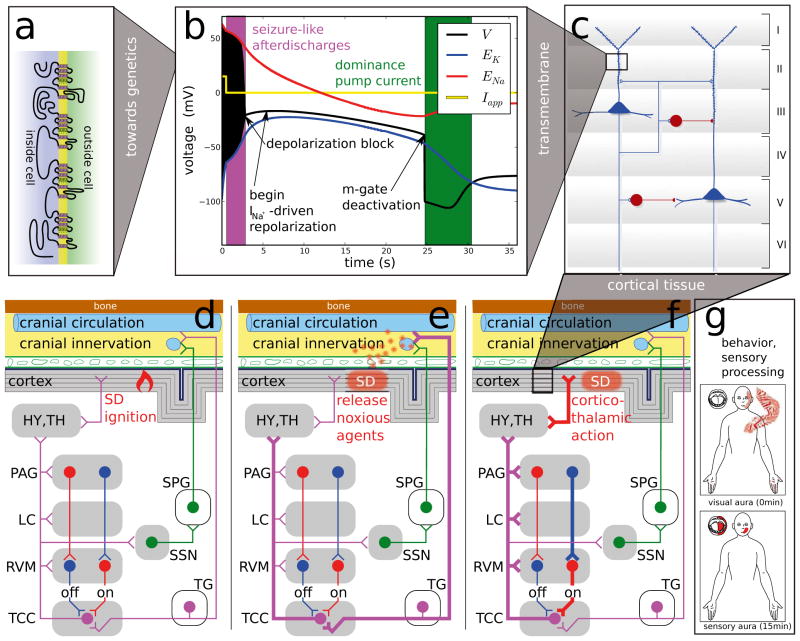
Figure 4.

Migraine affects neural activities across all levels. (a) Rare monogenic subtypes exist and genome-wide association study have revealed susceptibility loci for migraine with and without aura. (b) Disturbed functions of ion channel, proteins that regulate them, and pumps can be modeled by ion-conductance-based models. (c) Neuronal subpopulations and local circuits in specific brain regions, in particular, the layered cortex have also been investigated. (d) Higher-order networks of central nuclei and peripheral ganglia form the migraine generator network and its dynamical state may change during the course of an attack (e)–(f ). (g) Sensory processing can be perturbed in particular during the aura phase and behavioral changes occur in the prodromal phase such as food craving that can lead to false interpretation of triggers. (See main text for further detail.)

Migraine is a primary headache disorder characterized by recurrent episodes of head pain, often throbbing and unilateral sometimes preceded by neurological symptoms called aura. The known pathophysiologic mechanism suggests that this disorder should be considered as a neurovascular headache [20]. Migraine is a highly disabling disorder being according to the World Health Organization the seventh most disabling in the world and the fourth most disabling among women. Cluster headaches are also a primary headache disorder and the brainstem structures and subnetworks discussed below are also involved in cluster headache so that these concepts can likely be applied in some form to cluster headache, too.

Note that migraine is a chronic disorder with episodic manifestation, also referred to as episodic migraine, while the relative new term ’chronic migraine’ (CM) refers to chronification of the recurrent attacks, that is, more than 15 headache days per month over a 3 month period, at least 8 migrainous, and in the absence of medication overuse.

In migraine without aura (MO), attacks are usually associated with nausea, vomiting, sensitivity to light (photophobia) and sound (phonophobia), and attacks are worsened by movement. Migraine with aura (MA) involve in addition—but also rarely exclusively—neurologic symptoms (called aura) [21]. Migraine aura symptoms are most often visual field disturbances, but affect also other sensory modalities or cognitive functions [22]. Aura symptoms are caused by a wave of cortical spreading depression. Whether this wave also contributes to the headache phase in migraine is currently debated [23]. Epidemiological studies suggest that MA and MO share the same headache phase. However, on average the pain seems to be less severe and shorter lasting in MA than in MO [24].

The migraine cycle can be divided in four distinct stages and the headache-free interictal interval. The prodrome is characterized by feeling tired and weary, difficulty concentrating, yawning, polyuria, sweating, and fatigue are some typical features [19]. It lasts up to one day and occurs in about 60% of the reported cases. During the aura phase, all kind of sensory disturbances, visual most frequently, are reported. This phase lasts 5–60min and occurs in about 30% of the reported cases. Migraine headache is often unilateral and throbbing—though interestingly from a dynamical systems theoretical point of view, this seems to be not related to blood pulsation but is a signature of rhythms in the brain [25,26]. Migraine headaches last 4–72 hours and occur in about 95% of the cases. Last, the postdrome is characterized by tiredness, difficulty concentrating, weakness, dizziness, persistence of sensitivity to light and noise, lethargy, and fatigue, together often described as ‘headache hangover’. It lasts a few days and occurs in about 70% of the reported cases. Together with the attack-free interval these phases compose the migraine cycle with associated severe disabilities and reduced quality of life even between attacks [27].

5. Migraine theories

While we expect that quantitative methods such as computational neuroscience will become increasingly important in migraine research to keep up with the proliferation of imaging data and to confine current theories, it was the advent of non-invasive imaging that changed the view on this headache type in the first place with some intriguing qualitative observations. In the 1980s and into the mid-1990s, it became clear by studies of the clinical features of migraine and its physiological mechanisms that there is no clear correlation between blood flow changes and the headache but instead imaging studies suggested [28] that upstream events in the brainstem named ‘migraine generator’ (MG) [29] lead to the cascade resulting in migraine pain. Furthermore, imaging migraine with aura revealed that the phenomenon of cortical spreading depression (SD) is the neural correlate of migraine aura [30,31]. To date, the MG and SD theories are facing each other but are probably not irreconcilable.

In brief, the MG theory states that a dysfunction of the brainstem causes the pain and via further connections (directly and indirectly) the brainstem is also responsible for the neurological changes before the headache phase including symptoms in the prodromal phase and the aura phase, in particular, the MG is causing SD via a failure of vasomotor control (Figure 4d). The SD theory of migraine assumes that this cortical wave causes the neurological systems (aura) [32] and it can also cause the pain in the headache phase, which usually occur after the aura phase, but cf. [33]. In this theory, two independent pathways of increased pain traffic are suggested, a peripheral and a central pathway. The headache pain can either be triggered by a local release of noxious or inflammatory substances during the hyperemic phase of SD [23,34]. These substances are thought to be transmitted outward in the direction perpendicular to the cortical layers into the pain sensitive meninges. This transmission results in an activation of pain receptors (nociceptors) and local inflammation, which eventually triggers the migraine headache (peripheral pathway, Figure 4e). Or the alternative explanation is that SD leads to pain by a corticothalamic feedback that affects sensory processing by third-order neurons arising within the sensory thalamus. This is supported by the efficacy of calcitonin gene-related peptide receptor antagonists at the level of these neurons in migraine therapy [35] (central pathway, Figure 4f ). Probably, a combination of the peripheral and central pathway leads to this complex disorder and quantitative models as outlined below can help to disentangle the relative contributions and dependencies.

6. Computational models in migraine

Computational models of spreading depression date back to the mid-1970s. A simple rule-based cellular automata model was used to mimic the two-dimensional spread on the cortical surface, including spiral-shaped SD waves reentering around a functional block [36] that can also be observed experimentally [37]. Partial differential equations were used to describe the detailed physiological cellular events [38]. For a detailed review of SD modeling, including the mathematical description, see the excellent review by Miura et al. [39]. In the following, only basic approaches focusing on the principles of cellular dynamics and tissue pattern formation in SD are introduced. We start with cellular dynamics of SD and continue with the events in cortical tissue. The mathematical equations are given in an Appendix.

6.1 Cellular dynamics in SD

The focus in computational models of the cellular dynamics in SD is on transmembrane events that can be observed in in vitro experiments [40]. The advantage of such experiments is that the phenomenon of SD can be studied in isolation and the complex vasomotor feedback involved in SD can be neglected [41], though current modeling approaches include metabolic and perfusion effects on SD [42]. With this local focus set, SD is essentially a massive but temporary perturbation of ion homeostasis. The ion concentrations are under physiological conditions kept within a narrow range and their gradient across the cell membrane is treated in traditional computational models of Hodgkin-Huxley (HH) type as a constant battery, the reversal potential or Nernst potential [43]. During SD, however, ion concentrations can change by over one order of magnitude, so that the original HH approach to describe the potential changes across the excitable membrane must be extended. For instance, during SD the extracellular potassium concentration raises from 3mM within a few seconds to peak values around 55mM, plateaus at this level for about 30 seconds and recovers to the physiological range within one to two minutes [32]. Furthermore, neuronal activity is depressed due to the nearly complete elimination of the transmembrane ion gradients, in other words, the cells release almost all of their available energy—the Gibbs free energy—the supply for physiological neural activity [44]. This depressed activity state can spread throughout gray matter in the brain, hence this activity is named as SD (see below the section on spatial patterns forming in cortical tissue).

To model local cellular events in SD, Kirchhoff’s current law is used as first introduced in the HH framework [43]. The major extension, however, is that in addition to the original transmembrane potential V and the variables activating and inactivating conductances of transmembrane channels (voltage-gating variables, usually called m, n, and h) further functions and dynamic variables for the ion homeostasis are introduced. First, an ATP driven ion pump is modeled that exchanges intracellular sodium ions with extracellular potassium at a 3/2 ratio and therefore changes not only ion concentrations dynamically but also leads to a depolarizing transmembrane current I_pump. Second, extracellular and intracellular ion concentrations become dynamic variables and thus increase the phase space of the model. We refer to the Appendix A for the corresponding mathematical equations. Such an extended framework is able to model the long lasting dynamics on time scales of minutes, while, for example, a single action potential, which is described in the first generation HH-type framework, lasts about a millisecond, a time scale separation of about five orders of magnitude. This new time scale separation is the fundamental characteristic of this second generation HH-type framework.

The first generation of HH-type models for single cells is also called conductance-based models. In the parallel development of neural mass models for cell populations one often refers to rate- or activity-based modeling. In each case, the model is named after the respective dependent dynamical variables other than the transmembrane potential. In this terminology, the second generation HH-type models necessary to model SD are ion-conductance-based models. Note that ion-conductance-based models are necessarily ‘tissue-embedded’ single cell models because the amount of cell membrane surface area per unit tissue volume, in short, the surface area-to-volume ratio plays a significant role. While this factor does not affect HH type conductance-based models, in ion-conductance-based models it gives rise to the long time scale of SD excitation cycles as compared to much shorter actions potentials and may likewise cause slow modulations of activity in extended rate- or activity-based neural mass models.

With an ion-conductance-based model of a total of 9 dynamical variables the main features of SD that happen across the cell membrane can be modeled (see Figure 4b). Using electroneutrality and further symmetry constraints, ion-conductance-based models can be further reduced and become amenable for bifurcation and geometrical phase space analysis. On the other end towards physiologically more realistic ion-conductance-based models of SD, several dozens of dynamical variables in various electrically coupled neural compartments (~200, which effectively multiplies the number of dependent dynamical variables) can be modeled in tissue-embedded single cell models [39,45–47].

Although in reduced ion-conductance-based models the time course of the dynamic variables can be to some extent distorted as compared to more realistic models [39,45–47], main features of SD are revealed (Figure 4b). Two phases and three points stand out because of their significant mechanistic meaning in SD as an excitation phenomenon: the seizure-like after-discharges, the subsequent excitation block, the begin of a I_Na-driven transient repolarization, the m-gate deactivation that finally initiates a phase where the pump current I_pump can become dominant, see Figure 4b.

Of all these events highlighted in Figure 4b most notably is the recovery phase of SD at around 24.5 s. According to the computational models, recovery is due to a deactivation of the sodium activator m driven by a dominat I_Na that actually repolarizes V shortly after the seizure-like firing stops due to a depolarization block. After the deactivation of the sodium activator m, the pump current I_pump drives the membrane potential V (black) for several seconds outside the window of the two reversal potential of sodium and potassium, E_Na (red) and E_K (blue), respectively. The ignition of SD is due to a torus bifurcation (not shown, unpublished results) of the tonic seizure-like firing caused by the initial stimulation phase. This suggests that after the offset of the stimulation at 0.5 s the state of the dynamical system is already behind a canard-like trajectory that serves as a threshold causing firstly a brief phase of sustained (2–3 s) afterdischarges and then a long lasting recovery phase during which the system is refractory.

Next, we consider large-scale tissue events caused by SD. But before that it is worthwhile noting that cellular models often do not include lateral space, except for the original work by Miura and Tuckwell [38] and some recent approaches from the group of Miura [48] and an isolated work by Shapiro [46] considering osmotic forces and gap junctions. The compartments mentioned before extend in the vertical direction to model the apical dendritic tree of pyramidal cells in the cortex [45,47]. But the very detailed models by Kager, Wadman, and Somjen are not spatially extended to describe the lateral extension, that is, they describe SD not as an excitable phenomenon in a spatially extended system, called excitable media.

The lateral extension of cellular SD models is far from straight forward. Naively adding diffusion to the extracellular dynamical ion concentrations yields some insights but it does not reflect the necessary detail of neural microcircuits that needs to be considered to take the spatial continuum limit (Figure 4c). Neural field models, for example, describe this limit for rate- or activity-based neural mass models [49]. The problem is that the neural tissue is heterogeneous and the cell’s embedding needs to be considered in quite some detail for a lateral extension of cellular SD models. A bottom-up approach toward an ion-conductance-based medium model that lacks the support of an effective medium theory cannot expand from membrane to tissue level in a canonical way and therefore loses its advantage over the simpler top-down approaches. Likewise, a coarse-graining in time from individual spiking to rate or activity-based dynamics in simulated cell populations is needed for the relevant time scales in migraine. A first promising approach was made with an ion-conductance-based model in seizure spread [50].

6.2 Tissue events caused by SD

The Gibbs free energy-depleted and activity depressed state of SD described in the former section can spread through gray matter tissue by electrodiffusion due to newly formed ion gradient along the membranes in the neuronal and glial syncytium and the interstitial volume. In accordance with noninvasively imaged SD progression using high-field functional magnetic resonance imaging (fMRI) [31] and reported visual field defects [51], a macroscopic computational model of SD (see Appendix B) was proposed in which to each episodic migraine attack a particular spatio-temporal SD pattern is formed [12,52]. With this model a mechanism was suggested to explain the shape of SD in migraine as a discontinuous wave segment that spreads out in only one direction. In a nutshell, the mechanism is based on dissipative structures as self-organized localized solitary patterns [53,54] that become transient objects with critical slowing down—from a mathematical point of view a mechanism similar to the one of DNB—that is modulated by cortical folding, see Figure 3.

These are the tissue events of SD that are of clinical importance for migraine because we predict that they will determine not only the migraine aura but also the headache phase for two reasons. First, the spatio-temporal patterns of SD determine the transmission of noxious or inflammatory mediators in the direction perpendicular to the cortical surface into the pain sensitive meninges and then via peripheral pathway (Figure 4) the headache phase. This transmission must be significantly convergent to reach noxious threshold concentrations, whereby likewise the considerable heterogeneity of increased nociceptor density around pial arteries and dural venous sinuses can interfere with the distinctive self-organized patterns in the folded cortex. Second, the particular spatio-temporal pattern of SD probably also determines via the central pathway the specific corticothalamic feedback that affects sensory processing in terms of sensitization by third-order neurons (Figure 4f ). We suggested that the two major migraine subtypes, MO and MA, depend on the spatial SD patterns and the bifurcation that is responsible for their transient nature one being without critical slowing down and one showing critical slowing down, respectively [12,52].

The major advantage of generic, i.e., low dimensional, reaction-diffusion models of SD lies in the fact that they provide insight in the phase space structure of the whole class of models they represent. In fact, localized solitary patterns are not the only SD waves in the human cortex of clinical relevance. Re-entrant SD waves are believed to have the potential to worsen stroke outcome in incremental steps with each wave circling near the infarct core, while the same SD wave in the penumbra zone far from the infarct tissue could also have a beneficial component by stimulating blood flow [55]. The infarct core is a static anatomical block, whereas spiral waves and localized SD waves in migraine have a variable core (functional block) and variable left-off tissue, respectively [37,56]. These and other clinically important spatial pattern forming mechanisms can be understood in terms of phase space structures. These structures describe the migraine aura–ischemic stroke continuum as transitions of two-dimensional wave pattern in SD from retracting localized (migraine) to stationary waves (persistent migraine aura without infarct) to re-entrant waves (stroke) [57]. Therefore, the precise spatio-temporal SD pattern formation is of immense clinical interest [58].

To simulate the clinically observed patterns in migraine [31,51], a generic reaction-diffusion mechanism can be described in abstract terms of activator-inhibitor kinetics. In fact, simple activator-only kinetics date back to a mechanism of SD described in 1963 by Grafstein based on an otherwise unpublished suggestion by Hodgkin and Huxley, to date called the Grafstein-Hodgkin-Huxley (GHH) model [59]. The GHH model assumed that the extracellular potassium ion concentration is an activator in SD. We extended this scheme by introducing two inhibitory mechanisms, an immobilized inhibitor and a mean field inhibition (for details of the full model see [52]).

The abstract activator and inhibitor variables are lump variables. Unlike in the original GHH model, it is not necessary or even possible to identify particular physiological quantities, like [K⁺]_e, with them. Instead, the activator should be viewed as a positive feedback element with a bistable energy state. The activator and inhibitor or rather the respective networks of dynamical variables that constitute these elements can be described in great physiological detail on the cellular level (see the former section) yet they are also new emerging conceptual quantities that allows us to describe the phenomenon of SD directly on the macroscopic level. The high energy state (a stable fixed point) corresponds to the maintenance of homeostasis far from thermodynamic equilibrium and the low energy state (another stable fixed point) to the state where the cellular Nernst reversal potentials are eliminated, that is, a state at or near the thermodynamic Donnan equilibrium [44]. In the presence of inhibitors as recovery variables, which were not included in the GHH model, the low energy stable fixed point becomes a transient state that can spread through gray matter tissue by electrodiffusion as a depleted and activity depressed state.

7. Concluding remarks on translating theoretical concepts into neuromodulation applications

The design of new neuromodulation strategies in migraine requires to understand how electric and magnetic stimulation changes neural activity. Even more important are quantitative models of the network dynamics during this neurological condition to optimize stimulation protocols. In Sec. 6.1, we described cellular dynamics that are key to understand how electric and magnetic stimulation influences brain activity. The cellular dynamics are also the microscopic foundation of self-organized macroscopic tissue events, which are of direct clinical relevance. In Sec. 6.2, we show that on the macroscopic level SD manifests as a localized wave in the human cortex during migraine with aura. From the model we can predict that the macroscopic spatio-temporal SD patterns (shape, size, and duration) determine to some extent the clinical manifestation of a migraine attack [12].

As we argued in Sec. 5, the spatio-temporal SD events can determine the amount of noxious input into the pain sensitive structures (Figure 4e) as well as modulate corticothalamic feedback loops (Figure 4f ). However, the question about the most upstream event in the course of a migraine attack that would directly lead to the optimal target of preventative intervention is probably too naive. The ignition of SD is currently unknown but a failure of vasomotor control from the brainstem, which is part of the MG theory, is a likely scenario (Figure 4d). It further is plausible that these SD waves will in turn also affect the brainstem activity because SD itself causes a complex vasomotor reaction [41]. This allows only one conclusion: Migraine is an inherently dynamical disease with a complex network of interdependent events rather than a disease with a linear course from upstream to downstream events, a course that is also called into question by a rather variable cycle of recurrent episodic symptoms in migraine with phases such as the aura that occurs only in a fraction of the individual attacks [60].

The central question therefore is about different brain structures and in which phase of the migraine cycle they are promising neuromodulation targets (Figure 5) in the framework of complex dynamical systems and control theory [8]. We still lack a unified quantitative model combining the events in SD theory and MG theory of migraine (Sec. 5) to interpret their relation, simulate the impact of potential neuromodulation intervention, and make concrete predictions about optimized stimulations protocols that can be tested. In this situation, however, the theoretical framework of DNBs provides a sound basis to address these challenges because DNBs are based on a model-free concept and, if DNBs can be identified in migraine, they will help to develop a unified theory. Namely, DNBs will not only show whether a symptom is approaching or not, but also help to construct such a unified model explaining how the symptom appears, and providing a feedback-control-scheme to suppress the symptom.

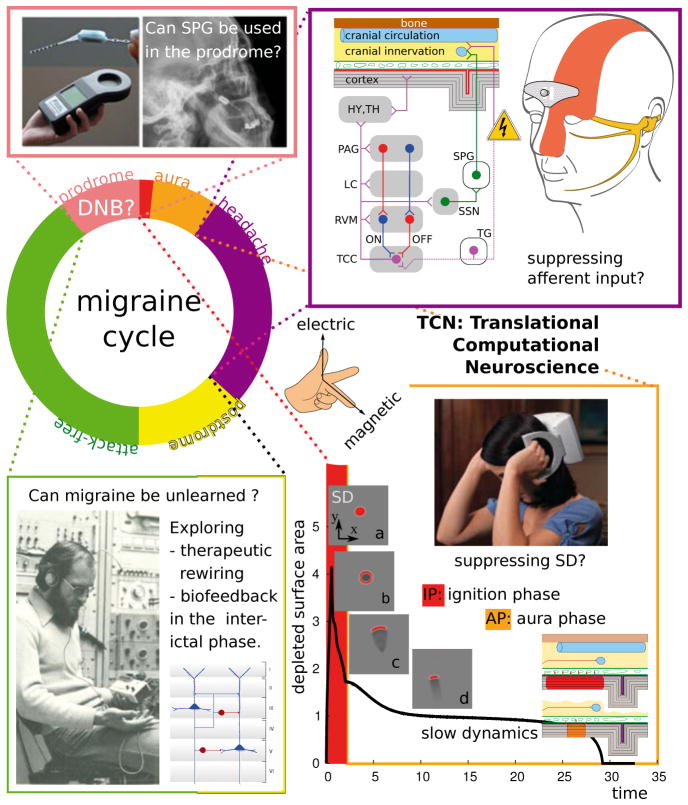
Figure 5.

Various neuromodulation techniques are currently investigated in chronic migraine, but note that, as of to date, there is no approved indication for neuromodulation with electric or magnetic stimulation for episodic migraine. We suggest to investigate these techniques also in episodic migraine and to use quantitative models and modern control theory to determine an optimal stimulation protocol, target structure and phase within the migraine cycle. Photograph top left (SPG stimulation): courtesy Autonomic Technologies, Inc. © 2013. Inset figure top right: courtesy of STX-Med © 2013. Photograph bottom right (TMS device): courtesy of Neuralieve, Inc. © 2013 (trading as eNeura Therapeutics).

We end this review by introducing briefly two neuromodulation techniques that are currently investigated in migraine in two different phases of the migraine cycle targeting two different brain structures. Then, we speculatively suggest a promising third neuromodulation technique that may be of particular use during the prodromal phase that could reflect a DNB (cf. Sec. 3). Furthermore, we also suggest taking the attack-free interval into account for prophylactic intervention.

Note that, as of to date, there is no approved indication for neuromodulation with electric or magnetic stimulation for episodic but only for chronic migraine (>15 headache days per month). In fact, due to the severeness of pain, most neuromodulation studies in headache research are or have been conducted among patients with refractory cluster headache. However, the field is rapidly increasing [13] and given that newer devices require noninvasive or minimally invasive implant surgery involving a new generation of intelligent control methods also less disabled patients with high frequency episodic migraine with unsatisfactory treatment response could benefit from efficient neuromodulation.

7.1 Transcutaneous electrical nerve stimulation

Transcutaneous and transcranial (see the next subsection) stimulations are the two noninvasive modes currently at hand. The transcutaneous electrical nerve stimulation (TENS) modulates neural activity by targeting noninvasively peripheral nerves. In migraine, a supraorbital transcutaneous stimulation (STS) was tested with a portable device that looks like a silver headband and targets the ophthalmic division of the trigeminal nerve that terminates in the central trigeminal nucleus caudalis (TNC) and the C1–C2 regions of the cervical spinal cord, together known as the trigeminocervical complex (TCC), see top right in Figure 5.

In a recent study, the stimulation was tested with biphasic rectangular AC impulses at 60Hz. The therapeutic gain (26%) is within the range of those reported for other preventive drug and nondrug migraine treatments [61]. The mode of action or even quantitative methods to test paradigms are currently missing, though it seems plausible that if central sensitization of second-order neurons is causing migraine pain, this method is suppressing the inbound sensory traffic which could add to sensitization, and it should therefore be used in the acute headache phase rather than prophylactically.

7.2 Transcranial magnetic and electrical stimulation

The transcranial stimulation targets not peripheral neurons but the cortex. Two noninvasive neuromodulation techniques are available in migraine, transcranial magnetic stimulation (TMS) and transcranial electrical stimulation (TES). A recent carefully sham-controlled larger trial with a portable TMS device was undertaken as a promising noninvasive neurostimulator for disrupting SD early in the aura phase [62], see bottom right in Figure 5. The results (effective in aborting migraine attacks) of this sham-controlled study were promising, i.e., it seems to disrupt SD, but that would limit its use to the acute aura phase. However, considering the concept of silent aura [63] and the mathematical model for SD [52], TMS could potentially be effective when used in the very early headache phase targeting the shorter lasting phase of SD. In either case, there is a clear need for further studies and the optimization of the stimulation protocol for targeting localized spatio-temporal reaction-diffusion patterns [52].

The simplest technology with the least safety issue is probably TES. Two versions of TES exist, the transcranial direct current stimulation (tDCS), in which cathodal tDCS inhibits while anodal tDCS increases neuronal firing. The alternating current stimulation (tACS) has not yet been clinically tested in migraine. Preliminary evidence was found for patients with chronic migraine having a positive, but delayed, response to tDCS applied to motor (anodal) and oribitofrontal (cathode) cortices [64]. In addition, computational simulations of current flow through brain regions were used to interpret the effects in this study. With the help of such simulations, a principal understanding of pain modulation can be gained, whether this modulation is due to the effect of TES on SD or on the dynamics of the pain matrix and deeper structures including thalamus and brainstem. Effective prophylactic therapy in migraine was also studied with cathodal tDCS over the visual cortex with the anode overlying the motor and sensory cortices [65].

7.3 Sphenopalatine ganglion stimulation

Beside the two mechanism explained by the SD theory (Figure 4e, f), also other mechanisms could activate pial and dural nociceptors and trigger the pain of the headache phase of migraine. It was suggested by Burstein and Jakubowski [66] that a common pathway for various migraine triggers could be provided by the pre- and postganglionic parasympathetic neurons in the superior salivatory nucleus (SSN) and sphenopalatine ganglion (SPG). A number of projections converging in the SSN seem to be coming from brain areas that can explain typical migraine triggers, for example stress, dietary, and external stimuli such as smell. Targeting the SSN through antidrome or feedback mechanisms of the SPG could therefore be a potential target in migraine (prevention).

Interestingly, it was also argued that for many if not all of the typical triggers the role of cause and effect is actually reversed and premonitory symptoms are mistaken as triggers [67,68]. For example, eating chocolate, as a typical food craving symptom before the headache phase of migraine, is a brain-driven response within the premonitory phase and not a trigger, i.e., the cascade of the attack has already started and the only symptom at that stage is the craving with all the other symptoms still to come. Likewise, sensitivity to light (photophobia) during the premonitory phase could mistakenly be identified as a trigger by light. In the context of DNB this is certainly plausible as this concept predicts a common subnetwork such as SSN and SPG to be involved in the premonitory symptoms.

Given the theory that the pre- and postganglionic parasympathetic neurons in the superior salivatory nucleus (SSN) and sphenopalatine ganglion (SPG) could be a common pathway for migraine triggers [66], minimally invasive sphenopalatine ganglion stimulation might be suited in particular in the prodromal phase in episodic migraine. A very innovative implantable battery-free SPG stimulator has been developed to apply on-demand stimulation for the treatment of migraine and other primary headache. In a pilot study (n=11), the potential of electrical stimulation of the SPG has already been shown in attack abortion, 2 patients were pain-free within 3 minutes of stimulation, 3 had pain reduction, 5 had no pain relief, 1 was not stimulated [69]. However, in this pilot study, the headache was allowed to intensify up to 6 hours before stimulation was initiated, where SPG stimulation might theoretically be less efficient to influence a migraine attack than it could have in the prodromal phase. More to the point, a recent paper described not only a marked abortive but also a preventative effect in cluster headache patients [70] which could best be explained by feed-back mechanisms from the SPG to the SSN and thus underlining the above mentioned theory and pointing towards the SPG as a suitable target for attack prevention. However, all this is based on a theoretical concept and it should be noted that in migraine research no valid studies have been published yet to prove that SPG stimulation could have a positive effect in this syndrome as well.

To summarize, already to date various neuromodulation methods for treatment of primary headache have been studied, beside the above mentioned also other invasive techniques such as deep brain stimulation and minimally invasive occipital nerve stimulation [71]. To fully realize the potential of computational models that can be translated into a new neuromodulation paradigm a modern control theory is needed. The challenge in the future will be to integrate the known mechanisms into a tractable theoretical migraine model, but also to obtain human data from clinical studies and identify DNB. Therefore, new clinical study designs are needed to investigate the macroscopic dynamics in migraine. For example, fMRI brainstem specific ROI-based imaging paradigms and fluorodeoxyglucose positron emission tomography (FDG-PET) combined with magnetic resonance imaging (MRI) could identify important neuronal centers in the brainstem and describe their connectivity pattern [72]. Such imaging methods together with quantitative methods and theoretical concepts are important to characterize dynamics in the migraine generator network and identify DNB over several migraine cycles in controls and patients suffering from episodic migraine.

8 Appendix: Model equations

8.1 Cellular models

To model local cellular events during SD, we start with Kirchhoff’s current law that was introduced as an equivalent membrane circuit by Hodgkin and Huxley [43]

$$\frac{\mathrm{d}V}{\mathrm{d}t}=-\frac{1}{C_m}(I_{{Na}^{+}}+I_{K^{+}}+I_{C{l}^{-}}+I_{\mathit{pump}}-I_{\mathit{app}})$$ (1)

The variable V is the potential difference or voltage across the membrane relative to the grounded extracellular side. The cell membrane has a capacity C_m. The currents I_ion are the transmembrane currents with ion ∈ {Na⁺,K⁺,Cl⁻}. I_app is an externally applied current.

In the original HH framework, an unspecified leak current was modeled but not a chloride current. The major extension, however, is the pump current I_pump, which can be modeled for example as [73]:

$$I_{\mathit{pump}}({Na}_i{K}_e)=\rho {\left(1+exp\left(\frac{25-{Na}_i}{3}\right)\right)}^{-1}{\left(1+exp(55-K_e)\right)}^{-1}$$ (2)

The pump current Ipump with pump rate ρ describes the ATP driven exchange of intracellular sodium ions with extracellular potassium at a 3/2 ratio.

The ion concentrations [ion] change due to fluxes proportional to the ion currents. The additional rate equations for intracellular ion concentrations are

$$\frac{\mathrm{d}[\text{ion}]}{\mathrm{d}t}=-\frac{\gamma }{\omega }(I_{\text{ion}}+\alpha I_{\mathit{pump}})$$ (3)

with α being 3, 2, and 0 for Na+,K+, and Cl−, respectively. The parameter γ converts currents to ion fluxes and depends on the membrane surface area A_m and Faraday’s constant F, γ= A_m/F. The parameter ω is the volume of the intracellular space (ICS).

In addition, also dynamical gating variables n, h and m have to be introduced, as in the original HH model. The potassium activator, sodium activator and sodium inactivator are defined by the voltage-dependent gating dynamical variables n, m and h, respectively. These are given by

$$\frac{\mathrm{d}p}{\mathrm{d}t}=\frac{1}{{\tau }_p}(p_{\infty }-p)$$ (4)

for p∈{n,m,h}.

8.2 Reaction-diffusion models

To simulate the clinically observed patterns in migraine [31,51], a generic reaction-diffusion mechanism can be described in abstract terms of activator-inhibitor kinetics of just two variables u and v, respectively. We extended the GHH model (see the main text) in the following way (also for details of the full model see Ref. [52]):

$$\epsilon \frac{\partial u}{\partial t}=u-\frac{1}{3}{u}^3-v+{\nabla }^{2}u$$ (5)

$$\frac{\partial v}{\partial t}=u+\beta +K\int \int H(u)\mathrm{d}x\mathrm{d}y$$ (6)

with H being the Heaviside step function and the space coordinates are given by x and y. Both activator u and inhibitor v are lump variables (see the main text). We set the parameter as follows: time scale separation ε=0.04, the threshold β=1.32, and the mean field coupling K=0.003.

There are two stable solutions of this model, namely the homogeneous steady state and the traveling wave. Moreover, there exists a saddle solution forming a localized solitary pattern whose stable manifold is the basin boundary of the stable solutions. By varying a control parameter, the stable traveling wave solution and the saddle solution collide causing the saddle-node bifurcation. The saddle-node bifurcation and the critical slowing down with this model suggest the applicability of DNB to detect SD.