Assessment of bone fragility with clinical imaging modalities

Abstract

Introduction

Osteoporotic fractures are a vital public health concern and have created a great economic burden to our society. Therefore, early diagnosis of patients with high risk of osteoporotic fractures is essential. The current gold standard for assessment of fracture risk is the measurement of bone mineral density using dual-energy X-ray absorptiometry. However, such techniques are not very effective in the diagnosis of patients with osteopaenia. Doctors are usually unable to make an informed decision regarding the treatment plan of these patients. In addition to bone mineral density, advanced imaging modalities have been explored in recent years to assess bone quality in other contributing factors, such as microarchitecture of trabecular bone, mineralisation, microdamage and bone remodelling rates. Currently, the microarchitecture of trabecular bone can be evaluated in vivo by high-resolution peripheral quantitative computed tomography techniques, which have a resolution of 80 µm. However, such imaging techniques still remain a high-end research tool rather than a diagnostic tool for clinical applications. Thus, the limited accessibility and affordability of high-resolution peripheral quantitative computed tomography have become major concerns for the general public. Alternatively, combining bone mineral density measurements with stochastic assessments of spatial bone mineral density distribution from dual-energy X-ray absorptiometry images may offer an economic and efficient approach to non-invasively evaluate skeletal integrity and identify the at-risk population for osteoporotic fractures. The aim of this critical review is to assess bone fragility with clinical imaging modalities.

Conclusion

High-resolution quantitative computed tomography imaging technique may provide direct measurements of microarchitectures of trabecular bone in vivo. However, it is an expensive method of imaging modality.

Introduction

Osteoporosis is a skeletal disease in which loss of bone mass and deterioration of bone microarchitecture cause a reduction in bone stiffness and strength, thus resulting in an increased risk of fragility fractures¹. Early diagnosis of patients with high risk of fragility fractures is important due to the elevated rate of morbidity and even mortality, which has made it a vital public health concern and a great economic burden to our society^2,3. The current gold standard for diagnosis of osteoporosis and assessment of fracture risk is the bone mineral density (BMD) measured using dual-energy X-ray absorptiometry (DXA).

Although BMD from DXA provides important information about risk of fragility fractures, assessments on BMD alone do not cover the full spectrum of the fracture risk. Numerous studies have indicated that bone strength is only partially explained by BMD^4,5. In fact, BMD is a measure of bone mass or quantity of bone. However, bone fragility is not only dependent on its quantity, but also its quality. Bone quality is defined as the totality of features and characteristics that influence a bone’s ability to resist fracture⁶. Such features may include, but may not be limited to, ultrastructure, microarchitecture, microdamage and remodelling rates in bone. Among the features, the microarchitecture of trabecular bone has been recognised as a major contributor to bone fragility.

There are several recently developed approaches that can provide complementary information for assessing fracture risks in addition to BMD. One of them is to develop high-resolution imaging modalities to directly visualise three-dimensional (3D) structure of trabecular bone. The underlying hypothesis is that bone architecture contributes to bone strength. With recent advancement in imaging techniques, high-resolution images using computed tomography (CT) and magnetic resonance imaging (MRI) could be directly used to assess 3D microarchitectures of trabecular bone.

Another approach is to make full use of the existing two-dimensional (2D) projection image modalities and to employ stochastic image-processing techniques to extract useful information on microarchitecture characteristics of bone. In this case, the resolution of the image is no longer essential. The important thing is to recover the information that is indicative of architectural characteristics of bone and can be used to assess the resistance of bone to fracture. To this end, the objective of this article is to review the current progress in using imaging modalities, both 2D projection images and 3D high-resolution images, to assess bone fragility in the clinical settings. The focus of this review article is on 2D imaging modalities since numerous review articles are available for 3D imaging modalities^6–9.

Discussion

The authors have referenced some of their own studies in this review. The protocols of these studies have been approved by the relevant ethics committees related to the institution in which they were performed.

2D imaging modalities

Radiographs and DXA images are two major modalities of 2D projection images for assessing bone fragility in the clinical settings. Conventional X-ray radiography offers higher resolution (up to 50 µm) for diagnosis of fragility fractures, whereas DXA images have lower resolution but provide a better estimation on average BMD. Improved prediction of bone fragility can be achieved when fractal and stochastic texture analyses of 2D projection images are conducted in addition to the measurement of BMD.

Fractal texture analysis of radiographs

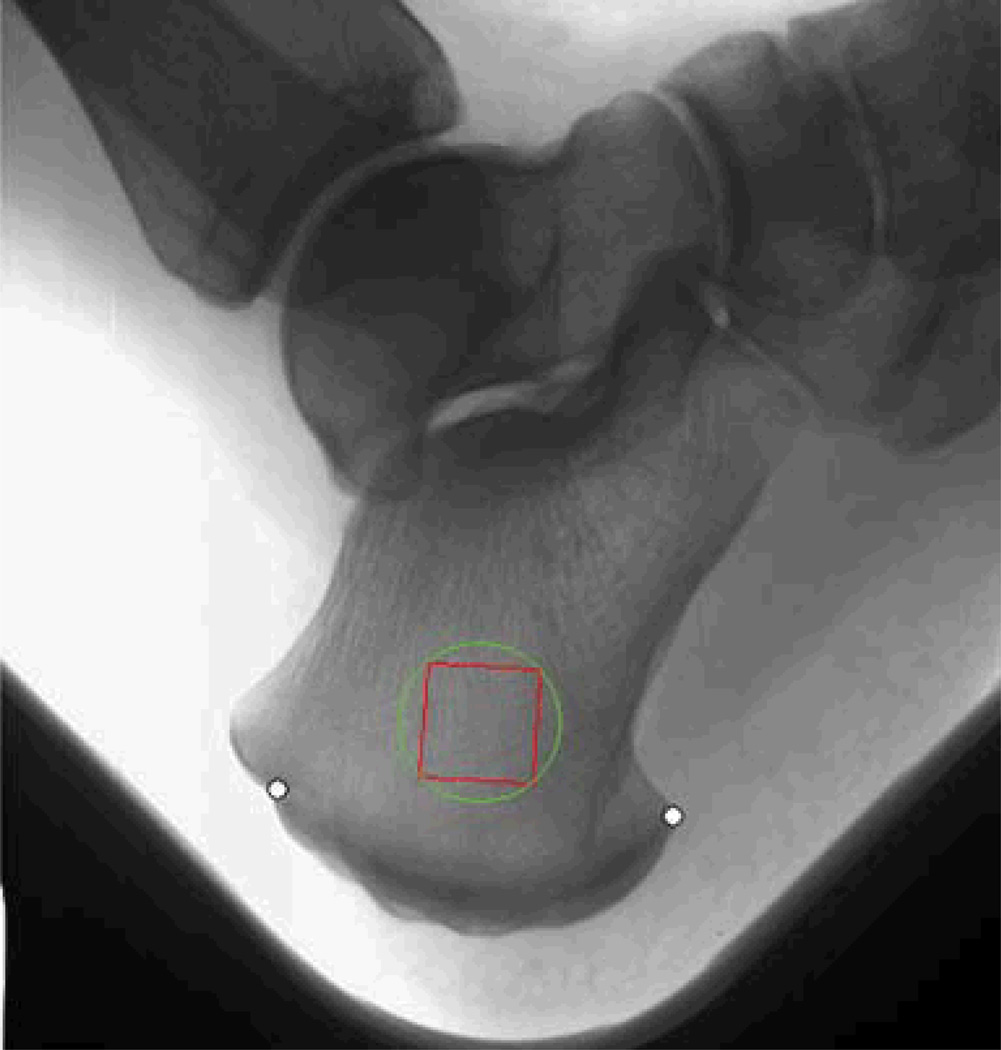
Fractal texture analysis, a useful imaging technique, has been successfully applied to high-resolution 2D radiography images (Figure 1) to extract the hidden geometric and microstructural features^10–19. Such analyses are based on the concept of fractal geometry. Fractal geometry can be used to define the complex objects that cannot be described by traditional geometric features, such as size and shape. Such objects possess a character of self-similarity, meaning that they can be split into different self-similar pieces at various scales or magnifications while the fractal geometry of these pasts remains similar to that of the whole object. Fractal dimensions are the characteristic dimensions of fractal geometry, with the dimension of a point, a line, a surface, and a volume being defined as 0, 1, 2, and 3, respectively. Different from conventional geometry, the fractal dimension is not an integer but fractional, representing something between the conventional dimensions (e.g. point, plane). Fractal dimension is a measure of how complex the structure of a self-similar object is, which is defined as a ratio of the logarithm of the number of self-similar pieces to the logarithm of the magnification factor. Fractal dimensions can be determined using a box counting algorithm¹⁰. This measure provides a statistical index of complexity of structure pattern and its changes with varying measuring scales.

Figure 1.

X-ray images were taken from calcaneus of postmenopausal women with a direct X-ray device. Texture analysis was performed on the region of interest to obtain texture parameters such as co-occurrence, run-length matrices and the fractal parameter H_mean (adapted from ref. 18, with permission from Springer Link).

In clinical studies, fractal analyses of trabecular bone from calcaneus and distal radius radiographs have helped distinguish the patients with osteoporotic fractures from those in an age-matched control group. For example, the fractal analysis of texture on calcaneus radiographs was able to discriminate osteoporotic patients with vertebral fracture from controls²⁰. In addition, multi-centre texture analyses on bone images from calcaneus with a direct digital X-ray device have demonstrated that three texture parameters (co-occurrence, run-length, and fractal parameter H_mean) were significantly lower in osteoporotic fracture cases than in control cases¹⁸. Fractal analysis was also applied to radiographs of distal radius and found that fractal dimensions were significantly different between subjects with and without hip fractures¹³. The power of fractal dimension analyses for predicting fracture risks is comparable to BMD for trabecular bones at the distal radius, but lower than that of total hip BMD¹³. In dental settings, fractal analysis of panoramic images has also detected osteoporotic changes in mandibular canine/premolar trabecular bone²¹.

In in vitro studies, fractal analysis of radiographs has been used to predict 3D microarchitecture of trabecular bone. For example, 2D texture analyses of calcaneus and femoral neck from micro-CT images^17,22, and femoral head from magnetic resonance images¹⁴ have predicted 3D microarchitecture parameters of the trabecular bones. Another study has examined the high-definition macro-radiography of trabecular bone in human lumbar vertebrae using the fractal analysis and has found that the horizontal and vertical trabecular organisation patterns are different between low- and high-BMD groups¹¹. The fractal feature of trabecular bone in knee osteoarthritis is a more sensitive marker of the disease than BMD¹⁶. Combining BMD values with fractal textural analysis of femoral radiographs from a high-resolution X-ray device has shown significant improvement for predicting the fracture load of human femurs, compared with the results obtained from either of the two measurements alone¹⁹.

In addition to plain radiographs, texture analysis has also been applied to other imaging modalities. For example, it has been applied to quantitative CT (QCT) of human vertebral bodies and photomicrography of transiliac crest biopsies and has helped distinguish osteoporotic bone structure from normal bone structure¹⁰. Fractal analysis is also used in high-resolution MRI of distal radius from cadavers²³. The fractal analysis provides the information independent of BMD in predicting failure loads of distal radius.

Although texture analysis on high-resolution radiographs has been performed to identify the parameters that are correlated with microarchitectures of trabecular bone, it has rarely been applied to 2D projection images from DXA scans. The reason is largely due to the limited resolution of DXA sans because fractal dimension analysis requires a large projection surface and distinguishable textures from high-resolution images²⁴. These constraints make it unsuitable for analysis of small surface with moderate resolution, such as DXA images.

Stochastic analysis of 2D projection images

Bone heterogeneity and random field

Although it was still debatable on what spatial resolution is required for clinical assessments of bone fragility, the current consensus is that the image resolution required for clinical evaluations may be much less than that needed in basic research⁶. The improvement of imaging resolution would become non-essential if useful information from bone microarchitecture, such as heterogeneity of spatial mineral distribution, can be extracted from the low-resolution images. Theoretical arguments and empirical data have indicated that the heterogeneity of mineral spatial distribution in bone may be used to reflect some features of trabecular architecture that contribute to the resistance of bone to failure^25,26. Therefore, there is the clinical significance to assess such spatial heterogeneity in bone. Luckily, variations of grey values in 2D projection images, such as DXA images, actually represent the spatial distribution of bone mineral. In addition, the variation of bone mineral distribution is statistically random as it results from numerous complex biological processes (e.g. mineralisation, bone remodelling) in a highly non-linear and unsystematic fashion. Thus, we need to adopt stochastic approaches to examine the 2D projection images and quantitatively assess the heterogeneity of spatial mineral distribution.

Stochastic processes and experimental variograms

Stochastic parameters can be used to represent spatial variations in BMD through a random field approach characterised by an exponential covariance function. Current techniques for quantifying bone heterogeneity consist of descriptive statistics such as mean and standard deviation. However, these parameters do not describe the spatial variations of bone properties. Stochastic assessment of distribution of BMD in 2D projections images of trabecular bone can be described by experimental variograms, which have been widely used in geosciences^27–29.

Previous studies have introduced experimental variograms to describe the inhomogeneity of bone properties^24,30,31. To determine experimental variograms, a semi-variance, γ(h), needs to be defined first as the half of the expected squared differences of BMD between any two locations with a lag distance of h.

$$\gamma (\mathbf{h})=\frac{1}{2}E[{\{Z(\mathbf{x})-Z(\mathbf{x}+\mathbf{h})\}}^2]$$ (1)

where Z(x) is a function describing the random field of BMD in 2D projection images; x and h are vectors; x is the spatial coordinates of the data location and h is the lag distance, representing the Euclidean distance and direction between any two data locations.

Then, the experimental variogram is calculated as an average of semi-variance values at the locations that have the same value of lag distance (h).

$$\widehat{\gamma }(\mathbf{h})=\frac{1}{2m(\mathbf{h})}\sum _{i=1}^{m(h)}E[{\{Z({\mathbf{x}}_{\mathbf{i}})-Z({\mathbf{x}}_{\mathbf{i}}+\mathbf{h})\}}^2]$$ (2)

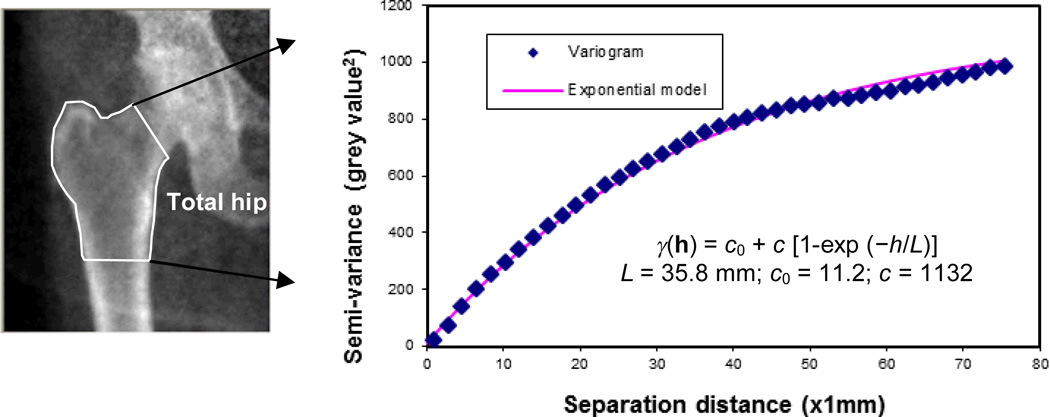
where m(h) is the number of data pairs for observations with a lag distance of h. A typical experimental variogram of DXA images at the hip region (Figure 2) indicated that semi-variance of BMD in DXA images increased with increasing lag distance and reached a plateau, also known as the sill of variograms. It is suggested that as the lag distance increased, the local BMD became more dissimilar on average. This is consistent with the description of a random field in that values at widely separated places are less similar.

Figure 2.

Stochastic assessment of bone mineral density distribution from DXA scans of hip. (a) DXA images; (b) variogram and exponential model to fit the experimental variogram.

Moreover, mathematical (authorised) models are needed to quantitatively describe the mineral distribution in bone using experimental variograms. Examples of simple authorised models are exponential, Gaussian and spherical models. Among them, exponential model fits well with experimental variograms and has the highest R² value in describing the distribution of BMD. Using the model, the semi-variance (γ) of BMD in DXA images can be represented by the following formula:

$$\gamma (\mathbf{h})=c_0+c(1-{\mathrm{e}}^{-h/L})$$ (3)

where γ(h) is the semi-variance as a function of lag distance (h); L (correlation length) describes the degree of smoothness or roughness in the map of BMD. A relatively larger correlation length implies a smooth variation, whereas a smaller correlation length corresponds to acute changes in BMD over the spatial domain; c₀ is the nugget variance, and c is the sill variance. The semi-variance converges to the sum of the nugget variance and the sill variance when the separation distance (h) approaches infinity.

The stochastic measures of BMD distribution from 2D projection images, i.e. correlation length (L), sill variance (c) and nugget variance (c₀), can be obtained by fitting the aforementioned exponential model to the experimental variogram using the least-square estimate.

Stochastic measures of BMD distribution from DXA images

A recent study has introduced the stochastic assessments of DXA images in predicting hip fractures for patients with osteopenia whose T-scores are between −1.0 and −2.5 (ref. 32). DXA scans of the total hip region obtained from 17 post-menopausal women with osteopaenia were analysed. The fracture group (N = 9) included subjects with a history of hip fractures, whereas the control group (N = 8) consisted of age-matched subjects without osteoporotic fractures. The stochastic parameters (i.e. correlation length, sill variance and nugget variance) were estimated from the distribution of BMD in the total hip region (Figure 2).

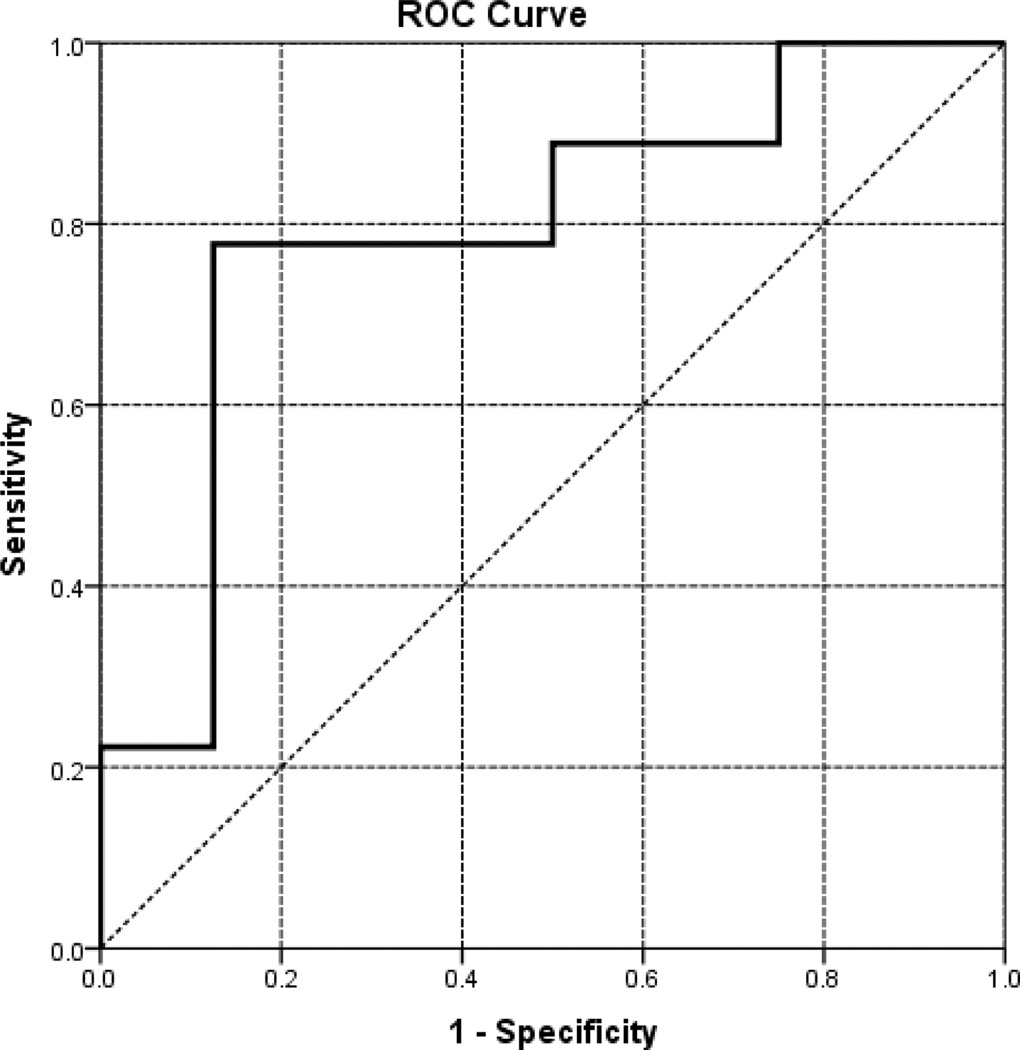
Logical regression models were used to estimate the combined power by both BMD and stochastic parameters in predicting the risk of hip fractures. The outcome of logical regression is represented by a receiver–operator curve (ROC; Figure 3). The area under the ROC (AUC) indicates the accuracy of the logical regression model, with AUC = 1 representing a perfect prediction, whereas AUC = 0.5 representing a worthless test. The analyses indicate that none of the measurement alone has a statistically significant power in predicting bone fracture risks (Table 1). However, the combined power with both BMD and stochastic parameters is statistically significant (p < 0.05) in predicting bone fractures, showing AUC = 0.792 with confidence intervals between 0.562 and 1.000 (Table 1, Figure 3).

Figure 3.

The ROC for a combination of BMD and stochastic parameters. ROC, receiver–operator curve.

Table 1.

The AUC for logistical regression models

Model	AUC	SE	p-value
BMD	0.553	0.146	0.7
Correlation length	0.736	0.131	0.102
Nugget variance	0.653	0.137	0.29
BMD + correlation length + nugget variance	0.792	0.117	0.043

AUC, area under the receiver–operator curve; BMD, bone mineral density; SE, standard error.

Stochastic measures of 2D projection images of trabecular bone

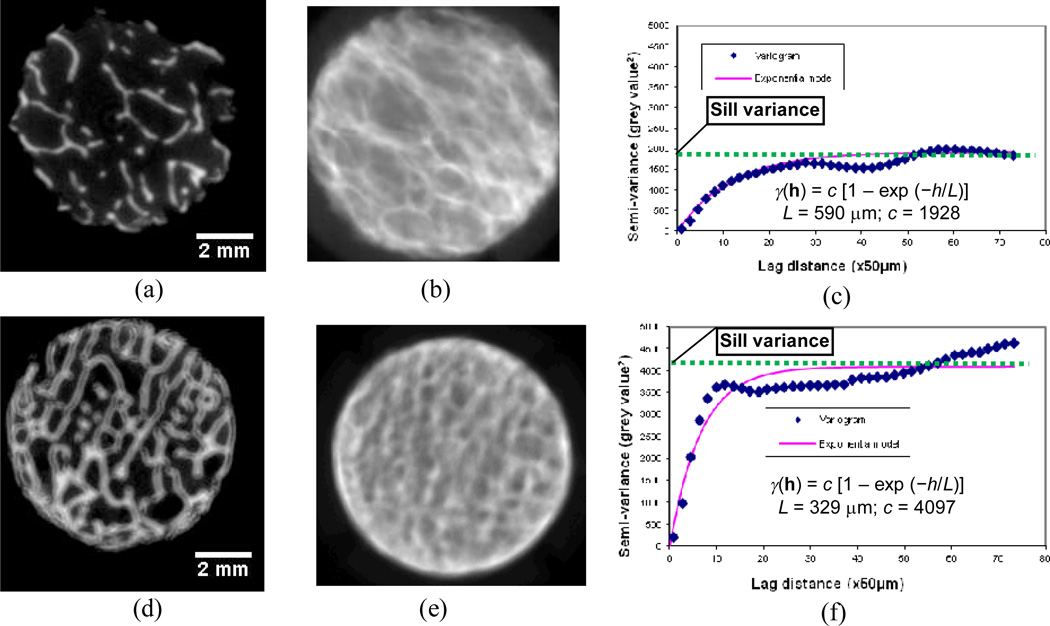
Assessments using stochastic analyses of 2D projection images are significantly correlated to the microarchitecture and mechanical properties of trabecular bone³³. Using a set of experimental data (micro-CT images and mechanical properties) of 15 cylindrical trabecular bone specimens from six male human cadavers (48 ± 14 years old)^34–37, a recent study was performed to verify the correlation of the stochastic assessments based on 2D projection images with the real microarchitecture and mechanical properties of the specimens. In this study, 2D projection images of trabecular bone were generated from high-resolution micro-CT scans by averaging the areal grey values of all scans. Stochastic assessments were performed on the 2D projection images through the aforementioned stochastic analysis. The specimens were divided into two groups with distinct bone porosities (Figure 4a, d). The corresponding 2D projection images exhibited a smoother variation of BMD distribution for the high-porosity group (Figure 4b) and a more acute variation of BMD distribution for the low-porosity group (Figure 4e). The semi-variance in the variogram of trabecular bone with a high porosity or low bone volume fraction (BV/TV = 0.13) reached the plateau slowly at a low sill variance (Figure 4c; c = 1928) whereas the other one (BV/TV = 0.33) arrived at the plateau relatively rapidly at a higher sill variance (Figure 2f; c = 4097).

Figure 4.

Quantification of spatial distribution of bone mineral density in 2D projection images. (a) a slice of micro-CT images with a low bone volume fraction (BV/TV) = 0.13; (b) 2D projection image of the specimen with low bone volume fraction; (c) the variogram of the trabecular bone specimen with low bone volume fraction; (d) a slice of micro-CT images of a dense specimen with BV/TV = 0.33; (e) 2D projection image of the dense specimen; (f) the variogram of the dense specimen.

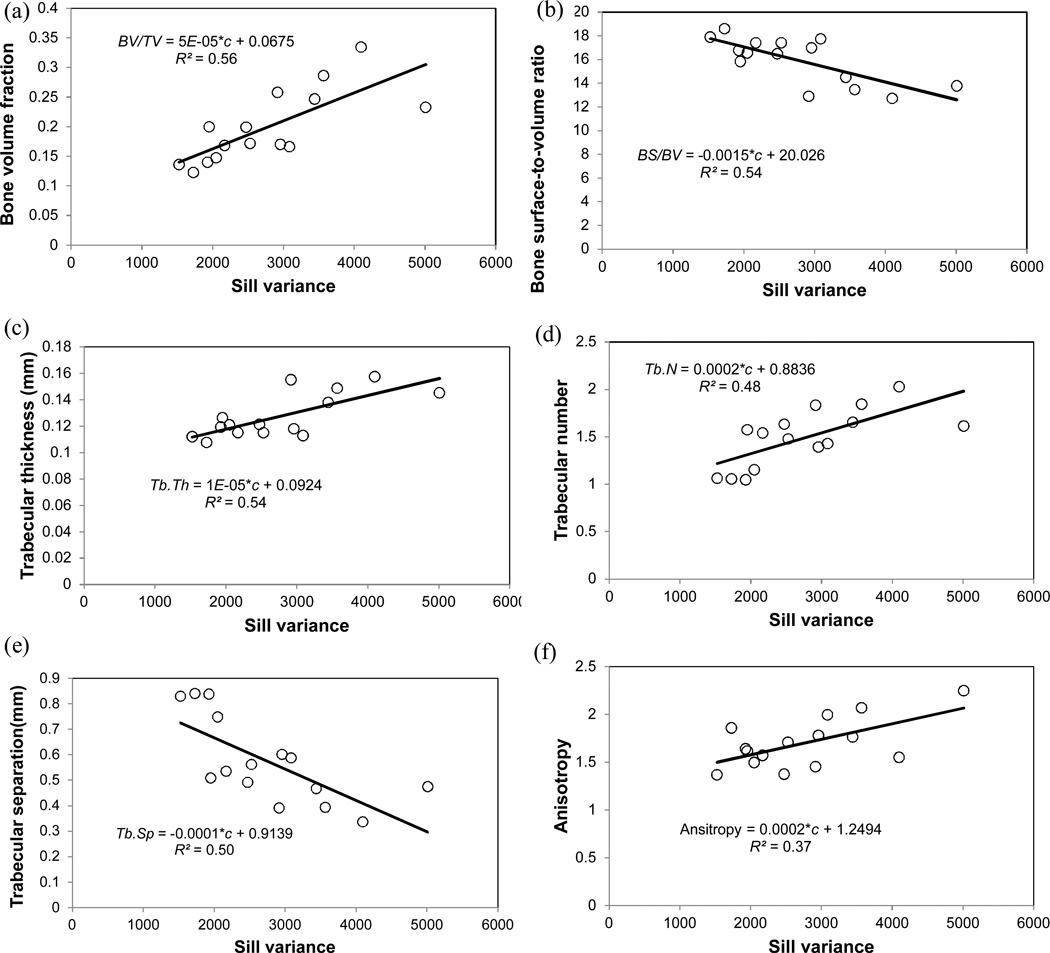
Significant positive relationships were observed between sill variance and the elastic modulus (Figure 5a, R² = 0.81, p < 0.001) and between sill variance and ultimate strength (Figure 5b, R² = 0.82, p < 0.001). Additionally, the sill variance of BMD distribution in bone was correlated with microarchitecture parameters. Linear regression analyses indicated a significant positive relationship between sill variance and bone volume fraction (Figure 6a, R² = 0.56, p = 0.001). Similar relationships were also observed between the sill variance of BMD distribution and other microarchitecture parameters, i.e. bone surface-to-volume ratio (Figure 6b, R² = 0.54, p = 0.002), trabecular thickness (Figure 6c, R² = 0.54, p = 0.002), trabecular number (Figure 6d, R² = 0.48, p = 0.004), trabecular separation (Figure 6e, R² = 0.50, p = 0.003), and anisotropy (Figure 6f, R² = 0.37, p = 0.02).

Figure 5.

Sill variance of bone mineral density distribution had significantly positive relationships with (a) elastic modulus (R² = 0.81, p < 0.001), and (b) ultimate strength (R² = 0.82, p < 0.001).

Figure 6.

Sill variance of distribution of bone mineral density had significantly positive relationships with microarchitecture parameters (a) bone volume fraction; (b) bone surface-to-volume ratio; (c) trabecular thickness; (d) trabecular number; (e) trabecular separation; and (f) anisotropy.

Moreover, combining BMD with the sill variance (Table 2) derived from 2D projection images (R² = 0.83) provided a better prediction of bone strength than BMD alone (R² = 0.63). Thus, it is promising to extend the stochastic assessment of 2D projection images to routine DXA scans, thus offering an improved methodology to predict bone fragility with marked clinical significance.

Table 2.

Regression analyses of combination of BMD and sill variance from high resolution 2D projection images (50 µm)

Model	R2	Adjusted R2	p-value
Strength ~ BMD	0.63	0.61	<0.001
Strength ~ BMD + sill variance	0.83	0.80	<0.001

BMD, bone mineral density; 2D, two-dimensional.

3D imaging modalities

The advantages of 3D imaging modalities are that the microarchitectures of trabecular bone can be directly assessed and trabecular bone can be separated from cortical bone. 3D CT and MRI have been used to assess bone fragility in both research and clinical settings.

Standard clinical CT scanners can be transformed into a QCT by placing a specific mineral-equivalent phantom to calibrate the image data⁶. Current techniques include single-slice technique, row-spiral technology and flat-panel volume system. Multi-slice spiral CT scanners have achieved an in-plane resolution of approximately 200 µm and slice thickness of 500 µm. It has been used in vivo to evaluate the lumbar spine, yet its performance with regard to differentiating patients with and without fractures has not been substantially better than BMD. The latest high-resolution peripheral QCT systems (HR-pQCT) are reported to achieve resolutions of up to 80 µm at tolerable radiation doses (Figure 7).

Figure 7.

Human tibia images obtained from HR-pQCT technique (Xtreme CT, Scanco Medical AG, Basserdorf, Switzerland). Imaging source is from www.scanco.ch.

Images of trabecular bone at appendicular sites can be obtained using MRI-based approach⁶. Such imaging technique makes use of specially designed coils in the newest high magnetic field clinical scanners. Such in vivo imaging technique can achieve an in-plane resolution of 150 µm and a slice of thickness of 250 µm³⁸. The apparent trabecular properties obtained from the MRI technique have shown strong correlations with measurements of trabecular microarchitecture from high-resolution techniques such as HR-pQCT³⁹. Some have reported that the patients with hip and vertebral fractures can be distinguished from control subjects using MRI-derived parameters³⁸. Future developments need to address the current limitations of high-resolution MRI, such as the requirement for specialised coils, the limitation to assessment at peripheral sites, and the relatively long acquisition times⁶.

One of the most promising 3D imaging techniques is HR-pQCT (i.e. in vivo micro-CT technique). The effectiveness of assessing trabecular microstructures of tibia and distal radius with HR-pQCT has been demonstrated in a number of recent studies in clinical settings. For example, deterioration of microstructure of distal radius and tibia has been observed in women during and after prolonged bed rest⁴⁰. Differences in bone microarchitecture are detected between post-menopausal Chinese-American and white women⁴¹. By examining the distal radius and tibia in daughter–mother pairs using HR-pQCT, it has been demonstrated that trabecular bone in childhood can be used to predict both trabecular and cortical morphology in adulthood⁴². In addition, HR-pQCT has also been used to monitor the usefulness of countermeasures of bone loss such as exercise and nutrition⁴⁰, whole-body vibration⁴³ and oral ibandronate⁴⁴.

Furthermore, in vitro studies have also verified the effectiveness of HR-pQCT in assessing bone microstructures. Comparison of bone microarchitecture of femoral necks evaluated by HR-pQCT and conventional histomorphometry has demonstrated that significant correlations were found between both techniques for trabecular bone volume, trabecular number, trabecular thickness, trabecular separation and trabecular connectivity⁴⁵. Individual trabecular segmentation-based morphological analysis has been applied to both HR-pQCT images and micro-CT images of human tibias and indicated that individual trabecular segmentation measurements of HR-pQCT images are highly reflective of the trabecular bone microarchitecture⁴⁶.

The major limitations to the HR-pQCT technique are that it needs specialised equipment, is restricted to evaluation at appendicular sites and employs ionising radiation, which may limit its use in certain patient populations.

Conclusion

HR-pQCT imaging technique may provide direct measurements of microarchitectures of trabecular bone in vivo. However, we have limited access to such facilities and the affordability is a major concern for the general public. Such an imaging modality may remain a high-end research tool to help understand bone fragility. On the other hand, the combination of BMD and stochastic assessment of distribution of BMD may offer an economic and effective approach to non-invasively evaluate skeletal integrity and identify the at-risk population for osteoporotic fractures.

Abbreviations list

AUC

area under the ROC

BMD

bone mineral density

CT

computed tomography

DXA

dual-energy X-ray absorptiometry

HR-pQCT

high-resolution peripheral QCT

MRI

magnetic resonance imaging

QCT

quantitative CT

ROC

receiver–operator curve

2D

two-dimensional

3D

three-dimensional