A comparison of binding surfaces for SPR biosensing using an antibody-antigen system and affinity distribution analysis

Abstract

The application of optical biosensors in the study of macromolecular interactions requires immobilization of one binding partner to the surface. It is often highly desirable that the immobilization is uniform and does not affect the thermodynamic and kinetic binding parameters to soluble ligands. To achieve this goal, a variety of sensor surfaces, coupling strategies and surface chemistries are available. Previously, we have introduced a technique for increasing the level of detail on the immobilized sites beyond an average affinity by determining the distribution of affinities and kinetic rate constants from families of binding and dissociation traces acquired at different concentrations of soluble ligand. In the present work, we explore how this affinity distribution analysis can be useful in the assessment and optimization of surface immobilization. With this goal, using an antibody-antigen interaction as a model system, we study the activity, thermodynamic and kinetic binding parameters, and heterogeneity of surface sites produced with different commonly used sensor surfaces, at different total surface densities and with direct immobilization or affinity capture.

Introduction

Biosensors have become an important tool in the study of macromolecular interactions, and many different design principles have been described that measure surface bound molecules label-free and with exquisite detection limits. These include optical biosensors based on surface plasmon resonance [1–3], resonant mirror [4], interference reflectometry [5, 6], and other optical evanescent wave principles [5, 7, 8], as well as quartz crystal microbalance biosensors [9]. In order to fully take advantage of the detection limits for analytes, all biosensors have in common the need for a sensing surface with high sensitivity and specificity. The latter is usually achieved through the creation of a surface layer of binding sites, usually through the surface immobilization of macromolecules, that can capture with high affinity its soluble binding partners (the analyte) flowing across the sensor surface, but is otherwise inert. Furthermore, for the purpose of biosensing in the study of macromolecular interactions, it is highly desirable, and often essential, that the surface attachment of the stationary binding partner does not diminish its binding energy or kinetics for the soluble analyte [1].

It is widely appreciated that creating such a specific surface with uniform ensemble of sites is a non-trivial task. For example, the proximity of the surface can add steric constraints and surface potentials contributing to the free energy of binding. Similar to the attachment of fluorophores or other extrinsic moieties in other biophysical techniques, the surface attachment of the macromolecule – covalent or through high-affinity capture – has the potential of altering the macromolecular conformation and/or access to the binding site. Due to the rugosity and microheterogeneity of the surface environment, heterogeneity of the surface sites may result [10]. Considering that in the overwhelming majority of published SPR biosensor studies random immobilization chemistries are used, and that often a significant fraction of the surface bound molecules has become inactive after immobilization (or after exposure to chemical ‘regeneration’ conditions that are designed to reversibly reduce the life-time of the bound state), it is easily conceivable that this could render a subset of molecules partially active. For these reasons, an ensemble of molecules that is well-described by a single set of thermodynamic parameters in solution may be expected to experience some dispersion of binding energies once immobilized to a surface. Many examples for heterogeneity of surface binding sites caused by immobilization have been reported [11–16].

In SPR biosensing, the most commonly employed surfaces have flexible polymeric linker layers, such as a carboxymethyl dextran brush. This has the virtue of separating the macromolecule from the surface to provide better access to the binding partner, suppress non-specific surface binding, and facilitate surface attachment [6, 10, 17]. On the other hand, diffusion through this layer has the potential to pose a limiting step for the binding kinetics [6, 18], and the non-uniform density distribution of the macromolecules in this layer could create microenvironments with different charge, pH, and surface crowding [10]. Interactions between immobilized protein and matrix are evident from altered dextran structure after immobilization or ligand binding [6, 19], and vice versa, for the fundamental reason that these forces must also act on the proteins. In some published cases, these matrix effects appear to be absent [20], but in others they dominate the surface binding signals [21, 22]. Clearly, tools to control for surface heterogeneity and other differences in the binding energetics are of critical importance for the use of optical biosensors to characterize macromolecular interactions.

SPR biosensing can provide data with excellent reproducibility and signal/noise characteristics, and therefore offers the possibility of detailed computational analysis. This contrasts with misfits of experimental data by overly simplistic, one or few site models found frequently in the literature. However, even though it is possible to embark on the development of ad hoc models with more complex reaction schemes that will invariably fit the data better, in the absence of independent confirmation they do not inspire much confidence [23, 24], especially in view of the experimental difficulties outlined above [25]. Recently, we have taken the opposite approach and introduced a data analysis model that we believe is closer to the experimental reality by not requiring the assumption of discrete classes of surface binding sites. Instead, it is based on modeling the data with an integral equation that describes the surface sites as a (quasi-)continuous two-dimensional distribution of affinity and kinetic rate constants [15]. Remarkably, this model routinely provides fits of the measured data with root-mean-square deviations (rmsd) on the order of the noise of data acquisition. We have previously used this model to demonstrate, with different antibody-antigen systems, the presence of heterogeneity and microheterogeneity in immobilized Fab fragments, as well as various classes of non-specific sites ascribed to the sensor surface [13–15]. For the study of protein interactions, resolving these sites allows us in a second stage to focus on the peak in the affinity/kinetic rate distribution that is presumed to reflect best native binding of molecules in solution [25–30].

The purpose of the present work was to demonstrate how the continuous affinity/kinetic rate distribution approach can be used to compare the performance of different sensor surfaces. To this end, we have collected SPR biosensor data of antigen binding to a monoclonal antibody immobilized with different chemistries, and different total immobilization density, to three different commercial sensor surfaces with different dextran coatings. We found significant differences in the surface site distributions, including the average values in the main peak for the affinity and kinetic rate constants, but also for the degree of transport limitation as well as non-specific binding. Although this pilot study is very limited in the repertoire of surface chemistries applied, it highlights the impact of the surface properties on the observed surface site affinity distributions, and indicates the utility of this analysis approach for more systematic experimental optimization.

Materials and Methods

Reagents

β₂-microglublin (B2MG) from human urine (catalog number: M4890) was purchased from Sigma-Aldrich (St. Louis, MO). A randomly biotinylated form of mouse monoclonal antibody to β₂-microglublin (anti-B2MG-biotin) was acquired from Abcam (Cambridge, MA, catalog number: ab21899). The capture molecule, streptavidin (SA) and D-biotin were purchased from Thermo Scientific Pierce Protein Biology Products (Rockford, IL, catalog numbers: 21125 and 29129). HBS-EP buffer (10 mM HEPES pH 7.4, 150 mM NaCl, 3.4 mM EDTA, 0.005% surfactant P20), reagents for amine coupling (N-(3-dimethylaminopropyl)- N’-ethylcarbodiimide hydrochloride, N-hydroxysuccinimide, and acetate buffers) as well as sensor chips C1, CM3 and CM5 were acquired from Biacore, GE Healthcare (Piscataway, NJ).

Sensor Surfaces and Binding Experiments

The antibody was coupled to the sensor surfaces C1, CM3, and CM5 by amine coupling using the standard protocol [31, 32]. Immobilization was performed with the antibody at 30 μg/mL at pH 5.5 using a flow rate of 5 μL/min. Alternatively, affinity capture by SA was used. For this purpose, SA at a concentration of 100 μg/mL in sodium acetate buffer, pH 5.5, was immobilized to the sensor surfaces C1, CM3, and CM5 using standard amine coupling, followed by injection of anti-B2MG-biotin at 25 μg/mL in the working buffer (HBS-EP) to capture the antibody, and application of biotin to block unoccupied sites. Consistent with reported binding constants of SA for biotin [33], dissociation of anti-B2MG-biotin from the SA functionalized surface was negligible during the course of the binding study. In both direct immobilization and capture approaches, the surface density of immobilized antibody on CM3 and CM5 sensor chips was varied; the immobilization level of SA (1000 – 2000 RU) and anti-B2MG-biotin (800 – 6000 RU), respectively, was controlled by varying the exposure time during immobilization. For each sensor chip, a reference surface was generated by mock derivatization without anti-B2MG-biotin antibody, and for affinity capture the same amount of SA was immobilized on the reference surface as the working surfaces on the same sensor chip.

SPR binding experiments were conducted in Biacore X and Biacore 3000 instruments (GE Healthcare, Piscataway, NJ), at a temperature of 25 °C, using HBS-EP as working buffer for all the experiments. A concentrated stock of B2MG (8.6 μM) was diluted in HBS-EP, and a series of 5 or 8 concentrations (0.1 – 100 nM) of B2MG were injected across the sensor surface at a flow rate of 5 or 10 μL/min. The time-course of binding was observed between 500 – 2000 sec, dependent on B2MG concentration. This was followed by the observation of the dissociation process for 2000 – 6000 sec, during which the surface was rinsed with HBS-EP buffer. Because the signal decreased to baseline level at the end of dissociation, a regeneration step was not necessary.

Data Analysis

Data analysis was conducted with the software EVILFIT [15]. First, sensorgrams were preprocessed using BIAevaluation (version 4.0.1, Biacore GE Healthcare, Piscataway, NJ), to subtract the signal response from the designated reference cell (including bulk refractive index changes), and to subtract remaining background signals measured in blank buffer injections. The net binding traces were aligned to assign 0 sec to the start of the injections, and exported into an .xls file. This file was loaded into EVILFIT, where the kinetic traces in each data set were globally fit at all concentrations with a model for continuous distributions of affinity constants and dissociation rate constant (see below). For a few data sets from surfaces with high surface density of immobilized molecules, the binding traces at all concentrations were globally analyzed using the distribution model combined with a two-compartment approximation of mass transport [14, 25]. The peaks of the calculated distribution were integrated to resolve the average equilibrium dissociation constant and dissociation rate constant.

Theory

The simplest model to describe the binding data from SPR biosensors is that of a single pseudo-first-order reaction, where binding of a single class of analyte to a single class of ligand on the surface is assumed. In this model, the binding sites on the surface exhibit a discrete affinity K_A, (K_A =1/K_D), and a signal at total binding capacity s_max. The kinetic association/dissociation process is described by the on-rate constant k_on and off-rate constant k_off (K_D = k_off/k_on) with the rate equation

$$\frac{ds}{dt}=k_{on}c(s_{\text{mnax}}-s)-k_{off}s$$ (1)

where the s is the measured signal (in RU) at time t after injection of analyte at concentration c. When steady-state binding is reached, the signal follows a Langmuir isotherm,

$$s_{eq}\left(c\right)=\frac{s_{\text{max}}}{1+{\left(K_{A}c\right)}^{-1}}$$ (2)

[34]. Assuming the association starts at t₀ s, we can obtain the signal, s_a for t s during association phase.

$$s_a(c,t)=s_{eq}\left(c\right)\left(1-e^{-(k_{on}c+k_{off})(t-t_0)}\right)$$ (3)

For dissociation after association with a contact time t_c, the time dependent signal change can be described as the following equation.

$$s_d(c,t)=s_a(c,t_c)e^{-k_{off}(t-t_c)}$$ (4)

In order to account for unknown degree of heterogeneity of the surface binding sites, we have extended this model to a two-dimensional distribution of equilibrium dissociation constants and rate constants, P(k_off, K_D), allowing for a range of K_D and k_off values [15]. In this model, the binding signal reported by the SPR biosensor is the linear superposition of the signals from binding to the different classes of surface sites, and can be expressed as a Fredholm integral equation

$$s_{obs}(c,t)=\iint s_1(c,t,k_{off},K_D)P(k_{off},K_d)d{K}_{d}d{k}_{off}$$ (5)

where s₁(c,t,k_off,K_D) denotes the binding traces of a single class of sites (following Eq. (2)-(4) at unit binding capacity s_max = 1 RU). The distribution of sites P(k_off, K_D) was calculated after discretization of Eq. (5) in a logarithmic grid of (k_off,i, K_D,i) values with 3 – 4 grid points per decade, through a global fit to several association and dissociation traces at different analyte concentrations. Tikhonov regularization was used at a confidence level of P = 0.95, to determine the most parsimonious distribution that is consistent with the data, showing only features that are essential to fit the data [15, 35]. Corrections for a decay of the binding surface with time introduced by Ober & Ward [36] are compatible with this calculation and have been implemented, although they were not required in the present work due to the absence of a chemical regeneration step. EVILFIT can be downloaded from https://sedfitsedphat.nibib.nih.gov/software/default.aspx with instructions at https://sedfitsedphat.nibib.nih.gov/tools/EVILFIT%20demo/Forms/AllItems.aspx, and a demo video at http://youtu.be/QXkXTN0gwck.

Besides heterogeneity, mass transport limitation is another major concern to complicate the binding data and interpretation. As shown previously [14], mass transport limited binding processes cannot be fit well with the standard distribution model Eq. (5). In the presence of limited mass transport, the analyte in the bulk does not migrate sufficiently fast due to hindered diffusion and/or fast association and slow dissociation. Therefore a depletion zone of analyte in the vicinity of the surface sites is formed during the association phase, and a retention zone exists during the dissociation phase. We have previously employed a two-compartment model to account for the transportation step for the cases with moderate mass transport limitation [37, 38]. In this model, the two compartments are designated as a bulk compartment with analyte concentration of c, and a hypothetical compartment at the surface with analyte concentration of c_surf. The rate equation for binding Eq. (1) is now extended by an additional transport of analyte molecule from one compartment to the other with a transport rate constant k_tr:

$$\frac{d{c}_{surf}}{dt}=k_{tr}(c-c_{surf})-\frac{ds}{dt}$$ (6)

$$\frac{ds}{dt}=k_{on}{c}_{surf}(s_{\text{max}}-s)-k_{off}s$$ (7)

In order to take both surface heterogeneity and mass transport limitation into account, we extend Eq. (7) to many classes of sites i, each reflecting a particular point P(k_off,i, K_D,i) of the distribution. We have shown that under steady-state conditions, where dc_surf/dt is negligible, this leads to the system of rate equations

$$\frac{d{s}_i}{dt}=k_{on,i}c(s_{\text{max},i}-s_i)-k_{off,i}{s}_i-\frac{k_{on,i}(s_{\text{max},i}-s_i)}{k_{tr}}\sum _{j=1}^N\frac{d{s}_j}{dt}$$ (8)

where binding to all classes of sites is coupled due to the their joint contributions to the depletion/retention zone [14]. As in the case where transport limitation is absent, for solving Eq. (8) we discretized the distribution with a logarithmic division of a K_D –range and k_off-range, both chosen sufficiently wide to ensure a global fit of the data at different concentrations to within the noise of data acquisition. In addition, limits on k_on values were imposed to facilitate the solution of Eq. (8). The transport rate constant was optimized by least-squares minimization [14]. The mass transport limited distribution model was implemented MATLAB (The MathWorks, Natick, MA) using scripts written in house.

Results and Discussion

Immobilization of anti-B2MG-biotin using amine coupling on C1, CM3 and CM5 sensor chips

First, we used amine coupling to immobilize anti-B2MG-biotin on the three types of sensor chips with different lengths of carboxymethylated dextran. The sensor chip CM5 matrix extends about 100-200 nm from the gold surface [39], whereas CM3 sensor chips have shorter dextran chains than CM5 with approximately 30% of the binding capacity [40], and C1 has a flat carboxylated surface with no dextran matrix.

For the C1 sensor chip, despite a sufficiently high antibody immobilization level of 800 RU, the application of a virtually saturating concentration of 100 nM of B2MG yielded only 15 RU maximum binding signal, which is only ~12% of the theoretically expected signal (data not shown). The concomitant low signal/noise ratio and comparatively large noise due to baseline uncertainties made the data acquisition unreliable. Thus, no titration series with analyte were generated for the binding system under study.

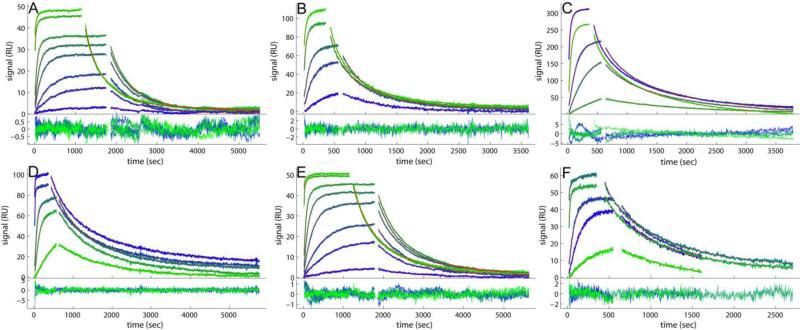
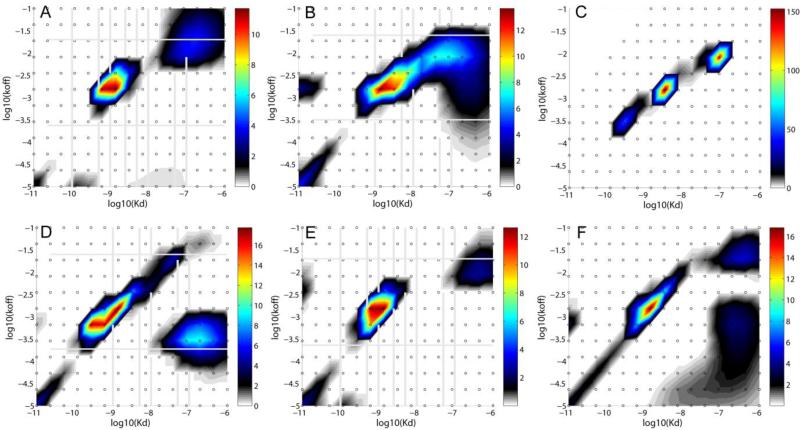
For the CM3 sensor chip, we were able to obtain different immobilization levels at 1350, 3200, and 4100 RU by adjusting the contact time of the ligand with the activated surface. Binding experiments yielded good data quality for all three surfaces (Figure 1A and Figure S1A-C), and excellent fits with the distribution model with low rmsd values for all the CM3 data sets at 0.30 – 0.40 RU, which is in the order of the noise of the data acquisition (Table 1). An example of the resulting surface site k_off - K_D distribution is shown in Figure 2A for the low density surface. The signal density of the peaks can directly be discerned from their color, which is scaled according to the color bar on the right side of the distribution plot. For the surfaces with all three different immobilization densities, a direct comparison of the families of surface binding traces, as well as their fits and resulting distributions, are shown in the Supporting Information Figures S1A-C and S2A-C, respectively.

Figure 1.

Comparison of the experimental data and fits for binding of soluble B2MG to a monoclonal IgG antibody immobilized on different sensor surfaces. Binding data (blue to green) and best-fit (red lines, virtually superimposed by the blue/green lines) from the affinity and kinetic rate constant distribution model without (A, B, D, E, F) and with two-compartment transport approximation (C). Excellent fits are achieved for all the data sets, with rmsd values listed in Table 1. For each panel, the binding traces and best-fits are shown on the top, and the residuals of the fit are shown on the bottom. (A) B2MG at 0.1, 0.5, 1.0, 2.5, 5.0, 10, 50 and 100 nM binding to a CM3 sensor chip with 1350 RU of anti-B2MG-biotin immobilized. (B) B2MG at 1.0, 5.0, 10, 50 and 100 nM binding to a CM5 sensor chip with 3000 RU of anti-B2MG-biotin immobilized. (C) B2MG at 1.0, 5.0, 10, 50 and 100 nM binding to a CM5 sensor chip with 6000 RU of anti-B2MG-biotin immobilized. (D) B2MG at 1.0, 5.0, 10, 50 and 100 nM binding to a C1 sensor chip with 1500 RU of anti-B2MG-biotin captured on the surface with 1500 RU of SA immobilized. (E) B2MG at 0.1, 0.5, 1.0, 2.5, 5.0, 10, 50 and 100 nM binding to a CM3 sensor chip with 800 RU of anti-B2MG-biotin captured on the surface with 880 RU of SA immobilized. (F) B2MG at 1.0, 5.0, 10, 50 and 100 nM binding to a CM5 sensor chip with 1000 RU of anti-B2MG-biotin captured on the surface with 1000 RU of SA immobilized.

Table 1.

Thermodynamic and kinetic parameters from the distribution analyses of the different surfaces

surface	immob (RU)	total signal (RU)	rmsd (RU)	major peak (RU)	Kd (nM)	koff (10-3 s-1)	kon (106 M-1s-1)	minor peak (RU)	peak ratio minor/major	activity* (%)	log10(ktr)
C1	800	15			n.d.					12
CM3	1350	86	0.30	37	1.2	1. 9	1. 6	42	1.13
CM3	3200	110	0.36	62	1.0	1.6	1.6	32	0.52	22
CM3	4100	100	0.40	82	1.1	1.4	1.3	8	0.10	16
CM5	3000	176	0.73	74	3.2	2.3	0.72	90	1.21	38
CM5	6000	461	1.59	254	2.4	1.2	0.49	183	0.72	50	9. 7
C1-SA	1500	175	0.83	78	0.80	1.1	1.4	73	0.94	75
CM3-SA	800	68	0.32	44	0.90	1.4	1.5	14	0.32	55
CM3-SA	2600	221	0.71	120	0.96	1.1	1.1	41	0.34	55	13 .1
CM5-SA	1000	143	0.71	143	1.4	1.7	1.3	43	0.30	93
CM5-SA	2000	135	0.76	97	2.2	1.9	0.87	-	-	44	7. 8

^*The activity is the ratio of maximum calculated total binding signal at saturation to the predicted binding capacity based on the immobilization signal, the molecular mass of the analyte and the ligand, and the binding stoichiomtry.

Figure 2.

Best-fit affinity and kinetic rate constant P(k_off, K_D) distribution from the global fit of all traces in corresponding panels of Figure 1. A: CM3; B: CM5 (low density); C: CM5 (high density); D: C1-SA; E: CM3-SA; F: CM5-SA. The distribution is modeled using a grid of 12 k_off values between 10^-5 and 10^-1 s^-1, and a grid of 15 K_D values between 0.01 nM and 1 μM, as indicated by the small circles, with Tikhonov-Phillips regularization on a P = 0.95 confidence level. Each distribution is depicted as a color temperature contour plot, with the color scale depicted in the color bar on the right side.

In this study, the distributions resulted from the analysis in EVILFIT vary from one data set to another, and for all three surfaces, heterogeneity of the surface sites is clearly observed (Figure 2). Often, in addition to the major peak several smaller peaks with different shapes are apparent, which reflect on the different properties of the surface. Even though it is a gross oversimplification to regard the distribution as two classes of sites, for pragmatic classification of the results we distinguish between a ‘major peak’ that contains the majority of the signal, and the ‘minor peak’ corresponding to the second most populated region in the affinity distribution space. (We believe this approach, now possible by the distribution analysis, is superior to an approach where the surface heterogeneity is blindly approximated by two discrete classes of sites, considering the a priori unknown heterogeneity of the surface and the considerable variation in the details of the distributions observed in the present study.) The major peak represents the binding event of interest at K_D of ~1 nM, k_off of ~1.5 – 2.0×10^-3 s^-1. These parameters are virtually independent of the immobilization level, and the signal attributed to these sites increases as more antibody is immobilized, although not strictly in proportion to the total immobilization density (Table 1). By contrast, for the minor peak both position and density vary between the three surfaces. We can only hypothesize about the nature of the sites, but considering that signals from ‘non-specific’ sites at the blank surface should largely be compensated for by subtraction of the reference cell signal, the most likely explanation appears to be that they are immobilized antibodies with reduced binding energy due to the local micro-environment and/or their particular orientation and cross-linking position. Interestingly, the signal contribution of these sites decreases with increasing total antibody immobilization level, and the fraction of the desired high-affinity binding sites among all available sites increases, despite the decreasing total surface activity (Table 1). Unfortunately, we also cannot distinguish the affinity of the individual molecules during the immobilization process, which makes the interpretation ambiguous. The material producing the additional 900 RU seems to be partially active and partially inactive, but perhaps is fortuitously blocking access to the previously generated lower-affinity sites, which one could speculate may be experiencing some degree of steric hindrance, for example, from the location in the interior of the matrix. In any event, the surface immobilization density dependence of the abundance of the low-affinity sites allows us to rule out purely random immobilization chemistry as the (sole) underlying cause.

For the CM5 sensor chip, two immobilization levels were explored, 3000 and 6000 RU. Figure 1B and Table 1 show a good fit of the 3000 RU data set in the surface site distribution model with an rmsd of 0.73 RU, with the best-fit distribution in Figure 2B. A comparison of the fits and the distributions of both surfaces can be found in Supplementary Figures S1D/E and S2D/E, respectively. The resulting k_off - K_D distributions yielded a similar peak pattern for the major and minor peaks as the CM3 surfaces, even though these two peaks appear slightly more distinct with the CM5 surface. For these surfaces, the minor peak signal is comparable to that of the major peak, indicating a binding surface with large interference of unwanted binding sites (Table 1). For example, at a comparable immobilization level of ~ 3000 RU, CM5 surfaces exhibited threefold more low-affinity sites, at comparable levels of high-affinity sites. Further, with the CM5 surfaces, we did not see masking of the lower affinity sites with increasing immobilization density, possibly related to the overall larger binding capacity of the longer-chain dextrans, which even at the experiments with 6000 RU is far from being exhausted.

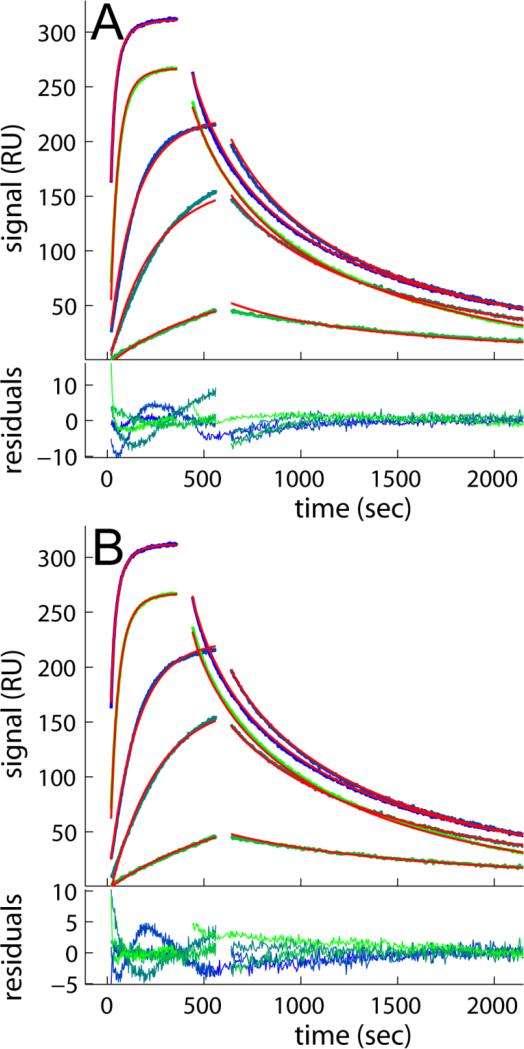
An aspect not observed with the CM3 surfaces is highlighted in Figure 3, where it can be discerned that the 6000 RU data set show more linear feature at the beginning of the association phase and shapes of the dissociation process that cannot be fit with the distribution model (Figure 3A) unless partial mass transport limitation is accounted for (with a best-fit transport rate constant k_tr of 10^9.7 RU×M^-1×s^-1) (Figure 3B). This is a well-known phenomenon of this surface at high binding capacities [14, 18]. As shown previously, limiting the mass transport could in principle be either a stagnant boundary layer or partitioning/diffusion within the dextran matrix [14, 18]. Even though the diffusion time of molecules in the bulk across a distance corresponding to the depth of the matrix, a few hundred nanometers, would be very short, the transport in the functionalized matrix is a coupled reaction/diffusion where propagation proceeds much differently and transport is substantially slowed down by many orders of magnitude due to the capture of freely diffusing molecules by the reactive sites, both specific and non-specific [41, 42]. The magnitude of this effect depends largely on the number of sites, but also on the surface and on crowding impacting the hydrodynamic friction, as well as on repulsive interactions and other factors modulating the diffusivity of the free analyte [18]. Interestingly, even after accounting for the mass transport influence, the average k_off and K_D of the major peak for both 3000 and 6000 RU data shows less tight binding, about 2- 3 fold lower than that of the CM3 surfaces. This is consistent with the results from the lower density CM5 surface, and mainly the result of a slower association, because the dissociation kinetics is similar with that of the CM3.

Figure 3.

Mass transport limited binding of B2MG at 1.0, 5.0, 10, 50 and 100 nM binding to CM5 sensor chip with 6000 RU of anti-B2MG-biotin. The effects of mass transport limitation on the binding progress data are highlighted in comparison of the best-fit distribution model not accounting (A) or accounting for mass transport limitation in a two-compartment approximation (B). Experimental traces are lines colored in blue to green, fits are the solid red lines, and residuals are shown in the bottom of each panel, with rmsd of 2.26 RU and 1.59 RU, for A and B, respectively.

Capturing anti-B2MG using streptavidin on C1, CM3 and CM5 sensor chips

The second immobilization approach used in the current study is high affinity capture with streptavidin (SA). The extremely high affinity binding between SA and biotin or biotinylated molecules lends itself to a stable capture. SA was immobilized on the sensor surfaces using amine coupling then anti-B2MG-biotin was captured on top of the SA layer, and unoccupied SA sites were blocked by biotin. A control experiment has been carried out to confirm there is no binding detectable between immobilized SA and the analyte, B2MG.

The C1 sensor chip once functionalized with 1500 RU of SA immobilized was able to capture 1500 RU of anti-B2MG-biotin antibody. The binding data generated from the resulting surface (C1-SA) yielded a nice fit with the surface site distribution model giving an RMSD of 0.83 RU as shown in Figure 1D and Table 1. Its distribution plot (Figure 2D) displays a major peak at a position similar to that of CM3 surfaces while slightly shifting to the left, indicating a small increase in affinity. In fact, the average K_D (0.80 nM) of this peak shows the highest affinity of all the distributions for the binding system of interest in the current study. The association rate constant is comparable with that of the CM3 surfaces, while the k_off value is 50% lower than the average value from the three CM3 data sets. The slower dissociation might be due to the stickiness of C1 surface since no polymer matrix support is present to minimize the adsorption of the protein by the hydrophobic surface. Since the capture agent, SA can specifically bind to the ligand, one might expect a more homogeneous binding surface in this approach than with the random chemistry of direct amine coupling. However, the antibody used here was also randomly biotinylated, and the randomness of the amine coupling did not seem to be the sole or major reason for heterogeneity on the CM3 surface (see above). In any event, the distribution of C1+SA data shows the surface is still heterogeneous, displaying a slightly broadened major peak and some minor peaks similar to those of the CM3 data. The most predominant of the minor peaks contributes similar amount of signal as the major peak (signal_minor/major=0.94), indicating a substantial population of undesired binding sites. On the other hand, this minor peak shows a much lower k_off (3.01×10^-4 s^-1) than that of the CM3 (low) and CM3 (high) surfaces (~2 ×10^-2 s^-1) and CM5 surfaces (5–9×10^-3 s^-1). We do not know the origin of this, but one could speculate it might be related to a greater hydrophobicity of the C1 surface or with electrostatic effects.

For the CM3 sensor chip two immobilization levels of SA were studied, with 800 RU and 2600 RU anti-B2MG-biotin captured on similar amounts of SA (Figure 1E and Supporting Information Figure 1G/H). The calculated distributions of both CM3+SA data sets (Figure 2E and Supporting Information Figure 2G/H) show again a similar overall pattern as those without SA, but with higher activity of the surface and higher ratio of high-affinity to low-affinity sites (Table 1). The ‘masking’ effect of lower affinity sites was not observed, suggesting a more uniform immobilization process. Notably, similar to the C1+SA surface, the major peak in the distributions of the CM3+SA surfaces has again a slightly higher affinity than on CM3 in the absence of SA (Table 1). For the CM3-SA at the high surface density we observed slight, but distinct mass transport limitation with k_tr of 10^13.1 RU×M^-1×s^-1.

Finally, CM5 sensor surfaces with different levels of SA immobilized were generated at final surface densities of anti-B2MG-biotin antibody of 1000 RU and 2000 RU, respectively (Figure 1F, and Supporting Information Figure S1 I/J). Consistent with the other surfaces, the major high-affinity peak of the CM5-SA surface is at slightly higher affinity than that of the CM5 surface in the absence of SA, and similar to CM3 surfaces (Table 1). Interestingly, the distribution at the high immobilization density of CM-5 is more uniform than that at low density, reminiscent of the findings of the CM3 surface (Figure 2F and Supporting Information Figure S2I/J).

With the same high-density CM5-SA surface, we found a strongly mass transport limited binding, with a best-fit estimate for k_tr of only 10^7.8 RU×M^-1×s^-1, which is the lowest transport rate constant of all surfaces created in this study,. This is remarkable as the total binding capacity of the surface for B2MG is significantly lower than that of the highly loaded CM5 surface, thus creating less of a depletion zone in the flow above the sensor surface, and at the same time the total macromolecular concentration is lower (2000 RU SA + 2000 RU anti-B2MG-biotin versus 6000 RU anti-B2MG-biotin), thus offering a less crowded surface. A third factor contributing to transport limitation are weak, transient non-specific sites that act as sinks for diffusion [41, 42]. It seems possible that SA might make the surface somewhat more ‘sticky’, providing a large number of weak, rapidly reversible sites for B2MG that would have gone undetected in our control experiment and be out of range of the distribution analysis [41]. This could also explain the mass transport influence of the highly loaded CM3-SA surface.

Conclusions

For binding studies using surface-based optical biosensing, it is important to consider the intrinsic potential problems of the presence of the surface and the immobilization. Although significant efforts have been devoted in the past decade to create a variety of specific immobilization strategies for creating ideal surfaces [10, 17, 43], many physical details of the binding surface are still unknown, and thus the heterogeneity of the surfaces and dispersion of affinities of sites generated with these strategies need more investigation. The same consideration also applies to the most commonly used surface for SPR biosensing that uses carboxylmethyl dextran as immobilization matrix. We and others have previously found that such surfaces with immobilized proteins using amine coupling indeed are often heterogeneous [11–16, 44–46], and the heterogeneity of the binding sites can cause substantial deviation of the experimental data from the pseudo-first-order kinetics. We believe surface site heterogeneity may be the rule rather than the exception. In order to account for the surface sites with different binding signature, we introduced a surface site affinity distribution model, which routinely exploits the high signal/noise ratio of the SPR binding traces, and can provide a better understanding of the behavior of the surface. In the current study, we explored the binding characteristics of different common sensor surfaces with this model. Our main focus was to evaluate the impact on the thermodynamic and kinetic binding parameters of two main immobilization strategies, the level of immobilization and length of the dextran matrix,.

Solely on the basis of the affinity distributions, the activity of the surface, and the dependence of both on the immobilization density and surface characteristics, unfortunately, it is still very difficult to unravel unambiguously which processes are taking place and are responsible for the altered affinity of the immobilized antibody in our model system. Systematic data from a much broader variety of sensor surfaces, a variety of interacting molecules, and different techniques (such as solution methods, and/or techniques that provide information perpendicular to the sensor surface [19]) will be required to shed more light on the origin of the observed affinity distributions. The present study is clearly limited in this regard, but may serve as a demonstration of the utility of the affinity distribution method for the study of sensor surface and immobilization properties.

Nevertheless, the approach provides more detailed information than previously available, and several clear conclusions can already be drawn. Importantly, it is very obvious that the type of sensor surface can have a very significant impact on the affinity of the immobilized macromolecule. The affinities we observed for the most abundant, high-affinity population of sites varied overall by 4fold, with consistently lower affinity when employing the long-chain CM5 surfaces, and generally higher affinity with SA capture. With regard to the dextran length, the distributions with short, 30 nm dextran of the CM3 surfaces were more uniform than those with longer dextran or without dextran, and binding was less transport limited. Although SA capture enabled us to obtain a functional C1 surface, it generally seemed that SA capture did not offer significant advantages in terms of uniformity of binding sites with the present system, which may be related to the chemically non-specifically biotinylated antibody. However, chemically random immobilization did not seem to be the major origin of the low-affinity sites, which we interpret to point towards heterogeneity of the physico-chemical micro-environment. Furthermore, SA appeared to alter the spectrum of ‘non-specific’ interactions, with detrimental impact on the mass transfer of the soluble B2MG through the matrix. Relevant for the analysis of SPR data, we observed that the idealizing assumption commonly made that the surface site properties are independent of the immobilization density, i.e. that different surface loading simply creates proportionally more sites for all classes, does not necessarily hold (consistent with our previous findings [13]). However, with the present method for determining the distribution of affinity and kinetic rate constants for different surfaces this assumption can be tested. More generally, given a particular system of interacting macromolecules, we believe this method will be a highly useful tool for the optimization of experimental conditions and assessing the performance of sensor chips and immobilization strategies.