Combining Solvent Thermodynamic Profiles with Functionality Maps of the Hsp90 Binding Site to Predict the Displacement of Water Molecules

Abstract

Intermolecular interactions in the aqueous phase must compete with the interactions between the two binding partners and their solvating water molecules. In biological systems, water molecules in protein binding sites cluster at well-defined hydration sites and can form strong hydrogen-bonding interactions with backbone and side-chain atoms. Displacement of such water molecules is only favorable when the ligand can form strong compensating hydrogen bonds. Conversely, water molecules in hydrophobic regions of protein binding sites make only weak interactions, and the requirements for favorable displacement are less stringent. The propensity of water molecules for displacement can be identified using inhomogeneous fluid solvation theory (IFST), a statistical mechanical method that decomposes the solvation free energy of a solute into the contributions from different spatial regions and identifies potential binding hotspots. In this study, we employed IFST to study the displacement of water molecules from the ATP binding site of Hsp90, using a test set of 103 ligands. The predicted contribution of a hydration site to the hydration free energy was found to correlate well with the observed displacement. Additionally, we investigated if this correlation could be improved by using the energetic scores of favorable probe groups binding at the location of hydration sites, derived from a multiple copy simultaneous search (MCSS) method. The probe binding scores were not highly predictive of the observed displacement and did not improve the predictivity when used in combination with IFST-based hydration free energies. The results show that IFST alone can be used to reliably predict the observed displacement of water molecules in Hsp90. However, MCSS can augment IFST calculations by suggesting which functional groups should be used to replace highly displaceable water molecules. Such an approach could be very useful in improving the hit-to-lead process for new drug targets.

Introduction

Water molecules are a key component of biological systems and act as ordered structural elements at binding interfaces.¹ The mediation of ligand binding by water molecules can have important consequences for binding affinity and specificity. Numerous examples of water-mediated protein–ligand interactions are known, including peptide binding in tyrosine kinase (Src),² binding of inhibitors to proteases,³ and carbohydrate-binding proteins.⁴ The consideration of individual water molecules in ligand design hinges on an accurate assessment of opposing thermodynamic contributions. This includes the entropic gain of displacing a highly ordered water molecule and the enthalpic loss of breaking water–protein hydrogen bonds.⁵ However, assessing the role of individual water molecules at the binding interface is a complex problem, as highlighted by the prediction that there is no direct correlation between the free energy of water molecules in the binding site and the affinity of bound ligands.⁶

Despite the difficulty in predicting and interpreting the roles of such water molecules, several attempts have been made at classifying binding site water molecules with respect to the likelihood of their “displaceability.”⁷⁻⁹ High displaceability in this context corresponds to displacement of the water molecule by a suitable chemical group on the ligand with an accompanying favorable change in the binding affinity. There are a variety of methods for identifying and ranking water molecules in binding sites, including physics-based methods and empirical methods. A physical method based on the double decoupling method employing thermodynamic integration (TI) to replica exchange Monte Carlo simulations was found to be successful in classifying water molecules as displaceable or conserved.⁶ However, such an approach requires extremely time-intensive calculations that must be performed on each water molecule individually. This drawback also affects free-energy perturbation (FEP) techniques, which have also been used to successfully predict the ease of displacement of ordered water molecules in protein binding sites.¹⁰ FEP predictions were found to correlate with the change in affinity for structural modifications that displaced the water molecules. However, the study also noted that a complete thermodynamic analysis is needed in order to accurately compute the effects of ligand modifications. Another approach employed machine learning to create a probabilistic water classifier.¹¹ This was found to be very good at predicting the location of water molecules and shown to have reasonable predictive power in classifying water molecules as displaceable or conserved. The structural features of water molecules in X-ray crystallographic structures, such as B-factors, accessibility to bulk solvent, number, and strength of protein-water hydrogen bonds, were used to develop multivariate logistic regression models for predicting the displacement of water molecules, yielding a prediction efficiency of 67%. An empirical method has also been developed that employs pseudo-Bayesian statistical analysis on predictions from the HINT scoring function¹² and the Rank algorithm,¹³ which is based on the number and geometric quality of hydrogen bonds for each water molecule. The method was found to be particularly useful for identifying strongly conserved water molecules.¹⁴

An alternative to the approaches described above is the use of inhomogeneous fluid solvation theory (IFST).¹⁵ IFST can be used to create a thermodynamic profile of the solvent surrounding a protein,^16,17 which can be used to identify binding hotspots.¹⁸ The free energies calculated by IFST are the contributions of regions of three-dimensional space to the solvation free energy of the solute.¹⁹ When this region is a highly occupied hydration site, ΔG can be thought of as the contribution of a specific water molecule to the solvation free energy of the solute. IFST has shown significant utility in drug development via Schrodinger’s WaterMap software. WaterMap has been used to explore the hydrophobic effect,²⁰ understand SAR,²¹ explain kinase selectivity,²² and predict binding affinities.²³ The advantage of IFST over other physics-based methods such as TI and FEP is that one simulation yields predictions for all the water molecules in a system. Recent work on IFST has focused on binding site prediction,²⁴ discretization on a Cartesian grid,²⁵ and investigating the effect of using different water models.²⁶ In this study, we employ IFST to predict the experimentally observed displacement of water molecules in a protein binding site.

When displacing a water molecule from a binding site in molecular design, consideration must be given to the functional group that replaces it. Multiple Copy Simultaneous Search (MCSS) is one of the oldest methods to predict energetically favorable positions of functional groups in protein binding sites.²⁷ The MCSS scoring function is based on the CHARMM force field²⁸ with interaction energies calculated from the difference between the bound and unbound states. The solvent effects are commonly taken into account by an approximation of dielectric screening from a distance-dependent dielectric model. An alternative approach to account for solvent effects is to couple the molecular mechanical energy component with polar and nonpolar solvation free energies derived from implicit solvent formalism in MM-PB/SA or GB/SA methods.^29,30 Implicit solvent approaches have gained widespread application in virtual screening, rescoring of docking poses, and estimation of ligand binding energies in ligand series.³¹⁻³⁶ The sorting of MCSS minima based on MM-PB/SA derived free energy estimates has yielded encouraging results.³⁷ MCSS analysis using probe molecules with different chemical characters provides what have been termed functionality maps. These functionality maps have been used for construction of ligands for numerous protein targets.³⁸

Other approaches have also been developed for computational solvent mapping and probe analysis. FTMap searches for favorable probe positions on protein surfaces using an empirical energy function including a desolvation term.³⁹ A clustering procedure is used to identify consensus probe binding sites which are identified as fragment-binding hotspots.¹⁴ The integral equation theory of liquids, known as the three-dimensional reference interaction site model (3D-RISM)^40,41 has also been used to find most probable positions of functional groups and small ligands on protein surfaces.⁴² This method has been applied to thermolysin with solvent probes for which experimental data were available, and reasonable agreement with experimental results was obtained.⁴³ More recently, methods employing molecular dynamics (MD) simulations using a mixture of explicit water and functional group probes have been introduced.⁴⁴ Guvench and MacKerell used a solvent mixture consisting of propane–benzene–water to construct probability density maps of probe binding preferences which corresponded to known ligand functional group preferences.⁴⁵ Seco and co-workers used a water–isopropanol mixture and evaluated druggability from their binding propensities on protein surfaces.⁴⁶ In other studies, more diverse sets of probe molecules have been used to assess the druggability of allosteric protein targets⁴⁷ and binding hotspots.⁴⁸ An important feature of these developments was the combined use of probe clustering and water displacement as indicators of hotspots. As summarized above, MD simulation based protocols using solvent-probe mixtures have been used previously to identify binding hotspots and predict target druggability. However, a direct assessment of relative displaceability of ordered water molecules has not been addressed in these studies. An effective method for providing such assessments would prove valuable in the hit-to-lead and lead optimization stages of drug development. In addition, an accurate ranking of water molecules making bridging interactions between the protein and the ligand can be also be used to make judicious choices about keeping or removing water molecules prior to molecular docking methods for virtual screening.⁴⁹⁻⁵²

The estimation of thermodynamic properties of water molecules at binding interfaces can provide very useful information for ligand design. The main aim of this study was to investigate the combination of hydration site free energies calculated by IFST with the MCSS scores of probe molecules in order to predict the observed displacement of water molecules. To calculate an experimental measure of displaceability, we used a large collection of ligand-bound structures of Heat shock protein 90 (Hsp90). The observed displacement was calculated from the frequency with which water molecules from the apo structure were displaced by a ligand. Hsp90 is well-known for its function as a molecular chaperone. Due to its important role in assisting protein folding, preventing self-aggregation, and cell cycle progression, it has been established as a valuable target in anticancer drug development. The structure of Hsp90 contains a highly conserved N-terminal domain that is linked, via a highly flexible linker, to a middle domain and a C-terminal domain.⁵³ The N-terminal domain contains an adenosine binding pocket, responsible for its ATPase activity, and has an unusual motif known as Bergerat fold, which is characterized by a rigid adenosine binding site and a flexible loop in phosphate binding region.⁵⁴ The ATPase activity of the N-terminal domain drives structural transitions required for chaperone functioning, and therefore it has been targeted in several drug discovery campaigns.⁵⁵ Water molecules have been a key aspect of structural studies on Hsp90,⁵⁶ and a key consideration in ligand design programs has been the role of four key water molecules in the binding site that are highly conserved in several complex structures.^57,58 Their systematic displacement and the resulting consequences on ligand optimization have also been the subject of recent investigations.^59,60 These factors make Hsp90 an ideal test case to assess the predictions of IFST.

Materials and Methods

Crystal Structure Analysis

A data set consisting of 103 ligand-bound X-ray crystallographic structures of Hsp90 (N-terminal domain) was compiled, based on Roughley and Hubbard’s work.⁵⁸ The structures can be organized into four groups: those based on a resorcinol substructure (41), those based on a (benz)-amide substructure (14), those based on an aminopyr(im)idine substructure (39), and those based on “second-site” fragments (9). Due to modifications around central scaffolds, this data set provides a systematic exploration of water displacement in the binding site. The set of crystal structures used in this work is reported in the Supporting Information. In addition, a crystal structure of the unbound closed-state conformation of Hsp90 (1YER) was used as the apo form of the receptor. All the structures were moved to the same reference frame by a rigid-body superimposition onto the ligand-bound crystal structure from 1UY6. From the superimposition, any water molecule in the apo structure lying within 2.0 Å of any of the ligand atoms in any structure was selected for subsequent analysis. For each of these reference water molecules, the observed displacement fraction (D) was defined from the fractional conservation (F).

1

2

F is obtained by counting the number of ligand-bound structures where a corresponding water molecule was present within 1.0 Å (N_hydrated) and then representing it as a fraction of total structures in the data set (N_total).

Structure Preparation

The protein structure of the apo form was initially prepared as follows. Atom coordinates were taken from the Protein Databank⁶¹ entry 1YER.⁶² This structure is of Hsp90 in the closed state. All crystallographic water molecules were deleted from the structure. The orientations of asparagine and glutamine residues were then checked using Schrodinger’s Preparation Wizard.⁶³ Residues Asn40, Asn105, Gln123, Gln133, and Gln194 were altered by switching the nitrogen and oxygen atoms to improve the hydrogen-bonding patterns. Histidine residues were also checked for orientation and protonation state using Schrodinger’s Preparation Wizard. Residues His154, His189, and His210 were flipped and assigned as epsilon protonated. All remaining histidines were assigned as delta protonated, but residue His77 was flipped. The residues lysine, arginine, aspartate, glutamate, cysteine, and tyrosine were also analyzed to check their protonation state. There was no evidence of any unusual protonation states, and thus all lysine and arginine residues were assigned as positively charged, all aspartate and glutamate residues were assigned as negatively charged, and all cysteine and tyrosine residues were assigned as neutral. The hydrogen-atom positions were then built using the HBUILD facility of CHARMM with the CHARMM27 energy function,^64,65 and the atomic charges were assigned from the CHARMM27 force field.^64,65

MCSS Calculations

The prepared protein structure was then subjected to MCSS calculations using eight different probe molecules. The probes were chosen to ensure that energetically favorable positions of polar, charged, hydrophobic, and aromatic functional groups were sampled. Two representative probes from each group were selected: methanol and ammonia (polar), ammonium ions and acetate ions (charged), methane and propane (hydrophobic), plus phenol and benzene (aromatic). All parameters for the probes were assigned using the MMFF94 force field.⁶⁶ The binding site region for MCSS calculations was defined as a 12.0 Å sphere around the centroid of all overlaid ligands. For each probe molecule, 500 copies were randomly placed in this sphere where any copy within 1.2 Å of any protein atom was removed. Energy minimizations were carried out in stages, and duplicate copies (within 0.2 Å of another copy) were removed at the end of each stage. The first stage was 500 steps of steepest descent; the second stage was 300 steps of steepest descent, and the final stages were 20 repetitions of 500 steps of conjugate gradient minimization. All minimizations were performed using a distance-dependent dielectric model with the default dielectric constant of 1.0. At the end of the MCSS run, probe copies with CHARMM interaction energies greater than +10.0 kcal/mol were removed. Finally, probe copies within 1.0 Å of each other were clustered together, and the copy with the lowest interaction energy was selected as the cluster representative. All of the above calculations were performed using the MCSS implementation in Accelrys Discovery Studio 3.1.

The raw probe scores from MCSS consist of the CHARMM interaction energy between the probe molecule and protein. These raw scores were size-normalized by multiplying by the ratio of water to probe molecular volume. This allowed us to compare the scores of probes with different sizes together. In two variations of the protocol, the normalized MCSS scores were combined with two different desolvation penalties: the experimental hydration enthalpy (MCSS-HE) and the experimental hydration free energy (MCSS-HFE). The experimental values of hydration enthalpy and hydration free energy for each probe were obtained from the literature.⁶⁷⁻⁷⁰ The MCSS derived probe positions were compared with the reference water molecules using the following procedure. A probe position was identified as corresponding to a reference water molecule if any of the probe heavy atoms was less than 1.5 Å from the oxygen atom of the water molecule. When multiple probe positions were obtained for a given water molecule, the best scoring pose was selected.

MM-GBSA Calculations

In a variation of the scoring protocol for MCSS-derived probe positions, the binding energy of each probe was calculated using an MM-GBSA approach:⁷¹

3

The free energy of each of the above terms is calculated from

4

E_MM is the energy calculated from the standard CHARMm energy function, which includes bonded and nonbonded terms. G_elec and G_np represent the electrostatic and nonpolar components of solvation free energy. G_elec represents the electrostatic component of solvation energy and was calculated using a variation of the standard GBSA model, referred to as the Generalized Born method with Molecular Volume integration (GBMV). The nonpolar contribution (G_np) to solvation free energy was calculated on the basis of the Surface Area (SA) model, which assumes a linear relationship between G_np and the solvent accessible surface area.⁷² A value of 5.0 cal/mol/Ų was used for the surface area coefficient in the SA model. The change in the solute entropy (TS) terms was assumed to be zero in this case. The MM-GBSA scores were also size-normalized using the method detailed above.

IFST Setup

For the MD simulation, the apo protein was first solvated with water molecules. Solvation was performed with the SOLVATE program,⁷³ version 1.0 from the Max Planck Institute to generate a sphere of radius 50 Å around the protein center. The system was then cut to form a rhombic dodecahedron (RHDO) with an edge length of 60 Å using the CHARMM program (version 34b1).²⁸ Water molecules were modeled with the TIP3P-Ewald,⁷⁴ TIP4P-2005,⁷⁵ and TIP5P-Ewald⁷⁶ water models in three separate systems. The water model has been shown to affect free-energy calculations in recent studies.⁷⁷⁻⁷⁹ Six sodium ions were included in all three systems to yield a net charge of zero. The ions were placed far from the Hsp90 binding site.

Equilibration

During all MD simulations, the heavy atoms were harmonically restrained using a 1.0 kcal/mol/Ų harmonic force, the RHDO was treated using periodic boundary conditions, and the electrostatics were modeled using the particle mesh Ewald method.⁸⁰ The system was first subjected to MD equilibration for 100 ps in an NPT ensemble. This stage of preparation was undertaken to equilibrate the density of the water molecules. The density of the water molecules plays an important role in IFST and is thus important to equilibrate. The system was then subjected to MD equilibration for 1 ns in an NVT ensemble. We ensured that the system was brought to equilibrium before continuing by verifying that the system reached a point where the energy fluctuations were stable.

Molecular Dynamics

Production simulations were performed for 5.0 ns at 300 K. All MD simulations were performed using the NAMD program version 2.8²⁸ with the CHARMM27 force field^64,65 allowing an MD time step of 2.0 fs. Electrostatic interactions were modeled with a uniform dielectric and a dielectric constant of 1.0 throughout the setup and production runs. van der Waals interactions were truncated at 11.0 Å with switching from 9.0 Å. All MD simulations were performed using NAMD compiled for use with the CUDA-accelerated GPUs. The 5.0 ns MD simulations required approximately 15, 20, and 25 h for the TIP3P-Ewald, TIP4P-2005, and TIP5P-Ewald water models on two four-processor GPU cores.

Hydration Site Identification

The first stage of the IFST analysis was to identify regions within the binding site with a high number density of water, termed hydration sites.¹⁷ We defined the center of the binding site as the centroid of the two water molecules W331 and W440 and considered the region within 12.5 Å of this centroid. We employed a radius of 1.2 Å for these hydration sites, in line with prior work.¹⁶ Hydration sites were identified by two methods. The first method was to place hydration sites at crystallographically determined water positions, and the second was to cluster water molecules from the MD simulation. For clustering, hydration sites were selected by sampling 5000 equally spaced snapshots from the MD trajectory and calculating the number density at Cartesian gridpoints within the binding site. A grid with a resolution 0.5 Å was generated around the centroid of the binding site. The number of water molecules within 1.2 Å from all 5000 snapshots was used to calculate the number density, and hydration sites were selected iteratively, starting at the gridpoint with the highest number density. No gridpoints were selected within 2.4 Å of an existing gridpoint, and the iteration terminated when the remaining gridpoints had a number density lower than 50% of the bulk value. The hydration site positions were then calculated as the mean position of all water molecules within 1.2 Å of each selected Cartesian gridpoint. The clustering required approximately 21, 27, and 34 h for the TIP3P-Ewald, TIP4P-2005, and TIP5P-Ewald water models on a single processor.

Energy Calculations

The interaction energy of each hydration site was calculated by sampling 1000 snapshots with one every 5.0 ps from the 5.0 ns simulation. The average interaction energy of every water molecule within the site was computed from the interaction with the solute (E_sw) and the other water molecules (E_ww). This was then combined with the average interaction energy of a water molecule determined from the bulk water simulation (E_bulk) to calculate the energy difference (ΔE) and binding energy difference (ΔE_bind) as shown in eqs 5 and 6, respectively:

5

6

The average number of water molecules in a hydration site is termed n. From a corresponding simulation of bulk water, E_bulk takes values of −9.81 kcal/mol, −11.33 kcal/mol, and −9.67 kcal/mol for the TIP3P-Ewald, TIP4P-2005, and TIP5P-Ewald water models. The binding energy can also be termed the normalized energy or the per water energy.

Entropy Calculations

The entropy of each hydration site was calculated by sampling 250 000 snapshots with one every 20 fs from the 5.0 ns simulation. The entropy difference was calculated from the contributions of the solute–water term (S_sw) and the water–water reorganization term (ΔS_ww). These terms can be calculated by integrating over the solute–water g_sw(r,ω) and water–water g_ww(r,r′,ω,ω′) correlation functions. The variable r represents the position of the water molecule with respect to the center of the hydration site, and the set of angles ω represents the orientation of the water molecule in the fixed protein reference frame. As in previous work, only contributions from two particle correlations were considered,^16,17 and vibrational entropy changes are not considered. Furthermore, the solute-water term was separated into translational (S_sw,trans) and orientational (S_sw,orient) contributions, and the orientational distributions were assumed to be independent of the position within the sites.¹⁶ These terms can be calculated for each hydration site as shown in eqs 7 and 8, respectively:

7

8

In these equations, k is Boltzmann’s constant, ρ° is the number density of bulk solvent, and Ω is the integral over the angles ω. The solute–water translational correlation functions were calculated using a bin size of 0.03 Å for the radial component, 10° for the φ angle and 1/18 for cos θ. The solute–water orientational correlation functions were calculated using a bin size of 10° for the φ and ψ angles and 1/18 for cos θ. The water–water reorganization term was also separated into translational (S_ww,trans) and orientational (S_ww,orient) contributions. The water–water translational pair probability densities were calculated as previously between water molecules in the hydration site and a set of subvolumes surrounding the hydration site.²⁶ A sphere of radius 3.6 Å around the hydration site was split into subvolumes using a bin size of 0.1 Å for the radial component, 12° for the φ angle and 1/15 for cos θ. The 3.6 Å cutoff is used because contributions to the translational entropy outside the first solvation shell are expected to be small.⁸¹ Due to the vast amount of data required for calculation of the solute–water–water triplet correlation function, a bulk water–water radial distribution function g_ww(R) was assumed as previously.¹⁵

9

g_sw(r′) is the translational probability density with respect to bulk water within a subvolume. For each hydration site, S_ww,orient was calculated from the mutual information (I_ww) between the orientations of water molecules in the hydration site and the orientations of water molecules in subvolumes surrounding the hydration site. A sphere of radius 3.6 Å around the hydration site was split into subvolumes using a bin size of 1/4 for cos θ and a bin size of 45° for the other Euler angles. The mutual information was then calculated between the hydration site and each of the subvolumes:

10

11

12

S_ww(ω_rel) is the water–water relative orientational entropy, where ω_rel is the relative orientation of two water molecules using a bin size of 10°. The full five-dimensional relative orientational entropies were estimated by using the second order entropy approximation generated by a truncation of the mutual information expansion.^82,83 These solute–water and water–water terms were then compared with the entropy of a water molecule determined from the bulk water simulation (S_bulk) due to other water molecules within 3.6 Å to calculate the entropy difference (ΔS) and entropy of binding (ΔS_bind) using eqs 13 and 14, respectively:

13

14

TS_bulk takes values of +3.54 kcal/mol, +3.94 kcal/mol, and +3.85 kcal/mol for the TIP3P-Ewald, TIP4P-2005, and TIP5P-Ewald water models based on the calculations described here. It is important to note that the values of a half in eq 13 have been removed from the definitions for S_ww,trans and S_ww,orient in eqs 9 and 10 (which has been the convention in previous work) such that eqs 13 and 14 correspond to eqs 5 and 6.

Free Energy Calculations

For each hydration site, the difference in free energy (ΔG) and the free energy of binding (ΔG_bind) is then calculated using eqs 15 and 16, respectively:

15

16

ΔE is assumed to be a good approximation for ΔH, as the PV term is expected to be negligible. The IFST calculations required approximately 7 min per hydration site.

Linear Regression Analysis

We hypothesized that the combination of best probe score and the corresponding water score should be reliable predictors of the observed displacement measure defined in this study. In order to assess this relationship, multiple linear regression analysis was performed in the R statistical computing package:

17

where β_o, β₁, and β₂ are coefficients and e represents the error term. Several models of this form were constructed using different formulations of the probe and hydration site scores. The probe scores corresponded to MCSS, MCSS-HE, MCSS-HFE, and MM-GBSA scores. For the hydration site score, seven IFST calculated properties were used: ΔG, ΔG_bind, ΔE, ΔE_bind, ΔS, ΔS_bind, and E_sw. The predictive power for each model was expressed as the adjusted coefficient of determination (R̅²), which is given by

18

where n is the number of samples and p is the number of variables in the model. The use of R̅² corrects for improvement in correlation arising just by the increase in number of variables. In all other instances, where correlation between any two variables is reported, we used the standard R² values.

Results

In the initial IFST analysis, hydration sites were placed on each crystallographic water molecule. This facilitates a direct comparison of observed displacement with various thermodynamic properties. The results of this analysis using water model TIP4P-2005 are summarized in Table 1. All of the crystallographic water positions bound favorably to the protein surface, as indicated by the corresponding hydration sites with negative ΔG values. Favorable ΔG values have also been noted in previous applications of IFST to proteins¹⁶ and model systems.⁷⁷ The free energy of hydration sites exhibited a moderately strong correlation with the observed displacement as indicated by an R² value of 0.57. Interestingly, some of the hydration sites with a highly favorable free energy corresponded to water molecules (e.g., W301 and W323) that are involved in bridging interactions and are retained by most of the ligands (Figure 1). Among the other thermodynamic properties of hydration sites calculated from IFST, E_sw and ΔE also demonstrated strong correlation with the observed displacement, with R² values of 0.62 and 0.58, respectively. The correlation was weak for other binding quantities ΔG_bind, ΔE_bind, and ΔS_bind. This is not unexpected, as the binding quantities do not consider the occupancy of the hydration site, which can be low or high. The correlation was also weak for ΔS, and this was not expected. However, the predictions are that enthalpic contributions tend to outweigh entropic contributions in determining the free energy. This is an interesting result that has also been noted in previous applications of IFST to proteins¹⁶ and model systems.⁷⁷ However, it may not be general for all systems or for all force fields. It is interesting to note that one of the hydration sites (W336) consistently appeared as an outlier in all correlation plots (Figure 2). The removal of this hydration site from the data set resulted in substantial improvement of correlation between observed displacement and thermodynamic properties, as indicated by R² values of 0.78, 0.82, and 0.81 for ΔG, E_sw, and ΔE, respectively. A clear explanation for why this hydration site is an outlier can be found by comparing W336 with W301. W301 is very close to W336 and hydrogen bonds to the same aspartate residue (Asp93). Interactions with Asp93 yield strongly favorable free energies for both hydration sites in comparison with hydration sites near uncharged residues. However, W301 makes a significantly more favorable contribution to the solvation free energy than W336 (−11.81 kcal/mol versus −8.28 kcal/mol). This corresponds to a significantly lower observed displacement for W301 compared to W336 (0.05 versus 0.99). Importantly, displacement of W336 is only achieved by a positively charged ligand moiety, presumably because the strong electrostatic interactions are necessary to overcome the strong interactions made by the water molecule. Thus, displacement of W301 must overcome even stronger water interactions and is rarely observed. This explanation provides the rationale for employing MCSS calculations, to allow the strength of interactions with water to be compared with the strength of interactions with probe molecules.

Table 1. Calculated Thermodynamic Properties of X-Ray Crystallographic Water Molecules and Corresponding Hydration Sites in the Binding Site of Closed Form Hsp90^a.

	X-ray crystallographic hydration sites								clustered hydration Sites
water	D	ΔG kcal/mol	ΔGbind kcal/mol	ΔE kcal/mol	ΔEbind kcal/mol	–TΔS kcal/mol	–TΔSbind kcal/mol	Esw kcal/mol	ΔG kcal/mol
W301	0.05	–11.81	–5.57	–13.46	–3.74	1.65	–1.83	–23.19	–11.78
W323	0.27	–9.07	–9.30	–8.59	–4.13	–0.48	–5.17	–14.41	–10.10
W324	0.57	–3.95	–3.10	–3.88	–0.13	–0.07	–2.97	–7.65	–3.98
W325	0.30	–6.55	–2.05	–6.70	1.08	0.15	–3.13	–14.44	–6.68
W328	0.09	–5.92	–6.17	–6.42	–2.90	0.50	–3.27	–10.36	–6.64
W336	0.99	–8.28	–6.47	–8.85	–3.16	0.57	–3.31	–14.58	–8.46
W338	0.92	–1.47	–0.95	–1.21	2.33	–0.25	–3.28	–3.32	–1.57
W346	0.18	–6.75	–3.69	–6.93	–0.43	0.18	–3.27	–13.45	–6.84
W357	1.00	–0.50	–0.71	–0.22	3.54	–0.27	–4.25	–1.14	–1.26
W379	0.95	–1.79	–2.86	–1.55	–0.52	–0.24	–2.34	–2.89	–1.68
W381	0.96	–1.81	–5.30	–1.46	–1.05	–0.34	–4.25	–2.71
W385	0.64	–2.37	–1.59	–2.37	1.03	0.00	–2.63	–5.29	–3.00
W405	0.97	–2.23	–1.88	–2.11	1.06	–0.12	–2.94	–4.82	–2.42
W412	0.70	–5.97	–5.94	–5.64	–2.70	–0.33	–3.24	–9.67	–7.03
W435	0.97	–2.43	–4.26	–1.91	0.10	–0.52	–4.36	–3.86	–3.55
W476	0.99	–1.27	–3.76	–0.91	0.04	–0.36	–3.80	–1.83	–4.84
W529	0.42	–6.62	–5.95	–6.11	–1.50	–0.51	–4.45	–11.11	–7.27
W536	0.89	–0.73	–1.54	–0.84	–0.90	0.11	–0.63	–1.41
W547	0.92	–1.40	–3.40	–1.06	–0.45	–0.34	–2.95	–1.96	–1.59
W598	0.81	–5.49	–7.92	–4.84	–3.34	–0.65	–4.58	–8.03	–5.51
R2 against D		0.57	0.13	0.58	0.19	0.27	0.00	0.62	0.50

^aThe water molecules are identified by their numbering in 1YER. D is the observed displacement fraction calculated using eq 2. Seven different IFST predictions are reported for hydration sites determined from crystallographic water molecule locations and the IFST free energy prediction is reported for hydration sites determined by clustering of water molecules from the MD trajectory. Not all crystallographic water molecules are identified by clustering.

Figure 1.

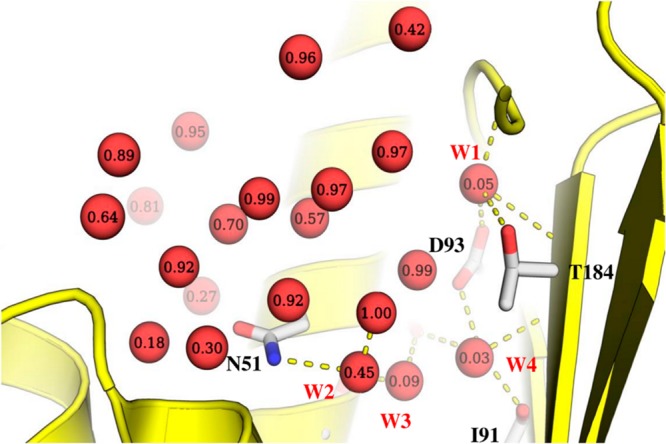
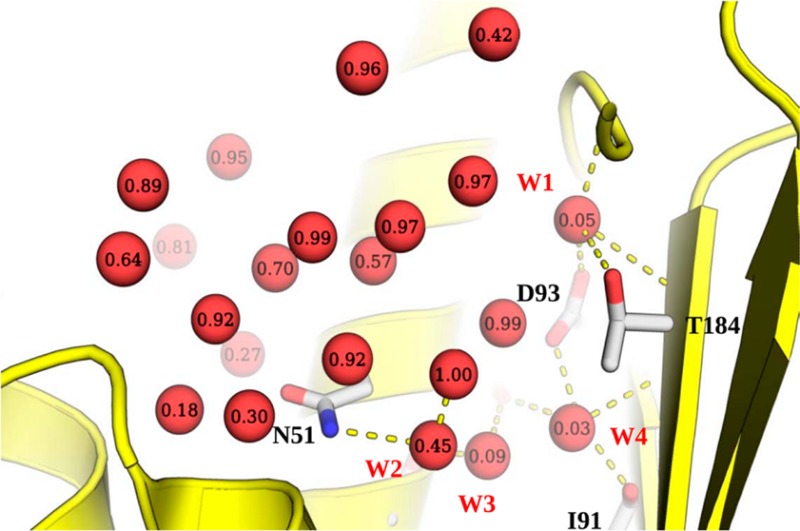
Water molecules in the binding site of Hsp90 N-terminal domain in the apo form (1YER). Each water molecule is labeled with the observed displacement fraction based on the analysis of 103 ligands considered in this study. A subset of four highly conserved water molecules (labeled W1–W4) is involved in several hydrogen bonds with the binding site. One of these water molecules (W2) was not seen in 1YER, and its position was derived by superposition of a liganded structure (1UY6).

Figure 2.

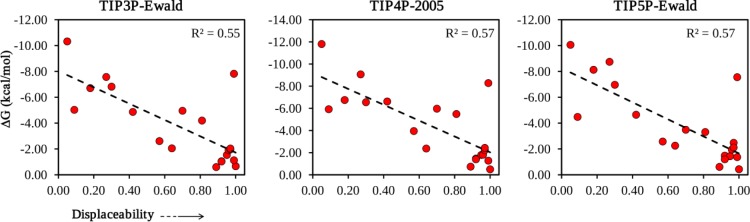
Correlation plots between the observed displacement from eq 2 and ΔG calculated from eq 15. IFST predictions were made using the water models TIP3P-Ewald, TIP4P-2005, and TIP5P-Ewald.

We also compared the effect of other water models in obtaining these quantities for hydration sites. The detailed results for each water model are given in the Supporting Information (Table S2). A comparison of the linear correlation between observed displacement and ΔG values from different models is shown in Figure 2. All three water models produced very similar results, with TIP3P-Ewald producing a very slightly lower correlation and TIP4P-2005 producing a very slightly higher correlation. From this point onward, the discussion of IFST results is based entirely on the TIP4P-2005 model for this reason.

In addition to placing hydration sites at crystallographic water positions, we also assessed the performance of the clustering protocol. The density cutoff was set to half the bulk density in order to identify all hydration sites. It was noted that some crystallographically observed water molecules have approximately the same number density as bulk water and were not predicted using a higher cutoff. Such hydration sites exhibit clustering of water molecules, leading to translational ordering and an unfavorable entropy contribution, but have a weakly favorable enthalpic component and thus a free energy that is approximately the same as bulk water. In terms of reproducing the crystallographic water positions from the simulation, the success rate (expressed as a percentage of crystallographic water molecules reproduced within 1.0 Å) was similar across different water models with TIP4P-2005 having the highest success rate of 80% (Table 1 and Table S2). Clustering identified 18 of the 20 displaceable water molecules within 1.5 Å and 16 within 1.0 Å. The failures all corresponded to crystallographic water positions with low occupancy and small free energy contributions as computed by IFST from the experimentally determined positions. This resulted in a slightly lower correlation with observed displacement (R² of 0.50) and suggests that placing hydration sites at crystallographic water positions may be more predictive.

The results of the MCSS calculations are summarized in Table 2. For each water position, the best scoring probe is reported using different formulations of MCSS. The raw MCSS scores reflect the CHARMM interaction energy between the probe and the protein, and desolvation penalties were applied to these raw scores. We tested the use of the hydration enthalpy (MCSS-HE) and the hydration free energy (MCSS-HFE) as desolvation penalties. The resulting scores were then normalized according to the relevant probe molecular volume. Finally, volume scaled MM-GBSA scores are also reported. The original MCSS output indicated a strong preference for charged groups for the majority of the hydration sites. This is most likely due to the crude approximation of solvent-screened electrostatic interactions in the distance-dependent dielectric model. The addition of desolvation penalties somewhat corrected for this trend by replacing nonpolar or polar probes in at least eight water positions. The MM-GBSA scores demonstrated the most significant differences, identifying polar molecules such as methanol and phenol as the most suitable probes for the majority of the hydration sites.

Table 2. Summary of the MCSS Probe Calculations from the 20 Hydration Sites in 1YER^a.

water	MCSS (kcal/mol)		MCSS-HE (kcal/mol)		MCSS-HFE (kcal/mol)		GBSA (kcal/mol)
W301	ammonia	–13.84	ammonia	–7.33	ammonia	–10.27	ammonia	–3.96
W323	ammonium	–44.42	ammonia	–8.59	ammonia	–11.53	phenol	0.34
W324	methanol	–13.06	methanol	–6.28	methanol	–9.80	methanol	–2.60
W325	acetate	–14.55	ammonia	–6.74	ammonia	–9.68	methanol	–5.76
W328	ammonium	–26.57	ammonia	–3.46	ammonia	–6.40	methanol	–3.27
W336	ammonium	–22.85	methanol	–4.06	methanol	–7.58	methanol	–5.31
W338	acetate	–8.69	propane	–1.08	propane	–4.64	methane	–4.01
W346	acetate	–14.55	ammonia	–5.62	ammonia	–8.56	methanol	–1.44
W357	acetate	–11.22	phenol	–2.56	phenol	–4.30	methanol	–4.13
W379	methanol	–7.20	phenol	–1.19	methanol	–3.94	benzene	–1.34
W381	ammonia	–20.13	ammonia	–13.62	ammonia	–16.57	phenol	–0.49
W385	ammonia	–11.54	ammonia	–5.04	ammonia	–7.98	methanol	–3.41
W405	acetate	–17.67	methanol	–5.38	methanol	–8.90	methane	–1.80
W412	acetate	–23.75	ammonia	–4.50	ammonia	–7.45	methanol	–1.14
W435	methanol	–12.19	methanol	–5.41	methanol	–8.93	phenol	–1.16
W476	phenol	–7.14	phenol	–3.76	phenol	–5.50	propane	–1.24
W529	ammonium	–31.98	ammonia	–6.27	ammonia	–9.21	methanol	–3.24
W536	acetate	–8.11	propane	–0.41	propane	–3.10	methanol	–2.30
W547	acetate	–14.55	phenol	–2.94	phenol	–4.68	propane	–1.04
W598	phenol	–4.51	phenol	–1.12	phenol	–2.86	phenol	–0.35

^aAll reported scores are volume corrected.

The important point to note from the MCSS analysis was that none of the different formulations had a significant correlation with observed displacement (Table 3). This is not unexpected, since capturing displaceability of water molecules solely from probe binding is unlikely, especially when probe scores contain crude approximations for solvation and entropic effects. The correlation between the different formulations of probe score and the predicted thermodynamic properties of water molecules was also mostly weak or insignificant. Volume-corrected MCSS scores showed R² values of 0.29 and 0.39 with ΔG and ΔG_bind of the corresponding hydration site. When best scoring MCSS probes are divided into polar and nonpolar categories, the correlation of scores with most of the IFST based properties is in opposite directions. For instance, polar probes have a correlation of 0.21 and 0.24 with ΔG and ΔH, respectively. On the other hand nonpolar probes have a correlation of −0.60 and −0.59 with ΔG and ΔH, respectively. This partially explains the nearly insignificant correlation when probes are considered together. In general, it was noticed that hydration sites with a large enthalpic component were associated with charged or polar probes whereas hydration sites with a small enthalpic component were associated with nonpolar probes.

Table 3. R² Coefficients of Determination for the Best MCSS Probe Scores with the Observed Displacement Fraction (D) and the IFST-Based Properties of Hydration Sites.

	MCSS	MCSS-HE	MCSS-HFE	GBSA
D	0.20	0.10	0.11	0.03
ΔG	0.29	0.12	0.13	0.04
ΔGbind	0.39	0.11	0.09	0.15
ΔE	0.23	0.11	0.12	0.07
ΔEbind	0.25	0.04	0.04	0.09
ΔS	0.00	0.01	0.02	0.30
ΔSbind	0.19	0.12	0.09	0.10
Esw	0.20	0.12	0.14	0.10

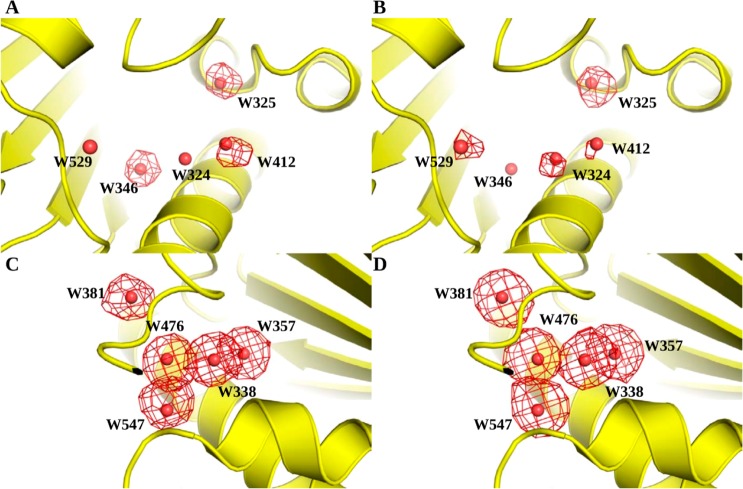
In order to qualitatively assess the MCSS results, we compared the distribution of probes in the binding site with that of the ligands. For each hydration site, ligand atoms within 1.0 Å of the crystallographic water molecule were obtained, which provided the distribution of atoms that most likely displaced it. These atoms were then divided into polar (N, O, S, P) and nonpolar (C) groups. The same procedure was then repeated for probes which provided the predicted distribution of functional groups around each hydration site. In Figure 3, these distributions are represented as an occupancy map on a 1 Å grid, where each grid point contains the amount of time it was occupied by an atom, represented as a fraction of the total number of atoms within 1 Å of the hydration site. First, we selected a set of hydration sites with highly favorable free energy (Figure 3A and B) and relatively high observed displacement. For at least three of these hydration sites (W325, W346, and W412), polar atoms comprised more than a 1/3 fraction of the displacing groups. W324 and W529 were displaced less frequently by polar groups. When compared with probe occupancies, this trend was somewhat reproduced. An important difference was that probe polar atoms more frequently occupied W324 and W529. On the other hand, probe polar atoms were less frequently observed for W346, which is frequently displaced by a polar ligand atom. The overlap between the ligand and probe occupancy maps was more pronounced for a set of less favorable hydration sites (Figure 3C and D), which were most frequently displaced by nonpolar functional groups (both in crystallographic ligands and probes). This can be rationalized on the basis that the optimal van der Waals interactions between (ligand/probe atoms and protein atoms) are more accurately reproduced by MCSS than the electrostatic interactions. Taken together, these results showed that hydration sites with highly favorable free energy (owing mostly to a strong enthalpic component) were displaced frequently by polar ligand atoms, and MCSS-based predictions for probes showed a similar trend. Conversely, hydration sites with less favorable free energy (with a decreased enthalpic but comparable or even large entropic component) were mostly displaced by nonpolar ligand and probe atoms. The number of distinct probes occupying the same energetically favorable site has been used before as an indicator of binding hot spots.^47,48 Prior to selection of the best scoring probe, we obtained the number of distinct probes identified at each hydration site and compared it with the observed displacement. The resulting correlation plot gives a weak R² value of 0.11. Hence, a clear relationship between diversity of probe binding and the likelihood of water displacement was not established from these data.

Figure 3.

A comparison of polar and nonpolar atom densities derived from crystallographic ligands (A and B) and MCSS-derived probe positions (C and D) in the Hsp90 binding site. Atoms around a given hydration site are represented as an occupancy map on a 1 Å grid, with grid points contoured at points where 30% of the total number of atoms within a 1 Å region around the hydration site are of the given type). (A and C) A set of highly favorable hydration sites with corresponding polar-atom occupancy maps compared across crystallographic ligands and probes. (B and D) A set of relatively less favorable hydration sites with corresponding nonpolar atom occupancy maps compared across crystallographic ligands and probes.

The results obtained from IFST calculations showed that the predicted free energy of hydration sites was a fairly reliable predictor of observed displacement. In order to assess whether the combination of IFST and MCSS probe analysis could improve the predictions, we used multiple linear regression models based on different combinations of hydration site thermodynamic properties and probe scores. The resulting data are summarized in Table 4, where the adjusted coefficient of determination is reported for each model. In most cases, the combination did not yield any improvement. The use of desolvation penalties derived from experimental data also did not lead to any improvement in predictions. However, as noted above, when the outlier W336 is removed from the data set, the adjusted R² values increased in some cases. For example, the highest value of adjusted R² (0.80) was obtained from a model combining E_sw values from IFST and probe GBSA scores. This also indicated that the use of GBSA to estimate probe desolvation penalties provided better results than constant desolvation penalties based on experimental hydration enthalpy or free energy values.

Table 4. The Adjusted Coefficients of Determination (R̅²) from Multiple Regression Analysis for Prediction of the Observed Displacement Fraction (D)^a.

	ΔG	ΔGbind	ΔE	ΔEbind	ΔS	ΔSbind	Esw
w/o MCSS	0.59	0.15	0.60	0.18	0.26	0.00	0.64
MCSS	0.52	0.12	0.54	0.17	0.42	0.18	0.59
MCSS-HE	0.52	0.08	0.54	0.15	0.26	0.02	0.58
MCSS-HFE	0.52	0.08	0.54	0.16	0.25	0.02	0.58
GBSA	0.52	0.16	0.54	0.21	0.20	0.08	0.59

^aEach model is derived from two predictors, indicated by row and column titles, and the value reflects strength of correlation with observed displacement. For comparison, R²’s for IFST values (without MCSS) are also given.

An important consideration in ligand design is the prioritization of ordered water molecules in the binding site for displacement and concomitant affinity gains. We selected a set of four water positions to assess the applicability of solvation thermodynamics and probe analysis in order to address such questions (Figure 1). Three of these water positions are already included in the set of reference water molecules derived from the apo structure (1YER). However, one additional water molecule is visible only in ligand bound Hsp90 (e.g., 1UY6). For consistency with previous studies, we refer to these water positions as W1, W2, W3, and W4.⁶⁰ The free energy of hydration sites corresponding to these water molecules, the best scoring probes (based on GBSA scores), and associated data are summarized in Table 5. These water molecules form a buried and tightly coordinated network of hydrogen bonds with the protein and/or ligand (Figure 1). The combined regression model based on IFST and MCSS predicts W2 to be the most displaceable in this group, whereas W2 and W3 are predicted to be moderately displaceable, and W1 is predicted to be very difficult to displace. The probe analysis predicts that W2 and W4 could be replaced by methane, whereas the W1 and W3 sites were most favorably filled by ammonia and methanol, respectively (Figure 4B and D). A collective picture emerges from the probe analysis that the binding site region containing W2 and W4 accommodates functional groups of nonpolar character, but W3 needs to retain hydrogen bonding interactions made by the displaced water molecules. This is also suggested by the good interaction energy (E_sw) for the W3 site.

Table 5. Summary of Hydration Site and Probe Analysis Data for Four Highly Conserved Water Molecules in Hsp90 Binding Site^a.

water	1YER water	GBSA (kcal/mol)		IFST ΔG (kcal/mol)	IFST Esw (kcal/mol)	observed displacement fraction (D)	predicted displacement fraction
W1	301	ammonia	–3.96	–11.78	–23.21	0.03	0.07
W2	NA	methane	–4.55	–2.44	–8.43	0.45	0.81
W3	328	methanol	–3.27	–6.64	–11.57	0.04	0.49
W4	303	methane	–2.68	–6.90	–16.11	0.03	0.47

^aW1, W3, and W4 correspond to 301, 328, and 303 from 1YER, whereas W2 is missing from 1YER. Thus, all IFST results are from corresponding hydration sites using the clustering protocol.

Figure 4.

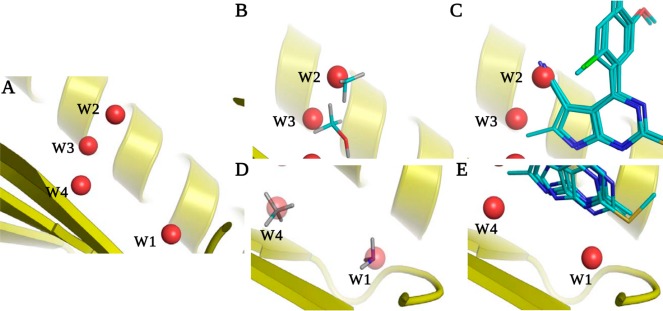
(A) A network of water molecules in the Hsp90 binding site. (B) W2 and W3 were predicted to be replaced by methane and methanol as most favorable probes. (C) In X-ray crystallographic ligands, W2 and W3 have been displaced by nitrile and methyl groups, respectively. (D) The best scoring probes corresponding to W1 and W4 were ammonia and methane, respectively. (E) In X-ray crystallographic ligands, W4 has been replaced by an ethyl group, but no reported examples were found for the displacement of W1 (it is not present in some structures but never overlaps with the ligand).

The IFST predictions agree well with experimental data on binding affinities for a pyrrolopyrimidine scaffold. Commensurate with this is a high predicted displacement, and indeed displacement of W2 by a nitrile group was shown to increase binding affinity approximately 250-fold (Figure 4C).⁵⁹ MCSS suggests a methyl probe is the most favorable replacement for W2 (with an MMGBSA score of −4.55 kcal/mol), but the methanol probe also scores highly (with an MMGBSA score of −4.13 kcal/mol), and this is consistent with displacement by a nitrile group that makes a hydrogen bond with Asn51. Thus, the experimental observations can be explained by IFST and MCSS due to the low ΔG for W2 in concert with a good probe score (Table 5). For the nitrile derivative, further displacement of W3 by a methyl group did not increase binding affinity. This was attributed to the attenuation of affinity gain by the loss of hydrogen bonding interactions for W3 and the clash of the new side chain. The rationalization based on IFST predictions is that the lack of significant gain in affinity is because W3 is not as easy to displace as W2 and that a nonpolar group is not the optimal replacement. Displacement of W3 alone by a polar substituent is predicted to be more fruitful. Further displacement of W4 by extending the methyl group to an ethyl group was shown to increase binding affinity 3-fold (Figure 4C). IFST and MCSS again rationalize this, with W4 predicted to be moderately displaceable by a nonpolar group such as methane. In addition, there is a small nonpolar cavity behind W3 that does not contain a water molecule. Such evacuated regions can provide unexpected boons in binding affinity,⁸⁴ and extension of the ethyl group to an isopropyl group may prove beneficial. It is interesting to note that the model predicts that W2, W3, and W4 are significantly more displaceable than has been observed experimentally. The recent experimental data⁵⁹ suggest that IFST is able to identify untapped potential at these sites. This would be very useful information in other established drug development projects.

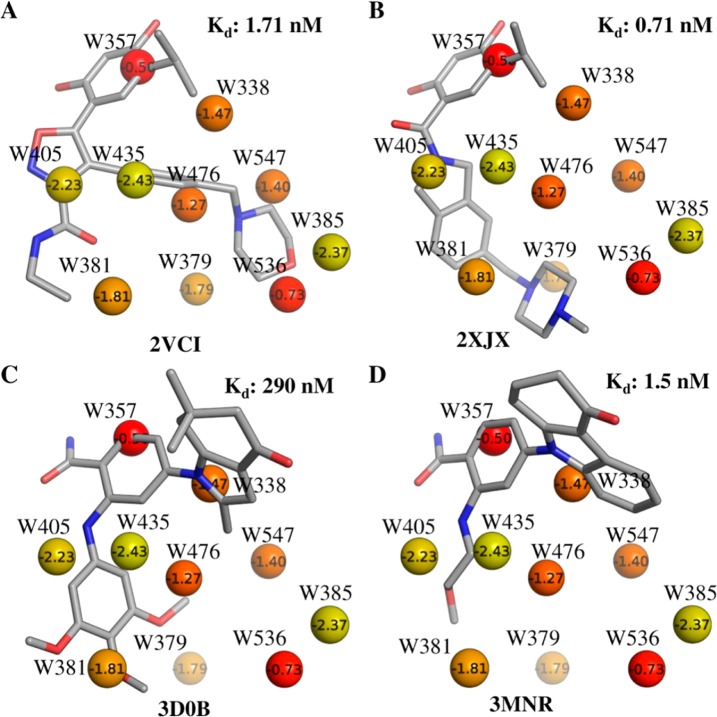
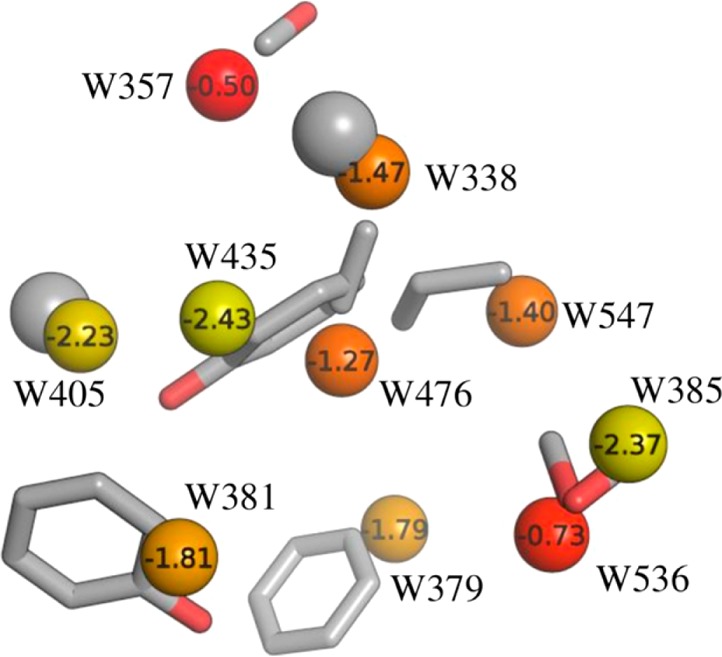
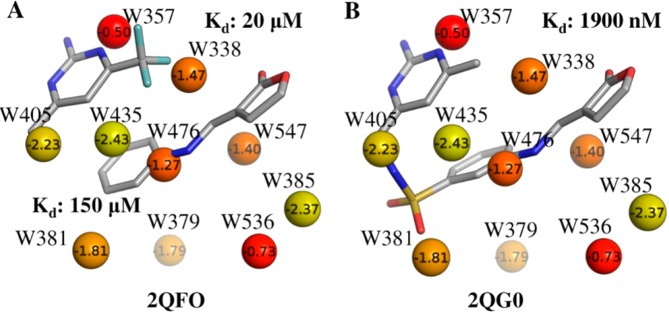
In order to further investigate the relationship between X-ray crystallographic ligands and thermodynamic properties of hydration sites along with associated functional groups, we selected a subset of unfavorable hydration sites including W338, W357, W379, W381, W385, W405, W435, W476, W536, and W547. The choice of these hydration sites was based on the fact that most of these are almost always displaced by the ligands (Table 1), and their calculated free energies lie in the range −0.5 kcal/mol to −2.5 kcal/mol. The remaining hydration sites had free energies less than −4.0 kcal/mol. The positions of the corresponding X-ray crystallographic water molecules and the most favored MCSS probes, based on MM-GBSA scores, are shown in Figure 5. The majority of sites are occupied by nonpolar groups, though some lower energy hydration sites are occupied by polar groups. This suggests an overall trend of prioritizing lower energy hydration sites for displacement with polar groups and high energy hydration sites with nonpolar groups. We performed a retrospective analysis of the different ligand series used in this study to see if a similar trend could be observed. Figures 6–8 summarize our analyses by showing representative ligands from different series. Binding affinities in these figures were obtained from BindingDB⁸⁵ or BindingMOAD.⁸⁶ First, we observe that W338 and W547 are commonly displaced by nonpolar groups in known inhibitors, which is consistent with the nonpolar MCSS probe positions. W338 is displaced by a nonpolar group in Figures 6A–C and 7A,B, whereas W547 is displaced by a nonpolar group in Figures 6C, 7A, and 8A–C. Similarly, for W357 the methanol probe position is consistent with the polar functionalities of known inhibitors in Figures 6A–C, 7A,B, and 8A,B.

Figure 5.

A subset of crystallographic water molecules in the Hsp90 binding site, labeled with the IFST-based solvation free energies in kcal/mol and colored from yellow to red representing low to high solvation free energy. The corresponding MCSS-derived probe positions overlaid for each site. The most favorable probe molecules based on MM-GBSA scores are shown.

Figure 6.

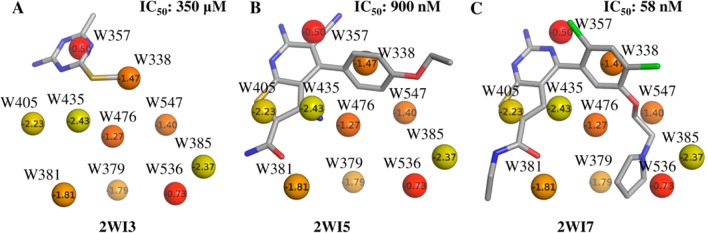
Representative ligands from aminopyri(mi)dine series overlaid on the crystallographic water molecules labeled with IFST-based solvation free energies in kcal/mol and colored from yellow to red representing low to high solvation free energy. These compounds represent hits from fragment and virtual screening (A and B) and an optimized clinical candidate (C).

Figure 8.

Representative ligands from “second-site” ligand series overlaid on crystallographic water molecules labeled with IFST-based solvation free energies in kcal/mol and colored from yellow to red representing low to high solvation free energy. (A) Two cocrystallized fragments in the Hsp90 binding site. (B) Ligand based on a methylsulfonamide linker.

Figure 7.

Representative ligands from resorcinol (A, B) and benzamide (C, D) series overlaid on the crystallographic water molecules labeled with IFST-based solvation free energies in kcal/mol and colored from yellow to red representing low to high solvation free energy.

In addition, we noticed that W405 and W435, which are relatively favorable hydration sites in this subgroup, are located in a hydrophobic cavity lined by Ala55, Ile96, Gly97, and Ile107. In the X-ray structure, the only hydrogen bond observed for this pair of water molecules is between W435 and the backbone carbonyl of Leu107. The MCSS predicted probes reproduce this pattern by favoring a methane in place of W405 and a phenol group in place of W435, retaining the hydrogen bond of W435 with the backbone carbonyl of Leu107. Such binding motifs where hydrogen bonding functionalities are enclosed in a hydrophobic environment can provide binding hotspots.¹⁷ The combination of IFST and MCSS can provide valuable information in this regard. Many of the potent Hsp90 inhibitors displace this pair of water molecules with a combination of polar and nonpolar groups, as predicted by probe analysis (Figure 6B, 7C,D).

Figures 6–8 provide different scenarios in ligand design where predicted displacement of water alongside probe analysis could prove useful. We emphasize that binding site hydration was not explicitly addressed during ligand design in these examples from the literature. However, the results are useful in understanding the utility of IFST and MCSS. In Figure 6, representative ligands from various stages of design (fragment/virtual screening hits 6A and B plus the clinical candidate 6C) are shown, which highlight the observation that stepwise disruption of binding site hydration (although not attempted in this particular ligand series) is a suitable route toward optimization. It is notable that all of the ligands in this study displace W357, which IFST predicts to make the least favorable contribution the solvation free energy among the 20 waters studied. W536 is predicted to make the second least favorable contribution to the solvation free energy and also appears to be a clear binding hotspot. The weaker inhibitors in Figure 6A and B do not displace it, whereas the high affinity clinical candidate in Figure 6C does displace it. This suggests that further affinity can be gained by molecules that do not displace W536, such as the inhibitor in Figure 8B. A systematic approach to ligand optimization should involve an assessment of binding site water molecules and the chemical functionalities suitable for displacing them. Figure 7 provides an example where core scaffolds from two distinct chemotypes (resorcinol in Figure 7A and B plus benzamide in Figure 7C and D) bind at similar locations, displacing the same hydration sites, W357 and W405, representing potent hydration sites for displacement. Apart from these two sites, different functional groups in each of these optimized candidates displace different water molecules. Consequently, the similarities between these functional groups and MCSS-predicted probes are interesting, e.g., methanol probes at W385 and W536 compared against the ligand in Figure 7A and phenol at W381 compared against the ligand in Figure 7C. Finally, in fragment linking approaches (shown in Figure 8A and B), the choice of linker can benefit from consideration of probes favorably displacing a water molecule. For example, the methylsulfonamide linker between the two fragments shown in Figure 8A displaces W381 in Figure 8B. MCSS favors a polar phenol probe at this site (Figure 6B), and the overlap of polar atoms between ligand and probe is noteworthy

To summarize, the results suggest that IFST and MCSS can be favorably combined to provide a useful binding site profile. The clustering of probes at a given location on the protein surface has been used as an indicator of binding hotspots, which can give rise to substantial gains in affinity for protein–ligand interactions. However, the use of probe calculations alone can result in false positives as they do not accurately consider the effects of solvation. IFST provides explicit accounting for water molecules, and hence a combination of both approaches can lead to better identification of hotspots in concert with advantageous functional groups for binding. Conversely, high scoring probe positions from MCSS that correspond to energetically favorable hydration sites can indicate strategically important sites where designing bridging interactions will be more appropriate.

Discussion

In this study, we have combined IFST calculations of solvent thermodynamics with MCSS probe analysis to predict the observed displacement of water molecules from protein hydration sites on Hsp90 and the best type of functional moiety to replace them, in the context of small molecule ligand design. IFST calculations of the hydration site free energies yielded a moderate correlation with the observed displacement, an encouraging result given the number and variety of ligands considered. Interestingly, the correlation with the total interaction energy (ΔE) is slightly better than the correlation with the free energy (ΔG), and the correlation with the protein interaction energy (E_sw) is even better. This can be rationalized on the basis that the enthalpic contributions to the solvation free energies are calculated to be significantly higher than the entropic contributions and that the loss of water–water interactions is less significant in the context of a ligand in the binding site that has already displaced the neighboring water molecules. This result suggests that approaches such as MCSS, which can calculate the interaction energy of water molecules with the protein, should work well in predicting observed displacement. However, there are two issues with this. The first issue is that the protein interaction energy from IFST is calculated from an explicit water simulation, and calculations based on a single water molecule that is not part of an ensemble will be different. The second issue is that the protein interaction energy from IFST is scaled by the occupancy of the site, and a calculation of the highest scoring single water molecule is not. Such a calculation is more analogous to the IFST binding quantities, which we have shown to have a weaker correlation with observed displacement.

To explore the application of IFST, we also calculated predictions based on three different water models, and in this case the results are very similar. All three water models predict hydration sites at very similar locations, and the R² between free energy predictions for the different water models is greater than 0.9 in all cases. In addition to predicting the observed displacement of water molecules, we considered whether MD simulations can reproduce crystallographic water positions. For TIP4P-2005, 18 out of the 20 crystallographic water positions were reproduced within 1.5 Å (Table 1). The other two water models had similar performance. It is important to note that a complete reproduction of crystallographic water positions is not always to be expected, as crystallographic water positions rely on an assignment of density from sometimes ambiguous data. We also compared two methods for placing hydration sites. The first was to place hydration sites at the positions of crystallographic water molecules, and the second was to place hydration sites by clustering the positions of water molecules from the MD simulations. The two approaches yield hydration sites at very similar positions with almost identical thermodynamic properties. This is shown by the high correlation between the free energies of the set of 18 equivalent hydration sites that are common between the two approaches (R² = 0.99). However, placing hydration sites at crystallographic water positions is slightly more predictive of the displacement, because the clustering procedure failures to identify all the crystallographic hydration sites. The IFST calculations show another interesting result, which is that the enthalpic contributions to the total free energy are commonly of greater magnitude than the entropic contributions. This has been noted previously^16,18 and may be a general result of IFST calculations. In contrast to the results of IFST, MCSS proved unsuccessful at predicting displacement and was unable to improve the predictions of IFST when the two were used in concert. However, MCSS does demonstrate a synergy with IFST when applied to ligand design. When IFST identifies a hydration site as highly displaceable, MCSS can predict the ligand functionality that should be used to displace it. Such information is harder to glean from IFST calculations alone, although two points should be noted. The first is that the positions of hydration sites predicted to have a highly favorable free energy are commonly found to overlap with polar ligand atoms. This is easily rationalized, as strong hydrogen bonding is the cause of both effects. In addition, the predicted orientation of the hydrogen bonding interactions for a water molecule is often recapitulated by the geometry of ligands, and this observation could be used in design. Conversely, hydration sites predicted to have a small free energy are commonly found to overlap with nonpolar ligand atoms.

Water displaceability is a difficult metric to capture from experimental data because displacement is Boolean for any given complex. In fact, almost every water molecule should be displaceable by some ligand, but this may be deleterious to the binding affinity. For example, displaceability data may be confounded if medicinal chemists have deliberately attempted to displace particular water molecules in cases where this is deleterious to the binding affinity. This will increase the frequency of displacement for a given water molecule in a case where displacement is not advantageous. For this reason, thermodynamic data may prove more useful in quantifying displaceability, but one still cannot quantify the specific contribution of a single water molecule to the binding affinity. Thus, we consider that the frequency of displacement from a large and varied data set of complexes is the best experimental data available. However, such data are still imperfect due to the bias of design by medicinal chemists. In addition, there are many cases where water molecules are subtly shifted rather than displaced, and this blurs such data. Despite these issues, IFST has proven to be a useful method for studying solvation thermodynamics, providing a perspective that is not available using other computational methods by decomposing solvation free energies into contributions from specific spatial regions. A similar perspective can be gained from FEP, by decomposing solvation free energies into contributions from specific species, including the water molecules.^87,88 FEP can also be used to selectively excite the individual degrees of freedom of water molecules and assess their contribution to the physicochemical characteristics of water.⁸⁹

In this work, we have shown that IFST can be used to identify binding hotspots and predict which water molecules should be advantageously displaced from a protein binding site. While a larger study would be needed to show that this is a general result, early results are promising and suggest that such an analysis performed on a new drug target would provide very useful information for ligand design. It may also show utility in identifying untapped potential for well-known drug targets. As noted previously, accurately predicting the effect of a ligand modification upon binding affinity cannot be achieved by considering any one factor and requires a comprehensive thermodynamic analysis of the ligand binding.¹⁰ However, given the vast number of potential ligands to be considered, there is a significant advantage in deriving useful information from IFST, which can be calculated from a single MD simulation.

Supporting Information Available

2-D diagrams of all the ligands in the four series investigated in this study are shown in Table S1, alongside the PDB codes of the corresponding Hsp90 X-ray crystal structures. IFST results for the reference water molecules based on the TIP3P-Ewald and TIP5P-Ewald water models are shown in Tables S2 and S3, respectively. This information is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

^⊥ These authors contributed equally to this work.

The authors declare no competing financial interest.