Multibody graph transformations and analysis

Abstract

This two-part paper uses graph transformation methods to develop methods for partitioning, aggregating, and constraint embedding for multibody systems. This first part focuses on tree-topology systems and reviews the key notion of spatial kernel operator (SKO) models for such systems. It develops systematic and rigorous techniques for partitioning SKO models in terms of the SKO models of the component subsystems based on the path-induced property of the component subgraphs. It shows that the sparsity structure of key matrix operators and the mass matrix for the multibody system can be described using partitioning transformations. Subsequently, the notions of node contractions and subgraph aggregation and their role in coarsening graphs are discussed. It is shown that the tree property of a graph is preserved after subgraph aggregation if and only if the subgraph satisfies an aggregation condition. These graph theory ideas are used to develop SKO models for the aggregated tree multibody systems.

1 Introduction

The investigation of the structural properties of multibody system dynamics remains an active area of research. Graph techniques have been developed for the systematic formulation of the equations of motion [20,24, 28, 30]. The sparsity structure of the equations of motion have been exploited to develop efficient dynamics computational algorithms [3, 7, 8, 23, 25]. Furthermore, analytical techniques such as system-level mass matrix factorization, and diagonalizing coordinate transformations have also been explored [1, 2, 9, 18, 19, 26] to simplify the dynamics formulations.

Recently, graph techniques have been used to identify general structural properties of tree multibody systems that underlie a broad family of analytical techniques and low-order algorithms for the systems [13-17]. It is seen that tree system dynamics can be described using abstract spatial kernel operator (SKO) models, and that several operator results including analytical mass matrix inversion follow directly from the SKO model structure—independent of the specific details of the system. Furthermore, these analytical results lead to a large family of low-order, scatter/gather recursive computational algorithms for important dynamics problems.

This two-part paper, further develops graph theory concepts and techniques for multibody system dynamics subjected to partitioning and aggregation graph transformations. Partitioning transformations decompose the system graph into simpler component subgraphs, while aggregation transformations collapse one or more component subgraphs into nodes to obtain coarser system graph representations. For example, a tree-topology system can be decomposed into a simpler tree of interconnected serial-chain segments in the system. In other instances, decompositions can reflect the natural structure of the system, e.g., a mobile platform with robotic arms equipped with multi-fingered hands for grasping and manipulating task objects. Applications of partitioning and decomposition techniques in multibody dynamics include: hierarchical dynamics and control; assembly of the overall equations of motion from those of simpler component subsystems; organizing dynamics computations (e.g., mass matrix, forward dynamics) from those of the component sub-systems for serial or parallel computations. Furthermore, partitioning techniques can help identify the sparsity structure of key dynamics matrices associated with the system dynamics that can be exploited to improve computational efficiency.

The contributions of this part are in the use of graph theory techniques to systematically study and derive results on the effect of partitioning and aggregation transformations on the SKO models for tree-topology systems. We derive the explicit partitioned structure of the system SKO model that is induced by partitioning transformations of the system graph. Since subgraph aggregation can destroy the tree graph structure, we derive rigorous sufficient conditions for tree structure preservation after the application of aggregation transformations. Preservation of the tree-topology structure leads to the natural question about the structure of the SKO model for the aggregated system. We derive explicit expressions for these aggregated SKO models. Our focus on SKO models is motivated by the easy availability of the large family of analytical and algorithmic techniques for these models. Furthermore, we show how the sparsity structure of key matrices and operators associated with tree-topology systems can be completely understood by applying the partitioning techniques developed in this paper. Part 2 of this paper [12] applies the aggregation transformation ideas developed here to develop constraint embedding techniques that extend the notion of SKO models to non-tree topology multibody systems.

The paper is organized as follows. Section 2 provides an overview of key graph theory ideas and the notion of SKO models. Section 3 focuses on partitioning transformations for SKO models. Toward this, the graph theory concepts of induced and path-induced subgraphs are introduced and their role in partitioning of abstract graphs is discussed. These ideas are used to partition dynamics models for tree multibody systems in Sect. 4. Section 5 studies the notion of subgraph aggregation for coarsening graphs. These ideas are subsequently used to apply aggregation transformations to dynamics models in Sect. 6. The aggregation techniques are then used to analyze the sparsity structure of the SKO model operators as well as the mass matrix in Sect. 7. The second part of this two-part paper uses the techniques derived here to develop a constraint-embedding technique that extends the notion of SKO models to nontree multibody systems.

2 Background: SKO models for tree multibody systems

Directed graphs (digraphs) provide natural mathematical constructs for describing the topology and connectivity of bodies in a multibody system. This section contains a brief review of key graph concepts and their use for multibody dynamics modeling.

2.1 Directed graphs and trees

A graph is a collection of nodes, and edges connecting pairs of nodes. A directed graph (also known as a digraph) is a graph where the edges have direction, i.e., an edge from one node to another is not the same as an edge in the reverse direction [27]. Each edge in a digraph defines a parent/child relationship between the node pair of that edge. Nodes defining an edge are said to be adjacent nodes. The node from which the edge emanates is referred to as the parent node, and the destination node is said to be the child node. The set of parent nodes of the kth node is denoted ℘ (k), and the set of its children nodes is C(k). Nodes without parent nodes are referred to as root nodes. Digraphs can have zero, one, or multiple root nodes. We assume that there is at most a single edge in the same direction between any pair of nodes, i.e., parallel edges between a pair of nodes are not allowed.

A node, j, is said to be the ancestor of another node, i, if there is a directed path from the node j to the node i. We use the notation i ≺ j (or equivalently j ≻ i) to indicate that node j is an ancestor of node i. The notation i ⊀ j implies that node j is not an ancestor of node i. Node i is said to be the descendant of node j if j is an ancestor of node i. A pair of nodes, i and j, are said to be related if one of them is the ancestor of the other; otherwise they are said to be unrelated.

1. A connected digraph is a digraph such that there is an undirected path connecting any pair of nodes, i.e., it is a digraph without disjoint components.

2. A rooted digraph is a connected digraph with a single root node that is the ancestor of every other node in the digraph.

3. A directed acyclic graph (DAG) is a connected digraph without any directed cycles, i.e., there is no directed path from any node back to itself.

4. A simply connected graph, or a polytree is a DAG in which nodes are not multiply connected, i.e., there is at most one directed path between any pair of nodes.

5. A tree, is a polytree where a node has at most one parent node, i.e., ℘ (k) contains at most one node for any node k. All trees have a unique root node.

6. A serial-chain is a tree where each node has at most one child. Unlike trees, serial-chains have the stronger property that all node pairs are related, i.e., for any pair of nodes in the serial-chain, one of the nodes is necessarily an ancestor of the other.

7. A forest is a collection of disjoint trees. Removing an edge or a node from a tree converts it into a forest. Adding a common root node to the independent trees in a forest converts them into a single tree.

A tree is said to be canonical¹ if the index of a parent node is always greater than the index of its child node, i.e., ℘ (k) > k for any node k. Every rooted digraph has a spanning tree, i.e., a tree that contains all the nodes in the digraph and whose edges belong to the digraph. The edges removed to convert a rooted digraph into its spanning tree are referred to as cut-edges. The adjacency matrix, 𝕊, for a digraph with n nodes is an n × n matrix where the (k, j) element is 1 if there is an edge between the kth and jth nodes, and zero otherwise.

2.2 Multibody digraphs

The standard digraph for a multibody system is a digraph with the inertial frame as the root node, and all the links in the system as the remaining nodes in the digraph. Thus, an n-link multibody system has a standard digraphwith n + 1 nodes.

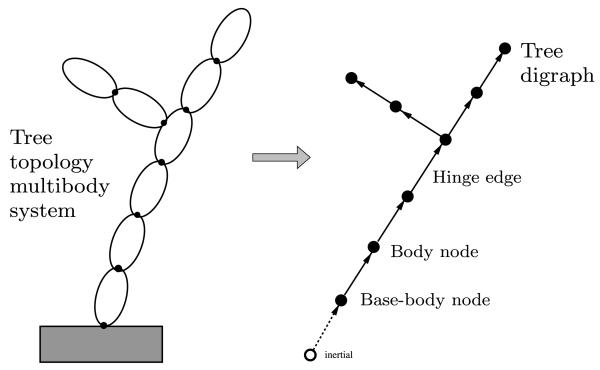
The edges in the digraphare defined by the motion constraints among the bodies, and between the bodies and the inertial frame. Thus, each hinge is represented by an edge, with the edges oriented from the inboard to the outboard body. Additional edges are assigned to other nonhinge motion constraints in the system. All motion constraints with respect to the inertial frame are defined so that edges from the inertial frame node to the link nodes are directed away from the inertial frame root node. These assignments result in a rooted digraph representation for the multibody system. Figure 1 illustrates the tree multibody system and its standard digraph. The convention is to depict the inertial frame node as unfilled, and the edges from the node as dashed lines. Multibody systems are classified as follows, based on the topology of their standard digraph:

• systems with tree standard digraphs are referred to as tree-topology systems;

• systems with serial-chain standard digraphs are referred to as the familiar serial-chain systems. They are special cases of tree-topology systems;

• systems with nontree standard digraphs are referred to as closed-chain or constrained systems. These digraphs can have directed cycles and/or multiply-connected nodes. Recall that every rooted digraph can be decomposed (nonuniquely) into a spanning tree together with a set of cut-edges. A decomposition into a spanning tree with n + 1 nodes and a set of cut-edges is often used when working with closed-chain systems.

Fig. 1.

The correspondence between a tree-topology multibody system and its standard tree digraph.

2.3 Equations of motion for tree-topology, rigid body systems

Consider a canonical n-link rigid body serial-chain system. The tip link is denoted link 1 and the base-body link as link n. The associated serial-chain tree associated with this graph is a strictly canonical tree with the parent/child relationship given by ℘(k) = k + 1.

Using 6-dimensional spatial coordinate-free notation with $\mathcal{V}\left(k\right)\in {\mathcal{R}}^6$ denoting the spatial velocity (angular and linear) of the kth link, $\stackrel{.}{\theta }\left(k\right)$ the kth hinge generalized velocities, H*(k) the kth hinge map matrix, $\mathfrak{l}(k+1,k)$ the vector between the (k + 1)th and kth body frames, and

$${\varphi }^{\ast }(k+1,k)=\left(\begin{array}{cc}\hfill \mathbf{I}\hfill & \hfill \tilde{\mathfrak{l}}(k+1,k)\hfill \\ \hfill 0\hfill & \hfill \mathbf{I}\hfill \end{array}\right)\in {\mathcal{R}}^{6\times 6}$$ (1)

the rigid body transformation matrix, the link-to-link spatial velocity relationship between the (k + 1)th links and its child body k can be expressed as [7, 11]:

$$\mathcal{V}\left(k\right)={\varphi }^{\ast }(k+1,k)\mathcal{V}(k+1)+H^{\ast }\left(k\right)\stackrel{.}{\theta }\left(k\right)$$ (2)

The overall velocity degrees of freedomfor the system is denoted $\mathcal{N}$ and is defined as the sum of all the individual hinge degrees of freedom.

Now, we introduce stacked vectors needed to define system level relationships. The stacked vectors $\mathcal{V}$ and θ are defined as

$$\begin{array}{cc}\hfill & \mathcal{V}\stackrel{\Delta }{=}\mathrm{col}{\left\{\mathcal{V}\right(k\left)\right\}}_{k=1}^n=\left[\begin{array}{c}\hfill \mathcal{V}\left(1\right)\hfill \\ \hfill \mathcal{V}\left(2\right)\hfill \\ \hfill ⋮\hfill \\ \hfill \mathcal{V}\left(n\right)\hfill \end{array}\right]\in {\mathcal{R}}^{6n},\text{and}\hfill \\ \hfill & \theta \stackrel{\Delta }{=}\mathrm{col}{\left\{\theta \right(k\left)\right\}}_{k=1}^n=\left[\begin{array}{c}\hfill \theta \left(1\right)\hfill \\ \hfill \theta \left(2\right)\hfill \\ \hfill ⋮\hfill \\ \hfill \theta \left(n\right)\hfill \end{array}\right]\in {\mathcal{R}}^{\mathcal{N}}\hfill \end{array}$$ (3)

The $\mathcal{V}$ stacked vector consists of the component body-level $\mathcal{V}\left(k\right)$ spatial velocity vectors combined into a single large vector. Correspondingly, the θ stacked vector consists of the component body-level θ(k) generalized coordinates combined into a single large vector. The link-level (2) relationship can now be expressed equivalently at the system level [11] as

$$\mathcal{V}={\mathcal{E}}_{\varphi }^{\ast }\mathcal{V}+H^{\ast }\stackrel{.}{\theta }$$ (4)

where the spatial operator ${\mathcal{E}}_{\varphi }\in {\mathcal{R}}^{6n\times 6n}$ is defined as

$$\begin{array}{cc}\hfill {\mathcal{E}}_{\varphi }& =\left(\begin{array}{ccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \varphi (2,1)\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \varphi (3,2)\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill \varphi (n,n-1)\hfill & \hfill 0\hfill \end{array}\right)\hfill \\ \hfill & =\sum _{k=1}^{n-1}{\mathrm{e}}_{k+1}\varphi (k+1,k){\mathrm{e}}_k^{\ast }\hfill \end{array}$$ (5)

${\mathrm{e}}_k\in {\mathcal{R}}^{6n\times 6}$ denotes a block-vector containing zero entries except for the kth slot which is a 6 × 6 identity matrix. The block-diagonal $H\in {\mathcal{R}}^{\mathcal{N}\times 6n}$ spatial operator is defined as follows:

$$\begin{array}{cc}\hfill H& \stackrel{\Delta }{=}\mathrm{diag}{\left\{H\right(k\left)\right\}}_{k=1}^n\hfill \\ \hfill & =\left(\begin{array}{cccc}\hfill H\left(1\right)\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill H\left(2\right)\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill H\left(n\right)\hfill \end{array}\right)\in {\mathcal{R}}^{\mathcal{N}\times 6n}\hfill \end{array}$$ (6)

The ε_φ spatial operator is in fact a BWA² matrix for the system digraph, and is referred to as a spatial kernel operator (SKO) for the system [14]. Observe that (4) is an implicit equation with $\mathcal{V}$ appearing on the both sides. However, it is explicit at the component-level, i.e., if we look at the kth row of this matrix equation, we obtain back the explicit (2) form.

The key difference between serial-chain and tree-topology multibody systems is that, in a tree system, bodies can have multiple children bodies. Examining the kinematic velocity relationships across the links, the interlink velocity relationship in (2) generalizes as follows for bodies in a tree-topology system:

$$\mathcal{V}\left(k\right)={\varphi }^{\ast }\left(\wp \right(k),k)\mathcal{V}\left(\wp \right(k\left)\right)+H^{\ast }\left(k\right)\stackrel{.}{\theta }\left(k\right)$$ (7)

That is, the spatial velocity of the kth link can be expressed as the sum of the rigidly propagated spatial velocity of the parent body and the relative spatial velocity, $H^{\ast }\left(k\right)\stackrel{.}{\theta }\left(k\right)$, across the kth hinge. Defining the $\mathcal{V}$ and $\stackrel{.}{\theta }$ stacked vectors and the H spatial operator in the same way as shown earlier, it is easy to verify that the following operator expression is a system-level re-arrangement of the component-level velocity relationship in (7)

$$\mathcal{V}={\mathcal{E}}_{\varphi }^{\ast }\mathcal{V}+H^{\ast }\stackrel{.}{\theta }$$ (8)

with ε_φ is defined more generally as [13, 15]

$${\mathcal{E}}_{\varphi }=\sum _{k=1}^n{\mathrm{e}}_{\wp \left(k\right)}\varphi \left(\wp \right(k),k){\mathrm{e}}_k^{\ast }$$ (9)

The ε_φ SKO operator continues to be a BWA matrix for the system digraph. This time, the φ(℘ (k), k) matrices are its 6 × 6 weight matrices. Observe that (4) and (8) have identical form, even though the former was derived specifically for a canonical serial-chain system, while the latter holds for arbitrary tree-topology systems.

For trees, ε_φ is nilpotent³ and, therefore, has a well-defined 1-resolvent,⁴φ = (I − ε_φ)⁻¹ [14]. φ is referred to as the spatial propagation operator (SPO) associated with the ε_φ SKO operator. Equation (8) can thus be transformed into the following explicit form:

$$\mathcal{V}={(\mathbf{I}-{\mathcal{E}}_{\varphi }^{\ast })}^{-1}{H}^{\ast }\stackrel{.}{\theta }={\varphi }^{\ast }{H}^{\ast }\stackrel{.}{\theta }$$ (10)

Differentiating the above leads to the following expression for the link spatial accelerations α:

$$\alpha ={\varphi }^{\ast }{H}^{\ast }\ddot{\theta }+\mathfrak{a}$$ (11)

where $\mathfrak{a}$ denotes the state-dependent Coriolis acceleration stacked vector.

With $\mathfrak{f}\left(k\right)\in {\mathcal{R}}^6$ denoting the interbody interaction spatial force between the parent ℘ (k) and the kth links, the following is the force balance expression for the kth body in a tree-topology system:

$$\mathfrak{f}\left(k\right)-\sum _{\forall j\in \mathrm{C}\left(k\right)}\varphi (k,j)\mathfrak{f}\left(j\right)=M\left(k\right)\alpha \left(k\right)+\mathfrak{b}\left(k\right)$$ (12)

where $M\left(k\right)\in {\mathcal{R}}^{6\times 6}$ is the kth link spatial inertia and $\mathfrak{b}\left(k\right)$ is the state-dependent gyroscopic spatial force for the kth body. Switching to the system-level stacked vector form, we obtain

$$\mathfrak{f}={\mathcal{E}}_{\varphi }\mathfrak{f}+M\alpha +\mathfrak{b}$$ (13)

where M is a block-diagonal spatial operator with link spatial inertias along the diagonal, and $\mathfrak{b}$ is the state-dependent stacked vector of gyroscopic terms. Continuing in this mode, the following expressions summarize the equations of motion for tree-topology systems:

$$\begin{array}{cc}\hfill & \mathcal{V}\stackrel{\left(8\right)}{=}{\mathcal{E}}_{\varphi }^{\ast }\mathcal{V}+H^{\ast }\stackrel{.}{\theta }\hfill \\ \hfill & \alpha ={\mathcal{E}}_{\varphi }^{\ast }\alpha +H^{\ast }\ddot{\theta }+\mathfrak{a}\hfill \\ \hfill & \mathfrak{f}\stackrel{\left(13\right)}{=}{\mathcal{E}}_{\varphi }\mathfrak{f}+M\alpha +\mathfrak{b}\hfill \\ \hfill & \mathcal{T}=H\mathfrak{f}\hfill \end{array}$$ (14)

$\mathcal{T}$ is the stacked vector of generalized forces. Using φ = (I − ε_φ)⁻¹, these expressions can be transformed from implicit ones into the following explicit operator expressions:

$$\begin{array}{cc}\hfill \mathcal{V}& ={\varphi }^{\ast }{H}^{\ast }\stackrel{.}{\theta }\hfill \\ \hfill \alpha & ={\varphi }^{\ast }(H^{\ast }\ddot{\theta }+\mathfrak{a})\hfill \\ \hfill \mathfrak{f}& =\varphi (M\alpha +\mathfrak{b})\hfill \\ \hfill \mathcal{T}& =H\mathfrak{f}\hfill \end{array}$$ (15)

Combining the expressions in (15) leads to

$$\mathcal{T}=\mathcal{M}\left(\theta \right)\ddot{\theta }+\mathcal{C}(\theta ,\stackrel{.}{\theta })$$ (16)

where

$$\begin{array}{cc}\hfill & \mathcal{M}\left(\theta \right)=H\varphi M{\varphi }^{\ast }{H}^{\ast }\in {\mathcal{R}}^{\mathcal{N}\times \mathcal{N}}\mathrm{and}\hfill \\ \hfill & \mathcal{C}(\theta ,\stackrel{.}{\theta })\stackrel{\Delta }{=}H\varphi (M{\varphi }^{\ast }\mathfrak{a}+\mathfrak{b})\in {\mathcal{R}}^{\mathcal{N}}\hfill \end{array}$$ (17)

$\mathcal{M}\in {\mathcal{R}}^{\mathcal{N}\times \mathcal{N}}$ denotes the mass matrix for the tree-topology system, and $\mathcal{C}\in {\mathcal{R}}^{\mathcal{N}}$ is the vector nonlinear Coriolis and gyroscopic velocity dependent terms.

2.4 SKO models for tree systems

References [13-15] have shown that SKO and SPO operators such as ε_φ and φ occur in internal-coordinate tree multibody kinematics and dynamics formulations. The occurrence of these operators is invariant to specific details such as body indexing, rigid/flexible links, regular or flexible/geared joints etc. Only the details of the weight matrices change with the system—not the SKO and SPO 1-resolvent properties. In general, the weight matrices can be nonsquare, noninvertible, and of nonuniform size. We formalize this general property with the definition of SKO models for multibody systems.

An SKO model for an n-links tree-topology multi-body system consists of the following:

1. A tree digraph reflecting the bodies and their connectivity in the system.

2. An ${\mathcal{E}}_{𝔸}$ SKO operator and associated SPO operator, $𝔸\stackrel{\Delta }{=}{(\mathbf{I}-{\mathcal{E}}_{𝔸})}^{-1}$

3. A full-rank block-diagonal, joint map matrix operator, H.

4. A block-diagonal and positive-definite spatial inertia operator, M.

5. Stacked vectors: $\stackrel{.}{\theta }$ ˙ denoting independent generalized velocities, $\mathcal{T}$ the generalized forces, $\mathcal{V}$ the node velocities, α the node accelerations, $\mathfrak{f}$ the interbody forces, $\mathfrak{a}$ the body Coriolis accelerations, $\mathfrak{b}$ the body gyroscopic forces, $\mathcal{N}$ the number of degrees of freedom, and equations of motion defined as:

   $$\begin{array}{cc}\hfill \mathcal{V}& ={𝔸}^{\ast }{H}^{\ast }\stackrel{.}{\theta }\hfill \\ \hfill \alpha & ={𝔸}^{\ast }(H^{\ast }\ddot{\theta }+\mathfrak{a})\hfill \\ \hfill \mathfrak{f}& =𝔸(M\alpha +\mathfrak{b})\hfill \\ \hfill \mathcal{T}& =H\mathfrak{f}\hfill \end{array}$$ (18)

   Thus,

   $$\mathcal{T}=\mathcal{M}\left(\theta \right)\ddot{\theta }+\mathcal{C}(\theta ,\stackrel{.}{\theta })$$ (19)

   where

   $$\begin{array}{cc}\hfill & \mathcal{M}\left(\theta \right)\stackrel{\Delta }{=}H𝔸M{𝔸}^{\ast }{H}^{\ast }\in {\mathcal{R}}^{\mathcal{N}\times \mathcal{N}}\text{and}\hfill \\ \hfill & \mathcal{C}(\theta ,\stackrel{.}{\theta })\stackrel{\Delta }{=}H𝔸(M{𝔸}^{\ast }\mathfrak{a}+\mathfrak{b})\in {\mathcal{R}}^{\mathcal{N}}\hfill \end{array}$$ (20)

   $\mathcal{M}$ is the symmetric and positive-definite mass matrix for the tree system and $\mathcal{C}$ is the vector of non-linear Coriolis and gyroscopic velocity dependent terms. Equation (20) is the Newton–Euler operator factorization of the mass matrix.

SKO models are also referred to by the (H, 𝔸, M) triplet of operators that define them.

References [13, 15] show that several analytical techniques and efficient algorithms follow directly from the SKO model structure for multibody systems. Examples of these include:

• Recursive $O\left(\mathcal{N}\right)$ procedures for computing SPO operator and stacked vector products.

• General $O\left(\mathcal{N}\right)$ Newton–Euler inverse dynamics algorithms.

• Solutions for the forward Lyapunov equations and decomposition of 𝔸X𝔹* operator product.⁵

• General $O\left({\mathcal{N}}^2\right)$ algorithm for computing the mass matrix.

• Solution for the backward Lyapunov equations and decomposition of 𝔸*X𝔹 operator product.

• Recursive algorithms for computing the 𝔸*X𝔹 operator product.

• The general $O\left(\mathcal{N}\right)$ articulated body inertia solution of the Riccati equation.

• The alternative Innovations Operator Factorization of the mass matrix.

• An analytical expression for the inverse of the mass matrix.

• The analytical expression for the determinant of the mass matrix.

• The general $O\left(\mathcal{N}\right)$ AB forward dynamics algorithm.

These results require no assumptions on the SKO model regarding the SKO weight matrices, the components of the other spatial operators, or the structure of the tree digraph. Thus, any multibody system formulation satisfying the requirements of the SKO model has available to it the full spectrum of these techniques and efficient algorithms.

3 Partitioning digraphs

In this section, we study the partitioning of SKO models for tree multibody systems. We begin with a discussion of partitioning concepts from graph theory and subsequently apply them to multibody systems.

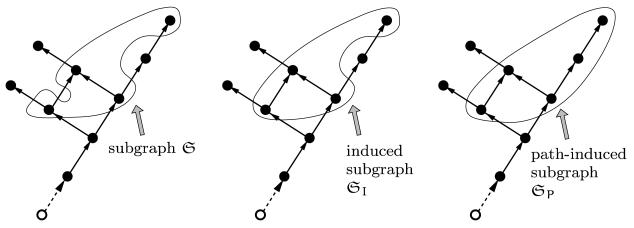
A subgraph $\mathfrak{S}$ of a digraph, $\mathfrak{T}$, is defined as a digraph containing a subset of the nodes and edges in $\mathfrak{T}$. $\mathfrak{S}$ is said to be induced if all edges in $\mathfrak{T}$ connecting node pairs in $\mathfrak{S}$ are also in $\mathfrak{S}$ [4, 27]. In other words, $\mathfrak{S}$ is induced if all node pairs in $\mathfrak{S}$ that are adjacent in $\mathfrak{T}$ are also adjacent in $\mathfrak{S}$. Thus, induced subgraphs preserve the adjacency property for node pairs, so that a pair of nodes in an induced subgraph are adjacent if and only if they are adjacent in the parent digraph. The induced subgraph ${\mathfrak{S}}_I$ for a subgraph $\mathfrak{S}$ is the minimal subgraph containing $\mathfrak{S}$ that is also an induced subgraph. A subgraph, and its induced subgraph, contain the same nodes, and differ only in the edges they contain.

A subgraph $\mathfrak{S}$ of $\mathfrak{T}$ is said to be path-induced if it contains all the paths (nodes and edges) in $\mathfrak{T}$ that connect node pairs in $\mathfrak{S}$. A path-induced subgraph has no missing nodes or edges for paths in $\mathfrak{T}$ that connect the nodes in $\mathfrak{S}$. Thus path-induced sub-graphs preserve the relatedness property for node pairs, so that a pair of nodes in a path-induced subgraph are related if and only if they are related in the parent digraph. The path-induced subgraph ${\mathfrak{S}}_P$ for a subgraph $\mathfrak{S}$ is the minimal subgraph of $\mathfrak{T}$ containing $\mathfrak{S}$ that is path-induced. Figure 2 illustrates a subgraph, and its induced and path-induced subgraphs. The path-induced property applies even to disconnected subgraphs. A path-induced subgraph, will generally contain more nodes and edges than the original subgraph or its induced subgraph. That is,

$$\mathfrak{S}\subseteq {\mathfrak{S}}_I\subseteq {\mathfrak{S}}_P$$ (21)

The following corollary shows that nontree path-induced sub-graphs are “complete”, in the sense that if such a subgraph contains part of a loop, then it must necessarily contain all the nodes and edges in the full loop, or, if it contains multiply-connected nodes, then all nodes and edges on paths connecting these nodes must also belong to the subgraph.

Fig. 2.

Examples of a subgraph $\mathfrak{S}$ and its induced and path-induced sub-graphs ${\mathfrak{S}}_I$ and ${\mathfrak{S}}_P$, respectively

Corollary 3.1 (Non-tree path-induced sub-graphs) Let $\mathfrak{S}$ be a path-induced subgraph of a digraph $\mathfrak{T}$.

1. If $\mathfrak{S}$ contains an edge that is a part of a directed cycle in $\mathfrak{T}$, then the full cycle must also be in $\mathfrak{S}$.

2. If $\mathfrak{S}$ contains a pair of multiply-connected nodes (i.e., nodes connected by more than one path), then all the paths connecting them must also be in $\mathfrak{S}$.

Proof

1. Since a directed cycle containing an edge, represents a directed path connecting the node pair for the edge, the path (and the cycle) must belong to $\mathfrak{S}$ since it is path-induced.

2. Similarly, all paths connecting a pair of nodes in $\mathfrak{S}$ must be in the subgraph since it is path-induced, and the result follows.

3.1 Partitioning by path-induced subgraphs

We now turn our attention to partitioning of digraphs. The following lemma shows that path-induced subgraphs are special in that they partition digraphs into component sub-graphs that are themselves path-induced.

Lemma 1 (Induced partitions of digraphs) Assume that $\mathfrak{S}$ is a path-induced subgraph of a digraph $\mathfrak{T}$. Define the $\mathcal{C}$ and $\mathcal{P}$ sub-graphs as follows:

• $\mathcal{C}$ child subgraph is the induced subgraph for the set of nodes that are not in $\mathfrak{S}$, but are descendants of the nodes in $\mathfrak{S}$, and

• $\mathcal{P}$ parent subgraph is the induced subgraph for the remaining nodes that are neither in $\mathfrak{S}$ nor in $\mathcal{C}$.

The $\mathfrak{S}$, $\mathcal{C}$ and $\mathcal{P}$ subgraphs represent a disjoint partitioning of the nodes in $\mathfrak{T}$. The following properties hold for the $\mathcal{C}$ and $\mathcal{P}$ subgraphs:

1. $\mathcal{C}$ is path-induced.

2. $\mathcal{P}$ is path-induced.

Proof

1. Assume that there are nodes i ≻ j ≻ k where i, $k\in \mathcal{C}$. Since j is a descendant of i, it must belong to either $\mathfrak{S}$ or $\mathcal{C}$. We will show that node j must necessarily belong to $\mathcal{C}$. First, since $i\in \mathcal{C}$, by definition there is a node $l\in \mathfrak{S}$ which is an ancestor of node i, i.e., l ≻ i ≻ j.

   If node j $j\in \mathfrak{S}$, we would have l ≻ i ≻ j. Since i $i\notin \mathfrak{S}$, this would contradict the assumption that $\mathfrak{S}$ is path-induced. Hence,$j\notin \mathfrak{S}$ and $j\in \mathcal{C}$. Therefore, $\mathcal{C}$ is path-induced.

2. Assume that there are nodes i ≻ j ≻ k, where i, $k\in \mathcal{P}$. We will show that node j must necessarily be in ≻.

3. If j $j\in \mathfrak{S}$, then, since node k is its child, k must be either in $\mathfrak{S}$ or $\mathcal{C}$, which would contradict our assumption that $k\in \mathcal{P}$. Thus $j\notin \mathfrak{S}$.

   If instead $j\in \mathcal{C}$, then there must a node $l\in \mathfrak{S}$ that is the ancestor of j, i.e., l ≻ j. This would imply that l ≻ k as well, since j ≻ k. Since k will then be a descendant of $l\in \mathfrak{S}$, it must belong to either $\mathfrak{S}$ or $\mathcal{C}$. This would contradict our assumption that $k\in \mathcal{P}$. Hence, node j must be in $\mathcal{P}$. This establishes that $\mathcal{P}$ is path-induced.

$\mathcal{P}$ contains nodes that are ancestors of the nodes in $\mathfrak{S}$ but are not themselves in $\mathfrak{S}$, together with all nodes that are unrelated with any of the nodes in $\mathfrak{S}$. While all nodes in $\mathfrak{T}$ belong to one of the $\mathfrak{S}$, $\mathcal{C}$ and $\mathcal{P}$ subgraphs, connecting edges between these subgraphs do not belong to any of the subgraphs.

4 Partitioning SKO models

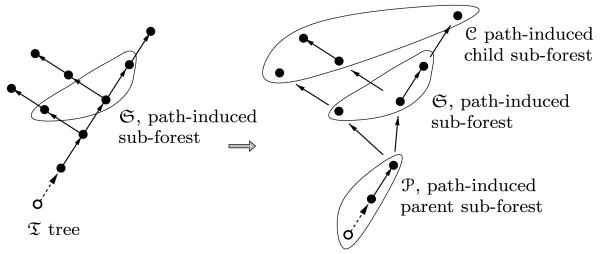
When $\mathfrak{T}$ is a tree digraph, a path-induced subgraph of $\mathfrak{T}$ is in fact a path-induced sub-forest, i.e., it is a collection of one or more disjoint path-induced subtrees. Thus, in the partitioning described in Lemma 1, $\mathfrak{S}$, $\mathcal{C}$, and $\mathcal{P}$ are all path-induced subforests. This is illustrated in Fig. 3. The partitioning process can be continued on the component sub-forests to further subdivide them into finer-grain path-induced subforests, if desired.

Fig. 3.

Illustration of the disjoint partitioning of a $\mathfrak{T}$ tree by a path-induced sub-forest $\mathfrak{S}$ into parent $\mathcal{P}$, and child $\mathcal{C}$ path-induced sub-forests

4.1 Partitioning SKO model operators

When $\mathfrak{T}$ is the tree digraph for an SKO model, the disjoint partitioning induced by a path-induced subgraph $\mathfrak{S}$ also partitions the bodies in the multibody system into disjoint component multibody systems, corresponding to the $\mathfrak{S}$, $\mathcal{C}$, and $\mathcal{P}$ path-induced subforests. Since these are subforests, each of the component systems have well-defined SKO spatial operators, denoted ${\mathcal{E}}_{{𝔸}_{\mathfrak{S}}}$, ${\mathcal{E}}_{{𝔸}_{\mathcal{C}}}$, and ${\mathcal{E}}_{{𝔸}_{\mathcal{P}}}$, respectively.

For ease of exposition, we assume that $\mathfrak{T}$ is a canonical tree. The $\mathfrak{S}$, $\mathcal{C}$, and $\mathcal{P}$ sub-graphs are then also canonical. Therefore, the ${\mathcal{E}}_{𝔸}$, ${\mathcal{E}}_{{𝔸}_{\mathfrak{S}}}$, ${\mathcal{E}}_{{𝔸}_{\mathcal{C}}}$, and ${\mathcal{E}}_{{𝔸}_{\mathcal{P}}}$ SKO operators are all strictly lower-triangular. The system-level ${\mathcal{E}}_{𝔸}$ SKO operator can be expressed in the following block-partitioned form:

$${\mathcal{E}}_{𝔸}=\left(\begin{array}{ccc}\hfill {\mathcal{E}}_{{𝔸}_{\mathcal{C}}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\mathcal{B}}_{\mathfrak{S}}\hfill & \hfill {\mathcal{E}}_{{𝔸}_{\mathfrak{S}}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill E_{\mathfrak{S}}\hfill & \hfill {\mathcal{E}}_{{𝔸}_{\mathcal{P}}}\hfill \end{array}\right)$$ (22)

The SKO operators of the individual subforests form the block-diagonal elements of ${\mathcal{E}}_{𝔸}$, with:

1. The ${\mathcal{E}}_{{𝔸}_{\mathcal{C}}}$ SKO operator for $\mathcal{C}$—with the smallest indices—being in the upper left corner.

2. The ${\mathcal{E}}_{{𝔸}_{\mathcal{P}}}$ SKO operator for $\mathcal{P}$—with the largest indices—being in the lower right corner.

3. The ${\mathcal{E}}_{{𝔸}_{\mathfrak{S}}}$_AS SKO operator for $\mathfrak{S}$ being in the middle.

4. ${\mathcal{B}}_{\mathfrak{S}}$ is a connector block, whose nonzero elements are for the parent/child edges between the nodes in $\mathcal{P}$ and their children in $\mathfrak{S}$.

5. $E_{\mathfrak{S}}$ is also a connector block, whose nonzero elements are for the parent/child edges between the nodes in $\mathcal{P}$ and their children in $\mathfrak{S}$.

6. The lower-left block is zero because none of the nodes in $\mathcal{C}$ are the children of the nodes in $\mathcal{P}$.

It is worth pointing out that the block lower-triangular structure of ${\mathcal{E}}_{𝔸}$ in (22) continues to hold even under the more relaxed condition where the component systems are not necessarily canonical systems themselves, but are only canonical with respect to each other. In this situation, the index of a node in $\mathcal{C}$ whose parent is in $\mathfrak{S}$ is required to be less than that of its parent. Similarly, the index of a node in $\mathfrak{S}$ whose parent is in $\mathcal{P}$ is required to be less than that of its parent.

Since the component systems are subforests, their corresponding SPOoperators are well-defined, and given by:

$$\begin{array}{cc}\hfill & {𝔸}_{\mathcal{C}}\stackrel{\Delta }{=}{(\mathbf{I}-{\mathcal{E}}_{{𝔸}_{\mathcal{C}}})}^{-1},{𝔸}_{\mathfrak{S}}\stackrel{\Delta }{=}{(\mathbf{I}-{\mathcal{E}}_{{𝔸}_{\mathfrak{S}}})}^{-1},\hfill \\ \hfill & {𝔸}_{\mathcal{P}}\stackrel{\Delta }{=}{(\mathbf{I}-{\mathcal{E}}_{{𝔸}_{\mathcal{P}}})}^{-1}\hfill \end{array}$$ (23)

The following lemma describes the corresponding partitioned structure of the system level SPO operator 𝔸 in terms of the SPO operators of the component systems.

Lemma 2 (Partitioning of the 𝔸 SPO operator) The 𝔸 SPO operator for the full system has the following partitioned structure corresponding to the partitioned structure of ${\mathcal{E}}_{𝔸}$ in (22):

$$𝔸=\left(\begin{array}{ccc}\hfill {𝔸}_{\mathcal{C}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {𝔸}_{\mathfrak{S}}{\mathcal{B}}_{\mathfrak{S}}{𝔸}_{\mathcal{C}}\hfill & \hfill {𝔸}_{\mathfrak{S}}\hfill & \hfill 0\hfill \\ \hfill {𝔸}_{\mathcal{P}}\left(E_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}{\mathcal{B}}_{\mathfrak{S}}\right){𝔸}_{\mathcal{C}}\hfill & \hfill {𝔸}_{\mathcal{P}}{E}_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}\hfill & \hfill {𝔸}_{\mathcal{P}}\hfill \end{array}\right)$$ (24)

Observe that the SPO operators for the component subgraphs are the block-diagonal elements of 𝔸.

Proof Start with the partitioned expression for ${\mathcal{E}}_{𝔸}$ in (22), and observe that

$$\begin{array}{cc}\hfill {𝔸}^{-1}& =(\mathbf{I}-{\mathcal{E}}_{𝔸})\hfill \\ \hfill & \stackrel{\left(22\right)}{=}\left(\begin{array}{ccc}\hfill \mathbf{I}-{\mathcal{E}}_{{𝔸}_{\mathcal{C}}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -{\mathcal{B}}_{\mathfrak{S}}\hfill & \hfill \mathbf{I}-{\mathcal{E}}_{{𝔸}_{\mathfrak{S}}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -E_{\mathfrak{S}}\hfill & \hfill \mathbf{I}-{\mathcal{E}}_{{𝔸}_{\mathcal{P}}}\hfill \end{array}\right)\hfill \\ \hfill & \stackrel{\left(23\right)}{=}\left(\begin{array}{ccc}\hfill {𝔸}_{\mathcal{C}}^{-1}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -{\mathcal{B}}_{\mathfrak{S}}\hfill & \hfill {𝔸}_{\mathfrak{S}}^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -E_{\mathfrak{S}}\hfill & \hfill {𝔸}_{\mathcal{P}}^{-1}\hfill \end{array}\right)\hfill \end{array}$$

The result follows by verifying that the product of this expression for 𝔸⁻¹, with 𝔸 in (24), is indeed the identity matrix.

If the $\mathcal{P}$ subgraph is empty, then the rows and columns for the parent subgraph do not exist in the partitioned structure. Similarly, if $\mathcal{C}$ is empty, then the corresponding columns and rows for the child subgraph do not exist in the partitioned structure.

4.2 Partitioning of an SKO model

The partitioning of the tree digraph for an SKO model also induces the following corresponding partitioning of the system-level block-diagonal H and M operators:

$$\begin{array}{cc}\hfill & H=\left(\begin{array}{ccc}\hfill H_{\mathcal{C}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill H_{\mathfrak{S}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill H_{\mathcal{P}}\hfill \end{array}\right)\text{and}\hfill \\ \hfill & M=\left(\begin{array}{ccc}\hfill M_{\mathcal{C}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill M_{\mathfrak{S}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill M_{\mathcal{P}}\hfill \end{array}\right)\hfill \end{array}$$ (25)

Observe that ($H_{\mathcal{C}},{𝔸}_{\mathcal{C}},M_{\mathcal{C}}$), ($H_{\mathfrak{S}},{𝔸}_{\mathfrak{S}},M_{\mathfrak{S}}$), and ($H_{\mathcal{P}},{𝔸}_{\mathcal{P}},M_{\mathcal{P}}$) define SKO models for the component tree-topology multibody systems associated with the $\mathcal{C}$, $\mathfrak{S}$, and $\mathcal{P}$ subgraphs, respectively.

The following corollary looks at the case where a system is partitioned into just outer and inner subsystems, and shows that the mass matrix subblock corresponding to the outer system is simply the mass matrix of the outer subsystem itself.

Corollary 4.1 (Mass matrix invariance of the outer sub-system) Consider an SKO model partitioned as in (22), but with empty $\mathcal{C}$. That is, the system is partitioned into inner, $\mathcal{P}$, and outer, $\mathfrak{S}$, SKO models. Then the overall SKO model mass matrix has the following partitioned structure:

$$\mathcal{M}=\left(\begin{array}{cc}\hfill {\mathcal{M}}_{\mathfrak{S}}\hfill & \hfill X\hfill \\ \hfill X^{\ast }\hfill & \hfill {\mathcal{M}}_{\mathcal{P}}+Y\hfill \end{array}\right)$$ (26)

where

$$\begin{array}{cc}\hfill & {\mathcal{M}}_{\mathfrak{S}}\stackrel{\Delta }{=}{H}_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}{\mathit{M}}_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}^{\ast }{H}_{\mathfrak{S}}^{\ast },\hfill \\ \hfill & {\mathcal{M}}_{\mathcal{P}}\stackrel{\Delta }{=}{H}_{\mathcal{P}}{𝔸}_{\mathcal{P}}{\mathit{M}}_{\mathcal{P}}{𝔸}_{\mathcal{P}}^{\ast }{H}_{\mathcal{P}}^{\ast },\hfill \\ \hfill & X\stackrel{\Delta }{=}{H}_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}{\mathit{M}}_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}^{\ast }{E}_{\mathfrak{S}}^{\ast }{𝔸}_{\mathcal{P}}^{\ast }{H}_{\mathcal{p}}^{\ast },\hfill \\ \hfill & Y\stackrel{\Delta }{=}{H}_{\mathcal{P}}{𝔸}_{\mathcal{P}}{E}_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}{\mathit{M}}_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}^{\ast }{E}_{\mathfrak{S}}^{\ast }{𝔸}_{\mathcal{P}}^{\ast }{H}_{\mathcal{P}}^{\ast }\hfill \end{array}$$ (27)

Proof The expressions in (26) and (27) are obtained by directly evaluating $\mathcal{M}=H𝔸M{𝔸}^{\ast }{H}^{\ast }$ using the following component partitioned expressions from (24) and (25):

$$\begin{array}{cc}\hfill & H=\left(\begin{array}{cc}\hfill H_{\mathfrak{S}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill H_{\mathcal{P}}\hfill \end{array}\right),𝔸=\left(\begin{array}{cc}\hfill {𝔸}_{\mathfrak{S}}\hfill & \hfill 0\hfill \\ \hfill {𝔸}_{\mathcal{P}}{E}_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}\hfill & \hfill {𝔸}_{\mathcal{P}}\hfill \end{array}\right),\hfill \\ \hfill & \mathit{M}=\left(\begin{array}{cc}\hfill {\mathit{M}}_{\mathfrak{S}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathit{M}}_{\mathcal{P}}\hfill \end{array}\right)\hfill \end{array}$$

Observe that ${\mathcal{M}}_{\mathfrak{S}}$ and ${\mathcal{M}}_{\mathcal{P}}$ are the respective mass matrices for the $\mathfrak{S}$ and $\mathcal{P}$ SKO models. Also, observe that the upper right sub-block ${\mathcal{M}}_{\mathfrak{S}}$ of $\mathcal{M}$ is independent of quantities associated with the $\mathcal{P}$ subgraph, i.e., the elements of the ${\mathcal{M}}_{\mathfrak{S}}$ mass matrix do not depend upon the properties or generalized coordinates of inboard bodies.

5 Aggregating sub-graphs

In this section, we use the partitioning techniques developed so far to study sub-structuring of SKO models using subgraph aggregation. We begin with the development of the aggregation concepts for digraphs and subsequently apply them to SKO models.

5.1 Edge and node contractions

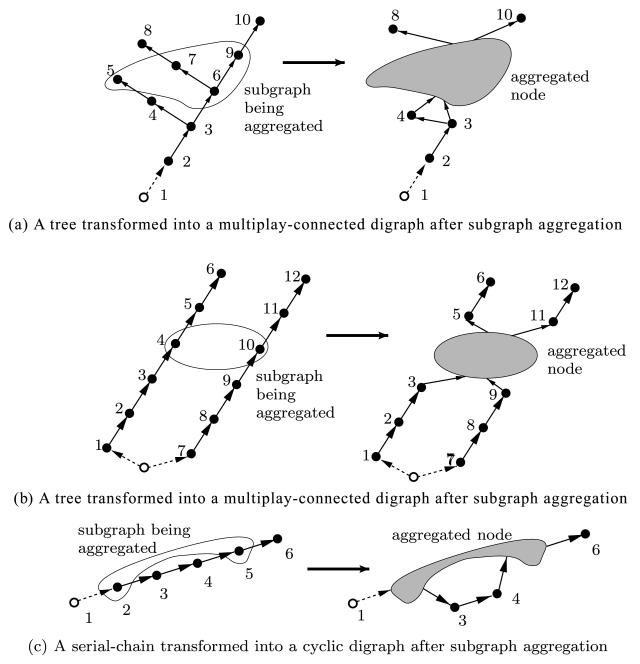
In graph theory, edge-contraction is referred to as the process of collapsing the node pair for an edge, into a single node [27]. The node and edge neighbors of the original pair of nodes become neighbors of the new aggregated node. Thus, the parent and children nodes of either of the original nodes (not including the node pair themselves) are the parent and children nodes of the aggregated node in the transformed digraph.

For a tree, the result of each such edge-contraction is once again a tree, with one fewer node. The edge-contraction process can be repeated to aggregate multiple edges in a tree. Thus, aggregating a sub-tree of a tree, using edge-contraction, results in a digraph that is also a tree.

Node-contraction is a more general concept that applies to pairs of nodes that are not necessarily connected by an edge. The node-contraction of a pair of nodes replaces the pair of nodes with a single aggregated node, where all the neighboring nodes and edges of the original pair become neighbors of the new aggregated node. Thus, edge-contraction is equivalent to node-contracting the node pair for an edge. Unlike edge-contractions, node-contractions generally do not preserve the tree property of a digraph. Node-contractions can be applied repeatedly to aggregate multiple nodes in a subgraph. Formally, subgraph aggregation is defined as the process of transforming a digraph by applying node-contraction to all the nodes in the subgraph. This is illustrated in Fig. 4. It shows examples of trees transformed into multiply-connected and cyclic digraphs, following subgraph aggregation. Later, we will examine the conditions under which the tree property is preserved following subgraph aggregation.

Fig. 4.

Examples of subgraph aggregation using node-contraction

The following lemma shows that aggregating a subgraph or its induced subgraph result in the same transformed digraph.

Lemma 3 (Aggregation of a subgraph and its induced subgraph) Let $\mathfrak{S}$ denote the subgraph of a digraph $\mathfrak{T}$. Then the new digraph, ${\mathfrak{T}}_{\mathfrak{S}}$, created by aggregating $\mathfrak{S}$, is the same as the one obtained by aggregating the induced subgraph, ${\mathfrak{S}}_I$, i.e., ${\mathfrak{T}}_{\mathfrak{S}}\equiv {\mathfrak{T}}_{{\mathfrak{S}}_I}$.

Proof $\mathfrak{S}$ and ${\mathfrak{S}}_I$ contain the same nodes, while the latter contains all the edges connecting the nodes as well. Node-contraction of a pair of nodes removes all edges connecting the node-pair. Thus, aggregating $\mathfrak{S}$ by node-contraction removes all edges connecting the nodes in $\mathfrak{S}$, whether or not the edges are in $\mathfrak{S}$ itself. This implies that the aggregation of $\mathfrak{S}$ or ${\mathfrak{S}}_I$ results in the same transformed digraph.

One implication of this lemma is that the nodes and edges missing from the transformed tree, after aggregating $\mathfrak{S}$, are precisely the nodes and edges in the ${\mathfrak{S}}_I$ induced subgraph of $\mathfrak{S}$.

5.2 Tree preservation after subgraph aggregation

Let $\mathfrak{S}$ denote a subgraph of a tree digraph, $\mathfrak{T}$. The aggregation of $\mathfrak{S}$ results in a new ${\mathfrak{T}}_{\mathfrak{S}}$ digraph, where all the nodes associated with the nodes in $\mathfrak{S}$ are replaced by a single node. We will henceforth refer to this aggregated node, as node $\mathfrak{S}$. Topologically, all the parent nodes of the $\mathfrak{S}$ subgraph, denoted $\wp \left(\mathfrak{S}\right)$, are now the parents of node $\mathfrak{S}$, and all the children nodes of the $\mathfrak{S}$ subgraph, denoted $\mathrm{C}\mathfrak{S}$, are now the children of node $\mathfrak{S}$. In general, ${\mathfrak{T}}_{\mathfrak{S}}$ obtained by this topological transformation will not be a tree.

The following defines the aggregation condition for subgraphs.

Assumption 1 (Aggregation condition) A subgraph $\mathfrak{S}$, of a tree digraph $\mathfrak{T}$, is said to satisfy the aggregation condition if:

1. $\mathfrak{S}$ is an induced subgraph, i.e., $\mathfrak{S}\equiv {\mathfrak{S}}_I$.

2. $\wp \left(\mathfrak{S}\right)$ contains exactly one node—one that is necessarily the ancestor of all the nodes in $\mathfrak{S}$.

The induced requirement for a $\mathfrak{S}$ satisfying the aggregation condition is a mild one since Lemma 3 states that aggregating a subgraph, or its induced subgraph, lead to the same transformed digraph. Some examples of a tree subgraph $\mathfrak{S}$, satisfying the aggregation condition, are:

• a single node

• a serial-chain segment

• a subtree

The following lemma shows that any subgraph of a tree satisfying the aggregation condition is a path-induced subgraph.

Lemma 4 (Aggregation condition and path-induced subgraphs) If a subgraph $\mathfrak{S}$ of a $\mathfrak{T}$ tree satisfies the aggregation condition, then it is path-induced, i.e., $\mathfrak{S}\equiv {\mathfrak{S}}_P$.

Proof Since $\mathfrak{S}$ satisfies the aggregation condition, it is an induced subgraph. An induced subgraph of a tree can differ from its path-induced subgraph in the nodes and edges that lie on the paths connecting nodes in $\mathfrak{S}$.

First, let us consider the case where the node sets are the same. Since $\mathfrak{S}$ is induced, there are no missing edges in $\mathfrak{S}$, and, therefore, even the set of edges are exactly the ones in the path-induced subgraph. Hence, $\mathfrak{S}$ and its path-induced subgraph are the same.

Let us now consider the case when the node sets are not the same. Then there exists a node k in the path-induced subgraph ${\mathfrak{S}}_P$ that is not in $\mathfrak{S}$. Node k must lie on a path connecting a pair of nodes in $\mathfrak{S}$. This implies that there is a node l on this path that belongs to $\wp \left(\mathfrak{S}\right)$. However, since k is in the interior of the path, node l is not the ancestor of all the nodes in $\mathfrak{S}$. This contradicts the assumption that $\mathfrak{S}$ satisfies the aggregation condition, which allows for only a single ancestor node for $\mathfrak{S}$. Hence, $\mathfrak{S}$ must be a path-induced subgraph.

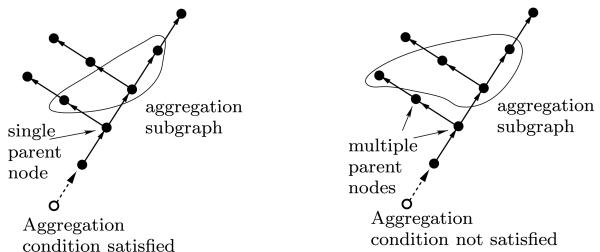
The converse is not true, i.e., not all path-induced subgraphs satisfy the aggregation condition. Figure 5 illustrates cases of path-induced subgraphs that do, and do not, satisfy the aggregation condition.

Fig. 5.

Examples of path-induced subgraphs that do, and do not, satisfy the aggregation condition

The following lemma shows that the aggregation condition is a necessary and sufficient condition for the ${\mathfrak{T}}_{\mathfrak{S}}$ aggregated digraph to be a tree.

Lemma 5 (Tree property after subgraph aggregation) Let $\mathfrak{S}$ denote an induced subgraph of a tree digraph $\mathfrak{T}$. Let us assume that $\mathfrak{S}$ is aggregated to create a new ${\mathfrak{T}}_{\mathfrak{S}}$ digraph with aggregated node $\mathfrak{S}$. Then the aggregated ${\mathfrak{T}}_{\mathfrak{S}}$ digraph is a tree if and only if the original sub-graph $\mathfrak{S}$ satisfies the aggregation condition.

Proof

1. First, let us assume the ${\mathfrak{T}}_{\mathfrak{S}}$ is indeed a tree, and we will show that $\wp \left(\mathfrak{S}\right)$ must contain a single node. Since ${\mathfrak{T}}_{\mathfrak{S}}$ is a tree, all of its nodes, including node $\mathfrak{S}$, can have at most one parent. Thus, $\wp \left(\mathfrak{S}\right)$ can have at most one node. The $\mathfrak{S}$ subgraph therefore satisfies the aggregation condition.

2. Now, let us consider the converse case, i.e., assume that $\wp \left(\mathfrak{S}\right)$ contains a single node that is the ancestor for all the nodes in $\mathfrak{S}$. We will prove that ${\mathfrak{T}}_{\mathfrak{S}}$ must then be a tree. We need to show that ${\mathfrak{T}}_{\mathfrak{S}}$ is not a polytree, is not multiply-connected, and does not have directed cycles.

   1. To show that ${\mathfrak{T}}_{\mathfrak{S}}$ is not a polytree, we need to focus only on node $\mathfrak{S}$ and show that it cannot have multiple parents. This follows directly from the assumption that $\wp \left(\mathfrak{S}\right)$ contains only one node.
   2. To show that ${\mathfrak{T}}_{\mathfrak{S}}$ is not multiply-connected, we need to focus only on the node $\mathfrak{S}$ and show that there is no node in ${\mathfrak{T}}_{\mathfrak{S}}$ from which there is more than one directed path to the node $\mathfrak{S}$. Since $\mathfrak{T}$ is a tree, it has no multiply-connected nodes. Thus, the only way for node $\mathfrak{S}$ to be multiply-connected is for multiple paths to end at node $\mathfrak{S}$. This would mean that the node $\mathfrak{S}$ has multiple parents—one from each of the paths that end on it. This would contradict the assumption that $\wp \left(\mathfrak{S}\right)$ contains a single node.
   3. Now, we show that ${\mathfrak{T}}_{\mathfrak{S}}$ cannot have directed cycles. Again, we need to focus on node $\mathfrak{S}$, and show that it cannot be part of a directed cycle. Assume that such a cycle exists. This implies that there are nodes $k,j\in \mathfrak{S}$, and a node $i\notin \mathfrak{S}$ such that k ≻ i ≻ j. In other words, there is a path from k to j containing node i. This would imply that there is a node, l, on the path from i to j that is a parent node for $\mathfrak{S}$. Since $\wp \left(\mathfrak{S}\right)$ contains only one node, l must be this ancestor node. This would imply that node l, and hence node i, is an ancestor of k. However we know that k is an ancestor of i. Hence, node $\mathfrak{S}$ is not part of any directed cycles.

Lemma 5 shows that preservation of the tree property after subgraph aggregation requires that the subgraph satisfy the aggregation condition. Intuitively, this result is not surprising, once we recall that edge-contractions preserve the tree property, and that the aggregation of a path-induced subgraph is equivalent to applying edge-contraction to all the edges in the subgraph.

5.3 The ${\mathfrak{S}}_A$ aggregation subgraph

The aggregation subgraph, for a subgraph $\mathfrak{S}$ of a tree, is defined as the minimal subgraph containing $\mathfrak{S}$ that also satisfies the aggregation condition. The aggregation subgraph of a subgraph $\mathfrak{S}$ is denoted ${\mathfrak{S}}_A$.

Lemma 6 (Properties of ${\mathfrak{S}}_A$)

1. ${\mathfrak{S}}_A$ is a path-induced subgraph.

2. The following containment relation holds

   $$\mathfrak{S}\subseteq {\mathfrak{S}}_I\subseteq {\mathfrak{S}}_P\subseteq {\mathfrak{S}}_A$$ (28)

3. ${\mathfrak{S}}_A$ is the subforest obtained by deleting the root node from the smallest subtree containing $\mathfrak{S}$.

Proof

1. By definition, ${\mathfrak{S}}_A$ satisfies the aggregation condition, and hence by Lemma 4, it is path-induced.

2. By definition, $\mathfrak{S}\subseteq {\mathfrak{S}}_A$. Hence, the path-induced subgraph of $\mathfrak{S}$, ${\mathfrak{S}}_P$, is contained in the path-induced subgraph of ${\mathfrak{S}}_A$, which is ${\mathfrak{S}}_A$ itself. This establishes the last containment in (28). The rest are restatements of (21).

3. Since ${\mathfrak{S}}_A$ satisfies the aggregation condition, it has a single parent node. Thus, with the parent node added in, the new subgraph is a subtree. The minimality of the sub-tree follows from the definition of a aggregation subgraph, which is required to be minimal.

This lemma helps us better understand the relationship between a subgraph, $\mathfrak{S}$, and its induced, path-induced and aggregation subgraphs. Starting with the $\mathfrak{S}$ subgraph, we obtain its induced subgraph ${\mathfrak{S}}_I$ by adding in the missing edges between the nodes in $\mathfrak{S}$. Furthermore, adding in any missing nodes and edges on paths connecting nodes in $\mathfrak{S}$ leads us to the path-induced ${\mathfrak{S}}_P$ subgraph. To obtain the ${\mathfrak{S}}_A$ aggregation subgraph, we need to further grow the path-induced subgraph until we get to the smallest sub-tree containing it, and then drop the root node from this subtree. The aggregation subgraph for a subgraph is important because, as shown by Lemma 5, while the aggregation of a subgraph $\mathfrak{S}$ will generally not preserve the tree property, aggregating ${\mathfrak{S}}_A$ instead ensures that the aggregated digraph remains a tree. Preserving the tree property is necessary requirement for the aggregated tree to have an SKO model.

6 Transforming SKO models via aggregation

6.1 SKO operators after body aggregation

Let $\mathfrak{T}$ be a tree digraph associated with a multibody system. We assume without loss in generality that it is canonical. Let $\mathfrak{S}$ denote a subgraph satisfying the aggregation condition. By Lemma 5, the aggregated ${\mathfrak{T}}_{\mathfrak{S}}$ digraph, with aggregated node $\mathfrak{S}$, is also a tree. Let us now develop an SKO model for the system with the ${\mathfrak{T}}_{\mathfrak{S}}$ aggregated tree.

To define SKO operators for ${\mathfrak{T}}_{\mathfrak{S}}$, we first need to assign weight dimensions to the nodes in ${\mathfrak{T}}_{\mathfrak{S}}$. All nodes unaffected by the aggregation process inherit the weight dimensions from the nodes in $\mathfrak{T}$. The weight dimension for node $\mathfrak{S}$ is defined as the sum of the weight dimensions of all the nodes in the $\mathfrak{S}$ subgraph, i.e.,

$$m_{\mathfrak{S}}\stackrel{\Delta }{=}\sum _{k\in \mathfrak{S}}{m}_k$$ (29)

Since the $\mathfrak{S}$ subgraph satisfies the aggregation condition it is path-induced. From Lemma 1, $\mathfrak{S}$ induces a disjoint partitioning of $\mathfrak{T}$ into path-induced parent $\mathcal{P}$ and child $\mathcal{C}$ subgraphs, respectively. These partitionedsubgraphs allow us to express the ε_φ SKO operator for $\mathfrak{T}$ in the partitioned form shown in (22):

$${\mathcal{E}}_{𝔸}=\left(\begin{array}{ccc}\hfill {\mathcal{E}}_{{𝔸}_{\mathcal{C}}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\mathcal{B}}_{\mathfrak{S}}\hfill & \hfill {\mathcal{E}}_{{𝔸}_{\mathfrak{S}}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill E_{\mathfrak{S}}\hfill & \hfill {\mathcal{E}}_{{𝔸}_{\mathcal{P}}}\hfill \end{array}\right)$$ (30)

Lemma 7 (SKO operator for the ${\mathfrak{T}}_{\mathfrak{S}}$ tree) With $\mathfrak{S}$ satisfying the aggregation condition, define the ${\mathcal{E}}_{𝔸}$_a matrix using the partitioned sub-blocks of (30) as follows:

$${\mathcal{E}}_{{𝔸}_a}\stackrel{\Delta }{=}\left(\begin{array}{ccc}\hfill {\mathcal{E}}_{{𝔸}_{\mathcal{C}}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\mathcal{B}}_{\mathfrak{S}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill E_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}\hfill & \hfill {\mathcal{E}}_{{𝔸}_{\mathcal{P}}}\hfill \end{array}\right)$$ (31)

The following facts hold for ${\mathcal{E}}_{𝔸}$_a:

1. ${\mathcal{E}}_{𝔸}$_a is an SKO operator for the original tree, $\mathfrak{T}$.

2. ${\mathcal{E}}_{𝔸}$_a is an SKO operator for the aggregated tree, ${\mathfrak{T}}_{\mathfrak{S}}$.

Proof

1. Since $\mathfrak{S}$ satisfies the aggregation condition, $\wp \left(\mathfrak{S}\right)$ contains a single node. Let us denote this node as node j. Comparing the expression for ${\mathcal{E}}_{𝔸}$_a in (31) with that of ${\mathcal{E}}_{𝔸}$ in (30), the only term that needs further examination to establish the SKO property is the $E_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}$ block, which differs from the $E_{\mathfrak{S}}$ block. Recall that the $E_{\mathfrak{S}}$ connector block contains non-zero entries for the edges connecting nodes in $\mathcal{P}$ to nodes in $\mathfrak{S}$ subgraphs. Therefore, $E_{\mathfrak{S}}$ has the form

   $$E_{\mathfrak{S}}=\sum _{l\in \wp \left(\mathfrak{S}\right)}{\mathrm{e}}_l\sum _{\begin{array}{c}\hfill k\in \mathfrak{S}\hfill \\ \hfill \wp \left(k\right)=l\hfill \end{array}}𝔸(l,k){\mathrm{e}}_k^{\ast }={\mathrm{e}}_j\sum _{\begin{array}{c}\hfill k\in \mathfrak{S}\hfill \\ \hfill \wp \left(k\right)=j\hfill \end{array}}𝔸(j,k){\mathrm{e}}_k^{\ast }$$ (32)
   In the above equations, we have taken some notational liberties; the e_x vectors represent appropriate size vectors for the $\mathfrak{S}$ and $\mathcal{P}$ subgraphs, instead of the full-sized ones for the $\mathfrak{T}$ tree. It follows that

   $$E_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}\stackrel{\left(32\right)}{=}{\mathrm{e}}_j\sum _{\begin{array}{c}\hfill k,i\in \mathfrak{S}\hfill \\ \hfill \wp \left(k\right)=j\hfill \end{array}}𝔸(j,k){\mathrm{e}}_k^{\ast }{𝔸}_{\mathfrak{S}}$$ (33)
   The $e_k^{\ast }{𝔸}_{\mathfrak{S}}$ product is the kth row of ${𝔸}_{\mathfrak{S}}$. Since ${𝔸}_{\mathfrak{S}}$ is an SPO operator, its kth row 𝔸(k, i) entry is nonzero only when node i is a descendant of the kth node. Hence, (33) can be reexpressed as

   $$\begin{array}{cc}\hfill E_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}& \stackrel{\left(33\right)}{=}{\mathrm{e}}_j\sum _{\begin{array}{c}\hfill k\in \mathfrak{S}\hfill \\ \hfill \wp \left(k\right)=j,k\succ i\hfill \end{array}}𝔸(j,k)𝔸(k,i){\mathrm{e}}_i\hfill \\ \hfill & ={\mathrm{e}}_j\sum _{\begin{array}{c}\hfill i\in \mathfrak{S}\hfill \\ \hfill j\succ i\hfill \end{array}}𝔸(j,i){\mathrm{e}}_i^{\ast }\hfill \end{array}$$ (34)

   In the last expression, j ≻ i, denotes the condition that the jth node is an ancestor of the ith node. From (34), it is clear that only the jth row of $E_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}$ is nonzero. The only nonzero entries in this row are for nodes in $\mathfrak{S}$ that are descendants of the jth node.⁶ Thus, each column of $E_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}$, has at most a single nonzero element, and since the central block of ${\mathcal{E}}_{𝔸}$_a is zero, this implies that the same column has only a single nonzero entry in the full ${\mathcal{E}}_{𝔸}$_a matrix as well. Thus, the single nonzero entry per column requirement for an SKO operator for $\mathfrak{T}$ is satisfied. Hence, ${\mathcal{E}}_{𝔸}$_a is an SKO operator for $\mathfrak{T}$.

2. We have seen that ${\mathcal{E}}_{𝔸}$_a is an SKO operator for $\mathfrak{T}$. For ${\mathfrak{T}}_{\mathfrak{S}}$, the central rows and columns of ${\mathcal{E}}_{𝔸}$_a correspond to the single $\mathfrak{S}$ node in the ${\mathfrak{T}}_{\mathfrak{S}}$ tree. For ${\mathcal{E}}_{𝔸}$_a to be an SKO operator for ${\mathfrak{T}}_{\mathfrak{S}}$, we need to show that it satisfies the SKO operator structural requirements, as represented by (9). That is, $E_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}$ must be of the form e_jX for some X. Equation (34) satisfies this requirement, and, thus, ${\mathcal{E}}_{𝔸}$_a is an SKO operator for ${\mathfrak{T}}_{\mathfrak{S}}$.

Having derived the expression for an ${\mathcal{E}}_{𝔸}$_a SKO operator for ${\mathfrak{T}}_{\mathfrak{S}}$, the following lemma derives the expression for the corresponding SPO operator for ${\mathfrak{T}}_{\mathfrak{S}}$.

Lemma 8 (The 𝔸_a SPO operator for the ${\mathfrak{T}}_{\mathfrak{S}}$ tree) Using the same assumptions and notation from Lemma 7, the SPO operator, 𝔸_a, for ${\mathfrak{T}}_{\mathfrak{S}}$ is given by the following expression:

$$\begin{array}{cc}\hfill {𝔸}_a& \stackrel{\Delta }{=}{\mathfrak{J}}_a𝔸\hfill \\ \hfill & \stackrel{\left(24\right)}{=}\left(\begin{array}{ccc}\hfill {𝔸}_{\mathcal{C}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\mathcal{B}}_{\mathfrak{S}}{𝔸}_{\mathcal{C}}\hfill & \hfill \mathbf{I}\hfill & \hfill 0\hfill \\ \hfill {𝔸}_{\mathcal{P}}\left(E_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}{\mathcal{B}}_{\mathfrak{S}}\right){𝔸}_{\mathcal{C}}\hfill & \hfill {𝔸}_{\mathcal{P}}{E}_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}\hfill & \hfill {𝔸}_{\mathcal{P}}\hfill \end{array}\right)\hfill \\ \hfill & \text{where}{\mathfrak{J}}_a\stackrel{\Delta }{=}\left(\begin{array}{ccc}\hfill \mathbf{I}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {𝔸}_{\mathfrak{S}}^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \mathbf{I}\hfill \end{array}\right)\hfill \end{array}$$ (35)

Proof Since Lemma 8 established ${\mathcal{E}}_{𝔸}$_a as an SKO operator for the ${\mathfrak{T}}_{\mathfrak{S}}$ tree, we need to show that ${𝔸}_a={(\mathbf{I}-{\mathcal{E}}_{{𝔸}_a})}^{-1}$ for it to be an SPO operator for ${\mathfrak{T}}_{\mathfrak{S}}$. Now

$$\begin{array}{cc}\hfill (\mathbf{I}-{\mathcal{E}}_{{𝔸}_a})& \stackrel{\left(22\right)}{=}\left(\begin{array}{ccc}\hfill \mathbf{I}-{\mathcal{E}}_{{𝔸}_{\mathcal{C}}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -{\mathcal{B}}_{\mathfrak{S}}\hfill & \hfill \mathbf{I}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -E_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}\hfill & \hfill \mathbf{I}-{\mathcal{E}}_{{𝔸}_{\mathcal{P}}}\hfill \end{array}\right)\hfill \\ \hfill & \stackrel{\left(23\right)}{=}\left(\begin{array}{ccc}\hfill {𝔸}_{\mathcal{C}}^{-1}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -{\mathcal{B}}_{\mathfrak{S}}\hfill & \hfill \mathbf{I}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -E_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}\hfill & \hfill {𝔸}_{\mathcal{P}}^{-1}\hfill \end{array}\right)\hfill \end{array}$$

The result follows by verifying that the product of the above, with 𝔸_a in (35), is the identity matrix.

Node $\mathfrak{S}$ in ${\mathfrak{T}}_{\mathfrak{S}}$ contains all the bodies associated with the nodes in the original subgraph $\mathfrak{S}$. Unlike regular rigid links, the geometry of node $\mathfrak{S}$ is variable, and depends on the hinge coordinates of the component links within the subgraph $\mathfrak{S}$. Such variable geometry bodies have been used in other dynamics modeling contexts [5, 10, 29].

6.2 SKO model for the ${\mathfrak{T}}_{\mathfrak{S}}$ aggregated tree

The key difference between the aggregated and the original tree is that the former treats the set of bodies in subgraph $\mathfrak{S}$ as a single body. The aggregation process provides a way of transforming and substructuring SKO models for tree-topology multibody systems into coarser SKO models. The aggregation process induces the following partitioning of the $\stackrel{.}{\theta }$, $\mathcal{V}$, $\mathfrak{f}$ and $\mathcal{T}$ stacked vectors:

$$\begin{array}{cc}\hfill & \stackrel{.}{\theta }=\left[\begin{array}{c}\hfill {\stackrel{.}{\theta }}_{\mathcal{C}}\hfill \\ \hfill {\stackrel{.}{\theta }}_{\mathfrak{S}}\hfill \\ \hfill {\stackrel{.}{\theta }}_{\mathcal{P}}\hfill \end{array}\right],\mathcal{V}=\left[\begin{array}{c}\hfill {\mathcal{V}}_{\mathcal{C}}\hfill \\ \hfill {\mathcal{V}}_{\mathfrak{S}}\hfill \\ \hfill {\mathcal{V}}_{\mathcal{P}}\hfill \end{array}\right],\hfill \\ \hfill & \mathfrak{f}=\left[\begin{array}{c}\hfill {\mathfrak{f}}_{\mathcal{C}}\hfill \\ \hfill {\mathfrak{f}}_{\mathfrak{S}}\hfill \\ \hfill {\mathfrak{f}}_{\mathcal{P}}\hfill \end{array}\right],\mathcal{T}=\left[\begin{array}{c}\hfill {\mathcal{T}}_{\mathcal{C}}\hfill \\ \hfill {\mathcal{T}}_{\mathfrak{S}}\hfill \\ \hfill {\mathcal{T}}_{\mathcal{P}}\hfill \end{array}\right]\hfill \end{array}$$ (36)

For the ${\mathfrak{T}}_{\mathfrak{S}}$ aggregated tree, the ${\mathcal{V}}_{\mathfrak{S}}$, ${\stackrel{.}{\theta }}_{\mathfrak{S}}$ etc., subvectors of the $\mathcal{V}$ and $\stackrel{.}{\theta }$ stacked vectors correspond to the single $\mathfrak{S}$ aggregate link. This partitioning of the system-level $\stackrel{.}{\theta }$ and $\mathcal{V}$ stacked vectors extends to other stacked vectors such as the Coriolis spatial accelerations vector $\mathfrak{a}$, the gyroscopic spatial forces vector $\mathfrak{b}$, and to the other spatial operators.

Lemma 9 shows that the transformed system with the aggregated tree possesses a well-defined SKO model, and defines the equations of motion for the model.

Lemma 9 (SKO model for an aggregated tree) Let (H, 𝔸, M) denote an SKO model with tree digraph $\mathfrak{T}$. Let $\mathfrak{S}$ be a subgraph of $\mathfrak{T}$ satisfying the aggregation condition. Then the (H_a, 𝔸_a, M) spatial operators define an SKO model for the ${\mathfrak{T}}_{\mathfrak{S}}$ aggregated tree, where

$$\begin{array}{cc}\hfill & H_a\stackrel{\Delta }{=}H{\mathfrak{J}}_a^{-1}\stackrel{\left(35\right)}{=}\left(\begin{array}{ccc}\hfill H_{\mathcal{C}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\underset{¯}{H}}_{\mathfrak{S}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill H_{\mathcal{P}}\hfill \end{array}\right)\text{and}\hfill \\ \hfill & {\underset{¯}{H}}_{\mathfrak{S}}\stackrel{\Delta }{=}{H}_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}\hfill \end{array}$$ (37)

H_a defines the new joint map matrix for the ${\mathfrak{T}}_{\mathfrak{S}}$ aggregated tree, with $H_{\mathcal{C}}$,$H_{\mathfrak{S}}$, and $H_{\mathcal{P}}$ denoting the component joint map matrices as defined in (25). The transformed version of the equations of motion from (18) are given by:

$$\begin{array}{cc}\hfill \mathcal{V}& ={𝔸}_a^{\ast }{H}_a^{\ast }\stackrel{.}{\theta }\hfill \\ \hfill \alpha & ={𝔸}_a^{\ast }(H_a^{\ast }\ddot{\theta }+\underset{¯}{\mathfrak{a}}),\hfill \\ \hfill & \text{where}\underset{¯}{\mathfrak{a}}\stackrel{\Delta }{=}{\mathfrak{J}}_a^{-\ast }\mathfrak{a}=\left[\begin{array}{c}\hfill {\mathfrak{a}}_{\mathcal{C}}\hfill \\ \hfill {\underset{¯}{\mathfrak{a}}}_{\mathfrak{S}}\hfill \\ \hfill {\mathfrak{a}}_{\mathcal{P}}\hfill \end{array}\right],{\underset{¯}{\mathfrak{a}}}_{\mathfrak{S}}\stackrel{\Delta }{=}{𝔸}_{\mathfrak{S}}^{\ast }{\mathfrak{a}}_{\mathfrak{S}}\hfill \\ \hfill \underset{¯}{\mathfrak{f}}& ={𝔸}_a(M\alpha +\mathfrak{b}),\hfill \\ \hfill & \text{where}\underset{¯}{\mathfrak{f}}\stackrel{\Delta }{=}{\mathfrak{J}}_a\mathfrak{f}=\left[\begin{array}{c}\hfill {\mathfrak{f}}_{\mathcal{C}}\hfill \\ \hfill {\mathfrak{f}}_{\mathfrak{S}}^{\prime }\hfill \\ \hfill {\mathfrak{f}}_{\mathcal{P}}\hfill \end{array}\right],{\mathfrak{f}}_{\mathfrak{S}}^{\prime }\stackrel{\Delta }{=}{𝔸}_{\mathfrak{S}}^{-1}{\mathfrak{f}}_{\mathfrak{S}}\hfill \\ \hfill \mathcal{T}& =H_a\underset{¯}{\mathfrak{f}}\hfill \end{array}$$ (38)

Thus,

$$\mathcal{T}=\mathcal{M}\ddot{\theta }+\mathcal{C}$$ (39)

with

$$\begin{array}{cc}\hfill & \mathcal{M}=H_a{𝔸}_a\mathit{M}{𝔸}_a^{\ast }{H}_a^{\ast }\in {\mathcal{R}}^{\mathcal{N}\times \mathcal{N}}\text{and}\hfill \\ \hfill & \mathcal{C}\stackrel{\Delta }{=}{H}_a{𝔸}_a(\mathit{M}{𝔸}_a^{\ast }\underset{¯}{\mathfrak{a}}+\mathfrak{b})\in {\mathcal{R}}^{\mathcal{N}}\hfill \end{array}$$ (40)

The mass matrix expression above represents the Newton–Euler operator factorization of the mass matrix for the SKO model of the aggregated system.

Proof Lemma 8 established that 𝔸_a is the SPO operator for ${\mathfrak{T}}_{\mathfrak{S}}$. With the central row and column of H_a corresponding to node $\mathfrak{S}$ in ${\mathfrak{T}}_{\mathfrak{S}}$, H_a is block-diagonal for ${\mathfrak{T}}_{\mathfrak{S}}$. Lastly, M has remained unchanged in going from $\mathfrak{T}$ to ${\mathfrak{T}}_{\mathfrak{S}}$. Thus, the structural requirements 1 through 4 for an SKO model in Sect. 2.4, are satisfied for the ${\mathfrak{T}}_{\mathfrak{S}}$ tree, by the (H_a, 𝔸_a, M) operators.

The equations of motion in (38) follow by substituting the expressions for H_a and 𝔸_a from (35) and (37) in the original equations of motion in (18).

Observe that, while $H_{\mathfrak{S}}$ is block-diagonal, ${\underset{¯}{H}}_{\mathfrak{S}}=H_{\mathfrak{S}}{𝔸}_{\mathfrak{S}}$ is no longer block-diagonal. Consequently, H_a is not block-diagonal for $\mathfrak{T}$ and the (H_a, 𝔸_a, M) operators do not satisfy the structural requirements for an SKO model for the original $\mathfrak{T}$. Nevertheless, the above lemma shows that these operators do satisfy the SKO model structural requirements for the ${\mathfrak{T}}_{\mathfrak{S}}$ tree. This implies that all of the SKO model formulation techniques and algorithms, including mass matrix factorization and inversion, are applicable to the SKO model of the aggregated tree.

The following corollary formally verifies that at the system-level, the mass matrix and Coriolis terms in the equations of motion are identical across the original and the aggregated systems. This of course is to expected, since the aggregation process only changes the form of the equations of motion and not the system dynamics.

Corollary 6.1 (Mass matrix invariance with aggregation) The mass matrix, $\mathcal{M}$, and the Coriolis vector, $\mathcal{C}$, of a tree-topology system remain unchanged after subgraph aggregation. In other words, the expressions for $\mathcal{M}$ and $\mathcal{C}$ in (40) agree with the quantities defined in (20), i.e.,

$$\begin{array}{cc}\hfill & \mathcal{M}=H𝔸\mathit{M}{𝔸}^{\ast }{H}^{\ast }=H_a{𝔸}_a\mathit{M}{𝔸}_a^{\ast }{H}_a^{\ast }\hfill \\ \hfill & \mathcal{C}=H𝔸(\mathit{M}{𝔸}^{\ast }\mathfrak{a}+\mathfrak{b})=H_a{𝔸}_a(\mathit{M}{𝔸}_a^{\ast }\underset{¯}{\mathfrak{a}}+\mathfrak{b})\hfill \end{array}$$ (41)

Proof First, we have

$$H𝔸\stackrel{\left(35\right),\left(37\right)}{=}\left(H_a{\mathfrak{J}}_a^{-1}\right)\left({\mathfrak{J}}_a{𝔸}_a\right)=H_a{𝔸}_a$$ (42)

Using this directly establishes the $\mathcal{M}$ equalities in (41). Moreover,

$$\begin{array}{cc}\hfill H𝔸(\mathit{M}{𝔸}^{\ast }\mathfrak{a}+\mathfrak{b})& \stackrel{\left(42\right)}{=}{H}_a{𝔸}_a(\mathit{M}{𝔸}^{\ast }\mathfrak{a}+\mathfrak{b})\hfill \\ \hfill & \stackrel{\left(35\right)}{=}{H}_a{𝔸}_a(\mathit{M}{𝔸}_a^{\ast }{\mathfrak{J}}_a^{-\ast }\mathfrak{a}+\mathfrak{b})\hfill \\ \hfill & \stackrel{\left(38\right)}{=}{H}_a{𝔸}_a(\mathit{M}{𝔸}_a^{\ast }\underset{¯}{\mathfrak{a}}+\mathfrak{b})\hfill \end{array}$$

This establishes the $\mathcal{C}$ equalities in (41).

The aggregation process provides a way to apply substructuring to develop alternative SKO models for a multibody system.

7 SKO model sparsity structure

Researchers have used system-level matrices and operators to analyze and exploit the sparsity structure of the mass matrix to develop efficient computational algorithms for the inverse and forward dynamics problems [3, 7, 21, 23]. In this section, we apply the partitioning and aggregation techniques developed to identify the sparsity structure of the SKO and SPO operators and the mass matrix for tree-topology systems.

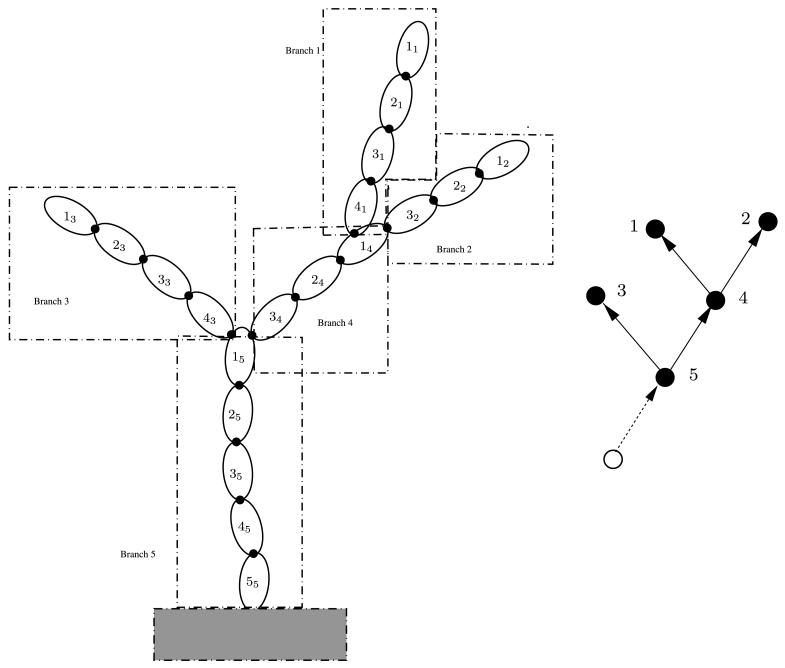
Tree and serial-chain subgraphs are always path-induced and satisfy the aggregation condition. Thus any tree system can be successively partitioned using such subgraphs. However, only in serial-chains are all node pairs related resulting in the most dense SKO and SPO operators. Thus, serial-chain subgraphs are well suited for analyzing the sparsity structure of SKO models. Toward this, the system digraph can be decomposed into disjoint serial-chain branch segments, which are subsequently aggregated to obtain a coarser tree model for the system. Figure 6 illustrates such a transformation of a tree with five serial-chain segments into a coarser tree with all the serial-chain segments aggregated into nodes.

Fig. 6.

Illustration of a tree-topology system on the left transformed into the coarser tree on the right by aggregating the serial-chain segments

The sparsity structure of the system’s spatial operators (e.g., SPO, mass matrix) directly reflects the structure of the aggregated tree. Subblocks of these matrices are associated with the aggregated serial-chain segment nodes, and are the most dense because all the nodes in a serial-chain are related. Equation (43) illustrates the sparsity structure of the system-level ${\mathcal{E}}_{𝔸}$ SKO operator via its decomposition in terms of the SKO operators for each of the aggregated serial-chain nodes

$${\mathcal{E}}_{𝔸}=\left(\begin{array}{ccccc}\hfill {\mathcal{E}}_{{𝔸}_1}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathcal{E}}_{{𝔸}_2}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathcal{E}}_{{𝔸}_3}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\mathcal{E}}_{{𝔸}_{4,1}}\hfill & \hfill {\mathcal{E}}_{{𝔸}_{4,2}}\hfill & \hfill 0\hfill & \hfill {\mathcal{E}}_{{𝔸}_4}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathcal{E}}_{{𝔸}_{5,3}}\hfill & \hfill {\mathcal{E}}_{{𝔸}_{5,4}}\hfill & \hfill {\mathcal{E}}_{{𝔸}_5}\hfill \end{array}\right)$$ (43)

ε_φj denotes the SKO operator for the jth branch segment. Also, when the kth branch is a child of the jth branch, the ${\mathcal{E}}_{𝔸}$_j,k block denotes the non-zero connector block between them. All other blocks are zero. The structure of ${\mathcal{E}}_{𝔸}$_j,k is as follows:

$${\mathcal{E}}_{{𝔸}_{j,k}}\stackrel{\Delta }{=}\left(\begin{array}{cccc}\hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 𝔸(1_j,n_k)\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \cdots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)$$ (44)

where 1_j denotes the tip body on the jth branch that is the parent of the n_k base-body of the kth branch. This partitioned structure of ${\mathcal{E}}_{𝔸}$ is a generalization of the partitioned structure in (22). We see that the only nonzero blocks in the lower-triangular part of the ${\mathcal{E}}_{𝔸}$ matrix in (43) are for the adjacent nodes in the aggregated tree.

With ${\varphi }_j\stackrel{\Delta }{=}{(\mathbf{I}-{\mathcal{E}}_{{\varphi }_j})}^{-1}$ denoting the SPO operator the jth branch, the overall structure of the system level 𝔸 SPO operator for Fig. 6 tree is illustrated in (45):

$$𝔸=\left(\begin{array}{ccccc}\hfill {𝔸}_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {𝔸}_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {𝔸}_3\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {𝔸}_{4,1}\hfill & \hfill {𝔸}_{4,2}\hfill & \hfill 0\hfill & \hfill {𝔸}_4\hfill & \hfill 0\hfill \\ \hfill {𝔸}_{5,1}\hfill & \hfill {𝔸}_{5,2}\hfill & \hfill {𝔸}_{5,3}\hfill & \hfill {𝔸}_{5,4}\hfill & \hfill {𝔸}_5\hfill \end{array}\right)$$ (45)

The 𝔸_j,k blocks denote the nonzero connector block between related serial-chain segments. All other blocks are zero. This partitioned structure of ${\mathcal{E}}_{𝔸}$ is a generalization of the partitioned structure in (24). The general expression for the 𝔸_j,k elements is:

$${𝔸}_{j,k}={𝔸}_j{\mathcal{E}}_{{𝔸}_{j,i}}{𝔸}_{i,k}\text{with}i\in \mathrm{C}\left(j\right),i\underset{¯}{\succ }k$$

In the above, ${𝔸}_{k,k}\equiv {𝔸}_k$. We see that the only nonzero blocks in the lower-triangular part of the 𝔸 matrix in (45) are for the related nodes in the aggregated tree.

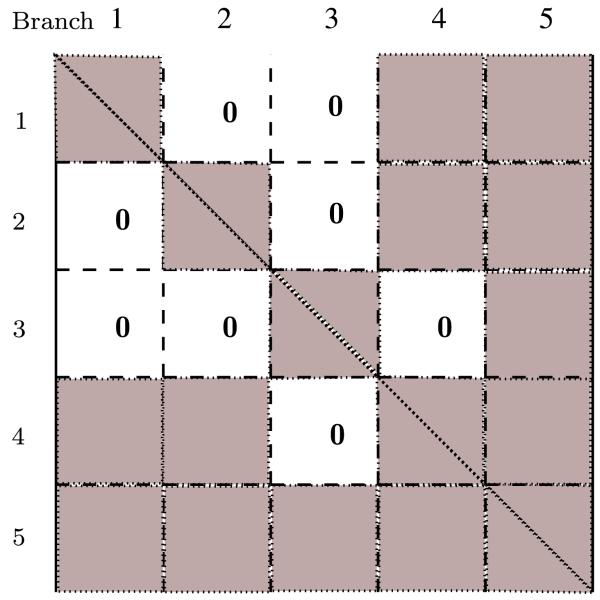
Figure 7 illustrates the sparsity structure of the mass matrix for the tree-topology system in Fig. 6. As expected, the sparsity structure of the mass matrix mirrors the sparsity of the 𝔸 SPO operator and its transpose. The block-diagonal of the mass matrix contains dense blocks, one for each of the branch segments in the tree. The off-diagonal blocks are zero for unrelated nodes in the aggregated tree. The topology dependency of the mass matrix’s sparsity structure was initially described in [22].

Fig. 7.

Structure of the mass matrix $\mathcal{M}$ for the tree topology system in Fig. 6

8 Conclusions

SKO models play a pivotal role in the analysis and algorithm development for tree multibody systems. In this paper, we have studied the effect of topological transformations on such SKO models. Path-induced subgraphs are shown to partition tree digraphs into parent and child path-induced subgraphs. We derive the relationship between the SKO models of the original multibody system and the SKO models of the partitioned subsystems. We further show that SKO models can be substructured into coarser SKO models by aggregating path-induced subgraphs into aggregated nodes. We show that the path-induced property for the aggregated subgraph is a necessary and sufficient condition for preserving the tree structure of the aggregated system and derive the SKO model for the aggregated system. Lastly, we use these topological insights to understand the relationship between the topological structure of the system digraph and the sparsity of the system SKO and SPO operators and its mass matrix. In the companion second part, we use these aggregation methods to develop a constraint embedding technique that extends the notion of SKO models from tree to closed-topology systems.

We anticipate future applications of these substructuring ideas in the development of parallel algorithms for distributing computations across component SKO models. Featherstone’s divide and conquer (DCA) forward algorithm [6] exemplifies such a use of a hierarchy of substructured component models to parallelize the solution for the forward dynamics problem. We also expect that partitioning and substructuring ideas to be useful in managing the dynamics computations for humanoid and legged robotic platforms subject to varying topologies and constraints. Furthermore, we anticipate the sparsity structure insights to facilitate the further development of sparsity based computational algorithms.