Optogenetic Activation of an Inhibitory Network Enhances Feed-Forward Functional Connectivity in Auditory Cortex

Summary

The mammalian neocortex is a highly interconnected network of different types of neurons organized into both layers and columns. Overlaid on this structural organization is a pattern of functional connectivity that can be rapidly and flexibly altered during behavior. Parvalbumin-positive (PV) inhibitory neurons, which are implicated in cortical oscillations and can change neuronal selectivity, may play a pivotal role in these dynamic changes. We found that optogenetic activation of PV neurons in the auditory cortex enhanced feed-forward functional connectivity in the putative thalamorecipient circuit and in cortical columnar circuits. In contrast, PV stimulation induced no change in connectivity between sites in the same layers. The activity of PV neurons may thus serve as a gating mechanism to enhance feed-forward, but not lateral or feedback, information flow in cortical circuits. Functionally, it may preferentially enhance the contribution of bottom-up sensory inputs to perception.

Introduction

Neurons communicate with each other in dynamically modulated circuits. Functional connectivity, a measure of interactions between neurons in these circuits, can change gradually during learning (McIntosh and Gonzalez-Lima, 1998) and formation of long-term memories, or can change rapidly depending on behavioral context and cognitive demands. While the mechanisms underlying long-term network plasticity have been extensively documented, those underlying rapid modulation of functional connectivity remain largely unknown. At the network level, functional connectivity is affected by up-down and oscillatory states of the neural network (Gray et al., 1989). Cortical inhibition plays a key role in this process (Cardin et al., 2009; Sohal et al., 2009; Womelsdorf et al., 2007). PV-positive interneurons, which make up more than half of the inhibitory neurons in the cortex (Celio, 1986), are particularly important as they provide strong feed-forward and feedback inhibition that can synchronize the cortical network (Cardin et al., 2009; Fuchs et al., 2007; Isaacson and Scanziani, 2011; Sohal et al., 2009). Their precise influence on cortical networks during sensory processing, however, remains unclear. In particular, to date no studies have addressed how PV neurons may differentially modulate responses in different layers of the neocortex, and how the anatomical organization of the cortex affects the flow of information through these networks.

Histological studies have shown that the cortex consists of defined layers with vertical projections between those layers (Lee and Winer, 2008; Linden and Schreiner, 2003; Winer and Lee, 2007). Functional connectivity within cortical networks has traditionally been investigated by measuring the cross-correlation between the spike trains of pairs of neurons (Douglas et al. 1989; Douglas and Martin, 1991). Still, little is known about functional connectivity under sensory stimulation or about the role of inhibition in the cortical network. We combine multiple computational approaches with optogenetic activation of PV neurons to determine how inhibitory activity modulates network connectivity within and across layers and columns of the cortex.

Results and Discussion

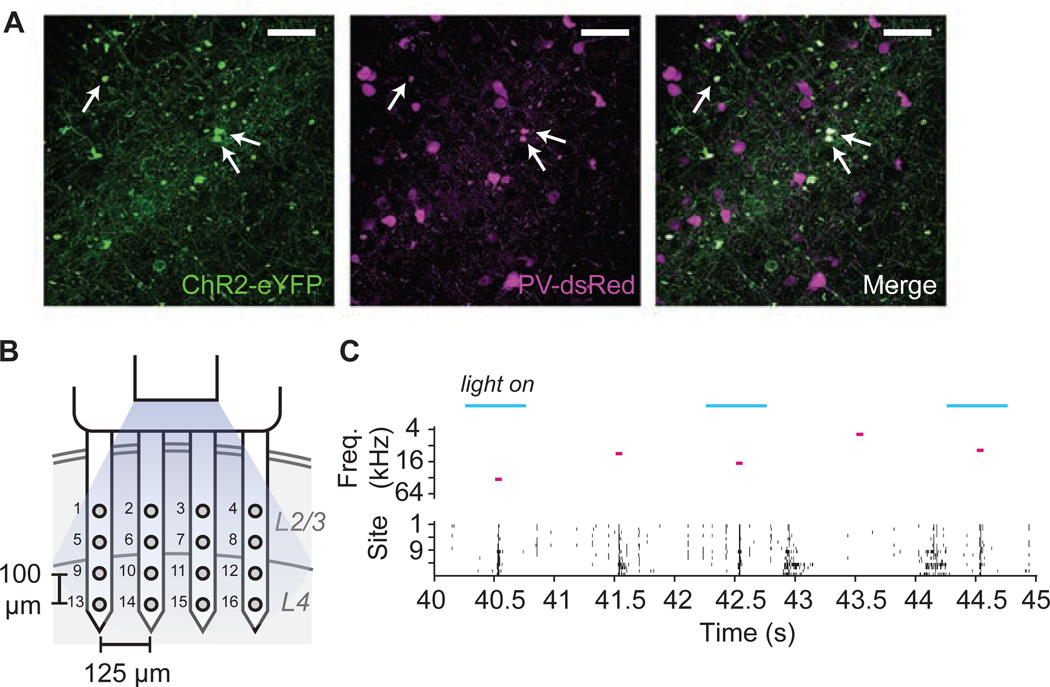
We targeted expression of the light-sensitive channel channelrhodopsin-2 (ChR2) to PV neurons in the mouse auditory cortex (Fig. 1A) using a Cre-dependent adeno-associated virus (Sohal et al., 2009). One month post-transfection, we recorded neural responses with a 4 × 4 polytrode in putative L2/3 through L4 of the primary auditory cortex (Fig. 1B) while playing pure tones to the contralateral ear and stimulating PV cells with blue light (Fig. 1C).

Figure 1.

Viral expression, recording setup and responses to pure tone and optogenetic stimulation. A. We injected PV-Cre mice with 1 uL of a Cre-inducible adeno-associated virus (AAV) in the right auditory cortex that resulted in transfection of the light sensitive ion channel ChR2 in PV cells. Histology confirmed the colocalization of ChR2-eYFP (left) to parvalbumin-positive cells in the auditory cortex (center, immunostained with dsRed, and see merge). Approximately 58% of PV cells were transfected with ChR2 (white arrows indicate examples of colocalization). White scale bar = 50 µm. B. Schematic depicting recording setup. A 4×4 silicon polytrode was lowered orthogonally to the cortex such that the deepest sites were located at a depth of ~500 µm. A 200 µm diameter optic fiber coupled to a 473 nm blue laser was positioned parallel to the polytrode, 1–2mm above the cortex to provide optogenetic stimulation during 50% of the trials. C. Light and sound stimulus conditions for example trials and corresponding spike raster plot. Input to the Ising model was a binary matrix including the light condition at each time point (blue bars represent the time during which the light was on and PV cells were being stimulated), the frequency of the pure tone stimulus that was presented at each time (represented by pink bars), and the spike data for each channel, binned at 5 ms. Sound and light conditions were randomly interleaved for each 1 second trial.

Using Ising models to recover functional connectivity in cortical circuits

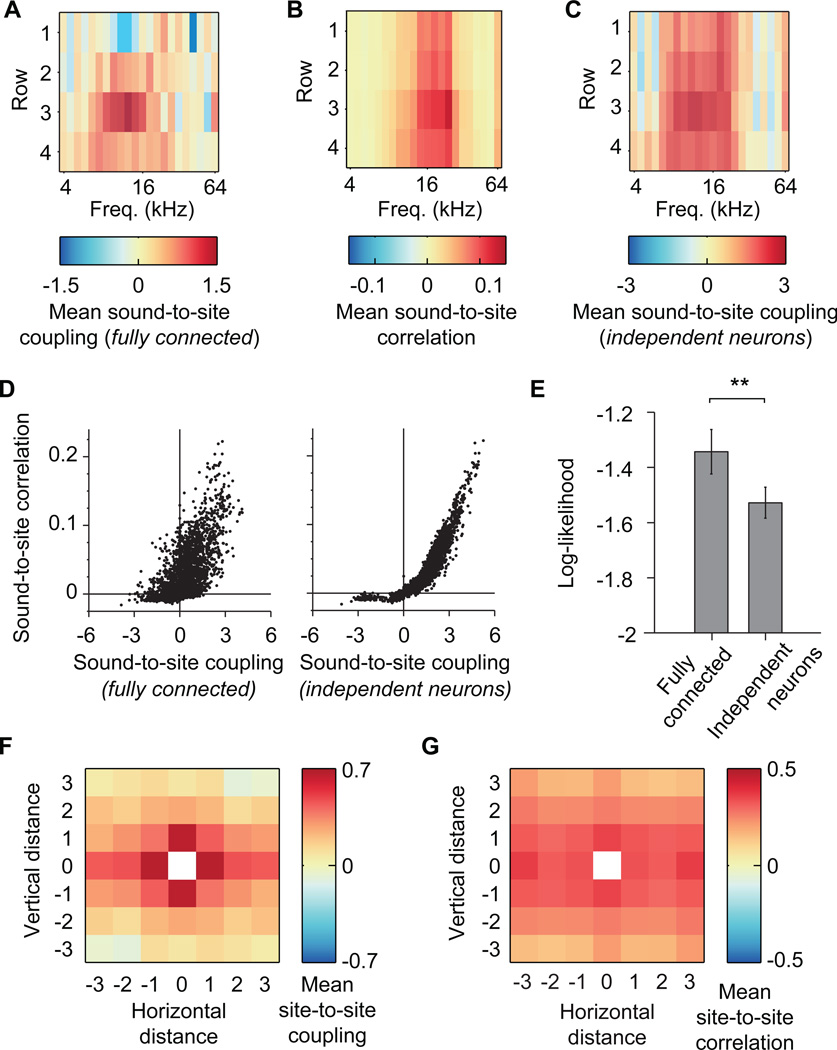
Functional connectivity between the recorded sites was quantified using Ising models, which have previously been used to model neural interactions in many different systems (Ganmor et al., 2011a, 2011b; Koster et al., 2012; Marre et al., 2009; Ohiorhenuan et al., 2010; Roudi et al., 2009a; Schaub and Schultz, 2012; Schneidman et al., 2006; Shlens et al., 2006, 2009; Tang et al., 2008). The Ising model describes the coupling (a measure of functional connectivity) between pairs of recording sites and between recording sites and external stimuli based on observed population firing patterns and corresponding stimuli (Fig. 1B,C). By considering all pair-wise interactions simultaneously, Ising models are less prone to false positive interactions that are inherent to traditional correlation analysis (Schneidman et al., 2006). For example, in a fully connected Ising model (see Methods), the strongest coupling to sounds occurred in rows 3 and 4 (Fig. 2A), corresponding to the thalamorecipient layers. By contrast, traditional correlation analysis indicated strong connectivity between sounds and sites in all rows (Fig. 2B). This false positive connectivity between sounds and activity in rows 1 and 2 is due to the absence of site-to-site interactions in the correlation analysis. In a reduced Ising model where recording sites were coupled to sound but not to each other, which we call the independent neurons model, positive couplings between neural activity and the sound stimulus were also present in all recorded layers and did not differ across depth (Fig. 2C, p = 0.55, Kruskal-Wallis ANOVA). Furthermore, pairwise correlations were more tightly correlated with couplings in the independent neurons model than in the fully connected model (Fig. 2D, correlations resampled 100,000 times, with the difference in correlations significant at bootstrapped p < 1 × 10⁻⁴). The fully connected model showed significantly higher log-likelihood on held-out data than the independent model (Fig. 2E, p = 0.013, Wilcoxon signed-rank test), suggesting a significant contribution of site-to-site interactions to neuronal activity.

Figure 2.

The Ising model recovers canonical cortical structure not observed with traditional correlation analysis. A. Mean sound-to-site coupling derived from one set of polytrode recording data using the fully connected model. When connections between sites are taken into consideration, the strongest couplings with sounds are seen in rows 3 and 4, corresponding to the putative thalamic input layers. B. Mean sound-to-site correlation from the same dataset as in A. Neural activity on all rows of the polytrode was positively correlated with sound presentation. C. Mean sound-to-site coupling derived from the same dataset as in A using the independent neurons model. When we assume the sites are not connected to each other, the coupling between neural activity and sound does not change as a function of depth (electrode row). D. Pairwise correlations as a function of Ising model couplings for the fully connected model of connectivity for all subjects and locations (left, Spearman ρ= 0.97). Pairwise correlations as a function of Ising model couplings for the independent neurons model of connectivity for all subjects and locations (right, Spearman ρ= 0.61). When connections between neurons are considered, couplings are more distinct from correlations. E. Ising model performance for the fully connected model and the independent neurons model. The fully connected model showed the highest log-likelihood on held out data. Data are presented as mean ± S.E.M. Asterisks indicate level of significance: ** = p < 0.01, Bonferroni corrected for multiple comparisons. F. Coupling between pairs of recording sites in the fully connected model as a function of horizontal and vertical distance collapsed across all locations. Laminar and columnar structure arises from the model in the form of strong positive couplings for horizontal and vertical distances = 0, compared to couplings between sites situated diagonally (horizontal and vertical distance ≠ 0), which are weaker. G. Mean correlation between sites as a function of horizontal and vertical distances collapsed across all locations. The correlation falls off strongly with vertical distance but remains more uniform across horizontal distance.

The Ising model can discover spatial structure within the network despite no prior knowledge of spatial locations of the polytrode recording sites. In the fully connected Ising model, coupling was stronger in the vertical and horizontal than diagonal directions (Fig. 2F), presumably due to neuronal projections within cortical columns and layers. In addition, coupling decreased more rapidly with vertical than horizontal distance—sites up to 375 µm apart horizontally were still more strongly coupled than sites 300 µm away vertically (p = 4.3 × 10⁻⁶, Wilcoxon rank sum test). Such connectivity structure was much less prominent in the pairwise correlations (Fig. 2G; ratio of column or layer/diagonal couplings = 1.26 ± 0.03 for correlations, 2.16 ± 0.20 for couplings; p = 0.001, Wilcoxon rank sum test). Thus, although the model is blind to the relative locations of the recording sites, the fully connected Ising model recovered known layer and column circuitry (Linden and Schreiner, 2003; Mountcastle, 1957).

Optogenetic activation of PV neurons enhances functional connectivity

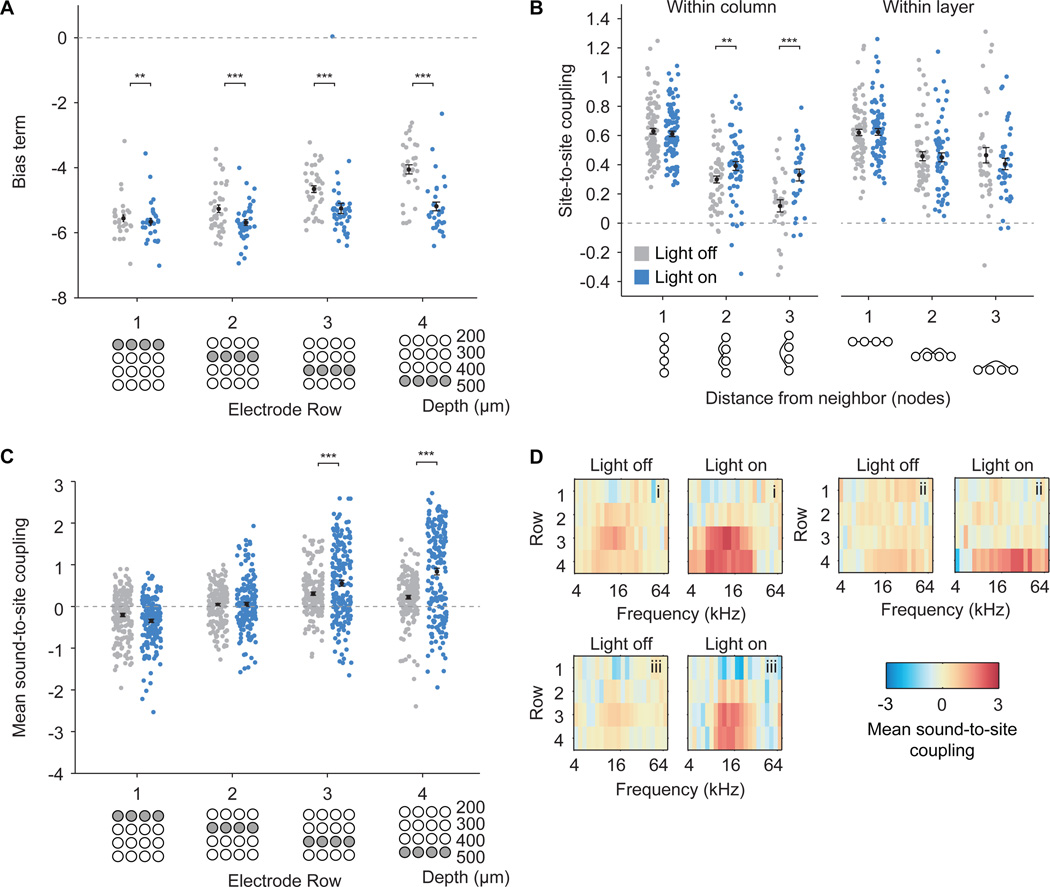
Using the fully connected Ising model, we analyzed how optogenetic activation of PV neurons influences functional connectivity in laminar, columnar, and thalamic input circuits of the primary auditory cortex. In keeping with PV neurons providing inhibitory input to connected pyramidal cells, we saw an overall reduction of the Ising model bias term in “light on” trials, reflecting reduced firing rates in all rows (Fig. 3A, Bonferroni-corrected p = 0.003, p = 0.0002, p = 8.4 × 10⁻⁶, and p = 8.7 × 10⁻⁵ for rows 1, 2, 3, and 4, Wilcoxon signed-rank tests). Furthermore, we found that stimulating PV neurons led to increases in vertical connectivity between sites within the same vertical column (Fig. 3B, Bonferroni-corrected p = 0.01 and p = 1 × 10⁻⁴ for coupling between sites within the same column, 2 and 3 rows away, respectively, Wilcoxon signed-rank tests), but did not change horizontal connectivity within layers (p > 0.05 for all comparisons, Wilcoxon signed-rank tests). Coupling between neural activity and sounds increased for sites in rows 3 and 4 during PV stimulation (Fig. 3C,D, Bonferroni-corrected p = 0.0003 and p = 8 × 10⁻¹³ for third and fourth rows, respectively, Wilcoxon signed-rank tests). These sites were likely located in the thalamorecipient input layers (layer 4 and deep layer 3). The increase in sound-to-site coupling in putative thalamorecipient layers was not an artifact of the response window selection (Fig. S1). Our findings indicate that activation of PV neurons results in enhanced functional connectivity specifically in thalamocortical input and cortical columnar circuits.

Figure 3.

Optogenetic activation of PV neurons decreases average firing rate while increasing functional connectivity within columns and from sounds to sites located in putative thalamorecipient layers. A. Bias term for the Ising model for each site in different rows on the polytrode, representing a proxy for the intrinsic firing rate of each site. Light stimulation significantly reduced the bias term in all layers, indicating an overall reduction of firing rate with PV stimulation. B. Site-to-site couplings as a function of the distance between the sites. Couplings are plotted between sites 1, 2, and 3 nodes away within a column or within a layer (see node diagrams below x-axis). Light stimulation significantly increased couplings within a column at distances 2 and 3 nodes away and did not change couplings within a layer. C. Soundto-site coupling averaged across sites in each row. During optogenetic stimulation, coupling between neural activity and sound stimulation increased in the putative thalamorecipient layers (rows 3 and 4). D. Examples of sound-to-site coupling in sites recorded from three different animals, plotted as a function of tone frequency and electrode row. In all cases, there was an increase in coupling to sounds in the putative thalamic input layers (rows 3 and 4) during light stimulation of PV neurons. Some locations showed decreases in coupling to sounds in the superficial layers during light stimulation, but this effect was not consistent across the population (see panel C). Asterisks indicate level of significance: * = p < 0.05, ** = p < 0.01, *** = p < 0.001, Bonferroni corrected for multiple comparisons. Errorbars and black marker in A–C depict mean ± S.E.M. See also Fig. S1.

PV stimulation enhances functional connectivity in the feed-forward direction

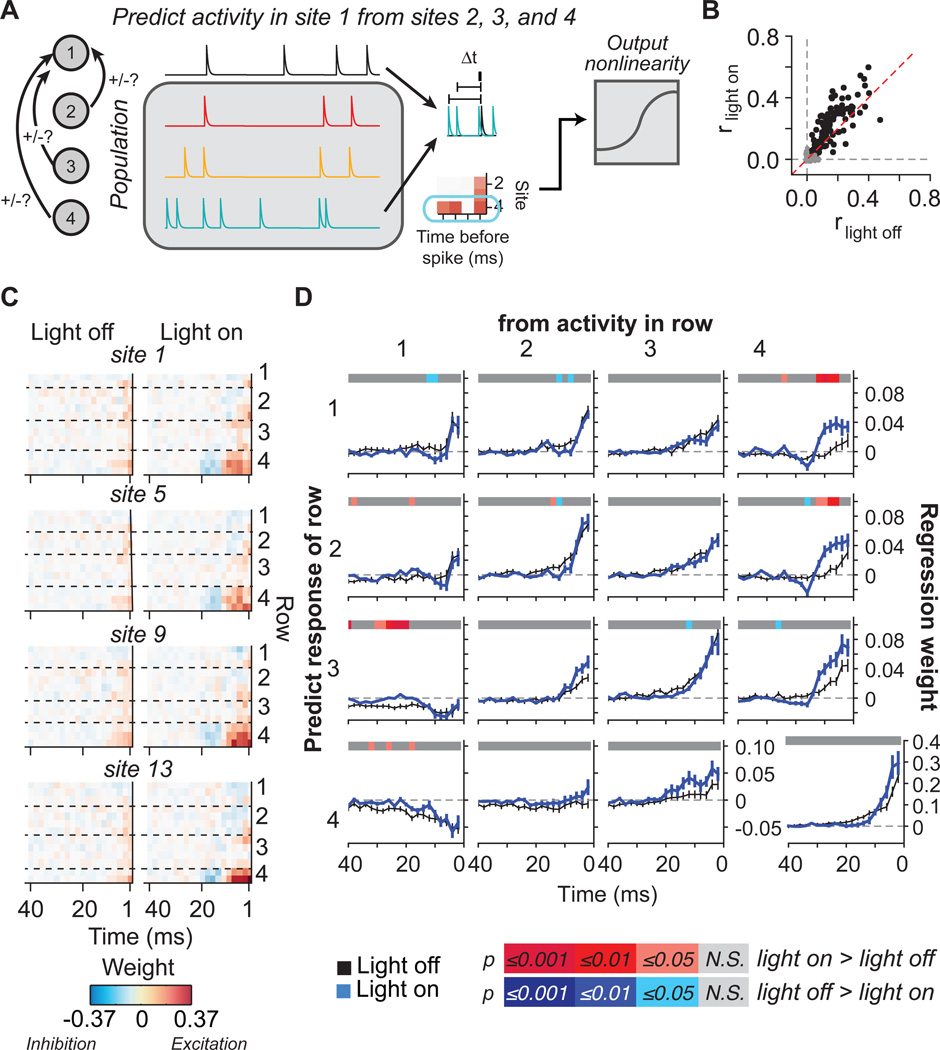
While the Ising model uncovers altered functional connectivity with inhibitory neuron stimulation, it is agnostic to the direction in which these changes occur. For example, the increased coupling within cortical columns during activation of PV neurons could be in the feed-forward, feedback, or both directions. To address this issue, we used vector autoregression (VAR) to derive a linear model that described how activity in one site was modulated by spikes in other sites as a function of time delay (Fig. 4A; see Methods for details). Unlike the Ising model, which describes dynamics within a fixed time bin, this model considers how inputs from different rows at different times affect the neural responses in a given time. Prediction of one site’s activity using the population activity was significantly better during the “light on” than the “light off” epochs (Fig. 4B, Wilcoxon signed-rank test, p = 4.0 × 10⁻¹⁰).

Figure 4.

PV neuron activation increases functional connectivity in the feed-forward direction. A. Schematic of the vector autoregression analysis. To model the interaction between the activity of sites at different depths, we fit a vector autoregression model (VAR) which predicts the activity for each site on the polytrode based on the activity of all other contact sites. In this schematic, neural activity in site 1 is predicted from activity in sites 2, 3, and 4. We fit a linear model that describes how spikes in each site modulate spiking in the predicted site at different time delays. For example, spikes in the teal trace often precede spikes in the black trace, so positive weights are assigned to site 4 at the relevant time delays. We then predict responses based on these weights and apply an output nonlinearity to improve response predictions. B. Prediction performance of VAR models is significantly higher when modeling spike trains during light “on” epochs compared to “off” epochs (p < 4.0 × 10⁻¹⁰, Wilcoxon signed-rank test). Prediction performance was assessed as the correlation between the response predicted by the VAR model and the actual response from held-out data. We used resampling to determine which models performed significantly better than chance, indicated in black. Gray points show VAR models that were excluded from further analysis. The red dashed line is the unity line y = x. C. Representative VAR model weights from one subject for sites on one shank of the polytrode. Each plot shows how the activity in sites from rows 1–4 modulates the activity of sites 1, 5, 9, and 13 respectively (on the left-most shank, see Fig. 1B). Excitatory drive is shown in red, inhibitory drive is shown in blue. Dashed lines separate channels in different rows on the polytrode. D. Average VAR model weights ( β_i from equation [4]) collapsed across all subjects and across contact sites in the same row show that light stimulation of PV cells results in stronger and longer excitatory drive from row 4 to rows 1 and 2. VAR model weights were significantly higher for light “on” epochs (Bonferroni-corrected p-value indicated by color on horizontal line, Wilcoxon-signed-rank test) when predicting rows 1–2 from activity in row 4. Row 2 also showed significantly more suppression from the putative thalamorecipient layer before the window of strong excitation starting at ~12 ms. When predicting row 3 activity from activity in superficial row 1, we found that PV stimulation reduced the inhibitory influence of row 1 on row 3, as evidenced by regression weights closer to zero. The strong increase in drive from row 4 to more superficial layers and the small regression weights in the feedback direction shows that PV stimulation increases drive in the feed-forward direction. Data are presented as mean regression weight across all sites and subjects ± S.E.M. See also Fig. S2.

We then examined the contribution of each site to predicting the activity of another site (i.e., the weight function in the linear model as a measure of functional connectivity; Fig. 4C,D). In general, neural activity was more strongly modulated by activity of sites in the same cortical layers rather than in different layers. However, these weights were not significantly altered by activation of PV neurons (Fig. 4D, diagonal subplots). By contrast, PV neuron activation significantly increased the weights for row 4 sites in predicting the activity of more superficial sites within a time window between 6 and 12 ms (Fig. 4D, far right subplots). There was also a small trend (not significant) of increased excitatory drive from row 3 to row 4, consistent with the primary input layer to auditory cortex arising in deep layer 3 and propagating information to layer 4 (Smith and Populin, 2001). Furthermore, inhibitory influences from superficial row 1 on activity in row 3 were lessened with PV neuron stimulation (Fig. 4D, first column, third row subplot), suggesting that the normal feedback inhibition from superficial layers is altered when PV neurons inhibit those cells. The double dissociation between the stronger baseline intra-layer influences and the light-activated increase for cross-layer influences supports our findings from the Ising model analysis that the activation of PV neurons specifically increases intra-column functional connectivity. The increased contribution of activity in row 4 to firing in superficial rows during light stimulation further suggests that the enhanced functional connectivity is in the feed-forward direction.

Qualitatively similar results were also observed when fitting the data in a generalized linear model (GLM) with an exponential nonlinearity (see Pillow et al., 2008), although predictive performance of the GLM as assessed by correlation was worse than the VAR model for both “light off” and “light on” conditions (p < 0.0001, Wilcoxon signed-rank tests; see Supplemental Methods and Fig. S2). These results, together with the increased sound-to-site coupling in the feed-forward thalamocortical circuit, suggest that activation of auditory cortical PV neurons may facilitate bottom-up information flow in the feed-forward direction.

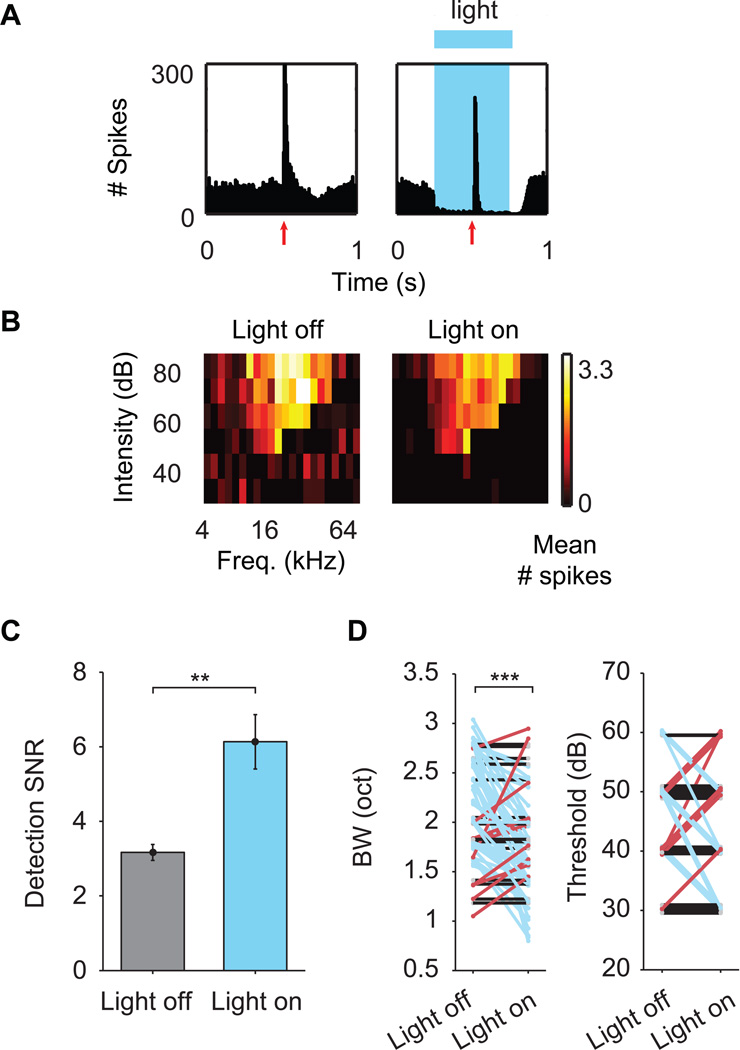
Activation of PV neurons increases detection signal-to-noise ratio in single recording sites

Previous studies have shown that optogenetic activation of PV neurons enhances stimulus feature selectivity and increases the signal-to-noise ratio in cortical neurons (Atallah et al., 2012; Lee et al., 2012; Sohal et al., 2009; Wilson et al., 2012). In our study, light activation of PV neurons induced strong suppression of spontaneous firing and weak reduction of tone-evoked responses (Mean % suppression ± SEM = 31.77 ± 0.03 % for spontaneous, 18.57 ± 0.03 % for evoked, see Fig. 5A,B for example peristimulus time histograms and receptive fields). This led to an increase in the detection signal-to-noise ratio (mean detection SNR ± SEM = 6.13 ± 0.73 for “light on” vs. 3.17 ± 0.21 for “light off” trials, p = 0.005 Wilcoxon signed-rank test, Fig. 5C). In addition, PV neuron stimulation significantly narrowed receptive field bandwidths (p < 0.001, Wilcoxon signed-rank test), without changing response thresholds at the characteristic frequency (p = 0.79, Wilcoxon signed-rank test, Fig. 5D). In sham-injected control mice not expressing ChR2, light stimulation did not cause any significant change in response properties (Fig. S3).

Figure 5.

PV neuron activation strongly suppresses spontaneous activity, weakly suppresses sound-evoked activity, and improves detection signal-to-noise ratio of responses. A. Example peristimulus time histogram of multiunit activity. Trials with no light stimulation (left) showed strong responses to pure tones played at 0.5 s (red arrow). When blue light was used to stimulate PV neurons between 0.25 and 0.75 s (right), responses to sound were still observed, but the overall evoked response was reduced. Spontaneous activity was reduced throughout the duration of the light stimulus. B. Example receptive fields during “light off” (left) and “light on” (right) trials separately for the same site in A. Each pixel in the plot represents the average number of spikes evoked by a stimulus at a particular frequency and intensity level. The reduction in spontaneous rate is evident in the decreased background spikes outside of the V-shaped receptive field. C. Detection signal-to-noise ratio (SNR; measured as a [# evoked - # spontaneous spikes]/[ # spontaneous spikes]) during “light off” (gray) and “light on” (blue) trials. Optogenetic activation of PV neurons results in a significant increase in the SNR compared to the no stimulation condition. Data are presented as mean SNR ± S.E.M. D. Receptive field bandwidths 20 dB above threshold (left) and receptive field thresholds (right) for receptive fields calculated from “light off” (no stimulation of PV neurons) and “light on” (stimulation of PV neurons) trials separately. Lines are colored according to whether a reduction (blue), increase (red), or no change (black) in bandwidth was observed. We observed a significant reduction in receptive field bandwidths during PV neuron stimulation (p <0.001, Wilcoxon signed-rank test) with no change in threshold. This indicates that stimulating PV neurons increases stimulus selectivity by narrowing the range of stimuli to which a site responds. Asterisks indicate level of significance: * = p < 0.05, ** = p < 0.01, *** = p < 0.001, Bonferroni-corrected Wilcoxon signed-rank tests. See also Fig. S3.

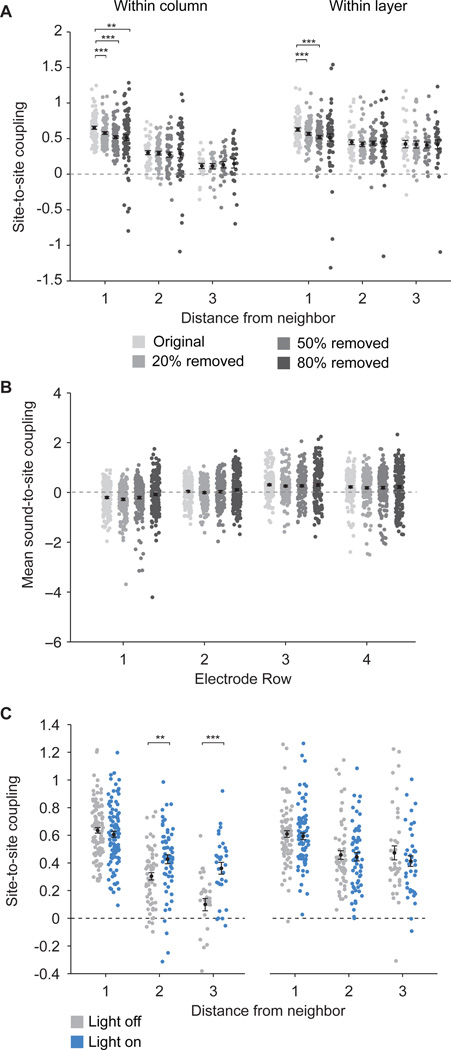
Reductions in spontaneous activity alone do not account for functional connectivity changes

To test the possibility that reduced spontaneous activity and increased detection SNR (Fig. 5A–C) caused the observed increases in site-to-site coupling (Fig. 3B), we randomly removed 20–80% of spikes recorded in “light off” trials to mimic the effects of PV stimulation with light and re-ran the Ising model analysis (see Methods). The mean site-to-site coupling strength was not increased by the random reduction of spontaneous and evoked spikes (Fig. 6A), but rather was reduced in sites one node away within the same column (p<0.001 for all comparisons, Bonferroni-corrected Wilcoxon signed-rank tests). No changes to coupling between sites 2 and 3 away within the column were seen (Bonferroni-corrected p>0.05, Wilcoxon signed-rank tests), even with reductions in activity that were far larger than the suppression caused by PV neuron stimulation (~32% suppression on average). There was also no change in sound-to-site coupling with these manipulations (Fig. 6B). Finally, to determine if the altered site-to-site coupling strength was due to changes in evoked activity, we removed sound-evoked spikes and re-ran the analysis with only the (unaltered) spontaneous activity. The coupling strength was still higher during activation of the PV neurons (Fig. 6C, Bonferroni-corrected p = 0.002 and p = 0.0002 for sites 2 and 3 away within a column, respectively, Wilcoxon signed-rank tests). These results indicate that the enhanced coupling by PV neuron activation was not due to the increased detection signal-to-noise ratio or reduced baseline activity. Rather, it reflects the state of the circuit connectivity, and is independent of sensory stimulation and responses.

Figure 6.

Manipulation of spontaneous and evoked activity on Ising model couplings. A. Random reduction of spikes in all layers during “light off” trials does not increase site-to-site couplings in the Ising model as did PV neuron stimulation. Instead, significant reductions in site-to-site couplings are seen in both column and layer couplings 1 node away for several levels of firing rate reduction (20, 50, or 80% reduction). B. Random reduction of spikes in all layers does not alter sound-to-site couplings. C. Removing sound-evoked periods from the spike trains does not change the effect of PV stimulation on site-to-site couplings, highlighting the importance of network connectivity over stimulus input. Data are presented as mean ± S.E.M.

Possible mechanisms for the enhancement of functional connectivity by PV neurons

In this study, we quantified functional connectivity in the auditory cortex with coupling from the Ising model and the weight function from vector autoregression. Both measures elucidate how the activity of a neuron or the presentation of a sound stimulus drives the firing of a target neuron. The specific mechanisms underlying the modulation of functional connectivity by PV neurons are not investigated in the present study, but could involve the modulation of synaptic connections and changes in global network states. For example, synaptic efficacy can be rapidly altered by the prior synaptic activity (Zucker and Regehr, 2002), which is likely influenced by the activity of PV neurons. Alternatively, by synchronizing network activity (Cardin et al., 2009; Sohal et al., 2009), PV neurons could set target neurons in a more excitable state when the projection neuron fires, thus enhancing their functional connectivity. The effects on column rather than layer connections may be related to anisotropic projection patterns of PV neurons (Packer and Yuste, 2011), whereby PV neurons preferentially inhibit pyramidal neurons located in the same vertical columns over distances 200 µm and greater.

Potential limitations

While both the Ising model and the VAR models allow us to analyze the relative changes to within vs. between layer connectivity with PV neuron stimulation, some caution should be taken when interpreting these functional connections in terms of synaptic interactions. With extracellular recordings it is not possible to reconstruct the synaptic connections between recorded (or stimulated) neurons. Coupling between neurons should be considered as a functional description rather than an anatomical one. For example, researchers have found that coupling weights in the Ising model do not necessarily correspond to synaptic connections in the network (Roudi et al., 2009b). The strength of the Ising model lies in its ability to distinguish direct from indirect interactions, for example in finding direct stimulus input to rows 3 and 4, representing the thalamorecipient layer. However, the symmetric nature of Ising model couplings means that directed interactions, such as combined excitatory/inhibitory influences (cell A excites B, but B inhibits A), cannot be uncovered. The VAR model addresses some of these caveats, since it can quantify directional interactions between recording sites and describe how neuronal firing is affected in different time periods. Our model shows that strong feed-forward drive is enhanced by PV stimulation, whereas feedback from superficial to putative thalamic input layers is not affected.

Implications for sensory perception

Specific enhancement of feed-forward connectivity has important implications in processing sensory information. Sensory perception is derived from both bottom-up sensory inputs and top-down stimulus expectations (Kording and Wolpert, 2004; Stocker and Simoncelli, 2006). Previous theoretical work indicates that sensory cortical neurons could integrate multiple sources of information by linear summation of population responses activated by each source. To achieve optimal integration under this scheme, however, the weight placed on each information source must be dynamically adjusted according to the quality of the information and task demands (Ma et al., 2006). Interestingly, the firing rate of fast-spiking neurons—likely PV neurons (Kawaguchi and Kubota, 1998; Toledo-Rodriguez et al., 2004)—appears to increase with demand of attention to external stimuli (Chen et al., 2008; Mitchell et al., 2007). Our results show that activation of PV neurons preferentially emphasizes bottom-up sensory information by increasing feed-forward connectivity, without changing the weight on top-down information presumably supplied through lateral or feedback connections. Thus, PV neurons may play an important role in optimal integration of sensory information with top-down expectations in sensory perception. These results could inform future work on mechanisms of sensory pathologies in patients with autism and schizophrenia, both of which are associated with PV neuron dysfunction (Gandal et al., 2012; Gonzalez-Burgos and Lewis, 2012).

Experimental Procedures

Subjects

The University of California-Berkeley Animal Care and Use Committee approved all procedures. Subjects included 11 adult PV-Cre mice (strain B6;129P2-Pvalbtm1(cre)Arbr/J, Jackson Labs), aged ~P100 at the time of recordings. 8 mice received an injection in the right auditory cortex at ~P60 with 1 µL of a Cre-dependent adeno-associated viral vector carrying a double-floxed inverted copy of the light-sensitive cation channel channel-rhodopsin-2 (pAAV-Ef1a-DIO-hChR2(H134R)-EYFP-WPRE-pA, 8 × 10¹² viral particles/mL, UNC Vector Core) using a glass micropipette (Drummond Wiretrol, 10 µL) attached to a Quintessential Stereotaxic Injector (Stoelting) and procedures described elsewhere (Cardin et al., 2010). To control for the effect of light stimulation or heating of the cortex in general, 3 mice were injected with saline using the same protocol. A small burr hole (0.7 mm in diameter) was made over the right auditory cortex (1.75 mm rostral to lambda on the temporal ridge (Franklin and Paxinos, 2008)), and virus (or saline) was delivered through a small durotomy. Each injection was performed in two stages, with 0.5 µL of virus injected at a depth of 500 µm and the remaining 0.5 µL injected at 250 µm, at a rate of 0.1 µL/s. Recordings were obtained after an infection period of approximately 1 month to ensure adequate expression of ChR2 throughout the auditory cortex, which was confirmed using GFP fluorescence goggles (BLS Ltd.).

Immunohistochemistry

Mice were perfused transcardially with cold 0.01M phosphate buffered saline (PBS, pH = 7.4), followed by 4% paraformaldehyde in 0.01M PBS. Brains were post-fixed in 4% PFA for 12h, and then cryoprotected in 30% sucrose for 18h. 50µm free-floating sections were cut using a cryostat (Leica CM3050). Every other section was incubated with blocking solution (10% normal goat serum in 0.01M PBS with 0.1% Triton X-100) for 45 minutes at room temperature (20°C), then incubated in primary antibody (PV 25 rabbit antiparvalbumin, Swant, 1:4000 dilution) at 4°C overnight. The next day, slices were incubated in secondary antibody (Alexa 594 goat anti-rabbit IgG, Invitrogen, 1:200 dilution) for 1.5h at room temperature. Sections were mounted on gelatin-subbed glass slides with Fluoromount-G (Southern Biotech) and cover-slipped. Adjacent sections not stained for PV were washed in 0.01 M PBS, mounted on slides, and left to dry for 48h. They were then Nissl stained with 0.5% cresyl (w/v) for identification of individual cortical layers.

Quantification of virus expression

The spread of the virus was scored by hand by analyzing each 50 µm coronal section for the presence of eYFP fluorescence using a Zeiss LSM 780 34-Channel AxioExaminer fixed stage upright confocal microscope (UC Berkeley Molecular Imaging Center). Colocalization of ChR2-eYFP to PV-positive cells was analyzed by acquiring confocal images and identifying cells from each fluorescence channel by hand using ImageJ’s cell counter plug-in.

Electrophysiological recording and stimuli

The right auditory cortex was mapped for each mouse under anesthesia using a cocktail of ketamine (100 mg/kg) and xylazine (10 mg/kg) and procedures described previously (Han et al., 2007). Following deflection of the temporal muscle, exposure of the auditory cortex, and removal of the dura mater, we performed a coarse mapping with tungsten electrodes (FHC, Inc.) to determine the location of primary auditory cortex based on rostrocaudal tonotopy and short spike latencies. We then recorded extracellular multi-unit neural activity in putative layer 2/3 through layer 4 of the right primary auditory cortex (Franklin and Paxinos, 2008; Oviedo et al., 2010) using a 4 × 4 silicone polytrode (NeuroNexus A4×4-3mm-100-125-177). 14/16 channels showed normal impedance measurements and were included in the analysis. A total of 350 multiunit sites (294 from ChR2-transfected animals, 56 from saline-injected controls) were used in our analyses. The polytrode was oriented parallel to the tonotopic axis and lowered orthogonally to the cortex such that the deepest contact sites were at a depth of approximately 500 microns from the pial surface (Fig. 1A). The extracellular signal was obtained using a TDT amplifier connected to TDT RX5 hardware (Tucker Davis Technologies, Inc.), using a sampling rate of 25 kHz. Spike times were calculated by thresholding the extracellular signal at 1.5 times the standard deviation of the signal-to-noise ratio and bandpass filtering between 300–3000 Hz, and were logged using custom software running on a Windows XP computer. Sound stimuli were presented to the contralateral ear through an electrostatic cannulated speaker (EC1, Tucker Davis Technologies, Inc.) controlled by TDT RX6 hardware, and calibrated to ensure less than 3% spectral distortion and a flat output (< 3 dB deviation) from 4–75 kHz (Brüel and Kjær microphone, preamplifier, and conditioning amplifier, using SigCal32 software). Sound stimuli were pure tones generated using MATLAB (25 msec length with 5 ms squared cosine ramp, sampling rate 156.25 kHz) played from 4 kHz to 75 kHz in 0.2 octave steps, for a total of 22 frequencies. Sounds were presented at 6 different loudness levels (20 – 70 dB SPL, 10 dB spacing) in a pseudorandom order with a 1 Hz repetition rate, and each frequency-intensity pair was repeated 3 times. For the 50 dB level, stimuli were presented an additional 12 times to obtain higher resolution data at this intermediate level. For each trial of length 1 second, a tone pip would play at 500 ms into the trial. For half of the trials, we stimulated ChR2-transfected PV neurons using a 500 msec pulse of 473 nm blue laser light (Shanghai Laser and Optics Century Co., model BL473T3) coupled to a 200 micron optic fiber (ThorLabs, BFL37–200) beginning at 250 ms into the trial and controlled by a TTL pulse delivered by the RX5 hardware. This stimulation protocol results in the continuous spiking of the PV neurons throughout the duration of the light pulse (Zhao et al., 2011). The laser output was calibrated using a power meter (ThorLabs, PM100D with sensor S120C and neutral density filter NE03A-A) to deliver light at an intensity of 1.2 mW, or ~40 mW/mm². This light intensity was chosen as the minimal light level that induced silencing of cortical activity throughout the light stimulation period. Photoelectric light artifacts (sharp transients locked to the onset of the light stimulus) were removed by excluding time points immediately surrounding the light onset (Cardin et al., 2010). Classical receptive fields were calculated for “light on” and “light off” trials separately by counting the number of spikes elicited by each frequency-intensity pair in a window defined by the peak of the PSTH. Receptive field thresholds were defined as the minimum sound intensity required to evoke a response (the intensity at the tip of the V-shaped receptive field). The receptive field bandwidths were calculated as the width of the frequency response in octaves 20 dB above the intensity threshold. Detection signal-to-noise ratio (SNR) was defined as [# evoked spikes - # spontaneous spikes]/[# spontaneous spikes] for “light on” and “light off” epochs separately.

Ising model fitting

Binary matrices of the sound stimulus condition and spiking data for “light off” and “light on” trials separately were used as input to the model. Spiking activity from each of the contact sites on the polytrode was binned into 5 ms time epochs such that for each bin, if a spike occurred during those 5 ms, the value was set to 1, and if no spikes occurred, the value was set to 0. The bin duration of 5 ms was chosen according to the average cross-correlation between all pairs of recording sites, which showed that the mean cross-correlation was approximately three times the standard deviation of the baseline correlation at 5 ms. The sound stimulus matrix consisted of values for 22 frequency bins for each of t time points, with values of 1 when a stimulus at a given frequency was present and 0 when the stimulus was absent. Since cortical responses to sound occur with a delay relative to stimulus onset, we set the sound matrix to 1 for a window starting at 15 ms after the onset of the sound and ending at 50 ms after sound onset, corresponding to when the cross-correlation between the sound stimulus onset and neural spiking responses reached approximately three times the standard deviation of the baseline cross-correlation. Fitting separate sound-to-site couplings for each time delay relative to the stimulus onset (from 0 to 100 ms after sound onset, see Supplemental Methods) did not change our result (Fig. S1). Only responses to the three highest decibel levels were used in the model (50, 60, and 70 dB). For each polytrode site, trials were randomized, the full data matrix was split into 10 equal chunks, and each model was estimated by holding out 1 of the data chunks and training on the remaining 90% of the data, and repeating this process 10 times for each possible training and validation set. This method, called 10-fold cross validation (Rohavi, 1995), was used to ensure an accurate estimate of the log-likelihood that is more robust to noise in the data.

The stimulus conditioned Ising model is defined as:

$$p(\mathbf{x}|\mathbf{s};\mathbf{J},\mathbf{W})=\frac{1}{Z(\mathbf{s},\mathbf{J},\mathbf{W})}\text{exp}({\mathbf{x}}^{\mathbf{T}}\mathbf{J}\mathbf{x}+{\mathbf{x}}^{\mathbf{T}}\mathbf{W}\mathbf{s}),$$ [1]

where x ∈{0,1}^N is the binary spike pattern for each time point, N is the number of recording sites, J∈ℝ^N×N is the site-to-site coupling matrix, W∈ℝ^N×M is the sound-to-site coupling matrix, M is the number of stimulus dimensions (in this case, sound frequencies presented), and s∈{0,1}^M is the stimulus input vector. A positive coupling value J_ij > 0 indicates that sites x_i and x_j tend to be active simultaneously, while a coupling J_ij < 0 indicates that when a spike occurs at site x_i, x_j will be more likely to remain silent, and vice versa. Similarly, a positive sound-to-site coupling value in W_ij indicates that spiking in x_i tends to increase during presentation of stimulus s_j, while a negative sound-to-site coupling value of W_ij indicates that spiking in x_i is suppressed during presentation of s_j. Both site-to-site and sound-to-site couplings are unitless (much like linear regression weights, for example), with the magnitude of coupling indicating the strength of the relationship between their firing patterns. We were interested in the effect of the light stimulus condition on coupling, so separate coupling matrices J and W were trained for the “light off” and “light on” trials.

To estimate the couplings, we used Minimum Probability Flow Learning (MPF) (Schaub and Schultz, 2012; Sohl-Dickstein et al., 2011a, 2011b) to minimize an L1 regularized version of the MPF objective function,

$$K(\mathbf{J},\mathbf{W})=\frac{1}{T}\sum _{\{\mathbf{x},\mathbf{s}\}}\sum _{\mathbf{x}\prime \in N(\mathbf{x})}\text{exp}(\frac{1}{2}[E(\mathbf{x}|\mathbf{s};\mathbf{J},\mathbf{W})-E(\mathbf{x}\prime |\mathbf{s};\mathbf{J},\mathbf{W})])+\lambda ({\Vert \mathbf{W}\Vert }_1+{\Vert \mathbf{J}\Vert }_1)$$ [2]

where the sum over {x, s} indicates a sum over all training observations, the neighborhood N(x) includes all states which differ from x by a single bitflip and the single state in which all bits are flipped, E(x|s;J,W)=−x^TJx−x^TW_s is the energy function of the Ising model,λ is the regularization strength, and T indicates the total number of training samples (in 5-ms binned time points).

The L1 regularization term λ(‖J‖₁+‖W‖₁)was included to prevent over-fitting to training data.λ was chosen by cross validation from ten values logarithmically spaced between 10⁻⁷ and 10⁻². Cross validation was performed by holding out 20% of the training data, training the model using the remaining 80%, repeating this 5 times, and choosing the λ with the best average log-likelihood across all light conditions and all sites. The choice of λ had little effect on the log-likelihoods of the model fit for “light off” trials, but there was improvement for the “light on” models at intermediate λ values. Thus, we chose to use the same value of λ irrespective of light condition. λ was set to 5.9 × 10⁻⁵.

Following selection of the regularization parameter, we fit the model using all of the training data, and the model log-likelihood, conditioned on the stimulus, was tested on the held out validation set. This was repeated 10 times for different validation sets, using the same regularization parameter. Coupling matrices shown in the figures are taken from the cross-validation iteration with the highest conditional likelihood on the validation set. We evaluated model likelihoods on held out data,

$$\text{log}L=\frac{1}{T}\sum _{\{\mathbf{x},\mathbf{s}\}}\text{log}p(\mathbf{x}|\mathbf{s};\mathbf{J},\mathbf{W})$$ [3]

The normalization constant Z(s, J, W) required in the calculation of p(x | s; J,W) was computed by exhaustive summation over all 2¹⁴ possible spiking states.

To test the effect of lowered baseline activity on Ising model couplings, we removed 20%, 50%, and 80% of spikes in all rows. Spikes were removed at random for each channel separately, and included both spontaneous and evoked data. We then re-ran the Ising model for the new manipulated spike data using cross-validation as before, and tested performance on a held-out set that had been manipulated similarly (20–80% spikes removed).

To test the effect of evoked activity, we removed all time points between 15 and 50 ms post-sound stimulus onset for each trial and fixed sound couplings to zero while training the model.

Vector Autoregression Modeling

To investigate the directionality of functional connections in the auditory cortex, we used vector autoregression (VAR) models (Lütkepohl, 2005), which are linear models that relate multiple, dependent time series, such as spike trains, by a sum of linear weights. Such models allow us to predict the spiking activity of each site in the polytrode as a function of the previous spiking activity at all other sites. We fit models of the form:

$${\hat{x}}_i(t)={\overline{x}}_i+\sum _{j=1}^N\sum _{\tau =1}^T{\beta }_i(\tau ,j)x_j(t-\tau )$$ [4]

where x̂_i(t) is the estimated response at recording site i at time t, x̄_i is the baseline firing rate of that site, β_iis a matrix of linear weights for the N simultaneously recorded sites over each of Ttime delays, and x_j(t−τ)is the response at recording site j at a given time in the past, (t−τ). T is the total number of time delays included in the analysis, and N is the total number of simultaneously recorded sites. We used delays up to 40 ms for each set of 14 simultaneously recorded sites. Those familiar with spectrotemporal receptive field (STRF) estimation will recognize this model as being essentially identical to a STRF (Aertsen and Johannesma, 1981; Theunissen et al., 2001; Wu et al., 2006), with the difference being that neural activity is predicted from other activity in the network rather than by a parameterization of the external stimulus.

To solve for the VAR weights, we used ridge regression which is less prone to over-fitting than ordinary least squares. Ridge regression, also known as L2-penalized or Tikhonov regularization, minimizes the mean-square-error (MSE) between the actual and estimated response while constraining the L2 norm of the regression weights. The strength of the L2 penalty is determined by the ridge parameter, λ ≥ 0 , where larger values of λ result in greater shrinkage of the weights (Asari and Zador, 2009; Machens et al., 2002; Wu et al., 2006). In ridge regression, we minimize the following error function:

$$E({\beta }_i)={\Vert x_i(t)-{\hat{x}}_i(t)\Vert }_2^2+\lambda {\Vert {\beta }_i\Vert }_2^2$$ [5]

Where x_i(t) is the true response of site i at time t, and the estimated response x̂(t) is given by equation [4] above. We estimated VAR weights using 80% of the data as a training set. Of the remaining 20% of the data, half was used for fitting the ridge parameter (10%) and half was used as a validation set to assess model performance (10%). The same recordings used in the Ising model were used in these analyses. Input to the model consisted of the binary spike trains binned at 2 ms for each of the channels on the polytrode. Separate models were fit for “light on” and “light off” trials. To find the optimal ridge parameter, we tested 10 logarithmically spaced ridge parameters between 10⁻² and 10⁵, then selected the value that resulted in the highest average correlation on the (ridge) test set across all sites on the polytrode and both “light on” and “light off” models. The same ridge parameter was used for both “light on” and “light off” models.

Since a neuron’s output is strictly positive and may scale nonlinearly with the input stimulus, we added an output nonlinearity to the model fitting (Wu et al., 2006). This nonlinearity does not change the weights of the model, but rather rescales the response predicted by the linear model to more accurately match the true response. We fit the nonlinearity as a univariate cubic spline that minimized the mean squared error between the actual and predicted responses on the training data. For both “light on” and “light off” models, adding the output nonlinearity significantly increased the predictive performance of the model (p = 4.6 × 10⁻¹⁰ and p = 4.4 × 10⁻¹⁶ for “light off” and “light on” respectively, Wilcoxon signed-rank test), though these increases were quite small (0.6 ± 0.1 % increase for “light off”, 1.5 ± 0.1 % increase for “light on”). The increase in correlation was significantly higher for “light on” over “off” (p = 6.4 × 10⁻¹³, Wilcoxon rank sum test), which is likely due to the overall lower firing rate during “light on” trials.

VAR model validation was performed by calculating the correlation coefficient between the response predicted by the model and the actual response on the held out validation set. Significance of the correlation between predicted and actual responses was determined using resampling. The predicted response was randomly reshuffled 100,000 times, and the correlation between the shuffled prediction and actual response was computed. Reshuffling was done using 526-ms (263-time bin) segments to preserve local temporal statistics (this length was chosen to limit accidental alignment of the 1000-ms stimulation protocol across shuffled samples). The p-value of the model prediction was then computed as the fraction of the 100,000 shuffled correlations that were higher than the actual correlation.

Statistical tests

To test differences in coupling, we used Wilcoxon rank sum tests (for comparing independent groups) or Wilcoxon signed-rank tests (for comparing paired groups) and corrected for multiple comparisons using Bonferroni correction. Parametric tests were not used because it was determined that the data being compared were not Gaussian distributed (Lilliefors test). Resampling techniques were used to obtain confidence intervals on correlation coefficients. Spearman rank correlations were used to test relationships between monotonically but not linearly related data, such as correlations and couplings in Fig. 2D. Values are reported as mean ± standard error unless otherwise stated.