RANKING TEM CAMERAS BY THEIR RESPONSE TO ELECTRON SHOT NOISE

Abstract

We demonstrate two ways in which the Fourier transforms of images that consist solely of randomly distributed electrons (shot noise) can be used to compare the relative performance of different electronic cameras. The principle is to determine how closely the Fourier transform of a given image does, or does not, approach that of an image produced by an ideal camera, i.e. one for which single-electron events are modeled as Kronecker delta functions located at the same pixels where the electrons were incident on the camera. Experimentally, the average width of the single-electron response is characterized by fitting a single Lorentzian function to the azimuthally averaged amplitude of the Fourier transform. The reciprocal of the spatial frequency at which the Lorentzian function falls to a value of 0.5 provides an estimate of the number of pixels at which the corresponding line-spread function falls to a value of 1/e. In addition, the excess noise due to stochastic variations in the magnitude of the response of the camera (for single-electron events) is characterized by the amount to which the appropriately normalized power spectrum does, or does not, exceed the total number of electrons in the image. These simple measurements provide an easy way to evaluate the relative performance of different cameras. To illustrate this point we present data for three different types of scintillator-coupled camera plus a silicon-pixel (direct detection) camera.

1. INTRODUCTION

A variety of electronic-readout cameras are currently available for use in electron microscopy. In addition to cameras that use a scintillator to first convert electrons into pulses of light, new types of direct-electron-impact, silicon-pixel cameras are also available from at least three manufacturers. Although the quality of images produced by these different types of camera is not expected to be equivalent, most users do not independently characterize this performance.

The preferred way to characterize electronic cameras is to estimate what is called the spectral detective quantum efficiency, DQE(s). The first step is to record an image of an opaque straight-edge, in order to measure the edge-spread function. Since the derivative of the edge-spread function is equal to the line-spread function of the camera, the Fourier transform of the estimated derivative gives an experimental estimate of the (one-dimensional) Modulation Transfer Function (MTF(s)) of the camera. The second step is to measure an “empty image”, i.e. the response of the camera when exposed to a uniform field of electron intensity (without any specimen). The azimuthally averaged modulus of the Fourier transform of the empty image, scaled so as to extrapolate to 1.0 at zero spatial frequency, is referred to as the (one-dimensional) “noise transfer function, NTF(s)”. The square of MTF(s), divided by the square of NTF(s), provides a specimen-independent measure of the degree to which the spectral signal-to-noise ratio in the camera output is degraded relative to that of the incident image. Multiplication of this ratio by the independently-determined detective quantum efficiency, DQE(0), produces the desired DQE(s) [1–4]. More recently, a similar approach has been developed that uses images of two-dimensional, opaque objects rather than a straight edge [5].

DQE(s) represents an excellent basis for comparing the performance of different types of camera – for a broader review, see section III. C. of [6]. Nevertheless, there are issues about what to use as an opaque edge (the shaft of the beam stop; a gold wire), where to place the opaque edge (as close as possible to the camera), and how to mathematically extrapolate both MTF (s) and NTF(s) to 1.0 at zero spatial frequency.

In the current work, we reconsider the simple approach, explored in the past but then abandoned, of using only uniformly illuminated “empty images” to evaluate the performance of any given camera. Rather than using a camera’s response to shot noise as a surrogate of how well it responds to signal, however, we ask, instead, how well the responses to shot noise do, or do not, approach the performance of an ideal camera. Two insights, already appreciated in earlier work, inform our approach.

First (as we show here) the one-dimensional spectral fall-off of the camera output is fitted reasonably well by a single Lorentzian function, as it is for digitized photographic film [7, 8]. As a result, the reciprocal of the spatial frequency at which the amplitude spectrum falls to 0.5 provides an estimate of the distance (number of pixels in the image) at which the line-spread-function for single-electron events falls to e⁻¹. By comparison, the ideal response for a single electron would be confined to a single pixel, in which case the Fourier amplitude spectrum would be flat rather than having a Lorentzian shape. We thus propose that the spatial frequency (expressed as a fraction of Nyquist frequency) at which the Fourier amplitude spectrum falls to 0.5 of its initial value can be used as one criterion to compare the extent to which different types of camera do, or do not, approach the performance of an ideal detector.

Second, we show that the value of the power spectrum at very low spatial frequencies can be used to estimate the excess noise that occurs in the camera output due to the finite width of the distribution of detector responses (e.g. pulse heights) for individual electron events. We formally show, in the limit of large N and when the distribution of electrons is uniform over the detector, that the value of the power spectrum is equal to $N(1+{\sigma }_{\mathit{\text{response}}}^2)$, where N is the number of electrons in the entire image and σ_response is the standard deviation of single-electron responses. We further show that the variance in the Fourier amplitude spectrum is equal to $(1-\frac{\pi }{4})$ times the power spectrum. It thus follows that the degree to which the power spectrum, normalized by N, approaches 1.0 can be used as a second criterion to compare the extent to which different types of camera do (or do not) approach the performance of an ideal detector.

As a demonstration of using these two criteria, we evaluate the performance of three different scintillator-based cameras as well as that of a silicon-pixel camera. In addition, we report examples of the extent to which the performance of two of these cameras is sensitive to the value of the electron energy.

2. METHODS

Data were recorded for four different camera systems, as follows. Images were recorded at 120 keV with a 4Kx4K TVIPS TemCam F416 camera (with 15.6 μm pixels) on an FEI Tecnai T12 microscope. Images were recorded at 120 keV and at 200 keV with a 4Kx4K Gatan UltraScan 4000 camera (with 15 μm pixels) on an FEI Tecnai F20 microscope. Images were recorded at 80 keV and at 300 keV with a 2Kx2K FEI Eagle camera (with 30 μm pixels) on an FEI Titan microscope. Images were recorded at 300 keV with a 4Kx4K Gatan K2 camera (with 5 μm pixels) on an FEI Titan microscope. The K2 camera was operated in the “linear” mode, in which electron responses were integrated on the sensor prior to readout.

Images consisting of uniformly distributed electron events, i.e. “empty images”, were recorded without any specimen in the electron beam. In order to minimize low-frequency variations in the intensity across the field of view of the camera, a large condenser aperture and a small illumination spot number were used, the illumination was spread to a diameter much larger than the field of view, and a flat-field correction (gain normalization) was performed, using the average of 20 images. Empty images were recorded with a total exposure of approximately 200 to 300 electrons per pixel for all scintillator-based cameras, whereas the electron exposure was about ten times less for images recorded with the K2 camera.

The analog-to-digital (ADC) counts in raw camera images were converted to the equivalent number of electrons per pixel by dividing the ADC counts per pixel by the calibrated number of counts per electron. Calibration of the number of electrons per pixel was based on two quantities: (1) the electron-microscope vendor’s calibration of the beam current measured on the viewing screen, which in turn was converted to the electron exposure rate at the specimen, and (2) the image magnification at the camera.

3. DATA REDUCTION AND NOMENCLATURE

The two-dimensional Fourier transform of the converted image intensities (i.e. the number of electrons per pixel) was calculated with SPIDER [9] command FT, which does not apply a scale factor to normalize the Fourier transform by the number of pixels in the image. Since SPIDER command PW – which computes the square of the Fourier transform produced by command FT – does apply a normalization factor, equal to half the number of pixels in an image, a customized script (available at http://cryoem.berkeley.edu/camera-ranking) was written to compute the “unnormalized” power spectrum. As is explained below, the corresponding power spectrum of randomly distributed Kronecker delta functions is equal to N, the total number of events in the image. In addition, our customized script also calculates the square root of the (un-normalized) power spectrum, i.e. the Fourier-amplitude spectrum. All plots were prepared in Matlab.

The one-dimensional power spectra and amplitude spectra shown here represent azimuthal averages of the two-dimensional spectra referred to above. It should be noted that such one-dimensional spectra represent averaged versions of central lines through the respective two-dimensional spectra, for which the noise decreases with increasing radius due to the increasing number of pixels contributing to the average. These averaged one-dimensional spectra represent, in turn, estimates of the power and the amplitude, respectively, of the Fourier transform of a one-dimensional projection of the two-dimensional point-spread function for (uncorrelated) single-electron events.

Lorentzian functions of the form $\frac{1}{1+{\left(\frac{s}{s_0}\right)}^2}$ were fitted to experimental Fourier amplitude spectra by varying three parameters, using the nonlinear regression function “nlinfit” in Matlab. One parameter, s₀, corresponds to the spatial frequency at which the Lorentzian function falls to a value of 0.5; the second parameter is used to scale the experimental Fourier amplitudes to this Lorentzian function; and the third parameter is a constant y-axis offset that is added to the Lorentzian function in order to improve the fitting to the experimental Fourier amplitudes.

4. RESULTS

4.1 The Fourier amplitude spectrum for registering single-electron events is closely approximated as a single Lorentzian function for currently available camera systems

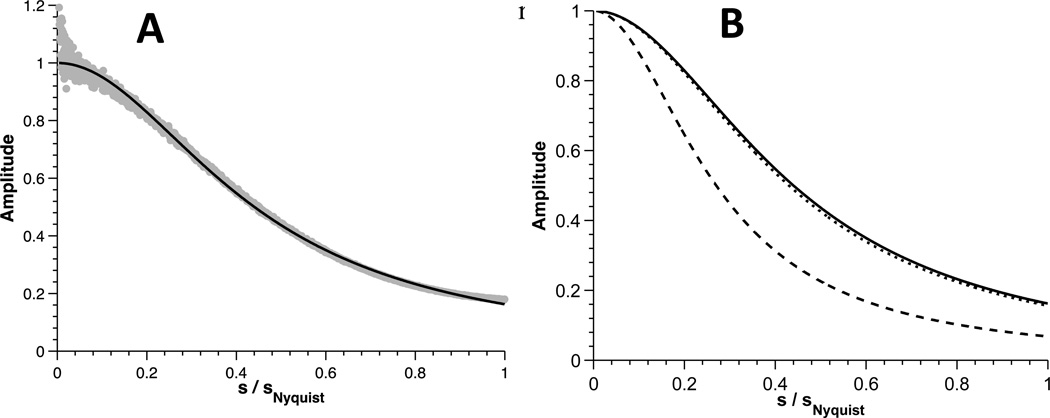
The azimuthally averaged Fourier amplitude spectrum of an empty image recorded with the TVIPS TemCam F416 camera, using 120 keV electrons, is shown in Figure 1A. Also shown in this figure is the fact that the sum of a single Lorentzian function plus a constant y-axis offset provides a three-parameter fit that closely matches the experimental data over nearly the entire domain, with a deviation of up to several per cent occurring only for frequencies close to the origin. Corresponding amplitude spectra, and the goodness of fit by single Lorentzian functions, are shown in Figure S1 for other cameras and other electron energies. Figure 1B compares three such Lorentzian curves, corresponding to measurements obtained for the TVIPS TemCam F416 camera (using 120 keV electrons), the Gatan UltraScan 4000 camera (using 200 keV electrons), and the Gatan K2 camera (using 300 keV electrons). The amplitude spectra are all normalized to 1.0 at the origin in order to facilitate the comparison of the relative falloff for each curve.

Figure 1.

Use of azimuthally averaged Fourier amplitude spectra of empty images to rank the performance of different electronic cameras. Individual Lorentzian functions, which are of the form $\frac{1}{1+{\left(\frac{s}{s_0}\right)}^2}$, are fitted to each Fourier amplitude spectrum. Three parameters – an overall scale factor for each experimental amplitude spectrum, an additive constant, and s₀, the spatial frequency at which the function is equal 0.5 – are varied to produce a least-squares best fit between the data and the analytical function. (A) The Fourier amplitude spectrum for the TVIPS TemCam F416 camera, obtained when using 120 keV electrons, is used to illustrate the fitting of a single Lorentzian function to the experimental amplitude spectrum. Corresponding figures for other cameras are shown in the Supplemental material. (B) Comparison of Lorentzian curves fitted to amplitude spectra for two types of scintillator-coupled camera and for a silicon-pixel camera. Solid line: TVIPS TemCam F416 camera, 120 keV electrons; dashed line: Gatan UltraScan 4000 camera, 200 keV electrons; dotted line, Gatan K2 camera, 300 keV electrons.

The spatial frequencies at which each such Lorentzian function falls to 0.5 are listed in Table 1. Since the Lorentzian function and the exponential function represent a Fourier-transform pair (see example 207 in http://en.wikipedia.org/wiki/Fourier_transform), the reciprocal of the spatial frequency at which the Lorentzian function falls to 0.5 is an estimate of the real-space distance at which the line-spread function for detection of single electrons falls to e⁻¹. The widths of the line-spread functions, estimated as the reciprocal of the spatial frequency at which the Lorentzian function falls to 0.5, are given in parentheses in Table 1.

Table 1.

Values of the spatial frequency, expressed as a fraction of Nyquist frequency, at which Lorentzian functions – fitted to the Fourier amplitude spectra of “empty” images – fall to 0.5, depending upon the type of detector and the electron energy. The sum of a single Lorentzian function plus a constant y-axis offset was fitted to the Fourier amplitude spectra (see Figure 1A for an example). Please refer to Figure S1 for fitted amplitude spectra for all other examples listed in this table. Values given in parentheses are the reciprocal of the respective values of the spatial frequency, i.e. the distance in number of pixels at which the nearly exponential linespread function falls to e⁻¹. Recall that Nyquist frequency is 1/(2 pixel).

	TVIPS F416 4kx4k 15.6 μm pixel	Gatan US4000 4kx4k 15.0 μm pixel	FEI Eagle 2kx2k 30 μm pixel	Gatan K2 4kx4k 5 μm pixel
80 keV	-	-	0.43 (4.7 pixels)	-
120 keV	0.44 Nyquist (4.5 pixels)	0.32 (6.3 pixels)	-	-
200 keV	-	0.27 Nyquist (7.4 pixels)	-	-
300 keV	-	-	0.35 (5.7 pixels)	0.43 (4.6 pixels)

4.2 The value of the power spectrum at the origin, normalized by the number of electrons in an image, can be used to estimate the variance in the camera response to single-electron events

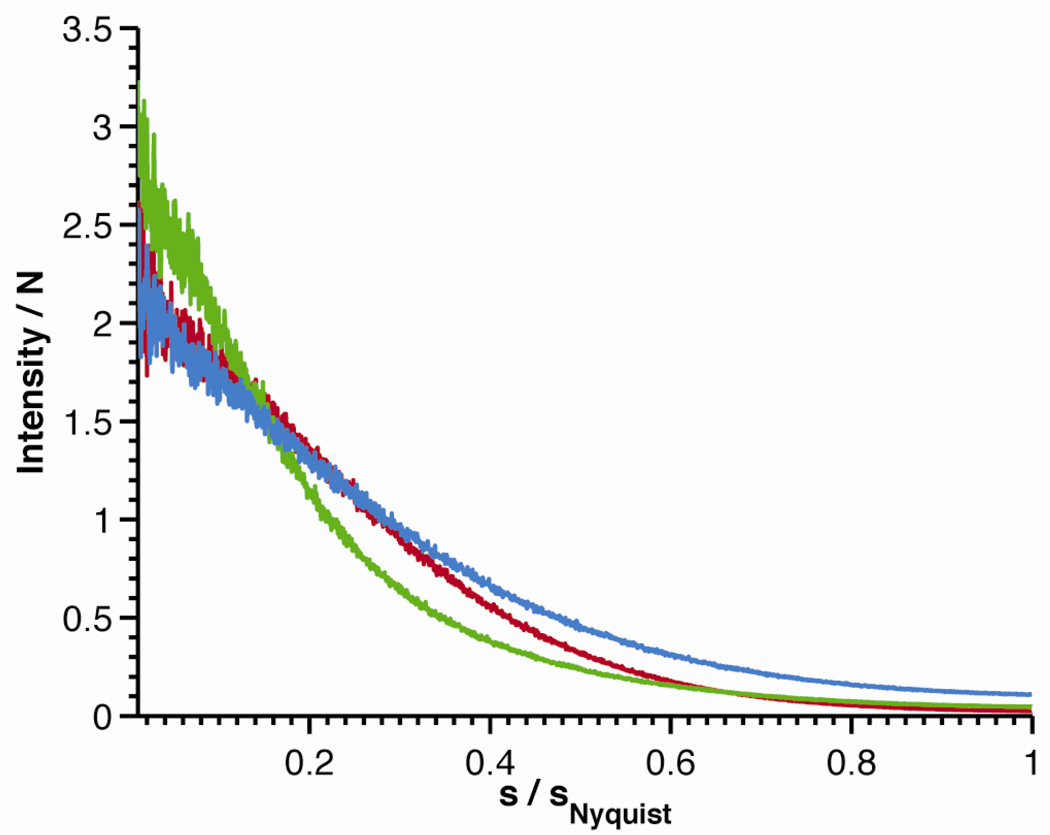
Three examples of power spectra of empty images are shown in Figure 2. The type of camera and the electron energy for these examples were chosen to be the same as for the Lorentzian functions, fitted to Fourier amplitude spectra, which were displayed in Figure 1B. Corresponding power spectra for all other cameras and electron energies are shown in Figure S2. All power spectra are normalized by the appropriate values of N, the total number of electrons in an image (please refer to section 3 for details on data reduction and nomenclature). Note that the normalized power spectra can rise to values that are much greater than 1.0 at the origin.

Figure 2.

Examples of azimuthally averaged power spectra of empty images that have been normalized by N, the total number of electrons in a given image. Only three examples are shown here for simplicity. Corresponding figures for other cameras are shown in the Supplemental material. Red curve: TVIPS F416 camera, 120 keV electrons; green curve: Gatan US4000 camera, 200 keV electrons; blue curve: Gatan K2 camera, 300 keV electrons.

The rationale for normalizing by N is based on the fact that the power spectrum of an empty image (i.e. shot noise as input) is equal to N for a perfect camera, i.e. one in which each electron is registered as a Kronecker delta function. To explain briefly, the Fourier transform of a single Kronecker delta function is the complex exponential function, whose magnitude is 1.0 and whose phase depends both on the spatial frequency and on the position of the delta function relative to the origin used to compute the Fourier transform. At any given spatial frequency the complex exponential function can thus be represented (in an Argand diagram) as a unit vector whose direction depends on the location of the delta function in real space. When N such delta functions are located randomly in real space, the Fourier transform thus becomes the sum of N unit vectors, each pointing in a random direction. As a result, the Fourier transform effectively takes a random walk (with unit step size) as one electron after another is added to the image. As is well known, the expected distance (from the origin) that is achieved in a random walk increases as the square root of the number of steps. The square of the amplitude of the Fourier transform, i.e. the power of the Fourier transform, thus increases linearly with N.

The derivation sketched out in the paragraph above indicates that the expectation value of the appropriately normalized power spectrum of an ideal, empty image should be 1.0 at all frequencies. Furthermore, if the camera is only semi-ideal in the sense that the response to single-electron events is a Kronecker delta function convoluted by a point-spread function with finite width, then the power spectrum will fall off with increasing resolution, but the value extrapolated to zero will still be 1.0. For the three examples shown in Figure 2, the power spectra of empty images all rise well above 1.0 as the curves are extrapolated to zero. The fact that a given (experimental) normalized power spectrum rises above 1.0 at low spatial frequency implies that the camera output contains some form of noise in excess of shot noise.

As was indicated in the Introduction, random variation in the magnitude of the camera response to single electrons represents one source of additional noise in the camera output. The degree to which this source of additional noise reduces the DQE was addressed quantitatively by Herrmann and Krahl [10]. However, a derivation showing how this excess noise is manifested in the Fourier spectra has not been described previously in the EM-camera literature to our knowledge. To do so, we again treat the Fourier transform as the result of a random walk in the complex plane. In this case, however, the step sizes – as well as the directions taken – vary randomly for each step. As is shown in the Supplementary material, the expected value of the power spectrum of an empty image then becomes $N(1+{\sigma }_{\mathit{\text{response}}}^2)$, where N is again the number of electrons in the entire image, and σ_response is the standard deviation of the distribution of single-electron responses. The corresponding value of DQE(0) given by this derivation is $\frac{1}{1+{\sigma }_{\mathit{\text{response}}}^2}$, in agreement with the result given by Herrmann and Krahl.

The variance of the values of single-electron responses (i.e. individual pulse heights) can thus be calculated from the amount by which the value of the power spectrum (extrapolated to the origin) exceeds 1.0. In the curve for the TemCam F416 camera, for example, using 120 keV electrons (shown in Figure 2), the power spectrum at low frequencies is about 2.1 times what it would be for an ideal camera, thus implying that the variance of the pulse-height distribution is about 1.1. For comparison, the power spectra for the UltraScan 4000 camera, using 200 keV electrons, is about 2.7 times what it would be for an ideal camera, thus implying that the variance of the pulse-height distribution is about 1.7. The values of the variance that we have measured for each camera in this study are listed in Table 2. For two of these cameras we were also able to make these measurements for two values of the incident electron energy.

Table 2.

Estimated variance of the detector response to single-electron events, derived from the excess noise (at low frequency) in the power spectra of empty images, depending upon the type of detector and the electron energy.

	TVIPS F416 4kx4k 15.6 μm pixel	Gatan US4000 4kx4k 15.0 μm pixel	FEI Eagle 2kx2k 30 μm pixel	Gatan K2 4kx4k 5 μm pixel
80 keV	-	-	0.1	-
120 keV	1.1	1.2	-	-
200 keV	-	1.7	-	-
300 keV	-	-	1.0	1.1

4.3 The variance of the Fourier amplitude spectrum of empty images provides an alternative measure of the excess noise

Although the average value (expected value) of the Fourier amplitude of an empty image merely represents a systematic background that can be subtracted (in quadrature) from the Fourier transform of a low-dose image, stochastic fluctuations in the Fourier-amplitude spectra represent irreducible noise in the data. The relative magnitude of these stochastic fluctuations, rather than the average value of the Fourier amplitude, determines the exposure-dependent signal-to-noise ratio for data recorded with one or another camera, assuming that the same number of electrons is used in all cases.

If a suitably large number of empty images is recorded (20, for example), the magnitude of the irreducible noise that is present in the Fourier amplitude spectra is easily estimated by simply computing the variance observed at each spatial frequency. As is derived in the Supplementary material, the expected value of the variance in the Fourier amplitude spectrum is equal to $N(1+{\sigma }_{\mathit{\text{response}}}^2)(1-\frac{\pi }{4})$ for empty images recorded with a semi-ideal camera (i.e. one for which single-electron events are registered as Kronecker delta functions with variable heights). Although the variance in the amplitude spectra for real cameras will fall off with resolution due to the non-zero width of the point-spread function, it is expected that the variance spectrum divided by the power spectrum should be constant. Furthermore, the ratio should be $(1-\frac{\pi }{4})=0.21$, if excess noise in the power spectra (and thus in the Fourier amplitude spectra) is due primarily to the variance in the response for single-electron events.

We have found that the ratio is indeed equal to 0.21 within experimental error. Graphs showing the value of this ratio as a function of spatial frequency are shown in Figure S3 for each of the cameras evaluated in this work.

5. DISCUSSION

As was stated above, an ideal camera for electron microscopes would record each electron as a Kronecker delta function that is located at the pixel where the electron first hits the camera. The relative performances of real camera systems necessarily fall short of this ideal in three ways. (1) Single-electron responses typically are not confined to single pixels, but instead they usually extend over a cluster of nearby pixels. The average width of these clusters determines the rate at which the Fourier transform falls off when the incident image consists of nothing but electron shot-noise. (2) In addition, these broadened responses often are not centered on the same pixel where the electron first hits the camera. The average displacement of the center of the cluster determines how rapidly the Fourier transform of the signal falls off relative to the Fourier transform of the noise [1, 3]. (3) Finally, instead of being the same for every electron, the magnitudes of single-electron events span a distribution of values. The variance in the magnitude of these output pulses determines the factor by which the noise in the output exceeds the irreducible noise in the input.

5.1 The relative cluster-size of single-electron responses can be measured by fitting a single Lorentzian function to the Fourier amplitude spectrum

In our current experiments, we confirm that the one-dimensional Fourier amplitude spectra of empty images are fitted quite well by a single Lorentzian function [5]. While the fitting is never perfect, and the accuracy varies between cameras, a single Lorentzian function is in all cases within a few percent of the experimental data. This fitting was improved slightly by including the added constant as a third parameter. The values of this parameter, which are given in the figure legend for Figure S1, varied from 0.06 to 0.13, depending upon the camera and the electron energy. We have not investigated whether a physical basis can be identified for this constant (spectrally “white”) term, but it may be that it is due, at least in part, to stochastic variance in the readout noise of the various cameras.

The fact that the amplitude spectra are well fitted by a single Lorentzian implies that the line-spread function for single-electron events is well approximated by a single exponential. In speaking of the line-spread function for single-electron responses (and the associated transfer function for shot noise), it is important to emphasize that single-electron responses are expected to vary randomly in terms of how many pixels participate in the response and the way in which the multi-pixel response is distributed relative to the point where the electron first hits the camera. In other words, no one instance of the response is likely to be the same as any other. The expression “line-spread function for single electrons” must thus be understood to refer to the average behavior of a large number of single-electron events. In this spirit, the reciprocal of the spatial frequency at which the one-dimensional Fourier amplitude spectrum of an empty image falls to 0.5 can be interpreted as the distance, in number of pixels, at which the line-spread function falls to 1/e of the initial value. The spatial frequency at which the amplitude spectrum of shot noise falls to 0.5 thus gives a useful comparison of how closely the performance of a given camera does, or does not, approach the ideal performance, in which the response to single electrons is confined to a single pixel.

5.2 The center of a cluster must converge to the initial point of electron impact as the size of the cluster converges to a single pixel

It may not be immediately obvious why the second shortcoming (identified above) causes the amplitude spectrum for (noise-free) signal to fall off more rapidly – with increasing resolution – than the amplitude spectrum for shot noise. To explain briefly, noise-free signal, at a given point in an image, is obtained in the limit that a large number of electrons is incident at exactly the same point in the image. When each such electron is registered over a cluster of several pixels, the center of which varies randomly in distance and direction from the initial point of impact, the resulting average of all such events is broader than is the average of the clusters themselves (i.e. when their centers are superimposed). The first type of average produces the noise-free pointspread function for signal, while the second average produces the point-spread function for noise. It is well known that NTF(s) thus is not, in most cases, a good estimate of MTF(s) for signal [3].

To the extent that the average cluster size becomes more and more narrow, however, the center of the cluster must also become more and more closely localized to the same pixel where the electron first hits the camera. It thus follows that MTF(s) must asymptotically approach NTF(s) as the rate at which NTF(s) falls off becomes less and less. In the limit that the MTF(s) and the NTF(s) fall off at the same rate, the signal-to-noise ratio in the camera output is no longer degraded by the fall off. In other words, one can boost the signal at high resolution, to compensate for the fall off, and the signal-to-noise ratio will remain unchanged. As a result, if two cameras have similar excess noise at low resolution (as do the TVIPS F416 camera and the Gatan US4000 camera at 120 KeV) the better camera is the one for which the Fourier amplitude spectrum of an empty image shows the slower decay as a function of increasing resolution.

5.3 The extent to which variations in the pulse height (magnitudes of single-electron responses) add to the noise in the camera output can be measured in terms of the value of the power spectrum at low spatial frequencies

It is important that the pulse height, i.e. the magnitude of the camera output, should be as constant as possible for each electron event. This is because random variations in the size of the response cause the noise in the camera output to be greater than the irreducible noise (shot noise) that is due to randomness in the spatial distribution of these events. The desired criterion of constant pulse height is not well met by currently available, scintillator-coupled CCD cameras, however. Instead, as we have shown here, the noise in the output is generally a factor of two or more greater than that expected for shot noise.

The extent to which the power spectra of images recorded with different cameras do – or do not – approach N, the total number of electrons in the image, is thus an important factor in ranking their relative performance (all else being equal). In this context, the development of camera systems that operate in an electron-counting mode provides one way to ensure a constant output for each electron event. It thus is expected that the noise level for such cameras will be significantly lower than it is for scintillator-coupled cameras, and – for the first time – the noise will actually approach the irreducible level set by shot noise.

In a related point, we emphasize that the noise in the computed Fourier amplitudes of an image is represented by random fluctuations in the Fourier amplitudes of a corresponding, empty image, rather than by the average value. As a result, the noise is characterized by the variance of the Fourier amplitudes, rather than by the power spectra of empty images. As we have stated above, the variance of the Fourier amplitude is smaller than the value of the power spectrum by a factor of $(1-\frac{\pi }{4})$.

Excess noise due to variation in the pulse-height distribution has been referred to as “Fano noise”, and the increment by which the power spectrum of an empty image exceeds N , the total number of electrons in the image, has been referred to as the “Fano factor” [6], in reference to the variance in number of ionization events (per increment of energy deposited) that was studied by Fano [11]. It is likely, however, that the pulse-height spectrum produced in currently used scintillators has a more complex origin than the effect studied by Fano. If the sensitive layer (scintillator) is relatively thick, multiple scattering can lead to wide variations in path length – and thus the amount of energy deposited – as an incident electron passes through. In addition, after electrons are transmitted through the sensitive layer, some – but not all – are back scattered and thus deposit even more energy. Thus we recommend to use the more general descriptors “excess noise” and “excess noise factor” when discussing electron microscope cameras. The methodology described for measuring the “Fano factor” (F in equation 17 of [6]) is, in fact, the same as what we have used to derive the values of the variance of the pulse-height distribution that are presented in Table 2. The magnitude of the excess noise factor that we observe for scintillators currently used on CCD cameras is almost 10 times greater, however, than that estimated by de Ruijter for a YAG scintillator [6]. The thickness of the sensitive layer (e.g. scintillator) relative to the range of the incident electron and the extent to which back scattering occurs in the material (if any) that supports the sensitive layer are likely to be major factors that influence the variance of the pulse-height distribution, i.e. the excess noise factor.

The accuracy with which one can measure the value of the power spectrum at low spatial frequency is limited by potential errors in the vendor-supplied calibration of the current density on the viewing screen. If very accurate values of the normalized power spectrum are required, it may thus be necessary to independently perform the beam-current calibration with a Faraday cup. There is also some uncertainty in estimating the mean value of the power spectrum at low spatial frequency, due in part to the fact that the low-frequency values are noisier (fewer pixels are included in the azimuthal average) and due in part to systematic errors (such as an imperfect flat-field correction). Nevertheless, this uncertainty is small relative to the amount by which the normalized power spectrum exceeds 1.0.

5.4. Some general remarks about ranking the performance of different cameras

Camera performance is determined by many factors. It is well-known, for example, that the performance of scintillator-based cameras is more ideal at low electron energy than at high, as is confirmed by the data in Table 1 and Table 2. This is understandable, since simulations of electron trajectories show that low energy electrons deposit their energy in a spatially more confined volume. The new silicon-pixel detectors, however, are expected to perform much better at high electron energy than at low [12], especially when the sensor is thinned in order to minimize backscattering of the primary electrons. When comparing camera performance, therefore, one must always do so for the electron energy at which the camera is intended to be used.

The data in Tables 1 and 2 also show (as is already well known) that the performance of scintillator-based cameras is better for a large pixel size. This improvement comes, of course, at the expense of a reduced field of view for a given resolution. The way in which the performance of silicon-pixel cameras depends upon pixel size is perhaps more complex. In any case, there is not yet a consensus about how to optimize the pixel size and the epilayer thickness as a function of the electron energy.

The methods presented here provide an easy way to measure and compare two of the factors that affect performance. While any improvement in performance is desirable, whether the measured differences are significant enough to be worth replacing one camera with another will ultimately have to be decided by the end user. One must be aware that there can be trade-offs in performance. As an example, the line-spread function could be better for one camera but at the same time the excess noise could be worse. Thus, while making the measurements (at the same electron energy) may be easy, ranking camera performance will only be easy if one camera performs better than another both with respect to line-spread function and with respect to excess noise.

5.5. These methods cannot be applied to a camera that is operated in an “electron counting” mode

The analysis of the power spectrum and Fourier amplitude spectrum of the camera output does not provide useful information about the camera performance when one uses a “cluster-imaging”, or “centroiding” algorithm [12], to convert the broadened camera output for single-electron events to Kronecker delta functions located at the centers of their respective, multi-pixel responses. This is because the camera output will appear to be perfect when one counts electrons – assuming, however, that the count rate is low enough to avoid pulse pileup (coincidences). A camera operated in the counting mode is, indeed, perfect in the sense that there is no additional noise due to finite variance in the magnitude of the camera response. The camera performance may not be perfect, however, because the location of the electron event in the output may still not coincide with the pixel location (or the subpixel location, in the case of centroiding) where the electron was incident on the camera. The performance of a camera that is operated in the counting mode must therefore be characterized by measuring DQE(s), as was done by McMullan et al. [13], rather than by measuring the power spectrum and the Fourier amplitude spectrum of the camera output.

6. CONCLUSIONS

We find that the one-dimensional, azimuthally averaged Fourier amplitude spectra of the output of four different camera systems, for randomly distributed incident electrons, are all well fitted by single Lorentzian functions. The widths of the corresponding (exponential) line spread functions are different, however, thus providing an easily measured criterion of how well a given camera system does, or does not approach the desired performance in which incident electrons are registered in, and only in, the pixel where the incident electron first hits the camera. We also find that the square of the Fourier transform at low frequency exceeds the number of electrons in the image, which is the value expected if every electron were registered with the same magnitude of response. We derive the result that the noise in the Fourier transform, i.e. the variance of the Fourier amplitude, is $(1-\frac{\pi }{4})$ times the power spectrum. The amount by which the power spectrum exceeds N (the number of electrons in the image) is thus an easily measured way to compare the relative noise level of different camera systems, for images recorded with identical electron exposures.

Highlights.

• ▪Fourier amplitude spectra of noise are well fitted by a single Lorentzian.
• ▪This measures how closely, or not, the response approaches the single-pixel ideal.
• ▪Noise in the Fourier amplitudes is (1 – π/4) times the shot-noise power spectrum.
• ▪Finite variance in the single-electron responses adds to the output noise.
• ▪This excess noise may be equal to or greater than shot noise itself.