The January Effect: Medication Reinitiation among Medicare Part D Beneficiaries

Abstract

The Medicare prescription drug program (Part D) standard benefit includes deductible, initial coverage, coverage gap and catastrophic coverage phases. As beneficiaries enter each phase, their out-of-pocket medication costs change discontinuously. The benefit cycle restarts on January 1^st of the next year. Taking advantage of variation in drug coverage, we study how individuals reinitiate discontinued medications in response to the non-linear price schedule.. Since some beneficiaries who receive low-income subsidies (LIS) have zero or fixed small copayments throughout the year, we perform a difference-in-difference analysis using the LIS group as a comparison. We find that individuals delay reinitiating important medications in December, and are significantly more likely to reinitiate in January than in other months. While we find some evidence that reinitiation is lower in the final months of the year, it is mostly driven by those who face higher prices due to the coverage gap. Our study suggests that individuals respond more to the current price of medications, and do not anticipate future prices as well as theory would suggest.

1. Introduction

A common feature of health insurance is the inclusion of discontinuous changes in patients’ out-of-pocket costs at various levels of spending. This could include deductibles, where consumers pay out-of-pocket up to a certain limit before an insurer will pay any expense; coverage limits, where patients pay all out-of-pocket costs after spending reaches a maximum threshold, or coverage gaps, where consumers pay 100% out-of-pocket for all medical costs incurred between an upper and lower threshold. From the insurance beneficiary’s perspective, this creates a non-linear price schedule. In the case of pharmaceuticals, this causes the price the beneficiary pays for a prescription to change throughout the year. As a result, patients may discontinue medications when prices are high, and/or reinitiate when prices are low. Forward-looking patients may also be able to anticipate these changes in the out-of-pocket price in advance, and adjust their consumption before the price changes. It is important to understand the role such pricing schemes play in individuals’ decisions to discontinue medications, and to resume treatment after discontinuation.

The Medicare prescription drug program (Part D) is an ideal setting to study how consumers respond to price non-linearities. Like many insurance plans, Medicare Part D is structured such that beneficiaries face different marginal out-of-pocket prices as they move through several spending phases throughout the year. The benefit cycle then restarts on January 1^st of each year. In 2008, the standard Part D benefit included a $275 deductible, an initial coverage period where the beneficiary paid 25% coinsurance for their drug spending between $275 and $2510, a coverage gap (or “doughnut hole”) where the beneficiary paid 100% out-of-pocket, and a catastrophic coverage period where the beneficiary paid 5% coinsurance after total spending reached $5726 (Figure 1). Since Part D’s initiation in 2006, the thresholds for each phase of coverage have changed slightly from year to year.

Figure 1.

Standard Medicare Part D Benefit Structure in 2008

In this paper, we estimate consumer responses to discontinuous price changes by taking advantage of the fact that the Part D benefit cycle restarts on January 1^st. The price changes individuals face as they enter the coverage gap or catastrophic coverage phases depend on cumulative drug spending throughout the year, so the price is endogenous to their consumption choice. The change in price at the beginning of a new cycle does not depend on consumer behavior, however. This exogenous change in marginal drug prices at the beginning of the year allows us to identify the impact of non-linear pricing on medication use. In addition, it enables us to examine anticipatory behavior by examining the likelihood of medication reinitiation in the months leading up to January 1^st.

In particular, we examine the effect of non-linear pricing on drug reinitiating behavior by determining whether individuals postpone filling prescriptions in December when anticipating a decrease in drug prices due to the beginning of a new policy cycle in January of the next year. We use pharmacy and medical claims data for the full population of Medicare beneficiaries who were discharged alive after an acute Myocardial Infarction (MI) in 2008. Our sample is then limited to those MI survivors who filled a prescription for a beta-blocker after discharge, and subsequently discontinued the drug for at least 30 days. This allows us to evaluate differences in beta-blocker reinitiation rates during different benefit phases.

One unique feature of Medicare Part D is the Low Income Subsidy (LIS) program where some qualifying beneficiaries have zero or a fixed, small copayment throughout the entire year. We take advantage of this variation in drug coverage and use a difference-in-difference approach to gain insight into consumer responses to different pricing schemes, using the LIS group as a comparison. Additionally, among the non-LIS population, we separately analyze subpopulations based on which phase they were in at the end of 2008, since they face different price changes at the beginning of the new cycle.

In our sample, approximately half of beneficiaries (n=115,863) who used beta-blockers after MI discontinued their medications during the study period, and approximately two thirds of those who discontinued their medications subsequently reinitiated use. Our results provide evidence that individuals delay reinitiating beta-blockers in December, and are more likely to reinitiate in January than in other months. However, our results also suggest that individuals make decisions based on the current price of medications, and do not respond much to future price decreases, even when it might be optimal to do so. Regardless of the cause of the delay in reinitiation, our results are important because cost-related non-adherence and medication discontinuation can have significant consequences, including increases the chance of uncontrolled symptoms and hospital admissions (Tamblyn et al., 2001).

The remainder of the paper is organized as follows: Section 2 discusses the study background and related literature, Section 3 introduces our methods and empirical model, Section 4 presents our results, and Section 5 concludes.

2 Background

Our study is related to several strands of literature in economics and health policy. First, several studies have examined the effects of non-linear pricing on medication use in Medicare. Much of this literature focuses on whether seniors reduce spending on medications after they enter the coverage gap compared with in the initial coverage phase (Duru et al., 2010; Gu et al., 2010; Fung et al., 2010; Schmittdiel et al., 2009; Zhang et al., 2012; Raebel et al., 2008). Previous researchers have found that those who entered the coverage gap were twice as likely to discontinue their medication, and beneficiaries reduced their monthly prescriptions by about 14 percent while in the doughnut hole (Polinski et al., 2011; Li et al., 2012; Zhang et al., 2009). Approximately a quarter non-LIS seniors who filled prescriptions entered the coverage gap in 2006, but only 4% reached the catastrophic coverage phase (Hoadley et al., 2008). Those with chronic conditions were more likely to enter the coverage gap and catastrophic coverage phase (Zhang et al., 2009).

One problem with examining the effect of the Medicare Part D coverage gap on medication usage is that the timing of entry into the gap is endogenous because it depends on how much beneficiaries spend during the year. This can lead to an overestimation of the effect of the gap if there is a short term increase in spending that causes entry into the gap (such as that due to an acute illness). It can also lead to an underestimation of the effect of the gap if individuals are forward looking, and decrease their spending in anticipation of reaching the gap.

Second, a few studies specifically examine medication reinitiation decisions. Joyce et al. (2007) studied private pharmaceutical plans that had capped benefits, and found that patients who faced a capped plan were more likely to discontinue medications, and were also more likely to reinitiate at the beginning of the year. For cardiac drugs, approximately 30% of patients discontinued their medications, and, of those, 30% reinitiated their medications. Colby et al. (2011) studied Medicare Part D and found that approximately one third of patients discontinued expensive medications for rheumatoid arthritis and cancer after reaching the coverage gap. Of those, about three quarters reinitiated their medications. However, those who discontinued in the doughnut hole were less likely to reinitiate.

Finally, our study is related to the literature on forward-looking behavior in the presence of non-linear price schedules. The theoretical literature predicts that forward-looking, rational individuals should respond to the predicted future end-of-year price, rather than the current spot price (Ellis, 1986; Keeler et al., 1977). In the case of pharmaceuticals, where spending is relatively predictable, this means that individuals should not vary consumption much throughout the year. Aron-Dine et al. (2012) demonstrated some anticipatory behavior by showing that individuals respond to changes in the expected future price when the spot price was held constant. However, the literature on the Medicare Part D coverage gap discussed above seems to suggest that individuals may also be sensitive to the spot price of medications.

Our study adds to the existing literature in several important ways. First, we focus on the change in out-of-pocket costs on January 1^st, the beginning of a new benefit cycle, where the date of the change is exogenous. Second, we identify a control group, the LIS group, which does not experience changes in out-of-pocket costs throughout the year. Finally, we test for short-term anticipatory behavior by examining the likelihood of medication reinitiation in the months leading up to January 1^st.

3. Methods

3.1. Data and Study Population

Our data come from the US Centers for Medicare and Medicaid Services’ Chronic Condition Warehouse and include 100% of Medicare beneficiaries who had an inpatient stay for MI in 2008. We identify beneficiaries who were discharged alive after an MI in 2008 and subsequently filled a prescription for a beta-blocker within 60 days after discharge. We follow each beneficiary until death or until the end of the study period on December 31, 2009. Our sample is then limited to those who discontinued beta-blockers at least once during the follow-up period, where we define discontinuation of medication as having a gap in drug possession for over 30 continuous days. In order to focus on the population that physicians would recommend to continue taking beta-blockers indefinitely, we exclude individuals from the sample if they were diagnosed with any condition or began any new medications that had a contraindication for beta-blocker therapy after their initial use of beta-blockers.¹ The study was approved by the institutional review board at the University of Pittsburgh.

Among those who discontinued beta-blocker use during the study period, we evaluate whether they reinitiated beta-blockers, and when they did so. In particular, we focus on reinitiations that occurred around the exogenous change in drug benefit as of January 1, 2009 when a new benefit cycle started for everyone regardless of their drug spending in 2008.

3.2. Models

We use two different survival models to estimate time until reinitiation from the end of discontinuation, censored at death or December 31, 2009 (the end of follow-up period). Our main specification is a Binary Time Series Cross-Sectional Model (BTSCS), described below. As a robustness check, we also perform a Cox Proportional Hazard Model.

3.2.1. Binary Time-Series Cross-Sectional Model

The BTSCS model is a discrete time survival model, where each month during the year is a discrete time period (Beck et al., 1998). Thus, the unit of analysis is person-month.

For this model, the hazard rate, h(t, x), depends on the time period, t, and covariates, x:

$$h(t,x)=Pr(T=t_i\mid T\ge t_i,X)$$

where T represents the reinitiation date. We then define the probability that an individual reinitiates as:

$$P(Y_{it}=1)={\lambda }_{it}$$

Since Y_it is only equal to 1 in the last period,

$$E({\lambda }_{it}\mid X)=h(t,x)$$

λ_it can depend on several variables

$${\lambda }_{it}={\beta }_0+{\beta }_1{X}_{1it}+{\beta }_2{X}_{2it}+\cdots +{\beta }_k{X}_{\mathit{kit}}$$

This flexible model is estimated with a logistic regression. The baseline hazard is specified using a cubic spline function representing the number of months since discontinuation. We perform the analysis using several specifications including three equally spaced splines, five equally spaced splines, and separate dummies for each time period. The results from these three specifications are not significantly different from each other, so only the results from the specification with three equally spaced splines are presented here.

Then, the actual month (e.g. February, March, etc.) enters the equation as a set of dummies, which gives a flexible form to estimate the effect of seasonality on reinitiation. This allows us to test whether there are higher or lower rates of reinitiation in particular months. We are especially interested in January, the months leading up to January, and those immediately following January, since this is when the benefit cycle resets. In addition, the model controls for the number of months since discontinuation; these months are different from calendar months because discontinuation occurs in different months for each individual.

In order to account for the fact that different months have different numbers of days, rather than using the actual calendar month, we generated time periods representing 30-day increments tied to January 1^st, 2009. For example, the month we refer to as “December 2008” is actually the 30-day period from December 2^nd to December 31^st, while “November 2008” is the period between November 2^nd and December 1^st, and so on. We cluster the standard errors at the individual level.

In addition, all regressions include gender, age, racial/ethnic group (non-Hispanic White, non-Hispanic Black, Hispanic, Asian, and other/unknown, all relative to White), disability status, and Medicaid eligibility. We also control for illness severity by including the number of chronic conditions the individual had been diagnosed with out of the 21 high-priority conditions listed by the Chronic Conditions Warehouse (Chronic Condition Warehouse, 2011).

3.2.2. Cox Proportional Hazards Model

The second specification uses the Cox Proportional Hazards Model. In this case, we model the number of days until reinitiation from 30 days after the date of discontinuation,² censored at death or December 31, 2009. Similar to the BTSCS model, we include dummies for each calendar month, as time-varying components. For example, if we follow an individual from November 15^th, the January dummy switches on after 47 days, and switches off after 77 days. Since this model is conceptually similar to the BTSCS model, we treat it as a robustness check.

3.3. Heterogeneous Groups

We perform our main analysis for several subpopulations by taking advantage of variation in individuals’ drug coverage. First, individuals who receive LIS have a fixed marginal price throughout the year, so we do not expect the reset of benefits on January 1^st to affect their rates of reinitiation. Second, among beneficiaries without LIS coverage, we separately analyze each subpopulation depending on which phase they were in at the end of 2008.³ Those who were in the catastrophic coverage phase (5% coinsurance) at the end of 2008 faced an increase in marginal price as the new benefit cycle started, and therefore we expect to observe a decreased reinitiation rate in January because the anticipated price increases at the beginning of the year. For those in the coverage gap at the end of 2008 and started their benefit cycle in January 2009, their marginal price decreased substantially from 100% to 25%. We anticipate these individuals were most likely to hold off reinitiating drugs in December and reinitiate in January. By comparing the effects for groups facing different price changes on January 1, 2009, we gain insight into consumer responses to different pricing schemes.

3.4. Difference-in-Differences

In order to separate out the seasonal or monthly effects on drug reinitiation from the price effects, we run a difference-in-difference specification using the BTSCS model. The treatment group includes non-LIS beneficiaries, while the comparison group includes those who received LIS. In addition, we compare non-LIS and LIS beneficiaries for two subgroups: those who entered the doughnut hole but did not enter the catastrophic phase anytime in 2008, and those who entered the doughnut hole before October 2008 but did not enter the catastrophic phase in 2008. For each specification, the LIS control group is selected such that their spending falls within the same range as the analogous non-LIS treatment group.

In each difference-in-difference specification, dummies for the November, December, January, and February, a dummy for being in the non-LIS group, as well as the interaction term between the non-LIS indicator and each of the month dummies are included. Each regression also includes the same controls used in the BTSCS models.

In order for our difference-in-difference specification to be valid, seasonal patterns of medication use in the LIS group would have to be similar to what they would be in the non-LIS group if the non-LIS group faced the same pricing scheme as the LIS group. Given that the LIS group has lower income, it is possible that they have different baseline patterns of medication use. However, it is likely that differences across time periods are relatively similar between the two groups. One of our earlier studies confirmed the underlying trend in medication use in the initial coverage period was parallel over time between LIS and non-LIS (Zhang et al., 2012).

3.5. Triple Difference

As noted above, the DD specification may be biased if there are different seasonal patterns of medication use between the LIS and non-LIS group. As an additional robustness check, we control for this by subtracting out the difference in seasonal use between LIS and non-LIS beneficiaries who did not reach the doughnut hole. Rather than comparing the non-LIS beneficiaries who reached the doughnut hole with one control group (i.e. LIS beneficiaries), this specification makes use of three control groups (i.e. LIS beneficiaries who reached the doughnut hole, LIS beneficiaries who didn’t reach the doughnut hole, and non-LIS beneficiaries who did not reach the doughnut hole), all of which should we would not expect to observe a January effect.

With this speciation, the assumption required to ensure an unbiased estimate is modified. We must now simply assume that the difference in seasonal patterns of medication use between the LIS and non-LIS is similar for those who did not reach the doughnut hole and those who did.

We define three differences, each of which is a meaningful measure of the January effect:

First Difference

$${\mathit{Jan}}_{\mathit{lis}=0}^{dh=1}-{\mathit{Other}}_{\mathit{lis}=0}^{dh=1}$$

Where ${\mathit{Jan}}_{\mathit{lis}=0}^{dh=1}$ refers to the adjusted average probability of reinitiation during the month of January, for individuals in the doughnut hole, who are non-LIS beneficiaries. Since the regression includes dummies for November, December, January, and February, ${\mathit{Other}}_{\mathit{lis}=0}^{dh=1}$ refers to the adjusted average probability of reinitiation in months other than those four for the analogous group of individuals.

The difference-in-difference, described above, removes seasonal variation by subtracting out the corresponding difference for individuals with low income subsidies.

Difference-in-Difference

$$({\mathit{Jan}}_{\mathit{lis}=0}^{dh=1}-{\mathit{Other}}_{\mathit{lis}=0}^{dh=1})-({\mathit{Jan}}_{\mathit{lis}=1}^{dh=1}-{\mathit{Other}}_{\mathit{lis}=1}^{dh=1})$$

The third difference adjusts for the fact that the LIS and non-LIS group may have different baseline utilization by taking out the difference-in-difference of the group of individuals that did not reach the doughnut hole:

Triple Difference

$$[({\mathit{Jan}}_{\mathit{lis}=0}^{dh=1}-{\mathit{Other}}_{\mathit{lis}=0}^{dh=1})-({\mathit{Jan}}_{\mathit{lis}=1}^{dh=1}-{\mathit{Other}}_{\mathit{lis}=1}^{dh=1})]-[({\mathit{Jan}}_{\mathit{lis}=0}^{dh=0}-{\mathit{Other}}_{\mathit{lis}=0}^{dh=0})-({\mathit{Jan}}_{\mathit{lis}=1}^{dh=0}-{\mathit{Other}}_{\mathit{lis}=1}^{dh=0})]$$

4. Results

4.1. Summary Statistics

Table I presents sample summary statistics for several key variables, for the total population, as well as for LIS and non-LIS groups separately. Across all three groups, slightly more than two-thirds of individuals who discontinued their beta-blockers, reinitiated beta-blockers at some point during the follow-up period. In the overall population, 59% of individuals had spending high enough to reach the doughnut hole, and 17% had spending high enough to reach the catastrophic coverage. Among those without LIS, 52% and 7% reached the doughnut hole and catastrophic coverage, respectively. The LIS group differed from the non-LIS group in several dimensions: those in the LIS group had more chronic conditions, and were more likely to be an ethnic/racial minority, disabled, or female.

Table I.

Unadjusted Characteristics of the Study Population

Variable	Overall Population (n=50,466)	LIS (n=25,427)	Non-LIS (n=25,039)
Female, %	54.3	57.8	50.7
Race, %
Non-Hispanic
White	77.1	63.0	91.4
Black	12.1	20.0	4.3
Hispanic	7.4	11.9	2.7
Asian	2.0	3.1	0.9
Other	1.4	2.0	0.7
Disabled, %	17.0	27.9	5.9
Age	74.2 ± 12.0	71.2 ± 13.4	77.3±9.4
Dual, %	44.4	86.5	-
No. of 21 high-priority CCW conditions	5.8 ± 2.0	6.1 ± 2.1	5.5 ± 1.9
Entered Doughnut Hole in 2008, %	58.9	65.7	52.0
Entered Catastrophic Coverage in 2008, %	16.8	27.0	6.5
Reinitiated during sample period, %	69.1	70.9	67.3

Plus-minus values are Means ± Standard Deviation.

Abbreviations: LIS = low income subsidies, this group includes duals and non-duals with low-income subsides for Part D; CCW= Chronic Condition Warehouse

21 high-priority CCW conditions include:

Acute Myocardial Infarction, Alzheimer’s Disease, Alzheimer’s Related Disorders/Senile Dementia, Atrial Fibrillation, Cancer (Colorectal, Endometrial, Breast, Lung, and Prostate), Cataract, Chronic Kidney Disease, Chronic Obstructive Pulmonary Disease, Depression, Diabetes, Glaucoma, Heart Failure, Hip/Pelvic Fracture, Ischemic Heart Disease, Osteoporosis, Rheumatoid Arthritis/Osteoarthritis, and Stroke/Transient Ischemic Attack

4.2. Binary Time Series Cross-Sectional Results

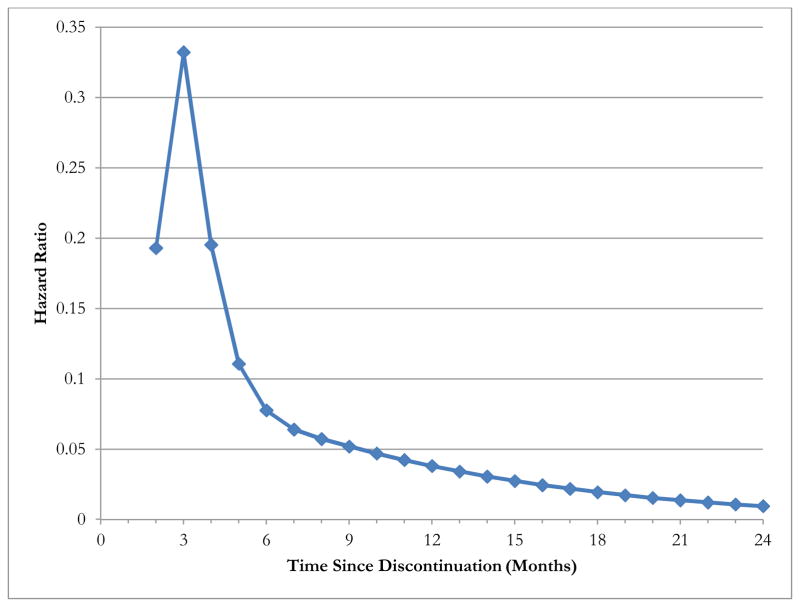
Figure 2 shows the baseline hazard function from the BTSCS model using three equally spaced cubic splines. The rate of reinitiation is highest in the second, third, and fourth months after discontinuation, and falls gradually in subsequent months. Since we define discontinuation as a period of at least 30 days without medication in possession, reinitiation in the first month is not possible. The spike in the third month suggests that, conditional on having at least a month without beta-blockers, individuals are most likely wait until the third month to reinitiate.

Figure 2.

Baseline Hazard Function with Three Equally Spaced Cubic Splines from Binary Time-Series Cross-Sectional Model.

Since we define discontinuation as a period of at least 30 days without medication in possession, reinitiation in the first month is not possible. The spike in the third month suggests that, conditional on having at least a month without medications, individuals are most likely wait until the third month to reinitiate.

Figure 3 shows the results from the BTSCS regressions. The key variables from these regressions are the calendar month variables. Since the January 2009 variable is excluded from the regression, the odds ratios for each month refer to the odds of reinitiating in each month as compared with January 2009. For the overall population, there is a significantly lower rate of reinitiation in the months leading up to January, while the rate of reinitiation in December is especially low. For example, we find that holding the baseline hazard rate constant, an individual has 20% lower odds of reinitiating in December 2008 than in January 2009. Additionally, we find lower reinitiation rates in the months immediately following January. Although most individuals do not face price increases after the end of January, one possible explanation for the decreased reinitiation in the subsequent months may be that individuals waiting for the price to decrease reinitiate in January rather than waiting any longer.

Figure 3.

Odds Ratios of Reinitiating Each Month Compared with January 2009 for Three Populations, After Adjusting for Covariates

Each of the three charts represents a separate logistic regression. For each chart, each bar represents the odds ratio of reinitiating discontinued medications in a particular month as compared to January. Since January is the excluded dummy variable in each regression, the odds ratio is 1.0. All regressions include controls for the amount of time since discontinuation, race, gender, age, disability status, number of chronic conditions, and Medicaid eligibility. The error bars display the 95% confidence intervals based on robust standard errors. The sample sizes differ from Table I because the unit of observation is person-months.

4.3. Heterogeneous Effects

Panels B and C of Figure 3 show the odds ratios of reinitiating among the LIS and non-LIS groups. As expected, the odds ratios for reinitiation in December are lower for the non-LIS population for the LIS group. We do observe a slight increase in reinitiations among the LIS group in January as compared with the three previous months, which is surprising since the price of medication for the LIS group does not vary throughout the year. This could imply that some of the observed increased rate of reinitiation in January may be explained by factors other than change in price, such as decreased access to medication over the holidays.

As a robustness check, Figure 4 shows the results from the Cox proportional hazard model. The results can be interpreted similar to those in Figure 3, and are generally similar. One difference is that we do not find any significant January effect for the LIS group, which provides stronger evidence that the main driver of the higher reinitiation in January among the non-LIS group is the change in price.

Figure 4.

Hazard Ratios of Reinitiating Each Month Compared with January 2009, Robustness Check Using Cox Proportional Hazard Models

Each of the three charts represents a cox proportional hazard regression. For each chart, each bar represents the hazard ratio of reinitiating discontinued medications in a particular month as compared to January. Since January is the excluded dummy variable in each regression, the odds ratio is 1.0. All regressions include controls for race, gender, age, disability status, number of chronic conditions, and Medicaid eligibility. The error bars display the 95% confidence intervals. The unit of observation is the individual, which is why sample sizes are different from those in Figure 3.

4.4. Difference-in-Difference Results

In order to determine whether the higher rates of reinitiation in January are due to the price differences rather than seasonal variation due to, for example, decreased access to medication over the holidays, we run a series of difference-in-difference specifications, which are shown in Table II.

Table II.

Odds Ratios of Reinitiation from the Difference-in-Difference Approach Comparing Beneficiaries with and without Low-Income Subsidies.

VARIABLE	(1) Full Population	(2) Coverage Gap End-of-Year	(3) Never Entered Gap
Non-LIS	0.957* (0.0226)	0.947 (0.0346)	1.010 (0.0372)
Nov	0.942* (0.0333)	0.950 (0.0526)	0.975 (0.0588)
Dec	0.928** (0.0323)	0.942 (0.0515)	0.885** (0.0538)
Jan	1.054 (0.0349)	1.082 (0.0561)	1.163*** (0.0648)
Feb	0.973 (0.0324)	0.968 (0.0513)	1.075 (0.0605)
Non-LIS* Nov	1.055 (0.0538)	1.074 (0.0820)	0.984 (0.0802)
Non-LIS* Dec	0.935 (0.0475)	0.862* (0.0660)	1.022 (0.0832)
Non-LIS* Jan	1.137*** (0.0528)	1.255*** (0.0863)	0.919 (0.0686)
Non-LIS* Feb	1.064 (0.0499)	1.082 (0.0779)	0.959 (0.0707)
Constant	0.0146*** (0.000919)	0.0148*** (0.00144)	0.0139*** (0.00137)
Observations	316,825	129,235	137,329

Each column represents a separate logistic regression using Binary Time-Series Cross-Sectional model. Besides the coefficients shown, each regression additionally controls for age, gender, race, disability status, number of chronic conditions, and a cubic spline function for the number of months since discontinuation. Robust standard errors are in parentheses. The unit of observation is person-month.

^***p<0.01,

^**p<0.05,

^*p<0.1

Abbreviations: LIS = low income subsidies, this group includes duals and non-duals with low-income subsides for Part D.

Column (1) of Table II compares the non-LIS individuals who face price changes throughout the year to those who received LIS, and did not face any price changes. The results show that the odds of reinitiating in January as compared to other months were 1.137 times higher in the non-LIS group, relative to the LIS group. The coefficients on the non-interacted November and December dummies show that reinitiation rates were lower for both groups in those months, which reiterates the results in Figure 3. Column (2) compares those who were in the doughnut hole at the end of 2008, and were most likely to experience a price change in January to all others. This regression shows that these individuals were significantly more likely to reinitiate in January. The odds ratio for December also provides evidence that reinitiation was lower in December than in other months, and was significant at the 10% level. Additionally, the reinitiation rate in December was significantly lower than either the reinitiation rates in November and January. Both of these comparisons are significant at the 5% level.

4.5. Triple Difference

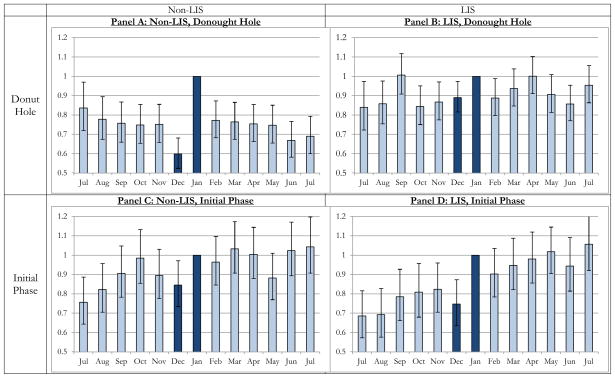
Figure 5 shows the monthly odds ratios of reinitiation for four groups, broken down by LIS status, and copayment phase at the end of the year. Panel A corresponds to the “First Difference” Non-LIS individuals who were in the doughnut hole at the end of 2008, were much more likely to reinitiate in January than other months, and less likely to reinitiate in December than other months, compared to LIS individuals. The difference between Panels A and B corresponds to our “Difference-in-Difference” specification. Since there is not much difference in reinitiation across calendar months for LIS individuals who had spending that would place them in the doughnut hole, we become more confident that the differences found in Panel A are due to pricing, rather than seasonal effects. However, it is possible that since LIS and non-LIS individuals have different incomes, they may have different underlying patterns of consumption. In order to control for this, we can look at the difference between Panels C and D. This includes two groups who both had spending low enough so that they could not have reached the doughnut hole, and thus should not be affected by the change in copayments at the beginning of the year. However, like the panels above them, both groups have different LIS status, and thus different incomes. Comparing these two panels, suggest that, if anything, the seasonal effects are actually stronger for the LIS group. Comparing the difference between Panels A and B vs. Panels C and D is similar to our “Triple Difference” calculation.

Figure 5.

Odds Ratios of Reinitiating Each Month Compared with January 2009 among Beneficiaries without Low-Income Subsidies, by Benefit Phase at the End of 2008.

Each of the charts represents a separate logistic regression. For each chart, each bar represents the odds ratio of reinitiating discontinued medications in a particular month as compared to January. Since January is the excluded dummy variable in each regression, the odds ratio is 1.0. All regressions include controls for the amount of time since discontinuation, race, gender, age, disability status, number of chronic conditions, and Medicaid eligibility. The error bars display the 95% confidence intervals based on robust standard errors.

The unit of observation is the person-month.

These differences are presented more formally in Table III. All of the results come from a logistic BTSCS regression where dummies for four calendar months (November, December, January, February) are interacted with both doughnut hole status, and LIS status. Each difference is calculated by bootstrapping the adjusted average probabilities and applying the formula described in the methods section. For comparing January to other months, the first difference suggests that non-LIS individuals in the doughnut hole are about 3.3 percentage points (P<0.0001) more likely to reinitiate in January than other months, and about 1.8 percentage points less likely to reinitiate in December (P<0.0001). The Difference-in-Difference estimates provide slightly smaller effects: individuals are 2.5 percentage points (P=0.001) more likely to reinitiate in January, and 1.2 percentage points (P=0.071) less likely to reinitiate in December. Finally, the Triple Difference calculations increase over the Difference-in-Difference calculations, but the standard errors increase. Individuals are 3.2 percentage points more likely to reinitiate in January (P=0.001), and 1.5 percentage points less likely to reinitiate in December (P=0.119).

Table III.

Bootstrapped Differences in Marginal Probabilities of Reinitiation: January and December vs. All Other Months.

		Marginal Effect Difference	Bootstrap Std. Err.	z	P>z
JAN	First Diff	0.0326741	0.005125	6.38	0
	Diff-in-Diff	0.0249281	0.00725	3.44	0.001
	Triple Diff	0.0319655	0.010049	3.18	0.001
DEC	First Diff	−0.0183698	0.004631	3.97	0
	Diff-in-Diff	−0.0122689	0.006797	1.81	0.071
	Triple Diff	−0.0148222	0.009516	1.56	0.119

All results come from 500 replications of a single logistic regression using Binary Time-Series Cross-Sectional model, followed by an estimation of the adjusted average probability. The regression controls for age, gender, race, disability status, number of chronic conditions, and a cubic spline function for the number of months since discontinuation, LIS status, donut hole status, calendar month dummies for November through February, and interactions between the LIS status, donut hole status, and calendar month dummies.

5. Discussion

This study focuses on the response of consumers to changes in prices due to non-linear pricing mechanisms in Medicare prescription drug benefits. In particular, we use the beginning of the Part D benefit cycle to estimate the effect of prescription drug prices on the timing of reinitiation of discontinued medication. We find that due to the design of the Part D benefit, beneficiaries who discontinued essential medications were likely to wait until the beginning of the year to reinitiate their use. This effect is strongest for those who were in the doughnut hole at the end of the year.

Our study is unique for several reasons. First, it is one of the first to examine the role of price in patients’ decisions to reinitiate medications. We find that 69.1% of individuals reinitiated their beta-blockers after stopping for at least 30 days, and that they were more likely to reinitiate in periods where prices were low. Second, we focus on price changes that occurred at an exogenously determined date, which mitigates the selection bias due to endogeneity in price change. This is an improvement compared with the previous studies that used endogenous price changes before and after Medicare patients entered the doughnut hole. Finally, we are able to remove seasonal trends in medication use by comparing our main study group to those who received LIS and did not experience changes in prices throughout the year, a natural built-in comparison group in our data.

Although our study design does not allow us to test whether beneficiaries are fully forward looking as predicted by Ellis (1986) and Keeler et al. (1977), we examine whether there is evidence that individuals are forward looking within a narrow time span. We find significant decreases in the likelihood of reinitiation in the final months of the year, which might suggest that some beneficiaries are anticipating the resumption of benefits at the beginning of the next calendar year. However, the final months of the year also had the peak number of individuals who were in the doughnut hole; thus, decreased medication use might simply reflect the higher prices that individuals face in those final months. More research is needed to determine whether any anticipatory behavior exists within similar insurance designs.

There are several important limitations to this study. First, we focus only on those who sdiscontinued their beta-blockers for at least 30 days. With regards to examining whether people are forward-looking, these individuals may be the least likely to exhibit anticipatory behavior, since they do not smooth their consumption across periods. Second, in our difference-in-differences specification, we use the seasonal variation in the LIS group to remove seasonal differences in the non-LIS group. Since the LIS group differs from the non-LIS group on several dimensions, the two groups may also have different seasonal patterns of medication use. Third, our analysis focus on reinitiating beta-blockers among those who recently survived an MI. The results might not be generalizable to all medications, or for the general population.

Overall, we find that individuals who ordinarily would have reinitiated medications at the end of the year have a tendency to wait until the reset of benefits at the beginning of the year. Despite the cause, this delayed effect on medication resumption might increase the chance of uncontrolled symptoms and hospital readmission. If people smoothed their consumption across periods with different prices as theory predicts, drug benefit designs that have various price phases might be a good way to limit drug claims with low marginal value. However, it appears that there is a growing body of evidence that individuals heavily weight the current price of medications when making decisions. In this case, this type benefit design may cause sub-optimal medication use and could lead to increased downstream costs.